Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Spatiotemporal stress and structure evolution in dynamically sheared polymer-like micellar solutions†
A. Kate
Gurnon
a,
Carlos R.
Lopez-Barron‡
a,
Aaron P. R.
Eberle
ab,
Lionel
Porcar
c and
Norman J.
Wagner
*a
aCenter for Neutron Science, Department of Chemical and Biomolecular Engineering, University of Delaware, Newark, DE, USA. E-mail: wagnernj@udel.edu; Tel: +1 302-831-8079
bNIST Center for Neutron Research, National Institute of Standards and Technology, Gaithersburg, MD, USA
cInstitut Laue-Langevin BP 156, F-38042 Grenoble Cedex 9, France
First published on 28th January 2014
Abstract
The complex, nonlinear flow behavior of soft materials transcends industrial applications, smart material design and non-equilibrium thermodynamics. A long-standing, fundamental challenge in soft-matter science is establishing a quantitative connection between the deformation field, local microstructure and macroscopic dynamic flow properties i.e., the rheology. Here, a new experimental method is developed using simultaneous small angle neutron scattering (SANS) and nonlinear oscillatory shear rheometry to investigate the spatiotemporal microstructure evolution of a polymer-like micellar (PLM) solution. We demonstrate the novelty of nonlinear oscillatory shear experimental methods to create and interrogate metastable material states. These include a precursory state to the shear banded condition as well as a disentangled, low viscosity state with an inhomogeneous supra-molecular microstructure flowing at high shear rates. This new experimental evidence provides insight into the complexities of the shear banding phenomenon often observed in sheared complex fluids and provides valuable data for quantitatively testing non-equilibrium theory.
1 Introduction
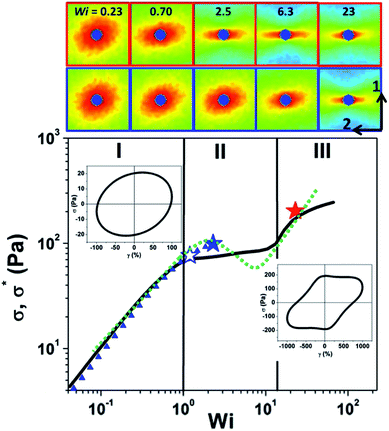
Complex fluids and soft materials are marked by a rich complexity of nonlinear flow behaviors. Even under the simplest of conditions for inertialess shear flow, nonlinear effects such as shear and vorticity banding,1,2 shear thickening,3 stick-slip flow, chaotic flows4 and shear-induced phase separation5 are common. This complex nonlinear flow behavior is attributed to the coupling between microstructure and deformation, which together, define the local stress that governs the kinematics of the flow field and hence, the local deformation. A long-standing, fundamental challenge in soft-matter science is establishing a quantitative connection between the deformation field, local microstructure and macroscopic dynamic flow properties i.e., the rheology. Predictive constitutive models designed to couple the molecular-scale structure to the macroscopic flow properties and processing characteristics are invaluable tools for practitioners formulating complex fluids in industries including energy production, paints and coatings, consumer healthcare products, foods, and drug delivery under varied nonlinear flow conditions.6,7 Particularly important are shear banding instabilities in entangled and branched polymer systems as well as model polymer-like or worm-like micellar solutions (PLM, WLM), which have recently received significant scientific interest.8 As such, theoretical and experimental research efforts have focused on defining and predicting the onset, processing conditions and underlying microstructure of the steady, shear banding states.8,9 Advances in the development of robust predictive models for the nonlinear flow behavior of PLMs7,10 benefit from local microstructure measurements in the steady shear banded state.11,12 The challenge now is to understand the dynamics of shear banding by measuring the spatiotemporal evolution of the microstructure and stress.An experimental signature of shear banding is a stress plateau evident over a significant range of shear rates,13 such that material flow rates can increase by orders of magnitude with small increases in stress (Fig. 1, solid black line). Three regions are identified: region I consists of an entangled, near equilibrium PLM viscoelastic solution, while region III is proposed to be a highly disentangled PLM solution that flows with a lower viscosity. At steady shear rates corresponding to region II, time-dependent metastable and unstable states are not experimentally accessible using traditional steady shear methods, but are evident in transient flows, such as start-up shear flow.14,15 A non-monotonic constitutive equation (Fig. 1, dotted line)1,2 is postulated to describe the shear banding response. In contrast to regions I and III where homogeneous flow is observed, the characteristic velocity profile in a Couette geometry for region II results in two separate, coexisting shear bands with different shear rates (Fig. 2C). The high shear band typically exhibits a strong flow alignment while the low shear band has a nearly isotropic microstructure.11,16,17 In region II, different states are probed using steady (Fig. 1, solid line) and oscillatory (Fig. 1, triangles and stars) shear experimental methods. Advances in instrumentation and theory have led to a strong interest in studying a broad range of complex fluids and soft materials by independently varying the effects of time- and length-scales through the use of nonlinear oscillatory shear rheology, also known as large amplitude oscillatory shear (LAOS).18–21 The LAOS method is well known in rheometry, but here it is used in a novel way to create and probe homogeneous metastable states of the PLM otherwise known to exhibit shear banding during steady shear.
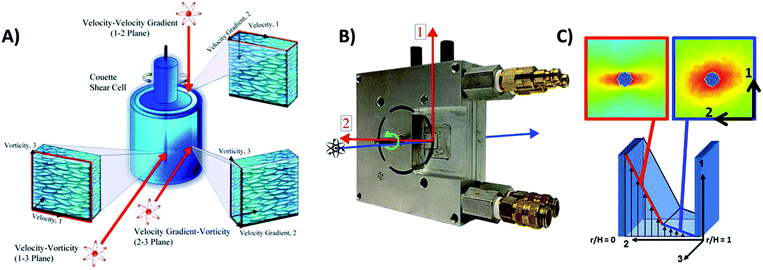
The microstructure of PLM materials during shear flow has been measured using flow-birefringence,15,16,22,23 small-angle light scattering (SALS),15,23 small-angle neutron/X-ray scattering (SANS/SAXS),24 nuclear magnetic resonance (NMR),25 and particle image velocimetry (PIV).15 Of direct implication to this work is rheology- and flow-SANS (rheo-SANS and flow-SANS) methods (Fig. 2A) as they have proven valuable for determining the three-dimensional microstructure of flowing complex fluids24 and are particularly well suited for probing the molecular and segmental length-scales of PLM solutions. Prior work has investigated the microstructure of PLMs in the velocity–vorticity [1–3] plane of flow (Fig. 2A) during steady16,26 and oscillatory shear.27 Unfortunately, experiments probing this plane of shear cannot spatially resolve the local microstructure across the shear bands, including possible shear-induced concentration differences,12 nor do they provide sufficient structural information to test predictions for the shear or normal stresses using stress-SANS relationships.11 A new, state-of-the-art flow SANS sample environment developed in our research group (Fig. 2B)24,28 enables simultaneous, quantitative measurements of the spatially resolved composition and microstructure alignment and orientation in the velocity–velocity gradient [1–2] plane of shear. Flow-SANS microstructure measurements made at two positions across the shear band during steady shear (Fig. 1 and 2C) illustrate the microstructural changes that occur with increasing shear rate from regions I to III in agreement with previously reported scattering results.11,16,17,29 The 1–2 flow-SANS sample environment enables quantitative assessment of molecular-based rheological constitutive equations for shear-banding fluids under steady and oscillatory shear flow.11,16,29
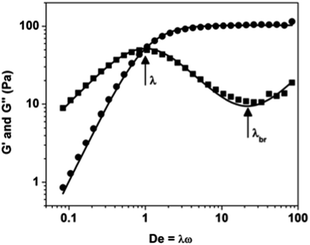
Experimental evidence and understanding for the temporal evolution of a material's microstructure during flow is essential to developing and testing molecular-based theory and robust constitutive equations for PLMs. Material timescales relaxation time, λ, and breakage time, λbr, (defined in Fig. 3) are particularly important for discerning the coupling between the microstructure and flow kinematics in time-dependent flows such as transient start-up or dynamic shear. Recent advances in SANS instrumentation now enable studying time dependent flow in the [1–3] plane20,27 and of greater value, in the [1–2] plane.28,29 In addition to these experiments, rheo-SALS (small angle light scattering)11,30 experiments are designed to probe the concentration and orientation fluctuations at the supra-molecular length-scale and illustrate the critical role of shear-induced concentration fluctuations prior to and during shear banding.15
The aim of this work is to investigate the nonequilibrium rheological and microstructural behavior of complex fluids under dynamic oscillatory shear conditions. The experimental identification of metastable states is of particular and significant value for testing and validating constitutive equations proposed for shear-banding fluids. Accurate representation of metastable states lies at the foundation of the proposed mechanism for shear banding.1,2,9 In order to achieve this aim two goals are to be completed; the first is to quantitatively define the spatiotemporal material microstructure and second, to predict the resulting shear stress properties from local microstructure measurements made across the velocity gradient direction of flow. These goals are achieved here by measuring the microstructure. The stress-SANS rule11 is used to predict the local stress response of a model PLM solution during LAOS.
2 Materials and methods
2.1 Materials
The model wormlike micellar solution investigated in this work is comprised of 5.1% w/w cetylpyridinium chloride monohydrate (CAS 6004-24-6) and 1.1% w/w sodium salicylate (CAS 54-24-7) at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 surfactant molar ratio in a 0.5 M NaCl and D2O brine. This concentration corresponds to a highly viscoelastic, shear banding solution in the semi-dilute regime and in the L1 or wormlike micellar phase.13,15,31 The sample is prepared by first combining the CPCl and NaSal and then adding the pre-mixed 0.5 M NaCl and D2O brine. The sample is thoroughly shaken and then placed in a water bath for 72 hours at 40 °C prior to experiments.
1 surfactant molar ratio in a 0.5 M NaCl and D2O brine. This concentration corresponds to a highly viscoelastic, shear banding solution in the semi-dilute regime and in the L1 or wormlike micellar phase.13,15,31 The sample is prepared by first combining the CPCl and NaSal and then adding the pre-mixed 0.5 M NaCl and D2O brine. The sample is thoroughly shaken and then placed in a water bath for 72 hours at 40 °C prior to experiments.
2.2 Rotational rheology
All rheological measurements were performed at 25 °C on TA Instruments ARES-G2 strain-controlled rheometer using a temperature controlled Couette geometry (27.7 mm bob diameter, 30 mm cup diameter). Steady shear rate sweeps are performed from shear rates of 0.1 to 100 s−1, waiting at each shear rate until equilibrium is achieved or 1 minute has passed (whichever is shorter). Small amplitude oscillatory shear measurements are made using a 0.01 strain amplitude and angular frequency sweep from 0.2 to 200 rad s−1. The single-mode relaxation time (λ = 0.42 s) and modulus (G0 = 103.2 Pa) of the PLM is defined with a single-mode Maxwell model (Fig. 3) fit to the SAOS experimental data and reported in Table 1.| Definition | Symbol | Value | |
|---|---|---|---|
| Relaxation modulus | Fig. 3 | G 0 | 103.2 Pa |
| Relaxation time | Fig. 3 | λ | 0.42 s |
| Breakage time | Fig. 3 | λ br | 0.019 s |
| Reptation time |
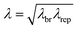
|
λ rep | 9.20 s |
| Mesh size | (kbT/G0)1/3 | ξ m | 34 ± 5 nm |
| Persistence length | Birefringence | l p | 24 ± 3 nm |
| Entanglement length | (ξm)5/3/(lp)2/3 | l e | 43 ± 15 nm |
| Contour length | G′′min/G0 = le/Lc | L c | 334 ± 100 nm |
| Cylinder length | SANS model (Fig. 5) | L c | 75 ± 15 nm |
| Length polydispersity | SANS model (Fig. 5) | 30% | |
| Micelle radius | SANS model (Fig. 5) | r cs | 1.8 ± 0.1 nm |
The PLM solution is investigated for its rheological and microstructural properties during large amplitude oscillatory shear, LAOS, (Fig. 4) defined by a frequency (f = 0.089 Hz or ω = 0.56 rad s−1 and f = 0.89 Hz or ω = 5.6 rad s−1) and strain amplitude (γ0) of deformation (5 or 10) for each condition. Only the alternance response of the LAOS experiment is reported here and in each case is achieved after 3 cycles of oscillation. Two dimensionless numbers define the alternance state of the sample: the Deborah number is the dimensionless timescale (De = λω), and the Weissenberg number is a dimensionless shear rate that also sets the strain amplitude (Wi = γ0ωλ or ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) λ). Three LAOS conditions are investigated and henceforth will be referred to as a [De, Wi] pair: [De = 0.23, Wi = 1.15], [De = 0.23, Wi = 2.3] and [De = 2.3, Wi = 23] (Fig. 1, stars). Each condition's stress and corresponding microstructure will be compared to that condition of equivalent Wi during steady state [De = 0]. These specific states are selected to probe the material at equivalent Wi that correspond to states just at the onset of shear-banding, in the metastable regime of shear banding, and in the high shear, region III of the steady-shear flow curve.
λ). Three LAOS conditions are investigated and henceforth will be referred to as a [De, Wi] pair: [De = 0.23, Wi = 1.15], [De = 0.23, Wi = 2.3] and [De = 2.3, Wi = 23] (Fig. 1, stars). Each condition's stress and corresponding microstructure will be compared to that condition of equivalent Wi during steady state [De = 0]. These specific states are selected to probe the material at equivalent Wi that correspond to states just at the onset of shear-banding, in the metastable regime of shear banding, and in the high shear, region III of the steady-shear flow curve.
2.3 Small-angle neutron scattering (SANS)
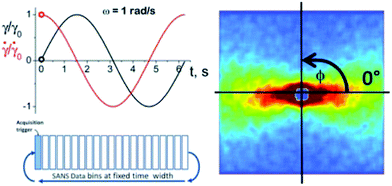
The spatiotemporal resolved (STR) microstructure changes on the PLMs segmental length scale in the [1–2] plane of shear are measured using 1–2 flow-STR small-angle neutron scattering (SANS).24,28,29 The novel sample geometry consists of a sealed Couette shear cell comprised of an inner rotating cylinder (d = 51 mm) and outer stationary cylinder with a shear gap of 1 mm and 5 mm pathlength28,29 (Fig. 2B). A complete description of the instrument, including mechanical drawings, is published.28 Spatially resolved SANS experiments are performed using a narrow slit aperture (0.1 mm × 3 mm).29 For each LAOS condition, microstructure measurements are made at two positions in the gap (r/H = 0.2 & 0.8) where H = rmax − rmin therefore r/H = 0 & 1 correspond to the inner rotating wall and outer fixed wall, respectively) (Fig. 2C). SANS experiments were performed at the Institut Laue-Langevin (ILL) Grenoble, France on the D-22 SANS instrument with a 6 Å incident neutron mean wavelength (λ) and a 11.2 m detector distance. The velocity–velocity gradient [1–2] plane SANS configuration defined for these experiments probes a range of scattering lengths (q = 0.03–0.4 nm−1) (real space length = 2π/q = 15–210 nm). Temperature was maintained at 25 °C using a circulating water bath.Time-resolved small-angle neutron scattering (t-SANS) methods20,32,33 are used to capture 30 different measured microstructures over the course of a single oscillatory cycle during LAOS experiments, Fig. 4. The experiment is designed such that at a given condition (gap position, strain amplitude and angular frequency) 30 discrete data bins (nb) are collected, each having a pre-determined and identical length of time, (ωnb)−1. The data is collected over multiple oscillation cycles such that statistically sufficient scattering events are recorded in each bin (typically 3 × 104 to 1 × 105 per bin). The complete set of results are presented as movies in the ESI (Movies S01–S03†).
The 2-D SANS scattering patterns are reduced using GRASP SANS reduction software34 provided by the Institut Laue-Langevin and Ber-SANS reduction software35 provided by the Helmholtz Zentrum Berlin. The analysis of the scattering results is performed using the SASET t-SANS analysis software package.36 The quantitative analysis of the 2-D 1–2 flow-STR SANS scattering patterns follows established methods11 resulting in an alignment factor (Af), defined in eqn 1 (ref. 11 and 37), and orientation angle (ϕ0). These parameters are calculated using the annular-averaged scattered intensity denoted Ic(q*, ϕ) where q* = 0.06 to 0.3 nm−1 (Fig. 5A, shaded region). For which over this particular q-range the intensity is averaged for each azimuthal angle (ϕ). Af takes a value between 0 (isotropic) and 1 (completely aligned, such as for a perfect nematic phase). The microstructure is defined by the principle axis of scattering (ϕ0) (Fig. 4) which takes values between −45° and 45° where ϕ0 = 0 is the flow direction. For an oscillating shear flow the sign of ϕ0 changes with a change in the shear flow direction.
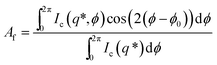 | (1) |
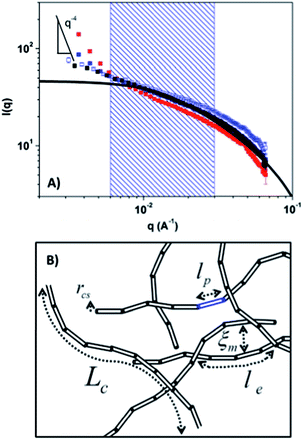 | ||
| Fig. 5 (A) Circular averaged 〈I(q)〉 vs. q for PLM: quiescent condition (black symbols); time averaged patterns for [De = 0.23, Wi = 1.2] (open blue symbols), [De = 0.23, Wi = 2.3] (closed blue symbols) and [De = 0.23, Wi = 23] (closed red symbols). Cylinder model with polydisperse length (solid black line), model parameters given in Table 1 shown for comparison to experimental results. Shaded region denotes the q-range (q* = 0.06 to 0.3 nm−1) from which ϕ0 and Af are defined. A Porod slope of q−4 is shown for reference. (B) Presents a schematic of the different length-scales for this PLM system as defined from rheology and SANS cylinder model fit (Table 1). | ||
The stress arising from the microstructure measured using SANS is predicted using the stress-SANS rule:11
σpxy = G0(CAf)1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2ϕ0) sin(2ϕ0) | (2) |
The stress-SANS coefficient (C = 11.2) is defined from steady shear SANS microstructure measurements in the linear regime (Wi = 0.1–1)38 and G0 is the shear modulus (103.2 Pa, Table 1).
2.4 Rheo-small-angle light scattering (Rheo-SALS)
Simultaneous rheology and SALS experiments are performed on the TA Instruments Discovery Hybrid Rheometer (DHR3) using the commercial DHR-SALS accessory and a 50 mm parallel quartz plate geometry. The 2-D light scattering measurements are made in the velocity–vorticity [1–3] plane of shear using cross-polarizers (HV, rheo-SALS, TA Instruments). Measurements are performed while a steady shear is applied at shear rates of 0.1, 0.56, 3.2, 5.6, 10, 18, 32 s−1. Rheo-SALS LAOS experiments are performed at identical conditions for those performed in the 1–2 STR flow-SANS experiments defined in the previous section. The SALS experiments are designed to probe longer length scales (q = 1.38 to 6.11 μm−1) (1–4.5 μm). The sheared SALS patterns are subtracted from a quiescent scattering pattern in order to accentuate the changes in microstructure upon shearing the sample. The experimental SALS results presented in Fig. (9) have the following color scheme: red is maximum scattering and black is minimum. Movies of these measurements are also presented in the ESI (Movies S04–S06†).3 Results and discussion
Fig. 5A shows SANS circular averaged angle-independent scattered intensity presented as 〈I(q)〉. The quiescent, equilibrium spectra is characteristic of a PLM. Flow-SANS measurements where 〈I(q)〉 is time-averaged over the oscillatory cycle and reported in Fig. 5A verify that the micellar phase persists for all LAOS conditions. A fit to a cylinder model with polydisperse length shows that the PLM maintains a cylindrical radius of 1.8 ± 0.1 nm. The important PLM length-scales defined in the schematic inset in Fig. 5B are determined from rheology and birefringence measurements and are reported in Table 1.The range of scattering vectors probed by SANS are appropriate for defining the stress-SANS relationships between microstructure and shear and normal stresses under flow.11,14,38 For [De = 0.23, Wi = 2.3] and [De = 2.3, Wi = 23] conditions there is an upturn in I(q) at low-q indicative of structures existing at larger length-scales outside of the measurable q-range using SANS. These are identified via rheo-SALS measurements that probe a lower q-range corresponding to larger length-scales.
Each of the three LAOS conditions will be discussed individually in terms of the spatiotemporal evolution of the stress and microstructure with respect to the oscillatory deformation. For [De = 0.23, Wi = 1.2] the equivalent Wi for steady shear corresponds to a condition at the onset of shear banding (at the border between regions I and II, Fig. 1, open blue triangle). The nonlinear stress response shown in Fig. 6 corresponds with microstructures measured at the inner and outer positions with slightly more alignment (Af) and flow orientation (ϕ0), observed nearer to the inner wall as expected for a shear-thinning fluid in Couette flow.15 The highest alignment indicating the greatest microstructural deformation corresponds to the largest stress response. We observe an isotropic scattering pattern that is indicative of an entangled PLM solution when the stress is at a minimum during the cycle.
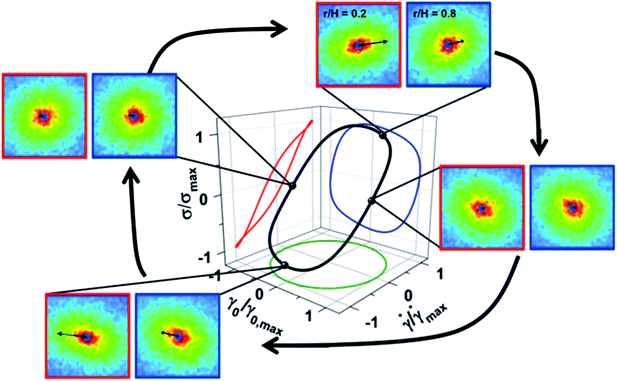 | ||
| Fig. 6 Lissajous–Bowditch diagram; normalized stress as a function of the imposed normalized strain and strain rate during LAOS with the elastic projection (blue line) and viscous projection (red line) for LAOS condition [De = 0.23, Wi = 1.2] where ω = 0.56 rad s−1 and γ0 = 5. SANS scattering patterns inner (r/H = 0.2) and outer (r/H = 0.8) positions have red and blue borders, respectively. For the 2-D SANS patterns the angle of the arrow reflects the average ϕ0 and the length of the arrow indicates the magnitude of Af. A movie for this condition showing the complete set of results is included in the ESI (Movie S01†). | ||
A comparison of the measured ϕ0 (Fig. 7A) and Af (Fig. 7B) during the oscillation cycle shows the microstructures are nearly equivalent for the two gap positions, confirming that a homogenous shear flow is present. Under these conditions, the PLMs have adequate time to deform with the applied strain rate (Fig. 7B) and maintain a structure primarily dependent upon the instantaneous direction and magnitude of the shear flow during LAOS. Fig. 7C shows quantitative agreement between shear stress measured by rheometry and the predicted shear stress at both positions in the gap calculated using the ϕ0 and Af values gained from SANS measurements and eqn (2) where the stress-SANS rule coefficient (C = 11.2) is defined from steady shear measurements.14,38 Thus, for this condition the validity of the stress-SANS rule relating segmental alignment to the polymeric stress tensor shows the material behavior is equivalent to that under steady shear conditions as expected from theory. Helgeson et al.11 propose critical values for the onset of shear banding (ϕ0 < 17° and Af > 0.18). In the instance here the values of ϕ0 and Af are substantially greater and lower, respectively, indicating that the microstructure throughout the oscillation is consistent with a near equilibrium flowing PLM that is entangled and not shear banding.
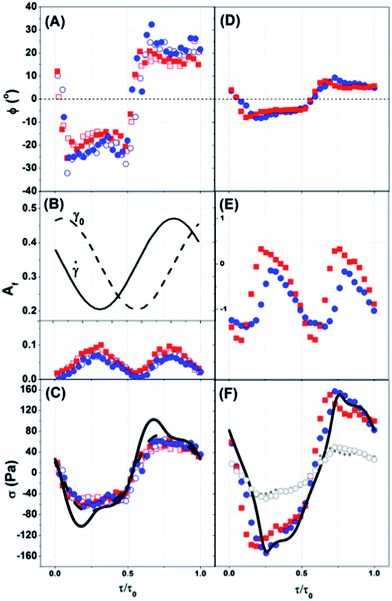 | ||
Fig. 7
ϕ
0 (A and D), Af (B and E) and σ (C and F) as a function of normalized time. Inset of (B) includes the imposed deformation strain (γ0) and strain rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ). Inner wall and outer wall positions are identified with red and blue, respectively. (A–C) [De = 0.23, Wi = 1.2] (open symbols) and [De = 0.23, Wi = 2.3] (closed symbols) where ω = 0.56 rad s−1 and γ0 = 5 and γ0 = 10. Rheometry experiment stress reported for [De = 0.23, Wi = 1.2] (dashed line) and [De = 0.23, Wi = 2.3] (solid line). Symbols in (C) use the stress-SANS rule (eqn (2)) and C = 11.2. (D–F) SANS results for [De = 2.3, Wi = 23] condition where ω = 5.6 rad s−1 and γ0 = 10. Rheometry experiment stress for [De = 2.3, Wi = 23] condition (solid line). Red and blue symbols in (F) use the stress-SANS rule (eqn (2)) and C = 112. Grey symbols use C = 11.2 inner position (closed symbols) and outer position (open symbols). ). Inner wall and outer wall positions are identified with red and blue, respectively. (A–C) [De = 0.23, Wi = 1.2] (open symbols) and [De = 0.23, Wi = 2.3] (closed symbols) where ω = 0.56 rad s−1 and γ0 = 5 and γ0 = 10. Rheometry experiment stress reported for [De = 0.23, Wi = 1.2] (dashed line) and [De = 0.23, Wi = 2.3] (solid line). Symbols in (C) use the stress-SANS rule (eqn (2)) and C = 11.2. (D–F) SANS results for [De = 2.3, Wi = 23] condition where ω = 5.6 rad s−1 and γ0 = 10. Rheometry experiment stress for [De = 2.3, Wi = 23] condition (solid line). Red and blue symbols in (F) use the stress-SANS rule (eqn (2)) and C = 112. Grey symbols use C = 11.2 inner position (closed symbols) and outer position (open symbols). | ||
The [De = 0.23, Wi = 2.3] LAOS condition (region II, Fig. 1, closed blue triangle) exhibits shear banding under steady shear at equivalent Wi. Interestingly, no shear banding is observed during LAOS as both ϕ0 (Fig. 7A) and Af (Fig. 7B) are equivalent at both measured positions across the velocity gradient direction of shear and correspond to homogeneous flow states.11 Start-up shear measurements at Wi = 9.2 show that it takes approximately ten relaxation times to establish steady shear banding at this value of Wi.14,15 Thus, at this moderate angular frequency of oscillation the sample does not have sufficient time during a cycle to establish a shear banded state; rather, the microstructure and stress of a homogeneous, metastable state is measured.
During LAOS a stress overshoot is observed prior to zero strain in the elastic projection (strain vs. stress) of the Lissajous curve, Fig. 8 (blue curve). The consequence of which is the observation of curious secondary loops in the viscous projection (strain rate vs. stress), Fig. 8 (red curve).39 With the exception of this stress overshoot, the stress predicted from the microstructure measurements using the stress-SANS rule (Fig. 7C) are in agreement with the measured rheology. A similar stress overshoot is also observed in start-up shear conditions performed on this same sample14 and is attributed to micellar chain stretch and subsequent disentanglement.
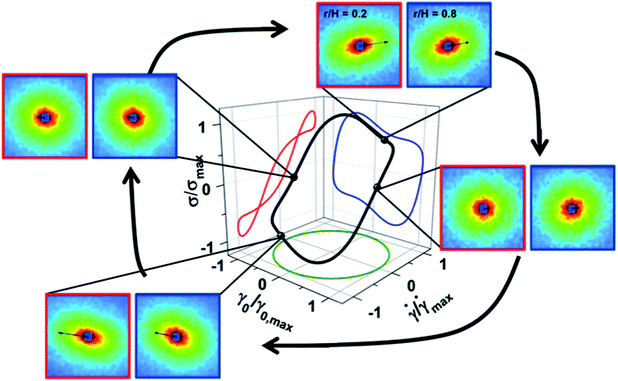 | ||
| Fig. 8 Lissajous–Bowditch diagram for [De = 0.23, Wi = 2.3] where ω = 0.56 rad s−1 and γ0 = 10. SANS scattering patterns follow the same legend as defined in Fig. 6. A movie for this condition shows the complete set of results is included in the ESI (Movie S02†). | ||
The violation of the stress-SANS rule in these overshoot stress states indicates nonlinear chain stretching and/or shear-induced concentration fluctuations.40 Evidence for the microstructural origin of the stress overshoot is identified in Fig. 9, where rheo-SALS results show a butterfly scattering pattern for states where the stress-SANS rule is violated for [De = 0.23, Wi = 2.3] (Fig. 9, right). No butterfly scattering pattern is evident for [De = 0.23, Wi = 1.2] (Fig. 9, left). In these systems, the contrast for light scattering comes from concentration and/or microstructure orientation fluctuations.15 Rheo-SALS experiments probe the supra-molecular length-scales comparable to the wavelength of light, much larger than that of a PLM segment. The stress and concentration fluctuation coupling is a well-known mechanism in viscoelastic polymer solutions41 and often observed as the classic SALS butterfly scattering pattern (Fig. 9, right).30,42,43
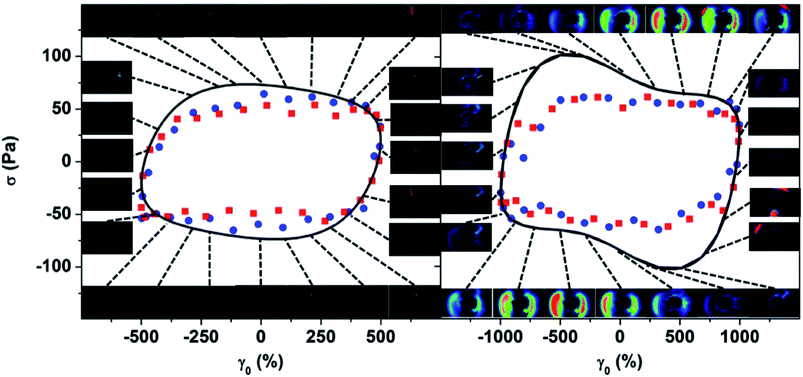 | ||
| Fig. 9 LAOS stress (σ) as a function of strain for [De = 0.23, Wi = 1.2] (left) and [De = 0.23, Wi = 2.3] (right). Points from local 1–2 SANS experiments using the stress-SANS rule (eqn (2)); inner and outer gap positions (red and blue points, respectively). Lines are results from rheometry LAOS experiments. Images are from rheo-SALS experiments with crosspolars where the dotted lines connect the image to the appropriate instantaneous strain in the cycle. SALS movies for each condition are included in the ESI: Movie S04 [De = 0.23, Wi = 1.2], Movie S05 [De = 0.23, Wi = 2.3] and Movie S06 [De = 2.3, Wi = 23].† | ||
SANS measurements also show the existence of this supra-molecular structure as an upturn in 〈I(q)〉 at low-q, Fig. 5A. This observation is consistent with the rheo-SALS measurements shown in Fig. 9 (right). Interestingly, the butterfly pattern (and the low-q increase in SANS intensity) does not persist through the entire oscillatory shear cycle. Instead, upon reduction in the shear rate the solution re-establishes homogeneity and the rheo-SALS butterfly pattern disappears until a comparable stress state is achieved in the opposite direction of flow.
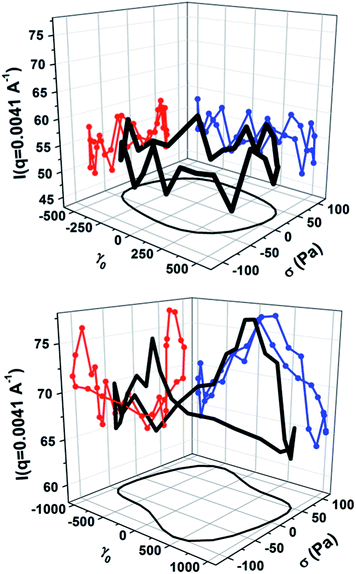
Fig. 10, at the time of this publication, is the first of its kind to define a structure parameter, I(q = 0.0041 Å−1) as a function of the strain deformation and stress response during LAOS. Note that in this unique “structure-Lissajous” plot the independent variables are taken as the strain and shear stress to enable direct observation of the microstructure's dependence on the stress state. For the [De = 0.23, Wi = 1.2] condition clearly there are no significant changes in low-q intensity during the oscillation cycle. This observation agrees well with Fig. 9 where no larger length scale microstructures are observed using rheo-SALS. For the [De = 0.23, Wi = 2.3] condition, the low-q intensity is larger indicating supra-molecular structures exist over the entire oscillatory cycle. In addition, the intensity at low-q demonstrates considerable changes over the course of the oscillation where the maximum stress corresponds with a maximum in I(q = 0.0041 Å−1) for SANS. The structure responsible for this increase in intensity grows and then appears at a later time in the oscillation cycle as observed in Fig. 9. It is clear that the microstructural changes occurring during LAOS are coupled over a range of length scales measured during SANS and SALS experiments. The nonequilibrium state with shear-induced concentration fluctuations qualitatively corresponds to metastable states that are a precursor to the shear banded state reported for flow start-up experiments.14,15 The microstructural transitions responsible for the stress overshoot and the anomalous double-looping behavior observed in the rheology (Fig. 8) are only now understood as the result of shear-induced concentration fluctuations.
The most nonlinear LAOS condition probed [De = 2.3, Wi = 2.3] is reported in Fig. 11 and corresponds to the state in region III of Fig. 1 (red star). At the higher Deborah number (De = 2.3) the angular frequency of oscillation is considerably faster than the relaxation time of the sample and therefore, the sample is not able to relax back toward an equilibrium state during the deformation cycle. LAOS under this condition creates a fundamentally different microstructure that oscillates around a highly flow-aligned state at both positions in the gap and does not return to an isotropic condition over the course of the oscillation cycle (Fig. 11). The small but distinguishable differences in ϕ0 and Af between the inner and outer spatial positions (Fig. 7D and E) are consistent with observations for a shear thinning material11,15 and demonstrate that there is no shear banding at this condition during LAOS. In particular, the ϕ0 and Af for both positions in the gap maintain ±5° (Fig. 7D) and Af > 0.1 (Fig. 7E) over the oscillation cycle and indicate that PLMs are always near a flow aligned state. The degree of flow alignment is much larger than what is observed for the lower De cases and is characteristic of that observed under steady shear in region III. Thus the PLMs are stretched to an aligned and oriented state that is largely maintained throughout the oscillation. The much lower viscosity of this state is consistent with it being largely disentangled.15
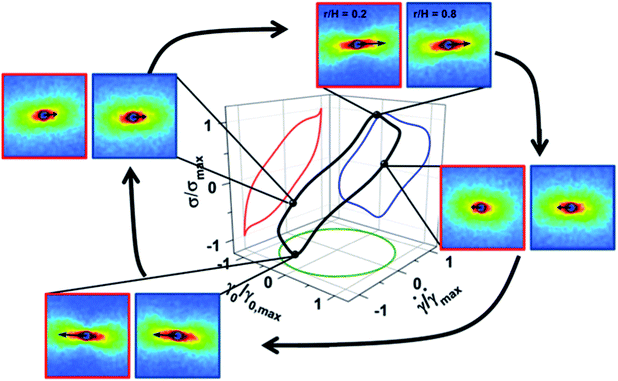 | ||
| Fig. 11 Lissajous–Bowditch diagram for [De = 2.3, Wi = 23] where ω = 5.6 rad s−1 and γ0 = 10. SANS scattering patterns follow the same legend as defined in Fig. 6. A movie for this condition showing the complete set of results is included in the ESI (Movie S03†). | ||
Fig. 7F (grey symbols) shows the predicted shear stress from the microstructural changes measured during flow-SANS using eqn (2) and the same stress-SANS rule coefficient (C = 11.2) and illustrates features similar to but in quantitative disagreement with the stress from rheometry measurements. This is not surprising as the shear-modified topology of the PLM in region III can be expected to yield a different relationship between stress and segmental alignment. Previous work shows that under nonlinear steady shear conditions the stress-SANS rule coefficient becomes a function of shear rate for conditions in region III, C = 112.14,38 Interestingly, when the stress-SANS rule coefficient for region III is used with the stress-SANS rule (eqn (2)) the stress defined from the SANS segmental microstructure measurements (Fig. 7F, red and blue symbols) is in quantitative agreement with the measured stress over the entire oscillation cycle despite the supra-molecular scale concentration fluctuations. Importantly, a strong persistent butterfly pattern is evident from the rheo-SALS experiment (Movie S06†). Thus, shear induced concentration fluctuations result in a shear-induced demixing on supra-molecular length scales. This behavior is characteristic of what is observed for steady shear conditions in region III.15
4 Conclusions
The achievement to create and study the detailed microstructure of metastable states in complex fluids provides quantitative understanding for the unique shear-banding rheology of PLMs as first identified nearly 30 years ago.13 The nonlinear viscoelastic metastable states (Fig. 1) now created and defined using LAOS methods provide both qualitative and quantitative understanding for the underlying material microstructure which leads to the shear banding phenomenon. Specifically, the Lissajous curves in Fig. 6, 8, and 11 are now understood to reveal the viscoelastic stress response from three distinct material states: an entangled PLM characteristic of region I that persists over the entire LAOS cycle, the metastable states where shear-induced concentration fluctuations first become evident and lead to steady shear banding in region II, and finally a more aligned, less viscoelastic material with shear-induced demixing is characteristic of region III.The 1–2 flow-SpatioTemporal Resolved SANS experimental method presented here provides a unique means to gain quantitative microstructural evidence for the origin of the nonlinear viscoelastic stress response from complex fluids. The ability to probe time-dependent microstructure and rheology provides new opportunities to interrogate and understand complex fluids. Measurements of metastable states become invaluable for validating advances in constitutive theory that are based on underlying microstructural features, such as chain scission.10 We anticipate that this new combined method of LAOS rheometry and 1–2 flow-STR SANS, which is now implemented and available at the NIST Center for Neutron Science (USA) and the Institute Laue-Langevin (France) will provide new opportunities to understand a broad range of nonlinear flow phenomena in shearing complex fluids.
Acknowledgements
This manuscript was prepared under cooperative agreements 70NANB7H6178, 70NANB10H256 from NIST, U.S. Department of Commerce. The statements, findings, conclusions and recommendations are those of the author(s) and do not necessarily reflect the view of NIST or the U.S. Department of Commerce. Additional data available in the ESI include movies of the SANS and SALS experiments.References
- J. K. G. Dhont and W. J. Briels, Rheol. Acta, 2008, 47, 1435–1528 CrossRef PubMed.
- P. D. Olmsted, Rheol. Acta, 2008, 47, 283–300 CrossRef CAS PubMed.
- N. A. Spenley, M. E. Cates and T. C. B. McLeish, Phys. Rev. Lett., 1993, 71, 939–942 CrossRef CAS.
- R. Ganapathy and A. K. Sood, Phys. Rev. Lett., 2006, 96, 1–10 CrossRef.
- A. Onuki, J. Phys.: Condens. Matter, 1997, 9, 6119–6157 CrossRef CAS.
- J. Bent, L. R. Hutchings, R. W. Richards, T. Gough, R. Spares, P. D. Coates, I. Grillo, O. G. Harlen, D. J. Read, R. S. Graham, A. E. Likhtman, D. J. Groves, T. M. Nicholson and T. C. B. Mcleish, Science, 2003, 301, 1691–1695 CrossRef CAS PubMed.
- R. G. Larson, Science, 2011, 333, 1834–1835 CrossRef CAS PubMed.
- M. E. Cates and S. M. Fielding, Adv. Phys., 2006, 55, 799–879 CrossRef CAS.
- S. Lerouge and J. F. Berret, Polymer Characterization: Rheology, Laser Interferometry, Electrooptics, Springer, 2010 Search PubMed.
- N. Germann, L. P. Cook and A. N. Beris, J. Non-Newtonian Fluid Mech., 2013, 196, 51–57 CrossRef CAS PubMed.
- M. E. Helgeson, P. A. Vasquez, E. W. Kalter and N. J. Wagner, J. Rheol., 2009, 53, 727–756 CrossRef CAS.
- M. E. Helgeson, L. Porcar, C. Lopez-Barron and N. J. Wagner, Phys. Rev. Lett., 2010, 105, 084501 CrossRef.
- H. Rehage and H. Hoffmann, J. Phys. Chem., 1988, 92, 4712–4719 CrossRef CAS.
- C. R. Lopez-Barron, A. K. Gurnon, A. P. R. Eberle, L. Porcar and N. J. Wagner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. Search PubMed , submitted.
- Y. T. Hu and A. Lips, J. Rheol., 2005, 49, 1001–1027 CrossRef CAS.
- E. Cappelaere, J. F. Berret, J. P. Decruppe, R. Cressely and P. Lindner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 1869–1878 CrossRef CAS.
- S. Lerouge, J. P. Decruppe and C. Humbert, Phys. Rev. Lett., 1998, 81, 5457–5460 CrossRef CAS.
- K. Hyun, M. Wilhelm, C. O. Klein, K. S. Cho, J. G. Nam, K. H. Ahn, S. J. Lee, R. H. Ewoldt and G. H. McKinley, Prog. Polym. Sci., 2011, 36, 1697–1753 CrossRef CAS PubMed.
- C. J. Dimitriou, L. Casanellas, T. J. Ober and G. H. McKinley, Rheol. Acta, 2012, 51, 395–411 CrossRef CAS.
- C. R. Lopez-Barron, L. Porcar, A. P. R. Eberle and N. J. Wagner, Phys. Rev. Lett., 2012, 108, 258301 CrossRef.
- A. K. Gurnon and N. J. Wagner, J. Rheol., 2012, 56, 333–351 CrossRef CAS.
- E. Cappelaere, R. Cressely and J. P. Decruppe, Colloids Surf., A, 1995, 104, 353–374 CrossRef CAS.
- S. Lerouge, J. P. Decruppe and J. F. Berret, Langmuir, 2000, 16, 6464–6474 CrossRef CAS.
- A. P. R. Eberle and L. Porcar, Curr. Opin. Colloid Interface Sci., 2012, 17, 33–43 CrossRef CAS PubMed.
- E. Fischer and P. T. Callaghan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 1–15 Search PubMed.
- H. M. Laun, R. Bung, S. Hess, W. Loose, K. Hahn, E. Hadicke, R. Hingmann, F. Schmidt and P. Lindner, J. Rheol., 1992, 36, 743–787 CrossRef CAS.
- S. Rogers, J. Kohlbrecher and M. P. Lettinga, Soft Matter, 2012, 8, 7831–7839 RSC.
- A. K. Gurnon, P. D. Godfrin, A. P. R. Eberle, P. D. Butler and N. J. Wagner, J. Visualized Exp., 2014, e51068, DOI:10.3791/51068.
- M. W. Liberatore, F. Nettesheim, N. J. Wagner and L. Porcar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 1–4 CrossRef.
- P. Thareja, I. H. Hoffmann, M. W. Liberatore, M. E. Helgeson, Y. T. Hu, M. Gradzielski and N. J. Wagner, J. Rheol., 2011, 55, 1375–1397 CrossRef CAS.
- J. F. Berret, D. C. Roux and G. Porte, J. Phys. II, 1994, 4, 1261–1279 CrossRef CAS.
- L. Porcar, W. A. Hamilton, P. D. Butler and G. G. Warr, Phys. Rev. Lett., 2004, 93, 198301 CrossRef CAS.
- S. A. Rogers, J. Rheol., 2012, 56, 1129–1151 CrossRef CAS.
- C. Dewhurst, Institut Laue-Langevin, GRASansP, 2008, http://www.ill.eu/instruments-support/instruments-groups/groups/lss/grasp/home/, Grenoble, France.
- U. Keiderling, BerSANS, Helmholtz Zentrum, HBZ, Berlin Search PubMed.
- M. Muthig, S. Prevost, R. Orglemeister and M. Gradzielski, J. Appl. Crystallogr., 2013, 46, 1187–1195 CAS.
- L. M. Walker and N. J. Wagner, Macromolecules, 1996, 29, 2298–2301 CrossRef CAS.
- A. K. Gurnon, M. Wassborough, C. Lopez-Barron, L. Porcar and N. J. Wagner, ACS Macro Letters Search PubMed , submitted.
- R. H. Ewoldt and G. H. McKinley, Rheol. Acta, 2010, 49, 213–219 CrossRef CAS PubMed.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press Inc., New York, 1986 Search PubMed.
- E. Helfand and G. H. Fredrickson, Phys. Rev. Lett., 1989, 62, 2468–2471 CrossRef CAS.
- T. Hashimoto and T. Kume, J. Phys. Soc. Jpn., 1992, 61, 1839–1843 CrossRef CAS.
- I. A. Kadoma, C. Ylitalo and J. W. Egmond, Rheol. Acta, 1997, 36, 1–12 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: See DOI: 10.1039/c3sm53113a |
| ‡ Present address: ExxonMobil Chemical Company, Baytown, Texas, USA. |
| This journal is © The Royal Society of Chemistry 2014 |