DOI:
10.1039/C3SM53070A
(Paper)
Soft Matter, 2014,
10, 4091-4109
Capillary attraction induced collapse of colloidal monolayers at fluid interfaces
Received
10th December 2013
, Accepted 18th February 2014
First published on 18th February 2014
Abstract
We investigate the evolution of a system of colloidal particles, trapped at a fluid interface and interacting via capillary attraction, as a function of the range of capillary interactions and temperature. We address the collapse of an initially homogeneous particle distribution and of a radially symmetric (disk-shaped) distribution of finite size, both theoretically by using a perturbative approach inspired by cosmological models and numerically by means of Brownian dynamics (BD) and dynamical density functional theory (DDFT). The results are summarized in a “dynamical phase diagram”, describing a smooth crossover from a collective (gravitational-like) collapse to local (spinodal-like) clustering. In this crossover region, the evolution exhibits a peculiar shock wave behavior at the outer rim of the contracting, disk-shaped distribution.
1 Introduction
Partially wetted colloidal particles can be strongly trapped at fluid interfaces. There they form colloidal monolayers, which constitute systems of low spatial dimensionality exhibiting a rich and interesting phenomenology. This is in part due to the effective capillary force acting between the particles, which is tied to the presence of a deformable fluid interface. Driven by basic research as well as application perspectives, capillary interactions have recently received renewed interest both in theory and in experiment, see, e.g., ref. 1–3 and references therein. If the colloidal particles deform the interface as a consequence of an external force acting on them, such as their weight or an externally imposed electric field among several actual experimental realizations, the dominant contribution to the capillary interaction is the so-called “capillary monopole”.† In the (experimentally realistic) limit of small interfacial deformations, this force is always attractive and has a range given by the capillary length  , where γ is the surface tension of the interface, g is the acceleration of gravity, and Δρ is the mass density difference between the fluids on both sides of the interface. In typical experimental configurations the interparticle separation (∼micron) is much smaller than λ (∼millimeter), so that any given particle interacts simultaneously with a huge number of neighbors. Furthermore, at separations smaller than λ, the capillary attraction varies logarithmically and is formally analogous to two-dimensional (2D) Newtonian gravity. In these circumstances, the capillary interaction is equivalent to “screened 2D Newtonian gravity”, with a screening length λ much larger than any microscopic length scale. Therefore we call this interaction “long-ranged”. In this context the tunability of such a system is of special interest. The range of the interaction may in principle be varied by changing the capillary length, which is accessible via changes of the surface tension of the interface, e.g., due to the addition of surfactants. Additionally, the relevant ratios of the interaction range to other length scales of the system (most notably, the interparticle separation and the system size) can be easily altered also by changing these other lengths in experimental setups.‡ Likewise, the amplitude of the capillary monopole and, correspondingly, the strength of the interaction are controllable by means of the external force. Therefore, for micron-sized colloidal particles, such a monolayer can serve as a 2D model system for studying the influence of a “long-ranged” interaction as a function of its parametric characteristics.
, where γ is the surface tension of the interface, g is the acceleration of gravity, and Δρ is the mass density difference between the fluids on both sides of the interface. In typical experimental configurations the interparticle separation (∼micron) is much smaller than λ (∼millimeter), so that any given particle interacts simultaneously with a huge number of neighbors. Furthermore, at separations smaller than λ, the capillary attraction varies logarithmically and is formally analogous to two-dimensional (2D) Newtonian gravity. In these circumstances, the capillary interaction is equivalent to “screened 2D Newtonian gravity”, with a screening length λ much larger than any microscopic length scale. Therefore we call this interaction “long-ranged”. In this context the tunability of such a system is of special interest. The range of the interaction may in principle be varied by changing the capillary length, which is accessible via changes of the surface tension of the interface, e.g., due to the addition of surfactants. Additionally, the relevant ratios of the interaction range to other length scales of the system (most notably, the interparticle separation and the system size) can be easily altered also by changing these other lengths in experimental setups.‡ Likewise, the amplitude of the capillary monopole and, correspondingly, the strength of the interaction are controllable by means of the external force. Therefore, for micron-sized colloidal particles, such a monolayer can serve as a 2D model system for studying the influence of a “long-ranged” interaction as a function of its parametric characteristics.
long-ranged interactions are a subject of active research in various branches of physics (see, e.g., ref. 6 and references therein), involving rather distinct scales. Ranging from cosmology down to chemotaxis in bacterial populations, a common feature of these systems is their temperature dependent instability with respect to clustering.7–10 In recent studies, we investigated this clustering instability in monolayers of micron sized particles driven by a monopolar capillary interaction,10–12 paying special attention to the influence of the ratio between the capillary length and the system size. In the formal limit λ → ∞, corresponding to 2D Newtonian gravity, cosmology offers a useful analogy for tackling the problem within the so-called “cold collapse” approximation, which is widely used to study clustering of collisionless matter: one neglects any force other than gravity (including diffusion by thermal motion). Within this approximation, the dynamical equations of our model are amenable to an analytical solution, which provides the basis for perturbative calculations when λ is finite. Numerical solutions and N-body simulations allow for going beyond the simplifying assumptions of the analytical approach.
Here our goal is to provide a complete characterization of the evolution induced by the clustering instability as a function of the relevant parameters of the system. In this respect, in ref. 10 and 12, a homogeneous particle distribution (either macroscopically extended or with periodic boundary conditions) was studied, while ref. 11 has addressed a radially symmetric (disk-shaped) distribution with a finite radius, which is more realistic from an experimental point of view. There a “dynamical phase diagram” was proposed in order to summarize the findings (see Fig. 1 in ref. 11): there is a region of stability at high temperatures, and a region of instability at low temperatures. In the latter region, the evolution proceeds as in the case of gravitational cold collapse if λ is larger than the system size, and as in the case of spinodal decomposition if λ is much smaller than the system size. There is no sharp borderline between these two limiting cases but instead a crossover region which exhibits characteristic features of both regimes. In a disk-shaped particle distribution, the presence of the explicit outer boundary brings into focus this crossover region as in the course of the collapse a shock wave-like structure is formed. First corresponding results are communicated in ref. 11. Here we elaborate and extend the theoretical model and the perturbative calculations underlying this study, including the proposed “dynamical phase diagram”. Resorting to Brownian dynamics (BD) simulations and dynamic density functional theory (DDFT) we investigate this diagram concerning the dynamic evolution of a disk-shaped finite distribution of particles. Both the BD and the DDFT results support the picture captured by the “dynamical phase diagram”.
The paper is organized such that in the next section we shall present the theoretical model. In Subsection 2.1 we shall introduce the definitions and the terminology used throughout the paper. We first recall briefly the theory for colloidal systems with monopolar capillary attractions and the model for the dynamical evolution. Next, in Subsection 2.2 we shall discuss the linear stability analysis of the homogeneous system, based on which we identify various dynamical regimes in the “dynamical phase diagram” as a function of the screening length λ and a rescaled, effective temperature. This will be followed by a formal definition of the cold collapse model, which serves as the baseline for the formulation of an analytical perturbation theory for the capillary collapse of colloids trapped at a fluid interface. The main results are summarized in Subsection 2.3 and certain derivations are given in Appendix A. In Section 3 we shall discuss the numerical methods we have applied in order to investigate the capillary collapse. In Section 4 we shall report on simulations for various setups so as to explore the “dynamical phase diagram” also for the case of finite-sized circular patches of particles, as a function of an effective temperature and of the range of the interaction. In order to render a comparison with future experiments feasible, in Section 5 we shall briefly discuss how a change of the interface tension affects the relevant variables for the setup of a homogeneous system or for that of a collapsing disk. Finally, in Section 6 we shall summarize and present our conclusions.
2 Theoretical model
2.1 Basic features and description of the dynamic evolution
We consider a two-dimensional set of interacting particles (Fig. 1). For the system under study, we map a distribution of spherical colloidal particles of radius R, which are trapped at a fluid interface, onto a two-dimensional distribution of disks in a flat reference plane. For small deformations of the interface as considered here, this renders a two-dimensional distribution of circular disks with radius R0.1,13,14 (The relationship between R and R0 depends on the contact angle of the interface at the particle surface.) Their dynamical model as used here is introduced in ref. 10 and is briefly recalled here.
 |
| | Fig. 1 Sketch of the system under consideration. Colloids are trapped at the interface between two fluids with surface tension γ. Around each colloid a dimple is formed because the external force f acting on each colloid pushes the colloids into the lower fluid (often water). The dimple depth is proportional to f/γ. Thus for micron-sized colloids with f caused by their own weight (or buoyancy) the depth is in the range of a few nm. Therefore the system is effectively two-dimensional, and the colloids interact via the attractive, long-ranged capillary pair potential Vcap(d) (see eqn (3)) in addition to short-ranged, repulsive interactions of different natures. This pair potential constitutes the dominant term of the colloidal interaction within the multipolar expansion which amounts to an expansion in terms of the inverse interparticle separation 1/d.2,13,14 The actual three-dimensional (3D) configuration is mapped onto a two-dimensional (2D) configuration of disks in a reference plane. | |
The particles are subject to capillary forces. These are generated by the interfacial deformation upon the action of an external force f on the particles (which in turn is, e.g., caused by the weight of the particles and their buoyancy at the interface) in the direction perpendicular to the reference plane. Within mean-field theory, the linearized Young–Laplace equation governing the interfacial deformation U(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ),
), ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ∈
∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2, is given by1,13
2, is given by1,13
| |  | (1) |
where
ρ(
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif)
) is the 2D particle number density field in the reference plane and
γ is the surface tension. (The interfacial deformation for micron-sized particles is in the nm range, which justifies the linearized approximation.) This interfacial deformation gives rise to an in-plane capillary force described by the areal force density
| |  | (2) |
The capillary force between two particles can be cast into a form such that a corresponding pair potential is given by
1| | 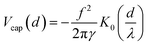 | (3) |
in terms of the modified Bessel function
K0, as obtained from Green's function for
eqn (1), and the center-to-center distance
d between the particles. The capillary length
λ acts as a cutoff for the interaction range because
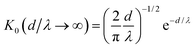
. In the opposite limit,
d ≪
λ, this potential coincides with the Newtonian gravitational interaction in
d = 2,
K0(
d/
λ → 0) ∼ ln(
λ/
d), which is nonintegrable in the sense of statistical mechanics,
i.e., it leads to a nonadditive (hyperextensive) internal energy. In view of this property and due to the wide separation of scales in colloidal systems,
λ =
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(mm) and
R0 =
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(μm), for the present purposes we call
Vcap(
d) a “long-ranged interaction”, as opposed to other interactions which will be called “short-ranged”.
Concerning the dynamics, we assume an overdamped motion for the particles adsorbed at the interface. For reasons of simplicity, as a first step we neglect hydrodynamic interactions§ so that the in-plane number density current of the particles is proportional to the driving force,
with an effective single-particle mobility
Γ.
Fshort is the sum of the areal thermodynamic force densities associated with thermal motion and with any other (short-ranged) interaction between the particles. Assuming local equilibrium, one can write

, where the 2D pressure field
p =
p(
ρ) is given by an appropriate equilibrium equation of state describing the macroscopic manifestation of the short-ranged forces. Therefore, the continuity equation for the particle number density is
| |  | (5) |
We introduce a characteristic particle density ρ0 and the length scale L0 associated with the size of the system. (For the homogeneous systems considered below, L0 is the side length of the periodically replicated square box and for the collapsing disk scenario, it is the initial radius of the particle-covered disk.) We also introduce the time scale ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) := γ/(Γf2ρ0), which is the so-called Jeans' time associated with the initial homogeneous density ρ0.10 This allows us to form the following dimensionless variables and quantities:
:= γ/(Γf2ρ0), which is the so-called Jeans' time associated with the initial homogeneous density ρ0.10 This allows us to form the following dimensionless variables and quantities:
| |  | (6a) |
| |  | (6b) |
In these terms,
eqn (1) and
(5) take the form:
| |  | (7b) |
It is useful to introduce the (dimensionless) chemical potential
μ =
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0b3.gif) γ
γ/(
f2ρ0L02) which is associated with the pressure
via the Gibbs–Duhem relationship:
¶| | 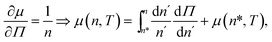 | (8) |
with a certain constant
n* so that
eqn (7b) can be also written as
| |  | (9) |
Alternatively, one can introduce a free energy functional
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
[
n,
w] (see
ref. 10), such that
| | 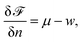 | (10) |
so that
eqn (7a) and
(7b) can be written as
| |  | (11) |
respectively. This establishes a formal analogy between
eqn (7) and the so-called dynamic density functional theory (DDFT)
16 for the ensemble-averaged density.
The dynamics described by these equations has been already the subject of previous studies.8,10–12,17 The main goal of the following analysis is the investigation of the dynamics as a function of the capillary length if the initial condition is a circular patch of colloidal particles, i.e., the solution of these equations with the property that w(r, t) is regular and with the boundary conditions
| |  | (12) |
and a so-called “top-hat” profile as the initial condition
| |  | (13) |
This initial configuration complements and is closer to experimental realizations than the idealized case of an infinitely extended homogeneous distribution. Compared with the cases of an infinitely extended system or a system in a box with periodic boundary conditions (as addressed in
ref. 8, 10, 12 and 17), the presence of an explicit boundary brings into focus the effect of changing the range of the capillary attraction relative to the system size, leading to a peculiar phenomenology.
11
For the following discussion we introduce the useful notions of the “cold limit” (Π → 0 in eqn (7b) or μ → 0 in eqn (9)) and of the “Newtonian limit” (κ → 0 in eqn (7a)). The first notion refers to the interpretation of vanishing pressure as a sort of athermal limit of the fluid; the second notion refers to the case that the capillary attraction (eqn (3)) becomes identical to Newtonian gravitational attraction in 2D (see, e.g., ref. 10 and 18). Regarding this latter notion, we briefly remark on the opposite limit κ → ∞, i.e., a very short-ranged capillary attraction. From the explicit integral of eqn (7a),
| |  | (14) |
one deduces
| |  | (15) |
in regions where the density field is smooth, and
eqn (7b) becomes
| |  | (16) |
with ∇(
n∇
w) ≈
κ−2∇(
n∇
n) = (
κ−2/2)∇
2(
n2). This is the diffusion equation for a fluid the equation of state
P(
n) of which accounts for the attractive force through the van der Waals-like contribution −
n2/(2
κ2). In view of that, one should note that, motivated by the wide scale separation mentioned above (
λ ≫
R0), we are interested in the comparison of the range of the interaction with a characteristic system size, as quantified by the parameter
κ. This is distinct from the more usual approach, in which the range would be compared with a microscopic length,
e.g., the particle radius.
2.2 Stability with periodic boundary conditions
We first review briefly the linear stability analysis of a homogeneous distribution in a finite square box with side length L0 and periodic boundary conditions. The findings can be summarized in a “dynamical phase diagram”, which is also useful for understanding qualitatively the mathematically more difficult case of a finite disk.
Consider the equilibrium, homogeneous state neq(r) = 1 with r ∈ [0, 1] × [0, 1] and periodic boundary conditions. In order to account for a locally perturbed density n(r, t) = 1 + δ(r, t) one introduces the Fourier transform of the density deviations:
| |  | (17) |
with the wavevectors (in units of 1/
L0)
| | k = 2π(mx, my), mx, my ∈ ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) . . | (18) |
Eqn (7) can be linearized in
δ resulting in
| | ![[small delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e125.gif) k(t) = k(t) = ![[small delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e125.gif) k(0)et/τ(k), k(0)et/τ(k), | (19) |
where in units of
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif)
the inverse characteristic time for each mode
k is given by
| |  | (20) |
in terms of Jeans' length
K−1 (in units of
L0) defined as
| |  | (21) |
(This quantity is actually the inverse of the isothermal compressibility of the fluid due to thermal motion and short-ranged forces,
i.e., in the absence of capillary attraction.)
Fig. 2 depicts 1/
τ(
k) for two qualitatively distinct cases characterized by the values of
K and
κ. In the cold (
K → ∞) Newtonian (
κ = 0) limit all modes grow at the same rate,
i.e.,
τ(
k) ≡ 1 (horizontal blue line in
Fig. 2(a)). (Actually, in this limit the growth of perturbations can be computed exactly beyond the linear regime; see the discussion in Subsection 2.3). A nonzero pressure (
K < ∞) causes a slowing down of the growth of the small-scale (
k → ∞) perturbations or even leads to damping (1/
τ(
k) < 0) due to the finite compressibility (red line in
Fig. 2(a)). The effect of a finite range of the attraction (
κ > 0) is to slow down the growth of the large-scale (
k → 0) perturbations (green line in
Fig. 2(a)). If
K/
κ < 1, all perturbations are damped (red curve in
Fig. 2(b)); if
K/
κ > 1, the amplitude of all Fourier modes below a critical wavenumber grow in time (blue curve in
Fig. 2(b)).
 |
| | Fig. 2 Examples of the dependence on k of the growth rate 1/τ(k) defined in eqn (20) for various values of the parameters K and κ (see the main text). In (a), K−1 = 1 for the red line and κ = 0.2 for the green line; in (b), K−1 = 1 and κ = 5 for the red line, and K−1 = 1 and κ = 0.2 for the blue line. | |
The analysis is facilitated by the introduction of a dimensionless parameter which we call “effective temperature”:
| | 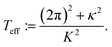 | (22) |
This parameter quantifies the ratio between the energy associated with thermal motion and short-ranged forces and with the potential energy of the capillary attraction.
Indeed, if for simplicity one considers an ideal gas, p(ρ) = ρkBT, in physical units eqn (22) turns into
| |  | (23) |
where the capillary potential energy of a pair of particles is ∼
f2/
γ (see
eqn (3)) and
| |  | (24) |
gives the approximate average number of neighbors with which any given particle interacts
via capillary attraction. This quantity allows one to quantify the notions of a “large system”, for which
Nneigh ∼
ρ0λ2 if
κ =
L0/
λ ≫ 1, and of a “small system”, with
Nneigh ∼
ρ0L02 if
κ =
L0/
λ ≪ 1.
In terms of these parameters Teff (eqn (22)) and κ, for a general system eqn (20) becomes
| |  | (25) |
so that the homogenous state is linearly stable (
τ(
k) < 0 for all allowed values of
k) if and only if
Teff > 1. As
Teff decreases, more and more modes at smaller length scales become unstable. This is visualized in
Fig. 3, which facilitates the discussion of the evolution of the density field in real space as a function of the two parameters
Teff and
κ characterizing the initial state. We have found that two properties are relevant in order to identify different “regimes of instability”: first, the number of unstable Fourier modes, as determined by the position of the zero in
Fig. 2, and second, the kind of mode exhibiting the fastest growth, determined by the position of the maximum in
Fig. 2.
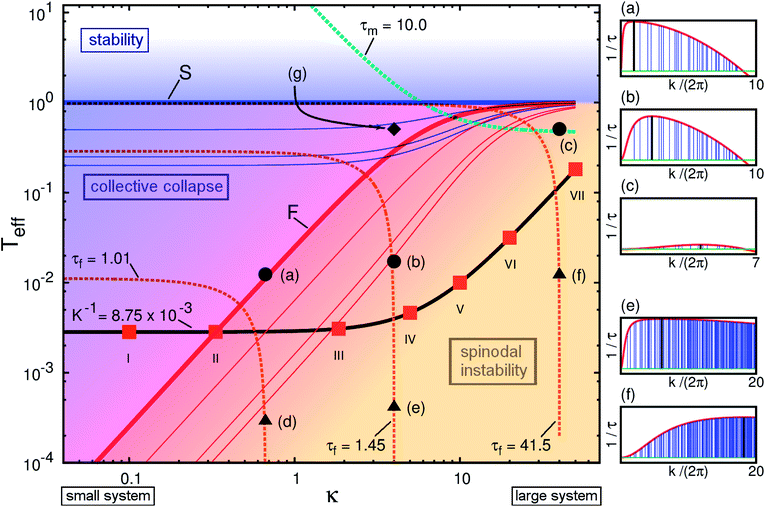 |
| | Fig. 3 Diagram showing the different “regimes of instability” for an initially homogeneous distribution with periodic boundary conditions in terms of Teff (eqn (22)) and κ = L0/λ. Blue lines, depending on the squared modulus m2 = mx2 + my2 of the mode indices, indicate the limit of stability for those modes (eqn (26)). The thick blue line S of absolute stability corresponds to m2 = 1; subsequent lines correspond to m2 = 2, m2 = 4, and m2 = 5. Red lines indicate that a mode with squared modulus m2 is the fastest growing one (eqn (27)). The thick red line F corresponds to m2 = 1. The thick black line is an iso-K line Teff(κ) = K−2[(2π)2 + κ2] (eqn (22)), containing the state points of the Brownian dynamics simulations presented in ref. 12 with a Jeans' length of K−1 = 8.75 × 10−3 (filled squares). Finally, the lines τm = 10 (i.e., the fastest mode has the characteristic time 10![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ) and τf = (1.01, 1.45, 41.5) (from left to right; the fundamental mode has the characteristic time 1.01 ) and τf = (1.01, 1.45, 41.5) (from left to right; the fundamental mode has the characteristic time 1.01![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , 1.45 , 1.45![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , and 41.5 , and 41.5![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , respectively) are given by eqn (28) and (29), respectively. The lines for given values of τf ≳ 1 indicate the transition region. The black symbols (symbols of different shapes correspond to different Jeans' lengths) indicate the systems consisting of a finite circular initial patch of particles investigated via simulations and are discussed in Section 4. For the points (a)–(c), (e), and (f), the corresponding inverse characteristic times 1/τ(k) (as shown in Fig. 2, see eqn (20)) are shown in the side panels on the right with the discrete modes indicated by blue vertical lines. Note that the horizontal scales for k vary whereas the vertical scale always ranges from −0.1 < 1/τ < 1. The green horizontal line corresponds to 1/τ = 0 and the vertical black lines indicate the maxima of 1/τ(k). , respectively) are given by eqn (28) and (29), respectively. The lines for given values of τf ≳ 1 indicate the transition region. The black symbols (symbols of different shapes correspond to different Jeans' lengths) indicate the systems consisting of a finite circular initial patch of particles investigated via simulations and are discussed in Section 4. For the points (a)–(c), (e), and (f), the corresponding inverse characteristic times 1/τ(k) (as shown in Fig. 2, see eqn (20)) are shown in the side panels on the right with the discrete modes indicated by blue vertical lines. Note that the horizontal scales for k vary whereas the vertical scale always ranges from −0.1 < 1/τ < 1. The green horizontal line corresponds to 1/τ = 0 and the vertical black lines indicate the maxima of 1/τ(k). | |
(1) The limit of stability given in Fig. 3 of a given mode k = 2π(mx, my) is determined using the conditions
| |  | (26) |
In particular, for the fundamental mode (k = 2π) this defines the line Teff = 1 of absolute stability (“line S” in Fig. 3).
(2) The loci in Fig. 3 where a given mode k = 2π(mx, my) exhibits the fastest possible growth is determined using the condition
| |  | (27) |
In particular, for the fundamental mode (
k = 2π) this defines the line
Teff = [1 + (2π/
κ)
2]
−1 (red “line F” in
Fig. 3) above which the fundamental mode is the fastest growing one.
||
It also proves to be useful to define the following loci:
(1) The maximum value  is given by
is given by
| |  | (28) |
which renders a line
Teff(
κ,
τm) with a parametric dependence on
τm. This time
τm is typically of order 1,
i.e., Jeans' time, and it can become significantly larger only close to the instability threshold,
Teff → 1, and for a “large system”,
κ → ∞; see in
Fig. 3 the blue dashed line corresponding to
τm = 10.
(2) The line along which the characteristic time τ(k = 2π) of the fundamental mode has a given value τf is given by
| |  | (29) |
As illustrated in
Fig. 3, these lines run parallel to the line S and then become vertical at a sharp value (
κ0/2π)
2 =
τf − 1. In this sense, the notion of a “small
vs. large system” is also quantified by the value of
τf − 1.
We can now summarize the overall picture in Fig. 3 as follows:
• In the region below the line S (stability limit) and above the line F (the fundamental mode is the fastest growing one) there are in general many unstable modes (thin blue lines), but the fastest growing one is the fundamental mode (i.e., with the smallest k), so that the evolution of the density field is dominated by features at the largest scales in real space (“collective collapse”). Furthermore, in this region the effect of a finite range of the capillary attraction i.e., κ ≠ 0 is irrelevant and the relative change in the growth rate between different modes is due to the effect of pressure (eqn (20)). This is the region of gravitational-like collapse, which proceeds on a time scale of the order of Jeans' time (because most part of this region lies well below the line τm = 10 and in the “small system” region, τf ≳ 1).
• In the region well below the red line F and in the “large system” region, i.e., far to the right of the lines τf ≳ 1, there are many unstable modes, but the fastest growing ones correspond to perturbations on small scales (compared to the size of the system), which evolve on a time scale substantially faster than the fundamental mode. Therefore, the evolution of the density field is dominated by the growth of small-scale perturbations of a certain preferred size (“local collapse”). This is the region of spinodal-like instability, which also proceeds on a time scale of the order of Jeans' time, except in the corner region κ → ∞, Teff − 1 small (note the location of the line τm = 10). In this corner the evolution appears to be substantially slowed down on the scale of Jeans' time and it corresponds precisely to the usual scenario of spinodal decomposition in fluids after quenching to a temperature below but not too far from the critical point (note that the spinodal line is actually the line S).
• The transition between the two regimes discussed above is smooth and corresponds roughly to the region below the line F but in the “small system” region, i.e., to the left of or around the lines τf ≳ 1. There the evolution consists of the simultaneous clustering at a rate of the order of Jeans' time of widely differing length scales, including both very small scales and the largest possible ones. This regime thus shares characteristic features of both the “spinodal instability” and the “gravitational instability”. Which feature dominates the structure formation (global or local collapse) depends critically on the distribution of the initial amplitudes of the density perturbations.
This picture is exemplified in ref. 12 with N-body simulations in a finite box with periodic boundary conditions corresponding to an initial dilute (ideal-gas) density with 1/K ≈ 8.75 × 10−3 fixed and values of κ ranging from 0.1 up to 100; in Fig. 3 the corresponding states are represented by filled red squares lying on the iso-K (thick black) line Teff(κ) = K−2[(2π)2 + κ2]. In these simulations all initial state points were chosen below the stability line S, and therefore the inherent mode instabilities led to clustering. For the two lowest state points (I and II) with κ < 1, perfect scaling of the time evolution of various geometric cluster measures with Jeans' time was observed, indicating the gravitational-like “collective collapse”. The third state point (III) with κ = 1.85 is located in the transition region and deviations from the above time scaling are noticeable. For all other state points (IV–VII) with κ ≥ 5, the dynamics became increasingly slow and the scaling with Jeans' time is completely lost. Together with the spatial information inferred from various snapshots (see Fig. 3 in ref. 12), these state points are characteristic of the spinodal regime.
2.3 Collapse of a finite-sized, radially symmetric distribution
As compared to the case discussed in the previous subsection, the theoretical analysis of a collapsing finite-sized disk is complicated by the fact that the unperturbed state is neither stationary nor spatially homogeneous. The theoretical description of such a system is facilitated by switching to Lagrangian coordinates. The details of this treatment are presented in Appendix A. Here we summarize and discuss the main results obtained from these calculations.
The Lagrangian trajectory field of volume elements is the mapping
such that
r is defined physically as the position at time
t of that volume element which was at position
x initially (
i.e., at time
t = 0);
x is called the Lagrangian coordinate of the volume element. The trajectory field allows one to express any other field as a function of the Lagrangian coordinates
x. In particular, the Lagrangian density field is given by:
| | | nL(x, t) := n(r = rL(x, t), t). | (31) |
Following the definitions and steps in Appendix A.1, the evolution equations for
n and
w (
eqn (7a) and
(7b)) can be put into their Lagrangian form (see
eqn (41d),
(41e), and
(47)). Mass conservation is a built-in property of the Lagrangian scheme, so that it is not violated regardless of the approximations done in the Lagrangian equations. The subsequent discussion is divided into two parts: the radially symmetric evolution of the initial profile given by
eqn (13) and the (linearized) evolution of perturbations to this initial profile.
Radially symmetric evolution.
It is described by Lagrangian trajectories of the form rL(x, t) = a(x, t)x. The formal solution for a(x, t) is derived in Appendix A.2. The theoretical analysis has been divided into steps of increasing difficulty.
(1) Newtonian (κ = 0), cold (Π = 0) limit. The evolution equation for nL (eqn (47)) can be solved exactly and the solution can be used to obtain a(x, t) from eqn (54). In this manner one finds (see Appendix A.2.1)
| |  | (32a) |
and
| |  | (32b) |
This is the so-called cold collapse solution, for which in the course of the evolution the disk shrinks and the density inside the disk does not depend on the radial position, so that all particles reach the center simultaneously. This is the 2D analogue of the cosmological “big crunch” solution (
i.e., a time-reversed “big bang” solution), where
a plays the role of the expansion factor and d
a/d
t that of the Hubble function.
(2) Finite screening (κ ≠ 0), cold (Π = 0) limit. Analytical results can be obtained using a perturbative approach in the two limiting cases of “small systems” (κ ≪ 1) and of “large systems” (κ ≫ 1). This amounts to approximately solving eqn (47) for nL by replacing the term proportional to κ2 by one corresponding to a reference solution. In the case κ ≪ 1, this is the cold-collapse solution given by eqn (32). The perturbative solutions for a(x, t) and nL(x, t) (eqn (63) and (64)) result in a deformation of the density profile during the collapse (see Fig. 4(a)). In particular, at the rim of the disk a peak forms which becomes singular before all matter collapses in the center. To the lowest order in κ, the radial position rsw and the time tsw for the occurrence of this shock wave are given by (eqn (72) and (73)):
| |  | (33) |
In the opposite limit of large system sizes,
κ ≫ 1, the collapse of the disk is slowed down substantially because initially the density field is homogeneous almost everywhere (see
eqn (16)). Thus one can use the initial condition as a reference solution as if it was stationary in order to obtain an approximate solution of
eqn (61). At the beginning, the dynamics is driven solely by the net capillary attraction near the density inhomogeneity at the rim and again a density singularity appears there (see
Fig. 4(b)). To the lowest order in
κ−1, this occurs at a time and a position given by (see the text following
eqn (77) and
(78))
| |  | (34) |
After this, the position of the singularity is shifted by the collapse of the disk, which occurs on a much longer time scale which is at least ≳1/
κ (see
eqn (78)).
 |
| | Fig. 4 In the cold limit time evolution of the radial density profile for a disk computed perturbatively (see eqn (63) and (64)). (a) Small systems: for κ = 2/3 the shock wave singularity appears at the radius rsw ≈ 0.17 and at the time tsw ≈ 1.086 (see eqn (33)). (b) Large systems: for κ = 10 the shock wave singularity appears at the radius rsw ≈ 0.9 and at the time tsw ≈ 1.9 (see eqn (34)). | |
Thus, the formation of a singularity is a generic feature of the cold limit. The time evolution is formally undefined beyond its appearance, but actually the singularity is regularized by the effect of a nonzero compressibility caused by corrections to the cold limit.
(3) Effects of nonzero Π. At nonzero temperatures, the pressure term in the evolution equation for n (eqn (7b) or, equivalently, the Lagrangian form in eqn (47)) can become important. If Π is sufficiently large (formally the limit of high temperature, T → ∞), pressure is the dominant term in the evolution equation and the initial density distribution ends up with two-dimensional evaporation instead of a collapse. This is the analogue of the region Teff > 1 shown in Fig. 3. We are more interested, however, in the case that the disk collapses and how a nonzero but still sufficiently low temperature T affects the evolution. In Appendix A.2.3 we show that a nonzero pressure quickly smoothens any finite steps in the initial density distribution. The analytical study of the effect of pressure on the density singularity, which forms as a divergence for Π = 0 and κ ≠ 0, is more difficult and we do not have explicit analytical results for this behavior, but it can be expected that the pressure will regularize also this singularity. This is clearly visible in our numerical solutions and in the simulated profiles (see Section 4 below). Thus the collapse will proceed beyond the time tsw and the regularized peak at the rim of the disk is shifted to the center in the manner of a shock wave.
Perturbations of radial symmetry.
This issue has been studied in Appendix A.3. For the Newtonian, cold limit one can solve the evolution equation for the Lagrangian density field exactly (see eqn (84)). There is enhanced clustering localized at initially overdense regions and depletion at underdense regions. In astrophysics this is called the “fragmentation instability”. For an initially small local overdensity, 0 < δn0 ≪ 1, the local time of collapse (signaled as a density singularity) is still of the order of Jeans' time, ts ≈ 1 − δn0. Again, it is difficult to treat the case of nonzero T and κ. However, for density perturbations localized near the center of the disk such that the effect of the boundary can be neglected, the calculations in Appendix A.3 show that the linear stability analysis of a time-independent, homogeneous state as discussed in Subsection 2.2 is useful also for this kind of perturbation. Particularly relevant observations are that the shortest temporal scale for the growth of perturbations is in general Jeans' time (see the line denoted as τm shown in Fig. 3) and that during disk collapse further fragmentation of the inhomogeneities is counteracted by a nonzero pressure.
Although Fig. 3 derives from the linear stability analysis of a stationary and homogeneous state, it is also useful in order to summarize and rationalize the picture which emerges from the theoretical analysis of the collapsing disk, with Teff and κ referring to the initial disk state. Thus, the disk collapses if Teff is well below 1. A generic feature of the disk-collapse is the formation of a singularity, eventually regularized by pressure, at the outer rim at a time slightly larger than Jeans' time. As an inbound shock wave this feature can dominate the evolution only in an intermediate transition region where κ is of the order of one and the time scale of the overall collapse is comparable to Jeans' time (see the lines denoted as τf in Fig. 3). If κ is very small, the gravitational-like global collapse is so fast that the formation of the singularity is practically unobservable. If κ is very large, the evolution is dominated by spinodal-like growth, on Jeans' time scale, of density perturbations with large wavenumbers inside the disk, while the collapse of the disk remains frozen and with it the singularity at the outer rim. This picture is confirmed by numerical calculations, as explained in the subsequent sections.
3 Brownian dynamics and particle based DDFT
The Brownian dynamics simulation introduced in ref. 12 relies on the particle-mesh method known from cosmological simulations. We first briefly recall the basic concept of this method, which provides the foundation of an easily applicable extension corresponding to a solution of a two-dimensional (2D) dynamic density functional theory (DDFT).
Within the simulation, the straightforward way to implement colloidal dynamics based on a pairwise additive potential such as the capillary potential of eqn (3) consists of summing all forces from all possible pairs of colloids. However, as explained after eqn (3), the potential in eqn (3) is long-ranged and non-integrable in 2D in a system of size L < λ. In using periodic boundary conditions, colloidal particles from periodic images will therefore contribute significantly to the total force acting on a single colloid. In order to obtain the correct value of the force experienced by a particle, the sum of the forces has to be extended over many periodic images. Alternatively, here we use the particle-mesh method, in order to exploit the underlying mean field character of eqn (1). It connects the average interfacial deformation U(r) with the average mean number density ρ(r). Provided one has access to the mean density, e.g., discretized on a grid or mesh, one can solve eqn (1)via Fourier transformation. The resulting mean interfacial deformation on the grid enables one to compute the capillary forces acting on the colloidal particles by means of interpolation, whereby the effect of periodic images is taken into account properly by the Fourier transform.
In order to simulate colloidal particles trapped at a fluid interface, one also has to consider the effect of the thermal heat bath provided by the fluid, as well as the nonzero size of the particles. In continuum theory, both aspects are taken into account by the presence of the (local) term ∝∇p(ρ) in eqn (5). Within BD simulations, the nonzero particle size is accounted for by short-ranged repulsive forces between the colloids. We use the cutoff and shifted repulsive part of the Lennard–Jones-potential (the so-called soft WCA potential, as used in ref. 12). Temperature enters by adding a stochastic noise term to the equations of motion of the particles. Hence, within BD one integrates the corresponding overdamped Langevin equation.
Thus, our BD simulations incorporate two different methods for the computation of the forces: the particle-mesh method for the long-ranged capillary forces and the direct summation of short-ranged repulsive forces. It would be even more convenient, if the particle-mesh method could be extended towards the short-ranged forces. Such an approach has been used in ref. 19 for describing the very dilute intergalactic medium. The same idea can be employed for eqn (9) because the forces ∝∇(μ − w) can easily be calculated for the discretized density grid. Since the fluctuations, giving rise to the noise present in BD simulations, are now also incorporated within a mean field approximation, this method describes the dynamical evolution of the discretized density according to an initial condition for the density field set by the distribution of particles at time zero. The evolution of the ensemble-averaged density field is obtained by averaging over initial conditions, i.e., the initial distributions of particles. In that manner, the obtained averaged evolution corresponds to the solution of the 2D DDFT defined by the evolution equation (11). We call it particle based, because in every time step one discretizes the density, i.e., one assigns all particles to points on the grid and calculates the forces ∇(μ − w) on the grid. Then, instead of integrating eqn (9) one interpolates these forces back to the positions of the particles which they occupied before they were assigned to grid points, and integrates their deterministic equations of motion. The next step, which is to discretize the density at time t + Δt, completes the evolution of the density as the basic quantity of our analysis. As has been pointed out in ref. 19, in comparison with the standard particle-mesh method, this discretization and integration scheme comes at the cost of an increased numerical noise at small scales of the order of the grid-spacing. However, for any physical observable noise we have studied so far, this increased numerical noise turned out to be not relevant.
4 Results from simulations
Using BD simulations and 2D DDFT as described in the previous section, we explore the “dynamical phase diagram” (Fig. 3) for the initial condition of a finite-sized patch of particles, arranged in a circular disk.** In order to locate in the Teff–κ plane of Fig. 3 the kind of evolution of a certain configuration, the value of the effective temperature (eqn (22)) is determined by the initial conditions inside the disk. To this end we recall the central result from the linear stability analysis in Subsection 2.2 and the perturbative analysis for the disk evolution in Subsection 2.3: when following an isothermal line†† from large capillary lengths λ (i.e., small cutoff parameters κ = L0/λ) down to λ = 2R, i.e., the value at which the range of the interaction equals the particle diameter, one first observes a collective collapse, followed by a regime where shock waves become visible and a spinodal decomposition stage for rather short-ranged attractions, i.e., λ/L0 ≪ 1 or κ ≫ 1.
We fix the effective temperature of the system by choosing a disk of radius L0 = 180R and setting the number of particles with radius R to N = 1804 so that ρ0 ≃ 574/L02. The associated Jeans' length‡‡ in units of L0 is K−1 = 0.018, corresponding to an isotherm containing the filled circles (a)–(c) shown in Fig. 3. For this isotherm we have carried out simulations at κ = 0.67 (collective collapse regime, τf = 1.01), κ = 4.0 (shock wave regime, τf = 1.45), and κ = 40.0 (spinodal regime, τf = 41.5). Fig. 5 shows the evolution of the radial density profiles of these three values of κ at various temperatures Teff. (In Fig. 5 the panels are ordered in the plane in correspondence to the locations of the points (a)–(f) in the “dynamical phase diagram” in Fig. 3.) The BD simulations are in line with the particle based DDFT (see Fig. 5(b)). For κ = 0.67 (point (a)) the evolution is dominated by the collective inbound motion, resembling almost the cold collapse scenario. For κ = 4.0 (point (b)) a pronounced shock wave is visible. The time scale for the collapse is stretched by a factor of ca. 4 compared with the time scale for the cold collapse. The fundamental mode, corresponding to the largest scales, still grows rather fast in this scenario: τf = 1.45 ≳ 1; therefore, this kind of evolution corresponds to the transition region between the collective collapse and the spinodal decomposition. In contrast, for the simulations with a rather large cutoff parameter κ = 40 (point (c)), associated with a data point in the regime of spinodal decomposition, quite a different picture emerges. As has been anticipated in Subsection 2.1, this limit corresponds to the diffusive regime with a comparatively short-ranged attractive force present (see eqn (16)). Inspecting the “dynamical phase diagram” (Fig. 3), one finds that point (c) is located in the top right corner. The amplitude for the growth of the fluctuations is rather small; for the fundamental mode it approaches zero. Since point (c) in the phase diagram is well above the line corresponding to τf = 41.5, the characteristic time of the fundamental mode will be even larger, leading to a very slow inbound motion of the density peak developing at the outer rim. In order to estimate the characteristic time for the collapse in this case, we rescale the density n in eqn (16) according to n′ = 2κn, which leads for a dilute system (Π(n) ≪ 1) to a rescaled characteristic time  . The collapse towards a close packed patch is therefore expected to occur at times t >
. The collapse towards a close packed patch is therefore expected to occur at times t > ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ′. This is in line with the observed slow inbound motion of the density peak. Additionally, at least one secondary peak in the inner part becomes visible for large times. These secondary peaks are much more pronounced if the effective temperature is lowered (see Fig. 5, panel (f)).
′. This is in line with the observed slow inbound motion of the density peak. Additionally, at least one secondary peak in the inner part becomes visible for large times. These secondary peaks are much more pronounced if the effective temperature is lowered (see Fig. 5, panel (f)).
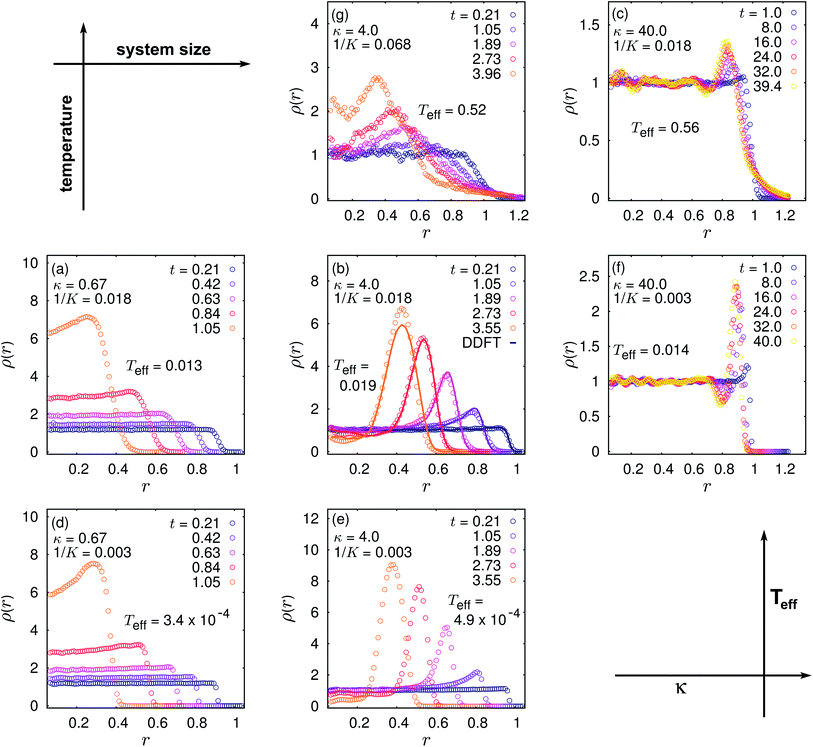 |
| | Fig. 5 Evolution of the radial density profiles corresponding to the points (a)–(g) in the “dynamical phase diagram” shown in Fig. 3. As indicated by the arrows, the reduced system size κ = L0/λ increases from left to right, the effective temperature Teff increases from the bottom panels to the top ones. Panels (a)–(c): density profiles of the effective temperatures Teff = 1.3 × 10−2 (a), Teff = 1.9 × 10−2 (b), and Teff = 0.56 (c) (corresponding Jeans' length: K−1 = 0.018) and for three values of the cutoff parameter κ = L0/λ. Panel (a): κ = 0.67, results of BD simulations (averaged over 120 runs), no clear signal of a shock wave is visible. Panel (b): κ = 4.0, comparison between 2D DDFT (colored lines, averaged over 120 runs) and the BD simulations (symbols). Panel (c): κ = 40.0, results of BD simulations (averaged over 500 runs). In contrast to (b), in (c) transient peaks resulting from clustering close to the center of the collapsing disk but separated from the shock wave become visible. Panels (d)–(f): radial density profiles at lower effective temperatures Teff = 3.4 × 10−4 (d), Teff = 4.9 × 10−4 (e), and Teff = 1.4 × 10−2 (f) (corresponding Jeans' length: K−1 = 0.003) for κ = 0.67, κ = 4.0, and κ = 40.0, respectively (BD, averaged over 500 runs). Panel (g): the same as above, at an effective temperature of Teff = 0.52 (corresponding Jeans' length: K−1 = 0.068) for κ = 4.0 (BD, averaged over 500 runs). An inbound traveling shock wave is observed clearly for τf ≳ 1, which is realized by the systems (b) and (e) (τf = 1.45). | |
Next we discuss an isotherm at a lower temperature which results in an effective temperature Teff about two orders of magnitude lower than the previous one (N = 3844, K−1 = 0.003); see the black, filled triangles (d), (e), and (f) in Fig. 3. (To this end the physical temperature does not need to be changed by two orders of magnitude. Such a shift can also be achieved by changing the initial number density or the capillary strength f via the particle size, because these quantities enter into the reduced pressure Π (eqn (6b)) and thus also into Jeans' length and into Teff.) In Fig. 5, panels (d), (e), and (f) show the radial evolution of the density, as in (a)–(c), for κ = 0.67 (point (d)), κ = 4.0 (point (e)), and κ = 40.0 (point (f)). In the latter two cases one observes peaks which are somewhat narrower than in (b) and (c), in line with the reduced pressure at lower temperatures. However, the qualitative behavior of the inbound motion is different. For κ = 4.0 the collapse is accelerated compared with point (b) (Fig. 5(b) corresponds to the same κ but to a higher Teff), and the position of the peaks is shifted to smaller radii. Inspecting the “dynamical phase diagram” (point (e) vs. point (b)), one finds that in the case of point (e) much more modes are unstable and grow considerably faster. Additionally, the value  of the maximum of 1/τ (see eqn (28)) almost reaches its upper limit
of the maximum of 1/τ (see eqn (28)) almost reaches its upper limit  . Both facts point towards a dynamics at large scales, which is accelerated compared with the setup at higher temperatures. However, the situation is different for κ = 40.0. Here for point (f), the overall inbound motion is slowed down even more than for point (c). (Fig. 5(c) corresponds to the same κ but to a higher Teff.) Again this may be explained on the basis of the outside panels (e) and (f) for 1/τ(k) in the “dynamical phase diagram”. In both cases, many modes are unstable; however, for point (f) the position of the maximum 1/τm of 1/τ(k) is shifted to large values of k, such that the nucleation of many small clusters with a narrow size distribution dominates the dynamics. The modes corresponding to large scales also grow, but less pronounced relative to the fastest growing modes at larger k. In this low temperature limit, the dynamics realizes a “bottom-up” scenario for the evolution of the system: The nucleation of small clusters happens at much shorter time scales compared to the overall collapse. This is in contrast to the “top-down” scenario for small values of κ or in the Newtonian limit. In this latter case, particularly at higher temperatures, the formation of small clusters is unfavorable, whereas the overall growth of modes corresponding to the large scales sweeps all particles to the final close packed patch. The inspection of panel (d) in Fig. 5 finally reveals the onset of the formation of a shock wave at low temperature and at late times. The corresponding point in the phase diagram (point (d)) lies well below the line F. Recalling that systems with identical fastest growing modes are located on the same thin red line in Fig. 3, we conclude that the fastest growing mode of point (d) is comparable to point (b). However, the value of κ = 0.67 is too small for the formation of a clearly visible shock wave. For that purpose, according to eqn (33) the formation point of the shock wave has to lie at somewhat larger values of κ, corresponding to a radial extent beyond the size of the close packed final cluster. This is the case for interaction ranges corresponding to κ ≳ 1.0.
. Both facts point towards a dynamics at large scales, which is accelerated compared with the setup at higher temperatures. However, the situation is different for κ = 40.0. Here for point (f), the overall inbound motion is slowed down even more than for point (c). (Fig. 5(c) corresponds to the same κ but to a higher Teff.) Again this may be explained on the basis of the outside panels (e) and (f) for 1/τ(k) in the “dynamical phase diagram”. In both cases, many modes are unstable; however, for point (f) the position of the maximum 1/τm of 1/τ(k) is shifted to large values of k, such that the nucleation of many small clusters with a narrow size distribution dominates the dynamics. The modes corresponding to large scales also grow, but less pronounced relative to the fastest growing modes at larger k. In this low temperature limit, the dynamics realizes a “bottom-up” scenario for the evolution of the system: The nucleation of small clusters happens at much shorter time scales compared to the overall collapse. This is in contrast to the “top-down” scenario for small values of κ or in the Newtonian limit. In this latter case, particularly at higher temperatures, the formation of small clusters is unfavorable, whereas the overall growth of modes corresponding to the large scales sweeps all particles to the final close packed patch. The inspection of panel (d) in Fig. 5 finally reveals the onset of the formation of a shock wave at low temperature and at late times. The corresponding point in the phase diagram (point (d)) lies well below the line F. Recalling that systems with identical fastest growing modes are located on the same thin red line in Fig. 3, we conclude that the fastest growing mode of point (d) is comparable to point (b). However, the value of κ = 0.67 is too small for the formation of a clearly visible shock wave. For that purpose, according to eqn (33) the formation point of the shock wave has to lie at somewhat larger values of κ, corresponding to a radial extent beyond the size of the close packed final cluster. This is the case for interaction ranges corresponding to κ ≳ 1.0.
The picture is completed by one more setup at the boundary between the gravitation-like, cold collapse and the transition regime marked by shock waves and in the vicinity of the line of stability (line S). This corresponds to point (g) in Fig. 3. The radial evolution is shown in panel (g) of Fig. 5 and shows the build-up and the evolution of the shock wave for κ = 4.0 at a rather high temperature (N = 121, K−1 = 0.097, Teff = 0.52). The peak is almost “molten” in the sense that it becomes rather broad whereas the inbound motion of the peak is again accelerated. Concerning the location in the “dynamical phase diagram”, point (g) is located well above the line τf = 1.45 and above the line F. It corresponds to a collective collapse at a high effective temperature. The overall inbound collective motion dominates the dynamics, whereas the high temperature disfavors the formation of smaller clusters. The evolution is slowed down significantly. (This is in contrast to point (c) for the same value of Teff but deeper in the spinodal regime (see Fig. 5(c)).) Note that point (g) is slightly outside the transition region where the shock wave is the dominant structure. The phenomenology is somewhat similar to the one for point (d) and the corresponding density evolution shown in panel (d) of Fig. 5 (κ = 0.67, N = 3844, K−1 = 0.003, Teff = 3.6 × 10−4). Here, with the onset of the shock wave becoming visible only at late times, the dynamics corresponds to an almost collective collapse. We note, however, that in this case the corresponding data point (d) is below the line F indicating that the transition region is not limited by a sharp borderline.
5 Experimental prospects for varying the capillary length
In actual experiments, a change of the capillary length 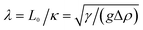 can be achieved by varying the surface tension γ ∝ λ2, e.g., by adding surfactants. In order to keep nonetheless both Jeans' time
can be achieved by varying the surface tension γ ∝ λ2, e.g., by adding surfactants. In order to keep nonetheless both Jeans' time ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = γ/(Γf2ρ0) and the amplitude of the capillary potential V0 = f2/(2πγ) (eqn (3)) constant, which allows the investigation of the isolated role of λ as a range parameter,
= γ/(Γf2ρ0) and the amplitude of the capillary potential V0 = f2/(2πγ) (eqn (3)) constant, which allows the investigation of the isolated role of λ as a range parameter, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) and V0 may be rescaled suitably by changing the particle radius R and the particle number density ρ0 of the monolayer, respectively. We assume that the external force f on the colloids is caused by their own weight, so that f ∝ R3. The rescaling
and V0 may be rescaled suitably by changing the particle radius R and the particle number density ρ0 of the monolayer, respectively. We assume that the external force f on the colloids is caused by their own weight, so that f ∝ R3. The rescaling| | | λ′ = ξλ, R′ = ψR, ρ′0 = ϕρ0, | (35) |
together with§§Γ−1 ∝ R leads to a rescaling of ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) and V0:
and V0:| | 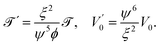 | (36) |
The requirements ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) =
= ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ′ and V0 = V′0 can be fulfilled by choosing
′ and V0 = V′0 can be fulfilled by choosing| |  | (37) |
Thus a change of λ by a factor ξ, while keeping ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) and V0 constant, requires moderate changes in ψ and ϕ of the particle radius R and of the density ρ0 of the system, respectively. Within a limited range, this appears to be experimentally accessible because it is state of the art to prepare colloids with designed radii, covering even several orders of magnitudes. Any change in density depends on the size of the colloids in the sense that close packing defines an upper limit R−2 for ρ0. Alternatively, one may allow for a moderate change of
and V0 constant, requires moderate changes in ψ and ϕ of the particle radius R and of the density ρ0 of the system, respectively. Within a limited range, this appears to be experimentally accessible because it is state of the art to prepare colloids with designed radii, covering even several orders of magnitudes. Any change in density depends on the size of the colloids in the sense that close packing defines an upper limit R−2 for ρ0. Alternatively, one may allow for a moderate change of  by keeping the density constant (ϕ = 1) and by using V′0 = V0, i.e., ψ6 = ξ2 (see eqn (36)). By expressing the time variable in terms of the corresponding characteristic time
by keeping the density constant (ϕ = 1) and by using V′0 = V0, i.e., ψ6 = ξ2 (see eqn (36)). By expressing the time variable in terms of the corresponding characteristic time ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , the various situations with fixed V0 are easily comparable. For the simulations presented throughout this work, we have only kept f2/γ constant and have ignored a possible dependence of f on λ(ref. 1). Therefore we have left both R and ρ0 unchanged. Further discussions on the values of the relevant scales for the instability (Jeans' time
, the various situations with fixed V0 are easily comparable. For the simulations presented throughout this work, we have only kept f2/γ constant and have ignored a possible dependence of f on λ(ref. 1). Therefore we have left both R and ρ0 unchanged. Further discussions on the values of the relevant scales for the instability (Jeans' time ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) and Jeans' length K−1) as a function of the system parameters applicable to various experimental situations can be found in ref. 10.
and Jeans' length K−1) as a function of the system parameters applicable to various experimental situations can be found in ref. 10.
6 Summary and conclusions
By studying a colloidal monolayer at a fluid interface and characterized by capillary attraction we have provided the theoretical foundation for a “dynamic phase diagram” of a paradigmatic system governed by long-ranged attractive interactions. The relevant parameters in this “dynamical phase diagram” are an effective temperature (proportional to the ratio of the energy of thermal motion and the capillary energy) and the range of the interaction relative to the characteristic size of the system. The latter parameter provides a smooth connection between infinitely ranged attractive interactions, which in the present case corresponds to 2D Newtonian gravity, and “short-ranged”, van-der-Waals-like attraction. In this diagram (Fig. 3) we find four regions of interest which we have explored via Brownian dynamics simulations and numerical computations within dynamic density functional theory. Above a critical temperature particles do not aggregate in spite of the attraction. Below this temperature we have identified three dynamical regimes for clustering which, however, are not sharply demarcated. At interaction ranges much larger than the system size (“small system” limit), we have found collective evolution, a global collapse associated with the fast growth of the spatially most extended modes, analogous to gravitational collapse. For interaction ranges much smaller than the system size (“large system” limit), the dynamics is dominated by local clustering analogous to spinodal decomposition; the nucleation of small clusters is overlaid by a rather slow global dynamics, with a large separation of time scales. In between we have predicted theoretically and have observed in simulations a transition region. For a finite-sized, disk-shaped distribution the dynamics is characterized by an inbound traveling shock wave. For a spatially homogeneous distribution with periodic boundary conditions, this transition region reveals itself in that observables (such as the total number of clusters) exhibit the onset of deviations in their temporal evolution from that valid for systems with infinitely ranged interactions.12
Appendix
A Cold collapse solution and perturbation theory
A.1 Lagrangian coordinates.
Here we recall briefly the Lagrangian formalism (see, e.g., ref. 20) and introduce the notation to be used throughout the Appendix. The key ingredient of the Lagrangian formalism is the Lagrangian trajectory field of volume elements, rL(x, t), defined physically as the position r at time t of that volume element which was at position x initially (i.e., at time t = 0); x is called the Lagrangian coordinate of the volume element. This field defines a mapwhich reduces to the identity at the initial time:
This map is assumed to be invertible, i.e., the trajectories of different volume elements do not cross each other.¶¶ The trajectory field allows one to express any other field as a function of the Lagrangian coordinates x and to introduce the Lagrangian fields for the density (nL), the long-ranged capillary potential (wL), the reduced pressure (ΠL), and the corresponding chemical potential (μL):
| | | nL(x, t) := n(r = rL(x, t), t), | (40a) |
| | | wL(x, t) := w(r = rL(x, t), t), | (40b) |
| | | ΠL(x, t) := Π(n = nL(x, t)), | (40c) |
| | | μL(x, t) := μ(n = nL(x, t)). | (40d) |
(We shall systematically use the subindex L in order to indicate that the corresponding field must be understood as a Lagrangian field,
i.e., as a function of
x and
t, whenever the same field has been already defined in Eulerian coordinates
r.) In general, Lagrangian and Eulerian fields will only coincide at the initial time. As explained below, the equations for the density evolution (
eqn (7)) can be transformed into the following equations for the Lagrangian fields:
| | ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) (x, t) := (∇xrL)−1, (x, t) := (∇xrL)−1, | (41a) |
| | 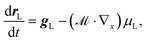 | (41b) |
| | nL = n0|det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) |, |, | (41c) |
| | gL := (![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ·∇x)wL, ·∇x)wL, | (41d) |
| | (![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ·∇x)·gL = −nL + κ2wL. ·∇x)·gL = −nL + κ2wL. | (41e) |
This is a complete set of equations for the determination of the trajectory field
rL(
x,
t) and all the other fields. ∇
x denotes the nabla operator with respect to the Lagrangian coordinate
x, while we use the customary notation d/d
t to indicate the Lagrangian time derivative,
i.e., derivative at fixed
x. The relationship with the Eulerian time derivative is a direct consequence of the definitions (
eqn (40)) of the Lagrangian fields:
| |  | (42) |
The dyadic product
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) −1
−1(
x,
t) is the Jacobian matrix of the map
x ↦
r,
i.e., (
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) −1
−1)
ij = ∂
rj/∂
xi. With this matrix, the transformation of the nabla operator ∇
x is given by
| | ∇ = ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) (x, t)·∇x. (x, t)·∇x. | (43) |
(The central dot · denotes a scalar product and, more generally, contraction of tensorial indices if the dyadic product
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif)
is involved.) In this manner,
eqn (41e) follows immediately from
eqn (7a) after introducing the acceleration field
g := ∇
w induced by capillary forces (see
eqn (41d)). One notices that
eqn (9) describes the advection of volume elements by the velocity field
g − ∇
μ (which is proportional to the acceleration in the overdamped approximation (see
eqn (4)) with the proportionality constant being one in terms of the dimensionless variables). Therefore, the dynamical equation obeyed by the trajectory of a volume element is
| |  | (44) |
which turns into
eqn (41b) upon transforming the nabla operators according to
eqn (43). Finally, since due to mass conservation the number of particles in a volume element, which is followed along its trajectory, is a dynamical invariant, one has
| | | n(r = rL(x, t), t)d2r = n(x, 0)d2x, | (45) |
and
eqn (41c) follows immediately because the Jacobian of the map
x ↦
r is
| |  | (46) |
Although
eqn (41c) is the formal solution of
eqn (7b), it will be useful to express
eqn (7b) (or
eqn (9)) in terms of Lagrangian fields:
| |  | (47) |
According to eqn (41c), a singularity in the density field, that is, a vanishing Jacobian (⇔det ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) = ∞) of the Lagrangian-to-Eulerian map x ↦ r, indicates that the map becomes multivalued. This shows up geometrically as the mutual crossing of the Lagrangian trajectories.20 This is prevented generically by the effect of the pressure, i.e., by the term involving μ. The “cold limit” (setting Π = 0 or, equivalently, setting μ → constant) is thus a singular limit because it reduces the order of the differential equation (see eqn (7) or (47)). It becomes a first-order partial differential equation and the Lagrangian trajectories coincide with the characteristic curves of eqn (7b): they are defined in the four-dimensional space (r1, r2, t, n) (with r = (r1, r2)) as solutions of the set of ordinary differential equations21
= ∞) of the Lagrangian-to-Eulerian map x ↦ r, indicates that the map becomes multivalued. This shows up geometrically as the mutual crossing of the Lagrangian trajectories.20 This is prevented generically by the effect of the pressure, i.e., by the term involving μ. The “cold limit” (setting Π = 0 or, equivalently, setting μ → constant) is thus a singular limit because it reduces the order of the differential equation (see eqn (7) or (47)). It becomes a first-order partial differential equation and the Lagrangian trajectories coincide with the characteristic curves of eqn (7b): they are defined in the four-dimensional space (r1, r2, t, n) (with r = (r1, r2)) as solutions of the set of ordinary differential equations21
| |  | (48) |
which precisely turns into
eqn (44) and
(47) upon using
t in order to parametrize the characteristic curves. The crossing of characteristic curves shows up in the solution as “a shock wave”. Therefore, the “cold limit” is not a uniformly valid approximation. Whenever any of these singularities appear, one should keep in mind that they are regularized physically by the effect of pressure.
A.2 Radially symmetric evolution.
Eqn (7) with the initial condition given by eqn (13) describes the collapse of the initial top-hat profile under the combined action of the capillary attraction and the gas pressure. The evolution preserves the radial symmetry of the initial configuration, so that the Lagrangian trajectories are radial and must have the form (x := |x|)with a certain amplitude function a(x, t). Geometrically, this describes the evolution of infinitesimally thin rings of matter with a radius ax. In this case one has the dyadic product (![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) is the identity 2nd-rank tensor)
is the identity 2nd-rank tensor)| |  | (50) |
where the last expression is the matrix representation of the dyadic in the basis {er = x/x, eφ} formed by the unit vectors for polar coordinates. Therefore, from eqn (41c) one obtains| |  | (51) |
with n0(x) given by eqn (13). (At the initial time one can use r and x interchangeably, see eqn (39).) This equation can be integrated rendering| |  | (52) |
where the integration constant A(t) controls the shape of the trajectories near the origin so that| |  | (53) |
because the density field nL(ξ, t) must be smooth at ξ = 0 before any singularity arises. Since the origin remains fixed during the collapse,  , one must take A(t) ≡ 0 and
, one must take A(t) ≡ 0 and| |  | (54) |
A.2.1 Newtonian, cold limit.
If both κ and Π vanish, the evolution reduces to the collapse of the disk under its own “gravitational” attraction, for which an analytically exact solution has been found (see, e.g., ref. 10 and 18). In this case eqn (47) reduces to| |  | (55) |
so that for a radially symmetric profile eqn (54) results in| |  | (56) |
(See also Appendix C in ref. 10 for the radially symmetric evolution in the Newtonian, cold limit.) For the initial condition in eqn (13) this gives| |  | (57) |
and| |  | (58) |
We note that the Lagrangian trajectories are defined even in the vacuum region (x > 1). There they describe the trajectories of test particles in the sense of field theory, i.e., of a dilute particle distribution which reacts to the force field without perturbing it. One can also compute the “gravitational” field wL(x, t) as the solution of eqn (41e), which reduces to ∇x2wL = a2(x, t)nL and has the solution| |  | (59) |
where C(t) is a, possibly time-dependent, additive constant. (The value of the field in the vacuum region x > 1 will not be relevant for our purposes.) Finally, the Eulerian density field can be obtained straightforwardly from eqn (40):| |  | (60) |
Therefore, the top-hat profile collapses without deformation and reaches an infinite density at time t = 1, when all rings of matter reach simultaneously the center. (This is an example in which the singularity is regularized by the gas pressure; the proper description of the later stages of the collapse must take into account the term Π in eqn (7b).) This homogeneous collapse is the counterpart to the cosmological scenario of a homogeneously contracting universe; the simultaneous collapse at the center would correspond to the “big crunch”.
A.2.2 Cold limit and κ ≠ 0 – a perturbative approach.
Here we first consider the cold limit, Π → 0, and investigate the effect of a non-vanishing value of κ. Eqn (47) is now| |  | (61) |
and cannot be solved exactly because of the dependence of wL on nL. However, one can study the solution perturbatively in the two opposite limits of “small systems” (κ ≪ 1) and “large systems” (κ ≫ 1). The idea is to solve the approximate equation| |  | (62) |
inside the disk, |x| ≤ 1, where ŵL and ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L are the fields evaluated in a reference solution, i.e., the unperturbed evolution, which depends on the limit one studies and will be specified below in each case. The solution of this equation inside the disk for the initial condition in eqn (13) is
L are the fields evaluated in a reference solution, i.e., the unperturbed evolution, which depends on the limit one studies and will be specified below in each case. The solution of this equation inside the disk for the initial condition in eqn (13) is| |  | (63) |
The evolution is completely determined if eqn (54) is used to calculate the perturbed radial trajectories:| |  | (64) |
The explicit dependence of both nL and a on x implies that, unlike in the Newtonian limit, the initial top-hat profile will deform during the evolution and an inhomogeneous density field will develop inside the collapsing disk. In particular, a singularity in the density field can emerge earlier than the global collapse at the center. The time ts(x) for the singularity at which the density of the matter ring, which started at x, diverges follows from eqn (63) and is given implicitly by
• Small systems, κ ≪ 1. In this limit the reference, unperturbed state is the Newtonian, cold limit computed previously with the fields ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L(x, t) and ŵL(x, t) given by eqn (58) and (59), respectively:
L(x, t) and ŵL(x, t) given by eqn (58) and (59), respectively:
| | 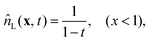 | (66a) |
| | 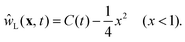 | (66b) |
However, the value of
C(
t), which is irrelevant in the Newtonian limit, must be determined as a function of
κ because the original
eqn (7a) is not invariant under a shift by a constant in the “potential”
w. The solution of
eqn (7a) with the boundary conditions given in
eqn (12) and for the Eulerian top-hat profile in
eqn (60) is given exactly as
| |  | (67) |
so that
| | 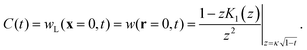 | (68) |
Expanding Bessel's function for
κ → 0 one finally obtains
| |  | (69) |
(
γe = 05772… is the Euler–Mascheroni constant). With this result, the density evolves according to
eqn (63) and
(64) in terms of the function
| |  | (70) |
which is obtained by inserting
eqn (66) and
(69) into the definitions in
eqn (63) and
(62). We note that the ratio
ŵL/
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L
L vanishes in time for
t → 1, so that the approximation leading to
eqn (62) is uniformly valid in time: if the term
κ2ŵL/
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L
L is a perturbation at the initial time, it will consistently remain so up to the collapse at time
t = 1.
As stated before, the emergence of a singularity is a generic outcome of the model equation (61). The time ts given implicitly by eqn (65) approaches 1 as κ → 0 (corresponding to the simultaneous collapse of all rings at the center), so that one can compute the time for the occurrence of the singularity consistently within the perturbation theory as
| |  | (71) |
after evaluating the integral in
eqn (70) at
t = 1. The physically meaningful time is the earliest one, which marks the appearance of the first shock wave and the limit of validity of the cold approximation. This earliest time corresponds to
x = 1,
i.e., the outer rim of the disk, so that the emergence of the shock wave occurs at the time
| |  | (72) |
The position of appearance of this shock wave is given by the outer rim of the disk:
| |  | (73) |
to the lowest order in
κ according to
eqn (64).
Fig. 4(a) shows an example of the density profile evolving according to this perturbative calculation.
• Large systems, κ ≫ 1. In this limit the reference state, which enters into eqn (62)via b(x, t), is the initial configuration,
| | ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L(x, t) = n0(x) = 1, (x < 1), L(x, t) = n0(x) = 1, (x < 1), | (74a) |
| |  | (74b) |
because d
nL/d
t can be neglected due to
eqn (15),
(61), and
(62). This simply indicates that the evolution proceeds over a time scale much larger than Jeans' time. The only exception is the behavior near the rim, where the discontinuity in the initial density renders the approximation given by
eqn (15) invalid. To be more specific, one can solve
eqn (7a) for the initial condition for
n as given by
eqn (13):
| |  | (75) |
Since Lagrangian and Eulerian coordinates coincide at the initial time (see
eqn (39)), one can use this result in
eqn (62) for
b(
x,
t) and obtain, with the additional approximation of large
κ,
| |  | (76) |
inside the disk, so that
B(
x,
t) =
tb(
x,
t) in the perturbative solutions (
eqn (63) and
(64)). As in the previous case, a singularity appears at a time
ts given by
eqn (65); in this case
| |  | (77) |
indicating the occurrence of two widely separated time scales in the evolution: one very slow compared with Jeans' time strictly inside the disk,
x < 1, and a fast one at the rim,
x = 1, where the shock wave,
i.e., the earliest singularity, forms at a time
tsw ≈ 2 − 1/
κ (compare with
eqn (72)). Nevertheless, in both cases the radial displacement given by
eqn (64) is very small,
| |  | (78) |
so that the physically meaningful singularity at the rim has a position
rsw =
a(1,
tsw) ≈ 1 − 1/
κ.
Fig. 4(b) illustrates the evolution of the density profile according to this perturbative calculation. Formally speaking, for points with
x < 1 the approximation in
eqn (76) is a short-time expansion with respect to the time scale of evolution (see
eqn (77)). Since this scale is much larger than Jeans' time, the approximation is also valid for describing the evolution on Jeans' time scale.
In summary, a nonzero value of κ induces a deformation of the initial top-hat profile by forming an enhanced density peak at the outer rim. For any value of κ the time scale for forming the singularity is of the order of Jeans' time, but the radial position of the peak depends strongly on the value of κ. The singularity eventually evolves into a shock wave when the effect of pressure becomes relevant locally.
A.2.3 “Hot” effects (Π ≠ 0).
Here we add a few remarks concerning the effect of the pressure Π in eqn (7b) on the radial evolution. Generically, the cold limit Π → 0 is singular because Π is associated with the highest order of the spatial derivatives in eqn (7b), so that one cannot neglect the term ∇Π uniformly throughout the disk. There are two particular aspects for which the effect of Π is relevant, that is the jump of the initial density at the outer rim of the disk and the formation of the shock wave, because both features are associated with the formal behavior ∇Π → ∞.
The initial discontinuity at r = 1 (see eqn (13)) implies that locally the early stages of the evolution will be dominated by the regularizing effect of the pressure, no matter how small Π is. In order to be specific we consider the ideal gas approximation, Π = εn, in which the small parameter ε → 0 can be identified with a dimensionless temperature (see eqn (6b)). The very early evolution of the density discontinuity can be described by neglecting locally any other force but pressure, so that in Eulerian coordinates
| |  | (79) |
In order to analyze the effect of pressure we introduce a new independent variable
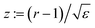
(centered at the initial density jump and rescaled in proportion to the, as it will turn out, thickness of the regularized discontinuity). This simplifies the equation as
ε → 0 at finite values of
z (
i.e., one effectively neglects the curvature of the regularized discontinuity and approximates it locally by a straight line):
| |  | (80) |
Expressed in terms of the original variables, the solution is given by the error function:
| |  | (81) |
This represents a regularized jump discontinuity or kink of thickness

. One can use this solution in order to determine self-consistently the time
tp beyond which the contribution of the pressure term no longer dominates
eqn (7b) even near
r = 1 compared with the term ∇·(
n∇
w), which is initially of order unity in terms of dimensionless quantities:
| |  | (82) |
The fact that this time is independent of
ε means that the regularization of the initial discontinuity takes a small but finite fraction of the total time of collapse in the Newtonian limit, which is of order 1 (see Subsection A.2.1 and
Fig. 4). However, this effect is spatially localized because the thickness of the resulting kink (
eqn (81)) vanishes as
ε → 0.
In the same manner, when a shock wave appears the density gradients can become so large that the effect of a small pressure eventually dominates the evolution in the localized regions of large gradients. This is the hallmark of the formation of a moving boundary layer. The involved mathematical analysis of this phenomenon is beyond the scope of the present study; here we confine our effort to the insight that this mechanism provides a qualitative explanation of the regularization of shock waves as observed in simulations.
A.3 Non-radially symmetric perturbations.
We now explore the robustness of the radially symmetric evolution against small perturbations of the initial radial symmetry. In this respect the ultimate goal is a generalization of the stability analysis as already carried out for the static (i.e., time-independent) homogeneous background (see Subsection 2.2). However, the mathematical problem is substantially more complicated, given that the unperturbed state, i.e., the radially symmetric density profile studied in the previous sections, is neither static nor homogeneous. Lagrangian perturbation theory has proved to be successful in the study of cosmological structure formation in an expanding homogeneous universe20,22 and, as it will turn out below, it is also helpful for the present problem. But, compared to applications in cosmology, progress is limited due to two difficulties: (i) the presence of the initial inhomogeneity at the boundary of the disk, and (ii) corrections to the Newtonian limit. Therefore, here we can address the full stability analysis only partially.
A.3.1 Newtonian, cold limit.
We first consider the exact solution in eqn (55) specialized to an initial density distribution of the form| |  | (83) |
i.e., a perturbation of the top-hat profile given by eqn (13). One can distinguish two cases.
(1) For perturbations inside the disk (x < 1) one has
| |  | (84) |
and a density singularity arises at the time
ts(
x) = [1 + δ
n0(
x)]
−1. Therefore any local overdensity (δ
n0 > 0) will grow faster and collapse earlier than the disk as a whole. This is the counterpart of the so-called “fragmentation instability” of a collapsing spherical cloud in astrophysics.
23,24
(2) For perturbations outside the disk (x > 1), representing in particular deviations from the circular shape of the initial disk, one has
| |  | (85) |
and a density singularity arises at the time
ts(
x) = 1/δ
n0(
x). For small perturbations (0 < δ
n0 ≪ 1), this time is larger than the time of collapse of the disk.
We emphasize that these results are exact, which is a peculiarity of the overdamped dynamics. In the astrophysical counterpart of this problem, the relevance of inertia prevents one from finding a closed equation for the density field analogous to eqn (55) and thus it is unavoidable to resort to perturbation theory. Nevertheless, the problem is not fully solved until the Lagrangian-to-Eulerian map rL(x, t) has been computed. Since this cannot be done exactly it is useful to apply Lagrangian perturbation theory. To this end, one defines a perturbation
| | δrL(r, t) := rL(r, t) − ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) L(x, t), L(x, t), | (86) |
of the trajectory, where the hat over a symbol denotes the reference, unperturbed evolution. The initial condition
holds by definition of the Lagrangian map (see
eqn (39)). Likewise, one defines perturbations of the Lagrangian fields as
| | δnL(x, t) := nL(x, t) − ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L(x, t), L(x, t), | (88) |
and similarly for δ
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif)
, δ
gL, δ
wL, and δ
μL.
Eqn (41) can be linearized with respect to the small perturbations:
||||| |  | (89a) |
| | 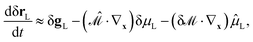 | (89b) |
| |  | (89c) |
| |  | (89d) |
| |  | (89e) |
| |  | (89f) |
where
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) ′L
′L := d
μ/d
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L
L,
![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) ′L
′L := d
Π/d
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L
L, δ
n0(
x) := δ
nL(
x, 0) represents the initial density perturbation, and
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0
0(
x) :=
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L
L(
x, 0) is the initial unperturbed density. These equations simplify significantly when specialized to the perturbed evolution of a top-hat profile in the Newtonian, cold limit, which amounts to setting
κ → 0,
μL → 0, and, restricting attention to the interior of the disk (
x < 1),
| |  | (90) |
with

(see
eqn (50),
(58) and
(59)). Under these conditions one obtains
| |  | (91a) |
| |  | (91b) |
| |  | (91c) |
| |  | (91d) |
| |  | (91e) |
In order to proceed one introduces the auxiliary field
| |  | (92) |
which can be viewed as a potential in Lagrangian coordinates: ∇
xϕL =
âδ
gL + δ
rL/(2
â).
Eqn (91b) and
(91d) reduce to
| |  | (93a) |
and
| |  | (93b) |
from which one obtains
***| |  | (94a) |
and
| |  | (94b) |
These equations can be integrated with the initial condition given in
eqn (87):
| | | ∇x × δrL(x, t) = â(t)∇x × δrL(x, t = 0) = 0, | (95a) |
| |  | (95b) |
These equations indicate that the mass clusters at the initially overdense regions (δ
n0 > 0; note that 1 −
â2 ≥ 0) while, consistently, the underdense regions (δ
n0 < 0) get depleted. Actually, the perturbations of the trajectories are parallel to the gravitational field generated by the initial density perturbation. This follows from the form of
eqn (95): the time dependence induced by
â(
t) can be factored out by a simple rescaling of the perturbation δ
rL, and the resulting equations are formally the field equations for the Newtonian gravitational field generated by a mass distribution given by δ
n0(
x). This property is the counterpart of the so-called Zel'dovich approximation in the context of cosmological structure formation (see
ref. 25 and references therein).
A.3.2 Small-scale, central perturbations.
The theoretical analysis beyond the cold, Newtonian limit is hampered by the fact that even the evolution of the reference, unperturbed state cannot be obtained in closed form. However, by focusing on perturbations localized close to the center of the disk (“central perturbations”), one can neglect the influence of the boundary so that one can take advantage of the results presented in Subsection 2.2.
The simplest case is the limit of large system sizes, i.e., κ ≫ 1. As argued in Subsection A.2.2, in this case the time scale of disk collapse is much larger than Jeans' time and, as far as the central perturbations are concerned, one can approximate the disk as a time-independent homogeneous distribution, namely the initial one, and the analysis presented in Subsection 2.2 holds. Therefore, according to Fig. 3, the fastest growing modes are the ones on small spatial scales and they are characterized by time scales of the order of Jeans' time (barring the exceptional case Teff → 1), which is consistent with the underlying approximations.
In the opposite limit of small system sizes, i.e., κ ≪ 1, we can establish a connection with the results presented recently in ref. 17, which deals, in the present language, with the stability in the Newtonian limit (κ = 0) of an infinitely extended disk (i.e., no boundary is considered). In this case one can argue that for the central perturbations the evolution of the reference state is indistinguishable from the cold, Newtonian limit during a certain initial period of time, because we have demonstrated before that the effect of the disk boundary is localized and that it takes some time for it to propagate into the interior of the disk. Thus, at early times eqn (89) can be evaluated in the region x ≪ 1 by again using eqn (90):
| |  | (96a) |
| |  | (96b) |
(compare with
eqn (93)). Furthermore, in order to be consistent with this approximation one has to neglect the term ∝
κ2 in
eqn (96b) because only perturbations with length scales much shorter than
κ−1 ≫ 1 are to be addressed. This leads to
| |  | (97a) |
and
| |  | (97b) |
(compare with
eqn (94)). Integration of
eqn (97a) implies ∇
x × δ
rL = 0 due to the initial condition given in
eqn (87) (compare with
eqn (95a)), while
eqn (97b) can be written in a more familiar form by introducing the so-called density contrast, defined as
| |  | (98) |
so that
| |  | (99) |
By introducing the Fourier transform in Lagrangian coordinates,
![[small delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e125.gif) L,k
L,k := ∫d
2xδ
L(
x)e
−ik·x, one obtains
| |  | (100) |
in terms of the time-dependent Jeans' length:
| |  | (101) |
This is the same expression as the one obtained for the stability of the homogenous state (see
eqn (19) and
(20)), restricted to modes with
k ≫ 1 ≫
κ (
i.e., valid only for perturbations of small length scales near the center of the disk). The only difference is the explicit time dependence of
K introduced by the background density
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L
L(
t). For realistic equations of state,
e.g., for hard disks, Jeans' length will decrease in time and in
Fig. 3 the effective state of the system for these “central perturbations” would describe a trajectory of steadily increasing
Teff ∝
K−2(
t). Thus, there is an increasing number of modes at small scales for which the effect of pressure will counteract the fragmentation instability. The solutions of
eqn (100) have been studied recently by Chavanis
17 for the particular choice
Π(
n) ∝
nα as a function of the polytropic index
α. The main conclusion follows from evaluating the time-dependent Jeans' length (see
eqn (101)),
K2(
t) ∝
â2(α−1), so that the amplitude of an initially unstable mode (
k <
K(
t = 0)) will eventually die out after a certain time (
k >
K(
t)) only if
α > 1 (corresponding to the critical index
γ4/3 introduced in
ref. 17 for the spatial dimension
d = 2)
†††.
Acknowledgements
J.B. thanks the German Research Foundation (DFG) for the financial support through the Collaborative Research Center (SFB-TR6) “Colloids in External Fields” Project N01. A.D. acknowledges support from the Spanish Government through Grants AIB2010DE-00263 and FIS2011-24460 (partially financed by FEDER funds).
References
- M. Oettel and S. Dietrich, Langmuir, 2008, 24, 1425 CrossRef CAS PubMed.
-
A. Domínguez, Capillary Forces between Colloidal Particles at Fluid Interfaces, in Structure and Functional Properties of Colloidal Systems, ed. R. Hidalgo-Alvarez, CRC Press, Boca Raton, FL, 2010, p. 31 Search PubMed.
- K. D. Danov and P. A. Kralchevsky, Adv. Colloid Interface Sci., 2010, 154, 91 CrossRef CAS PubMed.
- L. Botto, E. P. Lewandowski, M. Cavallaro Jr and K. J. Stebe, Soft Matter, 2012, 8, 9957 RSC.
- M. Brunner, C. Bechinger, W. Strepp, V. Lobaskin and H. H. von Grünberg, Europhys. Lett., 2002, 58, 926 CrossRef CAS.
- A. Campa, T. Dauxois and S. Ruffo, Phys. Rep., 2009, 480, 57 CrossRef CAS PubMed.
- E. Keller and L. A. Segel, J. Theor. Biol., 1970, 26, 399 CrossRef CAS.
- P.-H. Chavanis and C. Sire, Phys. A, 2008, 387, 4033 CrossRef PubMed.
- P.-H. Chavanis, Phys. A, 2011, 390, 1546 CrossRef CAS PubMed.
- A. Domínguez, M. Oettel and S. Dietrich, Phys. Rev. E, 2010, 82, 011402 CrossRef.
- J. Bleibel, S. Dietrich, A. Domínguez and M. Oettel, Phys. Rev. Lett., 2011, 107, 128302 CrossRef CAS.
- J. Bleibel, A. Domínguez, M. Oettel and S. Dietrich, Eur. Phys. J. E., 2011, 34, 125 CrossRef CAS PubMed.
- M. Oettel, A. Domínguez and S. Dietrich, Phys. Rev. E, 2005, 71, 051401 CrossRef CAS.
- A. Domínguez, M. Oettel and S. Dietrich, J. Chem. Phys., 2008, 128, 114904 CrossRef PubMed.
- J. Bleibel, A. Dominguez, F. Günther, J. Harting and M. Oettel, Soft Matter, 2014 10.1039/c3sm53043d.
- U. M. B. Marconi and P. Tarazona, J. Chem. Phys., 1999, 110, 8032 CrossRef CAS PubMed.
- P.-H. Chavanis, Phys. Rev. E, 2011, 84, 031101 CrossRef.
- P.-H. Chavanis and C. Sire, Phys. Rev. E, 2011, 83, 031131 CrossRef.
- N. Y. Gnedin and L. Hui, Mon. Not. R. Astron. Soc., 1998, 296, 44 Search PubMed.
-
T. Buchert, Lagrangian Perturbation Approach to the Formation of Large-Scale Structure, in Proceedings of the International School of Physics “Enrico Fermi”, ed. S. Bonometto, J. R. Primack and A. Provenzale, IOS, Amsterdam, 1997, vol. 132, p. 543; see also arXiv:astro-ph/9509005 Search PubMed.
-
R. Courant and D. Hilbert, Methods of Mathematical Physics, Wiley, New York, 1989, vol. II Search PubMed.
- S. Adler and T. Buchert, Astron. Astrophys., 1999, 343, 317 CAS.
- C. Hunter, Astrophys. J., 1962, 136, 594 CrossRef.
- S. J. Aarseth, D. N. C. Lin and J. C. B. Papaloizou, Astrophys. J., 1988, 324, 288 CrossRef PubMed.
- V. Sahni and P. Coles, Phys. Rep., 1995, 262, 1 CrossRef.
Footnotes |
| † In the absence of an external force, the dominant contribution is the “capillary quadrupole”, which is related to deviations from the spherical symmetry of the particles. See, e.g., ref. 4 for a recent review. |
| ‡ In this regard, we briefly remark on the possibilities offered by the technique of optical tweezers. They provide effective walls for the colloidal particles (see, e.g., ref. 5) but do not alter the interface, so that the system size is controllable without affecting the capillary forces acting on the particles. This is unlike the more direct method of confinement by means of physical walls, which may induce an undesired interfacial curvature or “external” capillary forces. |
| § This can be justified for dilute systems (see ref. 10 and 12). Nevertheless, recent results11,15 provide evidence that the main effect of the long-ranged hydrodynamic interaction on the dynamics of the capillary collapse consists of a reduction of the time scales, without altering the qualitative picture which we present here. |
| ¶ The additive function of only temperature is irrelevant for our present purposes, given that the system evolves under isothermal conditions. |
|| The fundamental mode can actually still be the fastest growing one in the region even below this line but above the line corresponding to the next mode,  . However, this is irrelevant for our purposes because the borders separating the different “regimes of instability” are not sharp anyhow. . However, this is irrelevant for our purposes because the borders separating the different “regimes of instability” are not sharp anyhow. |
| ** In order to minimize the effect due to periodic images of the disk within the particle-mesh method, we use a large simulation box with side length L = 800R ≈ 4.4L0, such that the disk is surrounded by empty space and therefore is substantially separated from its images. For the largest capillary length under consideration (λ = 1.5L0), the distance between the rim of the disk and its nearest periodic image is given by 3.4L0 ≈ 2.2λ. |
| †† We recall that the physical temperature T enters Jeans' length via K−1 = (dΠ/dn)1/2. Thus for the repulsive interaction taken to be of the hard core type, one has K−1 ∝ T1/2. Since the effective temperature Teff used in Fig. 3 is given by Teff = [(2π)2 + κ2]/K2 (eqn (22)), in the double-logarithmic Teff–κ plane of Fig. 3 an isotherm is a line which is horizontal for small κ and crosses over to a line with slope 2 at large κ due to Teff ∝ κ2. |
‡‡ As discussed in ref. 12, we employ an ideal gas equation of state for the initial condition to determine Jeans' length according to  with f2/(2πγ) = 0.89kBT (see eqn (3); this numerical value corresponds to the choice1R = 10 μm) so that K−1 ≈ 0.42ρ0−1/2. with f2/(2πγ) = 0.89kBT (see eqn (3); this numerical value corresponds to the choice1R = 10 μm) so that K−1 ≈ 0.42ρ0−1/2. |
| §§ The mobility is usually given by Γ = 1/(6πηR) where η denotes the dynamic viscosity. For half immersed particles at an air–water interface, we use the approximation Γ = 1/(3πηR) instead.12 |
| ¶¶ If this would happen, the corresponding system of equations would cease to have a unique solution. In this case, physical arguments would be required in order to extend the time interval of validity of the equations. |
|||| Linearization of terms involving the matrix ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) is achieved by applying the identities ln is achieved by applying the identities ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) det det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) = tr = tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) and and  , where , where ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) is the identity matrix and is the identity matrix and ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) −1 = ∇xrL (eqn (41a)). −1 = ∇xrL (eqn (41a)). |
| *** The vector field δrL and ∇x consist of two components. Both can be extended to three-component vectors by adding a third (“vertical”) component taken to be zero. This way ∇x × δrL is well defined and its only nonzero component is in the “vertical” direction. Accordingly, eqn (94a) reduces to a single equation for the “vertical” component. |
| ††† As pointed out in ref. 17, this conclusion only holds provided the initial amplitude of the unstable mode is sufficiently small so that its growth and subsequent decay can be described by the linearized theory. If after a certain time the amplitude enters the nonlinear regime, the conclusion concerning the asymptotic stability is no longer reliable. |
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article , where γ is the surface tension of the interface, g is the acceleration of gravity, and Δρ is the mass density difference between the fluids on both sides of the interface. In typical experimental configurations the interparticle separation (∼micron) is much smaller than λ (∼millimeter), so that any given particle interacts simultaneously with a huge number of neighbors. Furthermore, at separations smaller than λ, the capillary attraction varies logarithmically and is formally analogous to two-dimensional (2D) Newtonian gravity. In these circumstances, the capillary interaction is equivalent to “screened 2D Newtonian gravity”, with a screening length λ much larger than any microscopic length scale. Therefore we call this interaction “long-ranged”. In this context the tunability of such a system is of special interest. The range of the interaction may in principle be varied by changing the capillary length, which is accessible via changes of the surface tension of the interface, e.g., due to the addition of surfactants. Additionally, the relevant ratios of the interaction range to other length scales of the system (most notably, the interparticle separation and the system size) can be easily altered also by changing these other lengths in experimental setups.‡ Likewise, the amplitude of the capillary monopole and, correspondingly, the strength of the interaction are controllable by means of the external force. Therefore, for micron-sized colloidal particles, such a monolayer can serve as a 2D model system for studying the influence of a “long-ranged” interaction as a function of its parametric characteristics.
, where γ is the surface tension of the interface, g is the acceleration of gravity, and Δρ is the mass density difference between the fluids on both sides of the interface. In typical experimental configurations the interparticle separation (∼micron) is much smaller than λ (∼millimeter), so that any given particle interacts simultaneously with a huge number of neighbors. Furthermore, at separations smaller than λ, the capillary attraction varies logarithmically and is formally analogous to two-dimensional (2D) Newtonian gravity. In these circumstances, the capillary interaction is equivalent to “screened 2D Newtonian gravity”, with a screening length λ much larger than any microscopic length scale. Therefore we call this interaction “long-ranged”. In this context the tunability of such a system is of special interest. The range of the interaction may in principle be varied by changing the capillary length, which is accessible via changes of the surface tension of the interface, e.g., due to the addition of surfactants. Additionally, the relevant ratios of the interaction range to other length scales of the system (most notably, the interparticle separation and the system size) can be easily altered also by changing these other lengths in experimental setups.‡ Likewise, the amplitude of the capillary monopole and, correspondingly, the strength of the interaction are controllable by means of the external force. Therefore, for micron-sized colloidal particles, such a monolayer can serve as a 2D model system for studying the influence of a “long-ranged” interaction as a function of its parametric characteristics.

![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ),
), ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ∈
∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2, is given by1,13
2, is given by1,13
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ) is the 2D particle number density field in the reference plane and γ is the surface tension. (The interfacial deformation for micron-sized particles is in the nm range, which justifies the linearized approximation.) This interfacial deformation gives rise to an in-plane capillary force described by the areal force density
) is the 2D particle number density field in the reference plane and γ is the surface tension. (The interfacial deformation for micron-sized particles is in the nm range, which justifies the linearized approximation.) This interfacial deformation gives rise to an in-plane capillary force described by the areal force density
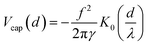
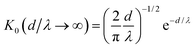 . In the opposite limit, d ≪ λ, this potential coincides with the Newtonian gravitational interaction in d = 2, K0(d/λ → 0) ∼ ln(λ/d), which is nonintegrable in the sense of statistical mechanics, i.e., it leads to a nonadditive (hyperextensive) internal energy. In view of this property and due to the wide separation of scales in colloidal systems, λ =
. In the opposite limit, d ≪ λ, this potential coincides with the Newtonian gravitational interaction in d = 2, K0(d/λ → 0) ∼ ln(λ/d), which is nonintegrable in the sense of statistical mechanics, i.e., it leads to a nonadditive (hyperextensive) internal energy. In view of this property and due to the wide separation of scales in colloidal systems, λ = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (mm) and R0 =
(mm) and R0 = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (μm), for the present purposes we call Vcap(d) a “long-ranged interaction”, as opposed to other interactions which will be called “short-ranged”.
(μm), for the present purposes we call Vcap(d) a “long-ranged interaction”, as opposed to other interactions which will be called “short-ranged”.
 , where the 2D pressure field p = p(ρ) is given by an appropriate equilibrium equation of state describing the macroscopic manifestation of the short-ranged forces. Therefore, the continuity equation for the particle number density is
, where the 2D pressure field p = p(ρ) is given by an appropriate equilibrium equation of state describing the macroscopic manifestation of the short-ranged forces. Therefore, the continuity equation for the particle number density is
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) := γ/(Γf2ρ0), which is the so-called Jeans' time associated with the initial homogeneous density ρ0.10 This allows us to form the following dimensionless variables and quantities:
:= γ/(Γf2ρ0), which is the so-called Jeans' time associated with the initial homogeneous density ρ0.10 This allows us to form the following dimensionless variables and quantities:


![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0b3.gif) γ/(f2ρ0L02) which is associated with the pressure via the Gibbs–Duhem relationship:¶
γ/(f2ρ0L02) which is associated with the pressure via the Gibbs–Duhem relationship:¶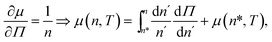

![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [n, w] (see ref. 10), such that
[n, w] (see ref. 10), such that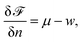







![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) .
.![[small delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e125.gif) k(t) =
k(t) = ![[small delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e125.gif) k(0)et/τ(k),
k(0)et/τ(k),![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) the inverse characteristic time for each mode k is given by
the inverse characteristic time for each mode k is given by


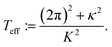




![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ) and τf = (1.01, 1.45, 41.5) (from left to right; the fundamental mode has the characteristic time 1.01
) and τf = (1.01, 1.45, 41.5) (from left to right; the fundamental mode has the characteristic time 1.01![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , 1.45
, 1.45![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , and 41.5
, and 41.5![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , respectively) are given by eqn (28) and (29), respectively. The lines for given values of τf ≳ 1 indicate the transition region. The black symbols (symbols of different shapes correspond to different Jeans' lengths) indicate the systems consisting of a finite circular initial patch of particles investigated via simulations and are discussed in Section 4. For the points (a)–(c), (e), and (f), the corresponding inverse characteristic times 1/τ(k) (as shown in Fig. 2, see eqn (20)) are shown in the side panels on the right with the discrete modes indicated by blue vertical lines. Note that the horizontal scales for k vary whereas the vertical scale always ranges from −0.1 < 1/τ < 1. The green horizontal line corresponds to 1/τ = 0 and the vertical black lines indicate the maxima of 1/τ(k).
, respectively) are given by eqn (28) and (29), respectively. The lines for given values of τf ≳ 1 indicate the transition region. The black symbols (symbols of different shapes correspond to different Jeans' lengths) indicate the systems consisting of a finite circular initial patch of particles investigated via simulations and are discussed in Section 4. For the points (a)–(c), (e), and (f), the corresponding inverse characteristic times 1/τ(k) (as shown in Fig. 2, see eqn (20)) are shown in the side panels on the right with the discrete modes indicated by blue vertical lines. Note that the horizontal scales for k vary whereas the vertical scale always ranges from −0.1 < 1/τ < 1. The green horizontal line corresponds to 1/τ = 0 and the vertical black lines indicate the maxima of 1/τ(k).

 is given by
is given by






 . The collapse towards a close packed patch is therefore expected to occur at times t >
. The collapse towards a close packed patch is therefore expected to occur at times t > ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ′. This is in line with the observed slow inbound motion of the density peak. Additionally, at least one secondary peak in the inner part becomes visible for large times. These secondary peaks are much more pronounced if the effective temperature is lowered (see Fig. 5, panel (f)).
′. This is in line with the observed slow inbound motion of the density peak. Additionally, at least one secondary peak in the inner part becomes visible for large times. These secondary peaks are much more pronounced if the effective temperature is lowered (see Fig. 5, panel (f)).
 of the maximum of 1/τ (see eqn (28)) almost reaches its upper limit
of the maximum of 1/τ (see eqn (28)) almost reaches its upper limit  . Both facts point towards a dynamics at large scales, which is accelerated compared with the setup at higher temperatures. However, the situation is different for κ = 40.0. Here for point (f), the overall inbound motion is slowed down even more than for point (c). (Fig. 5(c) corresponds to the same κ but to a higher Teff.) Again this may be explained on the basis of the outside panels (e) and (f) for 1/τ(k) in the “dynamical phase diagram”. In both cases, many modes are unstable; however, for point (f) the position of the maximum 1/τm of 1/τ(k) is shifted to large values of k, such that the nucleation of many small clusters with a narrow size distribution dominates the dynamics. The modes corresponding to large scales also grow, but less pronounced relative to the fastest growing modes at larger k. In this low temperature limit, the dynamics realizes a “bottom-up” scenario for the evolution of the system: The nucleation of small clusters happens at much shorter time scales compared to the overall collapse. This is in contrast to the “top-down” scenario for small values of κ or in the Newtonian limit. In this latter case, particularly at higher temperatures, the formation of small clusters is unfavorable, whereas the overall growth of modes corresponding to the large scales sweeps all particles to the final close packed patch. The inspection of panel (d) in Fig. 5 finally reveals the onset of the formation of a shock wave at low temperature and at late times. The corresponding point in the phase diagram (point (d)) lies well below the line F. Recalling that systems with identical fastest growing modes are located on the same thin red line in Fig. 3, we conclude that the fastest growing mode of point (d) is comparable to point (b). However, the value of κ = 0.67 is too small for the formation of a clearly visible shock wave. For that purpose, according to eqn (33) the formation point of the shock wave has to lie at somewhat larger values of κ, corresponding to a radial extent beyond the size of the close packed final cluster. This is the case for interaction ranges corresponding to κ ≳ 1.0.
. Both facts point towards a dynamics at large scales, which is accelerated compared with the setup at higher temperatures. However, the situation is different for κ = 40.0. Here for point (f), the overall inbound motion is slowed down even more than for point (c). (Fig. 5(c) corresponds to the same κ but to a higher Teff.) Again this may be explained on the basis of the outside panels (e) and (f) for 1/τ(k) in the “dynamical phase diagram”. In both cases, many modes are unstable; however, for point (f) the position of the maximum 1/τm of 1/τ(k) is shifted to large values of k, such that the nucleation of many small clusters with a narrow size distribution dominates the dynamics. The modes corresponding to large scales also grow, but less pronounced relative to the fastest growing modes at larger k. In this low temperature limit, the dynamics realizes a “bottom-up” scenario for the evolution of the system: The nucleation of small clusters happens at much shorter time scales compared to the overall collapse. This is in contrast to the “top-down” scenario for small values of κ or in the Newtonian limit. In this latter case, particularly at higher temperatures, the formation of small clusters is unfavorable, whereas the overall growth of modes corresponding to the large scales sweeps all particles to the final close packed patch. The inspection of panel (d) in Fig. 5 finally reveals the onset of the formation of a shock wave at low temperature and at late times. The corresponding point in the phase diagram (point (d)) lies well below the line F. Recalling that systems with identical fastest growing modes are located on the same thin red line in Fig. 3, we conclude that the fastest growing mode of point (d) is comparable to point (b). However, the value of κ = 0.67 is too small for the formation of a clearly visible shock wave. For that purpose, according to eqn (33) the formation point of the shock wave has to lie at somewhat larger values of κ, corresponding to a radial extent beyond the size of the close packed final cluster. This is the case for interaction ranges corresponding to κ ≳ 1.0.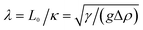 can be achieved by varying the surface tension γ ∝ λ2, e.g., by adding surfactants. In order to keep nonetheless both Jeans' time
can be achieved by varying the surface tension γ ∝ λ2, e.g., by adding surfactants. In order to keep nonetheless both Jeans' time ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = γ/(Γf2ρ0) and the amplitude of the capillary potential V0 = f2/(2πγ) (eqn (3)) constant, which allows the investigation of the isolated role of λ as a range parameter,
= γ/(Γf2ρ0) and the amplitude of the capillary potential V0 = f2/(2πγ) (eqn (3)) constant, which allows the investigation of the isolated role of λ as a range parameter, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) and V0 may be rescaled suitably by changing the particle radius R and the particle number density ρ0 of the monolayer, respectively. We assume that the external force f on the colloids is caused by their own weight, so that f ∝ R3. The rescaling
and V0 may be rescaled suitably by changing the particle radius R and the particle number density ρ0 of the monolayer, respectively. We assume that the external force f on the colloids is caused by their own weight, so that f ∝ R3. The rescaling![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) and V0:
and V0: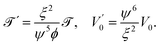
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) =
= ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ′ and V0 = V′0 can be fulfilled by choosing
′ and V0 = V′0 can be fulfilled by choosing
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) and V0 constant, requires moderate changes in ψ and ϕ of the particle radius R and of the density ρ0 of the system, respectively. Within a limited range, this appears to be experimentally accessible because it is state of the art to prepare colloids with designed radii, covering even several orders of magnitudes. Any change in density depends on the size of the colloids in the sense that close packing defines an upper limit R−2 for ρ0. Alternatively, one may allow for a moderate change of
and V0 constant, requires moderate changes in ψ and ϕ of the particle radius R and of the density ρ0 of the system, respectively. Within a limited range, this appears to be experimentally accessible because it is state of the art to prepare colloids with designed radii, covering even several orders of magnitudes. Any change in density depends on the size of the colloids in the sense that close packing defines an upper limit R−2 for ρ0. Alternatively, one may allow for a moderate change of  by keeping the density constant (ϕ = 1) and by using V′0 = V0, i.e., ψ6 = ξ2 (see eqn (36)). By expressing the time variable in terms of the corresponding characteristic time
by keeping the density constant (ϕ = 1) and by using V′0 = V0, i.e., ψ6 = ξ2 (see eqn (36)). By expressing the time variable in terms of the corresponding characteristic time ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , the various situations with fixed V0 are easily comparable. For the simulations presented throughout this work, we have only kept f2/γ constant and have ignored a possible dependence of f on λ(ref. 1). Therefore we have left both R and ρ0 unchanged. Further discussions on the values of the relevant scales for the instability (Jeans' time
, the various situations with fixed V0 are easily comparable. For the simulations presented throughout this work, we have only kept f2/γ constant and have ignored a possible dependence of f on λ(ref. 1). Therefore we have left both R and ρ0 unchanged. Further discussions on the values of the relevant scales for the instability (Jeans' time ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) and Jeans' length K−1) as a function of the system parameters applicable to various experimental situations can be found in ref. 10.
and Jeans' length K−1) as a function of the system parameters applicable to various experimental situations can be found in ref. 10.
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) (x, t) := (∇xrL)−1,
(x, t) := (∇xrL)−1,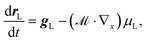
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) |,
|,![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ·∇x)wL,
·∇x)wL,![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) ·∇x)·gL = −nL + κ2wL.
·∇x)·gL = −nL + κ2wL.
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) −1(x, t) is the Jacobian matrix of the map x ↦ r, i.e., (
−1(x, t) is the Jacobian matrix of the map x ↦ r, i.e., (![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) −1)ij = ∂rj/∂xi. With this matrix, the transformation of the nabla operator ∇x is given by
−1)ij = ∂rj/∂xi. With this matrix, the transformation of the nabla operator ∇x is given by![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) (x, t)·∇x.
(x, t)·∇x.![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) is involved.) In this manner, eqn (41e) follows immediately from eqn (7a) after introducing the acceleration field g := ∇w induced by capillary forces (see eqn (41d)). One notices that eqn (9) describes the advection of volume elements by the velocity field g − ∇μ (which is proportional to the acceleration in the overdamped approximation (see eqn (4)) with the proportionality constant being one in terms of the dimensionless variables). Therefore, the dynamical equation obeyed by the trajectory of a volume element is
is involved.) In this manner, eqn (41e) follows immediately from eqn (7a) after introducing the acceleration field g := ∇w induced by capillary forces (see eqn (41d)). One notices that eqn (9) describes the advection of volume elements by the velocity field g − ∇μ (which is proportional to the acceleration in the overdamped approximation (see eqn (4)) with the proportionality constant being one in terms of the dimensionless variables). Therefore, the dynamical equation obeyed by the trajectory of a volume element is


![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) = ∞) of the Lagrangian-to-Eulerian map x ↦ r, indicates that the map becomes multivalued. This shows up geometrically as the mutual crossing of the Lagrangian trajectories.20 This is prevented generically by the effect of the pressure, i.e., by the term involving μ. The “cold limit” (setting Π = 0 or, equivalently, setting μ → constant) is thus a singular limit because it reduces the order of the differential equation (see eqn (7) or (47)). It becomes a first-order partial differential equation and the Lagrangian trajectories coincide with the characteristic curves of eqn (7b): they are defined in the four-dimensional space (r1, r2, t, n) (with r = (r1, r2)) as solutions of the set of ordinary differential equations21
= ∞) of the Lagrangian-to-Eulerian map x ↦ r, indicates that the map becomes multivalued. This shows up geometrically as the mutual crossing of the Lagrangian trajectories.20 This is prevented generically by the effect of the pressure, i.e., by the term involving μ. The “cold limit” (setting Π = 0 or, equivalently, setting μ → constant) is thus a singular limit because it reduces the order of the differential equation (see eqn (7) or (47)). It becomes a first-order partial differential equation and the Lagrangian trajectories coincide with the characteristic curves of eqn (7b): they are defined in the four-dimensional space (r1, r2, t, n) (with r = (r1, r2)) as solutions of the set of ordinary differential equations21
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) is the identity 2nd-rank tensor)
is the identity 2nd-rank tensor)



 , one must take A(t) ≡ 0 and
, one must take A(t) ≡ 0 and








![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L are the fields evaluated in a reference solution, i.e., the unperturbed evolution, which depends on the limit one studies and will be specified below in each case. The solution of this equation inside the disk for the initial condition in eqn (13) is
L are the fields evaluated in a reference solution, i.e., the unperturbed evolution, which depends on the limit one studies and will be specified below in each case. The solution of this equation inside the disk for the initial condition in eqn (13) is

![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L(x, t) and ŵL(x, t) given by eqn (58) and (59), respectively:
L(x, t) and ŵL(x, t) given by eqn (58) and (59), respectively: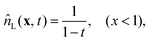
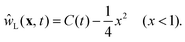

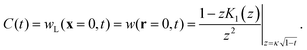


![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L vanishes in time for t → 1, so that the approximation leading to eqn (62) is uniformly valid in time: if the term κ2ŵL/
L vanishes in time for t → 1, so that the approximation leading to eqn (62) is uniformly valid in time: if the term κ2ŵL/![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L is a perturbation at the initial time, it will consistently remain so up to the collapse at time t = 1.
L is a perturbation at the initial time, it will consistently remain so up to the collapse at time t = 1.



![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L(x, t) = n0(x) = 1, (x < 1),
L(x, t) = n0(x) = 1, (x < 1),





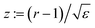 (centered at the initial density jump and rescaled in proportion to the, as it will turn out, thickness of the regularized discontinuity). This simplifies the equation as ε → 0 at finite values of z (i.e., one effectively neglects the curvature of the regularized discontinuity and approximates it locally by a straight line):
(centered at the initial density jump and rescaled in proportion to the, as it will turn out, thickness of the regularized discontinuity). This simplifies the equation as ε → 0 at finite values of z (i.e., one effectively neglects the curvature of the regularized discontinuity and approximates it locally by a straight line):

 . One can use this solution in order to determine self-consistently the time tp beyond which the contribution of the pressure term no longer dominates eqn (7b) even near r = 1 compared with the term ∇·(n∇w), which is initially of order unity in terms of dimensionless quantities:
. One can use this solution in order to determine self-consistently the time tp beyond which the contribution of the pressure term no longer dominates eqn (7b) even near r = 1 compared with the term ∇·(n∇w), which is initially of order unity in terms of dimensionless quantities:



![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) L(x, t),
L(x, t),![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L(x, t),
L(x, t),![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) , δgL, δwL, and δμL. Eqn (41) can be linearized with respect to the small perturbations:||||
, δgL, δwL, and δμL. Eqn (41) can be linearized with respect to the small perturbations:||||
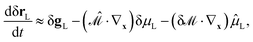




![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) ′L := dμ/d
′L := dμ/d![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L,
L, ![[capital Pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e106.gif) ′L := dΠ/d
′L := dΠ/d![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L, δn0(x) := δnL(x, 0) represents the initial density perturbation, and
L, δn0(x) := δnL(x, 0) represents the initial density perturbation, and ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0(x) :=
0(x) := ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L(x, 0) is the initial unperturbed density. These equations simplify significantly when specialized to the perturbed evolution of a top-hat profile in the Newtonian, cold limit, which amounts to setting κ → 0, μL → 0, and, restricting attention to the interior of the disk (x < 1),
L(x, 0) is the initial unperturbed density. These equations simplify significantly when specialized to the perturbed evolution of a top-hat profile in the Newtonian, cold limit, which amounts to setting κ → 0, μL → 0, and, restricting attention to the interior of the disk (x < 1),
 (see eqn (50), (58) and (59)). Under these conditions one obtains
(see eqn (50), (58) and (59)). Under these conditions one obtains
















![[small delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e125.gif) L,k := ∫d2xδL(x)e−ik·x, one obtains
L,k := ∫d2xδL(x)e−ik·x, one obtains

![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) L(t). For realistic equations of state, e.g., for hard disks, Jeans' length will decrease in time and in Fig. 3 the effective state of the system for these “central perturbations” would describe a trajectory of steadily increasing Teff ∝ K−2(t). Thus, there is an increasing number of modes at small scales for which the effect of pressure will counteract the fragmentation instability. The solutions of eqn (100) have been studied recently by Chavanis17 for the particular choice Π(n) ∝ nα as a function of the polytropic index α. The main conclusion follows from evaluating the time-dependent Jeans' length (see eqn (101)), K2(t) ∝ â2(α−1), so that the amplitude of an initially unstable mode (k < K(t = 0)) will eventually die out after a certain time (k > K(t)) only if α > 1 (corresponding to the critical index γ4/3 introduced in ref. 17 for the spatial dimension d = 2)†††.
L(t). For realistic equations of state, e.g., for hard disks, Jeans' length will decrease in time and in Fig. 3 the effective state of the system for these “central perturbations” would describe a trajectory of steadily increasing Teff ∝ K−2(t). Thus, there is an increasing number of modes at small scales for which the effect of pressure will counteract the fragmentation instability. The solutions of eqn (100) have been studied recently by Chavanis17 for the particular choice Π(n) ∝ nα as a function of the polytropic index α. The main conclusion follows from evaluating the time-dependent Jeans' length (see eqn (101)), K2(t) ∝ â2(α−1), so that the amplitude of an initially unstable mode (k < K(t = 0)) will eventually die out after a certain time (k > K(t)) only if α > 1 (corresponding to the critical index γ4/3 introduced in ref. 17 for the spatial dimension d = 2)†††.
 . However, this is irrelevant for our purposes because the borders separating the different “regimes of instability” are not sharp anyhow.
. However, this is irrelevant for our purposes because the borders separating the different “regimes of instability” are not sharp anyhow. with f2/(2πγ) = 0.89kBT (see eqn (3); this numerical value corresponds to the choice1R = 10 μm) so that K−1 ≈ 0.42ρ0−1/2.
with f2/(2πγ) = 0.89kBT (see eqn (3); this numerical value corresponds to the choice1R = 10 μm) so that K−1 ≈ 0.42ρ0−1/2.![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) is achieved by applying the identities ln
is achieved by applying the identities ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) det
det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) = tr
= tr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) and
and  , where
, where ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) is the identity matrix and
is the identity matrix and ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) −1 = ∇xrL (eqn (41a)).
−1 = ∇xrL (eqn (41a)).