 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Induced phagocytic particle uptake into a giant unilamellar vesicle
Andreas
Meinel
a,
Benjamin
Tränkle
a,
Winfried
Römer
bc and
Alexander
Rohrbach
*a
aDepartment of Microsystems Engineering (IMTEK), University of Freiburg, 79110 Freiburg, Germany. E-mail: rohrbach@imtek.de
bInstitute of Biology II, Albert-Ludwigs-University Freiburg, 79104 Freiburg, Germany
cBIOSS – Centre for Biological Signalling Studies, Albert-Ludwigs-University Freiburg, 79104 Freiburg, Germany
First published on 27th March 2014
Abstract
Phagocytosis, the uptake and ingestion of solid particles into living cells, is a central mechanism of our immune system. Due to the complexity of the uptake mechanism, the different forces involved in this process are only partly understood. Therefore the usage of a giant unilamellar vesicle (GUV) as the simplest biomimetic model for a cell allows one to investigate the influence of the lipid membrane on the energetics of the uptake process. Here, a photonic force microscope (PFM) is used to approach an optically trapped 1 μm latex bead to an immobilized GUV to finally insert the particle into the GUV. By analysing the mean displacement and the position fluctuations of the trapped particle during the uptake process in 3D with nanometre precision, we are able to record force and energy profiles, as well as changes in the viscous drag and the stiffness. After observing a global followed by a local deformation of the GUV, we measured uptake energies of 2000 kT to 5500 kT and uptake forces of 4 pN to 16 pN for Egg-PC GUVs with sizes of 18–26 μm and varying membrane tension. The measured energy profiles, which are compared to a Helfrich energy model for local and global deformation, show good coincidence with the theoretical results. Our proof-of-principle study opens the door to a large number of similar experiments with GUVs containing more biochemical components and complexity. This bottom-up strategy should allow for a better understanding of the physics of phagocytosis.
1. Introduction
Phagocytosis represents a central cellular mechanism in order to engulf particles into the cell membrane. Besides many approaches and studies investigating receptor mediated phagocytosis,1,2 only little is known about the bio-mechanical concepts used by cells to uptake particles such as bacteria, viruses, toxins or synthetic micro-containers.3–5 Particle uptake by zipper- or trigger-mechanisms involves actin reorganization as well as local membrane deformation.6–8 Although cell-mechanical concepts such as actin (de-)polymerization, myosin motor transport, membrane receptor clustering or filopodia activity are well-known,9 it is only partly clear which physical forces pull the particle to the inside of a cell. In particular, further insight is needed on how these forces are steered by bio-chemical factors such as various membrane proteins or by the ligands on the particle surface. If these forces remain too small, bacteria and toxins will not be internalized by the cell.An approach to analyse the relevant forces and to estimate the role of phagocytic key players is to reduce the complexity of the phagocytic system through using biomimetic systems. The simplest biomimetic variant is a giant unilamellar vesicle (GUV),10 where the chemical and mechanical properties of the spherical lipid bilayer membrane can be controlled in various manners.11–16 In order to engulf and internalize a particle, the spherical membrane of the GUV needs to be deformed significantly, as measured and modelled by several groups.8,17–22
Among various experimental techniques for GUV manipulation,10 optical tweezers are especially advantageous due to their ability to apply 3D forces between femto-Newtons23 and nano-Newtons24 without mechanical contact. In this way Dietrich et al.17 demonstrated that it is possible to ingest 7–18 μm large spheres into GUVs by using double beam optical tweezers. Later, effects of particle adhesion, diffusion, and coupling with GUVs have been studied with single beam optical tweezers.10 In combination with a fast 3D tracking system such as back-focal plane (BFP) interferometry the thermal position fluctuations of the trapped particle25,26 can be tracked nanometre precise at several 100 kHz – nearby living cells or in contact with them.27 Using BFP-interferometry, also the position fluctuations of lipid membranes have been measured in a broad dynamic range to estimate membrane properties.28
However, the measurement of force and energy profiles during the induced phagocytic uptake has not been achieved so far, which would enable a comparison to existing theories.
In the present study we describe the controlled internalization of a 1 μm small spherical particle into a GUV. Using 3D optical tweezers and 3D BFP-tracking, we were able to measure distance resolved forces and energies required for particle uptake. In parallel, we recorded the fluctuations of the particle on a μs time scale prior to binding, but also during uptake (in contact with the membrane) allowing us in both cases to extract the changes in viscosity and elasticity of the particle-GUV system. Our method allows a systematic comparison of energy profiles between GUV systems with different lipid compositions, but also comparisons to theoretical approaches.
2. Theoretical background and methods
2.1. Vesicle growth by electroformation
GUVs were prepared from egg phosphatidylcholine (Egg-PC) (Sigma-Aldrich), utilizing the method of electroformation.29 Therefore the lipids were dissolved in chloroform resulting in a stock concentration of 0.5 mg ml−1. In order to perform fluorescence microscopy, 1 mol% fluorescent lipid analogues (Bodipy FL-C5-HPC, Molecular Probes) were added to the stock solution. For electroformation, an ITO glass chamber was prepared using two facing ITO-coverslips that were coated with an 8 μl droplet of the stock solution.14,30 The vesicle formation was accomplished in a 300 mOsm sucrose solution by applying an alternating electric field (3 V RMS, 10 Hz) for a period of 2 h. The frequency was subsequently reduced to 4 Hz for 1 h enhancing the detachment of the formed vesicles from the ITO glass chamber.2.2. Reduction of membrane tension
In order to enable complete particle uptake, the membrane tension of the produced GUVs had to be reduced by decreasing their internal pressure. An intermediate evaporation of the GUV solution droplet during preparation induces an osmotic pressure difference, which subsequently vanishes through the flux of solution molecules from the interior of the vesicles to the extracellular space. A method to measure the membrane tension is GUV fluctuation spectroscopy,28 where thermal membrane fluctuations are analysed by their power spectral densities (PSD).2.3. Experimental setup
The phagocytic particle uptake enabled by the optical trap is sketched in Fig. 1a. A 1 μm polystyrene particle (Polysciences Inc.) is trapped by a focused laser beam (λ0 = 1064 nm, NA = 1.2, water) at powers between 10 and 50 mW inside the chamber. The 3D position tracking of the particle relative to the trap center is achieved by BFP-interferometry at rates of 0.1–1 MHz using a quadrant photodiode (QPD).27 The motion of the GUV is hindered by 20 μm large glass spheres (Microspheres PSi-20.0, Kisker). The chamber containing the GUV is moved by a 3D piezo stage (Tritor 102 CAP, Piezosystem Jena) in 80 nm steps over the distance yp relative to the trap center.2.4. Optical trapping and tracking
As sketched in Fig. 1a, the displacement b = (bx,by,bz) of the particle from the trap centre is used to determine the underlying forces and energies during the induced uptake process. The optical force Fopt,i (i = x,y,z) shows a linear behaviour for lateral displacements |bi| < λ/4, where λ = 1064 nm/1.33 = 800 nm denotes the wavelength of the trapping laser light:| Fopt,i(bi) ≈ −κibi | (1) |
The trap stiffness κi characterizes the strength of the optical trap in each direction and is determined by a Langevin calibration method.31
The corresponding optical energy Wopt,i(bi) ≈ 1/2κibi2 + Wi,0 results in a harmonic potential.
The 3D particle tracking is realized by interference of the unscattered laser light and light scattered at the particle. The resulting interference intensity in the BFP I(kx,ky,b), which depends on the particle position b, is recorded by using a QPD. The intensity profile I(kx,ky,b) is integrated over the four areas of the QPD, and provides four voltage signals Sn (n = 1,…,4). The linear composition of Sn defines the position signals Sx = ((S1 + S3) − (S2 + S4))/S0, Sy = ((S1 + S2) − (S3 + S4))/S0 and Sz = (S1 + S2 + S3 + S4)/S0. S0 is the sum signal without a scatterer. This operation is expressed by the function Qi, which forms the signal triplet Si (i = x,y,z) encoding the 3D particle position:
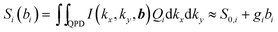 | (2) |
The detector sensitivity gi relates the QPD signals Si to the particle displacement bi. For small displacements, |bi| < λ/4 laterally and |bi| < λ/2 axially, this relationship is linear. The three sensitivities gi are obtained by the same Langevin calibration procedure in advance of each uptake experiment.
In the vicinity of the GUV, the interference pattern at the QPD may be altered by scattering of laser light at the GUV. This results in an additional intensity ΔI(kx,ky,d) and an additional sensitivity Δgi(d), which depends on the distance d to the GUV: 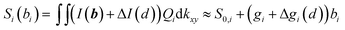 . It will be further discussed in Section 3.1. (for details, a manuscript is in preparation) that the change in sensitivity is small, i.e. |Δgi(d → 0)| < 0.1|gi| leading to a relative position tracking error of less than 10%.
. It will be further discussed in Section 3.1. (for details, a manuscript is in preparation) that the change in sensitivity is small, i.e. |Δgi(d → 0)| < 0.1|gi| leading to a relative position tracking error of less than 10%.
2.5. Fluctuation analysis
Due to the high photon densities available with the coherent BFP tracking technique, even particle fluctuations in the range of a few nanometres (nm) and on the scale of microseconds (μs) can be resolved. A common method in order to obtain relevant information about the Brownian motion of the particle is given by the autocorrelation (AC) function:ACi(τ) ≔ 〈bi(t)bi(t + τ)〉 = 〈bi(0)2〉e−τ/τ0,i = kBT/κi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−τκi/γi). exp(−τκi/γi). | (3) |
 | (4) |
Applying a linear fit function to ACi(τ) for τ ≤ 0.1 τ0,i allows one to determine the total stiffness κi and the total friction coefficient γi acting on the particle in all spatial directions. For the arrangement depicted in Fig. 1a, the two viscoelastic components are connected in parallel. Both the optical trap and the GUV-membrane represent damped oscillators with force constants κopt and κGUV and friction constants for the bead and GUV γb and γGUV such that
| κi = κopt,i + κGUV,iγi = γopt,i + γGUV,i | (5) |
The fluctuation width Δbi or variance Δbi2 = 〈bi2〉 − 〈bi2〉 can be obtained from the measured particle position histogram p(bi) from a piece of trajectory bi(t). After subtracting the mean value 〈bi〉 the squared fluctuation width reads:
 | (6) |
This expression is valid for all shapes of p(bi) = p0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(Wopt(bi) + WGUV(bi,d))/kBT)dbi, which obey Boltzmann statistics. Generally, it is defined by the harmonic trapping potential Wopt(bi) as well as by the distance dependent potential WGUV(bi,d) generated by the presence of the GUV. In summary, the particle fluctuations can be characterised by the three fluctuation variables κ, γ and Δb, which all provide relevant information about the local environment of the particle.
exp(−(Wopt(bi) + WGUV(bi,d))/kBT)dbi, which obey Boltzmann statistics. Generally, it is defined by the harmonic trapping potential Wopt(bi) as well as by the distance dependent potential WGUV(bi,d) generated by the presence of the GUV. In summary, the particle fluctuations can be characterised by the three fluctuation variables κ, γ and Δb, which all provide relevant information about the local environment of the particle.
2.6. Deformation model
The induced phagocytic particle uptake is accompanied by a successive deformation of the GUV until the engulfment is finally completed. This process can be mathematically described by a simple energy model considering the behaviour of the particle–GUV complex. The required deformation energy Gdef of a lipid bilayer sheet with membrane tension σ is based on the Helfrich energy,32 which, neglecting Gaussian and spontaneous curvature effects, can be expressed as: | (7) |
As sketched in Fig. 2a, the deformation of the GUV is comprised of a global (gl) and a local (lo) deformation:
| Gdef(hgl, hlo) = Ggldef(hgl) + Glodef(hlo) | (8) |
This energy increases with a global and a local indentation height, hgl and hlo, which are variables for the GUV deformation.
 | (9) |
Eqn (9) is derived from the assumption that the GUV volume is conserved during the deformation process, i.e. Rg3 = a2c.
The area of the ellipsoid is Aell = 2πa2(1 + (c/a)2(tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hε/ε)), where
hε/ε)), where  denotes the eccentricity. The increase in surface area is ΔAgl(hgl) = Aell(hgl) − Asp(hgl), with sphere surface Asp = 4πRg2.
denotes the eccentricity. The increase in surface area is ΔAgl(hgl) = Aell(hgl) − Asp(hgl), with sphere surface Asp = 4πRg2.
The global deformation energy Ggldef can be further separated into components for stretching and bending:
| Ggldef(hgl) = Gglstr(hgl) + Gglben(hgl) | (10) |
Using the mean curvature of an oblate ellipsoid 2Hell(hgl) = (c/a2 + a/c2) the global bending energy with bending modulus K is
| Gglben(hgl) = Gellben(hgl) − Gspben(hgl) = K/2[(2Hell)2Aell − (2Hsp)2Asp] | (11) |
The global stretching energy, which is typically much smaller than the global bending energy, is proportional to the increase in surface area,
 | (12) |
| Glodef(hlo) = Glostr(hlo) + Globen(hlo) | (13) |
Therefore we use the wrapping height of the bead pRb, p(θ) = 1 − cos(θ), and of the circle segment with wrapping height pRc, which defines the local indentation height
| hlo = p(Rb + Rc) = (1 − cos(θ))(Rb + Rc) | (14) |
R b + Rc represents the distance of the circle centres, and θ is the angle to the normal. q(Rb + Rc) is the normal projection and defines the flat circular area Ab,flat + Ac,flat = q2(Rb + Rc)2π that increases to Ab,bend + Ac,bend. Ab,flat = q2Rb2π is a circular area, and Ac,flat = q2((Rb + Rc)2 − Rb2)π is the area of the surrounding ring.
The increase in local surface area due to the deformation with an indenting sphere of radius Rb is ΔAsph ≈ Ab,bend − Ab,flat = π(pRb)2. The increase in local area due to the toroidal deformation is ΔAtor ≈ Ac,bend − Ac,flat = πqRc2(q + 2). The surface area of a torus between the polar angles [0;θ] is Ator = 2πRc2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ) + 2πRcRtθ ≈ 2πRcq(Rc + Rt) if θ < π/4. Here, Rc is the radius of the tube, and Rt is the radius of the torus ring. From eqn (14) we find p = hlo/(Rb + Rc) and
sin(θ) + 2πRcRtθ ≈ 2πRcq(Rc + Rt) if θ < π/4. Here, Rc is the radius of the tube, and Rt is the radius of the torus ring. From eqn (14) we find p = hlo/(Rb + Rc) and  , which can be inserted into ΔAtor(θ) and ΔAsph(θ) to obtain the local stretching energy as a function of hlo and Rbc = Rb + Rc
, which can be inserted into ΔAtor(θ) and ΔAsph(θ) to obtain the local stretching energy as a function of hlo and Rbc = Rb + Rc
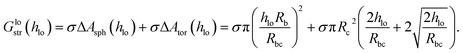 | (15) |
The local bending energy produced by the indentation of the bead is defined by the local curvature 2/Rb and the area Ab,bend = 2πRb2p of the cap with height pRb: Gsphben(θ) = K/2(2/Rb)2Ab,bend = 4πKp.
Similar to the approach of Deserno (eqn (31) in ref. 33), we calculate the curvature energy in the torus segment with opening angle θ. The energy as a function of the wrapping angle is simplified to  .
.
Therefore, we estimate the local bending energy to be
 | (16) |
The local and global deformation forces act in parallel, leading to the effect that the weaker global indentation distance is larger than the local one, such that hlo = Zhgl. Here, we approximate Z as the ratio Z = Ggldef(h0)/Glodef(h0) of global and local deformation energies at a distinct distance, e.g. h0 = 1 μm. Our approach assumes quadratic potentials Gdef(h) and corresponds to the inverse addition of spring constants for serially coupled oscillators. In consequence we can write:
| Gdef(h) = Globen(Zh) + Glostr(Zh) + Ggloben(h) + Gglostr(h) | (17) |
3. Experimental results
3.1. Influence of the GUV on bead trapping and tracking
Before facing the induced phagocytic uptake, the influence of the GUV membrane (as an additional scatterer) on particle trapping and BFP tracking has to be verified and discussed. Therefore we investigated the detector response of a single GUV using the experimental configuration sketched in Fig. 3a.35,36 The location dependent detector response for a freely diffusing GUV with radius Rg ≈ 9.4 μm (measured by fluorescence microscopy) was recorded while performing a fast periodic displacement of the laser focus yf with ft = 400 Hz along the y-direction passing both vesicle edges yle and yre. The movement of the laser focus over the trap length of Lt = 28 μm is achieved using galvanometric scan mirrors.The QPD-signal for the y-direction as a function of the focus position yf is shown in Fig. 3b for a constant laser power. An asymmetric response Sg(y) within a range of about 3 μm of the vesicle edges is shaded in bright green.37 As indicated, the distance between the zero-crossings can be used quite well to determine the vesicle radius Rg, which can also be read out from video microscopy. Within the vesicle (yle < yf < yre), the focus positions lead to a vanishing influence on the detector response (shaded in green). If the focus is far enough from the vesicle edge, the QPD-signal drops to zero again (grey shaded area).
The plot in Fig. 3c presents the detector responses in the vicinity of the right vesicle edge yre for a linearly varied laser power from 10–50 mW measured at a reference diode. The displacement by = yf − y0,r describes the distance of the focus position to the corresponding central zero-crossing of the detector response. The results clearly show that the shape and position of the signals Sg(y) do not change or shift laterally, although the laser power and thereby the optical forces are increased. In consequence, the optical forces on the GUV are negligible.
In the experiment, the position of the vesicle edge within the response function cannot be directly inferred. Therefore we performed a numerical simulation,38 where the interference of focussed unscattered light and light scattered at a GUV (Rg = 8 μm) is recorded and read out by a QPD. Fig. 3d shows that the edge of the GUV corresponds to the zero-crossing of the signal Sg(y) at y0,r.
The influence of the light scattered at the GUV on the signal of the trapped 1 μm polystyrene bead is relatively small. As shown in Fig. 3b–c, the maximum amplitude of the signal, Smax, at a laser power P = 50 mW is 0.1 V, whereas the maximum signal of the bead is 1.8 V. Although the scattered electric fields have to be added and not the interference intensities, the approximation to add simply the QPD signals is reasonable and helpful.35,39 Based on this approach, the change in position signal ΔI(d), in detector sensitivity Δg(d) and in position δb is less than 0.1 V/1.8 V = 6%. In summary, light scattering at the GUV has a negligible influence on both optical forces and position tracking of the particle.
3.2. Process of contacting the GUV
The study of a phagocytic particle uptake using a biomimetic system is initiated by the contact process between the GUV and the particle. Here, the particle position fluctuations in the vicinity of the GUV, measured at 1 MHz in all three directions, allow for the interpretation of the interaction process.The experimental procedure is shown in Fig. 4a. Here the unfixed GUV moves with the piezo-stage (PS) and is approached in 20 nm steps towards the trapped particle. At each position, 2 × 105 particle positions are recorded over 200 ms. Assuming thermal equilibrium, the fluctuation width Δbi (i = x,y,z) is a useful variable to characterize the interaction process. The plot in Fig. 4b reveals a slight decrease of the fluctuation width of the radial trajectory by(yp = vpt) upon contact at d = 0. It should be noted that the mean value of the displacements 〈by〉 (central red line) does not change more than ±5 nm upon contact with the unfixed GUV.
However, this is different with the lateral and axial friction factors γi(d) and force constants κi(d), which increase with decreasing distance d to the GUV (see Fig. 4c and d). γi and κi were obtained by linear fits to the AC-functions as described by eqn (4). An optimization procedure revealed that the most reliable results for linear fits were obtained for fitting intervals of 35 μs corresponding to 35 points in the AC data curve recorded for each piezo position yp. The total force constants (stiffness) were obtained through the constant part of the linear fit curve, κ = kBT/AC(0), whereas the friction coefficients were obtained from the slope of the linear fit curve. In addition, κ was positively cross-checked through evaluating the fluctuation width Δb, thus κ = kBT/Δb2.
The most important effect visible in Fig. 4c is the smooth increase in κy in the radial y-direction, indicating that no binding of the particle to the GUV-membrane occurs. A particle binding process to an interface is characterized by an abrupt increase in κ27,40 due to a sudden decrease in the fluctuation width of the particle. Therefore adhesion energies are not considered in our energy model as introduced in Section 2.6. Whereas the fluctuation width and thereby the force constants hardly change in tangential directions x and z, the friction experienced by the particle increases in all three directions. Remarkably, the friction factor γ and correspondingly the diffusion constant kT/γ change already prior to binding, and thus indicate a hydrodynamic coupling between the particle and GUV membrane.40 For yp > 2 μm, the bead is in closer contact with the GUV (the collision rate is increased) and the bead diffusion is influenced by the higher viscosity close to the lipid bilayer. Similar to the increase in γ close to a stiff wall, the increase in radial y-direction is larger than in tangential x, z-directions. This method may even allow distinguishing between different viscosities of the membrane due to different molecular compositions.
3.3. Induced phagocytosis
In this paragraph the phagocytic particle uptake induced by the optical trap is introduced. In the experiment, the uptake process is characterized by two parameters of the GUV: the vesicle radius Rg and the membrane tension σ. Both values are not known in advance, but methods in order to determine them are provided in the following. | ||
| Fig. 5 Complete induced phagocytic particle uptake. (a) Time series of fluorescent images demonstrating the deformation of the GUV. (b) Change in the half-axes of the ellipsoidal GUV extracted from Fig. 5a. (c) Measured deformation force as a function of the piezo-movement. The numbers correspond to the images in Fig. 5a. Fteth is the tether force. (d) Measured deformation energy profiles for different GUVs. (e) Simulated deformation energy profiles as a function of the indentation height h for GUVs with Rg0 = 9 μm, Rg1 = 13 μm, K0 = 10 kBT, σ0 = 30 kBT μm−2 = 0.12 × 10−3 pN nm−1 and Rc = K0/10 μm/kBT. (f) Simulated uptake energies at uptake lengths hut = 1 + Rg/3 for different GUV radii Rg and Λ. | ||
The 3D-tracking of the particle displacement from the trap centre allows for the determination of the 3D optical forces by integration of the potentials (see Section 2.4). The uptake force is dominated by the radial y-component, whereas the tangential directions make up a significantly smaller but still resolvable amount (not shown).
The deformation force profiles Fdef(yp) for four different vesicles shown in Fig. 5c in dependence of the piezo-position yp reveals a nonlinear behaviour corresponding to the frames (1)–(3) until the internalization process is completed at the uptake force Fut. Subsequently, the force drops off in the vicinity of frame (4), which corresponds to a relaxation process of the particle towards the trap centre. In frames (5) and (6) the particle reaches the equilibrium position accompanied by a non-vanishing force. Although badly visible in Fig. 5a, the remaining force likely belongs to a membrane tether indicating that the particle is not completely disrupted from the membrane and a tether is formed. The constant tether force is about Fteth ≈1.7 pN and can be calculated by  for a known membrane tension and bending modulus.41
for a known membrane tension and bending modulus.41
In Fig. 5c and d the measured profiles of the required forces and energies for complete particle uptake (ut) with maximum values Gut and Fut are displayed for different vesicle radii Rg. Vesicle sizes are determined by video microscopy. As illustrated, the required deformation energies for complete uptake vary between Gut = 2000–5500 kBT, whereas the forces range between Fut = 4–16 pN (kBT = 4 pN nm at T = 300 K). The required indentation height (piezo-movement yp) for the complete particle ingestion, the uptake length hut, is between 4.2 μm and 5.5 μm.
Results from the model. In Fig. 5d we have used the energy model introduced in Section 2.6 to prove its correctness and compare it with the experimental results. Fig. 5e shows four simulated energy profiles for different GUVs, where one profile (red curve) is separated into the global (red dash-dotted line) and local (orange dotted line) component of the total GUV deformation. The curves cannot be added on the same length scale h since hlo = Zhgl where Z = 0.1 in this example (see eqn (17)). We used the same radii Rg0 = 9 μm and Rg1 = 13 μm as in the experiment. The membrane tension was assumed to be σ0 = 30 kBT μm−2 = 0.12 pN μm−1 = 0.12 × 10−8 dyn cm−1 and the bending modulus K0 = 10 kBT,28 such that Fteth = 8π(Kσ)1/2 = 1.7 pN, which corresponds to the measured tether force. The radii for the two membrane curvatures for the local deformation were Rb = 0.5 μm for the bead and initially Rc = 2.5 μm for the torus tube. We than adapted the radius of curvature Rc to be proportional to K, such that Rc = K/10 μm/kBT. However, the effect of Rc on Gdef(h) was rather small. For the above mentioned parameters, deformation energies of up to 5500 kBT are reached for a local indentation hlo of up to 1 μm and a global indentation hgl of also up to 3 μm, resulting in a total indentation hlo + hgl of up to 4 μm. According to our model the main energy contribution for small indentations (h < 1 μm) results from the local deformation of the GUV. By changing the ratio Λ2 = (K/σ) between the bending modulus and the membrane tension, different local slopes of the energy curves can be obtained. The black curve displays a 4× decrease in σ, which results in an only slightly smaller energy profile, whereas a 4× decrease in K reduced the deformation energy significantly. In our case (σ0 ≈ 30 kBT μm−2 and K0 = 10 kBT) the bending rigidity influences the deformation energy profile much less than the membrane tension. A 4× decrease of the bending tension σ0 decreases the energy at h = 4 μm significantly. The 40% increase in GUV size (Rg0 → Rg1) leads to a 40% reduced deformation energy at h = 4.5 μm. From Fig. 5e we can estimate the uptake length hut to be about one third of the vesicle radius plus the diameter of the bead, such that Gdef(hut) was assumed as the uptake energy Gut in our model. The uptake length is the sum of the local and global indentation, hut = hlo + hgl = Rg/3 + 2Rb, where the particle is taken up and the free energy drops down. In Fig. 5f the overall increase of Gut with the vesicle radius is displayed for different ratios of Λ = sqrt(K/σ) = 0.3, 0.5 and 0.9, which are all values for vesicles with the mean stiffness. For vesicles with a decreased bending modulus Λ = 0.3, the uptake energy rises strongly with the vesicle radius. Uptake energies and vesicle radii found in the experiment are marked by black circles. Generally, rupturing and a possible tether formation are not included in our model.
Whereas the radial fluctuations are dominated by the membrane fluctuations and thereby define the steeper stiffness change Δκy, the reduced fluctuation volume of the trapped bead leads to a linear increase of Δκx, over the first micrometres. Only for a larger indentation of the bead at hlo ≈ 2Rb, κx also approaches the value of κm.
The changes in viscous drag are relatively small in the two tangential directions, i.e. Δγxz(yp)/Δγxz (yp = 4 μm) < 0.25, as shown in Fig. 6b. The increase in radial friction is more pronounced: Δγy grows smoothly until yp ≤ 3 μm and much stronger for yp > 3 μm until the maximal value of Δγy (hlo ≈ 2Rb) = γm is reached before the internalization of the particle. The maximal increase in friction γm ≈ pN ms μm−1 corresponds to a relative increase of 70%.
 in amplitude and in uptake length, here called relative piezo-movement β ∈ [0,1], as displayed in Fig. 7. In this way, the slopes of all curves can be well compared. β = 1 corresponds to the uptake length hut, i.e. the maximal indentation length, where the particle is taken up. We investigated four different GUVs made from Egg-PC. Fig. 7a shows their normalized energy profiles, which are characterized by a shallow energy increase likely due to a global, elliptical deformation of the GUVs, followed by a steeper increase likely due to a local deformation caused by the indenting particle. The black arrow to the left indicates the increasing GUV radius RGUV together with an earlier and smoother increase in deformation energy, likely due to a stronger influence of global deformation. By averaging over local and global effects, the energy profile can be approximated to be quadratic, Gdef,n(β) ≈ Cβ2. Fig. 7b displays the corresponding normalized force profiles Fdef,n(β), which, according to their slope, can be separated into ranges for global and local deformation. The latter comprises roughly 40% of the overall uptake length (β = 1).
in amplitude and in uptake length, here called relative piezo-movement β ∈ [0,1], as displayed in Fig. 7. In this way, the slopes of all curves can be well compared. β = 1 corresponds to the uptake length hut, i.e. the maximal indentation length, where the particle is taken up. We investigated four different GUVs made from Egg-PC. Fig. 7a shows their normalized energy profiles, which are characterized by a shallow energy increase likely due to a global, elliptical deformation of the GUVs, followed by a steeper increase likely due to a local deformation caused by the indenting particle. The black arrow to the left indicates the increasing GUV radius RGUV together with an earlier and smoother increase in deformation energy, likely due to a stronger influence of global deformation. By averaging over local and global effects, the energy profile can be approximated to be quadratic, Gdef,n(β) ≈ Cβ2. Fig. 7b displays the corresponding normalized force profiles Fdef,n(β), which, according to their slope, can be separated into ranges for global and local deformation. The latter comprises roughly 40% of the overall uptake length (β = 1).
The characteristics of the induced uptake process are influenced by the properties of the GUV–particle complex. In the experiments, the vesicle radius Rg, the membrane tension σ and, less obvious, the bending modulus K can be varied.28 As described in Section 2.2, the membrane tension σ has been reduced by the induced osmotic pressure difference in the sample. Due to the different GUV volumes, the resulting membrane tensions σ will also be different in each case.
 . Here, h designates the uptake length.
. Here, h designates the uptake length.
The dependency between the membrane tension σ and the membrane stiffness Δκm was further manifested by the results of Fig. 8b, where the radial GUV membrane fluctuations were measured directly in the centre of the focused laser (without bead) similar to the approach presented in ref. 28. Here, the membrane tension σ was estimated from the membrane fluctuation width Δby. Vesicle no. 2 (black curve in Fig. 5d) has the same size as vesicle no. 1 (blue curve), but reveals a 2-fold reduced fluctuation width Δby and a 4-fold increased membrane stiffness Δκm. As expected, a lower fluctuation width Δby results in a higher effective membrane tension σ. Considering the blue and the black uptake curves in Fig. 5d, the GUV with the lower σ results in a longer uptake length h and a reduced uptake energy Eut.
These findings are generalized in Fig. 8c–f. Fig. 8c displays the linear relationship of the final uptake energy and the product of the uptake force and the vesicle radius. The uptake energy Gut as a function of the uptake force times the uptake length, Fut × hut, results in a non-linear relationship due to the non-linear force profiles (not shown).
It can be seen in Fig. 8d and e that the uptake energy is approximately proportional to the membrane stiffness Δκm and to the maximal lateral friction coefficient γm briefly before internalization of the particle. In consequence, also the friction coefficient and the membrane stiffness have to be linear to each other as displayed in Fig. 8f.
4. Discussion
The goal of the present study has been the development and manifestation of a novel optical manipulation and measurement technique to study phagocytosis in a simple biomimetic system such as a GUV. It was our aim to obtain precise energy and force profiles together with supplementary physical parameters during phagocytosis, which we induced by optical tweezers and recorded by interferometric 3D particle tracking. It was a further aim to better understand the measured profiles by using an elastic deformation model considering global and local deformation effects due to indentation of a 1 μm large bead.4.1. BFP particle tracking near the membrane
The 1064 nm laser beam was focused by a NA = n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α = 1.2 water immersion objective lens resulting in a focusing angle of nearly α = 64°. If the optical trapped 1 μm latex particle is brought into contact with GUVs, which are 18–27 μm in diameter, the focused laser light will also hit the GUV. A first question to answer was whether the light scattered at the GUV could alter the optical trap and the particle tracking precision in the back focal plane (BFP) of the detection lens. The effect can be understood by the three beam interference leading to an additional intensity ΔI(x,y,d) in the focus and in the BFP ΔI(kx,ky,d), which depends on the distance between the focus and the GUV. By inspecting Fig. 1c, one can see that the most significant changes in the particle position signals occur in the radial y-direction, thus reducing the dimensions of the problem. It is demonstrated in Fig. 3 that these signals indeed represent the 3D particle position with a negligible small error of less than 10%, since the bipolar position signal of the GUV membrane is significantly smaller in amplitude than the signal resulting from the latex bead. Furthermore, a change in the laser intensity did not result in a position change of the free-floating GUV, meaning that optical forces on the GUV are negligible.
α = 1.2 water immersion objective lens resulting in a focusing angle of nearly α = 64°. If the optical trapped 1 μm latex particle is brought into contact with GUVs, which are 18–27 μm in diameter, the focused laser light will also hit the GUV. A first question to answer was whether the light scattered at the GUV could alter the optical trap and the particle tracking precision in the back focal plane (BFP) of the detection lens. The effect can be understood by the three beam interference leading to an additional intensity ΔI(x,y,d) in the focus and in the BFP ΔI(kx,ky,d), which depends on the distance between the focus and the GUV. By inspecting Fig. 1c, one can see that the most significant changes in the particle position signals occur in the radial y-direction, thus reducing the dimensions of the problem. It is demonstrated in Fig. 3 that these signals indeed represent the 3D particle position with a negligible small error of less than 10%, since the bipolar position signal of the GUV membrane is significantly smaller in amplitude than the signal resulting from the latex bead. Furthermore, a change in the laser intensity did not result in a position change of the free-floating GUV, meaning that optical forces on the GUV are negligible.
4.2. Mathematical deformation model
Our model estimates the deformation energy Gdef of a spherical lipid bilayer sheet, which can be separated into energy components for bending and stretching. These can be further separated into a global deformation, where the spherical GUV is transformed into an oblate spheroid and into the local deformation, where the indentation of the spherical bead leads to a small spherical deformation across the contact area of the bead and a toroidal deformation around this area. In both cases the change in membrane curvature as well as the change in membrane area had to be calculated. By using appropriate coordinate systems and variables, the expressions for these four energy terms could be reduced to handy expressions. Our approach is similar to that of Deserno et al.,33 although they present results in a more generalized way (e.g. by Λ2 = K/σ). The final energy profile Gdef(h) predicted by our model is a function of the local and global indentation height h = hlo + hgl. The model considers the GUV radius (here Rg = 9 μm and 13 μm), the bead radius (Rb = 0.5 μm), the membrane bending modulus for Egg-PC (K0 = 10 kBT), a membrane tension σ0 = 30 kBT μm−2 = 0.12 pN μm−1 estimated from the measured tether force , and the radius of the concave toroidal curvature from the local indentation (Rc = 2.5 μm), which however hardly affects the results.
, and the radius of the concave toroidal curvature from the local indentation (Rc = 2.5 μm), which however hardly affects the results.
The experimental parameters used correspond to a low tension membrane where Rg ≈ Λ = 0.57 μm and with a reduced membrane tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0 = Rb2σ0/K0 = (Rb/Λ)2 = 0.77, which is close to those expected for cellular membranes.19
0 = Rb2σ0/K0 = (Rb/Λ)2 = 0.77, which is close to those expected for cellular membranes.19
In the simulations both K and σ were varied by a factor of 4 to investigate the influence on the energy profile, which changes significantly more by reducing σ. In other words, the reduced membrane tension results in a longer uptake length which was also shown in the experiments, where vesicle no. 1 (blue curve) has a four times slower membrane stiffness Δκm relative to vesicle no. 2 (black curve). The strength of the model is that for reasonably estimated parameters K and σ, both the profile slope and the absolute deformation energies coincide well with the experiment. From Fig. 5d we could estimate the uptake length to be hut = Rg/3 + 2Rb, where the local indentation height 2Rb = 1 μm corresponds to complete wrapping of the particle. The global critical indentation height Rg/3 varies with the vesicle radius. The calculated energies Gut = Gdef(hut) at a typical uptake length of hut = Rg/3 + 1 μm are all in the range of some 1000 kBT.
The simulated energy profile for a local deformation (orange curve in Fig. 5e), although plotted over the whole range of 5 μm, does not reach values larger than the particle diameter = 1 μm. According to our theoretical model, the required energy for an estimated uptake increases nonlinearly with the vesicle radius Rg as shown in Fig. 5f. The increase is smaller for larger ratios Λ2 = K/σ.
The superposition of the local and global deformation energies confirm our mechanistic model and understanding that particle engulfment and uptake first lead to a global deformation followed by a local GUV deformation. The scale of the indentation lengths hlo and hgl are based on the harmonic approximation of the energy profiles, and use the concepts of serial connected spring constants, which add inversely. This serial connection of potential landscapes needs to be improved in the future if the energy profiles Gdef(h) become more complicated. Useful next steps would be to include the energies for tether formation and membrane rupturing in our model. In summary, our model represents a valuable approach to validate the observation, which can be extended and improved as proposed by others.19–21,34
4.3. Induced phagocytosis
The particle fluctuations in the vicinity of the membrane are recorded at the very high sampling rate of 1 MHz, enabling the investigation of the contact process between the particle and the GUV – before and after close contact with the membrane. As soon as the particle come into contact with the membrane, the particle's position fluctuations change both in amplitude and time, which can be analysed by the fluctuation width or the stiffness κ. In the case of sudden binding to the membrane, the fluctuation width changes instantaneously.27,40 However, Fig. 4 reveals a smooth increase in κ in the radial direction, indicating that the particle is slowly pressed against the membrane leading to a slow decrease of the fluctuation width.![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0 = 0.22 and
0 = 0.22 and ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0 = 1, respectively. These values vary with the GUV size and the maximal membrane stiffness Δκm, which have been evaluated from the fluctuations of the membrane alone or with the bead attached (Fig. 8a and b). As shown by Betz28 and confirmed by us in Fig. 8b, the membrane tension σ increases with the inverse membrane fluctuation width 1/Δby. In a proof-of-principle experiment we have demonstrated the increase of the membrane tension through 1/Δby with the membrane stiffness Δκm. However, further experiments and theoretical considerations have to be performed to understand the relationship between both quantities.
0 = 1, respectively. These values vary with the GUV size and the maximal membrane stiffness Δκm, which have been evaluated from the fluctuations of the membrane alone or with the bead attached (Fig. 8a and b). As shown by Betz28 and confirmed by us in Fig. 8b, the membrane tension σ increases with the inverse membrane fluctuation width 1/Δby. In a proof-of-principle experiment we have demonstrated the increase of the membrane tension through 1/Δby with the membrane stiffness Δκm. However, further experiments and theoretical considerations have to be performed to understand the relationship between both quantities.
This increase of the uptake energy with the membrane tension has been theoretically predicted by several authors.19,21,34 This prediction could be validated by the results shown in Fig. 8d, where uptake energies increase linearly with the membrane stiffness κi = kBT/〈bi2〉, which is the inverse squared fluctuation width 〈bi2〉 of the fully wrapped bead briefly before penetration. The physical and quantitative dependency between this membrane fluctuation parameter and the membrane tension σ still need to be evaluated. Interestingly, the uptake energy can also be estimated by analyzing the wrapped particle fluctuations on a very short time scale, resulting in the linear dependency to the radial friction coefficient γm as shown in Fig. 8e. Motions of the wrapped particle are strongly damped before the final uptake. Although the linear slope shown in Fig. 8f, can be concluded from the other two figures, this result is also far from being obvious and might be helpful for future uptake experiments.
It should be mentioned that biological cell membranes are characterized by unique permeability and adaptive mechanical properties, which means that under physiological conditions biomembranes are on the melting point, which means that they are on the switch between the gel and liquid–crystalline phase.45,46 The Egg-PC membranes we used have a relatively low melting point such that they are in the melted phase, such that no additional energy for melting is required. However, it remains an open question how the phase of the membrane influences their viscoelastic properties and the final uptake forces and energies.
Based on our experimental procedure and the present analysis, it should be possible to compare uptake energy profiles from different GUVs with more complex membrane compositions. Even systems with protein induced membrane deformations12 could be compared allowing one to investigate phagocytosis on a macromolecular level.
5. Conclusion
We succeeded in inducing the phagocytic uptake of a particle into a giant unilamellar vesicle (GUV) by means of optical tweezers.With increasing indentation length of the particle into the membrane, we measured membrane deformation energies that can be separated into two subsequent steps. We found uptake energies of 2000–5500 kBT for GUVs with different sizes and membrane tensions. Adhesion energies between the particle and the GUV that could lower the uptake energies were blocked, facilitating the analysis of global and local deformation energies of the GUV. In principle, the above-mentioned uptake energies can be brought up by conformational transitions of membrane-bound proteins. These uptake energies can be lowered by avoiding a global deformation of the GUV, as it is likely the case for biological cells. But, and this keeps this field of research very exciting, the uptake energies can be purely delivered by accessible adhesion energies between the particle and the host artificial cell. Our experimental procedure and theoretical model presented in this study should be applicable to other experiments as well with step-wise increased complexity, thus enabling a bottom-up strategy to understand the physics of phagocytosis.
Acknowledgements
The authors thank Dr Timo Betz for helpful comments and discussions as well as Prof. Dieter Braun for general support. B. Tränkle was supported by the Deutsche Forschungsgemeinschaft, grant number RO 3615/1. W. Römer was supported by the Excellence Initiative of the German Research Foundation (EXC 294), by a grant from the Ministry of Science, Research and the Arts of Baden-Württemberg (Az: 33–7532.20) and by a starting grant of the European Research Council (Programme “Ideas” no. ERC-2011-StG 282105).References
- P. Cossart and P. J. Sansonetti, Science, 2004, 304, 242–248 CrossRef CAS PubMed.
- T. Eierhoff, B. Stechmann, W. Römer, Pathogen and Toxin Entry – How Pathogens and Toxins Induce and Harness Endocytotic Mechanisms, in Molecular Regulation of Endocytosis, ed. B. Ceresa, InTech, 2012, pp. 249–256 Search PubMed.
- B. J. Reynwar, G. Illya, V. A. Harmandaris, M. M. Müller, K. Kremer and M. Deserno, Nature, 2007, 447, 461–464 CrossRef CAS PubMed.
- E. A. Evans and D. A. Calderwood, Science, 2007, 316, 1148–1153 CrossRef CAS PubMed.
- H. Kress, J. G. Park, C. O. Mejean, J. D. Forster, J. Park, S. S. Walse, Y. Zhang, D. Q. Wu, O. D. Weiner, T. M. Fahmy and E. R. Dufresne, Nat. Methods, 2009, 6, 905–909 CrossRef CAS PubMed.
- J. A. Champion and S. Mitragotri, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 4930–4934 CrossRef CAS PubMed.
- S. E. A. Gratton, P. A. Ropp, P. D. Pohlhaus, J. C. Luft, V. J. Madden, M. E. Napier and J. M. DeSimone, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 11613–11618 CrossRef CAS PubMed.
- S. Tollis, A. E. Dart, G. Tzircotis and R. G. Endres, BMC Syst. Biol., 2010, 4 DOI:10.1186/1752-0509-4-149.
- H. Kress, E. H. Stelzer, D. Holzer, F. Buss, G. Griffiths and A. Rohrbach, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11633–11638 CrossRef CAS PubMed.
- R. Dimova, S. Aranda, N. Bezlyepkina, V. Nikolov, K. A. Riske and R. Lipowsky, J. Phys.: Condens. Matter, 2006, 18, S1151 CrossRef CAS PubMed.
- H.-G. Döbereiner, O. Selchow and R. Lipowsky, Eur. Biophys. J., 1999, 28, 174–178 CrossRef.
- P. Sens, L. Johannes and P. Bassereau, Curr. Opin. Cell Biol., 2008, 20, 476–482 CrossRef CAS PubMed.
- D. L. Richmond, E. M. Schmid, S. Martens, J. C. Stachowiak, N. Liska and D. A. Fletcher, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 9431–9436 CrossRef CAS PubMed.
- W. Römer, L. Berland, V. Chambon, K. Gaus, B. Windschiegl, D. Tenza, M. R. E. Aly, V. Fraisier, J. C. Florent, D. Perrais, C. Lamaze, G. Raposo, C. Steinem, P. Sens, P. Bassereau and L. Johannes, Nature, 2007, 450, 670–U673 CrossRef PubMed.
- W. Römer, L.-L. Pontani, B. Sorre, C. Rentero, L. Berland, V. Chambon, C. Lamaze, P. Bassereau, C. Sykes and K. Gaus, Cell, 2010, 140, 540–553 CrossRef PubMed.
- K. Jaskiewicz, A. Larsen, D. Schaeffel, K. Koynov, I. Lieberwirth, G. Fytas, K. Landfester and A. Kroeger, ACS Nano, 2012, 6, 7254–7262 CrossRef CAS PubMed.
- C. Dietrich, M. Angelova and B. Pouligny, J. Phys. II, 1997, 7, 1651–1682 CrossRef CAS.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- M. Deserno, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2004, 69, 031903 CrossRef.
- C. C. Fleck and R. R. Netz, Europhys. Lett., 2004, 314 CrossRef CAS.
- S. Dasgupta, T. Auth and G. Gompper, Soft Matter, 2013, 9, 5473–5482 RSC.
- A. H. Bahrami, Soft Matter, 2013, 9, 8642–8646 RSC.
- A. Rohrbach, Opt. Express, 2005, 13, 9696–9701 CrossRef.
- A. Jannasch, A. F. Demirors, P. D. J. van Oostrum, A. van Blaaderen and E. Schaffer, Nat. Photonics, 2012, 6, 469–473 CrossRef CAS.
- A. Pralle, M. Prummer, E.-L. Florin, E. H. K. Stelzer and J. K. H. Hörber, Microsc. Res. Tech., 1999, 44, 378–386 CrossRef CAS PubMed.
- L. Friedrich and A. Rohrbach, Opt. Lett., 2012, 37, 2109–2111 CrossRef PubMed.
- H. Kress, E. H. Stelzer, G. Griffiths and A. Rohrbach, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2005, 71, 061927 CrossRef.
- T. Betz and C. Sykes, Soft Matter, 2012, 8, 5317–5326 RSC.
- M. I. Angelova and D. S. Dimitrov, Faraday Discuss. Chem. Soc., 1986, 81, 303–311 RSC.
- L. Mathivet, S. Cribier and P. F. Devaux, Biophys. J., 1996, 70, 1112–1121 CrossRef CAS PubMed.
- A. Rohrbach, C. Tischer, D. Neumayer, E. L. Florin and E. H. K. Stelzer, Rev. Sci. Instrum., 2004, 75, 2197–2210 CrossRef CAS.
- W. Helfrich, Z. Naturforsch., C: Biochem., Biophys., Biol., Virol., 1973, 28, 693–703 CAS.
- M. Deserno and W. M. Gelbart, J. Phys. Chem. B, 2002, 106, 5543–5552 CrossRef CAS.
- M. Deserno and T. Bickel, EPL, 2003, 62, 767 CrossRef CAS.
- M. Speidel, L. Friedrich and A. Rohrbach, Opt. Express, 2009, 17, 1003–1015 CrossRef CAS PubMed.
- M. Koch and A. Rohrbach, Nat. Photonics, 2012, 6, 680–686 CrossRef CAS.
- J. Lemiere, K. Guevorkian, C. Campillo, C. Sykes and T. Betz, Soft Matter, 2013, 9, 3181–3187 RSC.
- A. Rohrbach, Simulation software LightWave 1.1, 2013 Search PubMed.
- P. C. Seitz, E. H. Stelzer and A. Rohrbach, Applied Optics, 2006, 45, 7309–7315 CrossRef PubMed.
- F. Jünger, F. Kohler, A. Meinel, T. Meyer, R. Nitschke, B. Erhard and A. Rohrbach, Biophys. J. Search PubMed , in preparation.
- I. Derényi, F. Jülicher and J. Prost, Phys. Rev. Lett., 2002, 88, 238101 CrossRef.
- R. Dimova, C. Dietrich, A. Hadjiisky, K. Danov and B. Pouligny, Eur. Phys. J. B, 1999, 12, 589–598 CrossRef CAS.
- R. Dimova, B. Pouligny and C. Dietrich, Biophys. J., 2000, 79, 340–356 CrossRef CAS PubMed.
- I. Koltover, J. O. Rädler and C. R. Safinya, Phys. Rev. Lett., 1999, 82, 1991 CrossRef CAS.
- T. Baumgart, S. T. Hess and W. W. Webb, Nature, 2003, 425, 821–824 CrossRef CAS PubMed.
- O. G. Mouritsen, Eur. J. Lipid Sci. Technol., 2011, 113, 1174–1187 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |







