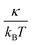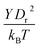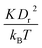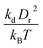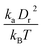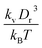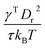DOI:
10.1039/C3SM52860J
(Paper)
Soft Matter, 2014,
10, 2961-2970
White blood cell margination in microcirculation†
Received
12th November 2013
, Accepted 22nd January 2014
First published on 24th January 2014
Abstract
Proper functioning of white blood cells is not possible without their ability to adhere to vascular endothelium, which may occur only if they are close enough to vessel walls. To facilitate the adhesion, white blood cells migrate toward the vessel walls in blood flow through a process called margination. The margination of white cells depends on a number of conditions including local hematocrit, flow rate, red blood cell aggregation, and the deformability of both red and white cells. To better understand the margination process of white blood cells, we employ mesoscopic hydrodynamic simulations of a three-dimensional model of blood flow, which has been previously shown to capture quantitatively realistic blood flow properties and rheology. The margination properties of white blood cells are studied for a wide range of hematocrit values and flow conditions. Efficient white blood cell margination is found in an intermediate range of hematocrit values of Ht ≈ 0.2–0.4 and at relatively low flow rates, characteristic of the venular part of microcirculation. In addition, aggregation interactions between red blood cells lead to enhanced white-blood-cell margination. This simulation study provides a quantitative description of the margination of white blood cells, and is also highly relevant for the margination of particles or cells of similar size such as circulating tumor cells.
1 Introduction
Leukocytes or white blood cells (WBCs) defend our body from various viral and bacterial infections and other foreign substances. They are normally located in the blood stream and in the lymphatic system, where they are able to monitor various chemical signals or stimuli. Once WBCs have detected a problem, e.g., an inflammation, their cellular machinery is able to facilitate transmigration into a surrounding tissue,1 which is necessarily preceded by their adhesion to vascular endothelium.2,3 However, the possibility of WBC interactions with a vessel wall, and therefore adhesion, is directly associated with the probability of being close enough to a vessel wall in blood flow. A number of experimental observations4–6 suggest that WBCs migrate toward vessel walls in blood flow, a process which is called margination. Thus, the WBC margination probability, which characterizes the fraction of time a WBC spends near a wall, directly affects the frequency of WBC adhesion.
A number of experimental observations7,8 and simulations9–12 of flowing blood have shown that red blood cells (RBCs) concentrate in the vessel center leading to a layer free of RBCs next to a wall. The migration of RBCs toward the vessel center has been attributed to a lift force,13–15 which arises from cell-wall hydrodynamic interactions in flow due to the non-spherical discocyte shape and high deformability of RBCs. Therefore, the migration effect for various cells is different due to the differences in size, shape, and deformability of blood cells, for instance between RBCs and WBCs. Different cell-wall hydrodynamic interactions of RBCs and WBCs lead to their segregation in flow such that WBCs are likely to be present near a wall. In fact, the lift force on WBCs is expected to be much lower than that on RBCs, since WBCs have a near-spherical shape and are not very deformable. This argument supports the fact that RBCs populate the vessel center, while WBCs may get marginated to the RBC free layer. Therefore, WBC margination in blood flow is mediated by RBCs.
Existing experimental4,6,16–18 and simulation19–21 studies have shown that WBC margination has a non-trivial dependence on various blood flow properties including hematocrit Ht, (i.e. RBC volume fraction), flow rate, vessel geometry, and RBC aggregation. Early in vivo experiments on WBC adhesion6 have shown a high WBC adhesion rate at low flow rates characteristic of venular blood flow and high Ht > 0.45. In vitro experiments on WBC adhesion in glass tubes17 suggested a similar dependence of WBC adhesion on the flow rate; however, they reported no significant dependence of WBC adhesion on Ht. One of the first simulation studies in two dimensions (2D)20 has also reported no significant effect of Ht on WBC margination. In contrast, WBC margination in microfluidic experiments18 has been found to be pronounced within an intermediate range of Ht ≃ 0.2–0.3, while at both lower and higher Ht values WBC margination has been reduced. Recent simulation work in 2D21 was able to reconcile the existing contradicting observations of WBC margination dependence on Ht, showing that a strong margination effect is achieved for an intermediate range of Ht values. At low Ht, WBC margination is weak due to a low concentration of RBCs, while at high Ht WBC margination is attenuated due to interactions of marginated WBCs with RBCs near a wall, which significantly limit the time WBCs spend near a wall. The apparent inconsistency with experiments17 and simulations,20 which suggests no dependence of WBC margination on Ht, has been reconciled due to the fact that the Ht values used in these studies fall almost entirely into the region of a strong WBC margination predicted in ref. 21. Furthermore, RBC aggregation has been found to result in an enhanced WBC margination and adhesion in both experiments6,16–18 and simulations.21
Even though the 2D simulations20,21 provide a qualitative picture of WBC margination, it is not clear whether WBC margination would display substantial changes in 3D. Another evident difference between 2D and 3D is that 2D simulations mimic blood flow in a slit geometry, while WBC margination in a tube geometry is of great interest, since it mimics an idealized blood vessel in microcirculation. To investigate WBC margination in idealized microvessels, we employ a particle-based mesoscopic simulation technique. WBC margination is investigated in 3D for a wide range of blood flow conditions including hematocrit, flow rate, and RBC aggregation, providing a quantitative description of WBC margination in microvessels. Our simulation results in 3D show a qualitatively similar dependence of WBC margination on Ht as in 2D, predicting a strong margination effect within an intermediate range of Ht values. Furthermore, WBC margination appears to be pronounced only for low enough flow rates characteristic of venular blood flow, consistent with existing experimental observations.6,16,17 In addition, we estimate the forces on a marginated WBC in the normal direction to the wall, which may aid in WBC adhesion.
2 Methods and models
To model blood flow we use a particle-based mesoscopic simulation technique called the smoothed dissipative particle dynamics (SDPD) method.22 Blood cells are represented by a network membrane model, since triangulated surfaces with curvature and stretching elasticity provide a very versatile approach to model the shapes and deformation of vesicles and cells in three dimensions.12,23–27 Cell membranes are coupled to a background fluid (i.e., blood plasma) through viscous friction. We briefly describe the employed cell model and the SDPD method.
2.1 Blood cell model
2.1.1 Membrane network model.
In simulations, a cell membrane is represented by a collection of Nv particles with coordinates {xi=1…Nv} interconnected by viscoelastic springs.27,28 The network of springs has a fixed connectivity and is characterized by the following energy| | | U({xi}) = Us + Ub + Ua+v, | (1) |
where Us is the elastic spring energy, Ub imposes membrane bending resistance, and Ua+v defines the area and volume conservation constraints. The spring's contribution Us mimics membrane elasticity, which is, for instance, supplied by a spectrin network for a RBC membrane. In addition, each spring may contain a friction term in order to incorporate a non-zero membrane viscosity similar to that of a lipid bilayer. The term Ub implies bending resistance of a cell membrane, while the area and volume conservation constraints mimic area-incompressibility of the lipid bilayer and incompressibility of a cytosol, respectively.
The vertices on a cell membrane are connected by Ns springs with the potential energy
| | 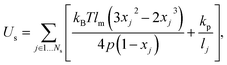 | (2) |
where
lj is the length of the spring
j,
lm is the maximum spring extension,
xj =
lj/
lm,
p is the persistence length,
kBT is the energy unit, and
kp is the spring constant. Note that each spring consists of the attractive wormlike chain potential and a repulsive potential such that a non-zero equilibrium spring length can be imposed. For the performance of different spring models for a RBC membrane, we refer to
ref. 28.
The membrane viscosity can be modeled by a viscous force assigned to each spring. Thus, we introduce dissipative and random forces for each spring FDij and FRij, respectively, similar to those in the theoretical framework of the fluid particle model.29 This force pair satisfies the fluctuation–dissipation balance in order to maintain a consistent membrane temperature and is given by
| | | FDij = −γTvij − γC(vij·eij)eij, | (3) |
| | 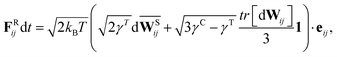 | (4) |
where
γT and
γC are dissipative parameters and the superscripts T and C denote the “translational” and “central” components,
vij is the relative velocity of spring ends,
tr[d
Wij] is the trace of a random matrix of independent Wiener increments d
Wij, and
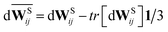
is the traceless symmetric part. Note that the condition 3
γC −
γT ≥ 0 has to be satisfied.
The bending energy of the RBC membrane is defined as
| | 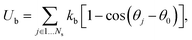 | (5) |
where
kb is the bending constant,
θj is the instantaneous angle between two adjacent triangles with the common edge
j, and
θ0 is the spontaneous angle. The area and volume conservation constraints are given by
| | 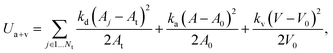 | (6) |
where
Nt is the number of triangles in the network,
At is the triangle area, and
kd,
ka and
kv are the local area, global area and volume constraint coefficients, respectively. The terms
A and
V are the total cell area and volume, while
A0 and
V0 are the desired total area and volume, respectively. More details of the RBC model can be found in
ref. 27 and 28.
2.1.2 Membrane elastic properties.
A linear analysis of a regular hexagonal network27,28 leads to relations between the model parameters and the membrane's macroscopic properties (e.g., shear, area-compression, and Young's moduli). For example, the membrane shear modulus is given by| | 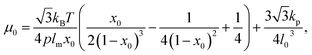 | (7) |
where l0 is the equilibrium spring length and x0 = l0/lm = 2.2. Furthermore, the area-compression K and Young's Y moduli can be computed as 2μ0 + ka + kd and 4Kμ0/(K + μ0), respectively. The model bending coefficient kb can be related to the macroscopic bending rigidity κ of the Helfrich curvature–elasticity model30 by 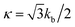 .23,31 Finally, the membrane shear viscosity is equal to
.23,31 Finally, the membrane shear viscosity is equal to 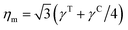 .
.
Cell macroscopic properties (μ0, K, Y, κ, and ηm) are selected as input variables, while the mesoscopic model parameters are calculated from the above equations without any further adjustment. For instance, the spring parameters can be uniquely computed for a given μ0 using eqn (7) and the fact that the spring force vanishes at l0. We also assume that x0 = 2.2 is a constant (see ref. 28), since it affects only non-linear cell deformation. The membrane bending rigidity and viscosity relations are rather straightforward, while the area and volume constraint coefficients are set large enough to properly approximate the incompressibility of the membrane and inner cytosol. We also employ a “stress-free” membrane model27,28 obtained by computational annealing, which assumes that the equilibrium length l0i of each spring is equal to the edge length after initial triangulation for i = 1,…,Ns. The “stress-free” model provides a membrane network free of local stress anomalies.
2.1.3 Inter-cell aggregation interactions.
The cell–cell aggregation interactions between RBCs32 are modeled phenomenologically using the Morse potential| | | UM(r) = De[e2β(r0−r)−2eβ(r0−r)], | (8) |
where r is the separation distance, r0 is the zero-force distance, De is the well depth of the potential, and β characterizes the interaction range. The Morse potential interactions are implemented between every two vertices of separate RBCs if they are within a defined potential cutoff radius rM. The Morse interactions consist of a short-range repulsive force when r < r0 and of a long-range attractive force for r > r0. However, such repulsive interactions cannot prevent two RBCs from an overlap. To guarantee no overlap among cells we also employ specular reflections of cell vertices on membranes of other cells.
The model for the above aggregation interactions describes only RBC–RBC interactions and is aimed to reproduce normal (healthy) RBC aggregation properties. RBC aggregation may change in several hematologic diseases and disorders (e.g., sickle-cell anemia, Gaucher's disease),33,34 which can be captured by proper tuning of the Morse potential strength. In some diseases (e.g., sickle-cell anemia) aggregation between RBCs and WBCs may also exist,35 where a similar modeling strategy can be employed. Finally, WBCs may adhere to vascular endothelium due to specific interactions between receptors on a WBC and ligands at a vessel wall.1 To model such interactions, the adhesive dynamics model of ref. 36 can be employed, which is based on the stochastic bond formation/dissociation strategy. Note that in this paper only the effect of RBC–RBC aggregation interactions is included.
2.2 Smoothed dissipative particle dynamics
SDPD22 is a particle-based mesoscale hydrodynamic simulation technique, which combines two frequently employed approaches: smoothed particle hydrodynamics37,38 and dissipative particle dynamics.39,40 The advantage of the SDPD approach is that the dynamic viscosity of a fluid and its equation of state can be input directly. Thus, the fluid compressibility can be well controlled. Nevertheless, the approximation for the simulated fluid viscosity is precise only if the cutoff radius and/or particle density are large enough. Therefore, it is always advisable to verify the value of the fluid viscosity independently in simulations.
The SDPD system consists of N point particles of mass mi, position ri and velocity vi. SDPD particles interact through three pairwise forces: conservative (C), dissipative (D), and random (R), such that the force on particle i is given by
| | 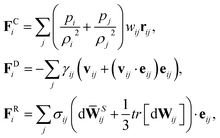 | (9) |
where
eij =
rij/|
rij| and
vij =
vi −
vj.
pi and
pj are particle pressures assumed to follow the equation of state
p =
p0(
ρ/
ρ0)
α −
b with
p0,
ρ0,
α, and
b being model parameters, see
Table 1. The particle density is calculated locally and defined as
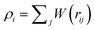
with
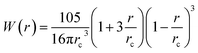
being the Lucy function, where
rc is the cutoff radius. Note that
W(
r) is chosen such that ∇
W(
r) = −
rw(
r) with
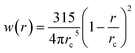
. The coefficients
γij and
σij define the strength of dissipative and random forces and are equal to
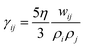
and
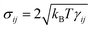
, respectively. The notation
tr[d
Wij] corresponds to the trace of a random matrix of independent Wiener increments d
Wij, and d
![[W with combining macron]](https://www.rsc.org/images/entities/b_char_0057_0304.gif) Sij
Sij is the traceless symmetric part.
Table 1 SDPD fluid parameters used in simulations. n is fluid's number density and η is the dynamic viscosity. In the simulation parameters, mass is given in units of fluid particle mass m=1, length in units of r'=2rc/3, and energy in units of E = 2.5kBT, where rc and kBT values are given in the table
|
p
0
|
ρ
0
|
α
|
b
|
r
c
|
η
0
|
n
|
k
B
T
|
η
|
| 100 |
3.0 |
7 |
80 |
1.5 |
100.0 |
3 |
0.4 |
107.6 |
The time evolution of velocities and positions of particles is determined by Newton's second law of motion
| | 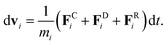 | (11) |
The above equations of motion are integrated using the velocity–Verlet algorithm.
2.3 Simulation setup and parameters
The solvent is represented by a collection of particles with the parameters outlined in Table 1. Note that the dynamic viscosity η is slightly larger than the desired viscosity η0, which has been computed from a Couette flow simulation. η will converge to η0 if we increase rc and/or n, which would also lead to a larger computational cost.
To define the cell shapes and the flow geometry, we introduce an effective RBC diameter 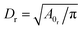 , which is based on the RBC membrane area A0r (the subscript ‘r’ corresponds to the red cell). Similarly, we define an effective WBC diameter
, which is based on the RBC membrane area A0r (the subscript ‘r’ corresponds to the red cell). Similarly, we define an effective WBC diameter 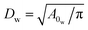 (the subscript ‘w’ corresponds to the white cell). The cell shapes (biconcave for a RBC and spherical for a WBC) are imposed by a combination of the cell area A0 and volume V0, which can be described by a reduced volume for both cells as V0r/(πDr3/6) = 0.642 and V0w/(πDw3/6) = 1.02. Note that the imposed WBC volume is 2% larger than the volume of a corresponding sphere, which leads to weak membrane tension and reduces WBC deformability, similar to a realistic WBC.41–43 The other cell membrane properties and parameters are given in Table 2. The blood cells are suspended in a Newtonian fluid (plasma), which is represented by a collection of SDPD particles. The cells are coupled to the fluid by friction which includes only dissipative and random forces.27,28
(the subscript ‘w’ corresponds to the white cell). The cell shapes (biconcave for a RBC and spherical for a WBC) are imposed by a combination of the cell area A0 and volume V0, which can be described by a reduced volume for both cells as V0r/(πDr3/6) = 0.642 and V0w/(πDw3/6) = 1.02. Note that the imposed WBC volume is 2% larger than the volume of a corresponding sphere, which leads to weak membrane tension and reduces WBC deformability, similar to a realistic WBC.41–43 The other cell membrane properties and parameters are given in Table 2. The blood cells are suspended in a Newtonian fluid (plasma), which is represented by a collection of SDPD particles. The cells are coupled to the fluid by friction which includes only dissipative and random forces.27,28
Table 2 Model parameters of red (RBC) and white (WBC) blood cells
| Type |
N
v
|
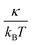
|
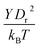
|
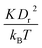
|
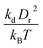
|
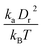
|
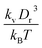
|
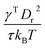
|
| RBC |
500 |
70 |
1.8 × 105 |
2.2 × 106 |
4.2 × 104 |
2.1 × 106 |
1.4 × 107 |
66.44 |
| WBC |
1000 |
1300 |
7.8 × 106 |
2.6 × 107 |
4.2 × 105 |
2.1 × 107 |
1.4 × 108 |
66.44 |
We simulate blood flow in a tube of diameter Dt = 3.08Dr, which is driven by a constant force applied to the solvent particles, equivalently to a constant pressure gradient. To characterize the flow, we define a dimensionless shear rate as
| | 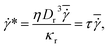 | (12) |
where
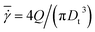
is the average shear rate (or pseudo-shear rate),
Q is the volumetric flow rate,
η is the solvent viscosity, and
τ =
ηDr3/
κr is a characteristic cell relaxation time. For comparison in physical units, we assume cell diameters
Dr = 6.5 μm and
Dw = 10 μm, which implies that
Dw ≃ 1.54
Dr, tube diameter
Dt = 20 μm, plasma viscosity
η = 1.2 × 10
−3 Pa s, temperature
T = 37 °C, membrane Young's modulus
Yr = 18.9 μN m
−1, and bending rigidity
κr = 70
kBT = 3 × 10
−19 J. Then, the characteristic RBC relaxation time is
τ = 1.1 s and therefore, the pseudo-shear rate
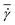
is roughly equivalent in magnitude to
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
* in inverse seconds.
RBC aggregation interactions, if used, were mediated by the Morse potential (eqn (8)). The Morse potential parameters were set to De = 0.75kBT, r0 = 0.046Dr, β = 9.75Dr−1, and rM = 0.17Dr. For more details see ref. 32.
3 Results and discussion
In the presentation of WBC margination results, for convenience, we schematically divide flow rates and Ht values in several groups. In the subsequent discussion, low flow rates are referred to as the rates of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≲ 20, intermediate flow rates are in the range of 20 ≲
* ≲ 20, intermediate flow rates are in the range of 20 ≲ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≲ 90, and high flow rates are for
* ≲ 90, and high flow rates are for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≳ 90. Physiologically, the high shear rates correspond to the rates in the arteriolar part of microcirculation, while low and intermediate shear rates are characteristic of venular blood flow.44,45 Similarly, we define low hematocrits as Ht ≲ 0.2, intermediate hematocrits as 0.2 ≲ Ht ≲ 0.4, and high hematocrits as Ht ≳ 0.4. Intermediate Ht values are specifically relevant for microcirculatory blood flow, while low Ht values may still be present in some parts of microcirculation.44 High Ht values are not likely to occur in healthy microvascular blood flow, but they are relevant within tumor microvasculature, since it is often subject to hemo-concentration due to plasma leakage.46
* ≳ 90. Physiologically, the high shear rates correspond to the rates in the arteriolar part of microcirculation, while low and intermediate shear rates are characteristic of venular blood flow.44,45 Similarly, we define low hematocrits as Ht ≲ 0.2, intermediate hematocrits as 0.2 ≲ Ht ≲ 0.4, and high hematocrits as Ht ≳ 0.4. Intermediate Ht values are specifically relevant for microcirculatory blood flow, while low Ht values may still be present in some parts of microcirculation.44 High Ht values are not likely to occur in healthy microvascular blood flow, but they are relevant within tumor microvasculature, since it is often subject to hemo-concentration due to plasma leakage.46
3.1 Physical basis of WBC margination
Fig. 1 shows sample snapshots from simulations for two different flow conditions. In the case of Ht = 0.3 and an intermediate flow rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 32, as displayed in Fig. 1a, a WBC is clearly marginated (i.e. located next to the wall), while for Ht = 0.2 and a high flow rate
* = 32, as displayed in Fig. 1a, a WBC is clearly marginated (i.e. located next to the wall), while for Ht = 0.2 and a high flow rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 115, as shown in Fig. 1b, a WBC remains in the vessel center. To characterize the WBC position within the tube, we measure its center-of-mass distribution over time, which reflects the probability of a WBC to be at a certain position r in the tube, as shown in Fig. 2. A peak near the position of 2r/Dt ≈ 0.5 (or r ≈ 5 μm) indicates that the WBC is marginated with high probability. At low Ht, WBC margination is weak, since the volume fraction of RBCs is not high enough to effectively push the WBC close to the wall; however, at low flow rates (
* = 115, as shown in Fig. 1b, a WBC remains in the vessel center. To characterize the WBC position within the tube, we measure its center-of-mass distribution over time, which reflects the probability of a WBC to be at a certain position r in the tube, as shown in Fig. 2. A peak near the position of 2r/Dt ≈ 0.5 (or r ≈ 5 μm) indicates that the WBC is marginated with high probability. At low Ht, WBC margination is weak, since the volume fraction of RBCs is not high enough to effectively push the WBC close to the wall; however, at low flow rates (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≈ 15), a WBC might still get marginated, as shown in Fig. 2a. It is noteworthy that even at low Ht a WBC is expelled from the tube center by RBCs. As hematocrit is increased, we observe stronger margination as being most efficient within the range of Ht = 0.2–0.4. However, at even higher Ht = 0.5 WBC margination seems to be attenuated, in particular, for low flow rates (
* ≈ 15), a WBC might still get marginated, as shown in Fig. 2a. It is noteworthy that even at low Ht a WBC is expelled from the tube center by RBCs. As hematocrit is increased, we observe stronger margination as being most efficient within the range of Ht = 0.2–0.4. However, at even higher Ht = 0.5 WBC margination seems to be attenuated, in particular, for low flow rates (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≈ 15). The mechanism for the margination attenuation phenomena at high Ht has been previously discussed in 2D simulations.21 It arises due to interactions of a WBC with RBCs in flow. In ref. 21 it has been shown that for low enough Ht the region in front of a marginated WBC remains virtually free of RBCs, which could otherwise interfere with the WBC and lift it off the wall. However, at large enough Ht due to RBC crowding, a marginated WBC may often encounter RBCs in front, which helps to effectively displace it away from the wall, leading to a lower margination probability than for lower Ht. The effect of hematocrit becomes weaker for higher flow rates (
* ≈ 15). The mechanism for the margination attenuation phenomena at high Ht has been previously discussed in 2D simulations.21 It arises due to interactions of a WBC with RBCs in flow. In ref. 21 it has been shown that for low enough Ht the region in front of a marginated WBC remains virtually free of RBCs, which could otherwise interfere with the WBC and lift it off the wall. However, at large enough Ht due to RBC crowding, a marginated WBC may often encounter RBCs in front, which helps to effectively displace it away from the wall, leading to a lower margination probability than for lower Ht. The effect of hematocrit becomes weaker for higher flow rates (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≈ 60), as seen in Fig. 2b(b), and a WBC is found to be marginated for essentially all investigated Ht values, but again most significantly in the range Ht = 0.2–0.4.
* ≈ 60), as seen in Fig. 2b(b), and a WBC is found to be marginated for essentially all investigated Ht values, but again most significantly in the range Ht = 0.2–0.4.
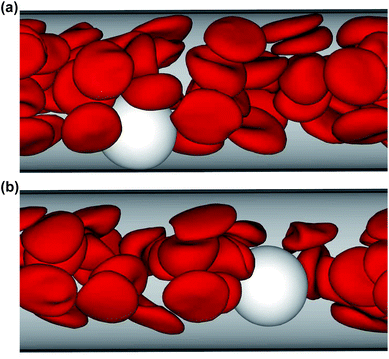 |
| | Fig. 1 Simulation snapshots of RBCs (red) and a WBC (white). The flow is from the left to the right. (a) Ht = 0.3 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 32; (b) Ht = 0.2 and * = 32; (b) Ht = 0.2 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 115. See also movies in the ESI.† * = 115. See also movies in the ESI.† | |
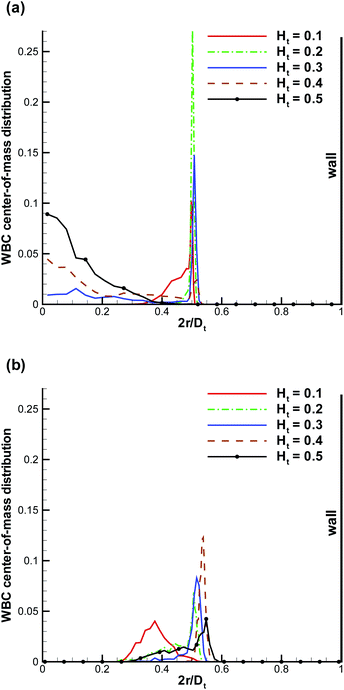 |
| | Fig. 2 WBC center-of-mass distribution with respect to the vessel position r normalized by Dt for various Ht values. (a) ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≈ 15, (b) * ≈ 15, (b) ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≈ 60. The center of the vessel is at 2r/Dt = 0, while the wall is at 2r/Dt = 1. * ≈ 60. The center of the vessel is at 2r/Dt = 0, while the wall is at 2r/Dt = 1. | |
To verify this mechanism in 3D, we plot in Fig. 3 the probability of RBCs to be around a marginated WBC for different Ht values, which is proportional to the local RBC volume fraction. The RBC distribution is calculated in a co-moving coordinate system of the WBC center-of-mass and with the condition that the WBC center is less than 0.5Dw (5 μm) away from the wall. This condition is equivalent to the WBC nearly touching the wall. An increase of Ht from 0.4 to 0.5 results in a substantial increase of RBC crowding in the region in front of a WBC, while for Ht ≤ 0.4 this region remains virtually void of RBCs. To demonstrate the quantitative differences in RBC crowding, one-dimensional cuts along the y-axis at an x position of 8 μm away from the WBC center are displayed in Fig. 4. At Ht = 0.5 a strong increase of the RBC presence in the region in front of a marginated WBC is clearly observed. This margination–attenuation mechanism at high Ht does not contradict the main hypothesis that WBC margination arises from a competition of lift forces on RBCs and WBCs and their interactions in flow, which would imply that margination should become even stronger at high Ht. We hypothesize that even at high hematocrit WBCs are constantly marginated due to the differences in lift forces and RBC–WBC interactions; however, WBCs are almost immediately sent back to the vessel center due to local interactions with RBCs near the wall. As a result, the time a WBC is marginated at high Ht can be short, which is reflected in the center-of-mass probability distribution. Finally, RBC aggregation interactions can improve WBC margination at higher Ht values, since the core of the flow consisting mainly of RBCs remains more compact due to inter-cell attractive interactions, which is consistent with findings in ref. 21. However, such an effect can only occur at low flow rates, because RBC aggregate structures are fragile and break up at high enough flow rates.
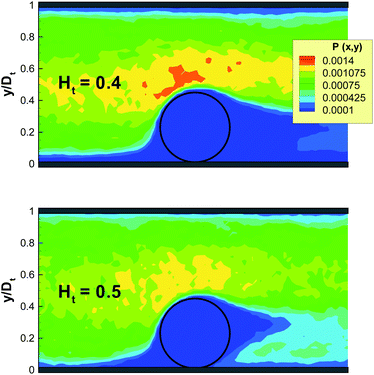 |
| | Fig. 3 Local RBC probability to be around a marginated WBC for Ht = 0.4 and Ht = 0.5 at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≈ 60. The probability is calculated in a co-moving coordinate system of the WBC center-of-mass and only for time instances, when the WBC center is within 0.5Dw (5 μm) from the wall. The black circle schematically shows a WBC. Only a part of the vessel is shown. No RBC aggregation is present. * ≈ 60. The probability is calculated in a co-moving coordinate system of the WBC center-of-mass and only for time instances, when the WBC center is within 0.5Dw (5 μm) from the wall. The black circle schematically shows a WBC. Only a part of the vessel is shown. No RBC aggregation is present. | |
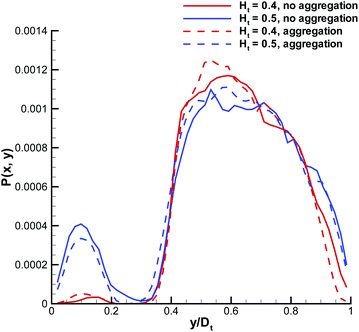 |
| | Fig. 4 Local RBC distribution cuts from the plots in Fig. 3 along the y-axis and 8 μm away from the WBC center. Both cases with and without RBC aggregation are shown. | |
3.2 WBC margination diagrams
To present our simulation data for a wide range of Ht values and flow rates, we construct WBC margination diagrams, which are based on a margination probability. The margination probability is defined as the probability of a WBC center-of-mass to be within a certain distance away from the wall, i.e., for rw < d, where rw is the distance of the WBC center-of-mass from the wall and d is a selected value. In principle, the margination probability is an integral of the WBC center-of-mass probability distribution from 0.5Dt − d to 0.5Dt. Fig. 5 shows two margination diagrams for d = 5 μm (i.e. the WBC membrane is nearly touching the vessel wall) and d = 5.5 μm (i.e. a distance of 0.5 μm between the WBC membrane and wall) without RBC aggregation interactions. Both diagrams show that WBC margination occurs in a certain range of Ht and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * values. In terms of hematocrit, the margination is mainly observed for Ht ∈ (0.2,0.4), which is consistent with hematocrit values in our microcirculatory system, where Ht magnitudes are lower than the systemic hematocrit of Ht = 0.4–0.45. As we mentioned before, margination at low Ht does not occur due to a low volume fraction of RBCs, since they are responsible for WBC margination, while at high Ht the margination effect also vanishes due to WBC–RBC interactions discussed above. With respect to the flow rate, we found WBC margination to occur mainly for
* values. In terms of hematocrit, the margination is mainly observed for Ht ∈ (0.2,0.4), which is consistent with hematocrit values in our microcirculatory system, where Ht magnitudes are lower than the systemic hematocrit of Ht = 0.4–0.45. As we mentioned before, margination at low Ht does not occur due to a low volume fraction of RBCs, since they are responsible for WBC margination, while at high Ht the margination effect also vanishes due to WBC–RBC interactions discussed above. With respect to the flow rate, we found WBC margination to occur mainly for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≲ 130. This range of
* ≲ 130. This range of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * covers mainly the flow rates encountered in the venular part of microcirculation, which is consistent with experimental observations that WBC margination and adhesion primarily occurs in venules and not arterioles.6,16,18 As an estimation, the flow rates in the venular part of microcirculation correspond to the range of
* covers mainly the flow rates encountered in the venular part of microcirculation, which is consistent with experimental observations that WBC margination and adhesion primarily occurs in venules and not arterioles.6,16,18 As an estimation, the flow rates in the venular part of microcirculation correspond to the range of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≲ 90, while in arteriolar part the flow rates are higher with
* ≲ 90, while in arteriolar part the flow rates are higher with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≳ 120.44,45
* ≳ 120.44,45
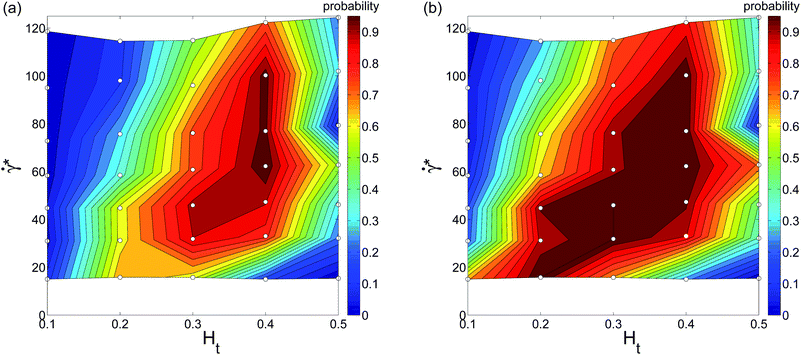 |
| | Fig. 5 WBC margination probability diagrams calculated for (a) rw < 5 μm and (b) rw < 5.5 μm, where rw is the distance of the WBC center-of-mass from the wall. The small white circles in the diagrams indicate performed simulations. No aggregation interactions between RBCs are imposed here. | |
To study the effect of RBC aggregation on WBC margination, we have also performed a set of simulations, where RBC aggregation has been explicitly included following the RBC aggregation model of ref. 32, which has been shown to reproduce the viscosity and shear-thinning behavior of whole blood very well. Fig. 6 presents the corresponding WBC margination diagrams for simulations where RBC aggregation interactions are included. The main effect of RBC aggregation is that the WBC margination region expands along the Ht axis such that RBC aggregation enhances WBC margination at high Ht values as well as at low hematocrit. As expected, a stronger effect of RBC aggregation is found at low ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * leading to WBC margination even at very low flow rates. Thus, RBC aggregation presents an additional force that expels WBCs from the RBC core due to attractive interactions between RBCs. At high enough flow rates, RBC aggregation does not play a significant role,32 and therefore there is no substantial change in the margination diagram at high
* leading to WBC margination even at very low flow rates. Thus, RBC aggregation presents an additional force that expels WBCs from the RBC core due to attractive interactions between RBCs. At high enough flow rates, RBC aggregation does not play a significant role,32 and therefore there is no substantial change in the margination diagram at high ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *. The RBC aggregation effect on WBC margination is qualitatively similar to that observed in simulations of 2D model systems.21 The comparison of Fig. 5 and 6 indicates that WBC margination could still be possible in the limit of
*. The RBC aggregation effect on WBC margination is qualitatively similar to that observed in simulations of 2D model systems.21 The comparison of Fig. 5 and 6 indicates that WBC margination could still be possible in the limit of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * → 0 for the case of RBC aggregation.
* → 0 for the case of RBC aggregation.
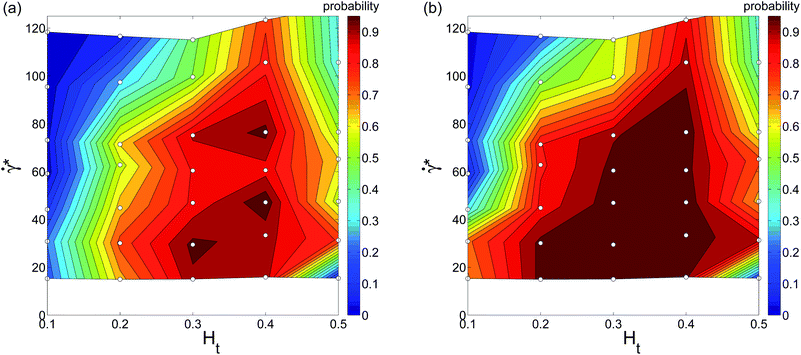 |
| | Fig. 6 WBC margination probability diagrams calculated for (a) rw < 5 μm and (b) rw < 5.5 μm for the case of RBC aggregation. The small white circles in the diagrams indicate performed simulations. | |
3.3 Deformation of a marginated WBC
A marginated WBC is subject to flow-induced deformation, since it experiences high shear stresses due to near wall fluid flow and RBCs. To quantify deformation of a marginated WBC we compute the ratios Dxw/D′w and Drw/D′w (shown in Fig. 7), which describe WBC deformation along the tube axis x and along the radial direction, respectively. Note that we use the notation Dw′ here, which is the WBC diameter calculated in equilibrium; it may slightly differ from Dw since the imposed WBC volume is 2% larger than the volume of a sphere with the diameter Dw. The WBC deformation does not seem to be very significant and lies within approximately 5%. Deformation of adhered WBCs in flow has been measured both experimentally6,47 and in simulations;48,49 these studies indicate a WBC deformation up to about 20–30% along the flow for comparable flow rates. The deformation of a WBC in shear flow is expected to be significantly lower than that of an adhered WBC due to cell spreading on the wall in the latter case. Thus, our modeled WBC approximates a nearly non-deformable sphere in flow, which is similar to observed shapes of flowing WBCs in experiments. The mechanical properties of WBCs have been measured in a number of experiments,41–43 which estimate cell stiffness and its cortical tension. A direct comparison of WBC mechanical properties is currently difficult, since our WBC model does not consider an inner cytoskeleton; however, the membrane tension of the modeled WBC has the right order of magnitude. The effect of WBC deformation on margination properties has been investigated for 2D model systems21 showing that a more deformable WBC exhibits a reduction in its margination at high flow rates, since the WBC shape may significantly depart from a sphere. In 3D, a similar trend is expected.
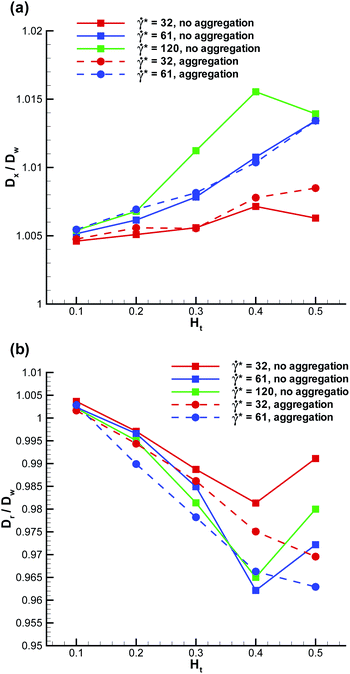 |
| | Fig. 7 Deformation of a marginated WBC (a) along the tube axis – Dxw/D′w and (b) along the radial direction – Drw/D′w. D′w denotes the WBC diameter in the absence of flow. | |
3.4 Force on a marginated WBC
WBC deformation in the radial direction appears to be stronger than that along the flow, see Fig. 7, which points to the existence of a compressive force normal to the wall. Similar conclusion can be drawn from the fluid flow, since blood plasma and RBCs have to go past a marginated WBC. We have measured the maximum force on a marginated WBC normal to the wall, defined as a cumulative force due to interactions with the blood plasma and RBCs, which is shown in Fig. 8. The positive force values indicate that a WBC is pushed towards the wall along the radial direction. The normal force on a marginated WBC is also expected to aid efficient WBC adhesion to the wall, which is important for proper WBC functioning.2,3 A recent simulation study50 has attempted to estimate the maximum pressure normal to the wall on a fixed spherical-like obstacle in blood flow, which mimics an adhered WBC. The reported values for the normal pressure are up to approximately 30 Pa. If we convert our maximum force of about 130 pN to a normal pressure by dividing the force by the area πDw2/4 we obtain the value of about 2 Pa. This pressure is much smaller than that predicted in ref. 50, which is expected to be due to the fixed obstacle position and a much stronger WBC confinement Dw/Dt = 0.75 used in ref. 50 in comparison to our simulations with Dw/Dt = 0.5.
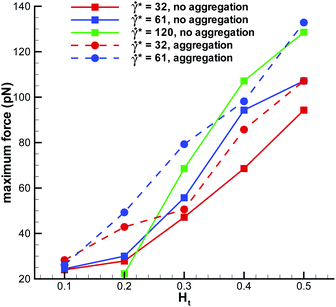 |
| | Fig. 8 Maximum force on a marginated WBC normal to the wall (radial direction). Positive force values indicate that a WBC is pushed toward the wall. | |
3.5 Effect of WBC margination on the flow resistance
We have also examined the effect of a marginated WBC on the blood flow resistance in a microvessel. To characterize the flow resistance, we define an apparent viscosity (or average blood flow viscosity), which is calculated by fitting the Poiseuille law to the measured flow rate. In order to quantify the effect of a WBC on the flow resistance, we present in Fig. 9 the relative flow resistance defined as the ratio of the computed apparent viscosity of blood with a WBC to the apparent viscosity without a WBC. At high flow rates (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≈ 120), the relative flow resistance is smaller than that for low flow rates. This is consistent with the observation in Fig. 5 that the WBC is poorly marginated at high flow rates and therefore, the resistance values mainly reflect the effect of an increased total volume fraction of cells due to the presence of a WBC. At intermediate and low flow rates, the presence of a WBC results in an increase of flow resistance by 10–30%. The relative resistance is clearly correlated with WBC margination such that WBC margination leads to a larger flow resistance. At low Ht, a WBC is not strongly marginated, and therefore the flow resistance is not significantly affected. At intermediate Ht values, where a WBC gets strongly marginated, the flow resistance reaches its maximum, while at high Ht the resistance due to a WBC slightly decreases, since WBC margination becomes less pronounced. The effect of RBC aggregation on the flow resistance due to a WBC is pronounced mainly at low flow rates, which is consistent with the RBC aggregation effect on WBC margination. Also, we expect that an increase in the flow resistance due to a marginated WBC will be smaller than 10–30% in larger vessels in comparison with the studied tube diameter of Dt = 20 μm.
* ≈ 120), the relative flow resistance is smaller than that for low flow rates. This is consistent with the observation in Fig. 5 that the WBC is poorly marginated at high flow rates and therefore, the resistance values mainly reflect the effect of an increased total volume fraction of cells due to the presence of a WBC. At intermediate and low flow rates, the presence of a WBC results in an increase of flow resistance by 10–30%. The relative resistance is clearly correlated with WBC margination such that WBC margination leads to a larger flow resistance. At low Ht, a WBC is not strongly marginated, and therefore the flow resistance is not significantly affected. At intermediate Ht values, where a WBC gets strongly marginated, the flow resistance reaches its maximum, while at high Ht the resistance due to a WBC slightly decreases, since WBC margination becomes less pronounced. The effect of RBC aggregation on the flow resistance due to a WBC is pronounced mainly at low flow rates, which is consistent with the RBC aggregation effect on WBC margination. Also, we expect that an increase in the flow resistance due to a marginated WBC will be smaller than 10–30% in larger vessels in comparison with the studied tube diameter of Dt = 20 μm.
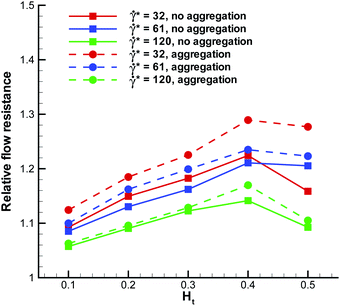 |
| | Fig. 9 Relative flow resistance for blood flow in a vessel with a WBC. It is defined as the ratio of calculated apparent viscosity with a WBC to the apparent viscosity of blood flow without a WBC. | |
3.6 Translational and rotational velocities of a marginated WBC
The WBC translational velocity can be used as an indicator for WBC margination, since the velocity of a marginated WBC is significantly lower than that in the vessel center, as has been pointed out in ref. 21. 3D simulation results for the translational velocity of a WBC for different flow rates and Ht values are shown in Fig. 10. A drop in WBC velocity is clearly observed when a WBC is marginated for the intermediate values of Ht = 0.2–0.4. Also, we notice that there is no significant dependence of the normalized translational velocity on the flow rate, so that this criterion can be universally applied for WBC margination detection. The opposite trend is found for the WBC angular velocity ω in blood flow, which is shown in Fig. 11. Here, ω increases with increasing Ht in the range Ht = 0.2–0.4, indicating that the rotational velocity of a marginated WBC is larger than that in the vessel center. Such an effect is expected due to larger shear rates near the wall than in the tube center. WBC rotational velocity is likely to be difficult to measure in experiments, so that this property cannot be employed easily for WBC margination detection. Finally, the rescaled angular velocity ωDw/(2ū) shows only a very weak dependence on ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *, which indicates that the scale factor 2ū/Dw captures the essential dependence of the angular velocity on the flow rate.
*, which indicates that the scale factor 2ū/Dw captures the essential dependence of the angular velocity on the flow rate.
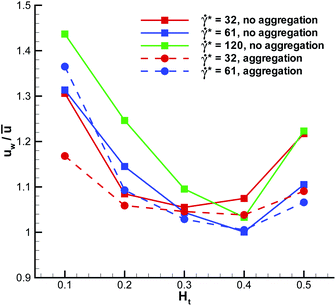 |
| | Fig. 10 Translational velocity of a WBC normalized by the average flow velocity for different flow rates and Ht values. | |
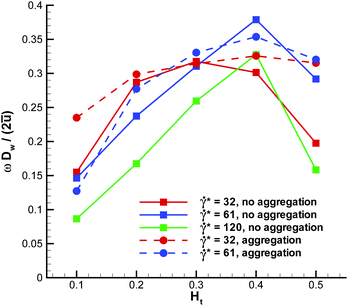 |
| | Fig. 11 Angular velocity of a WBC for different flow rates and Ht values. The angular velocity is directed perpendicular to the plane going through the tube axis and WBC center-of-mass. | |
4 Summary and conclusions
In blood flow, RBCs migrate toward the vessel center, while WBCs migrate or marginate to the walls. WBC margination is governed by flow-induced hydrodynamic cell-wall interactions (i.e., lift forces) and interactions among blood cells. We employed 3D mesoscopic simulations of blood flow to predict WBC margination for a wide range of Ht values and flow rates. WBC margination occurs mainly within a region of intermediate hematocrits, Ht = 0.2–0.4, and for relatively low flow rates, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≲ 130. This range of flow rates is characteristic of the venular part of microcirculation. RBC aggregation slightly enhances WBC margination, especially at high Ht values. The deformation of marginated WBCs appears to be rather small, remaining within a few percent of the undisturbed shape. The force on marginated WBCs is directed in the normal direction toward the wall, can reach a value of several hundred pico-newtons, and might aid in better WBC adhesion to the wall. Marginated WBCs also contribute to an increase in flow resistance with up to approximately 30% for vessel diameters of 20 μm. The effect of WBC margination on the flow resistance is expected to subside as the tube diameter is increased to values several times larger than the WBC diameter. Finally, we also presented translational and rotational WBC velocities, which might be used for the detection of WBC margination in experiments.
* ≲ 130. This range of flow rates is characteristic of the venular part of microcirculation. RBC aggregation slightly enhances WBC margination, especially at high Ht values. The deformation of marginated WBCs appears to be rather small, remaining within a few percent of the undisturbed shape. The force on marginated WBCs is directed in the normal direction toward the wall, can reach a value of several hundred pico-newtons, and might aid in better WBC adhesion to the wall. Marginated WBCs also contribute to an increase in flow resistance with up to approximately 30% for vessel diameters of 20 μm. The effect of WBC margination on the flow resistance is expected to subside as the tube diameter is increased to values several times larger than the WBC diameter. Finally, we also presented translational and rotational WBC velocities, which might be used for the detection of WBC margination in experiments.
The WBC margination results can be also used to predict margination of other micro-particles and cells in blood flow, if their size and mechanical properties are similar to those of WBCs. For instance, many circulating tumor cells have a similar size and are also rather stiff.43,51 Thus, the margination of many tumor cells is also expected primarily in the venular part of microcirculation, which would imply that the tissue invasion by tumor cells present in blood largely occurs from venules. The WBC margination results can be also employed in microfluidic devices for the separation of WBCs or circulating tumor cells from whole blood. In the future, we also plan to include adhesion of WBCs explicitly in order to study their adhesive interactions with vessel walls in blood flow.
Acknowledgements
A CPU time grant by the Jülich Supercomputing center is gratefully acknowledged. Dmitry A. Fedosov also acknowledges funding by the Alexander von Humboldt Foundation. We also thank the DFG Research Unit FOR 1543 “SHENC - Shear Flow Regulation in Hemostasis” for support.
References
- T. A. Springer, Annu. Rev. Physiol., 1995, 57, 827–872 CrossRef CAS PubMed.
- K. Ley and T. F. Tedder, J. Immunol., 1995, 155, 525–528 CAS.
- R. Alon, D. A. Hammer and T. A. Springer, Nature, 1995, 374, 539–542 CrossRef CAS PubMed.
- U. Bagge and R. Karlsson, Microvasc. Res., 1980, 20, 92–95 CrossRef CAS.
- H. L. Goldsmith and S. Spain, Microvasc. Res., 1984, 27, 204–222 CrossRef CAS.
- J. C. Firrell and H. H. Lipowsky, Am. J. Physiol., 1989, 256, H1667–H1674 CAS.
- H. L. Goldsmith, G. R. Cokelet and P. Gaehtgens, Am. J. Physiol., 1989, 257, H1005–H1015 CAS.
- G. R. Cokelet and H. L. Goldsmith, Circ. Res., 1991, 68, 1–17 CrossRef CAS.
- J. B. Freund and M. M. Orescanin, J. Fluid Mech., 2011, 671, 466–490 CrossRef.
- S. K. Doddi and P. Bagchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 046318 CrossRef.
- D. A. Fedosov, B. Caswell, A. S. Popel and G. E. Karniadakis, Microcirculation, 2010, 17, 615–628 CrossRef PubMed.
- D. A. Fedosov, H. Noguchi and G. Gompper, Biomech. Model. Mechanobiol., 2013 DOI:10.1007/s10237-013-0497-9.
- I. Cantat and C. Misbah, Phys. Rev. Lett., 1999, 83, 880–883 CrossRef CAS.
- M. Abkarian, C. Lartigue and A. Viallat, Phys. Rev. Lett., 2002, 88, 068103 CrossRef.
- S. Messlinger, B. Schmidt, H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 011901 CrossRef.
- M. J. Pearson and H. H. Lipowsky, Am. J. Physiol., 2000, 279, H1460–H1471 CAS.
- K. B. Abbitt and G. B. Nash, Am. J. Physiol., 2003, 285, H229–H240 CrossRef CAS PubMed.
- A. Jain and L. L. Munn, PLoS One, 2009, 4, e7104 Search PubMed.
- C. Sun, C. Migliorini and L. L. Munn, Biophys. J., 2003, 85, 208–222 CrossRef CAS.
- J. B. Freund, Phys. Fluids, 2007, 19, 023301 CrossRef PubMed.
- D. A. Fedosov, J. Fornleitner and G. Gompper, Phys. Rev. Lett., 2012, 108, 028104 CrossRef.
- P. Espanol and M. Revenga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 026705 CrossRef.
- H. S. Seung and D. R. Nelson, Phys. Rev. A, 1988, 38, 1005–1018 CrossRef.
- G. Gompper and D. M. Kroll, J. Phys.: Condens. Matter, 1997, 9, 8795–8834 CrossRef CAS.
- D. E. Discher, D. H. Boal and S. K. Boey, Biophys. J., 1998, 75, 1584–1597 CrossRef CAS.
- H. Noguchi and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 14159–14164 CrossRef CAS PubMed.
- D. A. Fedosov, B. Caswell and G. E. Karniadakis, Biophys. J., 2010, 98, 2215–2225 CrossRef CAS PubMed.
- D. A. Fedosov, B. Caswell and G. E. Karniadakis, Comput. Meth. Appl. Mech. Eng., 2010, 199, 1937–1948 CrossRef PubMed.
- P. Espanol, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 2930–2948 CrossRef CAS.
- W. Helfrich, Z. Naturforsch., C: J. Biosci., 1973, 28, 693–703 CAS.
- G. Gompper and D. M. Kroll, J.
Phys. I, 1996, 6, 1305–1320 CrossRef.
- D. A. Fedosov, W. Pan, B. Caswell, G. Gompper and G. E. Karniadakis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11772–11777 CrossRef CAS PubMed.
- T. Adar, R. Ben-Ami, D. Elstein, A. Zimran, S. Berliner, S. Yedgar and G. Barshtein, Br. J. Haematol., 2006, 134, 432–437 CrossRef CAS PubMed.
- J. Tripette, T. Alexy, M. D. Hardy-Dessources, D. Mougenel, E. Beltan, T. Chalabi, R. Chout, M. Etienne-Julan, O. Hue, H. J. Meiselman and P. Connes, Haematologica, 2009, 94, 1060–1065 CrossRef CAS PubMed.
- V. Chaar, J. Picot, O. Renaud, P. Bartolucci, R. Nzouakou, D. Bachir, F. Galacteros, Y. Colin, C. Le Van Kim and W. El Nemer, Haematologica, 2010, 95, 1841–1848 CrossRef CAS PubMed.
- D. A. Hammer and S. M. Apte, Biophys. J., 1992, 63, 35–57 CrossRef CAS.
- L. B. Lucy, Astron. J., 1977, 82, 1013–1024 CrossRef.
- J. J. Monaghan, Annu. Rev. Astron. Astrophys., 1992, 30, 543–574 CrossRef.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- P. Espanol and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef CAS.
- C. Dong, R. Skalak, K. L. Sung, G. W. Schmid-Schönbein and S. Chien, J. Biomech. Eng., 1988, 110, 27–36 CrossRef CAS.
- E. Evans and A. Yeung, Biophys. J., 1989, 56, 151–160 CrossRef CAS.
- M. J. Rosenbluth, W. A. Lam and D. A. Fletcher, Biophys. J., 2006, 90, 2994–3003 CrossRef CAS PubMed.
- A. S. Popel and P. C. Johnson, Annu. Rev. Fluid Mech., 2005, 37, 43–69 CrossRef PubMed.
- A. R. Pries, T. W. Secomb and P. Gaehtgens, Am. J. Physiol., 1995, 269, H1713–H1722 CAS.
- E. M. Sevick and R. K. Jain, Cancer Res., 1989, 49, 3513–3519 CAS.
- E. R. Damiano, J. Westheider, A. Tözeren and K. Ley, Circ. Res., 1996, 79, 1122–1130 CrossRef CAS.
- S. Jadhav, C. D. Eggleton and K. Konstantopoulos, Biophys. J., 2005, 88, 96–104 CrossRef CAS PubMed.
- V. Pappu and P. Bagchi, Comput. Biol. Med., 2008, 38, 738–753 CrossRef CAS PubMed.
- A. H. G. Isfahani and J. B. Freund, Biophys. J., 2012, 103, 1604–1615 CrossRef CAS PubMed.
- K. G. Phillips, P. Kuhn and O. J. T. McCarty, Am. J. Physiol., 2014, 306, C80–C88 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Two movies show simulation snapshots of blood flow with a marginated white blood cell and a non-marginated white blood cell for different hematocrits and flow rates. See DOI: 10.1039/c3sm52860j |
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article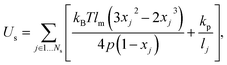
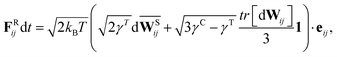
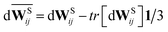 is the traceless symmetric part. Note that the condition 3γC − γT ≥ 0 has to be satisfied.
is the traceless symmetric part. Note that the condition 3γC − γT ≥ 0 has to be satisfied.
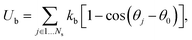
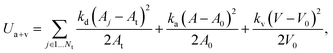
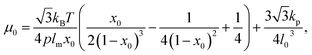
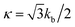 .23,31 Finally, the membrane shear viscosity is equal to
.23,31 Finally, the membrane shear viscosity is equal to 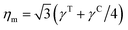 .
.
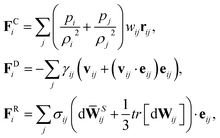
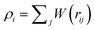 with
with 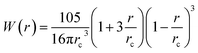 being the Lucy function, where rc is the cutoff radius. Note that W(r) is chosen such that ∇W(r) = −rw(r) with
being the Lucy function, where rc is the cutoff radius. Note that W(r) is chosen such that ∇W(r) = −rw(r) with 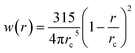 . The coefficients γij and σij define the strength of dissipative and random forces and are equal to
. The coefficients γij and σij define the strength of dissipative and random forces and are equal to 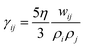 and
and 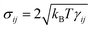 , respectively. The notation tr[dWij] corresponds to the trace of a random matrix of independent Wiener increments dWij, and d
, respectively. The notation tr[dWij] corresponds to the trace of a random matrix of independent Wiener increments dWij, and d![[W with combining macron]](https://www.rsc.org/images/entities/b_char_0057_0304.gif) Sij is the traceless symmetric part.
Sij is the traceless symmetric part.
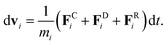
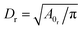 , which is based on the RBC membrane area A0r (the subscript ‘r’ corresponds to the red cell). Similarly, we define an effective WBC diameter
, which is based on the RBC membrane area A0r (the subscript ‘r’ corresponds to the red cell). Similarly, we define an effective WBC diameter 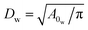 (the subscript ‘w’ corresponds to the white cell). The cell shapes (biconcave for a RBC and spherical for a WBC) are imposed by a combination of the cell area A0 and volume V0, which can be described by a reduced volume for both cells as V0r/(πDr3/6) = 0.642 and V0w/(πDw3/6) = 1.02. Note that the imposed WBC volume is 2% larger than the volume of a corresponding sphere, which leads to weak membrane tension and reduces WBC deformability, similar to a realistic WBC.41–43 The other cell membrane properties and parameters are given in Table 2. The blood cells are suspended in a Newtonian fluid (plasma), which is represented by a collection of SDPD particles. The cells are coupled to the fluid by friction which includes only dissipative and random forces.27,28
(the subscript ‘w’ corresponds to the white cell). The cell shapes (biconcave for a RBC and spherical for a WBC) are imposed by a combination of the cell area A0 and volume V0, which can be described by a reduced volume for both cells as V0r/(πDr3/6) = 0.642 and V0w/(πDw3/6) = 1.02. Note that the imposed WBC volume is 2% larger than the volume of a corresponding sphere, which leads to weak membrane tension and reduces WBC deformability, similar to a realistic WBC.41–43 The other cell membrane properties and parameters are given in Table 2. The blood cells are suspended in a Newtonian fluid (plasma), which is represented by a collection of SDPD particles. The cells are coupled to the fluid by friction which includes only dissipative and random forces.27,28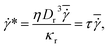
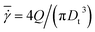 is the average shear rate (or pseudo-shear rate), Q is the volumetric flow rate, η is the solvent viscosity, and τ = ηDr3/κr is a characteristic cell relaxation time. For comparison in physical units, we assume cell diameters Dr = 6.5 μm and Dw = 10 μm, which implies that Dw ≃ 1.54Dr, tube diameter Dt = 20 μm, plasma viscosity η = 1.2 × 10−3 Pa s, temperature T = 37 °C, membrane Young's modulus Yr = 18.9 μN m−1, and bending rigidity κr = 70kBT = 3 × 10−19 J. Then, the characteristic RBC relaxation time is τ = 1.1 s and therefore, the pseudo-shear rate
is the average shear rate (or pseudo-shear rate), Q is the volumetric flow rate, η is the solvent viscosity, and τ = ηDr3/κr is a characteristic cell relaxation time. For comparison in physical units, we assume cell diameters Dr = 6.5 μm and Dw = 10 μm, which implies that Dw ≃ 1.54Dr, tube diameter Dt = 20 μm, plasma viscosity η = 1.2 × 10−3 Pa s, temperature T = 37 °C, membrane Young's modulus Yr = 18.9 μN m−1, and bending rigidity κr = 70kBT = 3 × 10−19 J. Then, the characteristic RBC relaxation time is τ = 1.1 s and therefore, the pseudo-shear rate 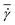 is roughly equivalent in magnitude to
is roughly equivalent in magnitude to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * in inverse seconds.
* in inverse seconds.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≲ 20, intermediate flow rates are in the range of 20 ≲
* ≲ 20, intermediate flow rates are in the range of 20 ≲ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≲ 90, and high flow rates are for
* ≲ 90, and high flow rates are for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≳ 90. Physiologically, the high shear rates correspond to the rates in the arteriolar part of microcirculation, while low and intermediate shear rates are characteristic of venular blood flow.44,45 Similarly, we define low hematocrits as Ht ≲ 0.2, intermediate hematocrits as 0.2 ≲ Ht ≲ 0.4, and high hematocrits as Ht ≳ 0.4. Intermediate Ht values are specifically relevant for microcirculatory blood flow, while low Ht values may still be present in some parts of microcirculation.44 High Ht values are not likely to occur in healthy microvascular blood flow, but they are relevant within tumor microvasculature, since it is often subject to hemo-concentration due to plasma leakage.46
* ≳ 90. Physiologically, the high shear rates correspond to the rates in the arteriolar part of microcirculation, while low and intermediate shear rates are characteristic of venular blood flow.44,45 Similarly, we define low hematocrits as Ht ≲ 0.2, intermediate hematocrits as 0.2 ≲ Ht ≲ 0.4, and high hematocrits as Ht ≳ 0.4. Intermediate Ht values are specifically relevant for microcirculatory blood flow, while low Ht values may still be present in some parts of microcirculation.44 High Ht values are not likely to occur in healthy microvascular blood flow, but they are relevant within tumor microvasculature, since it is often subject to hemo-concentration due to plasma leakage.46
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 32, as displayed in Fig. 1a, a WBC is clearly marginated (i.e. located next to the wall), while for Ht = 0.2 and a high flow rate
* = 32, as displayed in Fig. 1a, a WBC is clearly marginated (i.e. located next to the wall), while for Ht = 0.2 and a high flow rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 115, as shown in Fig. 1b, a WBC remains in the vessel center. To characterize the WBC position within the tube, we measure its center-of-mass distribution over time, which reflects the probability of a WBC to be at a certain position r in the tube, as shown in Fig. 2. A peak near the position of 2r/Dt ≈ 0.5 (or r ≈ 5 μm) indicates that the WBC is marginated with high probability. At low Ht, WBC margination is weak, since the volume fraction of RBCs is not high enough to effectively push the WBC close to the wall; however, at low flow rates (
* = 115, as shown in Fig. 1b, a WBC remains in the vessel center. To characterize the WBC position within the tube, we measure its center-of-mass distribution over time, which reflects the probability of a WBC to be at a certain position r in the tube, as shown in Fig. 2. A peak near the position of 2r/Dt ≈ 0.5 (or r ≈ 5 μm) indicates that the WBC is marginated with high probability. At low Ht, WBC margination is weak, since the volume fraction of RBCs is not high enough to effectively push the WBC close to the wall; however, at low flow rates (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≈ 15), a WBC might still get marginated, as shown in Fig. 2a. It is noteworthy that even at low Ht a WBC is expelled from the tube center by RBCs. As hematocrit is increased, we observe stronger margination as being most efficient within the range of Ht = 0.2–0.4. However, at even higher Ht = 0.5 WBC margination seems to be attenuated, in particular, for low flow rates (
* ≈ 15), a WBC might still get marginated, as shown in Fig. 2a. It is noteworthy that even at low Ht a WBC is expelled from the tube center by RBCs. As hematocrit is increased, we observe stronger margination as being most efficient within the range of Ht = 0.2–0.4. However, at even higher Ht = 0.5 WBC margination seems to be attenuated, in particular, for low flow rates (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≈ 15). The mechanism for the margination attenuation phenomena at high Ht has been previously discussed in 2D simulations.21 It arises due to interactions of a WBC with RBCs in flow. In ref. 21 it has been shown that for low enough Ht the region in front of a marginated WBC remains virtually free of RBCs, which could otherwise interfere with the WBC and lift it off the wall. However, at large enough Ht due to RBC crowding, a marginated WBC may often encounter RBCs in front, which helps to effectively displace it away from the wall, leading to a lower margination probability than for lower Ht. The effect of hematocrit becomes weaker for higher flow rates (
* ≈ 15). The mechanism for the margination attenuation phenomena at high Ht has been previously discussed in 2D simulations.21 It arises due to interactions of a WBC with RBCs in flow. In ref. 21 it has been shown that for low enough Ht the region in front of a marginated WBC remains virtually free of RBCs, which could otherwise interfere with the WBC and lift it off the wall. However, at large enough Ht due to RBC crowding, a marginated WBC may often encounter RBCs in front, which helps to effectively displace it away from the wall, leading to a lower margination probability than for lower Ht. The effect of hematocrit becomes weaker for higher flow rates (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≈ 60), as seen in Fig. 2b(b), and a WBC is found to be marginated for essentially all investigated Ht values, but again most significantly in the range Ht = 0.2–0.4.
* ≈ 60), as seen in Fig. 2b(b), and a WBC is found to be marginated for essentially all investigated Ht values, but again most significantly in the range Ht = 0.2–0.4.

![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 32; (b) Ht = 0.2 and
* = 32; (b) Ht = 0.2 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 115. See also movies in the ESI.†
* = 115. See also movies in the ESI.†
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * values. In terms of hematocrit, the margination is mainly observed for Ht ∈ (0.2,0.4), which is consistent with hematocrit values in our microcirculatory system, where Ht magnitudes are lower than the systemic hematocrit of Ht = 0.4–0.45. As we mentioned before, margination at low Ht does not occur due to a low volume fraction of RBCs, since they are responsible for WBC margination, while at high Ht the margination effect also vanishes due to WBC–RBC interactions discussed above. With respect to the flow rate, we found WBC margination to occur mainly for
* values. In terms of hematocrit, the margination is mainly observed for Ht ∈ (0.2,0.4), which is consistent with hematocrit values in our microcirculatory system, where Ht magnitudes are lower than the systemic hematocrit of Ht = 0.4–0.45. As we mentioned before, margination at low Ht does not occur due to a low volume fraction of RBCs, since they are responsible for WBC margination, while at high Ht the margination effect also vanishes due to WBC–RBC interactions discussed above. With respect to the flow rate, we found WBC margination to occur mainly for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≲ 130. This range of
* ≲ 130. This range of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * covers mainly the flow rates encountered in the venular part of microcirculation, which is consistent with experimental observations that WBC margination and adhesion primarily occurs in venules and not arterioles.6,16,18 As an estimation, the flow rates in the venular part of microcirculation correspond to the range of
* covers mainly the flow rates encountered in the venular part of microcirculation, which is consistent with experimental observations that WBC margination and adhesion primarily occurs in venules and not arterioles.6,16,18 As an estimation, the flow rates in the venular part of microcirculation correspond to the range of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≲ 90, while in arteriolar part the flow rates are higher with
* ≲ 90, while in arteriolar part the flow rates are higher with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≳ 120.44,45
* ≳ 120.44,45
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * leading to WBC margination even at very low flow rates. Thus, RBC aggregation presents an additional force that expels WBCs from the RBC core due to attractive interactions between RBCs. At high enough flow rates, RBC aggregation does not play a significant role,32 and therefore there is no substantial change in the margination diagram at high
* leading to WBC margination even at very low flow rates. Thus, RBC aggregation presents an additional force that expels WBCs from the RBC core due to attractive interactions between RBCs. At high enough flow rates, RBC aggregation does not play a significant role,32 and therefore there is no substantial change in the margination diagram at high ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *. The RBC aggregation effect on WBC margination is qualitatively similar to that observed in simulations of 2D model systems.21 The comparison of Fig. 5 and 6 indicates that WBC margination could still be possible in the limit of
*. The RBC aggregation effect on WBC margination is qualitatively similar to that observed in simulations of 2D model systems.21 The comparison of Fig. 5 and 6 indicates that WBC margination could still be possible in the limit of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * → 0 for the case of RBC aggregation.
* → 0 for the case of RBC aggregation.


![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≈ 120), the relative flow resistance is smaller than that for low flow rates. This is consistent with the observation in Fig. 5 that the WBC is poorly marginated at high flow rates and therefore, the resistance values mainly reflect the effect of an increased total volume fraction of cells due to the presence of a WBC. At intermediate and low flow rates, the presence of a WBC results in an increase of flow resistance by 10–30%. The relative resistance is clearly correlated with WBC margination such that WBC margination leads to a larger flow resistance. At low Ht, a WBC is not strongly marginated, and therefore the flow resistance is not significantly affected. At intermediate Ht values, where a WBC gets strongly marginated, the flow resistance reaches its maximum, while at high Ht the resistance due to a WBC slightly decreases, since WBC margination becomes less pronounced. The effect of RBC aggregation on the flow resistance due to a WBC is pronounced mainly at low flow rates, which is consistent with the RBC aggregation effect on WBC margination. Also, we expect that an increase in the flow resistance due to a marginated WBC will be smaller than 10–30% in larger vessels in comparison with the studied tube diameter of Dt = 20 μm.
* ≈ 120), the relative flow resistance is smaller than that for low flow rates. This is consistent with the observation in Fig. 5 that the WBC is poorly marginated at high flow rates and therefore, the resistance values mainly reflect the effect of an increased total volume fraction of cells due to the presence of a WBC. At intermediate and low flow rates, the presence of a WBC results in an increase of flow resistance by 10–30%. The relative resistance is clearly correlated with WBC margination such that WBC margination leads to a larger flow resistance. At low Ht, a WBC is not strongly marginated, and therefore the flow resistance is not significantly affected. At intermediate Ht values, where a WBC gets strongly marginated, the flow resistance reaches its maximum, while at high Ht the resistance due to a WBC slightly decreases, since WBC margination becomes less pronounced. The effect of RBC aggregation on the flow resistance due to a WBC is pronounced mainly at low flow rates, which is consistent with the RBC aggregation effect on WBC margination. Also, we expect that an increase in the flow resistance due to a marginated WBC will be smaller than 10–30% in larger vessels in comparison with the studied tube diameter of Dt = 20 μm.

![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *, which indicates that the scale factor 2ū/Dw captures the essential dependence of the angular velocity on the flow rate.
*, which indicates that the scale factor 2ū/Dw captures the essential dependence of the angular velocity on the flow rate.


![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≲ 130. This range of flow rates is characteristic of the venular part of microcirculation. RBC aggregation slightly enhances WBC margination, especially at high Ht values. The deformation of marginated WBCs appears to be rather small, remaining within a few percent of the undisturbed shape. The force on marginated WBCs is directed in the normal direction toward the wall, can reach a value of several hundred pico-newtons, and might aid in better WBC adhesion to the wall. Marginated WBCs also contribute to an increase in flow resistance with up to approximately 30% for vessel diameters of 20 μm. The effect of WBC margination on the flow resistance is expected to subside as the tube diameter is increased to values several times larger than the WBC diameter. Finally, we also presented translational and rotational WBC velocities, which might be used for the detection of WBC margination in experiments.
* ≲ 130. This range of flow rates is characteristic of the venular part of microcirculation. RBC aggregation slightly enhances WBC margination, especially at high Ht values. The deformation of marginated WBCs appears to be rather small, remaining within a few percent of the undisturbed shape. The force on marginated WBCs is directed in the normal direction toward the wall, can reach a value of several hundred pico-newtons, and might aid in better WBC adhesion to the wall. Marginated WBCs also contribute to an increase in flow resistance with up to approximately 30% for vessel diameters of 20 μm. The effect of WBC margination on the flow resistance is expected to subside as the tube diameter is increased to values several times larger than the WBC diameter. Finally, we also presented translational and rotational WBC velocities, which might be used for the detection of WBC margination in experiments.