Open Access Article
Open Access ArticleInfluence of internal viscoelastic modes on the Brownian motion of a λ-DNA coated colloid
Taiki
Yanagishima
a,
Nadanai
Laohakunakorn
b,
Ulrich F.
Keyser
b,
Erika
Eiser
*b and
Hajime
Tanaka
*a
aDepartment of Fundamental Engineering, Institute of Industrial Science, University of Tokyo, Komaba 4-6-1, Meguro-ku, Tokyo, 153-8505, Japan. E-mail: tanaka@iis.u-tokyo.ac.jp; Fax: +81-3-5452-6126; Tel: +81-3-5452-6125
bBiological and Soft Systems Sector, Cavendish Laboratory, JJ Thomson Ave, Cambridge, CB3 0HE, UK. E-mail: ee247@cam.ac.uk; Fax: +44 (0)1223-337000; Tel: +44 (0)1223-337007
First published on 13th January 2014
Abstract
We study the influence of grafted polymers on the diffusive behaviour of a colloidal particle. Our work demonstrates how such additional degrees of freedom influence the Brownian motion of the particle, focusing on internal viscoelastic coupling between the polymer and colloid. Specifically, we study the mean-squared displacements (MSDs) of λ-DNA grafted colloids using Brownian dynamics simulation. Our simulations reveal the non-trivial effect of internal modes, which gives rise to a crossover from the short-time viscoelastic to long-time diffusional behaviour. We also show that basic features can be captured by a simple theoretical model considering the relative motion of a colloid to a part of the polymer corona. This model describes well a MSD calculated from an extremely long trajectory of a single λ-DNA coated colloid from experiment and allows characterisation of the λ-DNA hairs. Our study suggests that the access to the internal relaxation modes via the colloid trajectory offers a novel method for the characterisation of soft attachments to a colloid.
1 Introduction
The dynamics of particles with internal degrees of freedom have attracted great scientific and industrial interest in recent years. Examples include polymer grafted micro- and nano-particles,1 hairy microgels,2,3 protein-bearing nanoparticles,4–6 ‘patchy’ particles,7 amongst many other novel constructs. A prominent subset of these consist of single colloids loaded with a localised ‘corona’ of proteins or polymers of similar diffusivity via grafting or adsorption, giving rise to ‘hairy’ particles. These include industrially and medically relevant examples, such as protein-loaded nanoparticles for biomedical applications,8 PEG-stabilised gold particles for cancer photoablation,9 the biocompatibilisation of magnetic resonance imaging contrast agents10 and mixed polymer-brush grafted colloids which can respond to their environment.11It has previously been established that the Brownian dynamics of such particles can be used for their characterisation. Most analyses work under the implicit assumption that macromolecular grafting simply increases the hydrodynamic size of the construct as a whole.12–14 This is intuitive and no doubt correct to first order.
However, this assumption leads to neglect of vital dynamic internal degrees of freedom including the motion of a colloid relative to its polymer corona. Despite the polymers being grafted to the microsphere, the whole structure can be very flexible, resulting in a potential lag between the response of the ‘corona’ and changes in colloid position. This raises a natural question of whether the whole structure simply behaves like it has become ‘bigger’. Not only can this lead to misestimation of the effect of the grafting, it opens up an interesting possibility that a polymer confined to move with the particle can, in fact, reflect its viscoelasticity in the particle trajectory while diffusing with it. Analysing such viscoelastic response may thus allow us to access the information on the polymer corona, which is usually difficult to obtain after the synthesis of a particle–polymer complex.
In this paper, we aim to address this by explicitly accounting for the presence of long fluctuating polymer chains and their influence on time-dependent correlations in the colloid position using Brownian Dynamics (BD) simulations. To our knowledge, this is the first systematic Brownian dynamics study of polymer-grafted colloids with a resolution of single chain steps in the layer. As an experimentally verifiable system, we chose λ-phage DNA grafted micron-sized polystyrene colloids in an aqueous solvent. The motivation for this was twofold (1) λ-DNA has a gyration size and diffusivity similar to those of micron-sized particles. (2) This diffusivity corresponds to a positional relaxation time on the order of seconds,15 allowing experimental examination using CCD video microscopy. To make a connection between simulation results and experiments, we introduce a simple theoretical model and check whether this model captures the essence of our simulation results. Then we apply the model to a single experimentally observed MSD of a colloid with λ-DNA hairs for characterising the hairs, sampling from a significantly longer trajectory than the maximum lag.
2 Simulation methods
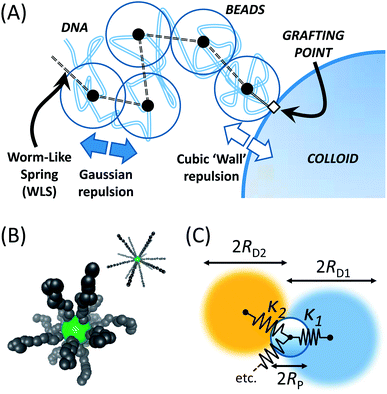
We simulate λ-DNA coated colloids (LDNACCs) using a Brownian Dynamics (BD) simulation method. As in well-established studies of polymer dynamics, we model each strand as a series of beads coupled by springs. The dynamical evolution of the position of each bead and the colloid itself is then represented by a Langevin equation, Ẋi = ξ−1iFi + Bi. Xi are the positions of the elements, Fi the total of the forces acting upon them, ξi are their drag coefficients and Bi is the stochastic Brownian force, with expected values 〈Bi〉 = 0 and 〈Bi(t)Bj(t + τ)〉 = 2kBTδ(τ)δ(i − j). ξi = 6πηr is defined via the Stokes force, where r = R when describing the colloid, and r = a for the beads with an effective hydrodynamic radius a.We adapt several approaches to realise a simulation of λ-DNA immobilised to a mobile colloid, namely a dynamically accurate coarse-grained model for free λ-DNA,16 its interaction with solid boundaries,17 and an explicit immobilisation method to pre-determined points on a translationally and rotationally mobile sphere.
Single strands are represented by a chain of Nb beads, connected via Ns = Nb − 1 springs, as given in Fig. 1(A). These springs adopt the force law proposed by Marko and Siggia,18 where a Finite Extensible Non-Elastic (FENE) and worm-like chain (WLC) force laws are combined into a worm-like spring force (WLS):
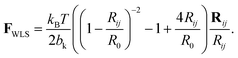 | (1) |
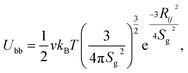 | (2) |
 | (3) |
As springs are connected directly to the colloid surface, it is clear that a torque is also acting on the sphere – it becomes paramount to rotate the colloid, and add rotational Brownian motion. Forces acting at the tether points are converted to torques vectorially and summed to give M and an effective angular velocity ωviaM = (8πηR3)ω. All grafting points are subsequently rotated using the unbiased rotation scheme of Beard et al.21 Radial positions were always rescaled to ensure location on the sphere surface.
Although many-body hydrodynamic interactions (HI) can affect polymer-chain dynamics,22,23 our main interest is the relative motion between a colloid and a corona of attached polymer chains. Because of the viscoelastic (not hydrodynamic) nature of the coupling, hydrodynamic interactions may lead to the renormalisation of the time scale, but not affect the basic behaviour, particularly given the low HI signature of double stranded DNA.24 Thus we ignore hydrodynamic interactions, whose incorporation is also computationally very costly, to access the long-time limiting behaviour.
Parameters for the model were chosen to match native λ-DNA. bk and v were set to be the same as in the study of Jendrejack,16bk = 0.106 μm, and v = 0.0012 μm3 as they are not expected to be different. Only a was adjusted to 0.047 μm, correcting for the free-draining case and the effect of any intercalating dye on the diffusion constant.15 Time steps were chosen to be 10−5 s, smaller than the translational diffusion time of the beads. Nb was set to 11 (or, 10 springs) for each strand. A colloid radius of 1.08 μm was chosen for comparison with experiments, as described later.
Due to the nature of the WLS spring law, unphysical forces can act when a Brownian step extends the spring beyond its natural contour length. Thus, the Langevin equation was integrated using an iterative backward Euler method and LAPACK routines.16 Due to the independence between Brownian terms on different elements that arises from the absence of hydrodynamics, most matrices dealt with here were sparse, requiring only elementary routines, such as Cholesky decomposition, for inversion and operation. All code was developed in Fortran 95.
Starting from a stretched state, the structure was allowed to equilibrate over several seconds, as illustrated in Fig. 1. Following relaxation, the trajectory of the central particle was recorded and mean-squared displacements found: 320 trajectories were simulated for a given number of chains Nc, each greater than 10 seconds in length, and averaged to find a characteristic MSD.
3 Theory
With the availability of mean-squared displacements for the trajectory of λ-DNA coated colloids, we require a means to interpret, fit and parametrise the results. For this, we need a physical model. Given the common description of polymers as viscoelastic entities, a general picture might consist of a colloid coupled to viscous spheres via springs. This is illustrated in Fig. 1(C).However, it is well known that polymers present a much more complex viscoelastic response than a single valued drag and elasticity.25 Further to this, λ-DNA colloids carry multiple strands, leading to a large variety of modes through which the colloid motion can relax. Given no previous knowledge of the number of strands coating the surface, the most productive (and accurate) interpretation of these beads are as representing different proportions of the polymer corona. This resembles a generalised Voigt model.
If one were to account for the presence of N beads, the Langevin equation of motion for such a system could be written as a system of N + 1 coupled equations
 | (4) |
| ξDiṙDi = κi(rp − rDi) + ζDi, | (5) |
| ξṙ = Kr + ζ, | (6) |
Without any loss of generality, one can begin to understand the general characteristics of the solution. By summing all of the terms on the left hand side together, there will always be an independent combination of coordinates, which consists entirely of Brownian noise terms.
 | (7) |
Due to the independence of the noise terms here (no HI), the MSD of this solution is found to be
 | (8) |
 , and d is the number of dimensions. On the other hand, eigenfunctions Xi with finite eigenvalue can be determined by solving the linear algebra problem defined by the matrix reduction given in eqn (6). This is equivalent to a Langevin equation for a Brownian particle inside harmonic confinement. Their MSDs are well known,25 given by
, and d is the number of dimensions. On the other hand, eigenfunctions Xi with finite eigenvalue can be determined by solving the linear algebra problem defined by the matrix reduction given in eqn (6). This is equivalent to a Langevin equation for a Brownian particle inside harmonic confinement. Their MSDs are well known,25 given by | (9) |
Note the change of index to j, and the mark ′ on the physical parameters. It is vital to recognize that these do not directly map to a mode i in the physical model. Thus, κ′j and τ′j are both effective confinements and relaxation times, functions of κi and ξi. Since each eigenvector denotes a linear superposition of the positions of the elements, the particle position can be recovered by a similar summation of these states.
Adding to this their orthogonality, the particle MSD simply becomes a weighted sum of the MSDs of each of these eigenfunctions, Y and Xi, resulting in a general expression
 | (10) |
Qualitatively, one can already see the general features of the MSD predicted from our hypothesis. At long times, the MSD approaches a purely diffusive one with a gradient that reflects the total hydrodynamic drag of the structure. At short times, a finite, positive contribution to the diffusivity derived from a first order Taylor expansion of the second term, leads to an effectively reduced drag.
3.1 CONTIN analysis
As we expect the response to be a sum of exponential decays, one might envision a means to explicitly identify these modes. Many such methods exist:26 here, we employ CONTIN, a regularisation based inverse Laplace-transform method commonly used to analyse dynamic light scattering correlation data.27 Firstly, we analyse simulated end-to-end vector autocorrelations for single DNA strands only, and secondly to the MSD of a DNA coated colloid. A MATLAB emulation28 is used with minor modifications.There is a significant added difficulty in the latter, in that the mean-squared displacements we expect do not converge. Exponential decay functions are notoriously non-orthogonal as it is, and any attempts to remove the linear term before decomposition relies on its absolute accuracy if subsequent analysis is to be used to extract meaningful parameters. This is obviously not feasible unless unfeasibly long trajectories can be measured, for virtually noise free long correlation time MSDs. We will see that we can employ alternative fitting methods which do not use such decomposition techniques, and avoid any conclusions which explicitly rely on such analysis.
4 Experimental methods
In order to test the predictions of the simulations and theory, we carried out an experiment to determine the MSD of a λ-DNA coated colloid trajectory. Polystyrene microspheres (Kisker Biotech, Germany) with a diameter of 2.16 μm were coated with λ-DNA using a protocol described in ref. 29, and dispersed in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of syringe filtered D2O and double distilled H2O to density match the colloid. The solution was buffered through addition of 10 mM tris(hydroxymethyl) aminomethane and 1 mM ethylenediaminetetraacetic acid (TE buffer) (Sigma Aldrich).
1 mixture of syringe filtered D2O and double distilled H2O to density match the colloid. The solution was buffered through addition of 10 mM tris(hydroxymethyl) aminomethane and 1 mM ethylenediaminetetraacetic acid (TE buffer) (Sigma Aldrich).
A 0.001% solution of λ-DNA coated particles was confined in a 120 μm thick glass chamber with Parafilm spacers, and imaged using an Eclipse Ti microscope (Nikon, Japan) in bright field illumination and a ‘Pike’ CMOS camera (Allied Visual Technologies, U.S.). Particles were chosen from around the middle of the chamber to eliminate hydrodynamic interaction with the boundaries. The field of view was reduced to allow faster sampling, around 150 frames per second, with videos extending to 30 seconds before the particle diffused out of the field of view. Two dimensional trajectories were obtained using particle tracking of video frames using a 2D kernel correlation followed by harmonic fitting to the correlation maximum.
5 Results and discussion
Firstly, we briefly describe simulation results of a single λ-DNA strand, free of grafting. We confirm that the ratio of the mean-square end-to-end distance 〈R02〉 to the mean-square radius of gyration 〈Rg2〉 is about 6, indicating that our polymer chain can indeed be regarded as a Gaussian chain. We also theoretically estimate the Rouse terminal relaxation time to be about 0.2 s with the parameters used, which is consistent with the relaxation time of the slowest mode (0.3 s) observed in Fig. 2, obtained via a CONTIN analysis of the end-to-end vector autocorrelation. These results support the validity of our simulation as well as the Gaussian nature of an individual chain.Following this confirmation, we go on to find the MSDs of simulated λ-DNA grafted colloids with a number of chains Nc ranging from 2 to 12, up to two seconds – these are given in Fig. 3. We can already see the features one would expect from a qualitative understanding of the dynamics. (1) For short times, the small Brownian fluctuations of the colloid are less affected by the DNA, as the DNA corona cannot respond to changes in colloid position. All MSDs are thus asymptotic to the bare colloid diffusivity, shown as a thick solid line marked Nc = 0 in the plot. (2) For long times, the whole structure may be translated by diffusion. The MSD gradients almost become constant with time, entering into an asymptotic diffusional regime with higher friction. The gradients become smaller for greater Nc, indicating higher friction for a colloid with more chains.
 | ||
| Fig. 3 MSDs from simulation (marked dots), from Nc = 2–12 from top to bottom. The MSD for free diffusion of a bare bead is marked with Nc = 0. A clear curvature is seen, asymptotic to a linear MSD with larger drag and at long correlation times. Lines denote fits using eqn (11), where good agreement is seen using tMAX = 0.2 s at all time scales, as seen on the main plot, and in a 〈x2〉t−1vs. log t plot (inset). | ||
With this encouraging development, we attempt a fit using the general MSD in eqn (10), using up to five modes to fit the behaviour. However, it became quickly obvious that (a) using a small number of terms, say 1 or 2, there is significant discrepancy with the fit and (b) once more than two terms are used, the confidence interval width of the parameters greatly increases, due to the same reasons given in Section 3.1. Though the fits are vastly improved, it becomes a redundant exercise when ones basis set can fit practically anything.
The inherent difficulty is further highlighted in a CONTIN analysis of the particle trajectory MSD, estimating the long time gradient by a linear fit within the 1 to 2 second correlation time domain, and subtracting the linear part. Not only is this analysis quantitatively unreliable, as any small error in the estimation will introduce a systematic error into the decay curve, but the peaks are significantly wider: this reflects coupling between modes. Nevertheless, a CONTIN analysis provides a general picture of the relaxation-time distribution compared to the distribution of a single DNA strand. A typical example is given in Fig. 2. Despite the difficulties, two key points to note here are (1) the qualitative distribution of peaks is similar and (2) the maximum relaxation time peak is always dominant.
This leads us to formulate an approximation which may allow us to quantitate the behaviour of the MSD without resorting to multiple exponential fits. We start by assuming that there is a single, dominant exponential decay mode beyond some empirically determined correlation time tMAX, whose relaxation time will most likely reflect some weighted average of the maximum peak. At times t > tMAX, there will be a constant contribution which arises from modes which have already decayed. The theoretical MSD we will fit thus becomes
 | (11) |
Eqn (11) is fitted to the simulated MSDs, with tMAX = 0.2 s. The efficacy of this method can be clearly seen in the excellent agreement between the simulated data and the fits, plotted both normally and as 〈x2〉t−1vs. t on a semilog scale (inset), demonstrating agreement on all time scales. This reflects the relative accuracy of a single mode fit when restricted to this domain, and vindicates our choice of tMAX.
We are finally able to parametrise the LDNACC dynamics by following the evolution of the relevant parameters, namely κ′, the characteristic confinement strength, τ′, the relaxation time, and ξ′tot, the drag associated with the whole structure. ξ′tot has an associated hydrodynamic radius Rtot = ξ′tot/(6πη) – we follow the evolution of Rtot − Rp to solely concentrate on what is associated with the DNA corona. These are given as a function of the number of chains Nc in Fig. 4.
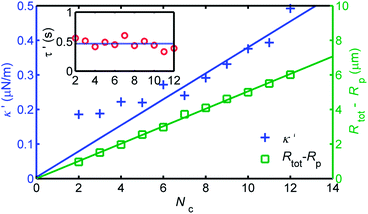 | ||
| Fig. 4 Evolution of effective structural parameters κ′, Rtot − Rp and relaxation time τ′ from fitting the MSDs found in Fig. 3. A linear increase in drag is associated with increasing Nc, while this is only recovered for the harmonic constant κ′ after an isotropic coating is restored for Nc ≥ 6. Interestingly, the relaxation time remains roughly constant τ′. | ||
Firstly, it is clear that Rtot − Rp goes up linearly with the number of chains attached. This is expected from previous studies,12 and corresponds to the previously held conception that grafted polymers add to the hydrodynamic profile of the whole particle. The magnitude of the gradient of the fit, is ≈0.50 μm per chain, corresponding to a stepwise increase similar to the radius of gyration of free λ-DNA.
Secondly, κ′ is also observed to rise with Nc, though linearly only for around Nc > 5 or 6. This is due to the lack of isotropy in the grafting for small numbers. Furthermore, a linear fit to Nc ≥ 6 passes through zero, as one might expect. The DNA corona clearly has linearly greater elasticity with a larger Nc. The gradient of this line is ≈0.033 μN m−1 per chain.
One can compare this to the elasticity associated with the slowest Rouse mode of single simulated DNA strands, given by25
 | (12) |
Thirdly, we can see that the characteristic relaxation time τ′ is roughly constant for the number of chains Nc. One might intuitively expect a decrease due to the increasing confinement κ′. However, if we recall that the relaxation time for a Brownian particle in harmonic confinement is the ratio of the drag coefficient and the harmonic constant, one can clearly attribute the constant behaviour of τ to the linear increase of both κ′ and the dissipation associated with the structure. This independence of τ′ on Nc can also be viewed as simply a natural consequence of the fact that the only relevant internal time scale for this polymer–colloid complex is the viscoelastic relaxation time of individual polymer chains. The estimated relaxation time τ′ is about 0.5 s, which is almost the same as the relaxation time of a grafted polymer (0.4 s) independently measured from CONTIN analysis of the end-to-end vector autocorrelation (see Fig. 3). This means that tMAX (= 0.2 s) is always located between the relaxation time of the slowest mode and that of the second slowest one, irrespective of Nc, guaranteeing the self-consistency of our choice of tMAX. We particularly stress that the agreement between the relaxation time τ′ and the slowest relaxation mode of a single DNA strand is consistent with the fact that the relevant spring constant per chain found from the LDNACC trajectories is the same order as that for the longest deformation mode of a single chain (see above).
Conversely, if one were to change the length of the DNA (e.g. use a longer strand to begin with, or use enzymatic cleavage), a change would be expected in τ′. An increased length would lead to an enlarged gyration radius, giving a decrease in κ′ and an increased ξ′eff, both working to increase the relaxation time.
It is clear that the MSDs found from simulation largely agree with our hypothesis, and that the theoretical expression we developed succeeds in parametrising the curves in such a way that the values found agree with what is expected from physical considerations.
Finally, we put these ideas to the test by fitting eqn (11) to an experimentally found MSD from a polystyrene microsphere coated with λ-DNA. Analysis was carried out on a particle trajectory monitored for more than 4500 continuous frames (≈30 seconds), determining a MSD with a 100 point maximum lag. This single particle characterisation opens up the exciting possibility that single building blocks of λ-DNACCs or any other ‘hairy’ system can be tuned for polydispersity through a tracer free, passive analysis. Though analysis for a single λ-DNACC is shown here, the same behaviour was seen in a clear majority of trajectories on different particles in the same sample.
The result is given in Fig. 5, where a comparison is given with what is expected from a bare bead, a linear fit to the first 5 points, and the theoretical fit produced above. It is clear that the particle does not simply behave like it is ‘bigger’ but displays a more complex diffusive motion. The MSD bows down to less than half of the diffusivity suggested by the first few points of the curve. However, it is apparent that the relaxation is faster than what is expected from simulation, with the majority of the decay happening before tMAX = 0.2 s. Instead, we set tMAX = 0.01 s, and effectively only omit the first point from the fit. This has the added benefit that the fit becomes robust against static errors, which can change the baseline of the MSD.
 | ||
| Fig. 5 An experimental MSD from a long trajectory of a single λ-DNA coated colloid. The MSD is predictably lower than what is expected from a bare bead, and there is a clear curvature downwards at longer lags compared to a linear fit to the first 5 points. Excellent agreement is found with a theoretical fit to eqn (11). | ||
We find excellent agreement with a theoretical fit, though the magnitudes of the parameters were somewhat different. Though Rtot − Rp = 2.00 μm is still of the order of magnitude of Rg of λ-DNA, the harmonic constant κ′ = 1.88 μN m−1 was significantly larger than in simulation. The relaxation time, as expected from qualitative observation, turned out to be much smaller, τ′ = 0.048 s.
The excellent functional agreement with the model indicates that the diffusive motion of the colloid is clearly affected by its coupling to the viscoelastic behaviour of λ-DNA grafted to it. On the other hand, there is a large discrepancy in the absolute values of τ′ and κ′ between experiments and simulations, despite the fact that the particle, the polymers, and the solvent viscosity are chosen to mimic experimental conditions. One plausible explanation is that there is adsorption of λ-DNA to the surface of the colloid. We note that Liu et al.30 indeed suggested such adsorptive interactions between the λ-DNA and the surface, which are neglected in our simulation. Having DNA in such close proximity to a surface will bias segments to positions closer to the surface, enhancing the elasticity experienced by the particle (i.e., increasing the spring constant κ′), reducing the long time hydrodynamic radius increase (i.e., decreasing Rtot − Rp), and shortening the relaxation time τ′. Furthermore, this may lead to loop formation, which can significantly increase the friction and the elasticity, as the effective number of chains Nc is largely increased. On this note, comparing the simulated and experimental τ′ and noting their proportionality to N2 in Rouse theory,25 an effective N can be estimated to be about 1/3–1/4 of the original N, which increases the spring constant about a factor of 3–4. Though such explanations provide a reasonable account for the experimentally observed behaviour, they are speculative: the origin of the discrepancy should be studied carefully in the future. Further verification will require confocal microscopy observation with high spatio-temporal resolution and deconvolution techniques or cryo-TEM studies to capture a high resolution image of the colloid and DNA corona.
6 Conclusions
It has been widely known that the long-time diffusional behaviour of a colloidal particle is affected by soft components, such as polymer hairs attached to it. Here we went a step further to access the dynamical information associated with the presence of polymer hairs from the trajectory of the colloid. We demonstrated by simulation and experiment that the Brownian motion of a polymer-grafted colloid is significantly affected by non-trivial dynamical coupling between the translational degrees of freedom of the colloid and the viscoelastic relaxation modes of the polymer hairs, and that this feature can be used for the previously impossible characterisation of the dynamical state of the polymers even after they are grafted to a colloid. This may even allow us to extract static information, e.g., interactions between polymers and the colloid surface.Though we have applied our methods to characterise the dynamics of λ-DNA coated colloids as a function of coverage, this whole procedure can find general use in parameterising the broad, non-linear evolution of the MSD for any polymer–grafted system, such as in nano-composite materials. This opens up the way for label-free single particle characterisation of all colloid–macromolecule hybrid systems, particularly where the positional relaxation times of the components are of similar magnitude. It is abundantly clear, from the simulation, theoretical framework and experiment, that there is a much more rich dynamics at work for the diffusive behaviour of these particles, and that we have presented a clear proof of principle that such a characterisation method provides more information and insight to the coupling of the viscoelastic response of the soft, polymer corona to the colloid motion.
7 Appendix
The simplest example of eqn (10) can be derived from the case where only one polymer bead is coupled to a colloid, making an asymmetric Brownian dumbbell.Here, the coupled Langevin equations become
| ξPṙP = κ(rD − rP) + ζP, | (13) |
| ξDṙD = κ(rP − rD) + ζD. | (14) |
Since the dimensions are decoupled, one can initially treat the problem in 1D. We solve this set analytically by re-assigning the variables to X and Y, given by X = rp − rD and Y = ζprp + ζDrD. The equations of motion change to
 | (15) |
| Ẏ = ζP + ζD | (16) |
| = ζY, | (17) |
X represents a Brownian motion in a harmonic potential, with an effective drag ξeff and spring constant κ, while Y represents free Brownian motion. Respective stochastic terms ζX and ζY are linear combinations of the Brownian terms for rp and rD. Their expectation values can be found trivially. The physical significance of these separate terms is clear – X reflects the internal, confined fluctuations of the colloid, whereas Y is the unconfined, slower diffusion of the whole structure. Their respective autocorrelation functions and MSDs are well known.25
By superimposing X and Y, we can analytically express the position of the colloid rp as  . The analytical MSD of rp is then found to be
. The analytical MSD of rp is then found to be
 | (18) |
 | (19) |
In the long time limit, the exponential and constant terms become negligible compared to the linear term 〈rP2〉 → 2dkBTt/(ξP + ξD), resulting in a reduced gradient compared to the short time limit.
Note that, in terms of the effective parameters introduced in eqn (10)
 | (20) |
| τ′ = ξeffκ−1 | (21) |
There is no constant to find here, as there is only one relaxation mode present.
Acknowledgements
TY would like to thank members of the Tanaka Soft Matter group for their patience and highly productive discussions. This work was sponsored by the Nano Doctoral Training Centre, Cambridge, UK (TY), the Ernest Oppenheimer Studentship (TY), the George and Lillian Schiff Foundation Award (TY and NL), Trinity College, Cambridge (NL) and the Cavendish Laboratory (EE). UFK was supported through an Emmy Noether grant from the Deutsche Forschungsgemeinschaft and an ERC starting grant. HT acknowledges support by Grants-in-Aid for Scientific Research (S) and Specially Promoted Research from JSPS and Aihara Project, the FIRST program from JSPS, initiated by CSTP.References
- M. Ballauff, Prog. Polym. Sci., 2007, 32, 1135–1151 CrossRef CAS PubMed.
- S. Tsuji and H. Kawaguchi, Langmuir, 2004, 20, 2449–2455 CrossRef CAS.
- B. R. Saunders, N. Laajam, E. Daly, S. Teow, X. Hu and R. Stepto, Adv. Colloid Interface Sci., 2009, 147–148, 251–262 CrossRef CAS PubMed.
- F. Caruso and C. Schüler, Langmuir, 2000, 9595–9603 CrossRef CAS.
- T. Cedervall, I. Lynch, M. Foy, T. Berggård, S. C. Donnelly, G. Cagney, S. Linse and K. A. Dawson, Angew. Chem., Int. Ed., 2007, 46, 5754–5756 CrossRef CAS PubMed.
- J. S. Gebauer, M. Malissek, S. Simon, S. K. Knauer, M. Maskos, R. H. Stauber, W. Peukert and L. Treuel, Langmuir, 2012, 28, 9673–9679 CrossRef CAS PubMed.
- G.-R. Yi, D. J. Pine and S. Sacanna, J. Phys.: Condens. Matter, 2013, 25, 193101 CrossRef PubMed.
- L. Treuel and G. U. Nienhaus, Biophys. Rev., 2012, 4, 137–147 CrossRef CAS.
- D. P. O'Neal, L. R. Hirsch, N. J. Halas, J. D. Payne and J. L. West, Cancer Lett., 2004, 209, 171–176 CrossRef CAS PubMed.
- M. Chanana, S. Jahn, R. Georgieva, J.-F. Lutz, H. Baumler and D. Wang, Chem. Mater., 2009, 21, 1906–1914 CrossRef CAS.
- B. Zhao and L. Zhu, Macromolecules, 2009, 42, 9369–9383 CrossRef CAS.
- A. S. Almusallam and D. S. Sholl, Nanotechnology, 2005, 16, S409–S415 CrossRef PubMed.
- K. M. Krueger, A. M. Al-Somali, M. Mejia and V. L. Colvin, Nanotechnology, 2007, 18, 475709 CrossRef.
- O. Ueberschär, C. Wagner, T. Stangner, K. Kühne, C. Gutsche and F. Kremer, Polymer, 2011, 52, 4021–4032 CrossRef PubMed.
- D. E. Smith, T. T. Perkins and S. Chu, Macromolecules, 1996, 29, 1372–1373 CrossRef CAS.
- R. M. Jendrejack, J. J. de Pablo and M. D. Graham, J. Chem. Phys., 2002, 116, 7752–7759 CrossRef CAS PubMed.
- R. M. Jendrejack, D. C. Schwartz, M. D. Graham and J. J. de Pablo, J. Chem. Phys., 2003, 119, 1165–1173 CrossRef CAS PubMed.
- J. F. Marko and E. D. Siggia, Macromolecules, 1995, 28, 8759–8770 CrossRef CAS.
- P. G. Bolhuis, A. A. Louis, J. P. Hansen and E. J. Meijer, J. Chem. Phys., 2001, 114, 4296 CrossRef CAS PubMed.
- P. Boucher, http://www.softimageblog.com/archives/115, 2006.
- D. A. Beard and T. Schlick, Biophys. J., 2003, 85, 2973–2976 CrossRef CAS.
- H. Tanaka, J. Phys.: Condens. Matter, 2005, 17, S2795–S2803 CrossRef CAS.
- K. Kamata, T. Araki and H. Tanaka, Phys. Rev. Lett., 2009, 102, 108303 CrossRef.
- F. Latinwo and C. M. Schroeder, Soft Matter, 2011, 7907–7913 RSC.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, 1988 Search PubMed.
- A. A. Istratov and O. F. Vyvenko, Rev. Sci. Instrum., 1999, 70, 1233–1257 CrossRef CAS PubMed.
- S. W. Provencher, Comput. Phys. Commun., 1982, 27, 229–242 CrossRef.
- I.-G. Marino, http://www.mathworks.com/matlabcentral/fileexchange/6523-rilt, 2007.
- U. F. Keyser, J. van der Does, C. Dekker and N. H. Dekker, Methods Mol. Biol., 2009, 544, 95–112 CAS.
- X. Liu, Z. Wu, H. Nie, Z. Liu, Y. He and E. S. Yeung, Anal. Chim. Acta, 2007, 602, 229–235 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |