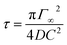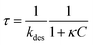Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Microfluidic Dynamic Interfacial Tensiometry (μDIT)†
Quentin
Brosseau
,
Jérémy
Vrignon
and
Jean-Christophe
Baret‡
*
Max-Planck Institute for Dynamics and Self-Organization (MPIDS), 37077 Göttingen, Germany. E-mail: jean-christophe.baret@ds.mpg.de
First published on 4th March 2014
Abstract
We designed, developed and characterized a microfluidic method for the measurement of surfactant adsorption kinetics via interfacial tensiometry on a microfluidic chip. The principle of the measurement is based on the deformability of droplets as a response to hydrodynamic forcing through a series of microfluidic expansions. We focus our analysis on one perfluoro surfactant molecule of practical interest for droplet-based microfluidic applications. We show that although the adsorption kinetics is much faster than the kinetics of the corresponding pendant drop experiment, our droplet-based microfluidic system has a sufficient time resolution to obtain quantitative measurement at the sub-second time-scale on nanoliter droplet volumes, leading to both a gain by a factor of ∼10 in time resolution and a downscaling of the measurement volumes by a factor of ∼1000 compared to standard techniques. Our approach provides new insight into the adsorption of surfactant molecules at liquid–liquid interfaces in a confined environment, relevant to emulsification, encapsulation and foaming, and the ability to measure adsorption and desorption rate constants.
Introduction
Amphiphilic molecules are ubiquitous in our daily lives, widely represented in natural systems1,2 and intensively used in the pharmaceutical, cosmetic, food and petroleum industries, among others.3,4 Surfactant molecules are used for example as detergents and dispersing materials, coating and foaming agents, emulsifiers and biocides, spanning a wide range of functions.5–7More than two hundred years after the first observations reported by Benjamin Franklin of the damping of waves on a lake by fatty acids,8 understanding the dynamics of surfactant films remains a challenge, both theoretically and experimentally. Interfacial rheology and adsorption dynamics are however key concepts in understanding foaming, emulsification and encapsulation processes9,10 as well as dynamic properties of biological membranes.11 Theoretically, understanding the dynamics of the surfactant requires an accurate description of the bulk molecular self-assembly, of the transport towards the interface and of the bulk–interface equilibrium.12–15 The latter point relies on the proper modelling of the surfactant interactions, especially in the case of ionic species,16,17 or of the interfacial reorganisation for oligomers and polymers.18,19 Experimentally, only a few methods enable a sensitive and direct measurement of molecular monolayer organization at the time-scale where the properties of the interface are influenced by the molecular self-assembly.15,20 Tensiometry is widely used for both equilibrium and dynamic measurements but provides limited information on adsorption–desorption processes due to the predominance of diffusion at large scales.13,21–23 Deviations of the experimental data from the minimal diffusive-limited model introduced by Ward and Tordai are almost systematically observed, and attributed to curvature effects,24–27 convective currents,23,28,29 or adsorption barriers.14,17 These adsorption barriers are revealed in the transfer-limited regimes which dominate at small dimensions21,30 and in convective systems,29,31 namely under the conditions relevant to emulsification or foaming. We address here the dynamics of surfactant adsorption in the context of microfluidic emulsification.
Microfluidics offers control for the manipulation of multiphase systems in confined environments. The possibility of measuring transient states at short time scales (∼ms) makes microfluidics especially appealing as a new tool to quantitatively study the physics and physico-chemistry of interfaces and emulsions.32–39 Microfluidic systems have been designed for interfacial tension measurement, for example making use of the deformation of a droplet entering a constriction.40 In the case of spheroidal shapes, the surface tension is obtained through the analysis of the rate of deformation and the velocity variation in the constriction.40–42 This type of analysis has further been used to obtain dynamic information on the interfacial properties of butanol with a time resolution of the order of one second.31 The dynamic processes of adsorption can influence emulsification at a much smaller time-scale,34,43–45 down to the limit of capillary breakup.46 To date, a direct quantitative measurement of the dynamic interfacial properties at the subsecond time-scale in the presence of surfactants is still lacking. In this manuscript we present a method usable for measuring the dynamic surface tension of droplets, with a resolution down to the millisecond. This method is not restricted to small droplet deformation and does not rely on assumption of specific droplet shapes during deformations. It is applied for the first time to the characterization of the adsorption properties of a block copolymer perfluoro surfactant of practical interest for biotechnology applications in microfluidics.47,48 We show for this surfactant that under flow conditions, adsorption is limited by the equilibrium between the bulk phase and the interface. This regime differs from the case of the pendant drop experiment, where the dynamics of adsorption of the perfluoro surfactant molecules is influenced for a large part by the surfactant bulk diffusion. In pendant drop tensiometry, convection is, in most cases, an undesired and uncontrolled side effect. However, as pointed out by Alvarez et al.,29 microfluidics provides new tools to control these convective effects for dynamic microtensiometry measurements. We propose here a new microfluidic approach to determine the kinetic properties such as the adsorption and desorption rate constants from the interface.
Materials & methods
Chemicals
The aqueous phase consists of Millipore water–ethanol (Sigma-Aldrich) mixtures and the oil phase in fluorinated oil HFE-7500 (3M, density ρ = 1.648 L−1). We used perfluorinated surfactant molecules, EA obtained as a kind gift from RainDance Technologies and used as received.47 The molecule is a non-ionic tri-block copolymer (PEG-PFPE) synthesised from two chains of Krytox FSL used as the fluorophilic part (Dupont) and a polyethylenoxide linker as the hydrophilic part. Dynamic Light Scattering (DLS) measurement showed a CMC of around 1.3 × 10−1 mol m−3, similar to the one obtained for a similar molecule (Fig. 1).39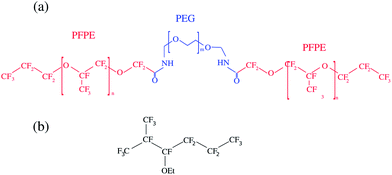 | ||
| Fig. 1 Chemical structure of the perfluorinated surfactant used. (a) The PEG-PFPE surfactant n = 12 and m = 34 (ref. 47) and (b) the HFE-7500 fluorinated oil. We consider the interfacial properties of the PEG-PFPE surfactant at the water–oil interface. | ||
Surfactant solutions
The surfactants are diluted in the oil from the pure phase to obtain three mother solutions of respectively 1.3 mol m−3, 2.6 mol m−3 and 5.2 mol m−3. These solutions are equilibrated for half a day, and then further diluted 10 fold. The operation is repeated to obtain an array of solution concentrations spanning 4 decades.Pendant drop tensiometry
The characterization of the bulk surfactant adsorption dynamics is performed using the pendant drop method (PAT 1M, Sinterface). A glass cuvette is filled with the aqueous phase. Before each measurement, the cuvette is rinsed with ethanol and Millipore water. The syringe and the tubing used to produce the droplet are rinsed with pure HFE and with the solution of the surfactant in oil being tested. Drops of oil and surfactant mixtures are formed at the tip of a needle into the water reservoir. The automatic generation of the droplet at the syringe outlet typically occurs within one second, limiting the accuracy of the measurement to time scales larger than 1 s. The size of the drop is kept constant during the analysis through a feedback loop based on real-time image processing of the drop volume. The drop volume and its interfacial area are obtained through a fit of the contour by the Young–Laplace equation fixing the density difference, Δρ = 0.62 g L−1, and the needle diameter. A calibration of the dimensions of the system is made before each series of measurements, or in the case of change in needle diameter. The measurement volume is chosen such that the drop reaches an equilibrium shape (corresponding to the equilibrium surface tension) without detaching from the needle. The volume varies between each experiment in the range 2–12 μL. The value of interfacial tension of the pure water–oil interface is measured at 49.5 mN m−1 ± 0.5 mN m−1 and constant over 105 s showing no trace of contaminant. The interfacial tension of the water–ethanol mixtures with pure oil is constant over the same time scale and concentration dependent (Fig. 4(c)). In the presence of the surfactant, the dynamic surface tension is monitored over a time scale varying from ∼102 s to 105 s, depending on the surfactant concentration.Device design
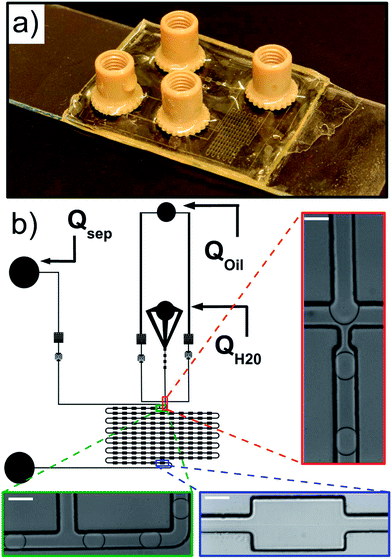
The microfluidic channel geometry is designed using QCad, with two oil phase inlets, one aqueous phase inlet and one outlet (Fig. 2 and the ESI†). Droplets are produced at a standard flow focusing junction.49 We designed an additional control on the droplet velocity and spacing independent of the droplet production using a side oil flow rate Qsep. The functional part of the device consists of a delay line with 121 successive chambers 300 μm wide and 500 μm long, each of them connected by a channel 100 μm wide and 500 μm long.Microfabrication
Microfluidic devices are produced using standard photolithography techniques50 through a polymer mask (Selba) and replica molded in Norland Optical Adhesive (NOA 81), a UV crosslinkable polymer. The non-crosslinked polymer has a low viscosity making device production straightforward.51 The cross-linked product exhibits good hydrophobic properties and is chemically and mechanically compatible with our emulsification system. In brief, a negative mold of the structure is prepared by photolithography of SU8-3050 on a silicon wafer. The structure is replica-molded in polydimethylsiloxane (PDMS, Sylgard 184) to obtain a soft positive mold. The NOA device is obtained in two parts. For the substrate, a flat NOA 81 layer is deposited on a microscope glass slide (VWR) and UV cured (365 nm, power 9 W, 20 s). For the structure, NOA 81 is deposited on the PDMS mold avoiding air bubble entrapment and cured under UV under the same conditions as above to obtain partially cross-linked interfaces.52 The holes for the tubing connection are punched with a biopsy needle of diameter 0.75 mm. Both parts are then brought into contact and a final curing (20 min) ensures irreversible bonding. Nanoport connectors (Upchurch scientific) are then glued on the connection holes (Loctite 3526, 3M). The device is finally hydrophobized by flowing an Aquapel solution through the channels and dried with nitrogen. The height H of the channel is H = 113 μm ± 5 μm, measured by interferometry (Veeco, Vision).Microfluidics
The fluids are injected from glass syringes (Hamilton, 5 mL) using syringe pumps (Nemesys, Cetoni) to control precisely the flow rates inside the microfluidic part. Syringes and the microfluidic chip are connected via PEEK tubing of outer diameter 0.75 mm.High-speed microscopy
The chip is mounted on an inverted microscope (Olympus IX71) and imaged using a ×20 microscope objective. The pictures of the droplets are recorded with a high speed camera (Phantom, V311) at a frame rate of 9100 pictures per second. The movies of droplet flow are recorded in each of the deformation chamber or in a subset of those.Image processing and data analysis
The droplet trajectory and shape is obtained by image processing of the high-speed movies through a home-made program. All parameters of interest rely on the detection of the two-dimensional projection of the contour of the droplet. The image background is averaged over all frames, and then subtracted to each frame. The droplet contour is defined as the outside edge of the droplet meniscus. We then compute the droplet projected area A, perimeter p, the center of mass positions xd, yd, large L and small l axes, and speed U. For one expansion, the number N of droplets is of order ∼10 and all quantities are averaged over the N droplets using linear interpolation along the x-axis. For each droplet, the deformation δ is defined as δ = (L − l)/(L + l) and is obtained as a function of position in the channel. The maximum deformation in the expansion δmax is obtained by a parabolic fitting of the deformation curve close to the maximum. The speed of the droplet at the maximum deformation Udefo is also extracted.Experimental results
We measure the kinetics of adsorption for a PEG-PFPE surfactant onto a water–fluorinated oil interface. First we use pendant drop tensiometry to extract the surfactant equilibrium parameters, such as the maximum coverage and the Langmuir equilibrium constant. Second we describe the principle of our microfluidic tensiometry measurements in the absence of the surfactant. Finally, we use these measurements as a calibration to determine the adsorption kinetics of PEG-PFPE inside the microfluidic chip.Dynamics of surfactant adsorption: pendant drop
The kinetics of surfactant adsorption with the PEG-PFPE surfactant is first measured using the pendant drop method. The interfacial tension γ is measured as a function of time for various surfactant concentrations C in the range C = 1.3 × 10−3 mol m−3 to C = 1.04 mol m−3, see Fig. 3. The interfacial tension decays from γ0 = 49.5 ± 0.5 mN m−1 to the equilibrium value γeq(C). γeq decreases with increasing surfactant concentration and the kinetics is faster at higher concentrations. For lower concentrations, the equilibrium values are sometimes not reached after 105 s. To further analyse the data, we refer to the diffusion limited adsorption originally derived by Ward and Tordai.13,14 The kinetics close to equilibrium is given by14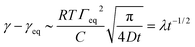 | (1) |
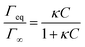 | (2) |
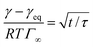 | (3) |
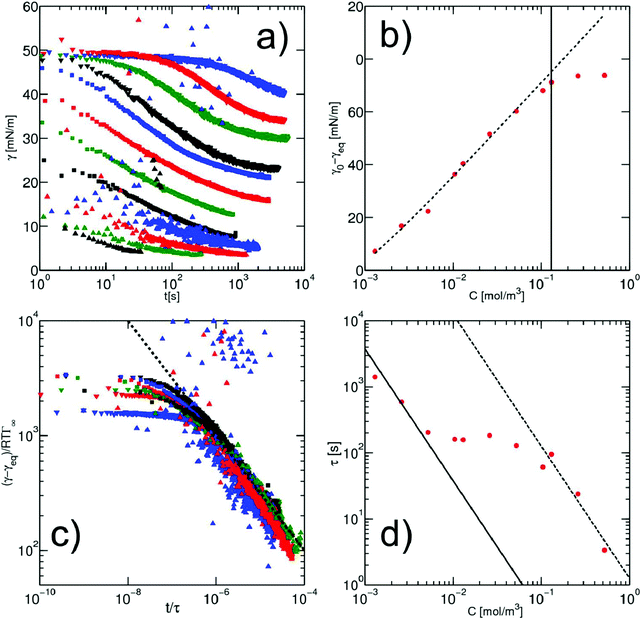 | ||
Fig. 3 (a) Dynamics of surface tension in the pendant drop method for the following surfactant concentrations: C = 1.3 × 10−3 mol m−3 ( ); C = 2.6 × 10−3 mol m−3, ( ); C = 2.6 × 10−3 mol m−3, ( ); C = 5.2 × 10−3 mol m−3, ( ); C = 5.2 × 10−3 mol m−3, ( ); C = 10.4 × 10−3 mol m−3, ( ); C = 10.4 × 10−3 mol m−3, ( ); C = 1.3 × 10−2 mol m−3, ( ); C = 1.3 × 10−2 mol m−3, ( ); C = 2.6 × 10−2 mol m−3, ( ); C = 2.6 × 10−2 mol m−3, ( ); C = 5.2 × 10−2 mol m−3, ( ); C = 5.2 × 10−2 mol m−3, ( ); C = 0.104 mol m−3, ( ); C = 0.104 mol m−3, ( ); C = 0.13 mol m−3, ( ); C = 0.13 mol m−3, ( ); C = 0.26 mol m−3, ( ); C = 0.26 mol m−3, ( ); C = 0.52 mol m−3, ( ); C = 0.52 mol m−3, ( ); C = 0.104 mol m−3, ( ); C = 0.104 mol m−3, ( ). (b) Equilibrium surface tension extracted from the long term kinetics equation (eqn (1)). The dotted line is a fitting of the isotherm, below the CMC, with the Langmuir equation (eqn (2)), with coefficients Γeq = 3.4 mol m−2 and κ = 3.1 × 103 mol3 m−2. The black line represents the CMC falling around 0.15 mol m−3. (c) Dynamic surface tension against the rescaled time ). (b) Equilibrium surface tension extracted from the long term kinetics equation (eqn (1)). The dotted line is a fitting of the isotherm, below the CMC, with the Langmuir equation (eqn (2)), with coefficients Γeq = 3.4 mol m−2 and κ = 3.1 × 103 mol3 m−2. The black line represents the CMC falling around 0.15 mol m−3. (c) Dynamic surface tension against the rescaled time 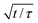 . The long term dynamics collapse on a t−0.5 power law (dashed line) (eqn (1)). (d) Evolution of the characteristic time τ with the surfactant concentration. The line represents theoretical values of τ, (eqn (3)), for different diffusion coefficients. The monomer diffusion is represented by the solid line with Dmonomer = 1 × 10−8 m2 s−1. The dotted line corresponds to a process of micellar diffusion with Dmicelles = 6 × 10−12 m2 s−1. . The long term dynamics collapse on a t−0.5 power law (dashed line) (eqn (1)). (d) Evolution of the characteristic time τ with the surfactant concentration. The line represents theoretical values of τ, (eqn (3)), for different diffusion coefficients. The monomer diffusion is represented by the solid line with Dmonomer = 1 × 10−8 m2 s−1. The dotted line corresponds to a process of micellar diffusion with Dmicelles = 6 × 10−12 m2 s−1. | ||
The rescaling of the surface tension kinetics with the parameters obtained from the fit shows that we obtain a power law with a −1/2 exponent over more than two decades in time (Fig. 3(c)). The scaling factor τ is then plotted as a function of the concentration (Fig. 3(d)). We find two asymptotic regimes where the relationship τ ∼ C−2 is satisfied. At high concentrations (above the CMC), we extract a diffusion coefficient Dmicelle = 6 × 10−12 m2 s−1, compatible with the diffusion coefficients of micelles of sizes ∼100 nm that have been measured using DLS (ESI Fig. 1;† comparable micelle sizes were obtained for a similar molecule here39). At low concentrations (below the CMC), the diffusion coefficient is Dmonomer = 1.5 × 10−9 m2 s−1. This value exceeds by about one order of magnitude the typical value that can be expected for such a nanometer sized molecule. A similar observation has been made for other surfactants in the pendant drop experiment, and might result from the existence of convective currents in an apparently quiescent fluid.23 The convective current might also originate from a flow induced by droplet deformation when the interfacial tension decreases. The apparent ‘superdiffusivity’ of our molecule is even clearer at the very early stage of adsorption. In this case, the fit of the experimental data by the early time kinetics of the Ward and Tordai model
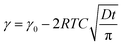 | (4) |
| Parameter | Value | Units |
|---|---|---|
| M w | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
g mol−1 |
| Γ ∞ | 3.4 × 10−6 | mol m−2 |
| κ | 3 × 103 | m3 mol−1 |
| CMC | 1.5 × 10−1 | mol m−3 |
| D C≪CMC* | 1.5 × 10−9 | m2 s−1 |
| D C≫CMC | 6 × 10−12 | m2 s−1 |
In the following, we consider the adsorption kinetics in a microfluidic chip.
Droplet deformation at a microfluidic expansion
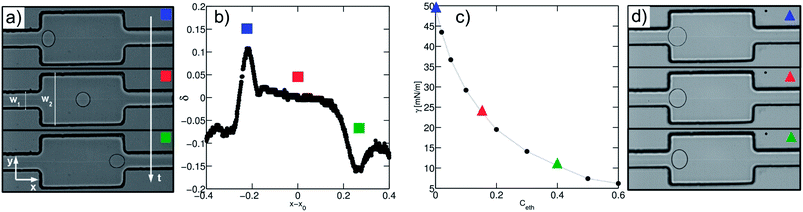
In a first series of experiments, we consider the case of solutions without a surfactant. We produce droplets at a frequency of ∼100 Hz. In a given expansion, the droplet is deformed in the direction perpendicular to the flow, with a maximum deformation δmax close to the entrance of the expansion (Fig. 4), as previously observed.40 For a fixed channel geometry, δmax is a function of the physical quantities: (i) the droplet velocity Udrop, (ii) the interfacial tension γ and (iii) the droplet radius R. The viscosities of both phases also control the deformation. In all experiments, the viscosity of the continuous phase is kept constant to 1.24 mPa s−1 and we found that the viscosity of the dispersed phase is not a relevant parameter, at least for the viscosities ranging from 1 to 10.8 mPa s−1 (ESI Fig. 3†). This result is consistent with the one obtained by Taylor showing that the deformation of sheared droplets is mainly controlled by the viscosity of the external fluid.41From the set of remaining physical parameters, two dimensionless numbers are expected to control the problem: (i) the capillary number calculated using the viscosity of the continuous phase, Ca = ηUdrop/γ and (ii) a geometrical number R* = 2R/W1 that relates the droplet radius R to a typical length, taken here as the channel width W1. Looking for a scaling relationship based on these two numbers, we first calibrate the dependence of the deformation on the speed and interfacial tension of the droplet. For a fixed droplet size, we vary the oil flow rate Qsep in the side injection channel. The maximal droplet deformation is measured as a function of the flow velocity. For water in oil (γ = 50 mN m−1), we observe that the deformation increases for increasing velocities, in qualitative agreement with previous experiments and theoretical expectations.40,42 The surface tension is then varied by adding ethanol in the dispersed aqueous phase without modifying significantly the viscosity ratio between the continuous and the dispersed phase (Fig. 5). All data collapse on a master curve when using the capillary number, indicating that the capillary number is the relevant dimensionless number of the problem. We find here a power law relationship δmax ∼ Ca2/3.
Fixing the flow velocity, we then varied the droplet size for a set of different surface tensions. We then rescaled the maximum deformation by Ca2/3 and obtained a good collapse of the data on a master curve (Fig. 5(b)). The master curve is in a good approximation to a power law:
| δmax = 0.8Ca2/3R*3.7 | (5) |
The resulting deformation is therefore a function of both the capillary number and a geometric dimensionless parameter. For Taylor sheared droplets, the power law exponent in Ca is 1. However when a droplet moves in an elongational flow field, the flow profile itself contributes to the deformation41,42,53 which is not captured in the Taylor sheared droplet. In addition, effects related to the confinement of the droplets in the channel might also contribute to the dissipation. We want here to point out that although the exponent of the capillary number can probably be derived from theoretical argument, there is no specific reason to obtain a power law relationship for the size dependence. The droplet size has probably a strong influence on the flow around the droplet due to the confinement, explaining the strong dependence of the droplet deformation on its size. Further hydrodynamic analysis including the effect of the confinement on droplet deformation is of interest and will be described in a later paper.
In the following, we will use the data relating deformation and surface tension (eqn (5)) as a phenomenological calibration of the system. The interfacial tension is expressed as a function of the droplet experimental δmax, Udefo, R and a constant k = 0.8, by the following expression:
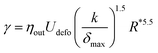 | (6) |
It is clear from the expression that a size fluctuation of 2% in droplet size (as usually obtained in microfluidic flow focussing) leads to a measurement error of ∼10% which sets the maximum resolution for the measurement (Fig. 6). Using all our experimental data, we can determine the surface tension γc obtained from the model equation as a function of the fluid–fluid interfacial tension γm (Fig. 6, inset).
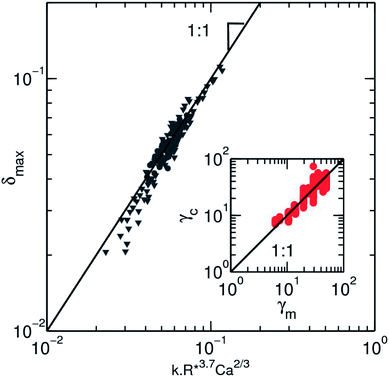 | ||
Fig. 6 Collapse of all experimental values on a master curve using the empirical scaling equation for the surface tension (eqn (6)). Both experimental data are represented, where the speed of the droplet ( ) and the size ( ) and the size ( ) are varied. The black line is a slope one as a guide for the eyes. The inset depicts the values of the surface tension for solution of ethanol in water and HFE-7500, as they are measured by the pendant drop method, γm, against the value calculated from the deformation profile in microfluidic channel γc. The black line has a slope 1 corresponding to an ideal match between the 2 measurements. The dispersion of the data from this match due to the error made on the deformation is visible here. ) are varied. The black line is a slope one as a guide for the eyes. The inset depicts the values of the surface tension for solution of ethanol in water and HFE-7500, as they are measured by the pendant drop method, γm, against the value calculated from the deformation profile in microfluidic channel γc. The black line has a slope 1 corresponding to an ideal match between the 2 measurements. The dispersion of the data from this match due to the error made on the deformation is visible here. | ||
Dynamics of surfactant adsorption: microfluidics
The surfactant adsorption is then measured in our microfluidic chip. Fixing the flow conditions to Qtot = 72 μL min−1 (QH2O = 2 μL min−1, Qoil = 50 μL min−1 and Qsep = 20 μL min−1), we measure the deformation of the droplet in a series of expansions distributed along a delay line. Along the whole channel, we observe a weak but measurable variation of the droplet size and speed (ESI, Fig. 4†). The apparent size of the droplet R* is varying at most by 4%, and velocities at most by 10%. These small variations integrate microfabrication uncertainties on the channel depth and the change of boundary conditions at the interface,54 and the changes in the lubrication layer thickness around a confined droplet. In the case of large droplets, the lubrication layer thickness given by Bretherton55 is of the order ∼HCa2/3. The order of magnitude for this layer in our case is at most 6 μm. Therefore it is not excluded that the change of surface tension upon adsorption would modulate the layer thickness leading to a change of the apparent droplet area. We believe that these variations are linked to the effect of surfactant adsorption, by modification of the Bretherton film or interface rigidification, as they are more pronounced at higher surfactant concentrations. In the following we will account for these variations by using the velocity and droplet size measured in the expansion considered.In the first expansion, the droplet remains circular with nonmeasurable deformation while larger deformations are observed at the end of the microfluidic channel, indicating that the surface tension has decreased (Fig. 7(a)). Using our calibration (eqn (6)) we derive the time evolution of the surface tension (Fig. 7(b)). Accounting for the apparent size and velocity of the droplet, we obtain plateau values of the surface tension for the highest surfactant concentrations, even in regions where the maximum deformation δmax still increases. As expected the values of the plateau depends on the surfactant concentration and are consistent with the pendant drop measurements (Fig. 7(c)).
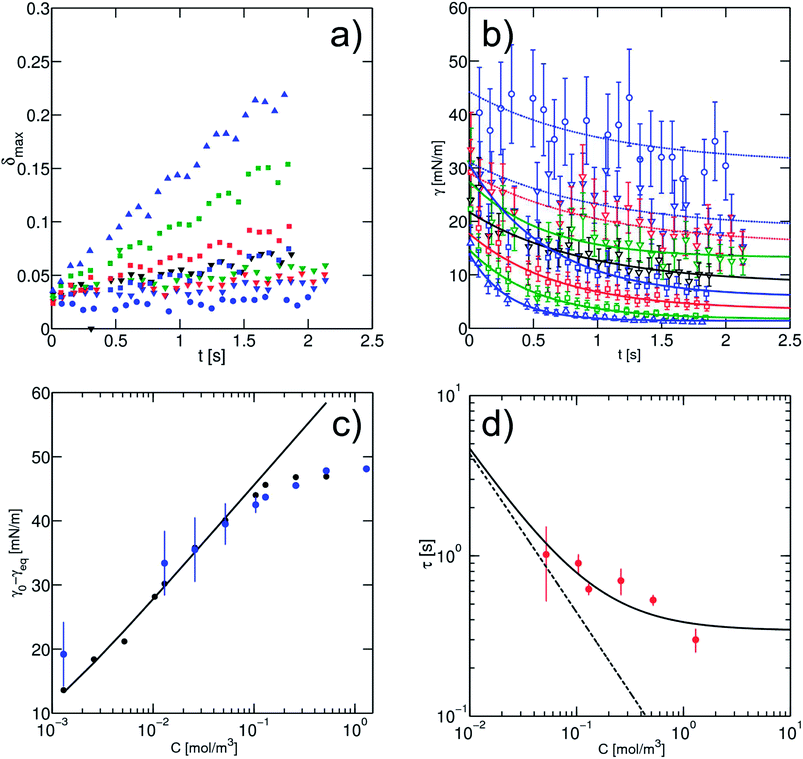 | ||
Fig. 7 (a) Maximum deformation of the droplet as a function of the time as recorded on-chip. Here the measured points correspond to a subset where one chamber out of five is analysed. The concentrations of surfactant used are: C = 1.3 × 10−3 mol m−3 ( ); C = 1.3 × 10−2 mol m−3, ( ); C = 1.3 × 10−2 mol m−3, ( ); C = 2.6 × 10−2 mol m−3, ( ); C = 2.6 × 10−2 mol m−3, ( ); C = 5.2 × 10−2 mol m−3, ( ); C = 5.2 × 10−2 mol m−3, ( ); C = 10.4 × 10−2 mol m−3, ( ); C = 10.4 × 10−2 mol m−3, ( ); C = 1.3 × 10−1 mol m−3, ( ); C = 1.3 × 10−1 mol m−3, ( ); C = 2.6 × 10−1 mol m−3, ( ); C = 2.6 × 10−1 mol m−3, ( ); C = 5.2 × 10−1 mol m−3, ( ); C = 5.2 × 10−1 mol m−3, ( ); C = 1.3 mol m−3, ( ); C = 1.3 mol m−3, ( ). (b) Surface tension derived from the maximum droplet deformation with the empirical scaling (eqn (6)). The open symbols correspond to the concentration in (a). The solid lines are the best fits found for each concentration, using an exponential fitting of the late kinetics, based on eqn (7). For the dotted line the fit has been done with values of τ fixed to one in order to extract the equilibrium surface tension. (c) Comparison between the equilibrium values of the surface tension as a function of the surfactant concentration from the pendant drop method ( ). (b) Surface tension derived from the maximum droplet deformation with the empirical scaling (eqn (6)). The open symbols correspond to the concentration in (a). The solid lines are the best fits found for each concentration, using an exponential fitting of the late kinetics, based on eqn (7). For the dotted line the fit has been done with values of τ fixed to one in order to extract the equilibrium surface tension. (c) Comparison between the equilibrium values of the surface tension as a function of the surfactant concentration from the pendant drop method ( ) and from microfluidic experiments ( ) and from microfluidic experiments ( ). The solid line is the fitting after the Langmuir equation (eqn (2)). The dashed line represents the CMC. (d) Characteristic time scales τ extracted from late on-chip kinetics (eqn (9)). Both lines represent the asymptotic expressions of τ in transfer limited, where micellar adsorption is allowed (solid line) and not allowed (dashed line) (eqn (10)), for a value of kdes = 6.5 × 10−3 s−1. ). The solid line is the fitting after the Langmuir equation (eqn (2)). The dashed line represents the CMC. (d) Characteristic time scales τ extracted from late on-chip kinetics (eqn (9)). Both lines represent the asymptotic expressions of τ in transfer limited, where micellar adsorption is allowed (solid line) and not allowed (dashed line) (eqn (10)), for a value of kdes = 6.5 × 10−3 s−1. | ||
At high surfactant concentrations, the interfacial tension reaches an equilibrium value in less than 1 s. At lower surfactant concentrations, the relaxation to equilibrium is slower and the equilibrium value is larger, as expected. We observe an increase in the experimental error at high surface tension because deformation of order 1% is at the limit of our optical resolution. The accuracy of the measurement is maximal at low surface tension (∼1 mN m−1) which makes the system interesting for highly efficient surfactants, possibly used for microemulsion production. This accuracy at low surface tension constitutes a significant improvement to the pendant drop method where low surface tension γ < 5 mN m−1, is at the limit of the method (ESI, Fig. 3†). In addition, the deformation experiments can be performed even for Δρ = 0, for which pendant drop tensiometry would fail.
We are now interested to extract the information on surfactant adsorption from the surface tension dynamics extracted on the chip. We first analysed the asymptotic behaviours. Contrary to the pendant drop experiments, a fit with a power law in t−1/2 was not possible. In contrast, the data could be fitted by an exponential relaxation, observed for example in transfer limited kinetics. We extracted from the fit the value of γeq and of the characteristic time τ as a function of the surfactant concentration according to eqn (7):
| γ − γeq ∼ exp(−t/τ) | (7) |
The equilibrium values obtained as a function of surfactant concentration are in full agreement with the pendant drop measurements showing the reliability of the method, see Fig. 7(c). In the transfer limited regime, the adsorption–desorption process is treated as a binding reaction involving a fixed number of binding sites at the interface. The definition of the adsorption and desorption rate constant kads and kdes, as well as the surface coverage as a function of time is obtained with:
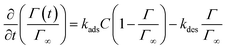 | (8) |
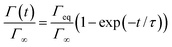 | (9) |
The Langmuir isotherm Γeq(C) is recovered with the Langmuir equilibrium constant expressed as κ = kads/kdes. The expression of τ is similar to the one reported by Li et al.30 Following the assumption that the surface tension changes are proportional to surface coverage changes, we obtain the expression for the relaxation time scale as a function of desorption rate and the Langmuir parameter κ. Unfortunately, the accuracy of our experimental data is satisfactory enough in the region of the CMC which does not provide a convenient range of concentrations to test this scaling. If the micelles contribute to the kinetics, assuming that neither the dissociation nor the diffusion is the limiting step, then the expression of τ is correct even above the CMC. In contrast if the dissociation is infinitely slow, the time scale is expected to reach a constant value above the CMC. The experimental data lie within these two asymptotic limits:
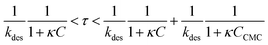 | (10) |
A value of kdes = 6 × 10−3 s−1 can be extracted from the behavior of τ (Fig. 7(d)). We use then the knowledge of κ to extract the adsorption rate kads = kdesκ = 18 m3 mol−1 s−1. The rate constants can also be expressed in the form22β* = kadsΓ∞ = 6 × 10−3 cm s−1. For clarity, all the data are provided in Table 2. Although the accuracy of the measurement value of kdes is limited by the large error bars due to the determination of the time-scale and the crude approximations of the model, we provide here the first estimate of the rate constants for the PEG-PFPE surfactant using our microfluidic chip, and a new on-chip tensiometry method to quantitatively analyse surfactant dynamics at the liquid–liquid interface.
| Parameter | Value | Units |
|---|---|---|
| κ | 3 × 103 | m3 mol−1 |
| Γ ∞ | 3.4 × 10−6 | mol m−2 |
| k des | 6 × 10−3 | s−1 |
| k ads = kdesκ | 18 | m3 mol−1 s−1 |
| β* = kadsΓ∞ | 6 × 10−3 | cm s−1 |
Discussion
We have designed a microfluidic system to measure the surfactant adsorption under the conditions relevant to emulsification processes and provide a measurement of the rates of adsorption and desorption. The adsorption on the chip is shown to be transfer-limited as one might expect in the presence of convective currents and at small dimensions. Quantitatively, the values we obtain for the adsorption rates provide estimates of the concentration cutoff above which the adsorption changes from diffusion limited to transfer limited.22 This concentration is expressed as Cmaxd = 0.01β*Γ∞/D = 4 × 10−3 mol m−3 in our case. A mixed-kinetic regime can be expected in the pendant drop experiments even in the absence of convection below the CMC. We hypothesize that the occurrence of the plateau in the pendant drop measurement between the two asymptotic regimes relates to this mixed-kinetic behaviour which suggests that a mixed-kinetic model has to be used to quantitatively analyse pendant drop experiments. In microfluidics, all experiments have been performed with concentrations above Cmaxd which confirms the influence of the transfer kinetics on adsorption.The cutoff length RDK = D/(Γ∞kads) (ref. 21) below which the adsorption processes are transfer limited is also estimated to be RDK ∼ 10 μm. In the pendant drop experiments, R ≫ RDK which is consistent with the diffusion limited regime observed at very small concentrations. In microfluidics, the adsorption is transfer limited even for droplet sizes around 100 μm as a result of the convective currents present in the system. Indeed the Peclet number Pe = UdropletL/D is of order 105 using the typical droplet velocity Udroplet ∼ 0.2 m s−1 and the droplet size as typical L. Another cutoff length can be defined to account for the convective currents by replacing the diffusive effects with convective effects. Comparing the typical speed of adsorption kadsΓ∞ describing the adsorption of molecules with the typical speed of the droplet relative to the oil (related to the amount of surfactant molecules available to the interface), we obtain a dimensionless number kadsΓ∞/U ∼ 3 × 10−4 indicating that the reaction kinetics is by far limiting the adsorption reaction in the presence of convection. Hence we do not expect significant changes in the kinetics when the flow rates are varied in the experiments.
In general, the values of κ, Γeq and the rate constants kads and kdes are all consistent with values obtained for other systems. For example, Γ∞ is within the same order of magnitude compared to the surfactant of the series CnEm which have a similar head group compared to our molecule.5,21 The long chain length of the perfluoro surfactant is therefore expected to be mainly oriented perpendicular to the interface without significantly folding onto the interface. A similar statement can be made based on the value of kads which is of the same order as the one of C14E8.5,21,29 Our method provides a measurement of the surface tension of a liquid–liquid interface during flow. We show here that we reach a transfer limited regime and this regime will dominate for droplet speeds even three orders of magnitude slower (i.e. around 200 μm s−1) for 100 μm droplets and for all speeds when the droplets are smaller than 10 μm.
Our results can be compared to the previous analysis of coalescence in microfluidic channels.34 The coverage required to stabilise the emulsion (estimated to be ∼10% (ref. 34) with a related surfactant) is reached in the early time kinetics (∼10 ms) where our current method is the least sensitive. Therefore making a direct link between dynamic tensiometry and the dynamics of emulsion stabilisation is not straightforward. In addition, emulsions are stabilised by Marangoni effects.56 The good agreement between the equilibrium values in pendant drop tensiometry and the microfluidic experiments shows that Marangoni stresses do not significantly influence the interfacial measurements in our range of parameters.57 However expanding the analysis to the data generated during the expansion and relaxation of the droplet could probably be used to measure interfacial rheology properties relevant to understand coalescence.10,31,56
Conclusions
In summary, we developed a method to measure surfactant adsorption in microfluidics through the deformability of droplets in shear flow. We exemplify its use on the analysis of adsorption of a perfluorinated surfactant of practical interest for microfluidic applications. Standard droplet tensiometry experiments provide estimates of the surfactant properties in a diffusion-limited case while the microfluidic platform shows that the kinetics of adsorption is transfer limited. The microfluidic experiments enable us to estimate the adsorption and desorption constant and provide equilibrium values compatible with the pendant drop experiments. Our microfluidic system can further be used to analyse the behaviour of other surfactant species, for example ionic species or more generally to analyse the transient states of active and reactive interfaces.Acknowledgements
The authors acknowledge the financial support from the Max-Planck Society and from the European Research Council (ERC) under the European Union's Seventh Framework Program (FP7/2007-2013/ERC Grant agreement 306385-sofi). The authors are grateful to B. Semin, V. Taly, M. Brinkmann, S. Herminghaus and J. Enderlein for helpful discussion. We also thank J. B. Hutchison for the kind gift of the surfactant used in the study.References
- Surfactans from renewable resources, ed. M. Kjellin and I. Johansson, Wiley, 2010 Search PubMed.
- K. Holmberg, Curr. Opin. Colloid Interface Sci., 2001, 6, 148–159 CrossRef CAS.
- M. J. Lawrence and G. D. Rees, Adv. Drug Delivery Rev., 2000, 45, 89–121 CrossRef CAS.
- Surfactants: Fundamentals and applications in the petroleum industry, ed. L. Schramm, Cambridge University Press, 2000 Search PubMed.
- M. J. Rosen, in Surfactants and Interfacial phenomena, John Wiley & Sons, Inc., 2004, pp. i–xiii Search PubMed.
- D. Weaire and S. Hutzler, The Physics of Foams, Oxford University Press, 1999 Search PubMed.
- J. Bibette, F. Leal-Calderon and P. Poulin, Rep. Prog. Phys., 1999, 62, 696–1033 CrossRef.
- B. Franklin, Philos. Trans. R. Soc. London, 1774, 64, 445–460 CrossRef.
- D. Langevin, Curr. Opin. Colloid Interface Sci., 1998, 3, 600–607 CrossRef CAS.
- D. Georgieva, A. Cagna and D. Langevin, Soft Matter, 2009, 5, 2063–2071 RSC.
- G. Enhoring, J. Appl. Physiol.: Respir., Environ. Exercise Physiol., 1977, 43, 198–203 Search PubMed.
- I. Langmuir, Proc. Natl. Acad. Sci. U. S. A., 1917, 3, 251–257 CrossRef CAS.
- A. Ward and L. Tordai, J. Chem. Phys., 1946, 14, 453 CrossRef CAS PubMed.
- J. Eastoe and J. S. Dalton, Adv. Colloid Interface Sci., 2000, 85, 103–144 CrossRef CAS.
- D. M. Colegate and C. D. Bain, Phys. Rev. Lett., 2005, 95, 198302 CrossRef.
- E. Lucassen-Reynders, J. Phys. Chem., 1966, 70, 1777 CrossRef CAS.
- A. Bonfillon, F. Sicoli and D. Langevin, J. Colloid Interface Sci., 1994, 168, 497–504 CrossRef CAS.
- V. B. Fainerman, S. A. Zholob, E. H. Lucassen-Reynders and R. Miller, J. Colloid Interface Sci., 2003, 261, 180–183 CrossRef CAS.
- F. Millet, P. Perrin, M. Merlange and J. Benattar, Langmuir, 2002, 18, 8824–8828 CrossRef CAS.
- J. Hutchison, D. Klenerman, S. Manning-Benson and C. Bain, Langmuir, 1999, 15, 7530–7533 CrossRef CAS.
- F. Jin, R. Balasubramaniam and K. Stebe, J. Adhes., 2004, 80, 773–796 CrossRef CAS.
- S. N. Moorkanikkara and D. Blankschtein, J. Colloid Interface Sci., 2006, 302, 1–19 CrossRef CAS PubMed.
- S. N. Moorkanikkara and D. Blankschtein, Langmuir, 2009, 25, 6191–6202 CrossRef CAS PubMed.
- X. Li, R. Shaw, G. Evans and P. Stevenson, Comput. Chem. Eng., 2010, 34, 146–153 CrossRef CAS PubMed.
- S. Lin, K. McKeigue and C. Maldarelli, AIChE J., 1990, 36, 1785 CrossRef CAS.
- V. Fainerman, S. Zholob, J. Petkov and R. Miller, Colloids Surf., A, 2008, 323, 56–62 CrossRef CAS PubMed.
- A. Makievski, G. Loglio, J. Kraegel, R. Miller, V. Fainerman and A. Neumann, J. Phys. Chem. B, 1999, 103, 9557–9561 CrossRef CAS.
- J. K. Ferri, C. Kotsmar and R. Miller, Adv. Colloid Interface Sci., 2010, 161, 29–47 CrossRef CAS PubMed.
- N. J. Alvarez, D. R. Vogus, L. M. Walker and S. L. Anna, J. Colloid Interface Sci., 2012, 372, 183–191 CrossRef CAS PubMed.
- B. Li, G. Geeraerts and P. Joos, Colloids Surf., A, 1994, 88, 251–266 CrossRef CAS.
- J. D. Martin and S. D. Hudson, New J. Phys., 2009, 11, 115005 CrossRef.
- C. Priest, S. Herminghaus and R. Seemann, Appl. Phys. Lett., 2006, 89, 134101–134103 CrossRef PubMed.
- N. Bremond, A. R. Thiam and J. Bibette, Phys. Rev. Lett., 2008, 100, 024501 CrossRef.
- J.-C. Baret, F. Kleinschmidt, A. E. Harrak and A. D. Griffiths, Langmuir, 2009, 25, 6088–6093 CrossRef CAS PubMed.
- A. R. Thiam, N. Bremond and J. Bibette, Phys. Rev. Lett., 2009, 102, 188304 CrossRef.
- A. R. Thiam, N. Bremond and J. Bibette, Phys. Rev. Lett., 2011, 107, 068301 CrossRef.
- N. Bremond, H. Domejean and J. Bibette, Phys. Rev. Lett., 2011, 214502 CrossRef.
- N. Bremond and J. Bibette, Soft Matter, 2012, 8, 10549–10559 RSC.
- Y. Skhiri, P. Gruner, S. Semin, Q. Brosseau, D. Pekin, L. Mazutis, V. Goust, F. Kleinschmidt, A. E. Harrak, J. Hutchison, E. Mayot, J. Bartolo, A. Griffiths, V. Taly and J. Baret, Soft Matter, 2012, 8, 10618–10627 RSC.
- J. T. Cabral and S. D. Hudson, Lab Chip, 2006, 6, 427–436 RSC.
- G. Taylor, Proc. R. Soc. London, Ser. A, 1934, 146, 501 CrossRef CAS.
- J. M. Rallison, Annual review of fluid mechanics, 1984, vol. 16 Search PubMed.
- S. L. Anna and H. C. Mayer, Phys. Fluids, 2006, 18, 121512 CrossRef PubMed.
- M. L. J. Steegmans, A. Warmerdam, K. G. P. H. Schron and R. M. Boom, Langmuir, 2009, 25, 9751–9758 CrossRef CAS PubMed.
- N. J. Alvarez, L. M. Walker and S. L. Anna, Langmuir, 2010, 26, 13310–13319 CrossRef CAS PubMed.
- M. Roch, M. Aytouna, D. Bonn and H. Kellay, Phys. Rev. Lett., 2009, 103, 264501 CrossRef.
- C. Holtze, A. C. Rowat, J. J. Agresti, J. B. Hutchison, F. E. Angile, C. H. J. Schmitz, S. Koester, H. Duan, K. J. Humphry, R. A. Scanga, J. S. Johnson, D. Pisignano and D. A. Weitz, Lab Chip, 2008, 8, 1632–1639 RSC.
- J.-C. Baret, Lab Chip, 2012, 12, 422–433 RSC.
- S. L. Anna, N. Bontoux and H. A. Stone, Appl. Phys. Lett., 2003, 82, 364–366 CrossRef CAS PubMed.
- Y. N. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 153–184 CrossRef CAS.
- E. Sollier, C. Murray, P. Maoddi and D. Di Carlo, Lab Chip, 2011, 11, 3752–3765 RSC.
- D. Bartolo, G. Degre, P. Nghe and V. Studer, Lab Chip, 2008, 8, 274–279 RSC.
- H. A. Stone and L. G. Leal, J. Fluid Mech., 1990, 220, 161–186 CrossRef CAS.
- K. Erk, J. Martin, J. Schwalbe, F. Phelan and S. Hudson, J. Colloid Interface Sci., 2012, 377, 442–449 CrossRef CAS PubMed.
- F. P. Bretherton, J. Fluid Mech., 1961, 10, 166–188 CrossRef.
- B. Dai and L. Leal, Phys. Fluids, 2008, 20, 040802 CrossRef PubMed.
- K. J. Stebe and D. Barthes-Biesel, J. Fluid Mech., 1995, 286, 25–48 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3sm52543k |
| ‡ Present address: Université de Bordeaux and CNRS Centre de Recherche Paul Pascal, 115 Avenue Schweitzer, Pessac, 33600, France. |
| This journal is © The Royal Society of Chemistry 2014 |