Cytoskeletal transition in patterned cells correlates with interfacial energy model

Abstract

A cell's morphology is intricately regulated by microenvironmental cues and intracellular feedback signals. Besides biochemical factors, cell fate can be influenced by the mechanics and geometry of the surrounding matrix. The latter point was addressed herein, by studying cell adhesion on two-dimensional micropatterns. Endothelial cells were grown on maleic acid copolymer surfaces structured with stripes of fibronectin by microcontact printing. Experiments showed a biphasic behaviour of actin stress fibre spacing in dependence on the stripe width with a critical size of approx. 15 μm. In a concurrent modelling effort, cells on stripes were simulated as droplet-like structures, including variations of interfacial energy, total volume and dimensions of the nucleus. A biphasic behaviour with regard to cell morphology and area was found, triggered by the minimum of interfacial energy, with the phase transition occurring at a critical stripe width close to the critical stripe width found in the cell experiment. The correlation of experiment and simulation suggests a possible mechanism of the cytoskeletal rearrangements based on interfacial energy arguments.

---

1 Introduction

Cells rely on environmental cues for the guidance of their identity and behaviour. Outside signals include myriads of biochemical inputs but also physical parameters such as substrate stiffness¹ and ligand anchorage² for adherent cells.³ Furthermore, substrate topology and geometry of the adhesive area are important for anchorage dependent cells. For example, cells show distinctive behaviours when confronted with differently shaped,⁴ spaced,⁵ or sized^6,7 adhesive patches. From these studies it can be concluded, that cell fate decisions like cell cycling, apoptosis and differentiation are controlled by size and morphology constraints in vivo as well as in vitro. In that way tissue formation, morphogenesis and regeneration are affected in development and wound healing. At the same time, the dysregulation of such functions has also to be considered to be involved in pathological processes like cancer development.

In the context of geometry sensing and mechanotransduction, the cell's cytoskeletal components are considered to be directly involved in the signalling process. In particular, actin is highly abundant in eukaryotic cells. Assembled into filaments and thick fibres, it forms an integral component of the cytoskeleton, next to microtubules and intermediate filaments. The fibres' capability of tensile contraction due to the presence of myosin motor proteins along with their strong involvement in the formation of focal and fibrillar adhesions makes them paramount for the adhesion, migration and orientation of cells.⁸ The actin stress fibres are the major source of strong intracellular tension and extracellularly applied traction force. Thus, the actin cytoskeleton actively determines the cells stability,⁹ shape¹⁰ and migratory behaviour.¹¹ Actin polymerization and depolymerization is a decisive process in migratory and adherent cells, hinging cell mechanics and biochemical signalling.¹²

Because of such fundamental relationships between mechanical and structural components of cells and their environment and the cell's behaviour, biophysical approaches are being used to reveal fundamental mechanisms. Numerous models have been developed to explain cell behaviour based on actomyosin activity and function, ranging from local, molecular scale to global scale on the level of whole cells or even tissues. Just to mention some of them, these models comprise constructions as in the tensegrity model¹³ or the characterization by active cable networks.¹⁴ There are models less dependent on the local structure, such as active gels,¹⁵ chord models,¹⁶ or, on a larger scale, the differential adhesion hypothesis incorporating cortical tension^17,18 as well as more abstract models such as the explanation of cell adhesion as a wetting process.¹⁹ Furthermore, by modelling of actomyosin fibres as force dipoles, predictions regarding cell polarity in response to substrate stiffness and anisotropy could be made.^20,21

These studies, both experimental as well as theoretical, indicate direct links of cell morphology to mechanical elements of the cell including the actin stress fibres and membrane tension. However, underlying mechanisms are still not fully understood. Therefore, we set off with a combined experimental and simulation approach to provide new facts and ideas in finding basic principles of cell regulation and tissue formation in the context of mechanobiology. In the experiments presented here, endothelial cells were grown on solid substrates with polymeric surface modifications and micropatterned with adhesion ligands arranged in stripes of different widths. The actin stress fibre pattern was studied in dependence on these parameters. Concurrently, cells were simulated as droplet-like structures with a constant volume and containing a non-deformable nucleus using an interfacial energy minimization approach. For simulations, the same lateral constraints and a cell size comparable to those seen in experiments were used. Surprisingly, cells in experiment and modelled cells exhibited biphasic behaviour in dependence on the stripe width at a similar length scale. Below a critical stripe width of approx. 15 μm, cells in the experiment showed a depletion of actin stress fibres in the central region and only formed stress fibres at the cell edges, coincident with the stripe borders. Simulated cells showed a bimodal behaviour in morphology, indicated by a change from a spread, high area state to a bulged, low area state below a critical stripe width of 15 μm. This value could be shifted by variation of interfacial energy (surface tension) within the simulation implying a correlation between actin cytoskeleton architecture and cell surface tension as the underlying regulatory parameter.

2 Materials and methods

2.1 Micropatterned substrates

2.1.1 Chemical preparation of substrates. Chemical modification of cover slips was performed according to a previous protocol.²² In brief, cover slips (Marienfeld GmbH & Co. KG, Lauda-Königshofen, Germany) were sonicated in deionized water and denatured ethanol, oxidized in an aqueous mixture of ammonia (29% w/w, Acros Organics, Geel, Belgium), hydrogen peroxide (medical grade, 35% w/w, MerckKGgA, Darmstadt, Germany) and deionized water at a ratio of 1 : 1 : 5 at 70 °C for 10 min, and incubated in 20 mM (3-aminopropyl)triethoxysilane (Sigma-Aldrich Chemie GmbH, Steinheim, Germany) in 2-propanol (Acros Organics) and deionized water at a 9 : 1 volume ratio at room temperature for 2 h. Copolymer solutions (poly(octadecene-alt-maleic anhydride) (POMA) (Polysciences Inc., Warrington, USA) MW = 50 000 g mol⁻¹, 0.16% w/w in tetrahydrofuran (Fluka, Deisenhofen, Germany); poly(propylene-alt-maleic anhydride) (PPMA) (Leuna-Werke AG, Germany), MW = 39 000 g mol⁻¹, 0.2% w/w in methylethylketone (Fluka); poly(ethylene-alt-maleic anhydride) (PEMA) (Sigma-Aldrich), MW = 125 000 g mol⁻¹, 0.3% w/w in tetraydrofuran and acetone (Merck) at ratio 1 : 2) were filtered with PTFE-filters (pore size 0.2 μm) and applied to dried substrates via spincoating (RC 5 Spin Coater, Suess Microtec, Germany) at 4000 rpm and 1500 rpm s⁻¹ for a total duration of 30 s. Substrates were tempered at 120 °C for 2 h and subsequently washed with the respective solvents to remove non-covalently attached polymers.

Prior to printing, cover slips were tempered at 120 °C for 2 h, to ensure anhydride moieties at the polymer surface to allow for a covalent attachment of the amine-terminated poly(ethylene glycol) molecules of the ink.

2.1.2 Microcontact printing. Poly(dimethyl siloxane) (PDMS) pre-polymer solution was prepared with Sylgard 184 (Dow Corning GmbH, Wiesbaden, Germany) by mixing the base and cross-linker at a 9 : 1 ratio and degassing in the desiccator until complete removal of bubbles. PDMS solution was put onto structured and hydrophobized silicon wafers (GeSiM, Großerkmannsdorf, Germany) and cross-linked at 50 °C for 8 h. Subsequently, stamps were cut from the PDMS sheet and hardened at 120 °C for 2 h. Stamps were washed with heptane for 24 h, followed by drying at 90 °C for 24 h.

Stamps intended for printing on PPMA and PEMA surfaces were activated by oxygen plasma at 10.15 W for 1 min (medium setting, Harrick plasma cleaner PDC-002, Laseranalytik Starna GmbH, Pfungstadt, Germany) and aminosilanized as described above followed by application of 0.1% PEMA (hydrolyzed) in ethanol. After evaporation of solvent and heating at 120 °C for 2 h, stamps were subjected to high pressure steam sterilization and stored in deionized water. Prior to printing, stamps were inked with 10 mM poly(ethylene glycol)-amine solution (Jeffamine M-1000, Huntsman, Everberg, Belgium) in deionized water for 60 s, dried in a nitrogen stream for 60 s and applied to the substrates with gentle pressure for 60 s.

Stamps intended for POMA surfaces were treated with oxygen plasma for 30 s (Harrick Plasma Cleaner PDC-002, medium setting), inked with 5 mM Jeffamine in ethanol for 10 s, dried under nitrogen for 60 s and applied to surfaces for up to 10 s.

Micropatterned cover slips were then dried at 80 °C for 3 h to ensure binding of Jeffamine to the copolymers. Before use, substrates were stored in deionized water for 24 h to become hydrolyzed. Substrates were rinsed repeatedly with PBS-citrate buffer (0.02 M Na-citrate, 0.1 M NaCl, 0.02% NaN₃, pH 5.5) and incubated with TAMRA-labelled fibronectin (for the labelling procedure of fibronectin using 5- (and 6)-carboxytetramethylrhodamine (TAMRA, Invitrogen, Carlsbad, CA) see Renner et al.²³) diluted with PBS/citrate to 50 μg ml⁻¹ for 1 h. After incubation, substrates were rinsed repeatedly with PBS and incubated with cell culture medium at 37 °C for at least 10 min.

2.2 Cell culture and staining

Primary human umbilical vein endothelial cells (HUVEC) were collected from human umbilical cords after a procedure described elsewhere.²⁴ Cells were passaged three times at maximum prior use. HUVEC were cultured at 37 °C and 5% CO₂ (HeraCell, Heraeus-Instruments, Osterode, Germany) in endothelial cell growth medium ECGM (Promocell, Heidelberg, Germany) containing 2% fetal calf serum. Cells were seeded with a density of approx. 1 × 10⁵ cm² to achieve a good distribution of single cells on micropatterned substrates. Cells were grown on micropatterned substrates for 50 min.

Cells were rinsed thrice with PBS and fixed with 4% paraformaldehyde (Fluka Chemie AG, Switzerland) in PBS at room temperature for 10 min. After rinsing with PBS, cells were treated with 0.1% TritonX (Fluka) in PBS. After rinsing with PBS, F-actin was stained with phalloidin-Alexa488 (dilution 1 : 200, Invitrogen, USA) for 1 h and mounted on a cover glass using Vectashield-DAPI (Vector Laboratories Inc., Burlingame, CA, USA) for staining the nucleus.

2.3 Image acquisition and analysis

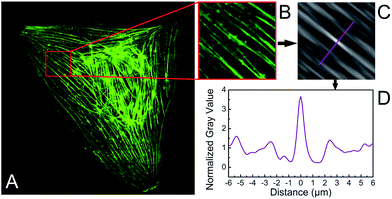
Fluorescence images of stained actin and prelabelled fibronectin patterns were acquired using confocal laser scanning microscopes (Leica DM IRBE SP1 and SP5) and a 40× oil immersion objective (HCX PL APO 40.0 × 1.25 OIL) directly on the substrate surface. Furthermore, we acquired z-stacks of xy-images of typical cells to reveal the 3D appearance of F-actin structures and the nucleus. Averaged distances between actin stress fibres were determined by processing images with a self-written macro in ImageJ (Rasband, W. S., National Institutes of Health, Bethesda, Maryland, USA, http://rsb.info.nih,gov/ij/, 1997–2008), similar to the method described elsewhere.²⁵ In short, images were background-corrected (rolling ball method, diameter 50 pixels), cropped to sections of 2ⁿ × 2ⁿ pixels with several actin fibres oriented in parallel (example shown in Fig. 1A), corresponding to a section size of roughly 10 to 20 μm with a resolution of 5–15 pixels per μm. These sections were autocorrelated, leading to a pattern of parallel stripes with a bright self-correlation maximum (called 0^th order maximum in this article) in the centre of the autocorrelation image (see Fig. 1B). The distance from the 0^th and 1^st order maximum was measured in a profile perpendicular to the actin stress fibre direction (see Fig. 1C). Note, that the 0^th order maximum is located in the centre of this profile and the origin of the abscissa was shifted to the 0^th order maximum for clarity. In this way, the distance between the 0^th and the 1^st order maximum can be directly read from the abscissa in both directions and can be taken as the average actin fibre distance in the related section of the cell. This approach was verified by direct measurements of typical distances of actin stress fibres chosen by visual inspection. Only sections of the cells were considered for the analysis, as a whole cell analysis lead to a strongly decreased signal-to-noise ratio because of the differently oriented parallel actin fibre regions. 3D visualization of confocal images was done using Volocity software (Perkin Elmer). In addition, the cell length and stripe width were measured directly from the images of actin and fibronectin patterns, respectively, and the cell basal area was determined from actin images by an ImageJ plugin.

Fig. 1 Autocorrelation analysis of actin stress fibre spacing. (A) From a microscopy image, a section with parallel stress fibres is chosen. (B) The 2D autocorrelation algorithm provides an autocorrelation image allowing the analysis of the mean actin stress fibre spacing in the section. (C) The spacing is determined from a cut through the central (self-correlation) maxima perpendicular to the stress fibre orientation and the distance between the 0^th and the 1^st order maxima.

2.4 Interfacial energy model

For simulation, the program Surface Evolver (Version 2.26, Kenneth Brakke, Mathematics Department, Susquehanna University, Selinsgrove, PA, USA; http://www.susqu.edu/brakke/evolver/evolver.html) was used to model the cells as liquid droplets spreading on micropatterned surfaces of striped wettability. The Surface Evolver can be applied to create surfaces and volumes, impose energetic boundary conditions and model the evolution of the given objects governed by minimization of energy. In this work, cell models started as cuboids on stripes with a given width. The cubic form was chosen as the starting configuration for simplicity and easy handling in the simulation. As we were only interested in the final equilibrium configuration the starting configuration was not considered as a relevant variable in the system, which is supported by the findings reported below. The contact angle, as defined by the Young equation, between the adhesive stripe and cuboid was set to 7° (equivalent to experimentally observed structures at cell adhesion contacts²⁶) and the contact angle between cuboid and the surrounding area was set to 180° (equivalent to non-spreading of cells on the non-adhesive substrate area). Both values set the lower and upper limit of the actual contact angle of the spread droplet at the border of adhesive and non-adhesive areas. Volume of the cuboids was set to 14 137 μm³, equal to the volume of a sphere with radius of 30 μm, and kept constant during each simulation. The surface tension of the free apical surface of the cell-droplet was set to 1, as the contact angle and surface tension are related according to Young's equation. To enhance similarity between the simulated structure and a cell, a solid sphere of 7 μm diameter was inserted into each cuboid as a fixed constraint for steric hindrance, in analogy to a cell's nucleus to inhibit extensive, non-physiological spreading in the case of flat cell morphologies. In the case of bulged droplets (narrow stripes, see also Fig. 5) it has no relevance as the sphere does not touch the droplet surface. For broad stripes and flat droplet morphologies the extensive spreading driven by the surface energy constraints (contact angle) is prevented by the solid sphere leaving the droplet morphology similar to an experimental cell morphology.

After definition of the initial conditions, triangulation was refined twice. To calculate the energy of each shape, contributions from a change of apical area (surface energy) as well as changes in the length of the contact line between the cell body and the adhesive area (line energy) were compared. After several iterations, the modelled cell's vertices were checked to not touch the hydrophobic area. Vertices in touch with the hydrophobic area were moved into the stripe region and the simulation continued in order to remedy the volume loss. At reaching a minimum energy configuration, triangulation was refined once and the model was iterated until recurrence of the minimum. Evolution of the droplet shapes was investigated on stripes of different widths ranging from 1 to 60 μm. In further simulations, volume, contact angle, nucleus size and surface tension were varied.

3 Results and discussion

3.1 Experiment

3.1.1 HUVEC adhesion on striped micropatterns. Early cell adhesion of HUVEC was investigated on micropatterned and non-patterned substrates 50 min after cell seeding. Cells were spread and showed round shapes when seeded on substrates without or with little lateral constraints (stripe width b > 40 μm). Cells adhered well to patterned substrates and did not spread to passivated (poly(ethylene glycol) modified) areas. Cells under strong lateral constraints were highly polarized in the direction of the stripes. On first sight actin fibres on the basal cell surface showed a distinct organization dependent on the stripe width as shown in Fig. 2. Actin fibres were almost randomly oriented on substrates with no or little constraints, Fig. 2A. On stripes with approximately 20 μm < b < 40 μm, actin fibres were found to be oriented with the stripe direction without changing the spacing between parallel fibres, see Fig. 2B. On very narrow stripes (b < 15 μm), many cells displayed only two actin stress fibres coincident with the stripe edge (see Fig. 2C) and were depleted of actin fibres in the central region.

Fig. 2 HUVEC on striped fibronectin micropatterns. The actin cytoskeleton pattern (green) changes with severity of lateral constraint (fibronectin – red): (A) random orientation of circularly spread cells, (B) parallel orientation along the stripe direction of polarized cells (stripe width: 27 μm), (C) depletion of actin fibres in the central cell region and two actin stress fibres at the stripe edge for highly polarized cells on very narrow stripes (stripe width: 13 μm). Scale bar: 20 μm.

3.1.2 Biphasic actin stress fibre spacing of HUVEC on micropatterns. To investigate the change in actin cytoskeleton architecture on the basal cell surface in more detail, distances between neighbouring parallel actin fibres were determined by autocorrelation analysis (see Materials and methods and Fig. 1). Quantification of actin fibre spacings yielded a mean distance of approximately 2 μm for cells growing on stripes with b > 25 μm as shown in Fig. 3. Cells on narrower stripes (10 μm < b < 20 μm) divided into two phenotypes, one with a regular spacing, whereas the other showed actin fibres only at the cell (stripe) edge. The latter behaviour led to a linear relationship between the stripe width and actin fibre spacing for cells on stripes with a width of 5–20 μm.

Fig. 3 Biphasic actin stress fibre spacing. (A) Actin stress fibre spacing in dependence on the stripe width. Open boxes characterize actin patterns with no stress fibres in the central cell region. Black (filled) boxes indicate regularly or arbitrarily organized actin patterns. (B) A histogram plot of actin stress fibre spacing in dependence on the stripe width better illustrates the biphasic behaviour with a linear relationship for stripe widths 5 μm < b < 20 μm and constant spacing for a stripe width b > 25 μm, as indicated by solid black lines. In between (10 μm < b < 25 μm) there is a continuous transition with an increasing stress fibre spacing indicated by the dotted black line.

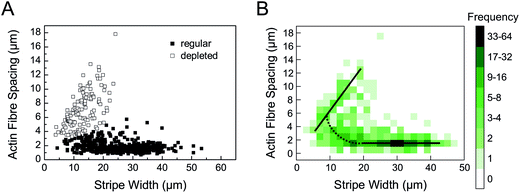
In addition to the stripe width, the influence of the physicochemical characteristics of the polymer substrates on actin fibre spacing was investigated, too. Previously, it had been shown that different maleic acid copolymer coatings can be used to alter ligand affinity due to wettability and charge density, affecting the spacing of fibronectin fibrils.²⁷ A similar influence on actin fibre spacing could be observed in this work as distances decreased with decreasing hydrophobicity of the polymer coating in the range of 2.0 μm to 1.7 μm for POMA and PEMA, respectively. However, this effect was only observed for non-patterned substrates and stripe widths b > 20 μm, i.e. cells with no or little lateral constraints. In comparison to the observations reported above, this effect was only minor and provided no significant impact for stripe widths b < 20 μm.

Furthermore, it has to be mentioned that reorganization of fluorescent-labelled fibronectin into fibrils below the adherent cells was only observed for no or little lateral constraints. No fibronectin fibrils could be detected for cells on narrow patterns. This observation implies a change in intracellular force regulation or adhesion contacts as myosin-driven transport along actin stress fibres out of focal adhesions is an essential parameter in fibronectin fibril formation.^28,29

The cell length and cell spreading area were also determined from actin stress fibre staining (data not shown). The cell length did not correlate with stripe width, while the basal cell area linearly increased with increasing stripe size.

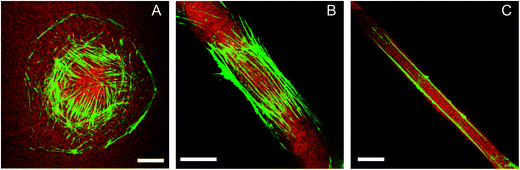
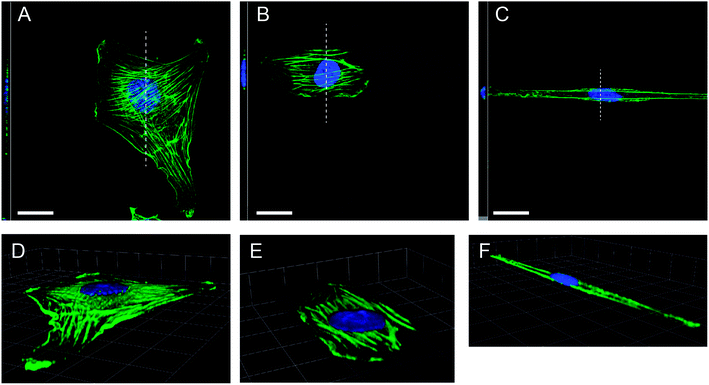
We additionally performed a 3D analysis of F-actin structures and the cell's nucleus for the different cell morphologies observed, see Fig. 4. As expected we observed elongated cell nuclei for cells on narrow stripes, while nuclei were found to be similarly positioned in the cells irrespective of the degree of constraint. The nuclei were located in the cell centre along the long axis of the cell and were tightly connected to the basal and apical cell surface. For very narrow stripes we partly observed a small expansion of the cell body including the nucleus onto the non-adhesive area which has to be attributed to a limited deformability of the nucleus, see also Fig. 4C and F. For the actin stress fibres it could be found that the major stress fibres stay near to the cell substrate. We did not find stress fibres on the apical cell surface, neither for the unconstrained cells on non-patterned substrates nor the highly constrained cells on the narrow stripes. In the case of cells on the narrow stripes we observed again that no stress fibres were formed in the cell centre. Only two single stress fibres (or bundles) are found along the cell edge parallel to the striped pattern. In this context we have to recall that we use staining of F-actin structures. Therefore, we should not attribute the lower number of inner stress fibres to a decrease of the overall actin content, which we do not expect during the short time period of the experiments.

Fig. 4 Three-dimensional confocal analysis of actin stress fibre distribution. Top view accompanied by vertical sections (left) of cells with stained F-actin (green) and cell nucleus (blue). The section is indicated by a dashed line. (Scale bar: 20 μm): (A) unconstrained cell, (B) cell with little constraints, (C) cell on a very narrow stripe. (E and F) Respective three-dimensional representations of the above cells (scaling mesh size: 12.4 μm).

3.2 Simulation

3.2.1 Modelling cell-droplets on striped micropatterns. In a concurrent simulation effort, cells on stripes were simulated with the software Surface Evolver. With this software, cells were modelled similarly to droplets, being assigned with an initial shape, incompressible volume, surface tension and contact angles between the different interfaces. However, droplets were not allowed to spread freely on surfaces, as an impenetrable, solid sphere mimicking the nucleus was incorporated into the droplet. Each simulation process was initialized with a cuboid cell-droplet tessellated by triangles. By minimizing energy, the cell-droplet structure was evolved until stable (see Materials & methods and Fig. 5). Starting parameters were chosen based on experimental observations: volume was equivalent to that of a cell with a diameter of 30 μm, the range of stripe widths equalled the one during experiments, the nucleus diameter was set to 7 μm, a small contact angle (7°), with respect to the Young equation, was given on adhesive stripes and a very large contact angle (180°) was set as an upper limit outside of stripes to prevent unbridled wetting. In that way the actual contact angle of a droplet touching the transition line of adhesive and non-adhesive area is between both limiting values. The contact angle on the adhesive stripe was chosen based on observations of the architecture of cell adhesion contacts.²⁶ However, our simulation shows that the observed behaviour is nearly universal for sufficiently small contact angles on the adhesive stripe. A limiting contact angle of 180° outside the adhesive stripes simulates the non-spreading of cell-droplets to this area. The interfacial energy of the free stripe surface is assumed to be negligible in comparison to the interfacial energy between the cell and the adhesive stripe.

Fig. 5 Simulation of cell-droplets leads to biphasic droplet morphology. (A) Starting configuration of simulation with a cuboid shape (free surface in green) and the central fixed sphere (blue) on a wettable stripe (red) with a width of 5 μm. (B) Equilibrium shape of a cell-droplet on a substrate with little lateral constraints (stripe width 20 μm) showing a flat and spread morphology. (C) Equilibrium shape of a cell-droplet on a substrate with a very narrow stripe (width 5 μm) showing a bulged droplet shape.

We do not use defined numbers of the interfacial tension as there is a broad variability of experimental values and estimates in the literature.³⁰ Numbers for the surface tension of free cell surfaces are reported in the range from 10⁻⁵ N m⁻¹,³¹ 10⁻⁴ N m⁻¹,³² up to 10⁻³ N m⁻¹.³³ Meaningful numbers of the interfacial tension at the cell–substrate interface are more difficult to obtain as they are difficult to measure and the cell–substrate interaction is heavily regulated in a receptor-specific and time-dependent manner. One can estimate lower boundaries by taking receptor–ligand interactions (i.e. integrin–fibronectin) in the range of 20 kT (see Li et al.³⁴) and a density of 200 receptors per μm² (ref. 35) leading to 10⁻⁵ N m⁻¹, a value which has been found in other studies,³⁶ too. Single cell force spectroscopy allows the quantification of the work of detachment of adherent cells, which together with estimates of the cell contact area results in values of interfacial tension in the range of 10⁻⁴ N m⁻¹ and 10⁻³ N m⁻¹.^37,38 Evaluating these estimates of the interfacial tension of the cell–substrate interface and the free cell surface suggests that the used ansatz for the contact angle on adhesive stripes of the droplet model is quite reasonable. However, we have to point out again that absolute numbers of the interfacial tension of cell-matrix adhesion have to be used with caution due to the multiple time-dependent biomolecular processes involved.

During simulation, aberrant cell shapes were observed as sometimes facets would overlap or wetting of the hydrophobic surface would occur. In these instances, vertices of the cell were reset to lie within the allowed region, triangulation was refined and iteration continued, see also Materials & methods.

The resultant structures were characterized by their area, composed of a basal and an apical component, as well as by the visual inspection of droplet morphology.

3.2.2 Cell-droplet shape transition at the critical stripe width. The simulation of cell-droplets yielded a biphasic behaviour in surprising coincidence with the experimental results. Two different morphologies could be observed. A transition between flat and spread cell-droplets and bulged droplets was observed with a decrease of the stripe width at around 15 μm, indicated by an abrupt change in the cell area (shown in Fig. 6A), in analogy to the behaviour of cells in the experiment.

Fig. 6 Biphasic behaviour of cell-droplets in dependence on lateral constraint. (A) A sharp increase in the surface area of the droplet at a critical stripe width of around 15 μm indicates the transition from the bulged shape to the flat shape, the latter one characterized by a much larger surface area. In the flattened morphology the surface area is almost independent of the stripe width. (B) The impact of surface tension on the transition between the two cell-droplet morphologies can be seen from the shift of the critical stripe width to lower values by a change in the interfacial energy of the free cell-droplet surface.

The reason for the switch between the two different morphologies in the simulation is the minimization of interfacial energy. On narrow stripes the gain in droplet-substrate interfacial energy by spreading on the stripe does not compensate the increase in the free droplet surface, thus limiting the spreading on the stripes.

This simulation result nicely fits to wetting experiments and modelling conducted by Gau et al.,³⁹ where water channels on narrow hydrophilic stripes also showed biphasic behaviour in morphology. Therein local channel bulging was observed and could be explained by minimal energy configurations and alternatively by a stability analysis based on contact angle and volume constraints.

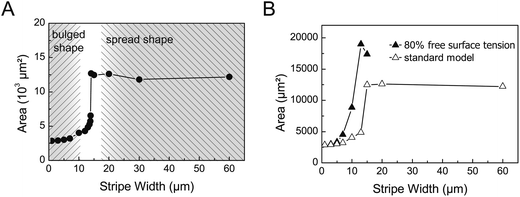
As the simulation of cell-droplets provided a critical stripe width for the transition between the two cell-droplet states which was similar to the stripe width characteristic for the change of the actin pattern in the cell experiments, we checked the sensitivity of different parameters of the model with respect to the critical stripe width. The simulation provided easy access to parameters such as the nucleus size, contact angle, volume and interfacial energy.

Variation of the nucleus size resulted in a more pronounced difference in the area between the bulged and spread state but had negligible impact on the critical stripe width. The latter is expected as the transition between both states is driven by interfacial tension and the nucleus does not touch the cell surface in the bulged state. This is noteworthy insofar as bulging was not observed to the same extent in the experiment. Rather, below the critical stripe width cells stayed elongated and a deformation of the nucleus was observed by the strong lateral constraints. An increase in the volume slightly shifted the transition region to broader stripes as bigger droplets would expose more area when spread. However, both parameters, the size of nucleus and cell volume, can be considered constant during cell spreading on the micropatterned substrates. Changes in the nuclear volume are only to be expected during the S-phase of the cell cycle (DNA synthesis). As endothelial cell cultures proliferate with a doubling time of approx. 20 hours⁴⁰ we do not consider changes of the nuclear volume in the time course of our experiment. Similarly the cell volume was shown to be almost constant during migration and non-migratory oscillations.^41–43 In that sense, we do not consider the cell volume as a relevant regulatory parameter in the experiments. However, one should consider variations in the volume of real cells as a possible parameter leading to a scatter of the data, i.e. the critical stripe width. This could also be the reason for the overlap of the different actin cytoskeleton patterns in the range of stripe width of 10 μm to 20 μm in cell culture experiments.

A variation of the contact angle on the adhesive stripe from 1° to 45° (as defined by the Young equation), while keeping surface tension of the apical surface constant, had little effect for small contact angles which can be understood from the Young's equation where the cosine function will remain nearly constant for small arguments. For larger contact angles, i.e. lowered interfacial energy at the basal side, an increase in the critical stripe width and a decrease of area gain due to flattening could be observed. However, the latter conditions of large contact angles on adhesive stripes cannot be considered relevant in the comparison to cells as such morphologies were not observed in the experiments.

In the standard simulation setup only relative changes of the interfacial energies between the free cell-droplet surface and basal cell-droplet surface were considered by varying the respective contact angle on the adhesive stripe. However, as we implemented the constraints of a non-deformable nucleus within the cell-droplet, the simulation can be extended to even lower surface energies of the free surface, beyond the range covered by the Young's equation, i.e. corresponding to negative values of the contact angle. In the simulation we still receive stable cell-droplet configurations, when lowering the surface tension of the free apical surface. This is equivalent to an increase in interfacial energy of the basal surface between the cell-droplet and substrate. This variation yielded a pronounced shift of the critical stripe width to smaller values, see Fig. 6B for lowering the surface tension of the apical surface to 80% of the standard model. Hence, the transition towards a bulged morphology is restrained to even smaller stripe widths as the energy cost for maintaining large apical surfaces is better compensated by a more favourable interaction between the droplet and substrate. This result can be interpreted in the following way. A lowering of the interfacial energy of the apical, free cell surface circumvents the transition to a non-spread (bulged) shape with high local membrane curvatures. Similarly, an increase in the cell–substrate interfacial tension (basal) would result in a similar phenomenon. This finding suggests an interesting ansatz for the interpretation of the biphasic characteristics of the actin stress fibre pattern in the cell experiments.

3.3 A hypothesis for the correlation of biphasic transitions in the actin stress fibre pattern and cell-droplet shapes on micropatterned substrates

Strikingly, two different systems, one being a living cell with its complex biochemistry and biophysics, the other one being an abstract model of a cell-reminiscent droplet predominantly determined by interfacial energies, both show intriguing similarities with regard to adaptation to lateral constraints of a micropatterned substrate: (i) both show different morphologies in dependence on lateral constraints and (ii) both systems exhibit transition regions at roughly the same critical stripe width of approx. 15 μm.

For the cell-droplet a dramatic morphology change is observed with bulging and a lowering of surface area for narrow stripes. For living cells we do not observe such a drastic morphology change of the whole cell. Cells stay very elongated with a similar length also on narrow stripes. Because bulging is not observed for the cells, the cell membrane touches the nucleus leading to a reshaping of the nucleus by the strong lateral constraints. So, we do find different situations for both systems on narrow stripes: bulged cell-droplets with no impact of the nucleus, elongated cells with the nucleus touching the cell membrane leading to strong interactions. Hence, for narrow stripes both systems are not compared with each other.

However, both systems show a transition in their characteristics at the same stripe width of approx. 15 μm, being the actin cytoskeleton pattern and the cell-droplet morphology, respectively. While one should be cautious to equate both systems and the respective causes and effects, the underlying physics and assumptions may allow the following hypothesis for the experimental findings in the actin stress fibre pattern. Interfacial energy, or surface tension respectively, was demonstrated to be the dominant parameter in the simulation part of this study. It is also expected to play an important role in the adhesion of real cells. The simulation suggested a lowering of apical (free) surface tension to shift the transition to a lower stripe width. (Similarly, the basal (cell–substrate) interfacial tension could be increased.) This argument can be used to suggest that lowering of free surface tension could allow the cell to circumvent strong shape changes (bulging) which otherwise would be required for surface energy minimization. Hence, an intracellular mechanism could regulate interfacial tension to circumvent morphology changes with a maintained minimal surface energy.

The reorganization of the actin cytoskeleton could be one way to allow for the lowering of cell surface tension. Here, the actin cortex at the cell membrane may play a role, which has already been known from other studies on cell shaping and force generation.¹⁷ In addition, the distinct changes in actin cytoskeleton architecture may be a hint for an active regulation of intracellular tension at actin stress fibres by the cytoskeletal signalling pathways. The latter argument is supported by our observation that very elongated cells do not form fibronectin fibrils, a process which is correlated with formation of focal and fibrillar adhesion sites as well as the occurrence of forces and transport along actin stress fibres. Hence, its absence indicates again changes in the intracellular organization of cytoskeletal components and force generators.

To fully understand the underlying regulatory principles, observations of the evolution and mutable reshaping of the actin cytoskeleton during cell spreading and adhesion on micropatterns would be beneficial in order to understand the dynamics of these processes. However live staining of actin structures of primary cells, i.e. endothelial cells in our case, is difficult to achieve without perturbing the cell function and viability. Also, assays with other cell lines may yield different results regarding cell forces and actin cytoskeleton architecture and are therefore beyond the scope of this paper.

Approaches to prove the raised hypothesis and to unravel underlying cell signalling mechanisms will need a range of other investigations to probe the force balance of the cells including investigation of adhesion forces, traction forces and overall cell mechanics. Here biophysical and biochemical perturbations are envisioned to probe distinct regulating cues of cell adhesion including changes of substrate stiffness, ligand affinity, actin depolymerization, inhibition of myosin motor activity, blocking downstream signalling pathways of intracellular stress fibre formation and tension generation, and others. Such a comprehensive analysis has to be left for future experiments as one has to tightly control different aspects of the strongly coupled signalling pathways in cell adhesion.

4 Summary

In this study, the actin stress fibre pattern of adherent endothelial cells was investigated under lateral constraints of adhesive striped micropatterns. A biphasic behaviour was observed with a transition near a stripe width of 15 μm, where on narrow stripes the spacing of two remaining actin fibres was linearly correlated with the stripe width, whereas on broad stripes actin fibre spacing was independent of the stripe width. Concurrently, cells were simulated as a quasi-droplet with a fixed integrated nucleus on wettable, striped micropatterns, only considering interfacial energies. Interestingly, the simulation yielded a biphasic behaviour, too, evidenced by a strong change of the cell area near a critical stripe width similar to the experimentally determined one. It is important to note that the parameters used in this model were derived from experimental observations and thus may have given a good approximation to experimental conditions. As interfacial energy was sufficient to explain the biphasic behaviour of cell-droplets under lateral constraints, we hypothesise that the observed cell behaviour concerning changes in the actin stress fibre pattern might be related to the cell's active regulation of interfacial energy. To attribute this to either membrane tension, changes in the actin cortex or intracellular tensions, more experiments are needed to be undertaken and better models have to be devised.

Acknowledgements

J.M., T. Paumer and T. Pompe thank Carsten Werner for supporting this work during their stay at the Max Bergmann Center of Biomaterials Dresden, Leibniz Institute of Polymer Research Dresden. A.M. acknowledges financial support by the Deutsche Forschungsgemeinschaft (Graduate School BuildMoNa).

References

1. D. E. Discher, P. Janmey and Y.-L. Wang, Science, 2005, 310, 1139–1143.
2. B. Trappmann, J. E. Gautrot, J. T. Connelly, D. G. T. Strange, Y. Li, M. L. Oyen, M. A. Cohen Stuart, H. Boehm, B. Li, V. Vogel, J. P. Spatz, F. M. Watt and W. T. S. Huck, Nat. Mater., 2012, 11, 642–649.
3. D. E. Discher, D. J. Mooney and P. W. Zandstra, Science, 2009, 324, 1673–1677.
4. L. Dike, C. Chen, M. Mrksich, J. Tien, G. Whitesides and D. Ingber, In Vitro Cell. Dev. Biol.: Anim., 1999, 35, 441–448.
5. M. Arnold, E. A. Cavalcanti-Adam, R. Glass, J. Blümmel, W. Eck, M. Kantlehner, H. Kessler and J. P. Spatz, ChemPhysChem, 2004, 5, 383–388.
6. C. S. Chen, M. Mrksich, S. Huang, G. M. Whitesides and D. E. Ingber, Science, 1997, 276, 1425–1428.
7. R. McBeath, D. M. Pirone, C. M. Nelson, K. Bhadriraju and C. S. Chen, Dev. Cell, 2004, 6, 483–495.
8. J. T. Parsons, A. R. Horwitz and M. A. Schwartz, Nat. Rev. Mol. Cell Biol., 2010, 11, 633–643.
9. C. Chen, R. Krishnan, E. Zhou, A. Ramachandran, D. Tambe, K. Rajendran, R. M. Adam, L. Deng and J. J. Fredberg, PLoS One, 2010, 5, e12035.
10. T. Yeung, P. C. Georges, L. A. Flanagan, B. Marg, M. Ortiz, M. Funaki, N. Zahir, W. Ming, V. M. Weaver and P. A. Janmey, Cell Motil. Cytoskeleton, 2005, 60, 24–34.
11. K. Hu, L. Ji, K. T. Applegate, G. Danuser and C. M. Waterman-Storer, Science, 2007, 315, 111–115.
12. V. Vogel and M. P. Sheetz, Curr. Opin. Cell Biol., 2009, 21, 38–46.
13. N. Wang, J. P. Butler and D. E. Ingber, Science, 1993, 260, 1124–1127.
14. I. B. Bischofs, F. Klein, D. Lehnert, M. Bastmeyer and U. S. Schwarz, Biophys. J., 2008, 95, 3488–3496.
15. K. Kruse, J. F. Joanny, F. Jülicher, J. Prost and K. Sekimoto, Eur. Phys. J. E: Soft Matter Biol. Phys., 2005, 16, 5–16.
16. C. M. Bidan, K. P. Kommareddy, M. Rumpler, P. Kollmannsberger, Y. J. M. Brechet, P. Fratzl and J. W. C. Dunlop, PLoS One, 2012, 7, e36336.
17. J.-L. Maitre, H. Berthoumieux, S. F. G. Krens, G. Salbreux, F. Jülicher, E. Paluch and C.-P. Heisenberg, Science, 2012, 338, 253–256.
18. M. L. Manning, R. A. Foty, M. S. Steinberg and E.-M. Schoetz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12517–12522.
19. E. Sackmann and R. F. Bruinsma, ChemPhysChem, 2002, 3, 262–269.
20. A. Zemel, F. Rehfeldt, A. E. X. Brown, D. Discher and S. A. Safran, J. Phys.: Condens. Matter, 2010, 22, 194110.
21. A. Zemel, F. Rehfeldt, A. E. X. Brown, D. E. Discher and S. A. Safran, Nat. Phys., 2010, 6, 468–473.
22. T. Pompe, S. Zschoche, N. Herold, K. Salchert, M.-F. Gouzy, C. Sperling and C. Werner, Biomacromolecules, 2003, 4, 1072–1079.
23. L. Renner, T. Pompe, K. Salchert and C. Werner, Langmuir, 2004, 20, 2928–2933.
24. J. R. Weis, B. Sun and G. M. Rodgers, Thromb. Res., 1991, 61, 171–173.
25. T. Pompe, C. Mitdank and C. Werner, J. Phys.: Condens. Matter, 2004, 16, S2421.
26. C. M. Franz and D. J. Müller, J. Cell Sci., 2005, 118, 5315–5323.
27. T. Pompe, K. Keller, C. Mitdank and C. Werner, Eur. Biophys. J., 2005, 34, 1049–1056.
28. Y. Mao and J. E. Schwarzbauer, Matrix Biol., 2005, 24, 389–399.
29. R. Pankov, E. Cukierman, Z. Katz, K. Matsumoto, D. C. Lin, S. Lin, C. Hahn and K. M. Yamada, J. Cell Biol., 2000, 148, 1075–1090.
30. J. L. Maitre and C. P. Heisenberg, Curr. Opin. Cell Biol., 2011, 23, 508–514.
31. D. Raucher and M. P. Sheetz, J. Cell Biol., 2000, 148, 127–136.
32. J. Y. Tinevez, U. Schulze, G. Salbreux, J. Roensch, J. F. Joanny and E. Paluch, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18581–18586.
33. I. B. Bischofs, S. S. Schmidt and U. S. Schwarz, Phys. Rev. Lett., 2009, 103, 048101.
34. F. Li, S. D. Redick, H. P. Erickson and V. T. Moy, Biophys. J., 2003, 84, 1252–1262.
35. P. W. Wiseman, C. M. Brown, D. J. Webb, B. Hebert, N. L. Johnson, J. A. Squier, M. H. Ellisman and A. F. Horwitz, J. Cell Sci., 2004, 117, 5521–5534.
36. R. Simson, E. Wallraff, J. Faix, J. Niewöhner, G. Gerisch and E. Sackmann, Biophys. J., 1998, 74, 514–522.
37. J. Friedrichs, K. R. Legate, R. Schubert, M. Bharadwaj, C. Werner, D. J. Müller and M. Benoit, Methods, 2013, 60, 169–178.
38. G. Weder, N. Blondiaux, M. Giazzon, N. Matthey, M. Klein, R. Pugin, H. Heinzelmann and M. Liley, Langmuir, 2010, 26, 8180–8186.
39. H. Gau, S. Herminghaus, P. Lenz and R. Lipowsky, Science, 1999, 283, 46–49.
40. T. Pompe, F. Kobe, K. Salchert, B. Jorgensen, J. Oswald and C. Werner, J. Biomed. Mater. Res., Part A, 2003, 67, 647–657.
41. M. P. Stewart, J. Helenius, Y. Toyoda, S. P. Ramanathan, D. J. Müller and A. A. Hyman, Nature, 2011, 469, 226–230.
42. H. Blaser, M. Reichman-Fried, I. Castanon, K. Dumstrei, F. L. Marlow, K. Kawakami, L. Solnica-Krezel, C. P. Heisenberg and E. Raz, Dev. Cell, 2006, 11, 613–627.
43. G. Salbreux, J. F. Joanny, J. Prost and P. Pullarkat, Phys. Biol., 2007, 4, 268–284.

---

Footnote

† Current address: Technische Universität Dresden, Institute of Materials Science, Dresden 01069, Germany.

---