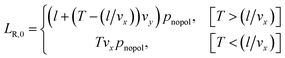Tuning the adhesive geometry of neurons: length and polarity control†
Caterina
Tomba
ab,
Céline
Braïni
a,
Beilun
Wu
a,
Nir S.
Gov
*c and
Catherine
Villard
*a
aUniv. Grenoble Alpes, Inst NEEL and CRETA, F-38042 Grenoble, France
bLTM c/o CEA Léti, Université Joseph Fourier, CNRS UMR 5129, 17 av des Martyrs, F-38054 Grenoble, France
cDepartment of Chemical Physics, Weizmann Institute of Science, Rehovot, Israel. E-mail: nir.gov@weizmann.ac.il
First published on 22nd January 2014
Abstract
Neurons acquire their functional and morphological axo-dendritic polarity by extending, from competing minor processes (neurites), one long axon among numerous dendrites. We employed complementary sets of micropatterns built from 2 and 6 μm wide stripes of various lengths to constrain hippocampal neuron shapes. Using these geometries, we have (i) limited the number of neuronal extensions to obtain a minimal in vitro system of bipolar neurons and (ii) controlled the neurite width during growth by the generation of a progressive cell shape asymmetry on either side of the cellular body. From this geometrical approach, we gained a high level of control of each neurite length and of the localization of axonal specification. To analyze these results, we developed a model based on a width and polarization dependent neurite elongation rate and on the existence of a critical neurite length that sets the axonal fate. Our data on the four series of micro-patterns developed for this study are described by a single set of growth parameters, well supported by experiments. The control of neuronal shapes by adhesive micro-patterns thereby offers a novel paradigm to follow the dynamical process of neurite lengthening and competition through the process of axonal polarization.
1 Introduction
Neurons are branched cells whose various stages of growth can be monitored in vitro. A fundamental step of neuronal development is the acquisition of polarity which results in both morphological and functional distinction between numerous dendrites and one long axon. In cultured hippocampal neurons, primary undifferentiated neuronal branches, or neurites, compete for the axonal fate by a race for the highest elongation rate.1 It is now well established that the various aspects of neuronal growth including branching, growth rate and axonal specification can be modulated by physical cues. Of note, these cues can be provided by the architecture of the brain itself, with the striking example of the in vivo migrating neurons constrained to adopt a bipolar geometry in their journey along micron-wide elongated glial cells.2 While the mechanical rigidity has proven to tune branching when approaching the extreme softness of the brain tissue,3 the topography provided by micro-pillars can increase the neurite elongation rate and thereby bias neuritic competition.4 Geometries imposed by adhesive micro-patterns are also an efficient way to control neuronal growth and to impose the localization of axonal specification, either by constraining neuronal shapes5 or by superimposing to these shapes a chemical gradient of adhesion.6 Poly-lysine constitutes a widely used polycationic coating on glass7 although laminin, a component of the extra-cellular matrix, is also commonly employed to foster axonal growth.8 Interestingly, varying the neurite width from 2 to 4 μm seems to have some influence on both neuronal growth and polarization.6 However a simple picture of the role of this geometric parameter would deserve an extensive study.The nascent axon is not only the longest neurite, but it also presents molecular specificities according to a characteristic spatial organization. In particular, a structure named the axonal initial segment (AIS) plays the role of a diffusion barrier at the axon base to ensure the establishment and the maintenance of polarity.9 The characteristic length of the AIS (30–40 μm) is also found in axotomy experiments where the remaining stump retains a memory of its axonal nature only when longer than 35 μm.10 A length threshold of 40 μm seems also to be required to stabilize the polarized state.11,12
In this work, we performed an in-depth study of the role of the neurite width in the process of neurite elongation and axonal specification. To that aim, we used geometric variations on the theme of a generic bipolar geometry imposed by poly-L-lysine micro-patterns. This non-specific coating against dendrite or axonal elongation was specifically chosen to dispose of a system where the shape is the only control parameter. Four series of micro-patterns allowing changes in the surface of adhesion between and along competing neurites were designed. The lengths of neurites were systematically measured, and the possible axonal nature of these neuronal extensions was assessed using the usual Tau-immunostaining.13,14 We provide for the first time experimental data that allow us to follow the dynamical neurite lengthening and competition through the process of axonal polarization. These data were compared to a simple model based on a width-dependent elongation rate modulated by a distance over which a neurite has the highest probability to become an axon. By unraveling the relationship between neuronal shapes and growth, our results support the existence of a critical length, close to the AIS length, that controls the axonal fate of a neuronal extension. Most of all, we provide in this work an original experimental paradigm to probe the impact of geometry on polarization.
2 Adhesive geometries and cells
We designed a minimal system of neurons characterized by two diametrically opposite neurites. This bipolar cell geometry was obtained by growing in vitro hippocampal neurons (see the Experimental section) on poly-L-lysine (PLL) adhesive stripes intercalated with 14 μm PLL disks designed to anchor the cell body (or soma). All patterns were derived from an initial geometry built from 2 μm and 6 μm wide stripes located on each side of the central disk (6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 pattern). Then, the length of either the 2 μm or the 6 μm wide stripe is progressively reduced and replaced by a 6 μm or 2 μm wide portion of length l, respectively. Patterns differ from the localization of these portions and are divided into two categories. In the first set of patterns (Fig. 1), the 6 μm (Fig. 1a) or 2 μm (Fig. 1b) wide portions of length l departs from the circular disk (i.e. from the soma). In the second set of patterns (Fig. 2), the non-modified portions of the 6
2 pattern). Then, the length of either the 2 μm or the 6 μm wide stripe is progressively reduced and replaced by a 6 μm or 2 μm wide portion of length l, respectively. Patterns differ from the localization of these portions and are divided into two categories. In the first set of patterns (Fig. 1), the 6 μm (Fig. 1a) or 2 μm (Fig. 1b) wide portions of length l departs from the circular disk (i.e. from the soma). In the second set of patterns (Fig. 2), the non-modified portions of the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 pattern in contrast remain near the adhesive disk. All patterns are defined by a simple nomenclature of type x
2 pattern in contrast remain near the adhesive disk. All patterns are defined by a simple nomenclature of type x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xy or y
xy or y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xy expressing the spatial succession of the 2 and 6 μm wide stripes.
xy expressing the spatial succession of the 2 and 6 μm wide stripes.
As an example, the typical morphology of cells grown on the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 patterns is given in Fig. 3. In this particular set of neurons, only the longest neuron (top) grown on the geometry characterized by l = 20 μm expresses the characteristic axonal Tau gradient on its longest, 2 μm wide neurite. Other examples of Tau staining are displayed in Fig. S1.†
26 patterns is given in Fig. 3. In this particular set of neurons, only the longest neuron (top) grown on the geometry characterized by l = 20 μm expresses the characteristic axonal Tau gradient on its longest, 2 μm wide neurite. Other examples of Tau staining are displayed in Fig. S1.†
3 Theoretical models
We model the elongation of the neurites along the adhesive strips, by considering the following observations.(1) The growth velocity is affected by the width of the adhesive stripe on which the neurite grows. We will consider the simplest scenario where the growth material synthesized at the soma level has to be distributed along the available surface at the neurite growth-cone, leading to a larger (smaller) velocity vtip when the width is smaller (wider).
(2) The neurites have a certain probability to turn into axons, which signals for the whole cell to polarize. This polarization event seems to depend on the absolute length of the neurite.11,12
(3) Following the polarization event the neurite that was “chosen” to become the axon may continue to grow at a different growth velocity βvtip (with β ≥ 1). The other neurite(s) continues to grow at a reduced growth velocity γvtip (0 ≤ γ ≤ 1), following the polarization event.
We now turn these assumptions into a calculation of the mean neurite length on the patterns shown in Fig. 1 and 2. For this we need to assume some probability density function that describes the probability for the neurite to undergo polarization, as a function of its length. Based on the notion of a critical length for this transition,11,12 we consider the following simple step-like cumulative probability to polarize
 | (1) |
 | (2) |
 | ||
| Fig. 4 Polarization cumulative probability Ppol(x) (eqn (1)) and the probability distribution function ppol(x) (eqn (2)) (inset). The parameters used are Lpol = 50 μm and σpol = 20 μm. | ||
We then divide the calculation into two cases, for the case of polarization along the right neurite and along the left neurite. We now demonstrate the calculations that result from our model for the x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xy patterns (shown in Fig. 1). A similar calculation follows along the same lines for the y
xy patterns (shown in Fig. 1). A similar calculation follows along the same lines for the y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xy patterns. For polarization along the right neurite, the length of the right neurite is given by the following
xy patterns. For polarization along the right neurite, the length of the right neurite is given by the following
 | (3) |
 | (4) |
 | (5) |
 | (6) |
The maximal value of xpol for the right neurite is
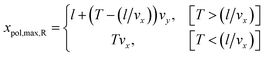 | (7) |
Over the possible range of xpol we need to integrate the lengths in eqn (3) multiplied by the probability that the right neurite polarizes at position xpol, which is given by ppol(x) (eqn (2)). In addition we need to multiply by the probability that the competing neurite has not already polarized itself by this time. This probability is given by the cumulative probability up to the position of the tip on the left neurite xpol,L corresponding to xpol on the right neurite
 | (8) |
The final mean length that we get is
 | (9) |
 | (10) |
For completeness, the overall probability for polarization of the left neurite is given by
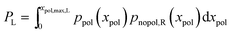 | (11) |
In a similar manner we calculate the length of the left neurite when the right one is polarized (〈LL,R〉) and the lengths for the case of polarization on the left neurite (i.e. 〈LL,L〉 and 〈LR,L〉). In order to get the total mean length along each side, we also need to consider the lengths of the neurites when no side has polarized. For the x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xy these lengths are given by
xy these lengths are given by
| LL,0 = Tvxpnopol | (12) |
where the probability for no polarization is given by pnopol = 1 − PR − PL, where PR is given in eqn (10).
Summing up the lengths on each neurite from all the possible polarization outcomes gives the final mean lengths: LL = LL,0 + 〈LL,R〉 + 〈LL,L〉 and LR = LR,0 + 〈LR,R〉 + 〈LR,L〉.
4 Results
The model presented above requires a set of parameters, namely the culture duration (T), the elongation rates of neurites constrained by either 2 and 6 μm wide stripes, the multiplicative coefficients controlling the change of these elongation rates after axonal specification (β for the axon and γ for the dendrite), and the characteristic lengths of the probability distribution function Lpol and σpol. The three first parameters are fixed by the experiments, with (i) T = 72 h (all neurons were fixed and analyzed after 3 days of culture) and (ii) v6 = 2 μm h−1 and v2 = 4 μm h−1, as roughly indicated from the data presented in Fig. 5 showing the evolution of the total neurite length for cells grown on symmetric x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x patterns (x = 2, 4 and 6 μm).
x patterns (x = 2, 4 and 6 μm).
 | ||
| Fig. 5 Influence of the stripe width on the total neurite length after 3 days of culture. The geometries used are sketched beside the graph. Errors bars denote the standard deviation. | ||
Fitting our model to the experimental data while keeping within the available constraints the values of the different parameters, we were able to obtain the values of Lpol, σpol, γ and β.
We want to emphasize here the limiting case of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 pattern. From the analysis of 180 neurons coming from 3 different cultures performed under the same conditions, 161 neurons exhibited a Tau immunostaining on the 2 μm wide stripe. Strikingly, none displayed this marker on the 6 μm wide side (of note, the 6 μm wide neurite is always the shortest) (see for example Fig. 6B, red symbols). Therefore, the 2
6 pattern. From the analysis of 180 neurons coming from 3 different cultures performed under the same conditions, 161 neurons exhibited a Tau immunostaining on the 2 μm wide stripe. Strikingly, none displayed this marker on the 6 μm wide side (of note, the 6 μm wide neurite is always the shortest) (see for example Fig. 6B, red symbols). Therefore, the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 pattern offers for the first time and to the best of our knowledge the first demonstration that the localization of axonal specification can be reliably set by geometrical constraints on the neurite width. Of note, neurons plated on the four different x
6 pattern offers for the first time and to the best of our knowledge the first demonstration that the localization of axonal specification can be reliably set by geometrical constraints on the neurite width. Of note, neurons plated on the four different x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xy or y
xy or y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xy sets of patterns were grown under slightly different conditions of culture (different serum batch, mice type, and temperature set-point of the incubator) that prevents a comparison of the length data obtained from these neurons with the ones of the 2
xy sets of patterns were grown under slightly different conditions of culture (different serum batch, mice type, and temperature set-point of the incubator) that prevents a comparison of the length data obtained from these neurons with the ones of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 pattern. Nevertheless, we made the choice to show on the same graphs the polarization data coming from all patterns, including the 2
6 pattern. Nevertheless, we made the choice to show on the same graphs the polarization data coming from all patterns, including the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 geometry.
6 geometry.
In Fig. 6A we compare the calculations of length presented in the previous section with the experimental data for the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62 pattern. In Fig. 6B we compare the calculated polarization probabilities PL and PR to the observed frequency of axons identified. In Fig. 7–9 we compare the calculated neurite lengths and the polarization probabilities to the observations for the other three patterns shown in Fig. 1 and 2. The points corresponding to the 2
62 pattern. In Fig. 6B we compare the calculated polarization probabilities PL and PR to the observed frequency of axons identified. In Fig. 7–9 we compare the calculated neurite lengths and the polarization probabilities to the observations for the other three patterns shown in Fig. 1 and 2. The points corresponding to the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 pattern in Fig. 8 and 9 are arbitrarily located at the coordinate l = 200 μm (and naturally at l = 0 μm in Fig. 6 and 7).
6 pattern in Fig. 8 and 9 are arbitrarily located at the coordinate l = 200 μm (and naturally at l = 0 μm in Fig. 6 and 7).
 | ||
Fig. 7 Pattern 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26. (A) Neurite lengths. (B) Polarization probabilities. All results after three days of growth. Symbols denote the experimental data and lines denote the result of the model calculation: circles (dashed line, LR) along the right neurite (here the xy branch) and squares (solid line, LL) along the left neurite (here the x branch). The red symbols correspond to the 2 26. (A) Neurite lengths. (B) Polarization probabilities. All results after three days of growth. Symbols denote the experimental data and lines denote the result of the model calculation: circles (dashed line, LR) along the right neurite (here the xy branch) and squares (solid line, LL) along the left neurite (here the x branch). The red symbols correspond to the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 pattern. The parameters used in this calculation are the same as in Fig. 6. 6 pattern. The parameters used in this calculation are the same as in Fig. 6. | ||
 | ||
Fig. 8 Pattern 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26. (A) Neurite lengths. (B) Polarization probabilities. All results after three days of growth. Symbols denote the experimental data and lines denote the result of the model calculation: circles (dashed line, LR) along the right neurite (here the xy branch) and squares (solid line, LL) along the left neurite (here the y branch). The red symbols correspond to the 2 26. (A) Neurite lengths. (B) Polarization probabilities. All results after three days of growth. Symbols denote the experimental data and lines denote the result of the model calculation: circles (dashed line, LR) along the right neurite (here the xy branch) and squares (solid line, LL) along the left neurite (here the y branch). The red symbols correspond to the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 pattern. The parameters used in this calculation are the same as in Fig. 6. 6 pattern. The parameters used in this calculation are the same as in Fig. 6. | ||
 | ||
Fig. 9 Pattern 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62. (A) Neurite lengths. (B) Polarization probabilities. All results after three days of growth. Symbols denote the experimental data and lines denote the result of the model calculation: circles (dashed line, LR) along the right neurite (here the xy branch) and squares (solid line, LL) along the left neurite (here the y branch). The red symbols correspond to the 2 62. (A) Neurite lengths. (B) Polarization probabilities. All results after three days of growth. Symbols denote the experimental data and lines denote the result of the model calculation: circles (dashed line, LR) along the right neurite (here the xy branch) and squares (solid line, LL) along the left neurite (here the y branch). The red symbols correspond to the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 pattern. The parameters used in this calculation are the same as in Fig. 6. 6 pattern. The parameters used in this calculation are the same as in Fig. 6. | ||
For all the cases we used the same set of parameters, given in the caption of Fig. 6.
5 Discussion
We first emphasize that the lengths corresponding to the four categories of patterns, namely 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62, 2
62, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26, 6
26, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 and 2
26 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62, were fitted by the same set of parameters. Among them, only Lpol, σpol, β and γ were free when running our model.
62, were fitted by the same set of parameters. Among them, only Lpol, σpol, β and γ were free when running our model.
The fits shown in Fig. 6–9 give for the two first parameters the values Lpol = 50 μm and σpol = 20 μm. The critical polarization length Lpol is therefore similar to the value of the AIS (i.e. 30–40 μm) found experimentally in ref. 11 and 12, although a little bit higher. Note that the probability to polarize into an axon has a significant spread around this critical length (see Fig. 4), in coherence with the experimental data reported in ref. 15. Interestingly, it has been shown that a differential neurite elongation obtained using adhesive geometries where only one neurite among four is allowed to extend beyond a length of ≥60 μm is highly favorable for the axonal specification of the longest neurite.16 Our findings are in very good agreement with these recent results that also indicate the existence of a critical length for the establishment of the neuronal axo-dendritic polarity.
Then, some specific modalities of hippocampal neuron growth first described by Ruthel and Banker17,18 and more recently by Flynn et al.19 might provide a better understanding of the significance of the parameters β and γ. These studies report that neurite elongation is mediated by periodic growth spurts produced by propagative growth-cone like structures (so-called waves) when reaching the neurite tip. We indeed observed the presence of waves in neurons on micro-patterns (see Fig. S2 and the associated movie in the ESI†). Interestingly, these authors found a difference in the periodicity of waves and in the amplitude of the wave-associated growth spurts between the nascent axon and the other minor processes (see Fig. 2 in ref. 19). From these specificities of waves, we expect a growth ratio between the nascent axon and the other neurites of about ∼2–4, which is in agreement with the value β/γ = 3 that came out of our model. We therefore emphasize that the adjustable parameters used in the model show a biological relevance.
We explored the sensitivity of our model to its adjustable parameters in the particular example of the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 62 patterns (see Fig. S3† and commentaries). One important feature here is that the polarization probability is very sensitive to Lpol. Interestingly, higher lengths (and higher polarization probabilities on the 62 branch) can be obtained for the shortest 6 μm wide stumps when increasing Lpol. This result is a direct consequence of the fact that, for relatively large Lpol values, the polarization decision is taken when the future axon tip has already reached the 2 μm wide portion. This increases the 62 branch probability to experience the fastest possible elongation rate βvtip2 during the period T of growth.
62 patterns (see Fig. S3† and commentaries). One important feature here is that the polarization probability is very sensitive to Lpol. Interestingly, higher lengths (and higher polarization probabilities on the 62 branch) can be obtained for the shortest 6 μm wide stumps when increasing Lpol. This result is a direct consequence of the fact that, for relatively large Lpol values, the polarization decision is taken when the future axon tip has already reached the 2 μm wide portion. This increases the 62 branch probability to experience the fastest possible elongation rate βvtip2 during the period T of growth.
The length data are well fitted by our model. The trend of the polarization rate is also correctly described by the model, although a systematic shift can be observed (see for example results on the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 pattern, Fig. 8B).
26 pattern, Fig. 8B).
To discuss the polarization fits, we first emphasize that the identification of polarized neurons, i.e. of axons, is based on the observation of specific markers, in our case Tau.13,14 This microtubule binding protein is distributed along a gradient revealing the distal part of the axon, about 100 μm away and more from the soma (see Fig. 3). Interestingly, the largest discrepancies between the model and the experimental data are observed when the Tau-staining should appear on a 6 μm wide portion. Under this condition of unusual neurite spreading (the spontaneous neurite diameter is indeed ∼1–2 μm on uniformly adhesive surfaces), the establishment of a Tau gradient might be impaired. To test this hypothesis, we additionally counted as axons the longest neurite in neurons that present a strong length asymmetry (i.e. a ratio greater than 2 between the neurite lengths) without however showing a Tau-staining. With these new sets of data we significantly reduced the shifts (see Fig. S4† and the particular improvement obtained for the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 pattern) without however obtaining a perfect match between the model and the experimental data. This point therefore remains an open issue.
26 pattern) without however obtaining a perfect match between the model and the experimental data. This point therefore remains an open issue.
6 Experimental
6.1 Neuron culture, labelling and imaging
Embryonic day E(18) hippocampi were dissected and then dissociated in MEM medium supplemented with 10% horse serum, 1% L-glutamine, 1% sodium pyruvate and 0.05% peni-streptomycine (Invitrogen). Neurons were plated on poly-L-lysine (Sigma, P2636) coated coverslips and kept first (for 3 hours) in the dissociation medium and then in the maintenance medium of neurobasal supplemented with 2% B27, 1% L-glutamine and 0.05% peni-streptomycine (Invitrogen). Neurons were fixed in 4% paraformaldehyde and immunostained with standard techniques, after a permeabilization step of 30 minutes in PBS supplemented with 2% BSA and 0.25% Triton. The following antibodies and respective secondary antibodies were used in the indicated dilutions: for microtubules, rat anti-tubulin antibody (clone YL1/2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500) and Alexa488 coupled (Invitrogen, 1
500) and Alexa488 coupled (Invitrogen, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250), for axons, Tau (clone Tau-1, Millipore, 1
250), for axons, Tau (clone Tau-1, Millipore, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500) and CY3 coupled (Invitrogen, 1
500) and CY3 coupled (Invitrogen, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250), for DNA, Hoechst (Invitrogen, 1
250), for DNA, Hoechst (Invitrogen, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000).
1000).
Isolated fixed neurons were analyzed with a right Olympus BX51 microscope.
6.2 Patterning
Poly-L-lysine patterns were transferred on silanized substrates (18 × 18 mm2 coverslips from VWR, ref. 631-1331). After an oxygen plasma cleaning step (50 W) of 2 min duration, silanization was performed in a liquid phase using 3-methacryloxypropyltrimethoxysilane (Bind-Silane, Sigma). Then, patterns were defined using UV classical photolithography steps, including Shipley S1805 photoresist spinning (4000 rpm, 0.5 μm thickness, 115 °C annealing step for 1 min), insulation through a mask, development (Microposit concentrate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, Shipley), oxygen plasma activation (50 W, 15 s), poly-L-lysine deposition (1 mg ml−1 overnight), and lift-off using an ultra-sound ethanol bath.
1, Shipley), oxygen plasma activation (50 W, 15 s), poly-L-lysine deposition (1 mg ml−1 overnight), and lift-off using an ultra-sound ethanol bath.
7 Conclusions
By combining experimental and modeling approaches of neuron growth and polarization under constrained geometries, this work provides an original system to explore some fundamental aspects of neuronal biology. In particular, using the proposed model we conclude that the tip elongation rate in neurites is width dependent. This finding should direct future research to reveal the underlying mechanism. One possible direction could be to explore the width-dependence of the propagative growth cone like structures (waves) that are associated with neurite elongation in these neurons.17 Finally, although indications for the existence of a critical length for axonal polarization already exist,16 our work indicates that this length, unlike the tip velocity, does not depend on the neurite width. This gives some new insight into the still mysterious phenomena of the establishment of axo-dendritic polarity. As a whole, by combining a novel experimental set-up and a simple physical model, our work helps to identify several key properties of neurite growth and polarization that a more microscopic model would have to account for. Furthermore, we have shown that by controlling the neurite width we can achieve an unequaled control over the localization of the axonal branch. This finding could have practical implications for the manipulation of in vitro neurons and the design of controlled neuronal micro-circuits.Acknowledgements
This work was funded by ANR-07-PCVI-0007 and the Nanosciences Fundation (Grenoble). We acknowledge support from the NanoFab facility of the Institut Néel and CNRS funding for the sabbatical stay of Prof. Nir S. Gov at the Institut Néel. We also acknowledge support from the Laboratoire d’excellence LANEF in Grenoble. We are indebted to A. Triller and his group, especially S. Colasse, for discussions and support in neuron culture.References
- C. G. Dotti, C. A. Sullivan and G. A. Banker, The establishment of polarity by hippocampal neurons in culture, J. Neurosci., 1988, 8, 1454 CAS.
- H. Troy Ghashghaei, C. Lai and E. S. Anton, Neuronal migration in the adult brain: are we there yet?, Nat. Rev. Neurosci., 2007, 8, 141–151 CrossRef PubMed.
- L. A. Flanagan, Y. E. Ju, B. Marg, M. Osterfield and P. A. Janmey, Neurite branching on deformable substrates, NeuroReport, 2002, 13(18), 2411–2415 CrossRef PubMed.
- L. Micholt, A. Grtner, D. Prodanov, D. Braeken and C. G. Dotti, et al., Substrate Topography Determines Neuronal Polarization and Growth In Vitro, PLoS One, 2013, 8(6), e66170, DOI:10.1371/journal.pone.0066170.
- S. Roth, M. Bisbal, J. Brocard, G. Bugnicourt, A. Andrieux, S. Gory-Fauré and C. Villard, How morphological constraints affect axonal polarity in mouse neurons, PLoS One, 2012, 7, e33623 CAS.
- R. Fricke, P. D. Zentis, L. T. Rajappa, B. Hofmann, M. Banzet, A. Offenhusser and S. H. Meffert, Axon guidance of rat cortical neurons by microcontact printed gradients, Biomaterials, 2011, 32, 2070–2076 CrossRef CAS PubMed.
- U. T. Ruegg and F. Hefti, Growth of dissociated neurons in culture dishes coated with synthetic polymeric amines, Neurosci. Lett., 1984, 49, 319–324 CrossRef CAS.
- T. Esch, V. Lemmon and G. Banker, Local presentation of substrate molecules directs axon specification by cultured hippocampal neurons, J. Neurosci., 1999, 19(15), 6417–6426 CAS.
- C. Leterrier, et al., End-binding proteins EB3 and EB1 link microtubules to ankyrin G in the axon initial segment, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 8826–8831 CrossRef CAS PubMed.
- S. Gomis-Rüth, C. J. Wierenga and F. Bradke, Plasticity of Polarization: Changing Dendrites into Axons in Neurons Integrated in Neuronal Circuits, Curr. Biol., 2008, 18, 992–1000 CrossRef PubMed.
- D. Seetapun and D. J. Odde, Cell-length-dependent microtubule accumulation during polarization, Curr. Biol., 2010, 20, 979–988 CrossRef CAS PubMed.
- H. Yamamoto, T. Demura, M. Morita, G. A. Banker, T. Tanii and S. Nakamura, Differential neurite outgrowth is required for axon specification by cultured hippocampal neurons, J. Neurochem., 2012, 123, 904–910 CrossRef CAS PubMed.
- K. S. Kosik and E. A. Finch, MAP2 and Tau Segregate into Dendritic and Axonal Domains After the Elaboration of Morphologically Distinct Neurites: An Immunocytochemical Study of Cultured Rat Cerebrum, J. Neurobiol., 1987, 7, 3142–3153 CAS.
- M. M. Black, T. Slaughter, S. Moshiach, M. Obrocka and I. Fischer, Tau is enriched on dynamic microtubules in the distal region of growing axons, J. Neurosci., 1996, 16, 3601–3619 CAS.
- G. Wainrib, M. Thieullen and K. Pakdaman, Intrinsic variability of latency to first-spike, Biol. Cybern., 2010, 103, 43–56 CrossRef PubMed.
- H. Yamamoto, et al., Differential neurite outgrowth is required for axon specification by cultured hippocampal neurons, J. Neurochem., 2013, 123(6), 904–910 CrossRef PubMed.
- G. Ruthel and G. Banker, Actin-dependent anterograde movement of growth-cone-like structures along growing hippocampal axons: a novel form of axonal transport?, Cell Motil. Cytoskeleton, 1998, 40, 160–173 CrossRef CAS.
- G. Ruthel and G. Banker, Role of moving growth cone-like “wave” structures in the outgrowth of cultured hippocampal axons and dendrites, J. Neurobiol., 1999, 39, 1–153 CrossRef.
- K. C. Flynn, C. W. Pak, A. E. Shaw, F. Bradke and J. R. Bamburg, Growth cone-like waves transport actin and promote axonogenesis and neurite branching, Dev. Neurobiol., 2009, 69, 761–779 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3sm52342j |
| This journal is © The Royal Society of Chemistry 2014 |