Boron–boron J coupling constants are unique probes of electronic structure: a solid-state NMR and molecular orbital study

Abstract

Diboron compounds are a part of a relatively unexplored, yet immensely useful, class of compounds. Their main use is for β-boration reactions where a boron center is rendered nucleophilic with the use of a metal catalyst or a Lewis base (alkoxide, amine, or NHC) to form a sp²–sp³ diboron compound. The reactivity of these reagents is largely dictated by the nature of the B–B bond (strength and polarity); however, no experimental methods have been used to directly probe both of these quantities. We demonstrate that unprecedented experimental information regarding the B–B bond may be obtained using ¹¹B solid-state NMR spectroscopy. For example, the ¹¹B quadrupolar coupling constants can be understood on the basis of the polarization of the B–B bond. ¹¹B double-quantum-filtered (DQF) J-resolved NMR spectroscopy was applied to easily and accurately measure J(¹¹B,¹¹B) coupling constants with high precision. These are shown to be well correlated with the orbital energy of the B–B σ-bonding natural bond orbital as well as the hybridisation states of the boron atoms in the bond. An increase in the p character of the bond by electron-donating ligands or via the formation of a sp²–sp³ diboron compound weakens the bond, increases the bond length, and decreases the J(¹¹B,¹¹B) coupling constants. These experiments provide a detailed experimental characterization of the B–B bond and may be useful in understanding the reactivity of diboron compounds and in designing new systems. The potential applicability of ¹¹B DQF J-resolved NMR spectroscopy towards analyzing complex mixtures of diboron compounds and towards measuring ¹¹B J coupling across multiple intervening bonds is also investigated and shows much promise.

---

Introduction

Understanding the electronic structure of molecular species is often the key to explaining reactivity and to designing more efficient reagents and catalysts. This is often achieved by performing quantum chemical calculations on model systems since experimental techniques specifically capable of shedding light on the detailed electronic structure of polyatomic compounds are relatively rare.¹ Electronic spectroscopies² are a primary option but, since the resolution is poor³ and the necessary bands may not be identifiable, their use may be limited. High-resolution single-crystal X-ray diffraction experiments can be used, in ideal situations, to image the electron density of a particular state akin to a molecular orbital.⁴ Similar measurements can be done using atomic force microscopy⁵ or laser tomography.⁶

Nuclear magnetic resonance (NMR) spectroscopy offers a different approach to gaining insight into the electronic structure of a molecule. The NMR properties which are measured are largely determined by orbitals localised primarily on the studied atom, and often consideration of only a handful of molecular orbitals may account for the value of a particular NMR parameter. For example, halogen nuclear quadrupolar coupling constants (C_Q) can be used to comment on the hybridisation state of the halogen and the nature of its bonding interactions.⁷ Although the resolution of the electronic states is much lower with NMR than with the aforementioned tomographic methods, NMR experiments are far more generally applicable and are less constrained by the nature of the sample.

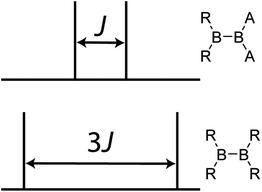
The understanding of bonding interactions is often of particular interest when performing electronic structure studies. Conveniently, these may be studied using the indirect nuclear spin–spin coupling interaction (J coupling) which is well known to depend on the overlap between the atomic orbitals of two nuclei.⁸J coupling has been extensively used in organic chemistry and structural biology to elucidate the backbone structure of a molecule⁹ as well as to determine its conformation.¹⁰ The relationship between J couplings and structure in inorganic systems is somewhat less explored because the vast majority of metals and metalloids possess quadrupolar nuclei for which it is difficult to extract the J coupling information, in part due to spectral broadening and/or relaxation due to the nuclear electric quadrupolar interaction. Recently, however, it has been shown that heteronuclear J coupling between quadrupolar nuclei can be determined using double-rotation (DOR) NMR.¹¹ Homonuclear J coupling information between quadrupolar nuclei can also be extracted using DOR NMR.¹² Robust J-resolved magic-angle spinning (MAS) NMR experiments, which can be applied to extract very precise, and small, J coupling constants for homonuclear quadrupolar spin pairs, have also been recently reported.¹³ This experiment yields a simple doublet for every homonuclear covalent bond. If the two nuclei are related by crystallographic inversion symmetry, the splitting of the doublet is amplified (e.g., 3J for a pair of spin-3/2 nuclei such as ¹¹B). Otherwise, the splitting is simply J (see Fig. 1). Note that it is the crystallographic symmetry which is important, not simply the molecular symmetry. Heteronuclear J coupling involving a quadrupolar nucleus and a spin-1/2 nucleus can be reliably measured using J spectroscopy,¹⁴ and has also been used to obtain 4-bond homonuclear correlation spectra of a quadrupolar nucleus.¹⁵

Fig. 1 A schematic representation of the result of a ¹¹B DQF J-resolved NMR experiment on a molecule wherein the boron atoms are not related by a crystallographic inversion centre (top) and a molecule wherein the boron atoms are related by crystallographic inversion symmetry (bottom). The symmetry in the bottom diboron system leads to an amplification of the J splitting (but not the coupling constant itself) by a factor of 3.

Much work is currently being done on the development of novel diboron reagents for use in β-boration reactions.^16–18 The β-boration reaction involves the attack of a nucleophilic boron site, from a diboron compound, onto an electron deficient alkene to form a C–B bond. The organoboron compounds that can then be formed are of tremendous synthetic use since the C–B bond can be easily converted to C–X, C–O, C–N, and even C–C bonds (using Suzuki-type cross-coupling reactions).¹⁹ Several groups have shown that the formation of a mixed sp²–sp³ diboron species substantially increases the reactivity.¹⁷ This is attributed to the electron donation of the additional group on the sp³-hybridised boron site which weakens the B–B bond and also induces a polarization of the bond that increases the nucleophilicity of the reactive sp²-hybridised boron site.^17,18 Recent studies also show that there is also much to learn concerning the reactivity of diboron systems whose chemistry is fairly unexplored.²⁰

In this Edge Article, we report on DQF J-resolved solid-state NMR measurements of the J(¹¹B,¹¹B) coupling constants in a series of diboron compounds in order to provide direct information on the B–B bond. Via density functional theory (DFT) calculations we decompose the J coupling into various natural bond orbital (NBO) and natural localised molecular orbital (NLMO) contributions²¹ and determine which structural and electronic factors contribute to the J(¹¹B,¹¹B) values. The sensitivity of J(¹¹B,¹¹B) to structure and symmetry is then leveraged as a screening technique to probe the nature of the B–B bond in a mixture of diboron reagents. Several ¹¹B–¹¹B J coupling constants ranging from 9 to 151 Hz have been measured either directly, or indirectly through ¹H NMR spectra, for various boranes in solution. These splittings are, however, rarely resolved for diboron compounds due to rapid quadrupolar relaxation.²²

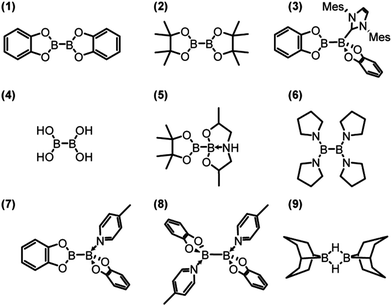
The compounds investigated in this paper, bis(catecholato) diboron (1), bis(pinacolato) diboron (2), [bis(catecholato) diboron]·IMes (3), tetrahydroxy diboron (4), pinacolato bis(2-hydroxypropyl)amino diboron (5), tetrakis(pyrrolidino) diborane (6), [bis(catecholato) diboron]·picoline (7), and [bis(catecholato) diboron]·dipicoline (8), are shown in Scheme 1. Some proof-of-principle experiments on samples 1 to 3 have been reported in a previous short communication.¹³ Compounds 1,²³2,^17d and 4 (ref. 24) are sp²–sp² diboron compounds with oxygen ligands. Compound 3 represents an intermediate in an NHC-catalysed β-boration reaction.^17a Compound 5 is a mixed sp²–sp³ diboron reagent designed for copper-catalysed β-boration reactions.^17b,e Compound 6 features nitrogen ligands²⁵ as opposed to oxygen ligands, and compounds 7 and 8, along with 1, form a series of compounds produced by a sequential addition of 4-picoline ligands.²⁶ Finally, 9-BBN (9), a popular hydroboration reagent, was also investigated due to its dimer structure²⁷ in order to determine whether it is possible to measure J(¹¹B,¹¹B) across multiple intervening bonds.

Scheme 1 Structures of the boron compounds discussed in the text.

Results and discussion

Boron-11 quadrupolar interactions and chemical shifts

The ¹¹B MAS NMR spectra for compounds 4, 5, 6, 8, and 9 are shown in Fig. 2. A ¹¹B multiple-quantum magic-angle spinning (MQMAS) NMR spectrum²⁸ of compound 6 is also shown, in which the two distinct boron sites are spectrally resolved. This is in agreement with the single-crystal X-ray structure that features two crystallographically distinct boron sites.²⁵ The parameters used for the simulations are given in Table 1. Generally, as can be expected, the three- and four-coordinate boron sites can be easily distinguished on the basis of their NMR parameters.²⁹ The spectra are affected by the electric quadrupolar interaction between the electric field gradient (EFG) tensor at the nucleus and the electric quadrupole moment of the nucleus (Q) as well as the isotropic chemical shift (δ_iso). The quadrupolar interaction is typically parameterised using the quadrupolar coupling constant (C_Q) and the asymmetry parameter (η) which describe the magnitude and axial asymmetry of the EFG tensor, respectively. The four-coordinate boron sites are more shielded, having isotropic chemical shifts ranging from 1 to 11.0 ppm whereas the three-coordinate boron sites have chemical shifts of 29.5 to 35.2 ppm. As can be also expected, the C_Q values are much smaller for the four-coordinate boron sites (<2.2 MHz) than for the three-coordinate boron sites (2.7 to 3.2 MHz) due to the higher tetrahedral symmetry of the former.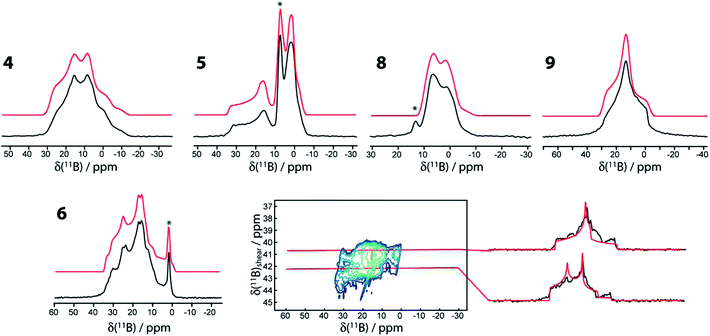

Fig. 2 ¹¹B MAS NMR spectra of compounds 4, 5, 6, 8, and 9 acquired at 9.4 T using a Hahn echo sequence. The MQMAS NMR spectrum of 6, including slices along the isotropic dimension, is also shown. In all cases the experimental spectra are in black and the simulations are in red. An asterisk denotes an impurity. A slight upwards tilt in the MQMAS spectrum of 6 is observed which is caused by the second-order quadrupolar-dipolar cross term interaction between ¹¹B nuclei and the ¹⁴N and ¹¹B nuclei.³⁶

Table 1 ¹¹B NMR parameters for the diboron compounds studied in this work

Compound	δ iso/ppm	C Q /MHz	η
a C Q = eV33Q/h and η = (V11 − V22)/V33 where Vii are the principal EFG tensor components ordered as |V33| ≥ |V22| ≥ |V11|, Q is the nuclear electric quadrupole moment, e is the fundamental charge and h is Planck's constant. Although only |CQ| can be measured using conventional means, the sign of CQ is obtained from DFT calculations. b No anisotropic lineshape was observed. c From ref. 13.
1	30.5 ± 0.5	2.85 ± 0.05	0.85 ± 0.05
2	31.5 ± 0.5	2.70 ± 0.05	0.85 ± 0.1
3 4-coordinate^c	1 ± 1^b	N/A^b	N/A^b
3 3-coordinate^c	34 ± 1	3.0 ± 0.1	0.90 ± 0.05
4	29.5 ± 1.0	3.2 ± 0.1	0.58 ± 0.05
5 4-coordinate	7.0 ± 0.5	(−)1.7 ± 0.1	0.7 ± 0.1
5 3-coordinate	34 ± 1	2.9 ± 0.1	0.90 ± 0.05
6 site A	31.2 ± 0.5	2.7 ± 0.1	1.00 ± 0.05
6 site B	35.2 ± 0.5	2.9 ± 0.1	0.50 ± 0.08
8	11.0 ± 0.5	(−)2.2 ± 0.05	0.15 ± 0.10
9	29 ± 1	(−)2.7 ± 0.1	1.00 ± 0.15

---

It can also be observed that upon the formation of a sp³-boron site by the coordination of a ligand to compounds 1 and 2 (i.e., giving compounds 3 and 5) there is a noticeable increase in the quadrupolar coupling constant and asymmetry parameter of the remaining three-coordinate boron site (i.e., the chemically active site in β-boration reactions). This site has maintained all of the same direct bonding interactions with its neighbouring atoms; however, a non-negligible change in C_Q of 200 kHz is observed. This change is in agreement with the model of Hoveyda whereby the binding of an additional ligand on one of the boron atoms polarises the B–B bond and induces a larger positive charge on the resulting four-coordinate boron center.^17a The increase in the asymmetry parameter originates from the increase in the intermediate V₂₂ EFG tensor component (see footnote to Table 1) which is calculated to be aligned along the B–B bond vector (vide infra). Since the sum of the EFG tensor components is always zero, the increase in |V₂₂| is seen here to also increase |V₃₃|, which is manifested in an increase in the magnitude of the quadrupolar coupling constant (C_Q = eV₃₃Q/h).

The impact of an additional ligand (see the structures of 3 and 5 in Scheme 1) is also evident from the deshielding of the three-coordinate ¹¹B resonances (by 3 to 4 ppm). The mechanism explaining this deshielding of the three-coordinate boron site has been well described for boronic acids and originates from a decrease of the smallest magnetic shielding tensor component caused by the interaction of ligand MOs with the unoccupied boron p orbital.³⁰

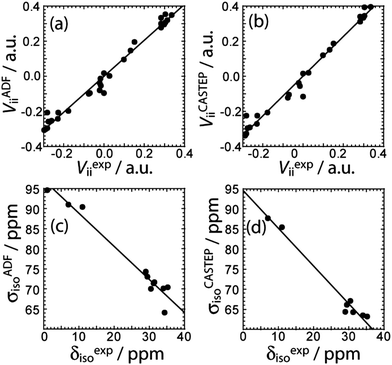
DFT calculations of the magnetic shielding and EFG tensors have been performed for these samples. Both cluster-based calculations, using a single molecule of the substance as input, and gauge-including projector-augmented wave (GIPAW) calculations,³¹ using the published crystal structures as input,^{17d,e,23–27} have been performed (see Experimental for further details). The chemical shifts and the EFG tensor components are both well-reproduced using both methods (see Fig. 3). The cluster-based calculations reproduce the experimental EFG tensor components better (slope of 1.02) than the PAW calculations, which systematically overestimate the EFG tensor components, as was previously mentioned³² (slope of 1.13). This overestimation has been attributed to molecular motions;³³ however, since the cluster-based calculations reproduce the EFG tensor components quantitatively, the overestimation likely originates from deficiencies of the pseudopotential used or the method itself. Conversely, the chemical shifts seem to be better reproduced by the GIPAW DFT calculations than by the cluster-based calculations (see Fig. 3). The plot correlating the calculated magnetic shielding with the experimental chemical shifts has a slope of −0.94 with GIPAW and −0.82 with cluster-based calculations; perfect agreement would give a slope of −1. Since not all compounds could be included in the GIPAW DFT calculations, due to the lack of a known crystal structure, it may be premature to conclusively state that GIPAW DFT calculations better reproduce the ¹¹B chemical shifts.

Fig. 3 Correlations between the experimental EFG tensor components and the calculated ones using (a) cluster model DFT (V^ADF_ii = 1.02V^exp_ii, R = 0.990) and (b) PAW DFT (V^CASTEP_ii = 1.13V^exp_ii, R = 0.989) are shown. The correlations between the experimental chemical shifts and the calculated magnetic shielding constants using (c) cluster model DFT (σ^ADF_iso = −0.825δ^exp_iso + 97.0 ppm, R = 0.980) or (d) GIPAW DFT (σ^CASTEP_iso = −0.941δ^exp_iso + 94.6 ppm, R = 0.988) are shown.

Boron–boron J coupling constants

¹¹B J-resolved NMR experiments using a J-based double-quantum filter¹³ have been performed on all of the samples in Scheme 1. The J-resolved spectra are shown in Fig. 4 and the J(¹¹B,¹¹B) values are listed in Table 2. The J-resolved spectra for compounds 1, 2, 4, and 8 have noticeably larger splittings than the other compounds (see Fig. 4). This originates from a symmetry-amplified J splitting effect which is present when the two nuclei are magnetically equivalent; for spin-3/2 nuclei such as ¹¹B, the amplification factor is 3 (see Fig. 1).¹³ The spin states associated with the quadrupolar central transition in these compounds are mixed which leads to a larger splitting in a J-resolved experiment.³⁴ This splitting is amplified whereas the actual J coupling constant is not. Once this effect is taken into consideration, it can be seen that all diboron systems have similar J coupling constants ranging from 136 to 98 Hz. Knowledge about either the molecular structure or the approximate magnitude of the coupling constant is, however, necessary in order to determine whether or not the J splitting is amplified; this is not a problem when comparing a series of analogous compounds as in the present case. We note that amplifications of the J splittings are also observed in MQMAS NMR spectra, however; this is due to the detection of mixed single and triple quantum coherences.³⁵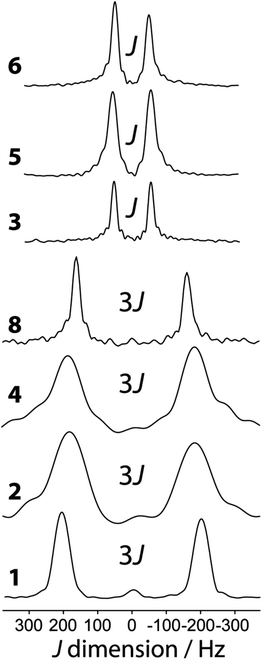

Fig. 4 Indirect dimension of the ¹¹B DQF J-resolved NMR experiments carried out on the diboron compounds shown in Scheme 1.

Table 2 J(¹¹B,¹¹B) coupling constants for the compounds in Scheme 1 extracted using ¹¹B DQF J-resolved NMR

Compound	J(^11B,^11B)/Hz
1	136 ± 1
2	120 ± 2
3	106.8 ± 0.6
4	121 ± 3
5	111 ± 3
6	98 ± 2
7	115 ± 4
8	108 ± 1
9	(−)10 ± 7

---

When the reaction of 1 with 4-picoline, intended to form compound 8, is halted prematurely,²⁶ some of the bis(catecholato) diboron will not have reacted and some will have ligated to one 4-picoline molecule as opposed to two, giving compound 7. Spectra of the resulting mixture provides a striking example of the excellent resolution which can be obtained in J-resolved experiments since the linewidth is governed by the spin–spin relaxation time constant.³⁴ A J-resolved spectrum of the reaction mixture extracted before the reaction was completed is shown in Fig. 5. It can be clearly seen that the symmetry-amplified doublet signals from 1 and 8 are present along with a smaller, unamplified doublet. The latter doublet can be attributed to compound 7 where only a single 4-picoline molecule has complexed to 1. The doublet splitting is smaller due to the absence of an inversion center relating the two boron sites in the crystal structure.

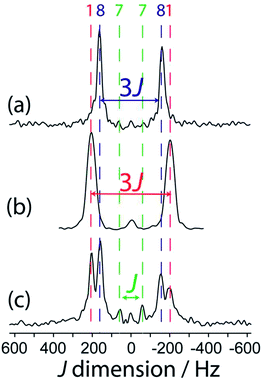Fig. 5 Indirect dimension of ¹¹B DQF J-resolved NMR spectra for (a) 8, (b) 1, and (c) a reaction mixture containing 1, 7, and 8, as marked by the colour-coded dashed lines.

It is interesting to comment on the tremendous spectral resolution which can be obtained for quadrupolar nuclei in powders using DQF J-resolved spectroscopy. In some cases, the resolution that can be achieved surpasses that which could be obtained using DOR NMR¹² or MQMAS NMR, for which the line widths are about an order of magnitude larger for these compounds.³⁶ This is in part due to the fact that the DQF J-resolved NMR experiment is insensitive to residual dipolar interactions (to ¹¹B and ¹⁴N, for example),³⁴ unlike DOR^11,12 and MQMAS,^36,37 and thus leads to narrower resonances. It is also interesting to notice that the J coupling constant steadily decreases from compound 1 to 7 and 8 with the addition of each 4-picoline ligand, which correlates with a lengthening of the B–B bond.²⁶ However, the spectral splitting greatly decreases when a single 4-picoline molecule is added, and then greatly increases when the second is added, since the inversion symmetry of the crystal is reinstated (see Fig. 1).²⁶ Thus, the NMR method not only provides excellent resolution of the mixture of compounds, but also gives direct evidence for the presence or absence of crystallographic inversion symmetry. Since the optimal double-quantum filter time depends on the J splitting and the samples have differing spin–spin relaxation times, this experiment is not quantitative. If the DQF efficiency was modeled numerically, or determined using pure forms of the various components, their proportions in the mixture could be quantified.

The J-resolved spectrum for symmetric compound 6 may be puzzling at first since the J splitting is not amplified (splitting of J = 98 ± 2 Hz). Diboron compounds with oxygen ligands prefer planar structures due to the stabilising effect of π delocalisation.³⁸ Diboron compounds with nitrogen ligands, however, have much weaker π delocalisation stabilisation energies and stronger hyperconjugation interactions.³⁸ That, combined with steric repulsion, means a staggered structure is often preferred in these systems.³⁹ The crystalline structure of 6 shows that it has a N–B–B–N dihedral angle of 76.4°. The two boron nuclei are not related by an inversion center and the splitting in the DQF J-resolved spectrum therefore is given by J rather than 3J.³⁴

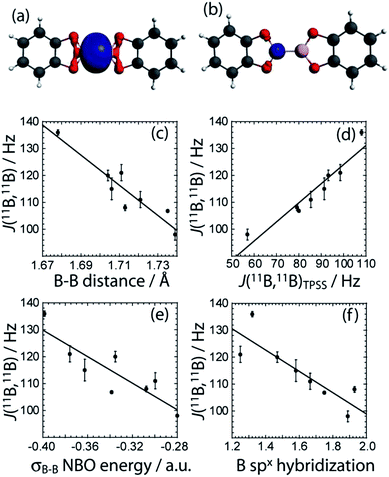
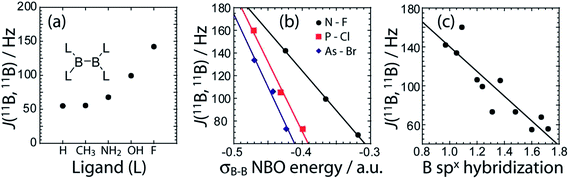
To gain a greater understanding of the factors that contribute to the J(¹¹B,¹¹B) values, we have analysed the J coupling in terms of natural bond orbitals (NBO)⁴⁰ and natural localised molecular orbitals (NLMO)^41,21 using the NBO 5.0 code⁴² implemented in the Amsterdam Density Functional (ADF) software.⁴³ NBOs are a set of very localized (strictly 1- to 3-centered) orbitals which best reproduce the Kohn-Sham orbitals whereas the NLMOs are expansions of the NBOs that include the longer range effects. As can be seen in Fig. 6, the experimental J(¹¹B,¹¹B) values are very well reproduced with DFT which serves to validate our theoretical approach.

Fig. 6 The σ_B–B NLMO and the boron core NLMO are depicted in (a) and (b), respectively (blue). The boron atoms are coloured pink, the carbon atoms are grey, the oxygen atoms are red, and the hydrogen atoms are white. The correlations between the experimental J(¹¹B,¹¹B) coupling constants and the (c) B–B bond length (J = 1072.2 Hz − d_B–B × 559.0 Hz Å⁻¹, R = 0.94), (d) TPSS/QZ4P computed J(¹¹B,¹¹B) values (J = 52.8 Hz − J^TPSS × 0.713, R = 0.95), (e) σ_B–B NBO energy (J = 31.38 Hz − E_NBO × 246.3 Hz a.u.⁻¹, R = 0.87), and (f) the hybridisation state of the boron orbitals in the σ_B–B NLMO (J = 178.12 Hz − x × 39.6 Hz, R = 0.86) are also shown.

For all the diboron compounds, nearly 100% of the J coupling originates from the Fermi contact (FC) mechanism. This mechanism involves the interaction of a nucleus with an electron situated at the nucleus. Since only s orbitals have a non-zero electron density at the nucleus, only orbitals with significant s character can contribute to J via the FC mechanism. This is clear when one examines the main NLMOs which contribute to the J coupling. For all diboron compounds, approximately 50% of the J coupling originates from the boron core orbitals and another 50% originates from the B–B σ-bonding orbital (see Table 3). Example NLMOs are depicted in Fig. 6. Perhaps surprisingly, the percentage contribution from the B–B σ-bonding orbital alone does not correlate with the J coupling or the bond length. Interestingly, the B–B σ-bonding orbital is polarised towards the empty boron p orbital in compounds 3, 5, 6, and 7, in agreement with the presence of σ_C–X (X = N or O) to p_B hyperconjugation.³⁸ This does not, however, seem to have an effect on the J coupling constant. This is perhaps expected since a pure boron p orbital cannot contribute to the J(¹¹B,¹¹B) coupling via the FC mechanism. Similarly, the π-delocalisation which is present in the planar diboron compounds (compounds 1, 2, and 4) does not affect the J(¹¹B,¹¹B) coupling. However, the J(¹¹B,¹¹B) values are well correlated to the B–B σ-bonding NBO energy (see Table 3 and Fig. 6). The J(¹¹B,¹¹B) values can then be used to directly report on the strength of the B–B σ bond, as the δ_iso and C_Q values can be used to report on the polarization of the bond, as described earlier.^17a

Table 3 Results from an NBO/NLMO analysis of the boron–boron bonds in compounds 1 to 8

Compound	B–B bond NLMO^a/%	B core NLMO^a/%	B–B bonding NBO energy/a.u.	B–B bond sp^x hybridisation^b
a These numbers correspond to the percentage of the J coupling which originates from those particular NLMOs. b The number indicated corresponds to the p character of the bond (x).
1	51.8	58.0	−0.399	1.32
2	50.5	62.0	−0.335	1.47
3	54.9	56.2	−0.339	1.17 and 2.33
4	59.0	56.0	−0.376	1.25
5	53.8	58.8	−0.300	1.38 and 1.67
6	47.0	65.1	−0.280	1.89
7	51.4	58.2	−0.363	1.21 and 1.95
8	46.0	52.4	−0.308	1.93

---

We can also analyze the hybridisation of the NLMOs and how they relate to the value of J. As can be seen in Table 3 and Fig. 6, the degree of hybridisation of the boron orbitals participating in the B–B bond also correlates strongly with the value of J(¹¹B,¹¹B). Compounds in which the boron s orbitals contribute more strongly to the B–B bond have a larger J coupling constant since the FC mechanism dominates the J coupling in this case. This larger s character is also consistent with a shorter B–B bond. This is fully consistent with the observed inverse correlation of the bond length with the value of J (see Fig. 6).

DFT calculations of the J coupling constants in a series of model, planar, diboron systems with various ligands were also performed and analysed within the NBO/NLMO framework. For these calculations, the B–B bond length was purposely fixed at 1.74 Å to eliminate the effects of bond length variations. This bond length was chosen as it is representative for these systems whose MP2 optimised bond lengths range from 1.758 Å to 1.714 Å.³⁸ As can be seen in Fig. 7(a), there is a dramatic increase in the calculated J(¹¹B,¹¹B) value as the ligand atom is changed from H to C, N, O, and finally F. This is consistent with our experimental observation that a diboron system with nitrogen ligands has a smaller J coupling constant than one with oxygen ligands. This increase in J coupling constant is also consistent with the increase in the strength of the B–B bond as the electronegativity of the ligands increases (Fig. 7(b)), and the increase in the boron s character of the bonding NLMO (Fig. 7(c)). These calculations then show that the differences in J coupling constants which are observed are caused by the differences in the s character of the bond and not directly by differences in bond length. The correlation between the J(¹¹B,¹¹B) values and the s character of the bond had been hypothesised nearly 40 years ago.⁴⁴

Fig. 7 In (a) the DFT calculated J(¹¹B,¹¹B) values are plotted as a function of the ligand (L). In (b), the DFT calculated J(¹¹B,¹¹B) values are plotted as a function of the NBO energy when various heavier ligands are used. In (c), the DFT calculated J(¹¹B,¹¹B) values are plotted versus the hybridisation state of the boron orbitals comprised in the σ_B–B NLMO.

Within the framework of the hybridisation concept, according to Bent's rule,⁴⁵ electron withdrawing groups will reduce the p character of the boron atomic orbitals and thus increase the relative s character of the boron orbitals participating in the boron–boron bond. This increase in s character decreases the orbital bond energy and shortens the boron–boron bond. Increased s character enables an increased contribution to J(¹¹B,¹¹B) via the FC mechanism. This is consistent with the smaller ¹¹B–¹¹B J coupling constant measured in tertrakis(dimethylamino)diborane⁴⁶ and the calculated ¹¹B–¹¹B J coupling constant in B₂H₄.⁴⁷ A similar effect dominates the J(¹³C,¹H) values of organic molecules.^8,48

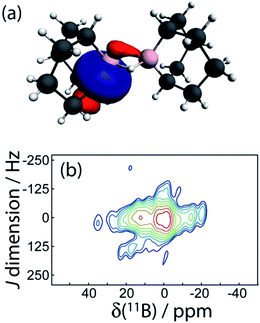
A potentially exciting application of ¹¹B DQF J-resolved spectroscopy is the structural study of borate glasses.⁴⁹ For example, ²⁹Si J-resolved spectroscopy is similarly used to probe the connectivities in silicate glasses where the number of nearest neighbours can unambiguously be determined even in a disordered structure.⁵⁰ We have then explored the possibility of measuring ¹¹B–¹¹B J coupling across multiple intervening bonds in 9. 9 is a common organic reagent used in hydroboration reactions but it exists as a dimer connected by two 3-centered B–H–B bonds in the liquid and solid states.²⁷ The boron nuclei are also related by an inversion center and thus the J splitting will be amplified by a factor of 3, aiding in the detection of a small J coupling constant. The ¹¹B J-resolved spectrum is shown in Fig. 8. Due to the small magnitude of the coupling and the short relaxation times of this sample, it was not possible to resolve a doublet; however, the mere presence of a J-DQF signal shows that there is a J coupling interaction between the two nuclei. From the spectrum it is possible to estimate the J coupling as 10 ± 7 Hz. This is consistent with the magnitude of the ¹¹B–¹⁰B J coupling measured in diborane (|J(¹¹B,¹⁰B)| = 1.3 Hz; |J(¹¹B,¹¹B)| = 3.8 ± 0.5 Hz).⁵¹ A two-bond J coupling constant would likely be even smaller than a J coupling across a 3-centered 2-electron bond. Therefore, in order to measure J(¹¹B,¹¹B) in borate glasses it may be advantageous to perform MAS NMR experiments at cryogenic temperatures to increase the spin–spin relaxation time constants.⁵²

Fig. 8 In (a), one of the four σ_C–B NLMOs is shown which is responsible for the J(¹¹B,¹¹B) coupling in 9. In (b), the ¹¹B DQF J-resolved NMR spectrum of 9 is shown; the presence of a signal is indicative of a non-negligible J coupling.

Interestingly, DFT calculations indicate that the two-bond J coupling constant is negative in 9 (J(¹¹B,¹¹B)_TPSS = −10.0 Hz), in contrast to the positive one-bond values for the diboron compounds. An NLMO analysis shows that this is because the two 3-centered bonds contribute negligible amounts to the J coupling whereas the B–C σ-bonding orbitals instead contribute most of the J coupling. These have a tail which connects to the other boron site (see Fig. 8). Since these orbitals have a node in between the two boron nuclei, the sign of the FC contribution to J coupling is inverted and the J coupling is negative.⁸

Conclusions

It has been demonstrated that ¹¹B DQF J-resolved spectroscopy is a robust tool for studying a variety of diboron compounds. The J(¹¹B,¹¹B) values which are measured with this method were demonstrated to be rich in useful electronic information. The J(¹¹B,¹¹B) values are shown to be correlated with the energy of the B–B σ-bonding NBO. Within a related series of compounds, a larger J coupling constant then directly correlates with a stronger B–B bond. The J coupling constants also directly report on the hybridisation of the boron orbitals which contribute to the B–B bond. Along with the EFG tensor data and ¹¹B chemical shifts it is then possible to gain experimental insight into the B–B bonding orbital as well as the polarization of the bond. This makes ¹¹B NMR a very powerful technique for screening potentially useful β-boration reagents. For example, diboron compounds with nitrogen ligands have noticeably weaker B–B bonds and may then have a higher reactivity towards electron deficient alkenes than diboron compounds with oxygen ligands.⁵³

It was also demonstrated that ¹¹B DQF J-resolved spectroscopy can be used as a high-resolution analysis technique for separating the signals from a mixture of diboron systems and identifying stable reaction intermediates. For the systems studied here, the resolution of this technique surpasses that of MQMAS and DOR NMR, which are some of the leading techniques used to obtain high-resolution NMR spectra of quadrupolar nuclei in solids. Additionally, the splittings observed in the J-resolved spectra indicate the presence or absence of crystallographic inversion symmetry.

Using the symmetry amplification of the J splitting in 9-BBN (9) it was possible to measure a rare example of a J coupling between two quadrupolar nuclei across multiple intervening bonds. This is an exciting advance towards studying amorphous systems such as borate glasses where measuring J coupling could yield unprecedented structural information.

Experimental

Compounds 1, 2, 4, 6, 9, 4-picoline, and bis(2-hydroxypropyl)amine were obtained from Aldrich and used without further purification. All reactions were performed using standard Schlenk and glove box techniques using anhydrous solvents. Samples 3,¹³5,^17b7, and 8 (ref. 26) were prepared using published literature procedures.

NMR experiments

All ¹¹B NMR experiments were performed at an applied external magnetic field of 9.4 T using a Bruker Avance III NMR spectrometer equipped with a Bruker 4 mm triple resonance MAS probe. The ¹¹B MAS NMR spectra were acquired using a spin-echo sequence to remove the probe background signal. The ¹¹B central-transition selective 90° pulse length was 20 μs and the echo delay was 80 μs for rotor synchronisation (ν_rot = 12.5 kHz). Between 8 and 192 transients were acquired for each sample using a relaxation delay of 4 s. The chemical shifts were referenced to F₃B·O(C₂H₅)₂ using NaBH₄ as a secondary reference (−42.06 ppm).⁵⁴ Spectral line shapes were simulated using WSolids1.⁵⁵

The ¹¹B DQF J-resolved MAS NMR experiments were performed using the published pulse sequence,¹³ 25 μs central-transition selective 90° pulses, and high-power ¹H decoupling. The MAS frequency was typically 12.5 kHz and the t₁ increments were set to either 40 μs or 80 μs for rotor synchronization. 36 t₁ slices of 64 to 540 transients were acquired and the spectra were processed in magnitude mode. Sample 9 was cooled to 0 °C in order to increase its spin–spin relaxation time constant and obtain sharper J-resolved signals. The DQF J-resolved MAS NMR experiments are straightforward to run, since only the double-quantum filter delay needs to be optimised, and are quite sensitive; a high quality J-resolved spectrum can be obtained in 2 h in a moderate applied magnetic field.

The ¹¹B MQMAS NMR spectrum of 6 was acquired using the 3-pulse z-filtered sequence with proton decoupling.⁵⁶ The excitation, conversion, and detection pulses lasted 4.5, 2.0, and 20 μs, respectively. 80 t₁ slices of 1560 scans were acquired with a t₁ increment of 80 μs and the spectrum was processed using the States method.⁵⁷

DFT calculations

GIPAW DFT calculations of the ¹¹B magnetic shielding and EFG tensors were performed using the CASTEP-NMR program (version 4.4).³¹ The published crystal structures were used as input.^{17d,e,23–27} The data were analysed using the EFGShield program (version 4.1).⁵⁸ Standard, on-the-fly generated ultrasoft pseudopotentials available within CASTEP were used for all atoms. A 610 eV kinetic energy cutoff and “fine” quality k-point grids were used in all cases. The generalised gradient approximation (GGA) DFT functional of Perdew, Burke, and Ernzerhof (PBE)⁵⁹ was used for all the calculations.

Cluster-model DFT calculations were performed using the ADF program (ver. 2009)⁴³ and the data were analysed using EFGShield.⁵⁸ The models consisted of a single molecular unit, with the exception of 4 for which the four neighbouring molecules, which form hydrogen bonds, were also included. The shielding and EFG tensor calculations used the revised PBE GGA functional of Zhang and Yang⁶⁰ whereas the J coupling calculations used the meta-GGA functional of Tao, Perdew, Staroverov, and Scuseria (TPSS).⁶¹ All calculations used the quadruple-zeta quadruple-polarised (QZ4P) basis set.⁶² The NBO/NLMO analysis of the J coupling constants was performed using the NBO program (version 5.0)⁴² which is incorporated into ADF.

Acknowledgements

F. A. Perras thanks NSERC for a graduate scholarship. D. L. Bryce thanks NSERC, the Canada Foundation for Innovation, and the Ontario Ministry of Research and Innovation for funding. Acknowledgment is made to the donors of The American Chemical Society Petroleum Research Fund for partial support of this research.

References

1. (a) R. G. Parr and W. Yang, Annu. Rev. Phys. Chem., 1995, 46, 701–728; (b) W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974–12980; (c) H. Chermette, J. Comput. Chem., 1999, 20, 129–154; (d) R. J. Bartlett and M. Musial, Rev. Mod. Phys., 2007, 79, 291–352.
2. (a) M. Kasha and S. P. McGlynn, Annu. Rev. Phys. Chem., 1956, 7, 403–424; (b) L. G. Parratt, Rev. Mod. Phys., 1959, 31, 616–645; (c) M. I. Al-Joboury and D. W. Turner, J. Chem. Soc., 1964, 4434–4441; (d) M. F. Chung and L. H. Jenkins, Surf. Sci., 1970, 22, 479–485.
3. L. Antonov and D. Nedeltcheva, Chem. Soc. Rev., 2000, 29, 217–227.
4. J. M. Zuo, M. Kim, M. O'Keeffe and J. C. H. Spence, Nature, 1999, 401, 49–52.
5. L. Gross, Nat. Chem., 2011, 3, 273–278.
6. J. Itatani, J. Levesque, D. Zeidler, H. Niikura, H. Pépin, J. C. Kieffer, P. B. Corkum and D. M. Villeneuve, Nature, 2004, 432, 867–871.
7. (a) C. H. Townes and B. P. Dailey, J. Chem. Phys., 1949, 17, 782–796; (b) F. A. Perras and D. L. Bryce, Angew. Chem., Int. Ed., 2012, 51, 4227–4230.
8. J. Autschbach and B. Le Guennic, J. Chem. Educ., 2007, 84, 156–171.
9. (a) A. Bax, R. Freeman and T. A. Frenkiel, J. Am. Chem. Soc., 1981, 103, 2102–2104; (b) D. Marion, L. E. Kay, S. W. Sparks, D. A. Torchia and A. Bax, J. Am. Chem. Soc., 1989, 111, 1515–1517.
10. (a) M. Karplus, J. Am. Chem. Soc., 1963, 85, 2870–2871; (b) F. R. Jensen and C. H. Bushweller, J. Am. Chem. Soc., 1969, 91, 3223–3225; (c) H. Kessler, C. Griesinger, J. Lautz, A. Müller, W. F. van Gunsteren and H. J. C. Berendsen, J. Am. Chem. Soc., 1988, 110, 3393–3396.
11. F. A. Perras and D. L. Bryce, J. Magn. Reson., 2011, 213, 82–89.
12. F. A. Perras and D. L. Bryce, J. Chem. Phys., 2013, 138, 174202.
13. F. A. Perras and D. L. Bryce, J. Am. Chem. Soc., 2013, 135, 12596–12599.
14. C. Fernandez and M. Pruski, Top. Curr. Chem., 2012, 306, 119–188.
15. M. Deschamps, F. Fayon, V. Montouillout and D. Massiot, Chem. Commun., 2006, 1924–1925.
16. S. Mun, J.-E. Lee and J. Yun, Org. Lett., 2006, 8, 4887–4889.
17. (a) K.-s. Lee, A. R. Zhugralin and A. H. Hoveyda, J. Am. Chem. Soc., 2009, 131, 7253–7255; (b) M. Gao, S. B. Thorpe and W. L. Santos, Org. Lett., 2009, 11, 3478–3481; (c) A. Bonet, C. Pubill-Ulldemolins, C. Bo, H. Gulyás and E. Fernández, Angew. Chem., Int. Ed., 2011, 50, 7158–7161; (d) C. Kleeberg, A. G. Crawford, A. S. Batsanov, P. Hodgkinson, D. C. Apperley, M. S. Cheung, Z. Lin and T. B. Marder, J. Org. Chem., 2012, 77, 785–789; (e) M. Gao, S. B. Thorpe, C. Kleeberg, C. Slebodnick, T. B. Marder and W. L. Santos, J. Org. Chem., 2011, 76, 3997–4007; (f) C. Pubill-Ulldemolins, A. Bonet, C. Bo, H. Gulyás and E. Fernández, Chem.–Eur. J., 2012, 18, 1121–1126; (g) J. Cid, H. Gulyás, J. J. Carbó and E. Fernández, Chem. Soc. Rev., 2012, 41, 3558–3570; (h) H. Gulyás, A. Bonet, C. Pubill-Ulldemolins, C. Solé, J. Cid and E. Fernández, Pure Appl. Chem., 2012, 84, 2219–2231; (i) C. Pubill-Ulldemolins, A. Bonet, H. Gulyás, C. Bo and E. Fernández, Org. Biomol. Chem., 2012, 10, 9677–9682; (j) A. Bonet, C. Sole, H. Gulyás and E. Fernández, Org. Biomol. Chem., 2012, 10, 6621–6623; (k) Y. Yamamoto, JP. Pat., WO 2013133203 A1, 2013.
18. J. Cid, J. J. Carbó and E. Fernández, Chem.–Eur. J., 2012, 18, 12794–12802.
19. K. Smith, in Organometallics in Synthesis: A Manual, ed. M. Schlosser, John Wiley & Sons, Ltd, Chichester, 2002, vol. 1, pp. 465–533.
20. (a) H. Braunschweig, A. Damme, R. D. Dewhurst, T. Kramer, T. Kupfer, K. Radacki, E. Siedler, A. Trumpp, K. Wagner and C. Werner, J. Am. Chem. Soc., 2013, 135, 8702–8707; (b) S. Litters, E. Kaifer, M. Enders and H.-J. Himmel, Nat. Chem., 2013, 5, 1029–1034; (c) H. Braunschweig, R. D. Dewhurst, C. Hörl, A. K. Phukan, F. Pinzner and S. Ullrich, Angew. Chem., Int. Ed., 2014, 53, 3241–3244.
21. J. Autschbach, J. Chem. Phys., 2007, 127, 124106.
22. (a) A. R. Siedle, Annu. Rep. NMR Spectrosc., 1988, 20, 205–314; (b) P. Greiwe, A. Bethäuser, H. Pritzkow, T. Kühler, P. Jutzi and W. Siebert, Eur. J. Inorg. Chem., 2000, 1927–1929.
23. W. Clegg, M. R. J. Elsegood, F. J. Lawlor, N. C. Norman, N. L. Pickett, E. G. Robins, A. J. Scott, P. Nguyen, N. J. Taylor and T. B. Marder, Inorg. Chem., 1998, 37, 5289–5293.
24. R. A. Baber, N. C. Norman, A. G. Orpen and J. Rossi, New J. Chem., 2003, 27, 773–775.
25. H. A. Ali, I. Goldberg and M. Srebnik, Eur. J. Inorg. Chem., 2002, 73–78.
26. P. Nguyen, C. Dai, N. J. Taylor, W. P. Power, T. B. Marder, N. L. Pickett and N. C. Norman, Inorg. Chem., 1995, 34, 4290–4291.
27. D. J. Brauer and C. Krüger, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 1684–1690.
28. L. Frydman and J. S. Harwood, J. Am. Chem. Soc., 1995, 117, 5367–5368.
29. H. M. Kriz and P. J. Bray, J. Magn. Reson., 1971, 4, 76–84.
30. J. W. E. Weiss and D. L. Bryce, J. Phys. Chem. A, 2010, 114, 5119–5131.
31. (a) M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744; (b) M. Profeta, F. Mauri and C. J. Pickard, J. Am. Chem. Soc., 2003, 125, 541–548; (c) T. Charpentier, Solid State Nucl. Magn. Reson., 2011, 40, 1–20; (d) C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azaïs, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779.
32. F. A. Perras and D. L. Bryce, J. Phys. Chem. C, 2012, 116, 19472–19482.
33. M. Dračínský and P. Hodgkinson, CrystEngComm, 2013, 15, 8705–8712.
34. F. A. Perras and D. L. Bryce, J. Magn. Reson., 2014, 242, 23–32.
35. G. Wu, S. Kroeker, R. E. Wasylishen and R. G. Griffin, J. Magn. Reson., 1997, 124, 237–239.
36. S. Wi and L. Frydman, J. Chem. Phys., 2000, 112, 3248–3261.
37. (a) J. McManus, R. Kemp-Harper and S. Wimperis, Chem. Phys. Lett., 1999, 311, 292–298; (b) G. Wu and K. Yamada, Chem. Phys. Lett., 1999, 313, 519–524.
38. I. Demachy and F. Volatron, J. Phys. Chem., 1994, 98, 10728–10734.
39. (a) Y. Mo and Z. Lin, J. Chem. Phys., 1996, 105, 1046–1051; (b) C. R. Watts and J. K. Badenhoop, J. Chem. Phys., 2008, 129, 104307.
40. J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218.
41. A. E. Reed and F. Weinhold, J. Chem. Phys., 1985, 83, 1736–1740.
42. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.0., Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2001.
43. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
44. J. Kroner and B. Wrackmeyer, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 2283–2290.
45. H. A. Bent, Chem. Rev., 1961, 61, 275–311.
46. F. Bachmann, H. Nöth, H. Pommerening, B. Wrackmeyer and T. Wirthlin, J. Magn. Reson., 1979, 34, 237–239.
47. B. Wrackmeyer, Z. Naturforsch B, 2004, 59, 1192–1199.
48. (a) N. Muller and D. E. Pritchard, J. Chem. Phys., 1959, 31, 768–771; (b) N. Muller and D. E. Pritchard, J. Chem. Phys., 1959, 31, 1471–1476.
49. N. S. Barrow, J. R. Yates, S. A. Feller, D. Holland, S. E. Ashbrook, P. Hodgkinson and S. P. Brown, Phys. Chem. Chem. Phys., 2011, 13, 5778–5789.
50. P. Florian, F. Fayon and D. Massiot, J. Phys. Chem. C, 2009, 113, 2562–2572.
51. T. C. Farrar and G. R. Quinting, Inorg. Chem., 1985, 24, 1941–1943.
52. M. Concistrè, E. Carignani, S. Borsacchi, O. G. Johannessen, B. Mennucci, Y. Yang, M. Geppi and M. H. Levitt, J. Phys. Chem. Lett., 2014, 5, 512–516.
53. J. Cid, J. J. Carbó and E. Fernández, Chem.–Eur. J., 2014, 20, 3616–3620.
54. S. Hayashi and K. Hayamizu, Bull. Chem. Soc. Jpn., 1989, 62, 2429–2430.
55. K. Eichele, WSolids1, version 1.20.15, University of Tübingen, Tübingen, Germany, 2011.
56. J.-P. Amoureux, C. Fernandez and S. Steuernagel, J. Magn. Reson., Ser. A, 1996, 123, 116–118.
57. D. J. States, R. A. Haberkorn and D. J. Ruben, J. Magn. Reson., 1982, 48, 286–292.
58. S. Adiga, D. Aebi and D. L. Bryce, Can. J. Chem., 2007, 85, 496–505.
59. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
60. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890.
61. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
62. E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.

---