Novel metal–organic framework linkers for light harvesting applications

Abstract

Metal–organic frameworks (MOFs) are composed of organic linkers and coordinating metals that self-assemble to form a crystalline material with tunable nanoporosity. Their synthetic modularity and inherent long-range order create opportunities for use as new functional electronic materials. Using quantum mechanical computational methodologies we propose novel conjugated organic linkers that are capable of forming the same one-dimensional infinite metal-oxide secondary building units (SBUs) as the well-known IRMOF-74. This structural arrangement allows for the formation of a continuous π–π stacking network that should enable charge transport in fashion analogous to organic semiconductors. The structural and electronic properties (fundamental and optical gaps) of the isolated proposed linkers were modeled using a non-empirically tuned long-range corrected functional that leads to significantly improved results compared with experimental benchmarks. In addition, periodic hybrid density functional calculations were employed to model the extended MOF systems. Our results demonstrate how the electronic properties of MOFs can be readily modified to have favorable orbital alignments with known electron acceptors that should facilitate charge transfer. The predicted properties are in good agreement with experiment (i.e. UV-Vis absorption spectra), demonstrating the power of this computational approach for MOF design.

---

Introduction

Metal–organic frameworks (MOFs) are receiving considerable attention due to their large surface area to volume ratios and tunable pore sizes. To date, research has primarily focused on applications relating to gas storage,^1–4 gas purification and separation,^5–9 chemical sensing,^10–12 and catalysis.^13–15 Recently, the light harvesting and intrinsic charge transport properties of MOFs have become of interest for electronic and photonic applications.^16–22 These efforts stem from both the success and shortcomings of current approaches based on organic materials, such as organic photovoltaics based on a bulk-heterojunction (BHJ) architecture. Although organic and organic–inorganic hybrid materials demonstrate exceptional promise for next-generation optoelectronic applications, the donor–acceptor interfaces in these systems are typically poorly ordered, leading to inefficient charge separation upon photoexcitation.²³ The potential utility of MOFs arises from a combination of their nanoporosity, which can accommodate guest molecules, and the ability to control donor–acceptor interactions and phase separation at the nanoscale, enabled by the long-range order inherent in these porous crystalline frameworks. For example, we recently showed that fullerenes and thiophenes, organic molecules typically used in OPV devices, can be stabilized within a MOF without phase segregation. The MOF host used in that investigation was MOF-177, a nominally passive (i.e. not charge conducting) structure that nevertheless performed the additional functions of light harvesting and energy transfer to the guest molecules by Förster resonance energy transfer (FRET).²²

In theory, however, MOFs can also be designed to play an active role, serving as one half of a donor–acceptor interface (the other half residing as guest molecules in the pores), thereby facilitating charge separation and transport in the device active layer. This requires the MOF to have specific electronic properties, including high charge-carrier mobility, broad spectral coverage, large absorption coefficients, and the appropriate orbital alignment with the opposing material residing in the pores, while retaining relevant geometrical parameters.^24–26 The MOF cavities or channels must also be sufficiently large to allow diffusion and accommodation of the infiltrated species (e.g. PCBM) in ample quantities. To date, nearly all MOFs are dielectric materials, particularly those with appreciable porosity; therefore, expansion of MOF applications to include optoelectronic devices requires the design and synthesis of new porous MOFs with semiconducting attributes.

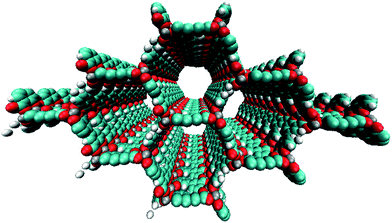
Creating a functional MOF-based electronic device is a major challenge given the synthetic complications and challenges associated with the integration of these materials in a structurally controlled manner. Several strategies have been proposed for designing electrically conducting MOFs (e.g., using transition metals, redox-active linkers, and hetero-bimetallic structures), but limited success has been achieved.^27,28 Nevertheless, the synthetic versatility of MOFs is encouraging and allows for facile tuning of their structural and electronic properties. There are three general approaches for altering the structural and electronic properties of MOFs: (i) changing the metal ion(s), (ii) modification of the organic linker(s) and/or (iii) infiltration of select molecules into the framework, resulting in the formation of new metal-to-ligand (ligand-to-metal) charge-transfer (MLCT (LMCT)) states. To our knowledge, the first reported porous, intrinsically conducting MOF is Cu[Ni(pdt)₂] (pdt²⁻ = pyrazine-2,3-dithiolate),²⁹ which is a p-type semiconductor with a conductivity of 1 × 10⁻⁴ S cm⁻¹ enabled by a redox mechanism. More recently, Sun and co-workers¹⁹ disclosed a manganese based MOF utilizing a thiophenol linker (2,5-disulfhydrylbenzene-1,4-dicarboxylic acid), referred to as Mn₂(DSBDC), a variant of IRMOF-74 (ref. 30–32) (see Fig. 1), that exhibits high intrinsic charge mobility. The same group¹⁸ also reported a tetrathiafulvalene (TTF) zinc-based MOF that exhibits a charge mobility of 0.2 cm² V⁻¹ s⁻¹. The proposed charge transfer (CT) mechanisms for these two systems are reportedly different. It is proposed that Mn₂(DSBDC) exhibits band transport through the infinite metal-oxide secondary building units (SBUs).³³ In contrast, charge hopping through the organic linkers is suggested as the conduction mechanism operative in the TTF MOF, since these groups are spaced ∼3.8 Å apart.

Fig. 1 A supercell representation of the periodic PBE optimized IRMOF-74-II(Mg) structure.

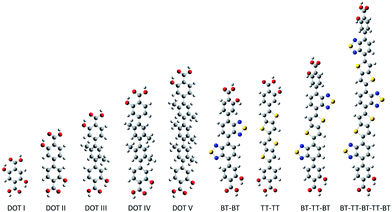
Here, we propose a new modular series of conjugated organic linkers (see Fig. 2) that are capable of forming the same infinite metal-oxide SBU as IRMOF-74 and acting as electron donors to well-known electron acceptors used in OPV, such as PCBM. Due to the nature of the proposed linkers and SBU, this new MOFs series allows for the formation of a continuous π–π stacking network potentially providing a direct route to facilitate charge transport. Synthesizing MOFs with these proposed linkers is feasible based on a previous study showing that the pore aperture of IRMOF-74 can be systematically increased. In that case, the organic linker (dioxidoterephthalate (DOT)) was lengthened to include up to 11 phenylene rings (DOT I–XI), creating an isoreticular series termed IRMOF-74-I to XI.³⁴ IRMOF-74 can also be readily synthesized with several different coordinating metals (IRMOF-74(M); M = Mg, Mn, Fe, Co, Ni, and Zn),^30,35 providing an unusually high degree of synthetic versatility (IRMOF-74-II(Mg) is shown in Fig. 1). We consider the Mg variant (IRMOF-74(Mg)) for its simple electronic structure (no d electrons); Mg²⁺ precludes MLCT or LMCT resulting in the localization of the frontier orbitals (HOMO and LUMO) entirely on the linkers and not on the metal. As a result, there is no competing CT state, enabling charge transfer and separation to occur only between the linker and the corresponding infiltrated electron acceptor. The electronic properties of the MOF, therefore, will be largely governed by the linker moiety. In addition, the high oxidation and low reduction potentials of Mg should prevent the metal ions in the framework from acting as charge carrier traps within an electrical device.

Fig. 2 The LC-BLYP/6-311G(d,p) optimized DOT I–VI linkers and proposed BT–TT linker series.

Here, we use a novel non-empirically tuned long-range corrected density functional theory (DFT) method^36–39 to demonstrate that these new linkers result in MOFs with the appropriate optoelectronic criteria and band-alignments with well-known electron acceptor components (i.e. PCBM) for light harvesting applications. To our knowledge, this is the first time that a non-empirically tuned density functional has been used to guide experimental MOF design. Specifically, we demonstrate that these MOF linkers are capable of absorbing light in the visible region and have large oscillator strengths compared to the parent DOT linker series. We validated our computational approach by synthesizing the BT–TT–BT linker and comparing its optical properties to several of the DOT linkers used in the IRMOF-74 series. These results and the corresponding synthetic protocol serve to demonstrate that the proposed linkers are chemically accessible in a straightforward manner using conventional synthetic methodologies and that the predicted and measured optical properties are in good agreement. In addition, we carried out periodic calculations for several of the extended MOF systems, confirming that the coordinating metal (Mg) does not interfere with the band edge. Consequently, useful information can be obtained by modeling the isolated linker allowing for rapid screening of potential organic linkers with desirable electronic properties. Finally, we discuss the confinement of electron acceptor materials within the MOF framework, showing that this can dramatically reduce the exciton diffusion length, an important factor governing efficiency in organic photovoltaics (OPV) and other optoelectronic devices.²⁴

Computational details and methodology

All density functional theory and time-dependent DFT (TDDFT) molecular orbital calculations were carried out using a non-empirically tuned long-range corrected (range-separated) density functional (LC-DFT) method. Recent theoretical work shows that range-separated functionals⁴⁰ are essential for modeling long-range charge-transfer and Rydberg states.^41–44 In addition, non-empirically tuned LC-DFT methods yield dramatic improvements for predicting fundamental and optical gaps over pure (nonhybrid) and hybrid functionals, when compared to experimental and/or results from more computational rigorous quantum mechanical methods.^36–38 The fundamental gap is defined as the difference in energy between the first ionization potential (IP) and the first electron affinity (EA), whereas the optical gap is the difference in energy between the lowest dipole-allowed excited state and the ground state. In general, the optical gap is smaller than the fundamental gap due to the Coulombic attraction between the excited electron and hole within the molecule. The improvements stem from the way the local DFT and nonlocal Hartree–Fock exchange are admixed. Range-separated functionals, in contrast with conventional hybrid functionals (i.e. B3LYP) that include a fixed percentage of Hartree–Fock exchange, incorporate nonlocal electron exchange as a function of the inter-electronic distance. As a result, the correct asymptotic behavior at large interelectronic distances is achieved. In LC-DFT, the electron repulsion operator 1/r₁₂ is separated into short-range (1st term) and long-range (2nd term) contributions: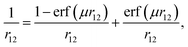where “erf” denotes the standard error function, r₁₂ is the interelectronic distance between electrons 1 and 2, and μ is the range-separation parameter in units of Bohr⁻¹. It has been demonstrated that μ is system dependent, but can be non-empirically tuned for a given system by minimizing the following function:^39,41

J²(μ) = [ε_HOMO(N, μ) + IP(N, μ)]². (2)

here, ε_HOMO(N, μ) is the energy of the HOMO, and IP is the ionization potential of the N electron system determined from the difference between the total energies of the N and N − 1 electron systems. In other words, the optimal μ value ensures that the negative of the HOMO energy is equal to the ionization potential. This is a fundamental condition within the Kohn–Sham DFT formalism (i.e., Janak's theorem⁴⁵), which justifies this self-consistent tuning of μ. Several slight variations of eqn (2) have been proposed (i.e. including the N + 1 system);⁴¹ however, the approach presented here carries the lowest computational burden. More importantly, the different approaches tend to produce similar results.⁴⁶ For example, for the BT–TT–BT linker considered here (see below), the optimal μ value differs by only 0.2% when the N + 1 state is included in the tuning procedure.

For the DOT-type linkers of the known IRMOF-74 series and new linkers proposed here, as well as for PCBM (PC₆₁BM), PC₇₁BM, P3HT (8 repeat units) and 2 × BT–TT–BT@PC₇₁BM (a molecular cluster containing 2 × BT–TT–BT linkers and PC₇₁BM), the optimal range-separated parameter was determined by varying μ from 0.1 to 0.4 Bohr⁻¹ in increments 0.1 Bohr⁻¹. For each value, full geometry optimizations were performed on the N-electron system followed by a single-point calculation of the +1 cation state (i.e., the N − 1 electron system). Plots of J² as a function of μ for all molecules are shown in Fig. S1;† the minimum of each curve was determined by cubic spline interpolation (optimal μ values are reported in Table 1). Finally, full geometry optimizations were carried out with the corresponding optimal μ value, followed by determination of the first 20 singlet excitations (10 singlet excitations for 2 × BT–TT–BT@PC₇₁BM) using TDDFT within the linear response formalism. Absorption spectra were determined by Gaussian convolution (full width at half-maximum of 3000 cm⁻¹) of the excitation energies and oscillator strengths to account for vibrational broadening of the spectrum at room temperature. All calculations were carried out within the Gaussian 09 package⁴⁷ using the LC-BLYP functional and the polarized 6-311G(d,p) basis set (6-31G(d,p) for 2 × BT–TT–BT@PC₇₁BM) with default SCF convergence criteria (density matrix converged to at least 10⁻⁸ Hartree) and DFT integration grid (75 radial and 302 angular quadrature points). For 2 × BT–TT–BT@PC₇₁BM, a smaller basis set was used, and fewer excitations were computed due to computational limitations associated with the size of the system (222 atoms). In addition, Grimme's empirical dispersion correction (S₆ = 1.20 and S_R6 = 1.10)⁴⁸ was used in order to take van der Waals interactions into consideration which are essential for modeling intermolecular interactions. During the geometry optimization of this cluster, the linkers (2 × BT–TT–BT) were fixed in the orientation obtained from the optimized periodic structure (see below) to maintain the configuration of the linkers within the MOF.

Table 1 Optimal μ values, HOMO–LUMO energies, fundamental gaps (HOMO–LUMO), optical gaps (S₀ → S₁ transition) and oscillator strengths of DOT I–V and the BT–TT series predicted at the LC-BLYP/6-311G(d,p) level of theory. All values are in eV; oscillator strengths are unitless

Linker	Optimal μ	HOMO	LUMO	Fundamental gap	Optical gap	Oscillator strength
DOT I	0.2715	−7.9	−0.6	7.3	3.3	0.115
DOT II	0.2507	−8.4	−0.5	7.9	4.1	0.304
DOT III	0.2089	−7.9	−0.4	7.5	4.1	0.407
DOT IV	0.2021	−7.8	−0.3	7.6	4.1	0.367
DOT V	0.1811	−7.7	−0.4	7.3	4.0	0.350
TT–TT	0.1829	−6.9	−1.0	5.8	3.1	2.161
BT–BT	0.1825	−7.4	−1.8	5.6	2.8	0.813
BT–TT–BT	0.1655	−6.7	−1.9	4.8	2.4	1.384
BT–TT–BT–TT–BT	0.1420	−6.2	−2.2	4.1	1.9	2.066
PCBM	0.1958	−7.4	−2.1	5.3	2.3	0.002
PC71BM	0.1724	−7.1	−2.2	4.9	2.2	0.006
P3HT	0.1419	−5.9	−1.0	4.9	2.6	2.434

---

Density functional theory calculations employing periodic boundary conditions were carried out on three MOFs (IRMOF-74-II(Mg), IRMOF-74–TT–TT(Mg) and IRMOF-74–BT–TT–BT(Mg)) using the Vienna ab initio simulation 5.2.12 package (VASP).^49–52 The Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional⁵³ with an energy cutoff of 500 eV was used for all geometry optimizations. Interactions between ions and electrons were described using projector-augmented-wave (PAW)^54,55 pseudo-potentials and a Γ-centered Monkhorst–Pack⁵⁶k-point grid of 4 × 4 × 12 was used for sampling the Brillouin zone. The structures were relaxed until all forces were smaller than 0.01 eV Å⁻¹. The tetrahedron method with Blöchl-corrections was used to determine the partial occupancies for each wavefunction.⁵⁷ Single-point calculations were carried out on the optimized PBE structures using the HSE06 hybrid functional^58,59 with a k-point grid of 2 × 2 × 6 using the Gaussian smearing method with a smearing width of 0.05 eV.

Results

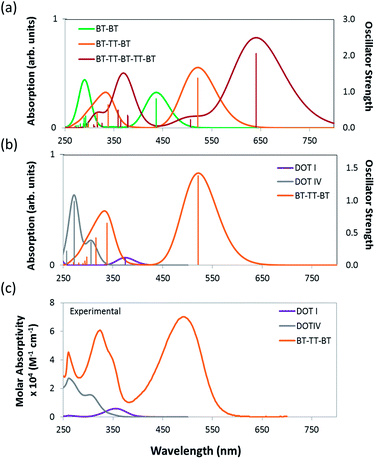
The predicted HOMO and LUMO energies, fundamental gaps (HOMO–LUMO), optical gaps (S₀ → S₁ transition), and oscillator strengths of DOT I–V (see Fig. 2) illustrate that the electronic structure of the IRMOF-74 series is not well suited to PV applications. Values of these properties are tabulated in Table 1 and were determined using the non-empirically tuned LC-BLYP functional. The predicted fundamental gaps for DOT I–V are all ∼7.5 eV. These values correspond to the molecule in the gas phase; thus, the large gaps are not unexpected. It has been shown that non-empirically tuned LC functionals predict fundamental gaps that are in very good agreement with experimental gas-phase measurements, as well as with more computationally intensive techniques such as many-body GW and CASPT2 (complete active-space second-order perturbation theory) methods.³⁶ The optical gaps, which are of primary importance for light harvesting, tend to be of similar energy in the gas and solid states and with the exception of DOT I are ∼4 eV. The large difference between the fundamental and optical gaps can be attributed to the magnitude of the exciton binding energy (fundamental gap–optical gap). For example, the experimental exciton binding energy of C₆₀ in the gas phase is 3.0 eV and is reduced to 1.4–1.6 eV in the solid state.⁶⁰

The TDDFT predicted optical gap of DOT I is 3.3 eV; this value is in near perfect agreement with the experimental absorption maximum occurring at 372 nm (3.3 eV; see Fig. 3). The predicted optical gaps for DOT II–V are blue shifted from this value, occurring at approximately 4.0 eV, again in near perfect agreement with experiment (see ESI† for all experimental details and absorption spectra; DOT V was not experimentally considered here). Comparing the experimental and Gaussian convoluted TDDFT absorption spectra (Fig. 3 and S2†), the accuracy of the non-empirically tuned range-separated functional is clearly evident. The correlation between the spectra extends beyond the S₀ → S₁ transition. For example, the S₀ → S₃ transitions are predicted to be stronger than the S₀ → S₁ transition for DOT II–IV, which is consistent with the experimental spectra. Although the DOT linkers allow for systematic control over the pore diameter of IRMOF-74, they absorb little, if any, of the visible spectrum, making them of little use for PV applications.

Fig. 3 The TD/LC-BLYP/6-311G(d,p) predicted absorption spectra and oscillator strengths (represented by the vertical lines) of BT–BT, BT–TT–BT and BT–TT–BT–TT–BT (a). (b) and (c) compare the predicted and experimentally determined absorption spectra of DOT I, DOT IV and BT–TT–BT (see SI for experimental details) respectively. The TDDFT predicted absorption spectra curves were determined by Gaussian convolution using a FWHM of 3000 cm⁻¹.

To create frameworks having the IRMOF-74 topology that are capable of harvesting visible light, chemical intuition and DFT suggest that modification of the organic linker is essential to achieving the desired optoelectronic characteristics. Although the literature of organic semiconductors provides many possibilities, the desire to incorporate these within the IRMOF-74 structure constrains the design process in two ways. In particular, IRMOF-74-n linkers must be linear and relatively rigid (Fig. 2), with intramolecular rotation largely confined to rotations of phenyl groups around the primary axis. They must also include the para-CO₂⁻ and ortho-OH⁻ functionalities that can coordinate with the metal ions to preserve the original topology. Among the many light-absorbing donor materials reported, those featuring electron-deficient benzo[c][1,2,5]thiadiazole (BT) and alternating thiophenes are among the most promising.^61–64 Fused and rigidified thiophene based building blocks lead to extended conjugation, narrower bandgaps and stronger intermolecular interactions. We therefore considered a new series of organic linkers composed of BT and/or alternating electron-rich thieno[3,2-b]thiophene (TT) moieties terminated with 2-hydroxybenzoic acid (see Fig. 2) for initial examination. The fused TT building block serves to enforce the geometrical parameters required for the formation of the same SBU as the IRMOF-74 series while simultaneously narrowing the optical gap.

The predicted electronic properties of the proposed linkers (i.e. BT–BT, TT–TT, BT–TT–BT, and BT–TT–BT–TT–BT) (Table 1) demonstrate that this series provides the ability to tune relevant optoelectronic features, such as the optical gap, while maintaining overall linker symmetry. Due to the conjugated nature of these molecules, they exhibit optical gaps that are significantly reduced relative to their DOT counterparts and also larger oscillator strengths for the S₀ → S₁ transition (see Table 1) compared to the DOT linker series. The emerging pattern indicates a decrease in the optical gap and an increase in the S₀ → S₁ oscillator strength as the number of alternating BT–TT moieties increases. This is consistent with the frontier orbital energies becoming more closely spaced as the delocalization length increases. As a result, the BT–TT–BT–TT–BT linker has the smallest optical gap (1.9 eV) of the linkers considered. The predicted absorption spectra of BT–TT, BT–TT–BT and BT–TT–BT–TT–BT (Fig. 3) illustrate that as the BT–TT length increases, the absorption shifts to the red with a concomitant increase in the oscillator strength, equivalent to an increase in molar absorptivity. The oscillator strength for the S₀ → S₁ transition of BT–TT–BT–TT–BT (f = 2.06) is more than fivefold higher than DOT V (f = 0.35) and more than 17 times that of DOT I (f = 0.11), indicating considerably enhanced photon absorption efficiency. Notably, the TT–TT linker has a larger oscillator strength (f = 2.16) for the S₀ → S₁ transition than BT–BT (f = 0.81), but similar fundamental and optical gaps, owing to the more electron rich nature of the moiety. This demonstrates that a rapid increase in oscillator strength, hence increased photon absorption efficiency, can be achieved through linking just two TT moieties.

To validate our theoretical approach, we synthesized the BT–TT–BT linker (as its protected methyl ester) and characterized its optical properties (see ESI† for experimental details). This provides an essential benchmark for our theoretical predictions and represents a critical first step toward the rational design of this new class of MOFs. The experimental absorption spectrum of BT–TT–BT relative to the predicted non-empirically tuned LC-BLYP spectrum are compared in Fig. 3. The experimentally determined absorption maximum (in dimethylformamide (DMF) at room temperature) for BT–TT–BT occurs at 490 nm, which is in good agreement with the predicted S₀ → S₁ excitation occurring at 2.4 eV (521 nm). Although not directly related to the absorption maximum, the predicted optical gap is consistent with these spectra, differing from the experimental maximum by only 0.15 eV (31 nm).

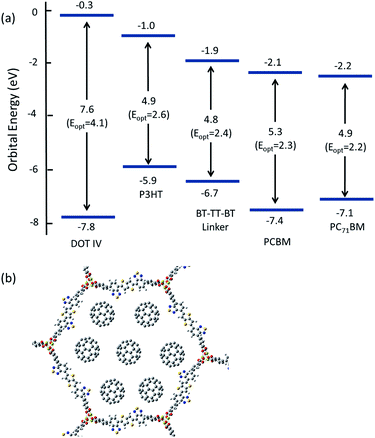
To ascertain whether the analysis of the isolated linkers can be related to the bulk MOF, we performed periodic DFT calculations for IRMOF-74-II(Mg), IRMOF-74–TT–TT(Mg), and IRMOF-74–BT–TT–BT(Mg). These systems were fully optimized at the DFT/PBE level of theory (optimized structures are shown in Fig. 1 and 4), followed by single-point calculations using the hybrid HSE06 functional. Hybrid functionals are well-known to more accurately predict bandgaps than GGA functionals (e.g. PBE); however, their use comes at significantly higher computational cost. The HSE06 (PBE) predicted bandgaps are 3.5 (2.5) eV, 2.5 (1.9) eV, and 2.0 (1.4) eV for IRMOF-74-II(Mg), IRMOF-74–TT–TT and IRMOF-74–BT–TT–BT respectively. The HSE06 values are systematically ∼0.5 eV smaller than the predicted optical gaps of the isolated linkers; this difference can in part be attributed to the surrounding dielectric (solid vs. gas phase) but is also an artifact of the functionals themselves. Not unexpectedly, the PBE predicted bandgaps are even smaller; upwards of 1 eV compared to the HSE06 results. Importantly, however, the pattern is consistent between the different methods. The total and partial densities of states, shown in Fig. 5, indicate that the frontier orbitals (valence and conduction band wavefunctions) are composed of C p-orbitals and have no contributions from the Mg valence s-orbital subshell. This indicates that the frontier orbitals are localized on the linkers; therefore, results predicted by considering the isolated linkers should provide an adequate representation of the electronic structure of the MOF. In the case of other metals that can be used to construct IRMOF-74 (Mn, Fe, Co, Ni, and Cu), however, the d-orbitals will likely be near the band edge, rendering this approximation invalid.

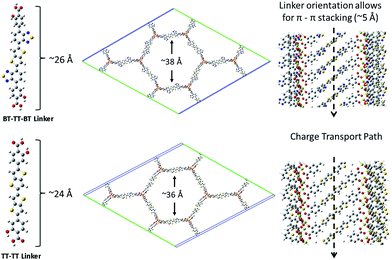Fig. 4 A schematic showing the BT–TT–BT and TT–TT optimized linkers, MOFs, linker length and pore cavity diameter, and the pi–pi stacking network.

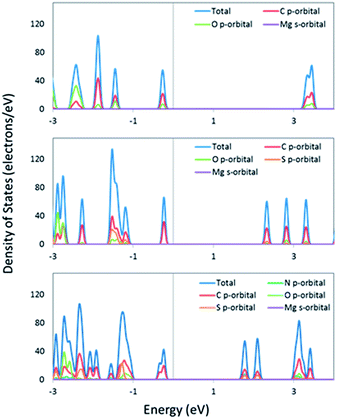Fig. 5 The total and partial density of states of IRMOF-74-II (top), IRMOF-74–TT–TT (middle), and IRMOF-74–BT–TT–BT (bottom). The Fermi energy has been placed at zero.

Discussion

The nanoporous nature of MOFs creates the potential to form a “nano-heterojunction,” in which the framework serves as an electron-donating light absorber that is infiltrated with an electron acceptor. The advantage of this configuration is that it confines both the donor and acceptor within a highly ordered chemical environment that, in principle, can be synthetically tuned to optimize light harvesting, exciton splitting, and charge transport. The IRMOF-74 topology is an excellent starting point for designing semiconducting MOFs with appreciable porosity because of its proven synthetic modularity and structural properties that should promote charge transport. A key feature of its structure is that the linkers stack (∼5 Å apart) in a perpendicular arrangement to form the sidewalls of the pores (see Fig. 1), in contrast with other well-known frameworks where the linkers are electronically isolated from each other (e.g. MOF-5, MOF-177, and HKUST-1).⁶⁵ This provides a potential route for charge transport through the organic linkers of the MOF. Supporting this proposed mechanism are prior studies demonstrating charge transfer between MOF linkers that are closely spaced.^66–69 However, as our calculations show, the linkers comprising the IRMOF-74 series (DOT I–XI) have large optical gaps, small oscillator strengths, and improper orbital alignments with known electron donor materials. For example, the HOMO and LUMO orbitals of PCBM lie between that of the DOT linkers (see Fig. 6); as a result, the IRMOF-74 series lacks the ability to absorb light in the visible region and transfer charge to PCBM. Recently, an alternative approach for predicting MOF band alignments, based on periodic DFT calculations, was proposed that allows for the conduction and valence bands of the MOF to be referenced to vacuum by taking advantage of the porous nature of the material.⁷⁰ Both methods provide only approximate values. Nevertheless, these carboxylate-based frameworks are expected to be insulators based on the magnitude of their bandgaps, making it impossible to conduct charge into or out of the framework.

Fig. 6 (a) HOMO–LUMO energies and fundamental and optical gaps of DOT IV, P3HT, BT–TT–BT, PCBM and PC₇₁BM predicted at the LC-BLYP/6-311G(d,p) level of theory (b) and a schematic illustrating how ample loading of PCBM or PC₇₁BM (C₆₀ was used for illustrative purposes) within the 1D pore channels of IRMOF-74–BT–TT–BT(Mg) is plausible.

In contrast, the electronic structure of the linkers in the series proposed here is designed for efficient light harvesting and to promote charge transport within the IRMOF-74 network. These molecules have the proper band alignment with known electron acceptors such as PCBM and PC₇₁BM, in that the HOMO (LUMO) of the linker, acting as an electron donor, is positioned below (above) the HOMO (LUMO) of the acceptor. We focus in this discussion regarding band alignment and CT on the BT–TT–BT linker for two reasons. First, its length will create large channels that facilitate infiltration of guest molecules and second, it has more favorable electronic properties than the linkers containing only the BT and TT moieties. As seen in Fig. 6, the predicted band alignments of the BT–TT–BT linker with respect to PCBM and PC₇₁BM indicate that this linker can act as an electron donor to either of these acceptors. Its light-absorbing properties (optical gaps and oscillator strengths) are also similar to those of P3HT (see Table 1), a well-known electron donor used in OPV. Notably, the linker/fullerene offset is close to the “ideal” donor–acceptor LUMO offset^26,71 of 0.3 eV (0.2 and 0.3 eV for PCBM and PC₇₁BM respectively), which is important for efficient exciton splitting. In contrast, the predicted LUMO offset between P3HT is much too large (1.1 eV for PCBM, which is in excellent agreement with the experimental value of 1.0 eV (ref. 26)). The predicted BT–TT–BT optical gap (2.4 eV) is also somewhat smaller than that of P3HT (2.6 eV), which is heading closer to the optimal bandgap of 1.5 eV for polymer absorbers used in OPV applications.²⁶ As our calculations show, the proposed BT–TT–BT–TT–BT linker approaches this ideal value. Together, these properties support our hypothesis that rigid MOF linkers comprised of alternating BT and TT groups are a promising strategy for synthesizing MOFs for exciton-based light harvesting and charge separation.

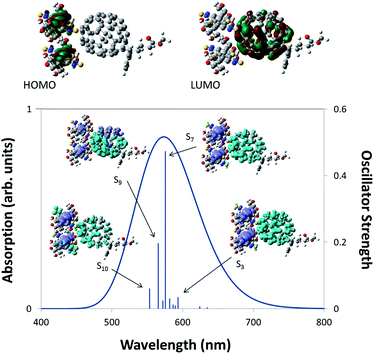
Additional evidence that charge transfer can occur between IRMOF-74–BT–TT–BT(Mg) and a fullerene derivative was obtained from TDDFT calculations of the 2 × BT–TT–BT@PC₇₁BM cluster model, which is representative of a fullerene guest within the MOF pore. The constrained optimized structure is shown in Fig. 7 along with images of the HOMO and LUMO. The localization of the HOMO on the linkers and the LUMO on PC₇₁BM indicates that charge transfer will occur upon absorption of photons with wavelengths of ∼500–700 nm. In addition, charge difference density (CDD)⁷² maps were generated for several of the dominant optically active transitions (see images within the absorption spectrum plot of Fig. 7). CDD maps enable visualization of the change in electron density upon excitation. These images show an increase in electron density on PC₇₁BM upon excitation, as represented by the light blue lobes, and a decrease in electron density on the linkers, as represented by the purple lobes. This is a clear indication that charge transfer should occur between IRMOF-74–BT–TT–BT(Mg) and PC₇₁BM.

Fig. 7 The HOMO, LUMO and the TDDFT (LC-BLYP/6-31G(d,p)) predicted absorption spectrum of 2 × BT–TT–BT@PC₇₁BM. The molecular images with the absorption spectrum plot show the change in electron density upon excitation (CCD maps). The purple and light blue regions represent a decrease (holes) and increase (electrons) in the electron density respectively.

In addition to proper band alignment, access to the pores and the ability to achieve high loading of electron acceptor molecules within them must be achievable to create an effective nano-heterojunction structure using a MOF. A dense acceptor loading is also needed to achieve the good orbital overlap between infiltrated acceptor molecules required for high charge mobility. The proposed IRMOF-74 variants have large 1D pore diameters, measuring ∼38 Å and ∼36 Å for IRMOF-74–BT–TT–BT and IRMOF-74–TT–TT, respectively (Fig. 4), which is sufficient to accommodate several fullerene molecules within the horizontal plane perpendicular to the pore channel (Fig. 6b). As these pores are one-dimensional channels, the pore limiting diameter (PLD) is the same as the largest cavity diameter (LCD). Diffusion of molecules this size into the pores should thus be rapid, as we demonstrated in a previous investigation of PCBM infiltration into MOF-177.²² In that case, the MOF LCD was ∼24 Å, but the PLD was only ∼16 Å, less than half that of IRMOF-74–BT–TT–BT and IRMOF-74–TT–TT. Nevertheless, nearly immediate PCBM uptake was observed upon exposure to a saturated solution, producing high loadings (22 wt%) comparable to those in BHJ OPV devices. We therefore expect that fullerene domains will form that are similar to those in conventional BHJ systems, but with more long-range order because the fullerene is confined within the 1D channels of the MOF. In a hypothetical thin-film BHJ device having a structure in which the MOF pore channels are perpendicular to the terminal contacts (anion/cathode), all the fullerene/acceptor and MOF/donor domains will have a continuous and direct path out of the active layer. In addition, the pores will confine the acceptors to be at most 20 Å (2 nm) from a donor, well within the maximum exciton diffusion length of 10 nm,²⁶ which is a major benefit of a MOF-based photovoltaic devices. Using the MOF as the electron donor, there would be virtually no exciton diffusion required if the pore channels are packed with fullerenes or any other acceptable electron acceptor with appropriately aligned electronic properties.

Conclusions

The proposed BT–TT series of linkers represent a new, previously unexplored class of MOFs that can be tailored specifically for light-harvesting with properties similar to those of well-studied organic semiconductors. Quantum mechanical periodic and molecular orbital calculations, including TDDFT using novel non-empirically tuned range-separated functionals, were used to extensively characterize their properties. This approach, which combines high-level theoretical treatments with bottom-up material design, represents an important step towards the synthesis of MOFs tailored for optoelectronic applications. We demonstrated that this modular BT–TT series is capable of forming the same infinite metal-oxide SBU as IRMOF-74, allowing a continuous π–π stacking network to be formed that could provide a route for high charge mobility. In these IRMOF-74 analogues, the linker is not merely structural, but is tuned to enable it to function as both a light harvester and an electron donor to electron acceptor molecules infiltrated within the pores. We expect, therefore, that light harvesting by these MOFs will be considerably more efficient than in typical carboxylate-type MOFs, which absorb primarily in the UV. As demonstrated, these linkers absorb visible light due to their relatively small optical gaps and large oscillator strengths, both of which agree well with experimentally determined trends and measured values. In addition, our results show that proper band alignment exists with well-known acceptor molecules, such as PCBM, to enable exciton splitting. Finally, the confinement of the acceptor molecules within the MOF should reduce the exciton migration distance considerably compared with typical bulk heterojunctions, a current factor that limits OPV performance.

The proposed MOF series and theoretical analysis represent a rational approach for predicting trends and guiding experimental efforts to develop MOF-based photovoltaic devices and functional electronic materials. The modularity of the proposed linker series allows for any BT–TT combination and pore diameter to be readily synthesized, affording the ability to systematically tune both the structural and electronic properties. Our results also demonstrate that accurate trends can be predicted from calculations based solely on the linkers, as long as the system is comprised of closed-shell metal ions such as Mg(II) that do not make orbital contributions near the band edges. Further modeling and experimental analyses are also underway to determine the charge transport characteristics of these MOFs. We are currently extending our approach to other potential organic linkers and MOF architectures that are expected to have favorable electronic properties for light harvesting, enhanced charge carrier mobility, minimal exciton diffusion distances, and high orbital overlap between adjacent linkers. Such architectures are promising not only for MOF-based solar cells, but also as well-controlled platforms for obtaining valuable fundamental knowledge regarding donor–acceptor interfaces, exciton diffusion lengths, and carrier mobility, due to the inherent structural order and nanoconfinement available in MOFs. Synthesis of these MOFs is currently underway in our laboratory.

Acknowledgements

This work was supported by the U.S. Department of Energy Office of Energy Efficiency and Renewable Energy SunShot Program under award number DE-FOA-0000387-1923 and Sandia National Laboratories' Laboratory Directed Research and Development (LDRD) Program. Sandia National Laboratories is a multi-program laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the U.S. Department of Energy's National Nuclear Security Administration under contract DE-AC04-94AL85000.

Notes and references

1. J. L. C. Rowsell, A. R. Millward, K. S. Park and O. M. Yaghi, J. Am. Chem. Soc., 2004, 126, 5666–5667.
2. A. R. Millward and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 17998–17999.
3. H. Wu, J. M. Simmons, Y. Liu, C. M. Brown, X.-S. Wang, S. Ma, V. K. Peterson, P. D. Southon, C. J. Kepert, H.-C. Zhou, T. Yildirim and W. Zhou, Chem.–Eur. J., 2010, 16, 5205–5214.
4. Q. Yang, V. Guillerm, F. Ragon, A. D. Wiersum, P. L. Llewellyn, C. Zhong, T. Devic, C. Serre and G. Maurin, Chem. Commun., 2012, 48, 9831–9833.
5. J. S. Seo, D. Whang, H. Lee, S. I. Jun, J. Oh, Y. J. Jeon and K. Kim, Nature, 2000, 404, 982–986.
6. J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504.
7. N. Nijem, H. Wu, P. Canepa, A. Marti, K. J. Balkus, T. Thonhauser, J. Li and Y. J. Chabal, J. Am. Chem. Soc., 2012, 134, 15201–15204.
8. A. Shigematsu, T. Yamada and H. Kitagawa, J. Am. Chem. Soc., 2012, 134, 13145–13147.
9. S.-M. Xie, Z.-J. Zhang, Z.-Y. Wang and L.-M. Yuan, J. Am. Chem. Soc., 2011, 133, 11892–11895.
10. L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. Van Duyne and J. T. Hupp, Chem. Rev., 2011, 112, 1105–1125.
11. M. D. Allendorf, R. J. T. Houk, L. Andruszkiewicz, A. A. Talin, J. Pikarsky, A. Choudhury, K. A. Gall and P. J. Hesketh, J. Am. Chem. Soc., 2008, 130, 14404–14405.
12. A. Lan, K. Li, H. Wu, D. H. Olson, T. J. Emge, W. Ki, M. Hong and J. Li, Angew. Chem., Int. Ed., 2009, 48, 2334–2338.
13. D. Farrusseng, S. Aguado and C. Pinel, Angew. Chem., Int. Ed., 2009, 48, 7502–7513.
14. C.-D. Wu and W. Lin, Angew. Chem., Int. Ed., 2007, 46, 1075–1078.
15. F. Vermoortele, M. Vandichel, B. Van de Voorde, R. Ameloot, M. Waroquier, V. Van Speybroeck and D. E. De Vos, Angew. Chem., Int. Ed., 2012, 51, 4887–4890.
16. H. A. Lopez, A. Dhakshinamoorthy, B. Ferrer, P. Atienzar, M. Alvaro and H. Garcia, J. Phys. Chem. C, 2011, 115, 22200–22206.
17. H.-J. Son, S. Jin, S. Patwardhan, S. J. Wezenberg, N. C. Jeong, M. So, C. E. Wilmer, A. A. Sarjeant, G. C. Schatz, R. Q. Snurr, O. K. Farha, G. P. Wiederrecht and J. T. Hupp, J. Am. Chem. Soc., 2012, 135, 862–869.
18. T. C. Narayan, T. Miyakai, S. Seki and M. Dincă, J. Am. Chem. Soc., 2012, 134, 12932–12935.
19. L. Sun, T. Miyakai, S. Seki and M. Dincă, J. Am. Chem. Soc., 2013, 135, 8185–8188.
20. D. Y. Lee, D. V. Shinde, S. J. Yoon, K. N. Cho, W. Lee, N. K. Shrestha and S.-H. Han, J. Phys. Chem. C, 2013 DOI:10.1021/jp4079663.
21. A. A. Talin, A. Centrone, A. C. Ford, M. E. Foster, V. Stavila, P. Haney, R. A. Kinney, V. Szalai, F. El Gabaly, H. P. Yoon, F. Léonard and M. D. Allendorf, Science, 2014, 343, 66–69.
22. K. Leong, M. E. Foster, B. M. Wong, E. D. Spoerke, D. Gough, J. C. Deaton and M. D. Allendorf, J. Mater. Chem. A, 2014, 2, 3389–3398.
23. R. R. Lunt, J. B. Benziger and S. R. Forrest, Adv. Mater., 2010, 22, 1233–1236.
24. T. M. Clarke and J. R. Durrant, Chem. Rev., 2010, 110, 6736–6767.
25. R. A. J. Janssen and J. Nelson, Adv. Mater., 2013, 25, 1847–1858.
26. B. C. Thompson and J. M. J. Fréchet, Angew. Chem., Int. Ed., 2008, 47, 58–77.
27. C. H. Hendon, D. Tiana and A. Walsh, Phys. Chem. Chem. Phys., 2012, 14, 13120–13132.
28. D. M. D'Alessandro, J. R. R. Kanga and J. S. Caddy, Aust. J. Chem., 2011, 64, 718–722.
29. Y. Kobayashi, B. Jacobs, M. D. Allendorf and J. R. Long, Chem. Mater., 2010, 22, 4120–4122.
30. N. L. Rosi, J. Kim, M. Eddaoudi, B. Chen, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 1504–1518.
31. T. M. McDonald, W. R. Lee, J. A. Mason, B. M. Wiers, C. S. Hong and J. R. Long, J. Am. Chem. Soc., 2012, 134, 7056–7065.
32. P. D. C. Dietzel, R. Blom and H. Fjellvåg, Eur. J. Inorg. Chem., 2008, 2008, 3624–3632.
33. O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714.
34. H. Deng, S. Grunder, K. E. Cordova, C. Valente, H. Furukawa, M. Hmadeh, F. Gándara, A. C. Whalley, Z. Liu, S. Asahina, H. Kazumori, M. O'Keeffe, O. Terasaki, J. F. Stoddart and O. M. Yaghi, Science, 2012, 336, 1018–1023.
35. P. D. C. Dietzel, Y. Morita, R. Blom and H. Fjellvåg, Angew. Chem., Int. Ed., 2005, 44, 6354–6358.
36. M. E. Foster and B. M. Wong, J. Chem. Theory Comput., 2012, 8, 2682–2687.
37. L. Kronik, T. Stein, S. Refaely-Abramson and R. Baer, J. Chem. Theory Comput., 2012, 8, 1515–1531.
38. S. Refaely-Abramson, R. Baer and L. Kronik, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075144.
39. T. Stein, L. Kronik and R. Baer, J. Am. Chem. Soc., 2009, 131, 2818–2820.
40. H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544.
41. T. Stein, L. Kronik and R. Baer, J. Chem. Phys., 2009, 131, 244119.
42. B. M. Wong, M. Piacenza and F. Della Sala, Phys. Chem. Chem. Phys., 2009, 11, 4498–4508.
43. R. Baer, E. Livshits and U. Salzner, Annu. Rev. Phys. Chem., 2010, 61, 85–109.
44. Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433.
45. J. F. Janak, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 18, 7165–7168.
46. G. García, J. M. Granadino-Roldán, A. Hernández-Laguna, A. Garzón and M. Fernández-Gómez, J. Chem. Theory Comput., 2013, 9, 2591–2601.
47. G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision D.01), Gaussian, Inc., Wallingford, CT, 2009.
48. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
49. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
50. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
51. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
52. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
53. J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539.
54. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
55. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
56. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
57. P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233.
58. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
59. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
60. M. Muntwiler and X. Zhu, in Dynamics at Solid State Surfaces and Interfaces: Volume 1-Current Developments, ed. U. Bovensiepen, H. Petek and M. Wolf, Wiley, 2010.
61. Y. Li, P. Sonar, L. Murphy and W. Hong, Energy Environ. Sci., 2013, 6, 1684–1710.
62. G. Dennler, M. C. Scharber and C. J. Brabec, Adv. Mater., 2009, 21, 1323–1338.
63. E. Bundgaard and F. C. Krebs, Macromolecules, 2006, 39, 2823–2831.
64. Z. B. Lim, B. Xue, S. Bomma, H. Li, S. Sun, Y. M. Lam, W. J. Belcher, P. C. Dastoor and A. C. Grimsdale, J. Polym. Sci., Part A: Polym. Chem., 2011, 49, 4387–4397.
65. Z. Xiang, D. Cao, J. Lan, W. Wang and D. P. Broom, Energy Environ. Sci., 2010, 3, 1469–1487.
66. P. M. Usov, C. Fabian and D. M. D'Alessandro, Chem. Commun., 2012, 48, 3945–3947.
67. B. D. McCarthy, E. R. Hontz, S. R. Yost, T. Van Voorhis and M. Dincă, J. Phys. Chem. Lett., 2013, 4, 453–458.
68. C.-W. Kung, T. C. Wang, J. E. Mondloch, D. Fairen-Jimenez, D. M. Gardner, W. Bury, J. M. Klingsporn, J. C. Barnes, R. Van Duyne, J. F. Stoddart, M. R. Wasielewski, O. K. Farha and J. T. Hupp, Chem. Mater., 2013, 25, 5012–5017.
69. C. R. Wade, M. Li and M. Dincă, Angew. Chem., Int. Ed., 2013, 52, 13377–13381.
70. K. T. Butler, C. H. Hendon and A. Walsh, J. Am. Chem. Soc., 2014, 136, 2703–2706.
71. D. B. Rodovsky, J. Peet, N. Shao, J. D. Azoulay, G. C. Bazan, N. Drolet, Q. Wu and M. Y. Sfeir, J. Phys. Chem. C, 2013, 117, 25955–25960.
72. M. Sun, J. Chem. Phys., 2006, 124, 054903.

---

Footnote

† Electronic supplementary information (ESI) available: Additional figures (J²vs. μ plots and computational and experimental absorption spectra) and full experimental details (synthesis and characterization). See DOI: 10.1039/c4sc00333k

---