The Houk–List transition states for organocatalytic mechanisms revisited

Abstract

The ten year old Houk–List model for rationalising the origin of stereoselectivity in the organocatalysed intermolecular aldol addition is revisited, using a variety of computational techniques that have been introduced or improved since the original study. Even for such a relatively small system, the role of dispersion interactions is shown to be crucial, along with the use of basis sets where the superposition errors are low. An NCI (non-covalent interactions) analysis of the transition states is able to identify the noncovalent interactions that influence the selectivity of the reaction, confirming the role of the electrostatic NCH^δ+⋯O^δ− interactions. Simple visual inspection of the NCI surfaces is shown to be a useful tool for the design of alternative reactants. Alternative mechanisms, such as proton-relays involving a water molecule or the Hajos–Parrish alternative, are shown to be higher in energy and for which computed kinetic isotope effects are incompatible with experiment. The Amsterdam manifesto, which espouses the principle that scientific data should be citable, is followed here by using interactive data tables assembled via calls to the data DOI (digital-object-identifiers) for calculations held on a digital data repository and themselves assigned a DOI.

---

Introduction

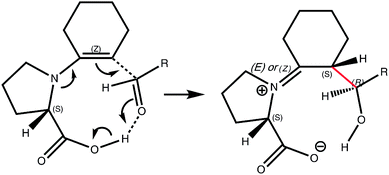
The promotion of a wide range of organic synthetic reactions using new generations of so-called organocatalysts (metal free systems) is highly topical. So too is the increasing adoption of computational modelling to chart the most probable mechanistic pathway and to establish the factors responsible for reactivity, selectivity, and particularly stereoselectivity.¹ In this regard, one report² in 2003 of computational investigation of the proline-mediated asymmetric intermolecular aldol reactions (Scheme 1) has achieved the rare distinction of having the key transition state model being named after the two principal authors; Houk and List. This computational model has informally become known as the gold standard for such investigations; since it exemplified the procedures for comparing computational modelling with experimental results for organocatalysed reactions and outlined a methodology for predicting the stereoselectivity of new organocatalysed reactions.

Scheme 1 Schematic mechanism for the intermolecular aldol reaction with proline as a chiral auxiliary, illustrating the cyclic transition state and key stereocentres created by bond formation between the enamine C=C and the carbonyl (red bond).

A one-proline mechanism based on enamine activation, the Houk–List model involves the transition state for stereogenic carbon–carbon bond formation. This is the rate-determining step² of the intermolecular aldol catalytic cycle in which the catalytically active enamine attacks an electrophile. The carboxylic acid group of proline plays a central role in the model, directing the electrophile to the Re face of the enamine. The enamine can be either anti or syn, relative to the acid, and the electrophile can offer two prochiral faces for attack, Re or Si, resulting in four different stereochemical outcomes (Scheme 2).

Scheme 2 The stereochemical possibilities for the asymmetric aldol reaction. Cahn–Ingold–Prelog conventions are shown for R = Ph.

Informed by extensive computational studies,^2–5 Houk and Bahmanyar suggested that the energy differences between these transition states, and so the origin and degree of stereoselectivity displayed by the reaction, depends on two critical structural elements: the relative degree to which each transition state can adopt a planar enamine, and the degree of electrostatic stabilisation provided to the forming alkoxide. A planar enamine allows for the greatest possible nucleophilicity of the terminal olefin while also reducing the geometric distortion experienced by the forming iminium group. The proton transfer from the carboxylic acid to the forming alkoxide was suggested as providing the majority of the electrostatic stabilisation and is key to the Houk–List model.^2,6 Smaller, yet important, stabilising contributions also result from NCH^δ+⋯O^δ− interactions from the pyrrolidine ring.⁷

Very good agreement between calculated and experimental stereoisomer ratios was observed, with the (S,R)-isomer most favoured for both R = Ph and ⁱPr (Scheme 2). The challenge of computational methods then is to establish a level of reliability which can be used to predict the outcome of further reaction variations. Any success of such models can then be used to build confidence for diversification to new reactions and mechanisms.

The Houk–List model has enjoyed a high degree of success in prediction of the stereochemical outcomes of a number of proline mediated reactions: from the inter-² and intramolecular⁵ aldol, Mannich,³ α-alkylation,⁸ and Michael reactions,⁹ among several others,¹ to the correct prediction of the outcome of reactions mediated by analogues of proline.^6,7,10–12 However, despite the apparently excellent comparison made between computational and experimental selectivities, for which this research became widely known, two significant issues have come to light regarding the details of the proline–cyclohexanone–benzaldehyde system. Houk has since disclosed that calculations carried out subsequent to publication, in which a greater volume of conformational space was investigated, revealed that structures of the transition states with lower energies exist;^1,13 potentially altering the predicted selectivity of the reaction. In addition, repetition of the experimental results by List found product selectivities to vary, with the reaction found to be extremely sensitive to both water content and to temperature. In the present article, we set out to establish whether the success of the Houk–List model as a concept, and the reportedly excellent agreement between computational and experimental results, is just coincidence or whether the faith in it is indeed justified.

Advances in computational methods

The ten years that have elapsed since the original report have seen many incremental, and sometimes dramatic, improvements to computational methods used. In the present article, we re-evaluate the Houk–List model by taking advantages of these; the gold standard itself must evolve. A more accurate computational model in turn allows the experimental findings to be subjected to improved scrutiny, which can potentially in itself result in suggestions for further experimental tests.

Because fully substituted reacting systems can often have >20 atoms and the organocatalysts themselves are potentially large molecules, the level of theory adopted to construct the Houk–List model in 2003 was (as always) a pragmatic compromise between the quality of the theory and the requirement to be able to compute the model in a reasonable time (a four day batch run is a typical resource available to most). The level originally selected by Houk and co-workers is commonly identified by the abbreviation B3LYP/6-31G*. Geometries, activation enthalpies, and free energies (ΔG₂₉₈) based on calculating the normal vibrational modes at this level were obtained for a gas phase model. To these energies (and at these geometries) various further corrections could be added using the previously computed geometries, including an estimation of the differential solvation energy computed for a polarizable continuum solvation model. This compound procedure was then applied to an exploration of the conformational space available to the system. Because this has many degrees of freedom for even quite simple reactions, only the most likely conformations were explored. So how can this basic approach be improved upon in 2014? We have focused on six aspects set out below:

1. The B3LYP density functional as used has, over the last twenty years, proven to be a very effective one for the study of reaction mechanisms, and it has been subjected to extensive testing and scrutiny during that period. In recent years, there have been attempts to benchmark the performance of B3LYP against more modern functionals.^14–16 As a result, one particular problem was identified with this functional; it captures only short range dynamic correlation energy and fails to capture longer range correlations. This term can be identified in part as the dispersion interactions between non-bonded atoms (also referred to as the non-covalent interactions or NCI). It is now recognised that the most effective way to correct a DFT method for dispersion terms is to add empirical corrections to the nuclear–nuclear repulsion terms, and three or more generations of methods have been developed over the last decade to achieve this. Grimme¹⁷ in particular has pioneered this approach and we have adopted his third generation procedure, known as D3, to correct the B3LYP method for these energy terms. Most modern functionals also incorporate such terms, and the ωB97XD method, which incorporates a version of Grimme's earlier D2 correction, was developed five years ago¹⁸ to specifically include both dispersion and the ability to reproduce reaction barriers.

2. The basis set quality is another feature that can be steadily improved, as computers have increased in speed, aspiring of course to a practical complete-basis-set limit (CBS). In 2003, the limit using conventional computational resources to the total number of basis functions that could be used for a modelling study was about 650 functions.¹⁹ For a 6-31G* basis set as used by Houk (the modern notation would be 6-31G(d), indicating only d-polarisation functions on non-hydrogen atoms) that would normally mean a limit of around 100 atoms, or perhaps up to about 120 if only the reacting core was specified at this level with sterically large substituents defined at a much smaller basis set level, say STO-3G.¹⁹ At this size, using a two or four parallel processing computer of the period, the second derivatives of the energy with respect to geometry (the Hessian, required to locate and characterise transition states) could be computed in about 170–200 hours of elapsed time. This would naturally limit the degree of conformational exploration that could be undertaken. The technological advances over a decade, the more common availability of 12/16-processor systems with much larger memory (improved from ∼4 Gbyte to ∼94 Gbytes) and faster algorithms for analytically computing the Hessian have reduced the elapsed time for such a calculation by a factor of about 100. Consequently, a much better level of basis set can now be deployed on molecules of such size. In the present study, we have used the TZVP basis,²⁰ a triple-ζ quality set with polarisation functions on both hydrogen as well as non-hydrogen atoms. This basis was selected since the Grimme-D3 dispersion corrections have been specifically parametrised for such basis sets. This now gives an opportunity to evaluate the errors due to basis-set-superposition that might have been incurred using the 6-31G* basis. For the system R = Ph (Scheme 1), this results in 556 basis functions for the calculation, compared with 376 for the 6-31G* basis and further allows selected intrinsic reaction coordinates (IRC) to be computed in a reasonable time. The IRC procedure requires the DFT-based Hessian to be evaluated 20–50 times, each taking about 1 hour using the TZVP basis, in order to map a full IRC. This requirement imposes a current practical limit of ∼800 basis functions for such a study. It is worth noting that this size of basis precludes the use of other Hamiltonians based on perturbative expansions such as MP2, an alternative procedure for evaluating dynamic correlation. Even on a very large memory 64-processor system, it was not possible to locate a single transition state for the TZVP basis in any reasonable time using this method.

3. It did prove feasible using the TZVP basis to perform a more systematic exploration of conformation space (Scheme 2), and even to apply the larger QZVP basis (1944 basis functions for R = Ph) to selected points.

4. The implementation of continuum solvation models has also improved considerably since 2003.²¹ Previously, optimisation of molecular geometries with such models was unreliable, since the first and second derivatives of the energy in a solvent continuum often resulted in small inhomogeneities due to the way in which the solvent cavity was constructed. York and Karplus²¹ revolutionised this with the introduction of an algorithm for obtaining a smoothed solvent cavity and since about 2010 it has been possible to fully optimise geometries within such a model.²² This means that a more self-consistent solvation approach can be undertaken, whereby the normal mode frequencies required to correct for thermal and entropy terms can be computed for geometries obtained using the solvation model at the relaxed solvation geometry, rather than simply being an ad hoc correction applied to a gas phase model. The reaction can develop charge separation during its course (to form a zwitterion), and (continuum model) solvation of charge-separated species can in turn have a significant impact upon their geometries and consequent properties.

5. The Houk–List model recognised the effect of solvent by correction for solvation free energies, but it did not also include the effects of discrete additional molecules in the model. For example, it is possible in any reaction that produces water as a product that at least one explicit water molecule could participate in the mechanism, either actively by acting as a proton relay or more passively by forming key additional hydrogen bonds. Indeed, mechanisms involving as many as four discrete waters acting as consecutive proton relays have been investigated. One consequence is that the overall free energy of the reaction can decrease. Of course, such a super-molecule can itself be treated by a continuum solvent model layered on top of the explicit model. Here we report an exploration of the role of water as both proton relay and as hydrogen bonding solvent.

6. In 2003, optimised geometrical coordinates, but no other derived properties (the full computed wavefunction, an IRC pathway, etc.) were inserted into paginated PDF documents as text and submitted as the ESI.† Re-using this data by extraction from the PDF document is non-trivial, as we ourselves experienced in re-using the original Houk–List data. The introduction²³ of open digital chemical data repositories in 2005 has revolutionised this aspect of data curation and citation.²⁴ All the results in the present study are presented in the form of interactive tables, themselves assigned a citable persistent digital-object-identifier (DOI), and in which the DOI assigned to individual calculations is used to retrieve and visually present the calculation log file from the appropriate digital repository.

Results and discussion

The Houk–List base model

The investigation began by locating the Houk–List transition states for the four stereochemical outcomes presented in Scheme 2. The original study located seven transition states for R = Ph and eight for R = ⁱPr. Two transition states differing in the conformation of the cyclohexene ring were located for each stereoisomer, apart from (S,R) anti R = Ph, where only one conformation was located. In the present study, we considered four conformations for each stereochemical outcome, resulting in 16 transition states for both R = Ph and R = ⁱPr. This expanded conformational analysis includes “chair” or “twist-boat” conformations for the cyclohexene ring and puckering of the proline ring away from or towards the proton transfer (Scheme 3).

Scheme 3 The four considered conformational possibilities for the asymmetric aldol condensation.

A repeat of the Houk–List calculations for R = Ph is presented in Table 1; calculated at the same theoretical level as previously employed² but including the additional conformations described above. As well as the relative DFT energy (ΔE), populations are shown based on the free energy (ΔG₂₉₈), the activation enthalpy (ΔH₂₉₈) and free energy of solvation; each of which were considered in the original study. Mindful that it is not practical to replicate the study by using the same versions of the computer codes that were available ten years earlier in 2003, a congruence of 0.01 kcal mol⁻¹ between the energy differences (ΔΔH₂₉₈) previously reported and those calculated using the modern versions of the codes²⁵ assures us that the basic methodology is highly reproducible.

Table 1 Transition state energies (R = Ph) calculated using the Houk–List method

Transition state		B3LYP/6-31G*							B3LYP/6-31G*/SCRF=DMSO^f
Isomer	Conf.	ΔE^c	Pop.^b	ΔΔG298^c	Pop.^b	ΔΔH298^c	Pop.^b	DOI^e	ΔE^c	Pop.^b	DOI^e
a Conformations considered in the original study from ref. 2. b % Populations based upon the conformations considered in the original study^2 in parentheses. c Relative energies in kcal mol^−1. Original conformations from ref. 2 shown in blue shade. d Relative energies from ref. 2. e Persistent identifiers (DOI) for digital repository entry. f Single point energy calculations for a solvation (CPCM) model at previously optimised gas-phase geometries (B3LYP/6-31G*). An interactive version of this table is archived at DOI: p9d.
(S,R) [anti]	1	0.00	98.45 (54.15)	0.00	99.51 (94.89)	0.00	98.75 (64.98)	10042/25001, pj3	0.00	99.40 (89.49)	10042/25809, pkn
	2	0.07		0.06		0.17		10042/25004, pj4	0.59		10042/25091, pkp
	3^a	2.36		1.60		2.29 [2.29]^d		10042/25002, pj5	1.87		10042/25090, pkq
	4	1.74		1.22		1.62		10042/25005, pj6	1.87		10042/25092, pkr
(S,S) [syn]	1^a	2.48	1.52 (44.34)	3.44	0.45 (4.26)	2.68 [2.68]^d	1.22 (33.59)	10042/25012, pkh	3.24	0.54 (8.79)	10042/25162, pk4
	2	2.60		3.07		2.72		10042/25015, pkj	3.48		10042/25163, pk5
	3^a	4.34		4.98		4.66		10042/25013, pkk	4.72		10042/25811, pk6
	4	3.70		4.29		3.92		10042/25016, pkm	4.48		10042/25164, pk7
(R,R) [ent-syn]	1	8.10	0.01 (0.28)	8.20	0.00 (0.09)	8.73	0.00 (0.15)	10042/25009, pkc	7.02	0.03 (0.81)	10042/25810, pkx
	2^a	5.48		5.73		5.88 [5.89]^d		10042/25011, pkd	4.65		10042/25099, pkz
	3	9.24		9.89		10.53		10042/25008, pkf	7.67		10042/25097, pk2
	4^a	7.11		7.39		7.91		10042/25010, pkg	5.81		10042/25098, pk3
(R,S) [ent-anti]	1	7.53	0.02 (1.23)	6.70	0.03 (0.76)	7.50	0.02 (1.27)	10042/25014, pj7	7.22	0.03 (0.90)	10042/25094, pks
	2^a	4.60		4.46		4.62 [4.62]^d		10042/25007, pj8	4.59		10042/25096, pkt
	3	8.59		8.10		8.69		10042/25003, pj9	8.26		10042/25093, pkv
	4^a	6.17		5.54		6.09		10042/25006, pkb	5.77		10042/25095, pkw

---

We find that the three additional conformations for the observed (S,R) anti product (conformations 1, 2 and 4) are all lower in free energy than the single conformation previously reported for that diastereomer (conformation 3).

The original study predicted high enantioselectivity, but low diastereoselectivity, for the reaction with benzaldehyde (based on ΔH₂₉₈). This was in good agreement with the ∼1 : 1 diastereomeric ratio that was experimentally determined by List. However, inclusion of these new low energy transition states changes the predicted diastereoselectivity of the reaction so that it is highly selective towards the (S,R) anti product and is no longer in good agreement with experiment.

Basis set superposition error

Having addressed the apparently incomplete exploration of conformational space, the next priority was to explore the effects of incorporating the changes in methodologies noted in the introduction. A recent article argued the importance of accounting for BSSE (basis set superposition error), as well as including dispersion corrections, for thermochemical calculations using the B3LYP/6-31G(d) method (the same level of theory used in the Houk–List study).²⁶ Compared to metal or protein based catalysts, typical organocatalytic systems consist of relatively few light main group elements. Therefore, the effects of BSSE are often assumed to cancel or be of a magnitude small enough to routinely ignore when calculating energies of organocatalytic transition states with similar connectivity. To test this assumption, we have evaluated the difference in BSSE between the anti and syn transition state geometries using the Boys–Bernadi counterpoise method for four basis sets: the original Houk–List 6-31G(d), the commonly used rather larger 6-311G(d,p), the triple-ζ-quality TZVP and the quadruple-ζ-quality QZVP. The calculations were performed in Orca (V. 2.9.1)²⁷ using benzaldehyde and the cyclohexanone–proline enamine as fragments, with overall geometries fully optimised at each respective level of theory.

These results (Table 2) clearly show that errors due to BSSE differences between stereoisomers can be of the order of 1 kcal mol⁻¹ at the original 6-31G(d) level selected in 2003. These relative errors are still relatively large (∼0.8 kcal mol⁻¹) for the larger 6-311G(d,p) basis and only become insignificant for the TZVP basis (∼0.2 kcal mol⁻¹). For the best QZVP basis set, even the absolute BSSE error has become insignificant (∼0.2 kcal mol⁻¹) although the general use of this basis is precluded because of computational cost. From these results, we suggest that the relatively compact TZVP triple-ζ-quality basis is the minimum appropriate for fidelity in stereochemical prediction, resulting in optimisations fast enough to allow exploration of multiple conformations when needed.

Table 2 Basis set superposition errors calculated for Houk–List transition state, R = Ph^a

Method	Isomer	Fragment (basis)^b								E (SE)^d	ΔE (SE)^d
		E (B)	DOI^c	E (CP–B)	DOI^c	CP (CP)	DOI^c	CP (CP–B)	DOI^c
a B = benzaldehyde, CP = cyclohexanone–proline derived enamine. Energies in Hartree. b Superposition error, E (SE) = E^CP–BCP(CP–B) − E^CP–BCP(CP) + E^CP–BB(CP–B) − E^CP–BB(B). c Persistent identifier for digital repository entry. d kcal mol^−1. An interactive version of this table is archived at DOI: qd7.
B3LYP/6-31G(d)	anti	−345.33656	10042/24751	−345.34328	10042/24752	−634.15131	10042/24754	−634.15629	10042/24753	7.34	1.13
	syn	−345.33879	10042/24755	−345.34629	10042/24756	−634.13923	10042/24758	−634.14522	10042/24755	8.47
B3LYP/6-311G(d,p)	anti	−345.43715	10042/24760	−345.44193	10042/24761	−634.32854	10042/24763	−634.33119	10042/24762	4.67	0.78
	syn	−345.43721	10042/24764	−345.44230	10042/24765	−634.31659	10042/24767	−634.32019	10042/24766	5.45
B3LYP/TZVP	anti	−345.47136	10042/24742	−345.47273	10042/24743	−634.37892	10042/24744	−634.37995	10042/24745	1.51	0.19
	syn	−345.47002	10042/24747	−345.47151	10042/24748	−634.37011	10042/24750	−634.37134	10042/24749	1.70
B3LYP/QZVP	syn	−345.50824	10042/26628	−345.50846	10042/26629	−634.44042	10042/26630	−634.44060	10042/26631	0.25	−0.04
	anti	−345.50635	10042/26625	−345.50655	10042/26624	−634.43077	10042/26626	−634.43090	10042/26627	0.21

---

The effects of the dispersion correction

To examine any effects a dispersion correction might have on energy and structure, the 16 transition states from the expanded conformational analysis (Scheme 3) were re-located for the benzaldehyde (R = Ph) and isobutyraldehyde (R = ⁱPr) systems. The geometries were optimised with the larger triple-ζ-quality TZVP basis set with inclusion of the CPCM solvation model, with and without DFT + D3 correction¹⁷ as applied to the B3LYP hybrid functional. Thus B3LYP+D3/TZVP/SCRF-CPCM=DMSO is now defined as our base standard.

The results of these calculations are summarized in Fig. 1 and Tables 3 (R = Ph) and 4 (R = ⁱPr). The most obvious geometrical effect is on non-bonded distances within the transition states, which can alter by up to 0.33 Å (Fig. 1). Smaller more subtle effects on the geometry of the reaction centre (Scheme 1) are induced. The creation of two stereogenic centres via the formation of a new C–C bond is accompanied by a key proton transfer from the carboxyl group to the oxygen of the carbonyl substrate. At the new base-level of theory, inclusion of the D3-correction for the transition state geometries for R = Ph and R = ⁱPr (Fig. 2) changes the optimised forming C–C length from 2.251 to 2.273 Å, the proton transfer geometry from 1.242/1.166 to 1.247/1.162 Å, and the planarity of the enamine from 174.9/174.8° to 177.2/176.1° (R = Ph). The corresponding changes for R = ⁱPr are 2.159 to 2.115 for the forming C–C bond, 1.154/1.262 to 1.151/1.269 Å for the proton transfer, and 175.5/173.7° to 178.5/176.1° for the planarity of the enamine. Larger variation is induced by a change of functional (to ωB97XD¹⁸); the latter values are similar to that obtained using MP2/6-31G(d,p)/SCRF=DMSO. We note that this smaller 6-31G(d,p) basis set is in fact the best basis for which a practical MP2 calculation can be run on the largest resource available to us, a 64-processor 88 Gbyte memory system.

Fig. 1 Computed selected bond lengths (Å) at B3LYP/TZVP/SCRF=DMSO (B3LYP+D3/TZVP/SCRF=DMSO) level of conformation 2 (Scheme 3) for R = Ph, showing the contraction in non-bonded distances when dispersion correction is included. An interactive version of this figure is archived at DOI: qd8.

Table 3 Calculated transition state properties for R = Ph (Scheme 2)

Transition state		B3LYP/TZVP/SCRF=DMSO				B3LYP+D3/TZVP/SCRF=DMSO
Isomer	Conf.	ΔE	ΔΔG298^a	Pop.	DOI^b	ΔE	D3^c	ΔΔG298^a	Pop.	DOI^b
a kcal mol^−1. b Persistent identifier (digital-object-identifier) for digital repository entry. c Grimme's D3 dispersion correction (ref. 17), in kcal mol^−1. d ωB97XD/TZVP/SCRF=DMSO, DOI: n47. e ωB97XD/TZVP/SCRF=DMSO, DOI: n48. f Hajos–Parrish mechanism, DOI: n49. g MP2(FC)/6-31(G)/SCRF=DMSO, DOI: ppd. h MP2(FC)/6-31(G)/SCRF=DMSO, DOI: ppf. i B3LYP/QZVP/SCRF=DMSO, DOI: p8h. j ΔΔG298 3.27 kcal mol^−1, DOI: p8g An interactive version of this table is archived at DOI: qcc.
(S,R) [anti]	1	0.00	0.00	99.94%	10042/24848	0.00	−36.52	0.05	99.30%	10042/24862, prz
	2	0.44	0.18		10042/24847, prf	0.25	−36.79	0.00^d^,^g^,^i (+20.5)^f		10042/24863, pr2
	3	1.04	1.68		10042/24849, prg	1.47	−35.99	2.20		10042/24864, pr3
	4	0.98	1.64		10042/24850, prh	1.07	−36.38	1.87		10042/24867, pr4
(S,S) [syn]	1	3.75	4.60	0.05%	10042/24859, prt	1.57	−38.93	3.04	0.68%	10042/24875, psf
	2	3.99	4.59		10042/24860, prv	1.73	−39.06	2.97^j		10042/24877, psg
	3	4.67	6.34		10042/24861, prw	2.70	−38.75	4.78		10042/24876, psh
	4	4.35	6.00		10042/24866, prx	1.96	−39.19	4.27		10042/24878, psj
(R,R) [ent-syn]	1	5.73	6.96	0.01%	10042/24855, prp	5.24	−37.11	7.05	0.01%	10042/24871, pr9
	2	3.99	5.43		10042/24857, prq	3.19	−37.56	5.14		10042/24872, psb
	3	6.16	7.72		10042/24856, prr	5.87	−37.08	7.59		10042/24873, psc
	4	4.70	6.31		10042/24858, prs	4.30	−37.22	5.93		10042/24874, psd
(R,S) [ent-anti]	1	7.34	7.51	0.00%	10042/24851, prj	7.51	−36.32	7.14	0.01%	10042/24868, pr5
	2	5.43	6.15		10042/24852, prk	5.35	−36.54	5.38		10042/24865, pr6
	3	8.06	7.78		10042/24853, prm	8.36	−36.24	7.88 (7.72)^e [8.11]^h		10042/24869, pr7
	4	6.19	6.52		10042/24854, prn	6.43	−36.44	5.81		10042/24870, pr8

---

Table 4 Calculated transition state properties for R = ⁱPr (Scheme 2)

Transition state		B3LYP/TZVP/SCRF=DMSO				B3LYP+D3/TZVP/SCRF=DMSO
Isomer	Conf.	ΔE^a	ΔΔG298^a	Pop.	DOI^b	ΔE^a	D3^c	ΔΔG298^a	Pop.	DOI^b
a kcal mol^−1. b Persistent (persistent-object-identifiers) for digital repository entry. c Grimme's D3 dispersion correction,^17 in kcal mol^−1. An interactive version of this table is archived at DOI: qcd.
(S,S) [anti]	1	0.00	0.00	100.00%	10042/24880, psq	0.00	−35.89	0.00	99.99%	10042/24895, ps9
	2	0.41	0.24		10042/24881, psr	0.19	−36.13	0.38		10042/24896, ptb
	3	0.75	0.32		10042/24882, pss	1.20	−35.41	0.59		10042/24898, ptc
	4	0.66	0.46		10042/24883, pst	0.70	−35.81	0.62		10042/25980, ptd
(S,R) [syn]	1	6.11	6.66	0.00%	10042/24891, ps5	4.99	−37.06	5.60	0.01%	10042/24906, ptp
	2	6.49	6.69		10042/24892, ps6	5.40	−37.10	5.59		10042/24908, ptq
	3	7.35	8.34		10042/24893, ps7	6.16	−37.11	7.08		10042/24907, ptr
	4	7.24	8.00		10042/24894, ps8	5.88	−37.31	6.92		10042/24909, pts
(R,S) [ent-syn]	1	7.71	8.36	0.00%	10042/24887, psz	8.56	−35.02	9.32	0.00%	10042/24902, ptj
	2	6.18	6.85		10042/24889, ps2	6.70	−35.42	7.39		10042/24903, ptk
	3	7.81	9.18		10042/24888, ps3	8.48	−35.18	9.77		10042/24904, ptm
	4	6.51	7.59		10042/24890, ps4	6.89	−35.54	8.08		10042/24905, ptn
(R,R) [ent-anti]	1	—	—	0.00%	—	—	—	—	0.00%	—
	2	6.77	7.06		10042/24884, psv	6.27	−36.48	6.96		10042/24899, ptf
	3	8.68	8.12		10042/24885, psw	8.63	−35.95	8.56		10042/24900, ptg
	4	6.55	6.55		10042/24886, psx	6.23	−36.24	6.41		10042/24901, pth

---

Fig. 2 Computed selected bond lengths at B3LYP+D3/TZVP/SCRF=DMSO for (a) R = ⁱPr conformation 1 (Scheme 3) in Å (original Houk–List values) and (b) R = Ph conformation 2 (original Houk–List values at the B3LYP/6-31G* level) [MP2(FC)//6-31G(d,p)/SCRF = DMSO], {ωB97XD/TZVP/SCRF=DMSO}.

An intrinsic reaction coordinate for R = Ph and R = ⁱPr computed at B3LYP+D3/TZVP/SCRF=DMSO (Fig. 3) shows C–C bond formation is synchronous in both cases with proton transfer. There is no sign of what Cremer²⁹ has referred to as a hidden intermediate, the frustrated formation of a minimum sandwiched between C–C bond formation and proton transfer.

Fig. 3 Computed intrinsic reaction coordinate (IRC) at the reference B3LYP/TZVP+D3/SCRF=DMSO level for (a) R = Ph, (b) R = ⁱPr. The corresponding digital repository identifiers are DOI: n46 and n45.

Energies resulting from the more complete conformational exploration are set out in Table 3 for R = Ph and in Table 4 for R = ⁱPr. These results include the effects of the D3-dispersion correction on the computed relative energies, the total superposition error for this correction ranging from −36 to −39 kcal mol⁻¹. Both the magnitude, and in particular the variation (∼3 kcal mol⁻¹), may come as a surprise, since the accepted wisdom tends to the belief that such corrections are only significant for much larger systems.

For both the R = ⁱPr and R = Ph systems, inclusion of D3 corrections results in an increase in the planarity of the enamine. Examining the enamine geometries for R = Ph, two clear trends appear; the enamine nitrogen is significantly (by 5 to 10°) less planar in the enantiomer, (R,R) and (R,S), conformations than compared to the (S,R) and (S,S) conformations. In addition, enamine planarity is loosely correlated to relative stability; the lowest energy structure has the most planar enamine and vice versa. The lowest energy structure, (S,R) conformation 2, has an almost totally planar enamine (177.2°) whereas the highest energy structure, (R,S) conformation 3, is highly pyramidalised (167.0°).

The results for R = Ph fully confirm the earlier conclusion that the (S,R) stereoisomer is the dominant species formed; the nearest alternative stereoisomer is conformation 2 of the (S,S) form, which emerges as 4.59 kcal mol⁻¹ higher in free energy using B3LYP/TZVP/SCRF=DMSO without dispersion correction, but the difference is reduced to 2.97 kcal mol⁻¹ at this basis if the D3 correction is included in the procedure. Overall, we see that inclusion of D3 corrections for this system tends to decrease the predicted enantioselectivity for this model, down to 98.6% ee from effectively 100%, without dispersion.

We also recalculated the transition states for the most important pair (R = Ph, conformation 2, (S,R), (S,S)) at the very large QZVP basis, resulting in an increase in the number of basis functions from 556 to 1944. The time taken for the DFT calculation scales as ∼N³–N⁴ (N = number of basis functions), an increase of ∼100 fold, making the use of such a large basis an impractical approach for general mechanistic exploration. ΔΔG^‡₂₉₈ increases slightly from 2.97 to 3.27 kcal mol⁻¹ (Table 3), a result that might be assumed to be close to the complete basis set (CBS) limit. This result is nevertheless still at odds with the reported apparent experimental diasteromeric ratio of between 1 : 1 and 4 : 1 (ΔΔG^‡₂₉₈ < 0.8 kcal mol⁻¹) but as we note in the introduction, the experimental value may be sensitive to both water content and temperature. Similar conclusions can be drawn for R = ⁱPr (Table 4).

The maximum difference in energy between the lowest energy conformer of the (S,R) form and the highest energy conformer of the least stable diastereomer (R,S) is 7.88 kcal mol⁻¹ (B3LYP+D3/TZVP), 7.72 kcal mol⁻¹ (ωB97XD/TZVP, which includes an implicit D2-dispersion correction) and 8.11 kcal mol⁻¹ (MP2/6-31G(d,p); it proved impractical to use the larger TZVP basis for this calculation), a result which is gratifyingly not overly sensitive to the method used.

Non-covalent interactions

In general terms, stereoselectivity is controlled by a combination of stereoelectronically-induced bond orientations in the transition state, but influenced by non-bonded weak interactions within the framework. Although the balance of these latter interactions can be difficult to compute from total energies alone, it has been recently shown³⁰ that the reduced density gradient (RDG) can be used to reveal the interactions that are present in the system (see ref. 28 for more details on the method).

This index enables the identification and characterization of weak interactions of various strengths as chemically intuitive RDG isosurfaces that reveal both stabilizing (hydrogen-bonding interactions in blue, van der Waals interactions in green) and destabilizing interactions (steric clashes in red, and weaker ones to yellow). This approach can be much more effective at revealing the non-bonded interactions present and also provide a more realistic analysis than pure topological indices such as QTAIM.³¹ Thus it represents a semi-quantitative and highly visual manner in which to analyse what is often merely described in a non-quantitative (and often intuitive) manner merely as transition state steric clashes and hydrogen bond/electrostatic attractions.

All NCI figures can be found in the interactive versions of Tables 2 and 3. In order to highlight certain features, three representative examples from the R = Ph reaction have been chosen. Fig. 4 dissects the diastereoisomer with the highest energy (ent-anti), the diastereoisomer with the lowest energy (anti) and the diastereoisomer with the highest dispersion correction (syn). The cutoff (ρ = 0.1 a.u.) has been chosen to isolate the purely non covalent interactions along with the C–C formation. At first glance, both the anti and the syn conformers show a greater RDG surface, which confirms the role of non-covalent interactions in stabilizing the diastereoisomeric transition states. For a more detailed analysis, the most relevant interactions have been highlighted in Fig. 4. The deep blue feature corresponds in all three cases to the forming C–C bond. It corresponds to a mid-range interaction, in-between covalent and non-covalent. Along with the C–C formation, two purely non-covalent regions appear:

Fig. 4 NCI analysis of several conformers of the computed transition state: (a) the lowest energy isomer, (b) the highest energy isomer (c) the highest D3 correction isomer (Table 3). The gradient isosurfaces (s = 0.5 a.u.) are colored on a BGR scale according to the sign (λ₂)ρ over the range −0.03 to 0.03 a.u.

1. The region of around the heteroatoms (C=O⋯N) shows stabilizing features in all the conformers. This feature is most important in the anti and syn conformers, whereas it is much weaker in the ent-anti and ent-syn ones. This 3D view coincides with previous approaches, which locate the relevance in the NCH^δ+⋯O^δ− interaction. However, along with the electrostatic interactions, green dispersive interactions appear elongating the NCI feature (see for example Fig. 4b) which highlight the importance of the planarity of this region (highlighted by the distances in Table 3) and which cannot be merely explained by electrostatics.

2. An extra region appears in the syn conformer (Fig. 3c), a green surface between the proline and the R = Ph group. This interaction can be identified as tilted T-shape interaction or as a π-facial hydrogen bond (a figure for such interactions is provided in the ESI† for reference). It is important to note that this new interaction, which stabilizes the syn conformers, had not been identified before by mere geometric inspection. However, its presence enables us to explain the fact that the syn conformers are the ones with the greatest dispersion correction (Table 3).

Thus, a combination of NCH^δ+⋯O^δ− electrostatics and dispersion (either in the NCH^δ+⋯O^δ− or T-shape/π-facial H-bond in the ring region) determine the outcome of the reaction, with only anti and syn as observable diastereoisomers (see the ESI† for a more detailed analysis). It should be noted that this balance of electrostatic and dispersive interactions highlights, once again, the necessity to include dispersion effects in the calculations, else the correct energetics and geometries would not be obtained.^32,33

Kinetic isotope effects

The utility of having a computed force constant model for the transition state is that it can yield kinetic isotope effects for the reaction.³⁴ For example, Meyer, Houk, and co-workers experimentally and computationally investigated ¹³C KIEs for the Hajos–Parish–Eder–Sauer–Wiechert reaction, suggesting that the rate determining step of the proline-mediated intramolecular aldol reaction occurs prior to C–C bond formation.³⁵ In contrast, for the proline-mediated intermolecular aldol reaction between acetone and o-chlorobenzaldehyde, Armstrong, Blackmond, and co-workers reported a normal isotope effect of k^H/k^D = 1.93–2.26 when using acetone-d₆.³⁶ Previous kinetic investigations of the reaction had led the researchers to expect an inverse isotope effect. The observation of a small, normal isotope effect implied that the final KIE was the result of a balance between normal and inverse isotope effects resulting respectively from synchronous proton transfer and C–C bond formation involving a change of C-hybridisation from sp². This implies that such isotope effects are indeed a sensitive measure of how realistic a computed transition state is. Computational modelling at the original Houk–List level of B3LYP/6-31G(d)/SCRF=DMSO level of theory had predicted a KIE of 1.97, thus offering further support for this hypothesis. This evidence also allowed the reasonable inference that nucleophilic addition of the enamine to the electrophile was indeed the rate determining step of the catalytic cycle by kinetic investigations, a process aided by a more or less synchronous proton transfer to the carbonyl oxygen from the carboxyl proton.

We felt it important to establish that the various corrections described above retain this behaviour. We report calculated KIEs (Table 5) for the proline-mediated intermolecular aldol reaction between cyclohexanone and benzaldehyde and also the acetone and m-chloro-benzaldehyde system for which previously measured values had been reported.³⁶ The calculations have been performed using the lowest energy transition states, as established in the previous section. The predicted isotope effects again reflect the synchronous nature of the reaction revealed by the IRC for R = Ph, exhibiting normal deuterium and carbon effects and a small inverse oxygen effect (R = Ph). The calculated isotope effects for the enamine formed from proline and acetone reacting with m-chloro-benzaldehyde in acetone-d₆ as solvent are more complex, since deuterium is incorporated into three distinct locations. Thus, the observed effect is a composite of a primary hydrogen KIE originating from the proton transfer and an inverse one originating from the isotope attached at the carbon forming the C–C bond. The agreement between experiment and theory is if anything even more congruent.

Table 5 Calculated^a kinetic isotope effects at 298 K, R = Ph

R	k ^H/k^D	k ^12C/k^13C=O	k ^12C/k^13C=C	k ^16O/k^18O=C
a B3LYP+D3/TZVP/SCRF=DMSO, derived from the thermally corrected free energy ΔG298 based on harmonic uncorrected frequencies, with appropriate isotope masses. b Reactant DOI: pn6. c d1 on OH. d d4 on OH and the three C–H groups on the cyclohexanone-derived enamine. e Reactant DOI: pn7. f Values for proton relay mechanism involving an additional water molecule. g d6 on OH and the five C–H groups on the acetone-derived enamine. h Reactant DOI: pn8. i Reactant DOI: ppb, transition state DOI: pn9 for the system reported in ref. 34.
Ph^b	4.37^c (3.01)^d	1.019	1.007	0.993
Ph^e^,^f	1.18^c	1.043	1.027	1.019
^iPr^h	4.05^c	1.026	1.0096	1.005
m-Cl-Ph^i	2.11 [1.93–2.26]^g	—

---

Passive explicit solvation

Patil and Sunoj have computationally investigated the role of explicit solvent molecules in the modeling of the proline-mediated conjugate addition reaction in polar protic solvents, at the mPW1PW91/6-31G(d) and B3LYP/6-31G(d) levels of theory.¹⁰ The researchers proposed, that only via the explicit inclusion of two methanol molecules in a cooperative hydrogen-bonding network between the carboxylic acid proton and the oxygen atoms of a nitro group, could the correct stereochemical outcome of the reaction be predicted. This study however is based on the use of total calculated energies for transition states, rather than the more correct thermal and entropy-corrected relative free energies for the reaction profile. In addition to molecules of solvent, additives such as triethylamine⁹ and DBU³⁷ have been shown to play an important role in determining the selectivity of proline-mediated reactions through their explicit inclusion in transition state calculations.

Here, we investigate not the role of additive but that of water in the Houk–List transition state. The first step of the catalytic cycle, which involves the formation of an enamine from the carbonyl compound and proline, liberates one water molecule. Potentially, this water could then participate in the subsequent reaction. Here, a single water molecule is introduced into the Houk–List model (R = Ph) as a passive solvent for one of the three oxygens via a hydrogen bond, augmenting the continuum solvation already applied. The effect this has on the relative energies of the anti and syn diastereomeric transition states is shown in Table 6. Addition of one explicit water molecule to the model was computed to induce only a small change in the computed free energy difference between (S,R) and (S,S) stereoselectivity, changing it from 2.97 to 3.15 kcal mol⁻¹. Models which include more water molecules were not studied, not least because the stochastic complexity increases rapidly.

Table 6 Passive explicit solvation of the Houk–List transition state, R = Ph^a

Transition state		B3LYP+D3/TZVP/SCRF=DMSO
Isomer	Conformation^d	ΔE^b	ΔΔG298^b	Pop.	DOI^c
a Model comprising one additional water molecule, hydrogen bonding in various locations. b kcal mol^−1. c Persistent identifier for digital repository entry. d As defined in Scheme 3. An interactive version of this table is archived at DOI: qcs.
(S,R) [anti]	1 (2)	0.37	1.08	99.31%	10042/25146, pk9
	1 (3)	0.22	0.00		10042/25147, pmb
	2 (1)	0.00	2.29		10042/25148, pmc
	2 (2)	0.72	1.55		10042/25149, pmd
	2 (3)	0.48	0.18		10042/25150, pmf
(S,S) [syn]	1 (1)	1.53	4.62	0.69%	10042/25151, pmg
	1 (2)	1.22	3.52		10042/25818, pmh
	1 (3)	1.65	3.74		10042/25152, pmj
	2 (1)	1.53	3.77		10042/25153, pmk
	2 (2)	1.50	3.58		10042/25154, pmm
	2 (3)	1.87	3.15		10042/25819, pmn

---

Proton relay mechanisms

Beyond a passive role, it is possible that a single molecule of water could participate directly in the Houk–List mechanism, acting as an active proton transfer relay between the proline carboxylic acid group and the incoming aldehyde (R = Ph) (Table 7). This results in the expansion of the ring size of the cyclic model by two atoms, thus allowing some stereochemical models previously excluded on the basis of strain to be included. Proton relay mechanisms in organocatalysis have precedent. One of the initial mechanistic proposals for the intermolecular aldol reaction, the HPESW reaction, involved a second molecule of proline acting as a proton transfer agent during C–C bond formation, based on the apparent observation of a non-linear effect.³⁸ This proposal was later discredited through experimental studies confirming the absence of non-linear effects in the proline-mediated aldol reactions.^4,39 Patil and Sunoj have also investigated the role of a proton-relay mechanism in hemiacetal-, iminium, and enamine formation for a model system mimicking the first step in the catalytic cycle of proline catalysis, at the mPW1PW91/6-31G(d) level of theory.⁴⁰ It was found that protic additives, such as methanol, allow for significantly lower activation energies of these pathways. The reported energies did not include the effects of entropy, which would be expected to result in significantly higher free energies of activation compared to those based on total energies alone. Here we present computed free energy differences for the proton relay mechanism, precisely isomeric with the passive mechanism described in the previous section.

Table 7 Proton relay mechanism, R = Ph^a

Transition state		B3LYP+D3/TZVP/SCRF=DMSO
Isomer	Conf.^d	ΔE^b	ΔΔG298^b	Pop.	DOI^c
a Based on conformations derived from the transition states described in Tables 1–4. b kcal mol^−1. c Persistent identifier for digital repository entry. d As defined in the ESI;† see DOI: rdp An interactive version of this table is archived at DOI: qc3.
(S,R) [anti]	1	3.79	5.15	23.03%	10042/25820, pp7
	2	4.21	3.65		10042/25821, pp8
	4	1.55	2.58		10042/25165, pp9
	5	0.03	0.69		10042/25155, pqb
	6	0.18	0.58		10042/25156, pqc
	7	2.88	3.43		10042/25822, pqd
	8	3.68	3.45		10042/25823, pqf
	9	2.85	3.12		10042/25166, pqg
	10	2.43	2.80		10042/25171, pqh
	11	2.70	3.95		10042/25167, pqj
	12	2.83	4.03		10042/25169, pqk
	13	2.15	3.96		10042/25172, pqm
(S,S) [syn]	1	4.78	6.26	76.97%	10042/25168, pqn
	2	3.65	3.56		10042/25170, pqp
	3	0.08	0.27		10042/25157, pqq
	4	0.00	1.06		10042/25158, pqr
	5	0.08	0.00		10042/25159, pqs
	6	0.95	0.93		10042/25173, pqt
	7	1.49	1.33		10042/25824, pqv
	8	2.56	2.56		10042/25825, pqw
	9	3.84	5.73		10042/25826, pqx
	10	3.00	4.90		10042/25827, pqz
	11	1.07	2.22		10042/25828, pq2
	12	0.36	1.42		10042/25832, pq3
	13	0.44	0.98		10042/25160, pq4

---

Four features are noteworthy.

1. The (S,S) diastereomer is now predicted as slightly lower in free energy than the observed (S,R) products.

2. The lowest free-energy for a proton-relay transition state is nevertheless 9.1 kcal mol⁻¹ higher than that of the passively solvated isomer. Because proton transfer reactions in particular can depend on the nature of the density functional used, we also evaluated this energy difference at the ωB97XD/TZVP level. The free energy difference of 6.4 kcal mol⁻¹ is smaller than using B3LYP+D3, but still clearly excludes the involvement of water in the proton-relay. This model would also predict the incorrect stereochemical outcome; it may not always be so, of course, for other mechanistic variations.

3. The intrinsic reaction coordinate (B3LYP+D3/TZVP/SCRF=DMSO, Fig. 5) indicates that the presence of the proton relay delays C–C bond formation; its length at the transition state is now a much shorter 1.920 Å (compared to 2.273 Å without such intervention). Only after this transition state is passed does the proton transfer commence. At a value of the IRC indicated with an arrow (Fig. 5b), C–C bond formation is largely complete (1.676 Å) and a so-called hidden intermediate is revealed in which a strong symmetric hydrogen bond between the proton relay and the carbonyl group manifests. The significance of detecting such intermediates is that the electronic influences at this geometry could be potentially targeted in order to induce the system to form a real intermediate; the relative timing of e.g. C–C bond formation and proton-relays can therefore be seen as a function of structure and substituents. This feature of a potential energy surface is relatively insensitive to e.g. the density functional procedure employed. Shown in Fig. 5c is the same reaction charted using the ωB97XD functional; the hidden intermediate occurs at the position in the IRC, but its profile is stronger (the gradient norm approaches zero more closely than with the B3LYP functional).

Fig. 5 The computed intrinsic reaction coordinate for the proton-relay mechanism for R = Ph @B3LYP+D3/TZVP/SCRF=DMSO, showing (a) the relative energy and (b) the gradient norm. The red arrow indicates the location of the hidden intermediate. The calculation is archived at DOI: n44. (c) The IRC recomputed at @ωB97XD/TZVP/SCRF=DMSO showing the gradient norm and the more prominent hidden intermediate. The calculation is archived at DOI: n43.

4. The kinetic isotope effects computed for this mechanism (Table 5) are very different from the one involving no intervention by water.

We therefore consider it unlikely that an explicit water molecule is actively involved in the rate-determining step for this reaction.

Hajos–Parrish mechanism

This mechanistic variation proposed by Hajos and Parrish⁴¹ for the intramolecular aldol reaction involves an initial proton transfer from the carboxyl group to the nitrogen of the enamine to form a zwitterion. This species can then react to form a C–C bond directly via a 6-membered ring transition state, accompanied by proton transfer from N to the carbonyl oxygen (Fig. 6a). The computed reaction IRC again reveals an entirely synchronous process, with C–C bond formation coincident with proton transfer. The free energy however (Table 3) is 20.5 kcal mol⁻¹ higher than the isomeric Houk–List model.

Fig. 6 Hajos–Parrish mechanism, R = Ph (see Table 2) showing (a) the computed B3LYP+D3/TZVP/SCRF=DMSO geometry, (b) the IRC energy profile and (c) the IRC gradient norm, DOI: n5d (d) the IRC energy profile for the Hajos–Parrish mechanism, R = Ph with inclusion of one water molecule acting as a proton relay and (e) the IRC gradient norm for the proton-relay mechanism, with hidden intermediates indicated with an arrow, DOI: n5n.

Interestingly, augmentation of the Hajos and Parrish variation with a proton-relay via a water molecule results in the reaction proceeding via the Seebach–Eschenmoser model.⁴² Here, the carboxylic acid is not acting as a directing group, as in the Houk–List model, but rather participates directly in the addition step as an enamine carboxylate, which is the proposed key reactive intermediate. In this mechanism, approach of the electrophile occurs on the opposite face of the pyrrolidine ring to the exocyclic carboxylate group, the free carboxylate then aids carbon–carbon bond formation via E2 elimination to the syn enamine, forming the exo-oxazolidinone.

E2 elimination and carbon–carbon bond formation are almost synchronous and these transition states are followed by two hidden intermediates (Fig. 6d and e), transfer of the proton from water to the newly formed alkoxide, accompanied by the final proton transfer from the nitrogen to the hydroxyl. However, this mechanism increases the overall activation energy even further (40.4 kcal mol⁻¹).

As with the proton-relay variation, we can conclude that the Hajos–Parrish variation, via the Houk–List or Seebach–Eschenmoser model, is also not viable for this reaction.

Substituted variations

For R = Ph, there is a 2.27 kcal mol⁻¹ difference in D3 dispersion stabilisation between the lowest energy (S,R) and (S,S) transition states (Table 3), the latter being the greater. This is reflected in a significant reduction in ΔΔG^‡₂₉₈ between (S,R) and (S,S) from +4.59 kcal mol⁻¹ (B3YLP/TZVP/SCRF = DMSO) to +2.97 kcal mol⁻¹ (B3LYP-D3/TZP/SCRF=DMSO). Even a simple visual inspection of the NCI surfaces for these transition states (Table 3) reveals two regions of interaction that are present in the (S,S) transition state, where the phenyl ring lies across the cyclohexene ring, but which are absent from the (S,R) transition state, where the phenyl ring protrudes into space (Fig. 7). The first is a π-facial interaction between the phenyl ring and an axial proton from the “chair” conformation of the cyclohexene ring, coloured as green (weakly stabilising). The second is a hydrogen bonding interaction between the ortho-proton of the phenyl ring and the oxygen of the carboxylic acid, coloured as light blue (moderately stabilising).

Fig. 7 NCI surface of the B3LYP+D3/TZVP/SCRF=DMSO computed transition state for (a) (S,R) R = Ph (conformation 2) (Table 3) and (b) (S,S) R = Ph (conformation 2) (Table 3).

These interactions are likely to contribute to the increased D3-dispersion stabilisation associated with the (S,S) transition state, as D3 correction has been shown to improve the description of weak hydrogen bonds.⁴³ Three models (Fig. 8) were devised to take advantage of these observations.

Fig. 8 Transition states for (a) 4-piperidinone–benzaldehyde–proline, (b) cyclohexanone–pyrrole-2-carboxaldehyde–Proline, (c) acetone–pyrrole-2-carboxaldehyde–proline.

(a) 4-Piperidinone–benzaldehyde–proline. This model aims to maximise the π-facial non-covalent interaction, observed in the syn transition state for R = Ph, between the proton at the 4-position of the cyclohexanone-derived enamine and the face of the aryl ring of the aldehyde.

(b) Cyclohexanone–pyrrole-2-carboxaldehyde–proline. This model aims to maximise the weak hydrogen bonding interaction, observed in the syn transition state for R = Ph, between the ortho-proton of the phenyl ring and the oxygen of the carboxylic acid of the bound catalyst.

(c) Acetone–pyrrole-2-carboxaldehyde–proline. This model aims to maximise the hydrogen bonding interaction, observed in the syn transition state for R = Ph, between the ortho-proton of the phenyl ring and the oxygen of the carboxylic acid of the bound catalyst and uses acetone, instead of cyclohexanone, as a less sterically demanding environment.

The striking feature of all three variations is the difference in the predicted outcome that addition of a dispersion correction has (Table 8). By model (c), with reduced steric congestion, the predicted ratio of the R/S diastereomers has inverted, but only when the dispersion correction is included. This result provides a compelling reason for including such corrections. It also suggests that an inspection of the computed NCI surfaces can give rapid visual clues for designing variations on the basic system. We suggest here that such procedures should be routinely included in protocols for mechanistic exploration.

Table 8 Houk–List Transition state analogues

4-Piperidinone–benzaldehyde–proline
Transition state		B3LYP/TZVP/SCRF=DMSO				B3LYP+D3/TZVP/SCRF=DMSO
Isomer	Conf.^a	ΔE^b	ΔΔG^b	Pop.	DOI^c	ΔE^b	ΔΔG^b	Pop.	DOI^c
a Alternative pyramidalisation of the secondary amine denoted by prime (′). b kcal mol^−1. c Persistent identifier for digital repository entry. An interactive version of this table is archived at DOI: qc4
(S,R) [anti]	1′	0.00	0.05	99.87%	10042/25119, pmp	0.00	0.00	93.82%	10042/25124, pmw
	1	0.58	0.00		10042/25120, pmq	0.35	0.12		10042/25125, pmx
	2	0.94	0.41		10042/25812, pmr	0.54	0.01		10042/25126, pmz
(S,S) [syn]	1′	4.70	5.25	0.12%	10042/25121, pms	3.19	4.36	6.14%	10042/25127, pm2
	1	3.70	4.13		10042/25122, pmt	1.00	1.86		10042/25128, pm3
	2	3.73	4.18		10042/25123, pmv	0.98	1.54		10042/25129, pm4
Cyclohexanone–pyrrole-2-carboxaldehyde–proline
(S,R) [anti]	1	0.00	0.00	98.44%	10042/25135, pm5	1.59	0.00	61.64%	10042/25139, pnf
	2	0.39	0.45		10042/25136, pm6	1.84	0.11		10042/25140, png
(S,S) [syn]	1	0.90	2.45	1.56%	10042/25137, pm7	0.00	0.19	38.36%	10042/25816, pnh
	2	1.54	2.92		10042/25138, pm8	0.59	0.51		10042/25141, pnj
Acetone–pyrrole-2-carboxaldehyde–proline
R	1	0.32	0.00	98.14%	10042/25130, pm9	2.41	0.34	47.04%	10042/25815, pnk
	2	0.00	0.17		10042/25131, pnb	1.83	0.10		10042/25133, pnm
S	1	0.75	2.52	1.86%	10042/25813, pnc	0.57	0.32	52.96%	10042/25132, pnn
	2	0.57	2.35		10042/25814, pnd	0.00	0.00		10042/25134, pnp

---

Computational procedures

The Gaussian 09 program, revision D.01 was used for all calculations excepting the BSSE evaluation, where ORCA 2.9.1 was employed, and thermal corrections were applied based on computed normal vibrational frequencies. Solvation models were using the polarizable conductor calculation model (CPCM) using smoothed reaction cavities, the geometries fully optimised, and vibrational frequencies at this geometry used to correct for thermal energies and entropy. Kinetic isotope effects were computed from the difference in thermally corrected free energies obtained from the calculated Hessian (force constant) matrix and appropriate atomic masses for the isotopes. Intrinsic reaction coordinate (IRC) evaluations were obtained using the following keyword in the Gaussian program: irc(calcfc,recalc=10,maxpoints=200,maxcycle=40,tight,cartesian,stepsize=7,lqa) (the outcome of such calculations can be very sensitive to the imposed parameters). All calculations were routinely archived in both of two digital repositories (DSpace-SPECTRa and Figshare) and assigned a digital-object-identifier (DOI). Some DOIs were contracted to a shorter form using the resource http://shortDOI.org/ NCI (non-covalent-interactions) were computed using the methodology previously described.^30,31 For NCI figures in tables, a Gaussian cube of the computed electron density at fine resolution was computed and converted to an NCI analysis using the resource at DOI: n5b, which is based on using the Jmol applet. The output of this process comprises a coordinate file (.xyz) and a compressed isosurface (.jvxl), which are visualised using Jmol or JSmol embedded in the interactive version of the table. For Fig. 4, data were obtained with the NCIPLOT program.⁴⁴ A density cutoff of ρ = 0.1 a.u. was applied and the pictures were created for an isosurface value of s = 0.5 and colored in the [−0.03,0.03] a.u. sign (λ₂)ρ range. Integrations described in the ESI† were carried out with an in-house program for cubic grids with a 0.1 a.u. increments along each side and re-scaled with respect to the total cube volume. Each data table or data figure is assigned a DOI in the Figshare repository (see footnotes), all retrievable as e.g.qd8. A 3D printable full-colour model of the lowest energy transition state for R = Ph can be obtained at http://shpws.me/pstF.

Conclusions

Computational modelling of the stereochemical outcome of catalysed solution-phase reactions has a stringent criterion for accuracy, defined in a sense by the equation ΔΔG^‡ = −RT ln K. The predicted relative transition state energy, ΔΔG^‡, has to be sufficiently accurate to result in reliable values for K, the ratio of the concentrations of two stereoisomers. In practice, this means achieving a computed accuracy for ΔΔG^‡ of <1 kcal mol⁻¹ or less for values of ΔΔG^‡ of between 2 and 5 kcal mol⁻¹. The lower limit here is typical of moderately stereoselective reactions and the latter is towards the top end of the most highly stereoselective reactions known. To do so will require a reasonable exploration of conformational space, and mechanistic variations such as implicit passive solvation, and active proton-relay interventions, and this all to be achieved using methodology which can be implemented with reasonable time-turnover on modern computational resources. We have tested an updated methodology to that used in establishing the original Houk–List model for the intermolecular aldol condensation catalysed by proline. A triple-ζ quality basis set is required to remove significant basis set superposition errors associated with the smaller 6-31G(d) basis set, coupled with a dispersion energy correction to the B3LYP functional. Alternatively, more modern functionals which already include such terms can be used. The solvation treatment now possible is both more accurate and more self-consistent, since thermal corrections to the free energy are evaluated from frequencies determined within the solvation model. It is possible to explore more conformational space for the basic reaction, and to augment the mechanism with either passive or explicit intervention of small molecules such as water.

Whilst routinely achieving accuracies in ΔΔG^‡ of <1 kcal mol⁻¹ is perhaps not entirely achievable at present, it surely will be in just a few years' time, as the density functionals and other methodologies continue to improve. Here progress may be hindered by the relative lack of accurate experimental data determined under standard kinetic conditions. Achieving a stochastic exploration of the mechanism using molecular dynamics is perhaps rather further off for these relatively complex mechanisms.

Acknowledgements

This work was supported in part by the French state funds managed by CALSIMLAB and the ANR within the Investissements d'Avenir program under reference ANR-11-IDEX-0004-02.

Notes and references

1. P. H. Cheong, C. Y. Legault, J. M. Um, N. Çelebi-Ölçüm and K. N. Houk, Chem. Rev., 2011, 111, 5042–5137.
2. S. Bahmanyar, K. N. Houk, H. J. Martin and B. List, J. Am. Chem. Soc., 2003, 125, 2475–2479.
3. L. Hoang, S. Bahmanyar, K. N. Houk and B. List, J. Am. Chem. Soc., 2003, 125, 16–17.
4. S. Bahmanyar and K. N. Houk, Org. Lett., 2003, 5, 1249–1251.
5. S. Bahmanyar and K. N. Houk, J. Am. Chem. Soc., 2001, 123, 11273–11283.
6. S. Bahmanyar and K. N. Houk, J. Am. Chem. Soc., 2001, 123, 12911–12912.
7. A. Armstrong, Y. Bhonoah and A. J. P. White, J. Org. Chem., 2009, 74, 5041–5048.
8. A. Fu, B. List and W. Thiel, J. Org. Chem., 2006, 71, 320–326.
9. M. P. Patil and R. B. Sunoj, Chem.–Eur. J., 2008, 14, 10472–10485.
10. K. N. Houk, P. H. Y. Cheong, J. S. Warrier and S. Hanessian, Adv. Synth. Catal., 2004, 346, 1111–1115.
11. Shinisha and R. B. Sunoj, Org. Biomol. Chem., 2007, 5, 1287–1294.
12. S. Mitsumori, H. Zhang, P. Ha-Yeon Cheong, K. N. Houk, F. Tanaka and C. F. Barbas 3rd, J. Am. Chem. Soc., 2006, 128, 1040–1041.
13. S. M. Bachrach, Computational Organic Chemistry, Wiley-Interscience, 2007, p. 337, See also ref. 1, p. 5051.
14. L. Simon and J. M. Goodman, Org. Biomol. Chem., 2011, 9, 689–700.
15. M. Korth and S. Grimme, J. Chem. Theory Comput., 2009, 5, 993–1003.
16. L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688.
17. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154119 , reviewed by S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228.
18. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
19. V. C. Gibson, E. L. Marshall and H. S. Rzepa, J. Am. Chem. Soc., 2005, 127, 6048–6051.
20. S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–556.
21. G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110–14115; D. M. York and M. J. Karplus, Phys. Chem. A, 1999, 103, 11060–11079.
22. J. Kong, P. v. R. Schleyer and H. S. Rzepa, J. Org. Chem., 2010, 75, 5164–5169.
23. J. A. Townsend, J. Downing, M. J. Harvey, P. B. Morgan, P. Murray-Rust, H. S. Rzepa, D. C. Stewart and A. P. Tonge, SPECTRa-T: Machine-based data extraction and semantic searching of chemistry e-theses, J. Chem. Inf. Model., 2010, 50, 251–261.
24. H. S. Rzepa, Emancipating data, Chemistry World, 2013. See http://www.rsc.org/chemistryworld/2013/09/open-repository-data-sharing-rzepa-figshare and http://www.force11.org/AmsterdamManifesto and the Data%20Citation%20Synthesis%20group.
25. The original code was Gaussian 98. We employed Gaussian 09, Revision D.01, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009.
26. H. Kruse, L. Goerigk and S. Grimme, J. Org. Chem., 2012, 77, 10824–10834.
27. F. Neese, The ORCA Program System, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78,  DOI:10.1002/wcms.81 and http://cec.mpg.de/forum/.
28. S. Ehrlich, H. F. Bettinger and S. Grimme, Angew. Chem., Int. Ed., 2013, 41, 10892–10895.
29. D. Cremer and E. Kraka, Acc. Chem. Res., 2010, 43, 591–601.
30. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
31. J. R. Lane, J. Contreras-García, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266.
32. T. Schwabe, R. Huenerbein and S. Grimme, Synlett, 2010, 1431–1441.
33. T. Hemery, R. Huenerbein, R. Frohlich, S. Grimme and D. Hoppe, J. Org. Chem., 2010, 75, 5716–5720.
34. See for example the use of KIE in resolving the mechanism of the benzidine rearrangement, W. Subotkowski, L. Kupczyk-Subotkowska and H. J. Shine, J. Am. Chem. Soc., 1993, 115, 5073–5076 and similarly for the epoxidation of ethene by peracid; T. Koerner, H. Slebocka-Tilk and R. S. Brown, J. Org. Chem., 1999, 64, 196–201.
35. H. Zhu, F. R. Clemente, K. N. Houk and M. P. Meyer, J. Am. Chem. Soc., 2009, 131, 1632–1633.
36. N. Zotova, L. J. Broadbelt, A. Armstrong and D. G. Blackmond, Bioorg. Med. Chem. Lett., 2009, 19, 3934–3937.
37. J. E. Hein, J. Bures, Y. H. Lam, M. Hughes, K. N. Houk, A. Armstrong and D. G. Blackmond, Org. Lett., 2011, 13, 5644–5647.
38. O. S. Puchot, E. Dunach, S. Zhao, C. Agami and H. B. Kagan, J. Am. Chem. Soc., 1986, 108, 2353–2357; C. Agami, J. Levisalles and C. J. Puchot, J. Chem. Soc., Chem. Commun., 1985, 441–442.
39. M. Klussmann, S. R. Mathew, H. Iwamura, D. H. Wells, A. Armstrong and D. G. Blackmond, Angew. Chem., Int. Ed., 2006, 45, 7989–7992; U. Pandya, A. Armstrong and D. G. Blackmond, Nature, 2006, 441, 621–623.
40. M. P. Patil and R. B. Sunoj, J. Org. Chem., 2007, 72, 8202–8215.
41. Z. G. Hajos and D. R. Parrish, J. Org. Chem., 1974, 39, 1615–1621 and discussed in Section 2.1 of ref. 1.
42. D. Seebach, A. K. Beck, D. M. Badine, M. Limbach, A. Eschenmoser, A. M. Treasurywala, R. Hobi, W. Prikoszovich and B. Linder, Helv. Chim. Acta, 2007, 90, 425–471.
43. W. Hujo and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 13942–13950.
44. J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.

---

Footnote

† Electronic supplementary information (ESI) available: An NCI figure along with a detailed analysis of the NCI interactions and their relationship to the D3 correction. See DOI: 10.1039/c3sc53416b

---