Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A catalytic role for methionine revealed by a combination of computation and experiments on phosphite dehydrogenase†
Kara E.
Ranaghan
ab,
John E.
Hung
c,
Gail J.
Bartlett
b,
Tiddo J.
Mooibroek
b,
Jeremy N.
Harvey
ab,
Derek N.
Woolfson
bd,
Wilfred A.
van der Donk
*c and
Adrian J.
Mulholland
*ab
aCentre for Computational Chemistry, School of Chemistry, University of Bristol, Bristol, BS8 1TS, UK
bSchool of Chemistry, University of Bristol, Bristol, BS8 1TS, UK. E-mail: Adrian.Mulholland@bristol.ac.uk
cDepartment of Chemistry and The Howard Hughes Medical Institute, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA. E-mail: vddonk@illinois.edu
dSchool of Biochemistry, Medical Sciences, University of Bristol, Bristol, BS8 1TD, UK
First published on 18th February 2014
Abstract
Combined quantum mechanics/molecular mechanics (QM/MM) simulations of the reaction catalysed by phosphite dehydrogenase (PTDH) identify Met53 as important for catalysis. This catalytic role is verified by experiments (including replacement by norleucine and selenomethionine), which show that mutation of this residue significantly affects kcat, without changing KM for phosphite. QM/MM and ab initio QM calculations show that the catalytic effect is electrostatic in nature. The side chain of Met53 specifically stabilizes the transition state for the hydride transfer step of the reaction catalysed by PTDH, forming a ‘face-on’ interaction with His292. To our knowledge, a defined catalytic role for methionine in an enzyme (as opposed to a steric or binding effect, or interaction with a metal ion) has not previously been identified. Analyses of the Protein Data Bank and Cambridge Structural Database indicate that this type of interaction may be relatively widespread, with implications for enzyme-catalysed reaction mechanisms and protein structure.
Introduction
Phosphite dehydrogenase (PTDH) catalyses the oxidation of phosphite (the widely used name for hydrogen phosphonate) to phosphate with the concurrent reduction of nicotinamide adenine dinucleotide (NAD+) to NADH.1 PTDH, originally isolated from the Gram negative bacterium Pseudomonas stutzeri (strain WM88), is useful for the regeneration of a catalytic pool of NADH,2 with applications in biotechnology and biocatalysis. Mutants have been developed with increased thermostability and catalytic activity, and reduced cofactor specificity, allowing the enzyme to use the phosphorylated form of NAD+, NADP+.3–5 The unusual reaction catalysed by PTDH involves a nucleophilic attack by water or hydroxide on phosphite, with direct displacement of a hydride leaving group to NAD+ (Fig. 1).6 Experiments have identified several residues that are probably involved in catalysis.5,7,8 Kinetic isotope effect (KIE) and pre-steady state measurements show that hydride transfer is fully rate-limiting for the reaction.9 Despite extensive experimental effort, many details about the reaction remain unclear, including the identity of the catalytic base that deprotonates water and the transition state structure of the phosphoryl transfer. His292 (in P. stutzeri) is an obvious candidate for the catalytic base in PTDH; however, phosphite would in that case have to bind in a monoprotonated state to explain the bell-shaped pH-rate profile for kcat/KM (phosphite).10 Such a ‘reverse protonation’ scenario where a group with a lower pKa (monoprotonated phosphite) is protonated and a group with a higher pKa (imidazolium of His292) is deprotonated is unusual but could account for the relatively low activity of the enzyme because only a small fraction of the phosphite and enzyme would be in the required protonation states at the optimal pH of 7.25.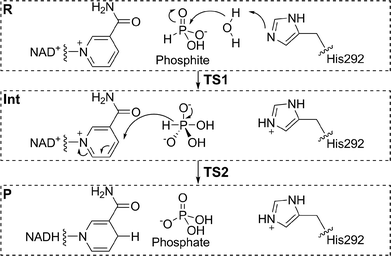 | ||
| Fig. 1 An associative mechanism, as modelled here, for the nucleophilic displacement reaction catalysed by PTDH, with His292 as the base.1 R = reactant state, Int = pentavalent intermediate, P = product. TS1 and TS2 are the transition states for the first and second steps. | ||
A crystal structure of a thermostable mutant PTDH (TS-PTDH) has been solved,11 which supports the proposed functions of several residues and also revealed another residue in the active site, Met53. This Met is absolutely conserved in PTDHs from different organisms, suggesting an important role (Fig. S1 in the ESI†). In a co-crystal structure of TS-PTDH with sulfite, a competitive inhibitor for phosphite,1 the sidechain of Met53 undergoes a large conformational change from the form with only NAD+ bound, such that the sulfur atom of Met53 forms a close contact with an oxygen of sulfite with a S–O distance of 3.1 Å (Fig. 2a). This observation is interesting, as methionine is more typically associated with hydrophobic interactions and steric effects. A search of the Catalytic Site Atlas12 reveals that methionine is present in 0.8% of enzyme active sites. Previously, it has been suggested that methionine can act as a weak hydrogen bond acceptor for backbone amide NH groups,13 and that it can form stabilizing (including non-hydrogen bond) interactions with other residues.14 Of course, it is also known as a ligand for metal ions in proteins.15 Methionine residues can be oxidized to methionine sulfoxide or methionine sulfone. However, there are very few suggestions of methionine residues playing a direct role in enzyme-catalysed reactions,16,17 and we have found none in which a clear catalytic function of a methionine sidechain has been identified. Identification and analysis of catalytic functions is one area in which the combination of mechanistic modelling and experiments is proving increasingly important in enzymology.18–25 This combined approach was central in the work here: the importance of Met53 in the PTDH reaction was initially identified from QM/MM simulations, and subsequently analysed and verified by experiments.
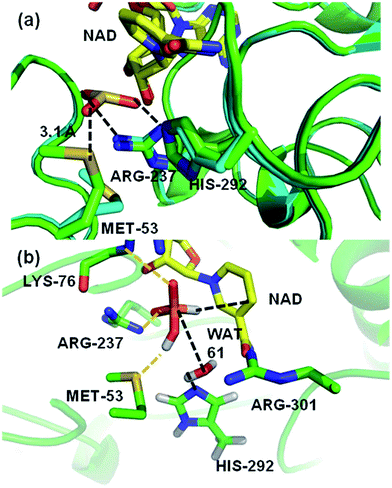 | ||
| Fig. 2 (a) A representation of the crystal structures of thermostable TS-PTDH with the NAD+ co-factor and sulfite inhibitor11 in green and the complex without sulfite in blue. NAD+ (shown with yellow carbons) and several key active site residues are shown as sticks and their interactions with the sulfite inhibitor are indicated by dotted lines. Arg237 is important for binding of the substrate and His292 is the putative base for the reaction.7 When sulfite is present, the Met53 sulfur (Sδ) to sulfite oxygen distance is 3.1 Å. In the absence of sulphite, the side chain of Met53 adopts a different orientation. (b) A representative snapshot of the PTDH ternary complex from QM/MM MD simulations showing important interactions in the active site. The black dotted lines indicate the distances involved in the reaction coordinate. | ||
Results and discussion
Insight into the PTDH ternary complex from QM/MM MD simulations
A computational model of the system was built from the co-crystal structure of TS-PTDH with NAD+ and the inhibitor sulfite11 (see Methods). The QM region was defined as phosphite, the nicotinamide ring of NAD+, a (crystallographic) water molecule (Wat61) involved in the reaction, and the imidazole ring of (neutral) His292 to act as the base (Fig. 1 and S2†). After optimization of the structure with quantum mechanics/molecular mechanics (QM/MM) methods at the AM1/CHARMM27 level of theory, the dynamics of the ternary complex of PTDH were explored through two separate 1 ns QM/MM molecular dynamics (MD) simulations initiated from different structures of the model taken from MM MD simulations. Fig. 2b shows a representative ‘snapshot’ of the ternary complex from one of the QM/MM MD simulations. Table S1† shows average interatomic distances for these interactions (see Methods for the definitions of hydrogen bonds used in the analysis). The protonated oxygen (O3) atom of phosphite donated a hydrogen bond to the sulfur atom of Met53 (Fig. 2b) in the majority of structures in one trajectory (86%) but only 40% of structures in the second trajectory, due to rotation of the hydroxyl group of phosphite and also some flexibility in the position of the sidechain of Met53.Mutagenesis of Met53
The presence of the hydrogen bond between phosphite and Met53 in these QM/MM simulations of the ternary complex suggested a possible role for Met53 in substrate binding, which had not previously been considered. Met53 mutants were constructed in 17X-PTDH and steady-state kinetic analysis was carried out to determine their activity relative to the parent 17X mutant (Table 1). 17X-PTDH differs from TS-PTDH through a Glu175Ala mutation, which allows the enzyme to use both NAD+ and NADP+.5 The KIEs, pH dependence, and pre-steady state kinetics observed with 17X-PTDH are all very similar to those observed with wild-type (wt) PTDH,8,9 indicating that these two proteins use the same catalytic mechanism. While the KM values for phosphite and NAD+ were little different from 17X-PTDH, kcat was reduced a factor of 50 and 200 for the Met53Ala and Met53Asn mutants, respectively (Table 1). The mutations might disrupt packing or orientation of side chains in the active site, but the small changes in KM for phosphite suggest the structure is not significantly altered.| k cat (s−1) | Relative kcat | K M,Phosphite (μM) | K M,NAD (μM) | k cat/KM,Phosphite (M−1 s−1) | D k cat | D k cat/KM | |
|---|---|---|---|---|---|---|---|
| a ND: not determined. Errors in parentheses were obtained from fitting data of triplicate experiments to the Michaelis–Menten equation. For experiments varying the phosphite concentration, the NAD+ concentration was held constant at 4 mM, and for experiments in which the NAD+ concentration was varied, the phosphite concentration was held constant at 2 mM. †Dkcat is the substrate deuterium kinetic isotope effect on kcat and Dkcat/KM is the substrate deuterium kinetic isotope effect on kcat/KM,Phosphite. | |||||||
| 17X-PTDH | 3.1 (0.1) | 1.0 | 28 (7) | 22 (6) | 1.1 (0.3) × 105 | 2.3 (0.1) | 2.1 (0.2) |
| M53N | 0.016 (0.001) | 0.005 | 17 (1) | 64 (1) | 920 (70) | ND | ND |
| M53A | 0.059 (0.001) | 0.019 | 100 (10) | 17 (1) | 590 (30) | 1.9 (0.1) | 1.9 (0.1) |
| Nle–PTDH | 0.11 (0.01) | 0.036 | 28 (1) | 21 (2) | 3900 (200) | 1.8 (0.1) | 1.8 (0.2) |
| Nle–PTDH–M53A | 0.072 (0.003) | 0.024 | 47 (7) | 7.8 (0.9) | 1500 (200) | ND | ND |
| SeMet–PTDH | 3.3 (0.1) | 1.1 | 110 (10) | ND | 3.0 (0.2) × 104 | ND | ND |
Mutagenesis experiments with proteinogenic amino acids are limited to crude replacements of Met. We therefore created two 17X-PTDH mutants with global replacement of methionine by the non-proteinogenic amino acids norleucine (Nle) and selenomethionine (SeMet). These analogues are closer in size to Met than any of the 19 other proteinogenic amino acids and have a methylene group or selenium atom in place of the sulfur atom, providing a clearer indication of electronic/electrostatic (rather than structural) effects. The protein synthesis machinery in E. coli tolerates methionine analogues,26,27 allowing for substitution of Met53 in PTDH by Nle or SeMet (see Methods and Fig. S1†). The kcat of Nle–PTDH is reduced by 25-fold, comparable to the Met53Ala mutant, with essentially identical KM values for both substrates compared to the parent 17X-PTDH (Table 1). This finding indicates that loss of an interaction with Met53 is responsible for the reduction in activity, rather than a change in the structure of the active site. The recombinant 17X-PTDH contains eight Met residues, including one in the hexa-histidine tag. Of these, only Met53 is near the active site. We therefore attribute the reduction in kcat in Nle–PTDH to replacement of Met53 with Nle. This conclusion is supported by the similarity of the kinetic parameters determined for Nle–PTDH–Met53Ala to those observed for the Met53Ala mutant (Table 1). Given the similar KM values of Nle–PTDH and 17X-PTDH, we cannot completely rule out that the observed activity with Nle–PTDH is the result of contamination with 17X-PTDH. In the absence of a good active site titration agent, it is difficult to experimentally address this possibility. However, if contamination with 17X-PTDH were responsible for the observed activity, the Nle substitution would have to be even more deleterious for activity than the observed 25-fold reduction in kcat. In contrast to Nle substitution, SeMet-substituted 17X-PTDH exhibited a kcat very similar to 17X-PTDH. As discussed below, the stabilizing contributions of selenium and sulfur in the transition state are also calculated to be similar. Altogether, these findings point to a catalytic contribution of the sulfur of Met53.
For 17X-PTDH, hydride transfer is fully rate limiting,9 as shown by KIE and pre-steady state kinetic measurements (Table 1). The KIEs for the Met53Ala mutant and Nle–PTDH were also obtained to determine if the rate-limiting step of the reaction changed with the substitution of Met53 (Table 1). In each case the KIEs, Dkcat and Dkcat/KM,Phosphite (i.e. the ratios kcat,H/kcat,D and (kcat,H/KM,H/kcat,D/KM,D)), are very similar in magnitude, as would be expected if the chemical step remained fully rate-limiting combined with a small commitment to catalysis.9 The observation that hydride transfer remains rate-limiting despite a large decrease in kcat has been reported previously for other mutants of PTDH.9 The slightly different magnitudes of the KIEs point to somewhat different transition states, which is not unexpected when mutating a residue that plays a stabilizing role in the transition state (vide infra). Solvent kinetic isotope effects (SIEs) can in some cases provide additional insight into the kinetic mechanism of a reaction that involves a proton transfer step. However, SIEs for PTDH are small (1.5) and complicated by changes in pKa values in H2O and D2O.10 Because SIEs have not been informative in these previous studies on PTDH, SIEs were not determined for the Met53 mutants.
The mutagenesis experiments on Met53 indicate that this residue is important in catalysis, rather than substrate binding. The Nle mutant has reduced activity, similar to the alanine mutant, providing good evidence that the sulfur atom in Met is important for catalysis. We cannot rule out that the different conformational preferences of the side chain of Nle compared to Met28 also play a role, e.g. affecting the ability of the Nle to take on the catalytically important conformation. Attempts to globally replace Met residues with their oxygen analogues were unsuccessful, presumably because of the known toxicity of methoxinine (O-methyl homoserine).29 On the other hand, substitution of Met53 with SeMet did not change kcat: this is consistent with a specific role of the chalcogen atoms in catalysis, and suggests that the catalytic effect is electrostatic/electronic.
QM/MM modelling of the reaction
From the significant decrease in kcat of the mutants, it is clear that Met53 plays some role in catalysis for PTDH. However, the experimental data did not identify the cause of this catalytic effect, e.g. whether the effect of Met53 mutation is due to a disruption of hydrogen bonds, a change in the steric environment of the active site, or some other interaction. Analysis of the catalytic role of Met53 was provided by QM/MM simulations and modelling. We modelled the reaction as an associative process (Fig. 1) using umbrella sampling molecular dynamics techniques (see Methods). AM1 has known limitations for modelling phosphorus,30 and the barriers here are, as expected, too high. This is not important for the application at hand, namely identification of potentially important interactions of the intermediates and transition states. We compare AM1 to correlated ab initio QM methods for this system below. The first step, attack on phosphorus by the water/hydroxide nucleophile was calculated to have a free energy barrier of 28.8 kcal mol−1, forming a pentacoordinated phosphorus intermediate (Int, Fig. 1) with an energy of 4.6 kcal mol−1 above the reactant complex (R). The calculated free energy barrier to the second step is 20.7 kcal mol−1 (relative to Int). The overall reaction energy (−45.1 kcal mol−1) was significantly exergonic (exoergic31). The apparent barrier (from the experimental kcat) to reaction is 16.4 kcal mol−1, significantly lower than the barrier calculated from simulations, because of the limitations of the AM1 method. Calculations on small models show that AM1 overestimates the exothermicity of the reaction by ∼25 kcal mol−1 (Table S2†).Structures from the reaction simulations were analysed to identify important interactions in the enzyme. The interactions between the QM and MM regions can be split into electrostatic and van der Waals components. Here, only the electrostatic energies are discussed in detail (the van der Waals energies are small and do not change significantly during the course of the reaction; the QM/MM van der Waals interaction with Met53 remains relatively constant along the path at ∼−3 kcal mol−1). Average electrostatic and van der Waals interaction energies along the reaction coordinate are given in Table S3.† In agreement with the hydrogen bonding patterns indicated in Fig. 2b, the largest contributions to the electrostatic stabilization energy were provided by Arg237, Arg301, Glu266, Lys76 and Gly77. In the simulations, the Met53 sidechain is observed to change position between Int and TS2, moving from a position close to the phosphite to one near the His292 ring (Fig. 3a). This stabilizes the positively charged histidine, as shown by a change in the interaction energy with Met53. The latter is on average slightly destabilizing in the first half of the reaction but becomes significantly stabilizing at TS2, providing an average of −7.9 kcal mol−1 stabilization (relative to R), the largest contribution of any neutral residue.
Further decomposition of the interaction between Met53 and the QM region in TS2 showed that this stabilizing interaction is mostly due to interaction between the QM region and the sidechain of Met53, rather than its backbone (see Table S3 in ESI†). A C–H⋯O hydrogen bond is present between the methyl group of Met53 and the amide oxygen of the NAD+ co-factor (Fig. 3a). This is a weak interaction, which does not make a significant contribution to stabilization; this interaction is lost in optimization of complexes in the gas phase. Rotation of the methionine methyl group also means that this C–H⋯O interaction is not present in all structures in the enzyme. See the ESI† for further discussion of the interaction between Met53 and NAD+. These interactions were not present in structures of R or Int.
Mulliken population analysis along the pathway shows the changes in charge distribution during the reaction (see Table S4 in ESI†). As expected, the atoms of phosphite and the nucleophilic water molecule undergo significant changes in charge at all stages of the reaction. The charge redistribution is less dramatic for the atoms of the NAD+ cofactor and catalytic base His292. The most significant changes in the partial atomic charges of His292 occur in the first step as it becomes protonated [partial atomic charge Nε: −0.275e in R, −0.238e in TS1 and −0.135e in Int]. There is some redistribution of charge around the histidine ring in the second half of the reaction, but the changes are small e.g. from −0.135e in Int to −0.126e in TS2 (Nε). The presence of Met53 also very weakly polarizes the partial atomic charges of the QM atoms (see Table S4 in ESI†).
The interaction between the Met53 sulfur atom and the positively charged histidine can be described as an n → π* interaction32 because it involves, at least in part, the delocalization of the lone pairs of electrons (n) on the sulfur atom into the antibonding orbitals of the histidine (π*). Clearly, the interaction here is largely electrostatic because it can be modelled by QM/MM methods; its primarily electrostatic nature is also demonstrated by NBO analysis (see ESI†).
Met53 stabilizes the transition state for the hydride transfer step (TS2), but not via hydrogen bonding. The present simulations indicate that this interaction specifically stabilizes TS2 only. Met53 is actually slightly destabilizing in R, TS1 and Int and provides an average of only −2.0 kcal mol−1 electrostatic stabilization to P as His292 and Met53 move further apart. Experimental data show that the step involving the hydride transfer is rate limiting, and hence stabilization of TS2 by Met53 is in accord with the observed reduction in kcat when this stabilization is removed by mutagenesis. In the modelled mechanism His292 becomes positively charged earlier in the mechanism (TS1), thus the interaction with Met53 might be expected to stabilize TS1 and Int also. However, our present simulations indicate that the required conformational change does not occur until TS2.
We cannot rule out the possibility of a concerted mechanism for the reaction in PTDH, but if that were the case, Met53 could also provide similar stabilization to the transition state, which geometrically would resemble the intermediate (Int) modelled here. In a dissociative process, however, protonation of His292 would occur after the rate-limiting hydride transfer event, and hence Met53 would not be expected to stabilize the transition state that governs kcat. As such, the findings here provide some indirect evidence for an associate mechanism and thus against a dissociative mechanism in PTDH if His292 is the catalytic base. The catalytic interaction between Met53 and His292 we have identified in PTDH also provides some support for the proposal that His292 is the catalytic base. According to the pH rate profile, His292 would be protonated throughout the reaction if a different residue acted as the catalytic base. Met53 might then be expected to form this type of interaction with His292 throughout and thus would not be catalytic. However, it is possible that the experimentally observed catalytic effect could be due to a change in position of Met53 during the reaction, i.e. moving to stabilize His292 during the reaction even if His292 does not function as the base. Thus, while the results provide some indirect support for His292 functioning as the base in the reaction, other potential mechanisms were modelled for comparison. Preliminary simulations of dissociative mechanisms, or with other residues as the base, led to unstable results, possibly due to limitations of the AM1 method for treating phosphorus.30 Met53 was found to give little or no stabilization in these simulations. The results presented here with the reaction modelled as an associative process, with His292 as the base, are most consistent with the experimental results. Results at this level of QM/MM theory should not be considered definitive, and therefore it will be useful to investigate the reaction mechanism further in future.
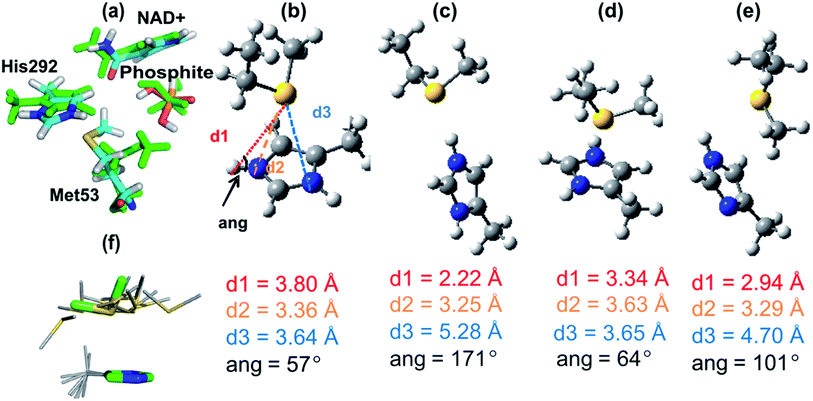
High-level QM investigation of His–Met interactions
To investigate the His–Met interaction in more detail, calculations at the MP2 (ref. 33)/aug-cc-pVTZ//MP2/6-31+G(d) level of QM theory were carried out on a small model representing the His292–Met53 sidechains, using Gaussian09 (ref. 34) and Molpro.35 Several different complexes were studied, using a 4-methyl-imizadole/imidazolium fragment to represent neutral and charged histidine, respectively, and methylthioethane to represent methionine. One complex was a face-on interaction between the imidazolium group and methylthioethane, similar to the interaction seen in the PTDH transition state structure, TS2 (Fig. 3b). The second complex had a (Nε–Hε⋯Sδ) hydrogen bond between the 4-methyl-imidazolium and methylthioethane fragments (Fig. 3c). A third complex contained methylthioethane and a neutral imidazole (Fig. 3d) in the same orientation as in the charged face-on complex. In the AM1/CHARMM27 TS2 structure (Fig. 3b), the sulfur of the methylthioethane fragment sits quite centrally over the imidazolium ring, with sulfur to nitrogen distances d2 and d3 of 3.36 and 3.64 Å, respectively, and a Nε–Hε–Sδ angle of 57°. When this structure was optimized in the gas phase at the MP2/6-31G(d) level of theory, a similar face-on complex was obtained with d2 and d3 of 3.63 Å and 3.65 Å, and a Nε–Hε–Sδ angle of 64° (Fig. 3d). There is good agreement between the geometry of the QM/MM and MP2 optimized complexes, particularly for d3 and the Nε–Hε–Sδ angle. The hydrogen-bonded complex between 4-methylimidazolium and methylthioethane (Fig. 3c) had a much shorter Sδ–Hε distance of 2.22 Å, and d2 and d3 values of 3.25 Å and 5.28 Å, respectively, and the Nε–Hε–Sδ angle (171°) was considerably larger. When a neutral complex of 4-methylimidazole and methylthioethane was optimized, the resulting geometry was intermediate between the face-on and hydrogen-bonded geometries with a Sδ–Hε distance of 2.94 Å and d2 and d3 values of 3.29 Å and 4.70 Å, respectively (Fig. 3e).The calculated interaction energies for these complexes at the MP2 (ref. 33)/aug-cc-pVTZ and SCS-MP2 (ref. 36)/aug-cc-VTZ levels of theory, including counterpoise correction for basis set superposition error, are given in Table 2. The strongest interaction was found for the hydrogen-bonded complex between 4-methylimidazolium and methylthioethane: −16.2 kcal mol−1 (MP2) and −14.9 kcal mol−1 (SCS-MP2). The face-on complex of the same fragments had a somewhat smaller, but still significant interaction energy: −10.4 and −9.0 kcal mol−1 at the MP2 and SCS-MP2 levels, respectively. These numbers are in quite good agreement with the average QM/MMele interaction energy of −5.0 kcal mol−1 with the sidechain of Met53 at TS2 in the QM/MM simulations, although indicating that this interaction energy is underestimated in the QM/MM simulations. It is encouraging that, despite the well-known limitations of the AM1 method, QM/MM methods at this level were able to identify this face-on interaction in good agreement with ab initio methods, in terms of both geometry and energy. It is important to point out, though, that these calculations show that the interaction with Met53 is likely to be underestimated at the AM1/CHARMM27 level of theory.
Ab initio interaction energies for methylselenoethane complexes differed by less than 1 kcal mol−1 from the values obtained for the methylthioethane complexes [−9.6 kcal mol−1 face-on complex; −15.5 kcal mol−1 hydrogen-bonded complex at the MP2/aug-cc-pVTZ level of theory]; this finding is consistent with our experimental finding that the SeMet-mutant and 17X-PTDH have similar activity. The interaction energy for the neutral model complex (Fig. 3e) was considerably smaller (−5.8 and −4.4 kcal mol−1, MP2 and SCS-MP2). The interaction energy of a neutral complex of 4-methylimidazole and methylthioethane, constrained to the geometry of the face-on complex, was even smaller (−0.57 kcal mol−1). The significantly smaller interaction energy for the neutral complex with the same geometry is consistent with this type of interaction only being observed between doubly protonated (charged) histidine and methionine. The hydrogen-bonded complex between positively charged His292 and Met53 (Fig. 3c), although stronger than the face-on interaction in the ab initio calculations, was not observed in the enzyme due to the constraints imposed by the other active site residues. The interaction energies calculated here are larger than the 2–3 kcal mol−1 contribution of Met53 to TS stabilization indicated by the experimental data, but are of the correct order of magnitude. It is important to note that the interaction energies calculated here are not directly comparable to the experimental ΔΔG‡ values for the mutations; e.g. Met53 forms other interactions in the active site, which are lost during the reaction.
Identification of Met–His interactions in crystal structure databases
To assess whether the face-on His–Met interaction identified by the QM/MM simulations is an isolated example or a more general phenomenon, crystal structures deposited in the Protein Data Bank (PDB)37 and the Cambridge Structural Database (CSD) were investigated (see ESI for details†). For the PDB search, the MP2/6-31+G(d) optimized geometry of the positively charged face-on complex (Fig. 3d) was used as a template. Approximately 80 structures within a RMSD of 1.0 Å of the template geometry were found (see Fig. 3f for examples), and ∼10% of these histidine sidechains were predicted (with PROPKA38) to be protonated at neutral pH. It is interesting that face-on interactions of this type are apparently present in other protein structures, suggesting they may be of more general importance. Some analysis of His–Met distributions was reported some years ago,14 but this specific type of interaction has not previously been identified. Close contact His–Met pairs were not identified within the CSD, but our initial inquiry did reveal analogous face-on interactions between an imidazolium ring and electron-rich atoms (see Fig. S3†). Analysis of the CSD for interactions between an imidazole group (neutral, protonated or coordinated) and electron-rich atoms (n = 2529, See ESI for full details†) revealed that such face-on interactions are a general phenomenon within the CSD and, moreover, are directional in nature (see Fig. S5†). This finding is reminiscent of earlier reports about anion–π and lone pair–π interactions with six-membered electron deficient aromatic rings39–41 and also Ar–X2 complexes where X is a heavy halogen.42 We note that the His–Met interaction discovered here in PTDH would not be identified by our structural search, because it is not present in the crystal structure; it is predicted to form only during the reaction (e.g. in the transition state). This stresses the importance of modelling reactions for analyzing enzyme mechanisms, because crystal structures (and simulations) of stable complexes may not contain all of the catalytically relevant interactions.Conclusions
QM/MM simulations and experiments identify a catalytic role for methionine in PTDH, which appears to be unprecedented. Analysis of protein and small-molecule structures indicates that face-on Met–His interactions are relatively widespread, with potential importance for the structure and function (e.g. catalysis) of other enzymes (particularly those in which histidine acts as a base). The combination of experiments, structural analysis and molecular simulation techniques demonstrate that Met53 is an important residue for catalysis by PTDH and provide an atomic description of its effects. Understanding of enzyme catalysis in general will benefit greatly from such multidisciplinary approaches. Altogether, our simulations, experiments and structural analysis provide a consistent picture in which methionine plays a catalytic role through transient stabilization of a positively charged histidine sidechain.Methods
General methods
For details regarding molecular biology procedures, protein expression and purifications and database analyses, see the ESI.†For MM and QM/MM simulations, a ‘reaction region', not subject to any positional restraints, was defined as a 21 Å sphere centred on O3 of NAD+. The region between 21 and 25 Å was defined as the ‘buffer region’: protein heavy atoms in this region were restrained using force constants scaled to increase with distance from the centre of the system.50,51 Atoms further than 25 Å from the centre of the system were held fixed. A stochastic boundary approach was used,30 and water was restrained to remain within the simulation system using a spherical deformable potential of radius 25 Å.52 The model system was heated to a temperature of 300 K and equilibrated for 100 ps before 1 ns of production MD was performed. Langevin dynamics were applied for atoms in the buffer region (the list of atoms in the buffer was updated every 50 steps), using friction coefficients of 250 ps−1 for protein heavy atoms and 60 ps−1 for water oxygen atoms,53 and a 1 fs time step. Non-bonded interactions, calculated using a 13 Å cut-off, were updated every 25 steps.
The QM region was defined as phosphite, a crystallographic water molecule (Wat61) positioned for reaction, the nicotinamide ring of NAD+ and 4-methylimidazole from His292: a total of 37 QM atoms, including 2 hydrogen (HQ) link atoms54 to satisfy the QM/MM boundary (with charges of MM host groups set to zero). The overall charge of the QM system was zero, from the −1e of monoprotonated phosphite and +1e of the NAD+ cofactor.
Two 1 ns QM/MM MD simulations were performed using two different starting geometries from the MM MD simulations. Umbrella sampling MD simulations were then used to model the reaction, using protocols similar to those applied successfully previously to other enzymes.50,51 Reaction coordinates for an associative mechanism were defined as Zstep1 = d(OH2–H2T) − d(H2T–NE2) − d(OH2–P)/Å for the nucleophilic attack on phosphite and Zstep2 = d(P–H1) − d(H1–C4N)/Å for the hydride transfer step (see Fig. 1). At each point along the relevant reaction coordinate, 5 ps of equilibration was carried out, followed by 50 ps of production QM/MM MD. Step 1 was sampled between reaction coordinate values of Zstep1 = −5.4 to 0.1 Å in 0.1 Å intervals, using a force constant of 200 kcal mol−1 Å−2. Each subsequent simulation was started from the 5 ps point of the preceding simulation. The value of Zstep1 was recorded at each step of the 50 ps dynamics simulation for statistical analysis. Step 2 was modelled in a similar way, in 0.1 Å intervals between Zstep2 = −3.8 to 2.2 Å. The reaction coordinate statistics for each step were combined using the weighted histogram analysis method (WHAM)55 to give the AM1/CHARMM27 free energy profile for the reaction.
Acknowledgements
This work was jointly supported by the National Science Foundation (NSF) and the Engineering and Physical Sciences Research Council (EPSRC) (NSF 0822536 to WAV and EPSRC EP/G002843/1 to AJM/KER and also EP/J014301/1 to DNW/GJB). AJM is an EPSRC Leadership Fellow (grant number: EP/G007705/01).Notes and references
- A. M. G. Costas, A. K. White and W. W. Metcalf, J. Biol. Chem., 2001, 276, 17429–17436 CrossRef CAS PubMed.
- J. M. Vrtis, A. K. White, W. W. Metcalf and W. A. van der Donk, Angew. Chem., Int. Ed., 2002, 41, 3257–3259 CrossRef CAS.
- T. W. Johannes, R. D. Woodyer and H. M. Zhao, Appl. Environ. Microbiol., 2005, 71, 5728–5734 CrossRef CAS PubMed.
- R. Woodyer, H. M. Zhao and W. A. van der Donk, FEBS J., 2005, 272, 3816–3827 CrossRef CAS PubMed.
- R. Woodyer, W. A. van der Donk and H. M. Zhao, Biochemistry, 2003, 42, 11604–11614 CrossRef CAS PubMed.
- J. M. Vrtis, A. K. White, W. W. Metcalf and W. A. van der Donk, J. Am. Chem. Soc., 2001, 123, 2672–2673 CrossRef CAS.
- R. Woodyer, J. L. Wheatley, H. A. Relyea and S. Rimkus, et al. , Biochemistry, 2005, 44, 4765–4774 CrossRef CAS PubMed.
- J. E. Hung, E. J. Fogle, H. D. Christman and T. W. Johannes, et al. , Biochemistry, 2012, 51, 4254–4262 CrossRef CAS PubMed.
- E. J. Fogle and W. A. van der Donk, Biochemistry, 2007, 46, 13101–13108 CrossRef CAS PubMed.
- H. A. Relyea, J. M. Vrtis, R. Woodyer and S. A. Rimkus, et al. , Biochemistry, 2005, 44, 6640–6649 CrossRef CAS PubMed.
- Y. Zou, H. Zhang, J. S. Brunzelle and T. W. Johannes, et al. , Biochemistry, 2012, 4263–4270 CrossRef CAS PubMed.
- C. T. Porter, G. J. Bartlett and J. M. Thornton, Nucleic Acids Res., 2004, 32, D129–D133 CrossRef CAS PubMed.
- P. Zhou, F. Tian, F. Lv and Z. Shang, Proteins: Struct., Funct., Bioinf., 2009, 76, 151–163 CrossRef CAS PubMed.
- D. Pal and P. Chakrabarti, J. Biomol. Struct. Dyn., 2001, 19, 115–128 CAS.
- J. Reedijk, J. Inorg. Biochem., 2012, 115, 182–185 CrossRef CAS PubMed.
- G. L. Holliday, C. Andreini, J. D. Fischer and S. A. Rahman, et al. , Nucleic Acids Res., 2012, 40, D783–D789 CrossRef CAS PubMed.
- G. L. Holliday, J. B. O. Mitchell and J. M. Thornton, J. Mol. Biol., 2009, 390, 560–577 CrossRef CAS PubMed.
- R. Lonsdale, K. E. Ranaghan and A. J. Mulholland, Chem. Commun., 2010, 46, 2354–2372 RSC.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- S. C. L. Kamerlin and A. Warshel, Proteins: Struct., Funct., Bioinf., 2010, 78, 1339–1375 CAS.
- K. Meier, A. Choutko, J. Dolenc and A. P. Eichenberger, et al. , Angew. Chem., Int. Ed., 2013, 52, 2820–2834 CrossRef CAS PubMed.
- L. Masgrau, A. Roujeinikova, L. O. Johannissen and P. Hothi, et al. , Science, 2006, 312, 237–241 CrossRef CAS PubMed.
- L. Y. P. Luk, J. J. Ruiz-Pernia, W. M. Dawson and M. Roca, et al. , Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 16344–16349 CrossRef CAS PubMed.
- D. H. Min, H. R. Josephine, H. Z. Li and C. Lakner, et al. , PLoS Biol., 2008, 6, 1802–1810 CAS.
- P. Thaplyal, A. Ganguly, B. L. Golden and S. Hammes-Schiffer, et al. , Biochemistry, 2013, 52, 6499–6514 CrossRef CAS PubMed.
- D. B. Cowie and G. N. Cohen, Biochim. Biophys. Acta, 1957, 26, 252–261 CrossRef CAS.
- R. Munier and G. N. Cohen, Biochim. Biophys. Acta, 1959, 31, 378–391 CrossRef CAS.
- S. H. Gellman, Biochemistry, 1991, 30, 6633–6636 CrossRef CAS.
- R. O. Roblin, J. O. Lampen, J. P. English and Q. P. Cole, et al. , J. Am. Chem. Soc., 1945, 67, 290–294 CrossRef CAS.
- J. Zurek, A. L. Bowman, W. A. Sokalski and A. J. Mulholland, Struct. Chem., 2004, 15, 405–414 CrossRef CAS.
- We use the term exergonic here, but note that IUPAC considers the terms exergonic and exoergic to be synonyms, http://goldbook.iupac.org/E02262.html.
- G. J. Bartlett, A. Choudhary, R. T. Raines and D. N. Woolfson, Nat. Chem. Biol., 2010, 6, 615–620 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseriaet al., Gaussian, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manbyet al., Molpro, 2006, http://www.molpro.net Search PubMed.
- S. Grimme, J. Chem. Phys., 2003, 118, 9095 CrossRef CAS PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- D. C. Bas, D. M. Rogers and J. H. Jensen, Proteins: Struct., Funct., Bioinf., 2008, 73, 765–783 CrossRef CAS PubMed.
- A. Frontera, P. Gamez, M. Mascal and T. J. Mooibroek, et al. , Angew. Chem., Int. Ed., 2011, 50, 9564 CrossRef CAS PubMed.
- T. J. Mooibroek and P. Gamez, CrystEngComm, 2012, 14, 1027–1030 RSC.
- T. J. Mooibroek and P. Gamez, CrystEngComm, 2012, 14, 3902–3906 RSC.
- A. C. Legon, Phys. Chem. Chem. Phys., 2010, 12, 7736–7747 RSC.
- P. C. Cirino, Y. Tang, K. Takahashi and D. A. Tirrell, et al. , Biotechnol. Bioeng., 2003, 83, 729–734 CrossRef CAS PubMed.
- B. R. Brooks, R. E. Bruccoleri, B. D. Olafson and D. J. States, et al. , J. Comput. Chem., 1983, 4, 187–217 CrossRef CAS.
- N. Foloppe and A. D. MacKerell, J. Comput. Chem., 2000, 21, 86–104 CrossRef CAS.
- A. D. MacKerell, D. Bashford, M. Bellott and R. L. Dunbrack, et al. , J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS.
- G. Vriend, J. Mol. Graphics, 1990, 8, 52–56 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura and R. W. Impey, et al. , J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS PubMed.
- E. Neria, S. Fischer and M. Karplus, J. Chem. Phys., 1996, 105, 1902–1921 CrossRef CAS PubMed.
- L. Masgrau, K. E. Ranaghan, N. S. Scrutton and A. J. Mulholland, et al. , J. Phys. Chem. B, 2007, 111, 3032–3047 CrossRef CAS PubMed.
- K. E. Ranaghan, L. Masgrau, N. S. Scrutton and M. J. Sutcliffe, et al. , ChemPhysChem, 2007, 8, 1816–1835 CrossRef CAS PubMed.
- C. L. Brooks, III and M. Karplus, J. Chem. Phys., 1983, 79, 6312 CrossRef PubMed.
- R. H. Stote and M. Karplus, Proteins: Struct., Funct., Genet., 1998, 23, 12–31 CrossRef PubMed.
- N. Reuter, A. Dejaegere, B. Maigret and M. Karplus, J. Phys. Chem. A, 2000, 104, 1720 CrossRef CAS.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Additional materials and methods, QM/MM model preparation, analysis methods for QM/MM structures, discussion of the Met–NAD+ interaction, NBO calculations, PDB and CSD searches, Tables S1–S6 and Fig. S1–S5. See DOI: 10.1039/c3sc53009d |
| This journal is © The Royal Society of Chemistry 2014 |