Proton transfer rates in ionized water clusters (H2O)n (n = 2–4)†
Abstract
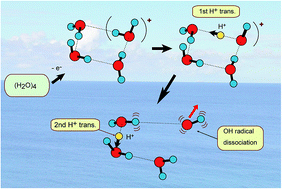
A proton transfer process is usually dominant in several biological phenomena such as the energy relaxation of photo-excited DNA base pairs and a charge relay process in Ser-His-Glu. In the present study, the rates of proton transfer along a hydrogen bond in a water cluster cation have been investigated by means of a direct ab initio molecular dynamics (AIMD) method. Three basic clusters, water dimer, trimer and tetramer, (H2O)n (n = 2–4), were examined as the hydrogen bonded system. It was found that the rate of the first proton transfer is strongly dependent on the cluster sizes: average time scales of proton transfer for n = 2, 3, and 4 were 28, 15, and 10 fs, respectively, (MP2/6-311++G(d,p) level) suggesting that proton transfer reactions are very fast processes in the three clusters. The second proton transfer was found in n = 3 and 4 (the average time scales for n = 3 and 4 were 120 fs and 40 fs, respectively, after the ionization). The reaction mechanism was discussed on the basis of theoretical results.

 Please wait while we load your content...
Please wait while we load your content...