Localization and shaping of surface acoustic waves using PDMS posts: application for particle filtering and washing

Abstract

We introduce a technique to control the position and effective area of the surface acoustic wave (SAW) acting on a fluid in a PDMS microchannel. The acoustic force can be localized at specific areas of the channels using a structured, ultra-thin PDMS foil beneath the microchannel. This setup enables shaping of the standing surface acoustic waves (SSAW) only by changing the geometry of the PDMS foil. In this way the effect is independent of the design of the acoustic transducer and even a single interdigitated transducer can be used to excite standing surface acoustic waves. The alignment of the assembly is very flexible allowing for different orientation of the microchannels with respect to the IDT. To demonstrate the significance and versatility of this technique we use a diagonal orientation to separate and wash particles of different size with a total deflection length of several wavelengths.

---

Introduction

Microfluidic sorting,^1–8 filtering^9–11 and deflecting^12–16 of cells and particles or manipulation of droplets,^17–22 in fluids plays an important role for application in various disciplines, like analytical chemistry, biotechnology or diagnostics. Many physical approaches from magnetics,^23–25 to electrophoresis^26–30 and optics^31–34 have been used to deflect objects. Also, acoustophoretic forces have been explored to manipulate particles,^21,35–37 drops,^38,39 cells^40–44 or cell media in a channel.^45,46 Some methods apply bulk acoustic waves.^47–52 In comparison, surface acoustic wave devices (SAW) are planar and more compact and can be easily integrated in microfluidic devices together with other functional features.^53,54 In order to achieve a good control over the fluid with SAW, a precise actuation of the acoustic path is required. This can be achieved by custom designed interdigital transducers (IDTs). For this purpose tapered IDTs (TIDTs) as well as parabolic shaped IDTs have been used.^17,20 Also the shaping of the acoustic path using phononic crystals has been demonstrated recently.^55,56 However, all these methods are limited by the inflexibility of the PDMS devices in combination with acoustic actuation as a result of the strong damping in PDMS. Damping occurs when the PDMS is in direct contact to the surface of the substrate along which the SAW propagates and this restricts the channels design and the applications significantly. Also, the alignment of channel and the IDT is laborious. The use of phononic crystals is more challenging in terms of chip fabrication. Therefore, it lacks a simple but versatile technique which combines ubiquitous PDMS fabrication by soft lithography with precise acoustic control of the fluid flow.

Here, we demonstrate a simple hybrid device which uses two straight IDTs and two layer PDMS lithography. Instead of shaping the acoustic path by IDT geometry²⁰ we use an ultra-thin layer of PDMS that defines the regions of acoustic actuation. This does not focus the acoustic energy, as has been reported earlier,^17,20 but instead enables the SAW to couple in only at specific positions of the microchannel. In most methods, the microchannel defines the flow of the fluid and, at the same time, the coupling of the acoustic force into the microchannel. However, our method overcomes this limitations enabling independent fluidic and acoustic control. Our method makes rapid prototyping a lot simpler, avoiding time-consuming fabrication of custom-made IDTs. A single IDT can be reused for many different experiments, because the PDMS microchannels is not bonded to the chip. Instead only two layer PDMS microchannels are needed, that are simpler and more rapidly produced and that are cheap and disposable. We can couple the SAW in any intended direction and at any designated position into the channel, not only parallel and at the borders of the microchannel, which are the interface between PDMS and the fluid. In contrast to other methods, the PDMS hybrid device neither needs exact alignment nor very thin channel walls to reducing damping effects. With two opposed IDTs a standing surface acoustic wave (SSAW) is excited, even if the IDTs are rotationally or laterally misaligned as long as the SAW still hits the post. Very recently, a similar approach using tilted-angled SSAW, was demonstrated to sort cells.⁵⁷ Using a PDMS post offers a high degree of flexibility so that the microchannel can even cross the IDT structure. In addition we can control the geometry of a SSAW simply by the PDMS device and without modifying the IDT design. We can even achieve SSAW with only a single tapered IDT exploiting the reflection of the primary wave. One IDT can be used for different positions and geometries of the acoustic force and different shapes of SSAWs are possible, just by changing the PDMS device. As an application of the PDMS post, we demonstrate the separation of 15 μm beads from 10 μm beads using SSAW. In comparison to other methods, separation via SSAW is not limited by a deflection length of λ/4 anymore.^58–60

Experiments and results

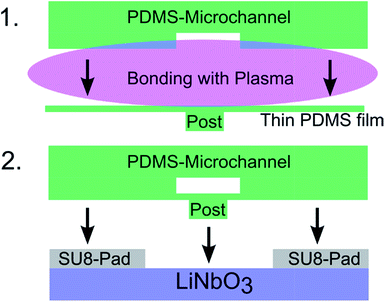
We use a surface acoustic wave (SAW) device, combined with a two layer PDMS mold. To excite SAWs propagating in opposite directions, we use in all experiments the same IDT device with two opposed, straight IDTs with a wavelength of 100 μm, an aperture of 1 cm and 20 finger pairs, as shown in Fig. 1. For the experiments with only a single IDT, we use two different tapered IDTs (TIDT) with different parameters, depending on the frequency requirement: TIDT1: 136–165 MHz, 65 finger pairs, 1200 μm aperture and TIDT2: 60–90 MHz, 12 finger pairs, 800 μm aperture. After the experiments we gently rinse the IDTs with water and isopropanol, dry it in a nitrogen flow and reuse it again for further experiments. The IDTs are produced by evaporating layers of 10 nm Ti, 50 nm Au and 10 nm Ti onto a 17.5 × 17.5 mm piezoelectric lithium niobate (128° Y-cut LiNbO₃) substrate.

Fig. 1 Micrograph of the experimental setup. PDMS hybrid (indicated by purple lines) device with microchannel (green area) and post (red area) is oriented diagonal to the two opposed IDTs. The Pads (orange arrows) guarantee that only the post has mechanical contact to the surface of the LiNbO₃ substrate.

Fig. 2 Schematic sketch of the hybrid device consisting of a PDMS microchannel, a thin PDMS film with post and a LiNbO₃ substrate with the IDT (IDT is not shown). For assembly, first the PDMS microchannel is bonded to the PDMS film with the post in ozone plasma. Then the PDMS composite is placed onto the LiNbO₃ chip.

For mechanical protection and electrical insulation 200 nm SiO₂ are sputtered onto the chips. Thin (20 μm height) SU-8 pads are deposited onto the chip via soft lithography. They serve as spacers, so that the microchannel does not directly contact the surface of the chip and only the post is in mechanical contact (Fig. 2).

The microchannel, with a height of 50 μm, is connected via PTFE tubes to an inlet and an outlet. We inject polystyrene microspheres (Polysciences Inc.) suspended in deionized water (MilliPore 18.2 MOhm cm). 1 mg BSA (bovine serum albumin, Serva Electrophoresis GmbH) per 1 ml water is added to shield the electrostatic interaction between the particles and PDMS and to avoid aggregations between the particles. The setup is then placed on a microscope (Axiovert 200M, Carl Zeiss) and movies are captured with a high-speed camera (Fastcam 1024 PCI, Photron). Each IDT is connected to a signal generator (SML 01, SML 02 or SMB100A, Rhode & Schwarz) and an amplifier (ZHL-1-2W, Mini-Circuits) and is excited with a total power of 23 up to 26.5 dBm. The two signal generators are coupled, enabling change of frequency for each IDT independently, thus controlling the position and velocity of the SSAW nodes. In the case of the TIDTs, only one signal generator and an amplifier was used. The total power used is 32 dBm. For tracking the beads the software plugin MTrackJ for ImageJ⁶¹ was used.

To prevent acoustic damping the PDMS-hybrid device is designed in such a way that the PDMS microchannel has no direct mechanical contact with the LiNbO₃ substrate. This is ensured by SU-8 spacers (Pads) as shown in Fig. 1. Only at the position of the post a mechanical contact is given (Fig. 2). It enables the SAW only at this specific position to couple into the microchannel. Everywhere else the SAW just propagates beneath the microchannel. With this design, the microchannel can be orientated at different angles with respect to the IDTs. In each micrograph of the figures a small inset indicates the orientation of the microchannel and the post to the IDTs.

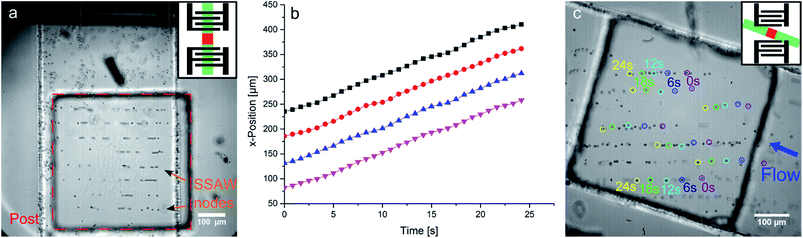
In the first experiment, we use a straight microchannel with two opposing IDTs with the same wavelength on both sides of the channel. The counter propagating SAWs of each IDT superpose to form a SSAW pattern on the substrate with lines of nodes and antinodes parallel to the IDTs. The polystyrene beads are forced into the pressure nodes of the SSAW. In this way, the pattern can be visualized.^62–65 However, the effect of the nodes onto the particles in the fluid can only be observed at a confined area in the channel. The standing surface acoustic wave (SSAW) affects and aligns the particles only at the localized region defined by the post position (Fig. 3a). Anywhere else in the channel there is no acoustic force and the beads simply follow the trajectory of the external fluid flow. This clearly demonstrates that the acoustic effect is limited to the region of the square shaped post (Fig. 3a).

Fig. 3 (a) Microchannel with squared post (500 × 500 μm) is orientated vertical to the IDT. Standing surface acoustic waves (SSAWs), which are visualized by 6 μm beads, are localized on the post. Beside the post there is no acoustic force and no alignment of beads. (b) By a small frequency mismatch (0.15 Hz) of the two frequency generators, the SSAW is moved in time, transporting beads trapped in the nodes vertically to the SSAW along the microchannel. The trajectories of four different SSAW nodes are tracked and linear fit is applied to measure the experimental velocities (v = 7.59 ± 0.03 μm s⁻¹), which are in very good agreement with the theoretical value (v = 7.5 μm s⁻¹). (c) Microchannel with squared post is aligned diagonal to the two opposed IDTs and a constant flow with a flow rate of approximately 5 μl h⁻¹ (blue arrow) is applied. The 6 μm beads are forced to stay in the pressure nodes of the SSAW and are thus deflected. For better visualization five images are overlaid and a few beads are marked at different times. This application can be used to filter or wash particles.

This principle can be exploited for particle transportation. We demonstrate that the SSAW can be used to transport trapped particles by the control of the node position. Changing the frequency of one of the two IDTs slightly by Δf = 0.15 Hz, the relative phase of the two SAWs is shifted constantly. As a result, the SSAW nodes propagates linear in time (Fig. 3b) towards one IDT at a velocity v = Δf·λ/2 (mathematical derivation: see notes). The measured average velocity v = 7.59 ± 0.03 μm s⁻¹ is in very good agreement with the theoretical value of v = 7.5 μm s⁻¹. The beads trapped in the pressure nodes follow the standing wave. As soon as the beads leave the position above the post, there is no SSAW, and therefore no acoustic force. Thus the beads away from the post simply follow the streaming of the fluid. In this way a controlled transportation along the post and perpendicularly to the SSAW is achieved with a transport velocity adjusted by the frequency shift Δf.

The SSAW can also be employed to transport beads along a stationary pressure node, parallel to the SSAW. Therefore, the two IDTs generate a SAW with the identical frequency, producing a SSAW on the post, which is constant in time. The microchannel is oriented diagonal to the IDTs and a flow (with a flow rate of ∼5 μl h⁻¹) to the channel is applied as shown in Fig. 3c. The flow is consequently diagonal to the SSAW, too. The beads entering the post are concentrated to the pressure node of the SSAW and follow these nodes. Leaving the post, the beads follow the flow again. The SSAW acts in this case as a guide for all beads above the post. This setup can be used for filtering or washing particles.

We show that beads can be transported along the post, either vertically with a moving SSAW (Fig. 3b) or parallel to the SSAW (Fig. 3c), by forcing the beads into the pressure nodes and an applied flow. The transportation velocity is limited by the friction force. The acoustic radiation force F_a in the SSAW has to be at least as large as the Stokes friction force F_r:^66–68

z is the position of the bead. ρ₀, ρ and c₀, c are the density and the acoustic velocity in the fluid and the particles, η is the viscosity of the fluid, ν is the frequency and λ is the wavelength of the SAW. v and r are the velocity and the radius of the particle and p₀ the static pressure. f₁ and f₂ are given as:

If the friction force is greater than the acoustic force, then the beads cannot follow the pressure nodes of the SSAW anymore. In our experiments only slow velocities are used to ensure that the friction force is always small enough.

To emphasize the significance and potential of this method even more, we demonstrate the filtering and separation of 15 μm beads from 10 μm beads (Fig. 4) in flow (with a flow rate of ∼1 ml h⁻¹). Here, the post is orientated at an angle of 19.5° to the IDTs. Two forces act on the beads, the Stokes-friction force in the flow and the acoustic force, which has a maximum in the pressure nodes of the SSAW and which depends on the particle radius r. The friction force (F_r ∼ r) acts in flow direction and the acoustic force (F_a(z) ∼ r³) acts parallel to the IDTs, diagonal to the microchannel. Above a critical radius, particles follow the nodes. Below the critical radius the friction force dominates the acoustic force, and particles are not hold by the SSAW significantly (see Fig. 4). As the post (375 μm width) is more narrow than the microchannel (500 μm width), the deflected beads are collected at the edge of the post, in the area where no post is present, since there the acoustic force vanishes. At this position, particles continue following the flow of the fluid, and the friction force dominates again. This behaviour is quantitatively analysed in the histogram (Fig. 4b), showing the concentration along the width of the channel for the incoming and outgoing particles of the two different sizes.

Fig. 4 (a) Separation of 15 μm beads from 10 μm beads with a rectangular post (375 μm width) in a microchannel (500 μm width). The micrograph shows an overlay of eight consecutive video frames taken at a time interval of 0.13 s with subtraction of the background. The white circles indicate the trajectories of some 15 μm beads. Initially when the SAW is off, the beads follow the flow (positions 1–3). After the SAW is switched on (position 3), the beads are follow a horizontal trajectory (position 3–6). The deflected 15 μm beads are transferred from section 1 to section 2. As soon as they have reached section 2 (position 7) no acoustic force acts on the particles and the beads follow the flow of the fluid again. In contrast the trajectory of the smaller particles (10 μm beads marked by yellow circles) is not affected by the acoustic field. (b) Histogram of the probabilities of the incoming and outgoing beads of the two different sizes (10 μm and 15 μm) along the width of the microchannel. The 10 μm beads are not significantly deflected by the SSAW (upper two diagrams). The 15 μm (lower two diagrams) are deflected into section 2. We tracked 60 to 80 particles for the inlet and 200 to 290 particles for the outlet. The applied flow rate is approximately 1 ml h⁻¹.

This setup demonstrates the key features to wash particles. Applying the SSAW, the 15 μm beads are transferred from the fluid flowing in section 1 to the fluid flowing in section 2. The fluids in both sections do not mix significantly, as can be seen from flow tracing particles (10 μm beads).

To study the effect of the relative orientation of the IDT to the post in more detail, a PDMS device with a rectangular post is aligned diagonally to the IDT. Here, the excited SAW is not parallel to the edges of the post anymore (Fig. 5). Interestingly, two types of patterns can be observed: one pattern (secondary pattern) diagonal to the IDTs but parallel to the edges of the post, and one parallel to the IDTs but diagonal to the post (primary pattern). The development of both patterns is relatively slow. Most of the beads travel to the intersections of both patterns over time.

Fig. 5 Temporal development of the SSAWs on a rectangle post (400 × 5000 μm) at different times after activation of the electric signal visualized with 1 μm beads. The two different patterns, caused by the reflections at the edges of the post (secondary pattern) and by direct interference of the two SAWs excited by the two opposed IDTs (primary pattern) occur. The result is a superposition of both effects. The development is relatively slow as the acoustic force is of the same order than the Stokes friction force.

We can understand this observation in the following way. A SSAW caused by direct interference of the two opposed, excited SAWs is stimulated (primary pattern). However, the incoming SAWs are also reflected at the edges of the post. Therefore, a second SSAW (secondary pattern) caused by the interference of reflected SAWs is excited (Fig. 5). When switching on the IDTs, both patterns establish. After a while the beads concentrate on the spots where both SSAW interfere constructively and thus the pressure node is most pronounced. This phenomenon is relatively slow as the acoustic force is of the same order as the friction force.

To verify that the visualized patterns are SSAWs excited by the two IDTs with a wavelength of 100 μm, the distances of adjacent pressure nodes are measured. For the primary pattern the distance d₁ is 50.4 ± 4 μm, for the secondary pattern d₂ = 52.2 ± 4 μm. This is in very good agreement with the theory as the pressure nodes intervals should be half a wavelength.

To examine the influence of the shape of the post, a circular post is used (Fig. 6). The primary pattern is unchanged but the secondary pattern alters drastically. The interferences of the reflections at the edges of the post are not straight anymore but leading to a circular secondary pattern, reflecting the shape of the post.

Fig. 6 Microchannel with circular post (with a radius of 150 μm) and 1 μm beads before (a) and after (b) switching on the IDT. Superposition of both SSAW patterns is visible. The linear pattern is caused by direct interference of the two IDTs and the circular pattern is caused by reflections at the edges of the post. The circular pattern is shaped by the geometry of the circular post.

Apparently, there are more patterns, induced by interference of reflected and incoming SAWs, but these are not as clear and pronounced as the primary and secondary patterns. The intervals of different nodes distances were measured (d₁ = 51 ± 6 μm and d₂ = 34 ± 6 μm) and it is clear that the different distances originate from different patterns.

The experiments demonstrate that the SSAW created by reflections (secondary pattern) can be directly controlled by the geometry of the post (Fig. 5 and 6). The SSAW induced by reflections, features the same geometry as the post. A rectangular post leads to a straight pattern parallel to the edges of the post. A circular post result in a circular pattern.

Our technique makes it is also possible to form SSAWs with only a single IDT. To demonstrate this, an elliptical post and one TIDT instead of the two opposed straight IDTs is used (Fig. 7 and 8). The primary pattern, caused by direct interference of the two incoming SAWs, no longer exists. Thus only a SSAW caused by interference of reflections at the edges of the post and the incoming wave is generated.

Fig. 7 Generating a SSAW with only one IDT is also possible. The pattern is caused only by reflections at the edges of the elliptical post (dimensions of 150 × 200 μm) and is shaped by the geometry of the post. With the higher frequency of 154 MHz (a) more nodes establish as with the lower frequency of 76 MHz (b). Concluding the average distance between the nodes rises from 9 ± 3 μm to 16 ± 3 μm. With changing frequency the position of the acoustic path is also changed, leading to a shift of the beads (see Fig. 8).

Fig. 8 SSAW induced by only one TIDT on an elliptical post (dimensions of 150 × 200 μm). By switching the frequency from 138 MHz (a), to 139 MHz (b) up to 140 MHz (c), the position of the acoustic path is slightly shifted, as indicated by the arrows below the images, and the beads can be transported along the SSAW. The average distance between the nodes is also changed slightly.

By changing the frequency of the tapered IDT, two effects appear. First, the distance between the pressure nodes is changed as it is direct related to the wavelength of the excited SAW, which is changed with frequency. In the experiment (Fig. 7) the frequency is reduced by a factor of ∼2 from 15 MHz to 76 MHz (by using two different IDTs), thus reducing the number of nodes. The average distance between the intervals of the nodes increases by a factor ∼2 from 9 ± 3 μm to 16 ± 3 μm.

With changing the frequency of a tapered IDT, the position of the acoustic path is also shifted. As a result the reflections are caused at different positions at the edges of the elliptical post and therefore the force of the pressure nodes of the SSAW are changed too (Fig. 8). This results in a shift of the pattern, but the shape remains the same. Polystyrene beads are always captured in the deepest pressure node and are following it as it is moving by changing the position of the node. Exploiting these two effects the polystyrene beads can be transported in two directions along the post.

Discussion

In the first experiments with two opposed IDTs mainly two patterns of SSAW were observed. Later, the remaining experiments with only one TIDT showed that there exist multiple patterns. Interferences of reflections and incoming SAW clearly explain observed elliptical pattern, when only a single TIDT is used. We can understand these reflections by following explanation: the incoming SAWs couple into the PDMS post. However, because the acoustic impedance Z = ρ·c of PDMS (Z = 1.048 × 10⁶ Ns m⁻³)⁶⁹ and air (Z = 444 Ns m⁻³)⁷⁰ have a large mismatch, a large part of the SAW is reflected at the boundaries of the PDMS post. The reflection coefficient R is given by:⁷¹. These reflections interfere with each other and the incoming SAWs, resulting in the different observed patterns. For the interface between PDMS and water, there is almost no reflection.⁶⁹ The additional patterns are probably also present in the first experiments, but assumedly not as pronounced as the other pattern and therefore could not be visualized by the polystyrene beads. In the experiment with a circular post, all these patterns seem to be visible as different node intervals were measured. ∼50 μm node intervals should be derived from the direct interference of the incoming waves (first pattern) or the interference of two reflected waves (secondary pattern). Smaller node intervals could be derived from the interference of incoming and reflected waves or perhaps from interference of various multiple reflected waves. Consequently both designs, elliptical and circular post, can be used to generate SSAWs with a single IDT, since in both cases the interference patterns generated by reflections and the incoming waves are visible.

We have also shown various applications of our technique, like transporting and alignment of particles. Moving particles with a propagating SSAW has already been demonstrated,^36,72,73 but our method enables to confine the effect on a distinct localized position in the channel and enables a vertical transportation of particles along the cannel by moving SSAW. The transportation velocity is limited by the friction force but also strongly depends on other parameters, such as the radius of the beads, the dimensionless parameters f₁ and f₂ and the wavelength as the acoustic force is related to these parameters. f₁ and f₂ are given by the densities and the acoustic velocities of particles and fluid. But more importantly is the dependence on the radius of the beads that enters to the third power to the acoustic force. The acoustic force is balanced by the Stokes friction which only linearly depends on r. Therefore, larger particles can be transported faster. Also, with higher frequency the acoustic force raises, so this would be a potential way for small particles.

Alignment of particles has also been demonstrated,^63,74 but as in the case of transportation, this could now be realized on localized regions of the channel. These two methods, as well as others, can greatly benefit by the technique we introduce and enhance functionality for a broader range of applications.

Additionally, as a SSAW perpendicularly to the channel can be excited without damping, alignment and sorting of object in this direction is feasible.

As a practical application, separation of 15 μm beads from 10 μm beads was demonstrated. By orientating the microchannel with the PDMS post diagonally towards the IDTs, only beads, for which the acoustic force dominates the friction force, are deflected. As soon as the beads exit the area with the post (section 1), the acoustic force vanishes and particles follow the fluid again (section 2). Similarly, the 15 μm beads are collected at a specific region of the channel, but are not pushed against a wall. This method enables a deflection with SSAW of more extended distances, as compared to other methods which are limited by a deflection length of λ/4.^58–60 The same device also demonstrates the washing of the 15 μm beads, by transferring the beads from medium flowing in section 1 to medium flowing section 2. Here, the tracer particles (10 μm beads) indicate that the fluid media in both sections do not mix significantly.

Generally one would expect the interface between section 1 and section 2 to be identical with the post boundary, however as can be seen from diagram 4b, there is a slight deviation. This deviation is caused by the limited field of view of our microscope at this magnification, which limits the tracking of the full trajectories of some particles.

Defining the outlet with a width of 185 μm, which is a bit larger than the section 2 in Fig. 4, we get a purity before sorting of 55 ± 4%. After sorting the purity is boosted to 72 ± 4% with a sorting efficiency of 80 ± 4%. These values could be increased dramatically by focusing all particles to section 1 before sorting. As we only wanted to show an application of our method, we did not want to make the device more complex then absolutely necessary.

The throughput for filtering and washing could be easily increased by rising the flow rates or the concentrations of the particles. As the acoustic force has to be at least as large as the friction force, the power has to be risen, too.

Conclusion

We have shown a new robust technique which allows excellent control of the acoustic force of a SAW in a PDMS microchannel. With the structured feature embedded in the ultra-thin PDMS foil below the microchannel, the SAW can be localized for almost every specific application. Further, the SAW can be coupled into the microchannel in every designated direction and is not damped until it reaches the post. The microchannel can be orientated at any angle towards the IDT(s) and can even cross the IDT(s). We have demonstrated different basic functions and applications of this technique, like shaping the geometry of SSAWs, or generating a SSAW with only a single TIDT. It is possible to transport assemblies of beads above the post by changing the position of the acoustic path of a TIDT. Beads can also be transported by a moving SSAW, which is generated by two opposed, identical IDTs, but one is excited with a slightly different frequency. Guiding of particles is also very simple to implement: a SSAW forces beads to travel along the post parallel to the SSAW but diagonal to the flow of the fluid. Based on this principle a label-free filtering and washing device has also been shown, separating 15 μm beads from 10 μm beads. The deflection length depends only on the post dimensions and not on the wavelength anymore.

Our technique is an extension and complement to current state of the art SSAW techniques, as the device is simple to produce and can be easily integrated with other on-chip components. The full enclosure of the sample into a PDMS environment makes it biocompatible and avoids direct sample exposure to the surrounding air and suppresses cross-contamination. It is useful for further development of micro total analysis systems (μTAS) particularly when the PDMS composite is used as a sample containing disposable and the IDT chip is reused. This technique provides a simple platform to for manipulating single objects, filtering, washing, separating and pattering particles or other objects, such as cells. Because only one chip design can be reused for various operations our technique allows the less experienced user to use and exploit the multiple advantages acoustofluidics offers.

In the future different post geometries, such as triangles, should be examined in further experiments for a better quantification of the effects and to extend the field of applications. With different or more complex designs a controlled transportation of beads in the microchannel over even larger distances and in various direction is feasible and will be the focus of investigations. Other application, like localized acoustic tweezers, or the washing of particles or cells could easily be realized, as fixing single particles at distinct positions in the microchannel is possible.

Calculation of moving SSAW velocity

Amplitude y(x) of the superposition of two counter-travelling waves with same Amplitude and an angular frequency difference of Δω.

y(x) = Ae^i(ωt−kx) + Ae^i(ωt+kx)

= Ae^iωt(e^−ikx + e^i(Δωt+kx))

= Ae^{i(ω+Δω/2)t}(e^{−i(Δωt/2+kx)} + e^{i(Δωt/2+kx)})

= 2Ae^{i(ω+Δω/2)t} cos(Δωt/2 + kx)

This results in a velocity of the moving SSAW of v = Δf/2λ

Variables

A	Amplitude of single wave
F	Frequency
ω = 2πf	Angular frequency
k	Wavenumber
t	Time

Acknowledgements

R. R. and T. F. acknowledge support by the “Bayerisches Staatsministerium für Umwelt und Verbraucherschutz”. T. F. thanks the DFG for financial support. R. R. and V. S. thank Achim Wixforth for his support and Lothar Schmid for helpful discussions.

References

1. Y. Chen, T.-H. Wu, Y.-C. Kung, M. a Teitell and P.-Y. Chiou, Analyst, 2013, 138, 7308–7315.
2. T. Franke, S. Braunmüller, L. Schmid, A. Wixforth and D. a Weitz, Lab Chip, 2010, 10, 789–794.
3. S. Li, X. Ding, F. Guo, Y. Chen, M. I. Lapsley, S.-C. S. Lin, L. Wang, J. P. McCoy, C. E. Cameron and T. J. Huang, Anal. Chem., 2013, 85, 5468–5474.
4. L. Mazutis, J. Gilbert, W. L. Ung, D. a. Weitz, A. D. Griffiths and J. a Heyman, Nat. Protoc., 2013, 8, 870–891.
5. T. Franke, A. R. Abate, D. a Weitz and A. Wixforth, Lab Chip, 2009, 9, 2625–2627.
6. S. Kapishnikov, V. Kantsler and V. Steinberg, J. Stat. Mech.: Theory Exp., 2006, 2006, P01012.
7. Y. Chen, A. A. Nawaz, Y. Zhao, P.-H. Huang, J. P. McCoy, S. J. Levine, L. Wang and T. J. Huang, Lab Chip, 2014, 14, 916–923.
8. L. Schmid, D. A. Weitz and T. Franke, Lab Chip, 2014, 14, 3710–3718.
9. P. Sethu, A. Sin and M. Toner, Lab Chip, 2006, 6, 83–89.
10. D. Di Carlo, J. F. Edd, D. Irimia, R. G. Tompkins and M. Toner, Anal. Chem., 2008, 80, 2204–2211.
11. V. VanDelinder and A. Groisman, Anal. Chem., 2007, 79, 2023–2030.
12. G. Destgeer, K. H. Lee, J. H. Jung, A. Alazzam and H. J. Sung, Lab Chip, 2013, 13, 4210–4216.
13. V. Skowronek, R. W. Rambach, L. Schmid, K. Haase and T. Franke, Anal. Chem., 2013, 85, 9955–9959.
14. J. Oakey, R. W. Applegate, E. Arellano, D. Di Carlo, S. W. Graves and M. Toner, Anal. Chem., 2010, 82, 3862–3867.
15. G. Destgeer, S. Im, B. Hang Ha, J. Ho Jung, M. Ahmad Ansari and H. Jin Sung, Appl. Phys. Lett., 2014, 104, 023506.
16. D. J. Collins, T. Alan and A. Neild, Lab Chip, 2014, 14, 1595–1603.
17. M. Sesen, T. Alan and A. Neild, Lab Chip, 2014, 14, 3325–3333.
18. L. Schmid and T. Franke, Appl. Phys. Lett., 2014, 104, 133501.
19. R. R. Pompano, W. Liu, W. Du and R. F. Ismagilov, Annu. Rev. Anal. Chem., 2011, 4, 59–81.
20. D. J. Collins, T. Alan, K. Helmerson and A. Neild, Lab Chip, 2013, 13, 3225–3231.
21. Y. Xie, D. Ahmed, M. I. Lapsley, M. Lu, S. Li and T. J. Huang, J. Lab. Autom., 2014, 19, 137–143.
22. A. Wixforth, C. Strobl, C. Gauer, A. Toegl, J. Scriba and Z. v. Guttenberg, Anal. Bioanal. Chem., 2004, 379, 982–991.
23. S. Miltenyi, W. Müller, W. Weichel and A. Radbruch, Cytometry, 1990, 11, 231–238.
24. E. Mirowski, J. Moreland, A. Zhang, S. E. Russek and M. J. Donahue, Appl. Phys. Lett., 2005, 86, 243901.
25. K. E. McCloskey, J. J. Chalmers and M. Zborowski, Anal. Chem., 2003, 75, 6868–6874.
26. S. E. Yalcin, A. Sharma, S. Qian, S. W. Joo and O. Baysal, Electrophoresis, 2010, 31, 3711–3718.
27. N. A. M. Yunus, H. Nili and N. G. Green, Electrophoresis, 2013, 34, 969–978.
28. C. Zhang, K. Khoshmanesh, A. Mitchell and K. Kalantar-Zadeh, Anal. Bioanal. Chem., 2010, 396, 401–420.
29. J. Zhu, T.-R. J. Tzeng and X. Xuan, Electrophoresis, 2010, 31, 1382–1388.
30. U. Kim, J. Qian, S. a Kenrick, P. S. Daugherty and H. T. Soh, Anal. Chem., 2008, 80, 8656–8661.
31. M. M. Wang, E. Tu, D. E. Raymond, J. M. Yang, H. Zhang, N. Hagen, B. Dees, E. M. Mercer, A. H. Forster, I. Kariv, P. J. Marchand and W. F. Butler, Nat. Biotechnol., 2005, 23, 83–87.
32. S. B. Kim, S. Y. Yoon, H. J. Sung and S. S. Kim, Anal. Chem., 2008, 80, 2628–2630.
33. I. M. White, S. H. Yazdi and W. W. Yu, Microfluid. Nanofluid., 2012, 13, 205–216.
34. K. S. Lee, S. Y. Yoon, S. B. Kim, K. H. Lee, H. J. Sung and S. S. Kim, Microfluid. Nanofluid., 2012, 13, 9–17.
35. S.-C. S. Lin, X. Mao and T. J. Huang, Lab Chip, 2012, 12, 2766–2770.
36. X. Ding, S.-C. S. Lin, B. Kiraly, H. Yue, S. Li, I.-K. Chiang, J. Shi, S. J. Benkovic and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11105–11109.
37. C. D. Wood, S. D. Evans, J. E. Cunningham, R. O’Rorke, C. Wälti and A. G. Davies, Appl. Phys. Lett., 2008, 92, 044104.
38. L. Schmid and T. Franke, Lab Chip, 2013, 13, 1691–1694.
39. R. D. O'Rorke, C. D. Wood, C. Wälti, S. D. Evans, A. G. Davies and J. E. Cunningham, J. Appl. Phys., 2012, 111, 094911.
40. T. M. Geislinger and T. Franke, Biomicrofluidics, 2013, 7, 44120.
41. P. Augustsson, C. Magnusson, M. Nordin, H. Lilja and T. Laurell, Anal. Chem., 2012, 84, 7954–7962.
42. F. Petersson, A. Nilsson, C. Holm, H. Jonsson and T. Laurell, Lab Chip, 2005, 5, 20–22.
43. Y. Chen, S. Li, Y. Gu, P. Li, X. Ding, L. Wang, J. P. McCoy, S. J. Levine and T. J. Huang, Lab Chip, 2014, 14, 924–930.
44. J. Shi, D. Ahmed, X. Mao, S.-C. S. Lin, A. Lawit and T. J. Huang, Lab Chip, 2009, 9, 2890–2895.
45. P. Augustsson, L. B. Åberg, A.-M. K. Swärd-Nilsson and T. Laurell, Microchim. Acta, 2008, 164, 269–277.
46. F. Petersson, A. Nilsson, H. Jönsson and T. Laurell, Anal. Chem., 2005, 77, 1216–1221.
47. C. R. P. Courtney, C.-K. Ong, B. W. Drinkwater, P. D. Wilcox, C. Demore, S. Cochran, P. Glynne-Jones and M. Hill, J. Acoust. Soc. Am., 2010, 128, EL195–EL199.
48. O. Jakobsson, C. Grenvall, M. Nordin, M. Evander and T. Laurell, Lab Chip, 2014, 14, 1943–1950.
49. P. Mishra, M. Hill and P. Glynne-Jones, Biomicrofluidics, 2014, 8, 034109.
50. P. B. Muller, M. Rossi, Á. G. Marín, R. Barnkob, P. Augustsson, T. Laurell, C. J. Kähler and H. Bruus, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 023006.
51. P. Glynne-Jones, C. E. M. Démoré, C. Ye, Y. Qiu, S. Cochran and M. Hill, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2012, 59, 1258–1266.
52. Y. Qiu, H. Wang, C. E. M. Demore, D. a Hughes, P. Glynne-Jones, S. Gebhardt, A. Bolhovitins, R. Poltarjonoks, K. Weijer, A. Schönecker, M. Hill and S. Cochran, Sensors, 2014, 14, 14806–14838.
53. S. Haeberle and R. Zengerle, Lab Chip, 2007, 7, 1094–1110.
54. P. S. Dittrich, K. Tachikawa and A. Manz, Anal. Chem., 2006, 78, 3887–3908.
55. Y. Bourquin, R. Wilson, Y. Zhang, J. Reboud and J. M. Cooper, Adv. Mater., 2011, 23, 1458–1462.
56. J. Reboud, Y. Bourquin, R. Wilson, G. S. Pall, M. Jiwaji, A. R. Pitt, A. Graham, A. P. Waters and J. M. Cooper, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15162–15167.
57. X. Ding, Z. Peng, S.-C. S. Lin, M. Geri, S. Li, P. Li, Y. Chen, M. Dao, S. Suresh and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2014, 1–6.
58. O. Jakobsson, C. Grenvall, M. Nordin, M. Evander and T. Laurell, Lab Chip, 2014, 14, 1943–1950.
59. J. Shi, H. Huang, Z. Stratton, Y. Huang and T. J. Huang, Lab Chip, 2009, 9, 3354–3359.
60. J. Nam, Y. Lee and S. Shin, Microfluid. Nanofluid., 2011, 11, 317–326.
61. E. Meijering, O. Dzyubachyk and I. Smal, Methods Enzymol., 2012, 504, 183–200.
62. J. Shi, H. Huang, Z. Stratton, Y. Huang and T. J. Huang, Lab Chip, 2009, 9, 3354–3359.
63. J. Shi, X. Mao, D. Ahmed, A. Colletti and T. J. Huang, Lab Chip, 2008, 8, 221–223.
64. X. Ding, S.-C. S. Lin, M. I. Lapsley, S. Li, X. Guo, C. Y. Chan, I.-K. Chiang, L. Wang, J. P. McCoy and T. J. Huang, Lab Chip, 2012, 12, 4228–4231.
65. J. Nam, H. Lim and S. Shin, Korea-Australia Rheology Journal, 2012, 23, 255–267.
66. M. Wiklund and H. M. Hertz, Lab Chip, 2006, 6, 1279–1292.
67. H. Bruus, Lab Chip, 2012, 12, 1014–1021.
68. M. Settnes and H. Bruus, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 016327.
69. I. Leibacher, S. Schatzer and J. Dual, Lab Chip, 2014, 14, 463–470.
70. R. Weast, M. Astle and W. Beyer, CRC handbook of chemistry and physics, 90th edn, 1988.
71. L. Landau and E. Lifshitz, Course of theoretical physics, 1980.
72. L. Meng, F. Cai, Z. Zhang, L. Niu, Q. Jin, F. Yan, J. Wu, Z. Wang and H. Zheng, Biomicrofluidics, 2011, 5, 044104.
73. S. B. Q. Tran, P. Marmottant and P. Thibault, Appl. Phys. Lett., 2012, 101, 114103.
74. X. Ding, J. Shi, S.-C. S. Lin, S. Yazdi, B. Kiraly and T. J. Huang, Lab Chip, 2012, 12, 2491–2497.

---

Footnote

† Electronic supplementary information (ESI) available: Movie of a moving SSAW on a squared post. See DOI: 10.1039/c4ra13002b

---