Rapid evaluation of the interaction energies for carbohydrate-containing hydrogen-bonded complexes via the polarizable dipole–dipole interaction model combined with NBO or AM1 charge†
Jiao-Jiao Hao and
Chang-Sheng Wang*
School of Chemistry and Chemical Engineering, Liaoning Normal University, Dalian 116029, P. R. China. E-mail: chwangcs@lnnu.edu.cn
First published on 17th December 2014
Abstract
The polarizable dipole–dipole interaction model, which explicitly involves the permanent dipole–dipole interaction, the van der Waals interaction, the polarization contribution and the covalency interaction, has been proposed in our lab for N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C–H⋯O
C and C–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen-bonded complexes containing amides and peptides. In this paper, the polarizable dipole–dipole interaction model is further developed and applied to hydrogen-bonded complexes containing ribose, deoxyribose, fructose, glucose, maltose and sucrose. We regard the chemical bonds O–H, C–H and C–O in ribose, deoxyribose, fructose, glucose, maltose and sucrose molecules as bond dipoles. The magnitude of the bond dipole moment varies according to its environment. The parameters needed are first determined from the training dimers. The polarizable dipole–dipole interaction model is then applied to a series of carbohydrate-containing hydrogen-bonded complexes. The calculation results show that the polarizable dipole–dipole interaction model not only can produce the equilibrium hydrogen bond distances compared favorably with those produced by the MP2/6-31+G(d,p) method and can produce the interaction energies in good agreement with those yielded by the high quality counterpoised-corrected MP2/aug-cc-pVTZ method, but is much more efficient as well, demonstrating that the polarizable dipole–dipole interaction model and the parameters determined are reasonable and useful.
C hydrogen-bonded complexes containing amides and peptides. In this paper, the polarizable dipole–dipole interaction model is further developed and applied to hydrogen-bonded complexes containing ribose, deoxyribose, fructose, glucose, maltose and sucrose. We regard the chemical bonds O–H, C–H and C–O in ribose, deoxyribose, fructose, glucose, maltose and sucrose molecules as bond dipoles. The magnitude of the bond dipole moment varies according to its environment. The parameters needed are first determined from the training dimers. The polarizable dipole–dipole interaction model is then applied to a series of carbohydrate-containing hydrogen-bonded complexes. The calculation results show that the polarizable dipole–dipole interaction model not only can produce the equilibrium hydrogen bond distances compared favorably with those produced by the MP2/6-31+G(d,p) method and can produce the interaction energies in good agreement with those yielded by the high quality counterpoised-corrected MP2/aug-cc-pVTZ method, but is much more efficient as well, demonstrating that the polarizable dipole–dipole interaction model and the parameters determined are reasonable and useful.
Introduction
Carbohydrate recognition through noncovalent interactions, which is known to mediate cell adhesion, the infection of a cell by pathogens, the distribution and reactivity of proteins within cells, and many aspects of the immune response, has attracted a great deal of attention.1–3 Among the various noncovalent interactions, hydrogen bonding plays an important role in carbohydrate recognition and also in many other chemical and biological processes.4–13 For example, the X-ray crystal structures of protein–carbohydrate complexes invariably reveal intensive hydrogen bonding between host and guest.4,5 Cocinero et al. explored carbohydrate–peptide interactions in the gas phase using double-resonance IR-UV spectroscopy and DFT method. They found that the carbohydrates are bound through hydrogen bonding to the dipeptide chain.6 Paul et al. carried out molecular dynamics simulation to investigate the role of trehalose molecules on the change in the structural and dynamical properties of aqueous N-methylacetamide (NMA) solution. They observed that on addition of trehalose, water–NMA hydrogen bonds were replaced by NMA–trehalose. However, trehalose has essentially no effect on changing the total number of hydrogen bonds formed by a single NMA molecule with solution species.7 Zhao et al. found that the intermolecular hydrogen bond in the electronic excited state is greatly strengthen for coumarin chromophores and weakened for thiocarbonyl chromophores, and the radiationless deactivations can be dramatically influenced through the regulation of electronic states by hydrogen bonding interactions.8,9 Carcabal et al. found that the water molecule can insert into the carbohydrate at a position where it can replace a weak intramolecular interaction by two strong intermolecular O–H⋯O hydrogen bonds and the insertion can produce significant changes in the conformational preferences of the carbohydrates.10 Because carbohydrate-related hydrogen bonding plays a significant role in chemical and biological processes, evaluating the strengths of these hydrogen bonding interactions is important.In the past decades thanks to accurate results of both computational and experimental studies, great progress has been achieved in the studies of hydrogen bond.14–34 High quality ab initio methods, such as the Møller–Plesset perturbation theory14 and coupled cluster technique,15,16 have become standard now in calculations of the structures and energetic properties of simple hydrogen-bonding systems.17,18 Riley and Hobza assessed the performance of the MP2 method, when paired with several different medium and extended basis sets, for the accurate computation of interaction energies of small hydrogen-bonded complexes, they found that the MP2/aug-cc-pVTZ method produces very good result for hydrogen bonding interactions.19 A comparison of experimental and computed energies of model peptide backbone structures concluded that MP2 energetics are within about 1 kcal mol−1 of those evaluated experimentally.20 Although high level ab initio methods such as MP2 and CCSD(T) can produce accurate hydrogen bonding interaction energies for small hydrogen-bonded complexes, they are limited when applied to large systems such as carbohydrates, proteins and nucleic acids due to excessive CPU time and enormous capacities of hard disk required.
Aiming at accurately and rapidly modeling the interactions for hydrogen-bonded complexes in large biosystems, the polarizable dipole–dipole interaction model has been proposed and applied to hydrogen-bonded complexes containing amides, peptides, uracil, and thymine.35,36 In this paper the polarizable dipole–dipole interaction model was further developed and applied to hydrogen-bonded complexes containing ribose, deoxyribose, fructose, glucose, maltose and sucrose. The calculation results show that the equilibrium hydrogen bond distances and the interaction energies predicted by the polarizable dipole–dipole interaction model compare well with the corresponding values obtained from MP2 calculations, demonstrating that the polarizable dipole–dipole interaction model is reasonable and useful.
The polarizable dipole–dipole interaction model
In the polarizable dipole–dipole interaction model, we use eqn (1) to produce the equilibrium hydrogen bond distances and use eqn (2) to calculate the interaction energies.35
 | (1) |
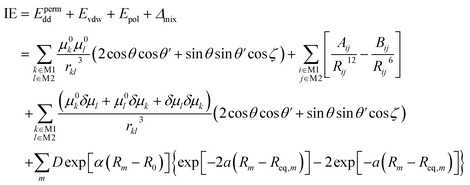 | (2) |
The permanent dipole–dipole interaction Epermdd between the molecule M1 and the molecule M2 is calculated via eqn (3). Similar expressions have been derived by a number of authors.37–40
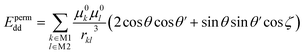 | (3) |
In eqn (3), μ0k and μ0l are the permanent bond dipole moments and μ0k belongs to the molecule M1 while μ0l belongs to the molecule M2. rkl is the distance between the two bond dipole centers. The summation k covers all bond dipoles in the molecule M1 and the summation l covers all bond dipoles in the molecule M2.
The van der Waals interaction Evdw between the molecule M1 and the molecule M2 is calculated via eqn (4) in which Aij = εij(R*ij),12 Bij = 2εij(R*ij),6 R*ij = R*i + R*j, εij = (εiεj)1/2. R*i and εi are the van der Waals radius parameter and the van der Waals well depth parameter of the ith atom, respectively.
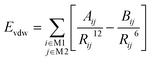 | (4) |
The summation i covers all atoms in the molecule M1 and the summation j covers all atoms in the molecule M2.
When the molecule M1 and the molecule M2 approach each other, polarization happens. The permanent bond dipole moment μ0k of the isolated molecule M1 changes to μk = μ0k + δμk, where δμk stands for the bond dipole moment increment induced by the second molecule M2 (the environment of the molecule M1). We refer to δμk as the induced bond dipole moment. The polarization contribution Epol to the total interaction energy is calculated via eqn (5).
 | (5) |
The summation k covers all bond dipoles in the molecule M1 and the summation l covers all bond dipoles in the molecule M2.
The covalency and other mixed contribution Δmix to the total interaction energy is estimated via eqn (6). Supposing there exist m hydrogen bonds between the molecules M1 and M2, Rm stands for the distance between the donor H atom and the acceptor O atom of the mth hydrogen bond, Req,m is the equilibrium hydrogen bond distance between the H atom and the O atom of the mth hydrogen bond. D, α, a, and R0 are the parameters depending on the hydrogen bond type.
 | (6) |
The summation m covers all hydrogen bonds between the molecule M1 and the molecule M2.
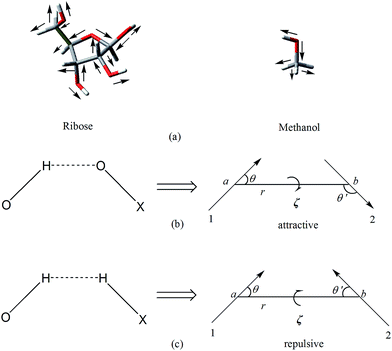
In this paper, we further applied the polarizable dipole–dipole interaction model to hydrogen-bonded complexes containing ribose, deoxyribose, fructose, glucose, maltose and sucrose. As shown in Fig. 1a, we regard the C–O, O–H and C–H bonds of these molecules as bond dipoles. There exist 16 bond dipoles in a ribose molecule and 5 bond dipoles in a methanol molecule. Therefore, for a complex composed of one ribose and one methanol, there are total 80 dipole–dipole interactions between the two molecules. The interaction between two permanent dipoles μ0k and μ0l in which μ0k belongs to molecule M1 while μ0l belongs to molecule M2 may be attractive or repulsive depending on the relative orientation of the two dipoles. The interaction is attractive when the relative orientation is like Fig. 1b and repulsive when the relative orientation is like Fig. 1c.
Parameterization
In order to use eqn (1) to predict the equilibrium hydrogen bond distances, the permanent bond dipole moment μ0, the van der Waals radius parameter and well depth parameter R*i and εi should be known first. In this paper, the values of the permanent bond dipole moments μ0 for O–H, N–H, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, C–O, and C–H are taken from ref. 41 directly, the value of the permanent bond dipole moment μ0 for Cα–H (Cα–H is the bond formed between a hydrogen atom and an α-carbon atom, and the definition for the α-carbon is the same as that adopted in AMBER99 force field42) is taken from ref. 35 directly, the values of the van der Waals parameters R*i and εi for the atoms except the sp3 oxygen and the hydrogen attached to the sp3 oxygen are taken directly from AMBER99 force field.42 The van der Waals radius and well depth parameters R*i and εi for the sp3 oxygen and the hydrogen attached to the sp3 oxygen need to be parameterized.
O, C–O, and C–H are taken from ref. 41 directly, the value of the permanent bond dipole moment μ0 for Cα–H (Cα–H is the bond formed between a hydrogen atom and an α-carbon atom, and the definition for the α-carbon is the same as that adopted in AMBER99 force field42) is taken from ref. 35 directly, the values of the van der Waals parameters R*i and εi for the atoms except the sp3 oxygen and the hydrogen attached to the sp3 oxygen are taken directly from AMBER99 force field.42 The van der Waals radius and well depth parameters R*i and εi for the sp3 oxygen and the hydrogen attached to the sp3 oxygen need to be parameterized.
In order to determine the van der Waals parameters R*i and εi for the sp3 oxygen and the hydrogen attached to the sp3 oxygen, six dimers (Fig. S1†) are chosen as training dimers. Geometry optimizations for the training dimers are first carried out at the MP2/6-31+G(d,p) level and the equilibrium hydrogen bond distances RMP2eq(H⋯O) are obtained. Then the value of eqn (1) is calculated only varying the distance R(H⋯O) between proton donor hydrogen atom and proton acceptor oxygen atom from 1.7 to 20 Å with other structural parameters fixed at the optimized values of its dimer. The energy curves of the training dimers are obtained and the equilibrium hydrogen bond distance Req(H⋯O) is determined by eqn (1). Then the van der Waals parameters R*i and εi for the sp3 oxygen and the hydrogen attached to the sp3 oxygen are adjusted in order to make Req(H⋯O) as close to RMP2eq(H⋯O) as possible for these dimers. The values of the van der Waals parameters R*i and εi are thus determined.
As soon as the equilibrium hydrogen bond distance Req(H⋯O) of a hydrogen-bonded dimer is determined via eqn (1), the NBO charges are calculated by using B3LYP/6-31G(d) method to obtain the atomic partial charge q in the dimer and q0 in the monomer. The induced bond dipole moment δμ is then estimated via δμ = d(q − q0). Therefore, for a hydrogen-bonded complex, the value of eqn (2) can be calculated if the parameters D, α, a, and R0 are known.
The parameters D, α, a, and R0 for the N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bond have been determined35 and will be used directly in this work. The parameters D, α, a, and R0 for the O–H⋯O hydrogen bond are determined as following: the accurate interaction energy curves of the training dimers in Fig. S1† are first calculated at the CP-corrected MP2/aug-cc-pVTZ level. The parameters D, α, a, and R0 for the O–H⋯O hydrogen bond are then derived from fitting to these CP-corrected MP2/aug-cc-pVTZ interaction energy curves via eqn (2).
C hydrogen bond have been determined35 and will be used directly in this work. The parameters D, α, a, and R0 for the O–H⋯O hydrogen bond are determined as following: the accurate interaction energy curves of the training dimers in Fig. S1† are first calculated at the CP-corrected MP2/aug-cc-pVTZ level. The parameters D, α, a, and R0 for the O–H⋯O hydrogen bond are then derived from fitting to these CP-corrected MP2/aug-cc-pVTZ interaction energy curves via eqn (2).
The parameters derived from the training dimers are listed in Table 1 together with the permanent bond dipole moments μ0 and the van der Waals parameters εi and R*i for other atoms. In Fig. S1† are listed the equilibrium hydrogen bond distances predicted by eqn (1) and by the MP2/6-31+G(d,p) method. Fig. S1† shows that eqn (1) produces the equilibrium hydrogen bond distances in good agreement with those obtained by the MP2/6-31+G(d,p) method. With respect to the MP2/6-31+G(d,p) equilibrium hydrogen bond distances, eqn (1) exhibits a mean unsigned error (MUE) of 0.023 Å and a root mean squared error (RMSE) of 0.028 Å. In Table S1† are the interaction energies of these training dimers predicted by eqn (2) and by the CP-corrected MP2/aug-cc-pVTZ method. Table S1† shows that for all the training dimers, eqn (2) produces the interaction energies as accurately as those produced by the CP-corrected MP2/aug-cc-pVTZ method. With respect to the CP-corrected MP2/aug-cc-pVTZ interaction energies, eqn (2) exhibits an MUE of 0.16 kcal mol−1, an RMSE of 0.24 kcal mol−1 and an MRE of 2.7%. These comparisons indicate that the parameters determined in this work are reasonable.
| Description | Value |
|---|---|
| Parameters for bond dipole moments μ0 (Debye) | |
| a The values taken from ref. 41.b The values taken from ref. 35.c The values taken from AMBER99 force field.d The values obtained in this work using the training dimers. | |
| μ0 (O–H) | 1.51a |
| μ0 (N–H) | 1.31a |
μ0 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
2.65a |
| μ0 (C–O) | 0.70a |
| μ0 (C–H) | 0.30a |
| μ0 (Cα–H) | 0.70b |
| Parameters for van der Waals interactions | R*i (Å) | εi (kcal mol−1) | |
|---|---|---|---|
| Carbon | Any sp3 carbon | 1.9080c | 0.1094c |
| Any carbonyl sp2 carbon | 1.9080c | 0.0860c | |
| Nitrogen | sp2 nitrogen | 1.8240c | 0.1700c |
| Oxygen | sp2 oxygen | 1.6612c | 0.2100c |
| sp3 oxygen in water | 1.6210d | 0.2104d | |
| sp3 oxygen in alcohols and carbohydrates | 1.6500d | 0.1700d | |
| Hydrogen | H attached to N | 0.6000c | 0.0157c |
| H attached to C | 1.1000b | 0.0157c | |
| H attached to Cα | 1.0000b | 0.0157c | |
| H attached to sp3 oxygen in water | 0.7500d | 0.0157d | |
| H attached to sp3 oxygen in alcohols and carbohydrates | 0.5800d | 0.0157d | |
It should be pointed out here that eqn (2) can produce not only the accurate interaction energies, but the accurate equilibrium hydrogen bond distances as well. Tables S2 and S3† show that both eqn (1) and (2) can yield accurate equilibrium hydrogen bond distances, however, eqn (1) is more efficient than eqn (2) and that is the reason why we use eqn (1) to predict the equilibrium hydrogen bond distances.
Application
The equilibrium hydrogen bond distances
Eqn (1) and the parameters listed in Table 1 are used to predict the equilibrium hydrogen bond distances for hydrogen-bonded complexes containing ribose, deoxyribose, glucose, fructose, sucrose and maltose (Fig. 2 and 3). In Fig. 2 and 3 are also given the equilibrium hydrogen bond distances Req(H⋯O) predicted by eqn (1). For relatively small complexes (Fig. 2), the equilibrium hydrogen bond distances Req(H⋯O) are also calculated by using the MP2/6-31+G(d,p) method and the results are listed in Fig. 2. For more complicated complexes (Fig. 3), the equilibrium hydrogen bond distances Req(H⋯O) are calculated by using the B3LYP/6-31+G(d,p) method and the results are listed in Fig. 3. | ||
| Fig. 2 The testing dimers. The equilibrium hydrogen bonding distances predicted by eqn (1) are given in the corresponding position. Values in parentheses are obtained from MP2/6-31+G(d,p) calculations. All distances are in Å. | ||
 | ||
| Fig. 3 The testing dimers. The equilibrium hydrogen bonding distances predicted by eqn (1) are given in the corresponding position. Values in parentheses are obtained from B3LYP/6-31+G(d,p) calculations. All distances are in Å. | ||
Fig. 2 shows that eqn (1) produce the equilibrium hydrogen bond distances for these complexes in good agreement with those produced by the MP2/6-31+G(d,p) method. With respect to the MP2/6-31+G(d,p) hydrogen bond distances, eqn (1) exhibits an MUE of 0.025 Å and an RMSE of 0.029 Å, demonstrating that eqn (1) can yield accurate equilibrium hydrogen bond distances for these carbohydrate-containing hydrogen-bonded complexes.
Fig. 3 shows that eqn (1) produce the equilibrium hydrogen bond distances for these complicated complexes in good agreement with those produced by the B3LYP/6-31+G(d,p) method. With respect to the B3LYP/6-31+G(d,p) equilibrium hydrogen bond distances, eqn (1) exhibits an MUE of 0.015 Å and an RMSE of 0.021 Å, further demonstrating that eqn (1) can yield accurate equilibrium hydrogen bond distances for carbohydrate-containing hydrogen-bonded complexes.
The interaction energies
Based on the structures obtained via eqn (1), the interaction energies were obtained by using eqn (2) in which the polarization contribution Epol is estimated either with the NBO atomic charges at the B3LYP/6-31G(d) level (hereafter we refer to as eqn (2) with NBO charge) or with the AM1 atomic charges at the AM1 level (hereafter we refer to as eqn (2) with AM1 charge). Based on the structures obtained at the MP2/6-31+G(d,p) level or at the B3LYP/6-31+G(d,p) level, the interaction energies were obtained by using CP-corrected MP2/aug-cc-pVTZ method. In Table 2 are listed the interaction energies IE obtained via eqn (2) and via the CP-corrected MP2/aug-cc-pVTZ method. In Table 2, the data in the second column are the interaction energies obtained by the CP-corrected MP2/aug-cc-pVTZ method, the data in the third column are the interaction energies obtained by eqn (2) with NBO charge, the data in the sixth column are the interaction energies obtained by eqn (2) with AM1 charge.| Dimers | IEMP2 | Eqn (2) with NBO charge | Eqn (2) with AM1 charge | AMBER99 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| IE | ΔE | δ (%) | IE | ΔE | δ (%) | IE | ΔE | δ (%) | ||
| a ΔE = IE − IEMP2, δ = |ΔE ÷ IEMP2| × 100%, all energies are in kcal mol−1. | ||||||||||
| 1 | −11.29 | −10.35 | 0.94 | 8.3 | −10.53 | 0.76 | 6.7 | −10.62 | 0.67 | 5.9 |
| 2 | −11.19 | −10.28 | 0.91 | 8.1 | −10.46 | 0.73 | 6.5 | −10.11 | 1.08 | 9.7 |
| 3 | −10.21 | −9.56 | 0.65 | 6.4 | −9.56 | 0.65 | 6.4 | −9.23 | 0.98 | 9.6 |
| 4 | −9.02 | −9.26 | −0.24 | 2.6 | −9.31 | −0.29 | 3.2 | −9.21 | −0.19 | 2.1 |
| 5 | −13.69 | −14.26 | −0.57 | 4.2 | −14.39 | −0.70 | 5.1 | −12.54 | 1.15 | 8.4 |
| 6 | −13.78 | −14.60 | −0.82 | 6.0 | −14.71 | −0.93 | 6.7 | −12.48 | 1.30 | 9.4 |
| 7 | −19.18 | −18.20 | 0.98 | 5.1 | −18.26 | 0.92 | 4.8 | −18.4 | 0.78 | 4.1 |
| 8 | −10.07 | −9.39 | 0.68 | 6.7 | −9.47 | 0.60 | 6.0 | −9.19 | 0.88 | 8.7 |
| 9 | −12.00 | −12.84 | −0.84 | 7.0 | −13.05 | −1.05 | 8.8 | −9.99 | 2.01 | 16.8 |
| 10 | −12.34 | −12.99 | −0.65 | 5.2 | −13.14 | −0.80 | 6.5 | −9.14 | 3.20 | 25.9 |
| 11 | −12.95 | −13.27 | −0.32 | 2.5 | −13.44 | −0.49 | 3.7 | −12.12 | 0.83 | 6.4 |
| 12 | −20.55 | −20.09 | 0.46 | 2.2 | −20.53 | 0.02 | 0.1 | −18.4 | 2.15 | 10.5 |
| 13 | −9.64 | −8.92 | 0.72 | 7.4 | −9.03 | 0.61 | 6.3 | −8.41 | 1.23 | 12.8 |
| 14 | −8.16 | −7.39 | 0.77 | 9.4 | −7.37 | 0.79 | 9.7 | −8.21 | −0.05 | 0.6 |
| 15 | −11.83 | −12.27 | −0.44 | 3.7 | −12.53 | −0.70 | 5.9 | −10.56 | 1.27 | 10.7 |
| 16 | −9.94 | −9.23 | 0.71 | 7.1 | −9.21 | 0.73 | 7.3 | −10.41 | −0.47 | 4.7 |
| 17 | −24.90 | −23.98 | 0.92 | 3.7 | −24.31 | 0.59 | 2.4 | −23.52 | 1.38 | 5.5 |
| 18 | −14.99 | −13.81 | 1.18 | 7.9 | −14.01 | 0.98 | 6.5 | −13.77 | 1.22 | 8.1 |
| 19 | −15.09 | −13.89 | 1.20 | 8.0 | −14.08 | 1.01 | 6.7 | −13.05 | 2.04 | 13.5 |
| 20 | −11.02 | −10.04 | 0.98 | 8.9 | −10.14 | 0.88 | 8.0 | −9.31 | 1.71 | 15.5 |
| 21 | −10.65 | −9.53 | 1.12 | 10.5 | −10.03 | 0.62 | 5.8 | −10.04 | 0.61 | 5.7 |
| 22 | −10.60 | −9.60 | 1.00 | 9.4 | −9.98 | 0.62 | 5.8 | −9.89 | 0.71 | 6.7 |
| 23 | −11.69 | −10.38 | 1.31 | 11.2 | −10.70 | 0.99 | 8.5 | −11.13 | 0.56 | 4.8 |
| 24 | −12.67 | −12.08 | 0.59 | 4.7 | −12.25 | 0.42 | 3.3 | −11.91 | 0.76 | 6.0 |
| 25 | −12.98 | −12.69 | 0.29 | 2.2 | −12.89 | 0.09 | 0.7 | −13.23 | −0.25 | 1.9 |
| 26 | −22.58 | −19.97 | 2.61 | 11.6 | −20.78 | 1.80 | 8.0 | −17.07 | 5.51 | 24.4 |
| Mean unsigned error (MUE) | 0.84 | 0.72 | 1.27 | |||||||
| Root mean squared error (RMSE) | 0.96 | 0.80 | 1.67 | |||||||
| Mean relative error (MRE) | 6.5 | 5.7 | 9.2 | |||||||
Table 2 shows that eqn (2) predicts the interaction energies for these complexes in good agreement with those produced by the CP-corrected MP2/aug-cc-pVTZ method. For example, for the ribose–acetone dimer 3, we regard one C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and six C–H bonds of the acetone and four O–H bonds, six C–O bonds and six C–H bonds of the ribose as bond dipoles, therefore there exist 112 dipole–dipole interactions. There exists a traditional O–H⋯O(sp2) hydrogen bond in the dimer 3. The interaction energy of the dimer 3 predicted by eqn (2) includes all these permanent dipole–dipole interactions, as well as polarization interaction, van der Waal interaction, and covalency contribution. Table 2 shows that the interaction energy IE of −9.56 kcal mol−1 predicted by eqn (2) with NBO charge and by eqn (2) with AM1 charge has a difference of 0.65 kcal mol−1 from the value of −10.21 kcal mol−1 predicted by the CP-corrected MP2/aug-cc-pVTZ method and the relative error is only 6.4%. For the fructose-deoxyribose dimer 15, we regard all the O–H, C–H, and C–O bonds of the fructose and deoxyribose molecules as bond dipoles, therefore there exist nineteen bond dipoles in the fructose molecule and fifteen bond dipoles in the deoxyribose molecule and total 285 dipole–dipole interactions between a fructose molecule and a deoxyribose molecule. Table 2 shows that for the dimer 15, the interaction energies IE of −12.27 kcal mol−1 predicted by eqn (2) with NBO charge has the differences of 0.44 kcal mol−1 from the value of −11.83 kcal mol−1 predicted by the CP-corrected MP2/aug-cc-pVTZ method, the interaction energies IE of −12.53 kcal mol−1 predicted by eqn (2) with AM1 charge has the differences of 0.70 kcal mol−1 from the value of −11.83 kcal mol−1 predicted by the CP-corrected MP2/aug-cc-pVTZ method. The relative error is only 3.7% and 5.9%, respectively. Table 2 shows that eqn (2) with NBO charge yields the CP-corrected MP2/aug-cc-pVTZ interaction energies within the relative error limits of 12% for all the testing dimers. Compared with the CP-corrected MP2/aug-cc-pVTZ interaction energies, eqn (2) with NBO charge exhibits an MUE of 0.84 kcal mol−1, an RMSE of 0.96 kcal mol−1 and an MRE of 6.5%. eqn (2) with AM1 charge yields the CP-corrected MP2/aug-cc-pVTZ interaction energies within the relative error limits of 10% for all the testing dimers. Compared with the CP-corrected MP2/aug-cc-pVTZ interaction energies, eqn (2) with AM1 charge exhibits an MUE of 0.72 kcal mol−1, an RMSE of 0.80 kcal mol−1 and an MRE of 5.7%. In Table 2 are also listed the interaction energies IE predicted by the well-known force field AMBER99 method. Compared with the CP-corrected MP2/aug-cc-pVTZ interaction energies, AMBER99 exhibits an MUE of 1.27 kcal mol−1, an RMSE of 1.67 kcal mol−1 and an MRE of 9.2%. These comparisons demonstrate that the polarizable dipole–dipole interaction model can yield accurate interaction energies for these hydrogen-bonded complexes, better than AMBER99 method.
O bond and six C–H bonds of the acetone and four O–H bonds, six C–O bonds and six C–H bonds of the ribose as bond dipoles, therefore there exist 112 dipole–dipole interactions. There exists a traditional O–H⋯O(sp2) hydrogen bond in the dimer 3. The interaction energy of the dimer 3 predicted by eqn (2) includes all these permanent dipole–dipole interactions, as well as polarization interaction, van der Waal interaction, and covalency contribution. Table 2 shows that the interaction energy IE of −9.56 kcal mol−1 predicted by eqn (2) with NBO charge and by eqn (2) with AM1 charge has a difference of 0.65 kcal mol−1 from the value of −10.21 kcal mol−1 predicted by the CP-corrected MP2/aug-cc-pVTZ method and the relative error is only 6.4%. For the fructose-deoxyribose dimer 15, we regard all the O–H, C–H, and C–O bonds of the fructose and deoxyribose molecules as bond dipoles, therefore there exist nineteen bond dipoles in the fructose molecule and fifteen bond dipoles in the deoxyribose molecule and total 285 dipole–dipole interactions between a fructose molecule and a deoxyribose molecule. Table 2 shows that for the dimer 15, the interaction energies IE of −12.27 kcal mol−1 predicted by eqn (2) with NBO charge has the differences of 0.44 kcal mol−1 from the value of −11.83 kcal mol−1 predicted by the CP-corrected MP2/aug-cc-pVTZ method, the interaction energies IE of −12.53 kcal mol−1 predicted by eqn (2) with AM1 charge has the differences of 0.70 kcal mol−1 from the value of −11.83 kcal mol−1 predicted by the CP-corrected MP2/aug-cc-pVTZ method. The relative error is only 3.7% and 5.9%, respectively. Table 2 shows that eqn (2) with NBO charge yields the CP-corrected MP2/aug-cc-pVTZ interaction energies within the relative error limits of 12% for all the testing dimers. Compared with the CP-corrected MP2/aug-cc-pVTZ interaction energies, eqn (2) with NBO charge exhibits an MUE of 0.84 kcal mol−1, an RMSE of 0.96 kcal mol−1 and an MRE of 6.5%. eqn (2) with AM1 charge yields the CP-corrected MP2/aug-cc-pVTZ interaction energies within the relative error limits of 10% for all the testing dimers. Compared with the CP-corrected MP2/aug-cc-pVTZ interaction energies, eqn (2) with AM1 charge exhibits an MUE of 0.72 kcal mol−1, an RMSE of 0.80 kcal mol−1 and an MRE of 5.7%. In Table 2 are also listed the interaction energies IE predicted by the well-known force field AMBER99 method. Compared with the CP-corrected MP2/aug-cc-pVTZ interaction energies, AMBER99 exhibits an MUE of 1.27 kcal mol−1, an RMSE of 1.67 kcal mol−1 and an MRE of 9.2%. These comparisons demonstrate that the polarizable dipole–dipole interaction model can yield accurate interaction energies for these hydrogen-bonded complexes, better than AMBER99 method.
Although hydrogen bonds are widely studied, the physical origin of hydrogen bonds is not fully revealed even after 100 years of research. Our model contains the electrostatic permanent dipole–dipole interaction term, the polarization term, the van der Waals term and the covalency contribution, therefore potentially provides a means of disentangling the contributions made to the interaction energy by electrostatic, polarization, van der Waals (dispersion/repulsion), and others (covalency and other mixed effects). In Tables S4 and S5† are listed the interaction energy components predicted by eqn (2) with NBO charge and by eqn (2) with AM1 charge: the permanent dipole–dipole interaction Epermdd, the polarization interaction Epol, the van der Waals interaction Evdw and the covalency contribution Δmix. For example, Table S4† shows that for the deoxyribose–thymine dimer 1, the largest component of the interaction energy is the permanent dipole–dipole interactions Epermdd (−5.75 kcal mol−1), which contributes 55.5% of the overall stabilization, the next in importance is the van der Waals interaction Evdw (−2.43 kcal mol−1), which contributes 23.5%, and the third contribution to the stabilization is the covalency contribution Δmix (−1.42 kcal mol−1), which contributes 13.7%, and the last contribution to the stabilization is the polarization interaction Epol (−0.75 kcal mol−1), which contributes 7.3%, respectively. For the ribose–methanol dimer 8, the largest component of the interaction energy is Epermdd (−5.73 kcal mol−1), which contributes 61.0% of the overall stabilization, the next in importance is Δmix (−2.80 kcal mol−1), which contributes 29.8%, and the last contributions to the stabilization are Epol (−0.64 kcal mol−1) and Evdw (−0.22 kcal mol−1), which contribute 6.9% and 2.3%, respectively. These results suggest that although the nature of hydrogen bonding varies from system to system, the permanent dipole–dipole interactions are the most important part, consistent with previous observations.43–46
The efficiency
We like to point out here that the polarizable dipole–dipole interaction model not only can produce accurate equilibrium hydrogen bond distances and interaction energies for carbohydrate-containing hydrogen-bonded complexes, but is much more efficient as well. For example, Table 3 shows that for the ribose–methanol dimer 8 which contains 26 atoms, it takes about 6 hours 39 minutes (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 seconds) CPU time to carry out a CP-corrected MP2/aug-cc-pVTZ single-point calculation to obtain the interaction energy on the DELL server with 16 Intel Xeon CPUs, 96 GB memory, and a 4.0 TB hard disk. However, it takes only 1 minute 8 seconds (68 seconds) CPU time to obtain the interaction energy by using the polarizable dipole–dipole interaction model combined with NBO charges, that is, eqn (2) with NBO charge is about 350 times faster than the CP-corrected MP2/aug-cc-pVTZ method. Among the 1 minute 8 seconds CPU time, 1 minute 6 seconds CPU time is spent on calculating the NBO charge of the ribose–methanol dimer and of the monomers by using B3LYP/6-31G(d) method. For the glucose–gly dipeptide dimer 17 which contains 43 atoms, it takes about 75 hours 11 minutes (270
940 seconds) CPU time to carry out a CP-corrected MP2/aug-cc-pVTZ single-point calculation to obtain the interaction energy on the DELL server with 16 Intel Xeon CPUs, 96 GB memory, and a 4.0 TB hard disk. However, it takes only 1 minute 8 seconds (68 seconds) CPU time to obtain the interaction energy by using the polarizable dipole–dipole interaction model combined with NBO charges, that is, eqn (2) with NBO charge is about 350 times faster than the CP-corrected MP2/aug-cc-pVTZ method. Among the 1 minute 8 seconds CPU time, 1 minute 6 seconds CPU time is spent on calculating the NBO charge of the ribose–methanol dimer and of the monomers by using B3LYP/6-31G(d) method. For the glucose–gly dipeptide dimer 17 which contains 43 atoms, it takes about 75 hours 11 minutes (270![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 660 seconds) CPU time to carry out a CP-corrected MP2/aug-cc-pVTZ single-point calculation to obtain the interaction energy on the DELL server with 16 Intel Xeon CPUs, 96 GB memory, and a 4.0 TB hard disk. However, it takes only 1 minute 52 seconds (112 seconds) CPU time to obtain the interaction energy by using the polarizable dipole–dipole interaction model combined with NBO charges, that is, eqn (2) with NBO charge is about 2400 times faster than the CP-corrected MP2/aug-cc-pVTZ method. Among the 1 minute 52 seconds CPU time, 1 minute 50 seconds CPU time is spent on calculating the NBO charge of the glucose–gly dipeptide dimer and of the monomers by using B3LYP/6-31G(d) method. For the more complicated sucrose–maltose dimer 26 which contains 90 atoms, it takes about 304 hours 55 minutes (1
660 seconds) CPU time to carry out a CP-corrected MP2/aug-cc-pVTZ single-point calculation to obtain the interaction energy on the DELL server with 16 Intel Xeon CPUs, 96 GB memory, and a 4.0 TB hard disk. However, it takes only 1 minute 52 seconds (112 seconds) CPU time to obtain the interaction energy by using the polarizable dipole–dipole interaction model combined with NBO charges, that is, eqn (2) with NBO charge is about 2400 times faster than the CP-corrected MP2/aug-cc-pVTZ method. Among the 1 minute 52 seconds CPU time, 1 minute 50 seconds CPU time is spent on calculating the NBO charge of the glucose–gly dipeptide dimer and of the monomers by using B3LYP/6-31G(d) method. For the more complicated sucrose–maltose dimer 26 which contains 90 atoms, it takes about 304 hours 55 minutes (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 097
097![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 seconds) CPU time to carry out a CP-corrected MP2/aug-cc-pVTZ single-point calculation to obtain the interaction energy on the DELL server with 16 Intel Xeon CPUs, 96 GB memory, and a 4.0 TB hard disk. However, it takes only 6 minute 25 seconds (385 seconds) CPU time to obtain the interaction energy by using the polarizable dipole–dipole interaction model combined with NBO charges, that is, eqn (2) with NBO charge is about 2800 times faster than the CP-corrected MP2/aug-cc-pVTZ method. Among the 6 minute 25 seconds CPU time, 6 minute 23 seconds CPU time is spent on calculating the NBO charge of the glucose–gly dipeptide dimer and of the monomers by using B3LYP/6-31G(d) method. These comparisons indicate that the polarizable dipole–dipole interaction model is much more efficient than the CP-corrected MP2/aug-cc-pVTZ method and the bigger the system, the more efficient the polarizable dipole–dipole interaction model.
700 seconds) CPU time to carry out a CP-corrected MP2/aug-cc-pVTZ single-point calculation to obtain the interaction energy on the DELL server with 16 Intel Xeon CPUs, 96 GB memory, and a 4.0 TB hard disk. However, it takes only 6 minute 25 seconds (385 seconds) CPU time to obtain the interaction energy by using the polarizable dipole–dipole interaction model combined with NBO charges, that is, eqn (2) with NBO charge is about 2800 times faster than the CP-corrected MP2/aug-cc-pVTZ method. Among the 6 minute 25 seconds CPU time, 6 minute 23 seconds CPU time is spent on calculating the NBO charge of the glucose–gly dipeptide dimer and of the monomers by using B3LYP/6-31G(d) method. These comparisons indicate that the polarizable dipole–dipole interaction model is much more efficient than the CP-corrected MP2/aug-cc-pVTZ method and the bigger the system, the more efficient the polarizable dipole–dipole interaction model.
The polarizable dipole–dipole interaction model combined with AM1 charge (eqn (2) with AM1 charge) is even more efficient. For example, for the ribose–methanol dimer 8 which contains 26 atoms, it takes only 2 seconds CPU time to obtain the interaction energy by using the polarizable dipole–dipole interaction model combined with AM1 charge, that is, eqn (2) with AM1 charge is about 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 times faster than the CP-corrected MP2/aug-cc-pVTZ method. For the glucose–gly dipeptide dimer 17 which contains 43 atoms, it takes only 2 seconds CPU time to obtain the interaction energy by using the polarizable dipole–dipole interaction model combined with AM1 charge, that is, eqn (2) with AM1 charge is about 135
900 times faster than the CP-corrected MP2/aug-cc-pVTZ method. For the glucose–gly dipeptide dimer 17 which contains 43 atoms, it takes only 2 seconds CPU time to obtain the interaction energy by using the polarizable dipole–dipole interaction model combined with AM1 charge, that is, eqn (2) with AM1 charge is about 135![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times faster than the CP-corrected MP2/aug-cc-pVTZ method. For the sucrose–maltose dimer 26 which contains 90 atoms, it takes only 3 seconds CPU time to obtain the interaction energy by using the polarizable dipole–dipole interaction model combined with AM1 charge, that is, eqn (2) with AM1 charge is about 365
000 times faster than the CP-corrected MP2/aug-cc-pVTZ method. For the sucrose–maltose dimer 26 which contains 90 atoms, it takes only 3 seconds CPU time to obtain the interaction energy by using the polarizable dipole–dipole interaction model combined with AM1 charge, that is, eqn (2) with AM1 charge is about 365![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times faster than the CP-corrected MP2/aug-cc-pVTZ method. These comparisons also indicate that the polarizable dipole–dipole interaction model is much more efficient than the CP-corrected MP2/aug-cc-pVTZ method and the bigger the system, the more efficient the polarizable dipole–dipole interaction model.
000 times faster than the CP-corrected MP2/aug-cc-pVTZ method. These comparisons also indicate that the polarizable dipole–dipole interaction model is much more efficient than the CP-corrected MP2/aug-cc-pVTZ method and the bigger the system, the more efficient the polarizable dipole–dipole interaction model.
Conclusions
In this paper, the polarizable dipole–dipole interaction model is further developed to predict the hydrogen bond distances and interaction energies for carbohydrate-containing hydrogen-bonded complexes. The calculation results show that the hydrogen bond distances obtained from the polarizable dipole–dipole interaction model are in good agreement with those obtained from the corresponding MP2 and B3LYP method, and the interaction energies obtained from the polarizable dipole–dipole interaction model are in good agreement with those obtained from the CP-corrected MP2/aug-cc-pVTZ method, demonstrating that the polarizable dipole–dipole interaction model and the parameters determined in this work are reasonable and useful. The comparisons of the CPU times spent by the CP-corrected MP2/aug-cc-pVTZ method and by the polarizable dipole–dipole interaction model (eqn (2) with NBO charge or eqn (2) with AM1 charge) indicate that the polarizable dipole–dipole interaction model is much more efficient. We hope the polarizable dipole–dipole interaction model can provide a new way for rapidly and accurately estimating the interaction strength for carbohydrate-containing hydrogen-bonded complexes.Up to now, the polarizable dipole–dipole interaction model is only applied to the complexes containing N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C–H⋯O
C, C–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and O–H⋯O hydrogen bonds and therefore needed to be further improved. One direction of improving this model is to extend this model to various base pairs in DNA and RNA which can be characterized as hydrogen-bonded complexes. Another direction of improving this model is about how to describe the covalent interaction Δmix as physically as possible. In this paper, eqn (6) is just a fitting formula because no available methods exist at present that can be used to describe the covalent interaction of a hydrogen bond physically and precisely. We hope that the covalent interaction of a hydrogen bond can be described physically and precisely in the future and this depends on deeply understanding the nature of hydrogen bonding. Compared to the general force field which usually includes bonded terms (i.e., stretches, bends, and torsions) and nonbonded terms, our model only includes the nonbonded terms. We here take the intramolecular geometry as rigid so only nonbonded interactions contribute to the interaction energy. This limitation will be eliminated in an improved form of our model that will also handle bonded interactions. The studies on these directions are ongoing in our laboratory.
C, and O–H⋯O hydrogen bonds and therefore needed to be further improved. One direction of improving this model is to extend this model to various base pairs in DNA and RNA which can be characterized as hydrogen-bonded complexes. Another direction of improving this model is about how to describe the covalent interaction Δmix as physically as possible. In this paper, eqn (6) is just a fitting formula because no available methods exist at present that can be used to describe the covalent interaction of a hydrogen bond physically and precisely. We hope that the covalent interaction of a hydrogen bond can be described physically and precisely in the future and this depends on deeply understanding the nature of hydrogen bonding. Compared to the general force field which usually includes bonded terms (i.e., stretches, bends, and torsions) and nonbonded terms, our model only includes the nonbonded terms. We here take the intramolecular geometry as rigid so only nonbonded interactions contribute to the interaction energy. This limitation will be eliminated in an improved form of our model that will also handle bonded interactions. The studies on these directions are ongoing in our laboratory.
Acknowledgements
We acknowledge the National Natural Science Foundation of China (20973088, 21173109, 21133005), the Program for Liaoning Excellent Talents in University (LR2012037) and Program for Leading Figures in Dalian, China.Notes and references
- H. Lis and N. Sharon, Chem. Rev., 1998, 98, 637–674 CrossRef CAS PubMed.
- A. P. Davis and R. S. Wareham, Angew. Chem., Int. Ed., 1999, 38, 2978–2996 CrossRef.
- F. Y. Avci and D. L. Kasper, Annu. Rev. Immunol., 2010, 28, 107–130 CrossRef CAS PubMed.
- F. A. Quiocho, Pure Appl. Chem., 1989, 61, 1293–1306 CrossRef CAS.
- W. Weis and K. Drickamer, Annu. Rev. Biochem., 1996, 65, 441–473 CrossRef CAS PubMed.
- E. J. Cocinero, P. Çarçabal, T. D. Vaden, B. G. Davis and J. P. Simons, J. Am. Chem. Soc., 2011, 133, 4548–4557 CrossRef CAS PubMed.
- S. Paul and S. Paul, J. Phys. Chem. B, 2014, 118, 1052–1063 CrossRef CAS PubMed.
- G. J. Zhao and K. L. Han, J. Phys. Chem. A, 2007, 111, 2469–2474 CrossRef CAS PubMed.
- G. J. Zhao and K. L. Han, Acc. Chem. Res., 2012, 45, 404–413 CrossRef CAS PubMed.
- P. Carcabal, R. A. Jockusch, I. Huming, L. C. Snoek, R. T. Kroemer, B. G. Davis, D. P. Gamblin, I. Compagnon and J. Oomens, J. Am. Chem. Soc., 2005, 127, 11414–11425 CrossRef CAS PubMed.
- M. M. Deshmukh, L. J. Bartolotti and S. R. Gadre, J. Phys. Chem. A, 2008, 112, 312–321 CrossRef CAS PubMed.
- E. C. S. Kaposta, P. Çarçabal, E. J. Cocinero and P. Hurtado, J. Phys. Chem. B, 2013, 117, 8135–8142 CrossRef PubMed.
- C. M. Altaner, L. H. Thomas, A. N. Fernandes and M. C. Jarvis, Biomacromolecules, 2014, 15, 791–798 CrossRef CAS PubMed.
- C. Moller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef CAS.
- R. J. Bartlett and M. Musial, Rev. Mod. Phys., 2007, 291 CrossRef CAS.
- J. Shen, E. Xu, Z. Kou and S. Li, Phys. Chem. Chem. Phys., 2011, 13, 8795–8804 RSC.
- J. Šponer, P. Jurečka and P. Hobza, J. Am. Chem. Soc., 2004, 126, 10142–10151 CrossRef PubMed.
- P. Jurečka, J. Šponer, J. Černy and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993 RSC.
- K. Riley and P. Hobza, J. Phys. Chem. A, 2007, 111, 8257–8263 CrossRef CAS PubMed.
- W. Chin, F. Piuzzi, I. Dimicoli and M. Mons, Phys. Chem. Chem. Phys., 2006, 8, 1033–1048 RSC.
- R. Vargas, J. Garza, R. A. Friesner, H. Stern, B. P. Hay and D. A. Dixon, J. Phys. Chem. A, 2001, 105, 4963–4968 CrossRef CAS.
- Y. L. Zhao and Y. D. Wu, J. Am. Chem. Soc., 2002, 124, 1570–1571 CrossRef CAS PubMed.
- F. Jiang and Y. D. Wu, J. Am. Chem. Soc., 2014, 136, 9536–9539 CrossRef CAS PubMed.
- C. S. Wang, Y. Zhang, K. Gao and Z. Z. Yang, J. Chem. Phys., 2005, 123, 024307 CrossRef PubMed.
- J. S. Arey, P. C. Aeberhard, I. C. Lin and U. Rothlisberger, J. Phys. Chem. B, 2009, 113, 4726–4732 CrossRef CAS PubMed.
- X. N. Jiang and C. S. Wang, Sci. China: Chem., 2010, 53, 1754–1761 CrossRef CAS PubMed.
- Y. Li and C. S. Wang, Sci. China: Chem., 2011, 54, 1759–1769 CrossRef CAS.
- P. Jurečka, J. Černy, P. Hobza and D. R. Salahub, J. Comput. Chem., 2006, 28, 555–569 CrossRef PubMed.
- S. Scheiner, J. Phys. Chem. B, 2006, 110, 18670–18679 CrossRef CAS PubMed.
- S. Scheiner, J. Phys. Chem. B, 2009, 113, 10421–10427 CrossRef CAS PubMed.
- C. R. Jones, P. K. Baruah, A. L. Thompson, S. Scheiner and M. D. Smith, J. Am. Chem. Soc., 2012, 134, 12064–12071 CrossRef CAS PubMed.
- Y. Zhang and C. S. Wang, J. Comput. Chem., 2009, 30, 1251–1260 CrossRef CAS PubMed.
- C. L. Sun, X. N. Jiang and C. S. Wang, J. Comput. Chem., 2009, 30, 2567–2575 CrossRef CAS PubMed.
- X. N. Jiang and C. S. Wang, ChemPhysChem, 2009, 10, 3330–3336 CrossRef CAS PubMed.
- S. S. Li, C. Y. Huang, J. J. Hao and C. S. Wang, J. Comput. Chem., 2014, 35, 415–426 CrossRef CAS PubMed.
- X. C. Gao, C. Y. Huang and C. S. Wang, Comput. Theor. Chem., 2014, 1048, 46–53 CrossRef CAS PubMed.
- H. Margenau and N. R. Kestner, Theory of Intermolecular Forces, Oxford Pergamon Press, New York, 2nd edn, 1971 Search PubMed.
- A. J. Stone, The Theory of Intermolecular Forces, Oxford Clarendon Press, United Kingdom, 2nd edn, 2013 Search PubMed.
- A. D. Buckingham, Q. Rev., Chem. Soc., 1959, 13, 183–214 RSC.
- A. D. Buckingham, Adv. Chem. Phys., 1967, 12, 107–143 CrossRef CAS.
- J. A. Dean, Lange's Handbook of Chemistry, McGraw-Hill, Inc., New York, 1998 Search PubMed.
- J. Wang, P. Cieplak and P. A. Kollman, J. Comput. Chem., 2000, 21, 1049–1074 CrossRef CAS.
- C. F. Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, Chem.–Eur. J., 1999, 5, 3581–3594 CrossRef CAS.
- A. Hesselmann, G. Jansen and M. Schütz, J. Am. Chem. Soc., 2006, 128, 11730–11731 CrossRef CAS PubMed.
- J. Ran and P. Hobza, J. Phys. Chem. B, 2009, 113, 2933–2936 CrossRef CAS PubMed.
- Z. Lu, N. Zhou, Q. Wu and Y. Zhang, J. Chem. Theory Comput., 2011, 7, 4038–4049 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The training dimers used to derive the parameters needed in this work (see Fig. S1); the interaction energies obtained by the CP-corrected MP2/aug-cc-pVTZ method (IEMP2), and by eqn (2) with NBO charge (IE) for the six training dimers (see Table S1); the equilibrium hydrogen bond distances Req(H⋯O) obtained by MP2/6-31+G(d,p), by eqn (1) and (2) (see Table S2); the equilibrium hydrogen bond distances Req(H⋯O) obtained by B3LYP/6-31+G(d,p), by eqn (1) and (2) (see Table S3); the interaction energy components obtained by eqn (2) with NBO charge (see Table S4); the interaction energy components obtained by eqn (2) with AM1 charge (see Table S5); Cartesian coordinates for all the hydrogen-bonded complexes considered in this work (see Table S6). See DOI: 10.1039/c4ra12814a |
| This journal is © The Royal Society of Chemistry 2015 |