Systematic theoretical investigation of geometries, stabilities and magnetic properties of iron oxide clusters (FeO)_n^μ (n = 1–8, μ = 0, ±1): insights and perspectives

Abstract

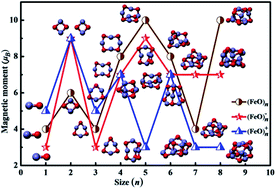
The structural properties of neutral and charged (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters have been studied using an unbiased CALYPSO structure searching method. As a first step, an unbiased search relying on several structurally different initial clusters has been undertaken. Subsequently, geometry optimization by means of density-functional theory with the Perdew and Wang (PW91) exchange–correlation functional is carried out to determine the relative stability of various candidates for low-lying neutral, anionic and cationic iron oxide clusters obtained from the unconstrained search. It is shown that the mostly equilibrium geometries of iron oxide clusters represent near planar structures for n ≤ 3. No significant structural differences are observed between the neutral and charged iron oxide clusters beyond sizes with n = 6. The relative stabilities of (FeO)_n^μ clusters for the ground-state structures are analyzed on the basis of binding energies and HOMO–LUMO gaps. Our theoretical results confirm that the binding energies of neutral and anionic (FeO)_n^0/− tend to increase with cluster size. Cationic (FeO)_n⁺ exhibits a slight downward trend. It is worth noticing that (FeO)₅ and (FeO)₄^−/+ are the most stable geometries for (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters. Lastly, an evident local oscillation of magnetic behavior is present in the most stable (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters, and the origin of this magnetic phenomenon is analyzed in detail.

---

1 Introduction

A cluster is an ensemble of bound atoms or molecules that is intermediate in size between a molecule and a bulk solid. The knowledge of the geometric structures of low-lying clusters can provide detailed information for understanding how the different properties evolve as individual atoms are brought together to form nanostructures and solids, and investigating the minimum size at which clusters begin to exhibit similar properties of the corresponding bulk systems.^1–5 In recent years, due the development of new experimental techniques and rigorous ab initio calculation methods, binary clusters consisting of metals (especially transition metals) and oxide clusters have attracted much attention for two major reasons: first, metal oxide clusters can be used as models for the metal oxide materials and metal oxide surfaces and second, oxidation can be used as a new way to modulate the electronic structure and properties of clusters.^6–10

Iron oxide clusters and nanoparticles are of primary significance in a wide spectrum of subjects ranging from astrophysics and astrochemistry to nanomedicine and materials science. Iron monoxide nanoparticles are now thought of being responsible for the 21 μm emission feature in post-asymptotic giant branch stars.^11,12 In nanomedicine, iron oxide nanoparticles and alternating magnetic fields are used to produce local hyperthermia in cancer therapy.¹³ Among other materials science implications,¹⁴ recent work by Lin et al.¹⁵ shows that iron oxide nanoparticle and graphene nanoribbon composites display remarkable potential in new-generation lithium-ion battery anodes. Advancing to fundamental physicochemical characteristics, it is worth noticing that of all metal oxide clusters, iron oxide ones are of particular interest because of their remarkable electronic and structural features. It is now fairly obvious that in-depth studies on iron oxide clusters not only provide a new avenue to detailed information about the interaction between oxygen and iron but also provide insight into the chemical processes in corrosion, biological oxygen transport, and oxide film formation.^16–18 In addition, some iron oxide clusters, such as Fe₂O₃, seem to be potential candidates for CO oxidation and NO reduction which are undesirable chemical products in many industrial processes and their removal is one of the most important industrial and environmental problems nowadays.¹⁹

On the experimental side, Wang et al. reported the first study of a series of small Fe_nO_m clusters, containing up to four Fe and six oxygen atoms in molecular beams, by using size-selected anion photoelectron spectroscopy.²⁰ Their results indicated that small Fe_nO_m clusters can be viewed as sequential oxygen atom adsorption to the surfaces of the Fe_n (n = 3, 4) clusters, leading to nearly linear increase of the electron affinity with the number of O atoms. Shin et al. studied the neutral cluster distribution of iron oxide clusters formed by laser ablation of iron metal and reaction of the metal plasma plume with oxygen in the gas phase under a wide variety of experimental conditions, including oxygen concentration and 193 nm ionization laser power, among other variables.^21,22 The most stable clusters observed under conditions of excess oxygen are of the form Fe_mO_m and Fe_mO_m+1,2. Wang et al. measured the infrared spectra of mass-selected oxygen-rich cation complexes in the gas phase and studied the geometric and electronic structures of iron dioxygen Fe(O₂)_n⁺ (n = 3–5) cluster by infrared photodissociation spectroscopy.²³ In order to elucidate the growth behavior of the iron oxide clusters, Gutsev et al. investigated the electronic and geometrical structures of oxygen-rich neutral and negatively charged FeO_n clusters by employing density functional theory with generalized gradient approximation.²⁴ However, a systematic theoretical understanding of the interaction of oxygen with iron is still lacking, in particular for large architectures.

In order to systematically study the interaction of oxygen with iron and structural evolution in iron oxide clusters, we here present extensive structure searches to explore the global minimum geometric structures of neutral and charged iron oxide clusters in the size range of 2 ≤ n ≤ 8, by combining our developed CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) method with the density functional theory. Our first goal of this work is to gain a fundamental understanding of the ground state geometric structures in iron oxide clusters. The second one is to reexamine a number of neutral and charged low-energy isomers of small iron oxide clusters that have been reported previously by experiments or density functional calculations. Thirdly, we are also motivated to explore the physical mechanism of the magnetic behaviors of neutral, anionic and cationic iron oxide clusters and provide relevant information for further theoretical and experimental studies. In what follows, we will first describe the computational methodology in Section 2, and then present our results and discussions in Section 3. Finally, a summary is given in Section 4.

2 Computational method

Our cluster structure prediction is based on the CALYPSO method.^25–28 A local version of particle swarm optimization (PSO) algorithm is implemented to utilize a fine exploration of potential energy surface for a given non-periodic system. The bond characterization matrix (BCM) technique is employed to eliminate similar structures and define the desirable local search spaces. This structure prediction method has been benchmarked on LJ clusters with cluster sizes up to 150 atoms. High search efficiency is achieved, demonstrating the reliability of the current method. The significant feature of this method is the capability of predicting the stable structure with only the knowledge of the chemical composition. It has been successful in correctly predicting structures for various systems.^28–30 The evolutionary variable structure predictions of neutral and charged iron oxide clusters are performed ranging from 2 to 8. Each generation contain 30 structures, 70% of which are generated by PSO. The others are new and will be generated randomly. We followed 50 generations to achieve the converged structure. The lowest-energy candidate structures of the global minimum for each size are further to perform geometric optimization using all-electron density-functional theory within generalized gradient approximation in the PW91 functional, as implemented in the Gaussian 09 package.³¹ The convergence thresholds of the maximum force, root-mean-square (RMS) force, maximum displacement of atoms, and RMS displacement are set to 0.00045, 0.0003, 0.0018, and 0.0012a₀, respectively. The effect of the spin multiplicity is also taken into account in the geometric optimization procedure. Meanwhile, the vibration frequency calculations are performed at the same level theory to assure the nature of the stationary points.

In order to test the reliability of our calculations, we have calculated the neutral and anionic two-atom clusters (FeO, FeO⁻, O₂, O₂⁻, Fe₂ and Fe₂⁻) through many different functionals (B3LYP,^32,33 TPSS,³⁴ PW91,^32,35 BP86,³³ PBE³⁴ and B3PW91 ^32,35,36) with the 6-311+G* basis set. The calculated results are summarized in Table 1. It is seen that the PW91 method gives results of bond lengths (r), vibration frequencies (ω) and dissociation energies (D) of the two-atom dimers closest to the experimental values.^37–45 To further confirm the reliability of the computational method, the vertical detachment energies (VDEs = E_{neutral at optimized anion geometry} − E_{optimized anion}) and adiabatic electronic affinities (AEAs = E_{optimized neutral} − E_{optimized anion}) for the ground state of (FeO)_n⁻ (n = 1–8) clusters are also calculated. The theoretical results as well as the experimental data are listed in Table 2. The agreement between the experimental data and the calculated results is also excellent. The reasonable agreement between the calculated values strengthens our choice of theoretical methods.

Table 1 Calculated values of bond length r (Å), frequency ω (cm⁻¹) and dissociation energy D (eV) for the FeO, FeO⁻, O₂, O₂⁻, Fe₂ and Fe₂⁻ molecules at different level

Clusters	Multi.	Para.	Methods						Exp.
			B3LYP	TPSS	PW91	BP86	PBE	B3PW91
a Ref. 37.b Ref. 38.c Ref. 39.d Ref. 40.e Ref. 41.f Ref. 42.g Ref. 43.h Ref. 44.i Ref. 45.
FeO	5	r	1.63	1.61	1.61	1.61	1.61	1.60	1.62^a
		ω	910	913	908	909	905	912	881^b
		D	4.37	5.07	4.49	5.33	5.46	4.80	4.20^b
FeO^−	4	r	1.65	1.63	1.63	1.63	1.63	1.64	1.63^b
		ω	812	858	855	854	851	826	849^f
		D	6.31	6.28	6.86	6.77	6.79	6.11
O2	3	r	1.21	1.22	1.22	1.22	1.22	1.20	1.21^c
		ω	1633	1544	1546	1537	1549	1677	1580^c
		D	5.19	5.35	5.05	5.89	6.06	5.25	5.12^h
O2^−	2	r	1.35	1.37	1.36	1.36	1.36	1.33	1.28^c
		ω	1165	1092	1101	1096	1103	1203	1131^c
		D	5.77	5.78	5.56	6.45	6.49	5.66
Fe2	7	r	1.98	2.00	2.01	2.01	2.01	1.98	2.02^d
		ω	428	406	400	402	397	431	418^g
		D	1.38	1.93	1.48	2.31	2.47	1.18	1.15^i
Fe2^−	8	r	2.05	2.06	2.06	2.06	2.07	2.04	2.10^e
		ω	369	355	352	353	349	370	270^e
		D	1.35	2.24	1.73	2.61	2.71	1.46	1.90^i

---

Table 2 The calculated vertical detachment energies (VDEs) and adiabatic electronic affinities (AEAs) for the ground state of (FeO)_n⁻ (n = 1–8) clusters at PW91/6-311+G* level, compared to the experimentally measured VDEs and AEAs from the photoelectron spectra

Species	VDE (eV)		AEA (eV)
	This work	Exp.^a	This work	Exp.^a
a Ref. 20.
FeO^−	1.37	1.50	1.36	1.50
(FeO)2^−	1.25	1.35	1.31	1.36
(FeO)3^−	2.28	2.34	2.21	2.20
(FeO)4^−	2.89	2.90	2.80	2.70
(FeO)5^−	3.24		2.93
(FeO)6^−	3.52		3.50
(FeO)7^−	3.87		3.03
(FeO)8^−	4.02		3.06

---

3 Results and discussions

3.1 Geometrical structures

Using the computation scheme described in Section 2, a large number of optimized isomers for (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters are obtained. All earlier known structures, experimentally and theoretically, are successfully reproduced by our current structure searches. Here, we only select several low-lying isomers for each size of neutral, anionic and cationic species. According to their energies from low to high, the neutral, anionic and cationic isomers are designated by na^0/*^/+, nb^0/*^/+ and nc^0/*^/+. Where “n” is the number of iron and oxide atoms. These clusters are presented in Fig. 1–3, respectively. Meanwhile, the corresponding electronic state, point symmetry and relative stabilities along with vibration frequencies for the lowest-energy and selected low-lying isomers are also calculated and summarized in Table 3. In the following section, we briefly describe the main characteristics of the neutral and charged iron oxide clusters, in terms of their geometry, symmetry, point group, spin state and relative energy.

Fig. 1 Lowest-energy and low-lying structures of (FeO)_n (n = 1–8) clusters. The red and blue balls represent oxygen and iron atoms, respectively.

Fig. 2 Lowest-energy and low-lying structures of (FeO)_n⁻ (n = 1–8) clusters. The red and blue balls represent oxygen and iron atoms, respectively.

Fig. 3 Lowest-energy and low-lying structures of (FeO)_n⁺ (n = 1–8) clusters. The red and blue balls represent oxygen and iron atoms, respectively.

Table 3 The electronic states, symmetries, relative energies (ΔE), and vibration frequencies of (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters

	Sta.	Sym.	ΔE	Freq.		Sta.	Sym.	ΔE	Freq.		Sta.	Sym.	ΔE	Freq.
1a	^5Σ	C∞v	0.00	82, 259	1a*	^4Σ	C∞v	0.00	76, 315	1a^+	^4Σ	C∞v	0.00	79, 286
2a	^7B	C2	0.00	113, 688	2a*	^10A	C2	0.00	144, 625	2a^+	^10B	C2	0.00	108, 685
2b	^9B	C2	0.14	185, 680	2b*	^6A	C2	0.07	243, 702	2b^+	^4B	C2	0.58	161, 733
2c	^11B	C2	1.04	87, 662	2c*	^6Bg	C2h	0.50	37, 863	2c^+	^12B	C2	1.12	195, 644
3a	^5A′′	Cs	0.00	89, 579	3a*	^4A2	C2v	0.00	157, 687	3a^+	^6A	C1	0.00	74, 685
3b	^13A2	C2v	0.14	141, 708	3b*	^8A1	C2v	0.95	110, 686	3b^+	^14A′′	Cs	0.43	97, 684
3c	^7A′′	Cs	0.64	85, 701	3c*	^8A	C1	1.94	57, 893	3c^+	^8A	C1	0.65	44, 750
4a	^9A	C2	0.00	39, 619	4a*	^8A	C2	0.00	49, 661	4a^+	^8A	Cs	0.00	129, 649
4b	^9A′	Cs	0.24	136, 700	4b*	^6A	C1	0.68	32, 654	4b^+	^6B	C2	0.12	37, 744
4c	^11B	C2	0.92	41, 753	4c*	^6A	C1	1.58	65, 877	4c^+	^4A	C2	0.13	50, 710
5a	^11A	C1	0.00	78, 643	5a*	^10A′′	C1	0.00	54, 701	5a^+	^4A′	Cs	0.00	21, 708
5b	^9A	C1	0.11	51, 720	5b*	^12A′′	C1	0.18	19, 691	5b^+	^4A	C1	0.66	74, 657
5c	^9A	C1	1.24	85, 696	5c*	^6A	C1	1.70	63, 675	5c^+	^4A′	Cs	0.89	31, 735
6a	^9A	C1	0.00	50, 747	6a*	^8A	C1	0.00	51, 698	6a^+	^8A	C1	0.00	34, 708
6b	^7A	C1	0.95	56, 691	6b*	^10A	C1	0.41	48, 725	6b^+	^6A	C1	0.03	38, 716
6c	^9A	C1	1.00	62, 920	6c*	^8A	C1	1.80	66, 660	6c^+	^8A	C1	1.17	64, 769
7a	^5A	C1	0.00	62, 680	7a*	^8A	C1	0.00	72, 675	7a^+	^4A	C1	0.00	56, 648
7b	^9A	C1	0.92	67, 681	7b*	^4A	C1	0.98	41, 782	7b^+	^10A	C1	0.45	48, 667
7c	^9A	C1	0.98	26, 953	7c*	^8A	C1	1.61	32, 912	7c^+	^8A	C1	1.45	28, 880
8a	^11A	C1	0.00	41, 706	8a*	^8A	C1	0.00	58, 659	8a^+	^4A	C1	0.00	48, 694
8b	^13A	C1	0.86	38, 761	8b*	^8A	C1	0.48	24, 691	8b^+	^10A	C1	0.37	30, 640
8c	^9A	C1	1.17	46, 777	8c*	^6A	C1	1.33	48, 706	8c^+	^6A	C1	1.12	41, 682

---

For neutral iron oxide clusters, the calculated results indicate that the planar ring structures are slightly more stable than the distorted isomers for n ≤ 3. Conversely, the ground state structures begin to exhibit the hollow three-dimensional (3D) configurations at n = 4. Our theoretical results show that the ground state of (FeO)₂ is ⁷B, followed by other two states ⁹B(2b) and ¹¹B(2c). The three isomers have the same point symmetry of C₂. The Fe–O bond length in ground state is 1.79 Å which is almost the same as the bond length of (CuO)₂ measured by Wang et al.⁴⁶ Besides, the structure (2b), which is only 0.14 eV higher in energy than the ground state, shows a butterfly structure with the Fe–Fe bond for the “body” of the insect plus four Fe–O bonds at the edges of the “wings”. In fact, the lowest energy structure of (FeO)₄ is an open ring structure with the C₂ point symmetry, and the O atoms located at the apex are slightly tilted. From Fig. 1, we can clearly see that the higher sizes in this sequence consist of structures built via vertically assembling stable rings to form layer-like structures. For example, the ground state structure of (FeO)₅ is a approximate hollow triangular prism with a (FeO)₃ ring at the bottom. Subsequently, for (FeO)₇, the most stable structure is a tower structure, which can be constructed by one (FeO)₃ ring and one (FeO)₄ ring. This interesting phenomenon has also been observed in (MnO)_n clusters.⁴⁷ The structural evolution also shows that the layered structures become energetically more favorable for n ≥ 5. This may be due to the enhanced complex interaction between iron and oxygen atoms as the increasing of the cluster size.

For anion clusters, the ground state structure of (FeO)₂⁻ (2a*) is a flat structure of diamond (¹⁰A) with bond length Fe–O = 1.85 Å. It is in good agreement with the similar theoretical result reported by Shiroishi et al. (1.87 Å).⁴⁸ The ground state structure of (FeO)₆⁻ shows an approximate hollow triangular prism, which can be viewed as a (FeO)₄ ring on each sides. The isomers (6b*) and (6c*) are less stable than the respective ground state (6a*) by 0.41 eV and 1.80 eV, respectively. For (FeO)₈⁻, a “cage-shaped” structure with ⁸A state is obtained. The relative high octet spin multiplicity is more stable than sextet and quartet state. In order to gain more insight into the electronic properties of the iron oxide clusters, the vertical detachment energies (VDEs) and adiabatic electronic affinities (AEAs) of the ground state of (FeO)_n⁻ (n = 1–8) clusters are also predicted. The theoretical results are listed in Table 2 together with available experimental values for comparison.²⁰ It can be seen from Table 2 that the calculated AEA values of (FeO)_n⁻ (n = 1–4) clusters are mostly in good agreement with experimental values, with the average discrepancy of 4%. These results further give us confidence to confirm that our searched lowest-energy structures are true minima. However, there is no any available experimental data to compare with our obtained VDE and AEA results for (FeO)_n⁻ (n = 5–8) clusters. Thus, we hope that our theoretical results would provide more available information for further experimental investigation.

For cationic charged iron oxide clusters, the geometrical optimization of the final structures confirm that the (FeO)_n⁺ clusters become more compact and symmetrical. The ground state structures begin to show layer-like structures at n = 4, as shown in Fig. 3. For the (FeO)₃⁺ cluster, the preferred lowest energy structure is a hexagon ring. This configuration is similar to the structure of (ZnO)₃ reported by Wang et al.⁴⁹ The low-lying isomers (3b⁺) and (3c⁺) have the similar structures but higher electronic states (¹⁴A′′) and (⁸A), which lead to the deviation of energy. (FeO)₄⁺ is an approximate hollow triangular prism with C_s symmetry. It can be viewed as the result of the removal of a FeO chain from the neutral (FeO)₅ cluster. Interestingly enough, the lowest-energy structure of (FeO)₅⁺ is similar to the corresponding neutral and anionic clusters. This phenomenon can be also found in other low-lying isomers (5c and 5c*, 6c* and 6c⁺ etc.), just with small distortions. The present calculations indicate that within each size, the Fe atom tends to form the largest probable number of bonds with O atoms, which is similar to iron sulfur clusters.⁵⁰

As discussed above, we find that the ground state structures of (FeO)_n^0/−/+ clusters are “ring structures” when n ≤ 3, which is similar to the previous reported Fe_nO_m clusters.⁵¹ When n ≥ 4, the ground state structures of (FeO)_n^0/−/+ exhibit layer-like 3D configurations. It should be pointed out that all the low-lying structures are found to prefer high spin state. There are no significant differences between the neutral and charged clusters.

3.2 Relative stabilities and HOMO–LUMO gaps

It is well known that the magnitude of binding energy per atom E_b gives information about the strength of chemical bonds in the clusters. The E_b is defined as follow:where E(Fe), E(O), E(O^μ) and E(Fe_nO_n^μ) are the total energies of the corresponding atoms or clusters, respectively. For the most stable structures of neutral and charged iron oxide clusters, the size-dependent binding energies are plotted in Fig. 4(a). It can be seen from Fig. 4(a) that the binding energies for (FeO)_n^0/− tend to increase with size, as previously observed in (ZnO)_n clusters,⁴⁹ while a slight downward trend is found for (FeO)_n⁺. Besides, the anionic (FeO)_n⁻ clusters are almost as stable as the neutral ones. For (FeO)_n⁺, the E_b values are obviously higher than those of (FeO)_n clusters indicating that the cationic clusters become more competitive energetically than the neutral clusters. This implies that the deprivation of an extra electron can enhance the stability of the neutral (FeO)_n clusters.

Fig. 4 Size dependence of the binding energy per atom E_b (a) and HOMO–LUMO energy gap E_gap (b) for the lowest-energy structures of (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters.

The highest occupied-lowest unoccupied molecular orbital (HOMO–LUMO) energy gaps have been proved to be a powerful tool to represent the ability of the molecule to participate in the chemical reaction in some degree. The larger values of HOMO–LUMO energy gaps correspond to a stronger chemical stability. The calculated values of HOMO, LUMO and HOMO–LUMO energy gaps for the lowest-energy (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters are listed in Table 4. In addition, the HOMO–LUMO energy gap E_gap as a function of the cluster size n is presented in Fig. 4(b). It can be seen from Table 4 that the values of HOMO and LUMO for (FeO)_n⁻ clusters are higher than those of their corresponding neutral and cationic clusters. The local maximum values (0.57 eV, 0.51 eV, 0.58 eV) of HOMO–LUMO energy gaps are found at n = 5 for neutral and n = 4 for charged iron oxide cluster, respectively. This indicates that these clusters are more stable than their neighboring clusters. From Fig. 4(b), we can clearly find a conspicuous valley appear at (FeO)₆⁻, meaning that the stability of (FeO)₆⁻ cluster is increased when removing an extra electron.

Table 4 HOMO/LUMO energies and the gaps between them for the lowest-energy (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters. All of energies are in eV

Cluster size	(FeO)n			(FeO)n^−			(FeO)n^+
	HOMO	LUMO	HO–LU gap	HOMO	LUMO	HO–LU gap	HOMO	LUMO	HO–LU gap
n = 1	−4.55	−4.08	0.47	1.40	1.79	0.39	−13.09	−12.89	0.20
n = 2	−4.28	−3.84	0.44	0.55	0.95	0.40	−10.87	−10.50	0.37
n = 3	−4.90	−4.78	0.12	0.36	0.77	0.41	−11.23	−11.12	0.11
n = 4	−5.23	−5.04	0.18	−0.45	0.07	0.51	−10.52	−9.94	0.58
n = 5	−5.58	−5.01	0.57	−0.74	−0.26	0.47	−10.01	−9.81	0.20
n = 6	−5.14	−4.77	0.37	−1.03	−0.90	0.13	−10.03	−9.75	0.28
n = 7	−5.04	−4.58	0.46	−1.34	−0.91	0.42	−9.10	−8.90	0.20
n = 8	−5.09	−4.92	0.17	−1.02	−0.82	0.20	−9.06	−8.93	0.13

---

Fig. 5 shows the molecular orbital energy levels of the three relative stable (FeO)₅, (FeO)₄⁻ and (FeO)₄⁺ clusters together with their molecular orbital maps. The blue and red lines show the occupied orbital while the yellow and azure lines represent the unoccupied orbital. It can be seen from Fig. 5 that the (FeO)₅ is characteristic of the degeneration of the molecular orbital energy level of HOMO and LUMO, which probably leads to its largest value for the energy gap. Moreover, to understand the relative stability of the remaining clusters, we have also calculated the molecular orbital energy levels of their lowest-energy structures, as shown in Fig. S1–S4 (see ESI†). In addition, we can also note that their highest occupied molecular orbitals with bonding character between O-2p and Fe-3d orbitals as shown in their molecular orbital plots. The result is further confirmed by calculating molecular orbital maps of the HOMO−1 and LUMO+1 of (FeO)₅, (FeO)₄⁻ and (FeO)₄⁺ clusters (see Fig. S5†).

Fig. 5 Calculated molecular orbital energy levels of (FeO)₅, (FeO)₄⁻ and (FeO)₄⁺ clusters together with the molecular orbital maps of the HOMOs and LUMOs.

3.3 Magnetic property

The calculation of magnetic moments is foremost in elucidating how transition metal atoms can be affected in binary mixed clusters. Here, the spin magnetic moments of the most stable (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters have been calculated and the results are presented in Fig. 6. From Fig. 6, we can see that the spin magnetic moments of the ground state (FeO)_n^0/+ exhibit a remarkable oscillation. The same behavior is easily discernible in the corresponding anionic clusters when n < 6, while the ground state of (FeO)₆⁻, (FeO)₇⁻ and (FeO)₈⁻ clusters possess the same spin magnetic moments 7 μ_B. Our calculations also show that the spin magnetic moments of neutral (FeO)_n clusters is consistently 1 μ_B higher than those of their corresponding anions, except for the case n = 2, 7, 8. It is probably attributable to the fact that the attachment of the extra electron to the neutral ground state leads to a slight decrease of magnetic moments. In order to further understand the distribution of the magnetism, we calculated the local magnetic moments on the Fe atoms of (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters. The results are summarized in Table 5. From Table 5, it can be easily inferred that the local magnetic moments mainly come from Fe-3d states, while the 4s and 4p states only have a weak contribution. Within each size, the spin magnetic moments of the clusters closely relate to the local magnetic moments on Fe atoms. For example, the local magnetic moments (8.4 μ_B) of Fe atoms in (FeO)₅⁻ cluster is almost equal to the total magnetic moments (9.0 μ_B) of (FeO)₅⁻ cluster.

Fig. 6 Size dependence of spin magnetic moments together with the corresponding geometries for the lowest-energy structures of (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters.

Table 5 The local magnetic moment (μ_B) of the Fe atoms of (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters for the lowest-energy structures

Clusters	Moment (μB)
	Fe
	3d	4s	4p	Local
FeO	2.86	0.46	0.09	3.41
(FeO)2	5.34	0.10	0.12	5.56
(FeO)3	3.33	0.11	0.01	3.45
(FeO)4	6.75	0.14	0.04	6.93
(FeO)5	8.89	0.22	0.03	9.14
(FeO)6	7.09	0.14	0.11	7.34
(FeO)7	3.42	0.09	0.05	3.56
(FeO)8	9.41	0	0.04	9.45
(FeO)^−	2.84	−0.29	0.02	2.57
(FeO)2^−	6.78	0.64	0.38	7.8
(FeO)3^−	2.75	−0.03	−0.03	2.69
(FeO)4^−	6.12	0.02	0.01	6.15
(FeO)5^−	8.20	0.04	0.2	8.44
(FeO)6^−	6.24	0.69	0.03	6.96
(FeO)7^−	5.48	0	0.12	5.60
(FeO)8^−	6.98	0	−0.05	6.93
(FeO)^+	3.54	0.23	0.03	3.8
(FeO)2^+	7.16	0.1	0.08	7.34
(FeO)3^+	3.99	0.13	−0.05	4.07
(FeO)4^+	6.37	0.12	0.03	6.52
(FeO)5^+	2.86	0.04	−0.05	2.85
(FeO)6^+	6.28	0.16	0	6.44
(FeO)7^+	2.12	0.02	0.01	2.15
(FeO)8^+	2.87	0.3	−0.02	3.15

---

In order to explore the origin of the magnetic behavior, the total density of states (TDOS) and partial density of states (PDOS) of (FeO)₃ and (FeO)₅ for neutral clusters, (FeO)₂⁻ and (FeO)₅⁻ for anionic clusters as well as (FeO)₂⁺ and (FeO)₅⁺ for cationic clusters are discussed. Overall, the total DOS show clear spin polarization near the Fermi energy, as Fig. 7 illustrated. By comparing the total and partial DOS, it is obviously found that the total magnetic moments mainly come from Fe-d states, while the magnetic moments of O-s and O-p states are nearly negligible, indicating that spin polarization is mainly localized on the Fe atoms. This result is in agreement with the findings of Palotás et al.⁵²

Fig. 7 Calculated total DOS and partial DOS of (FeO)₃ [(a) and (b)], (FeO)₅ [(c) and (d)], (FeO)₂⁻ [(e) and (f)], (FeO)₅⁻ [(g) and (h)], (FeO)₂⁺ [(i) and (j)], (FeO)₅⁺ [(k) and (l)] clusters. The Fermi level is indicated by the vertical dashed line.

Generally, the hybridization between s, p, and d states causes the closed-shell Fe atoms to have an incomplete d-shell configuration, which is usually responsible for the magnetism of transition-metal clusters. The up- and down-spin sub-bands of the Fe-d states of (FeO)₅ and (FeO)₃ (see Fig. 7(b) and (d)) appear similar to each other while the sub-bands of the O-p states of (FeO)₅ cluster are more closely spaced in comparison to that of (FeO)₃ cluster, which enhances the depletion of Fe-d states through p–d hybridization. This may be due to the fact (FeO)₅ has a larger magnetic moment than the (FeO)₃ cluster. In addition, systematically sharp and prominent peaks are observed in the DOS of Fe-d states in (FeO)₂⁻ and (FeO)₂⁺ clusters, as shown in Fig. 7(f) and (j). The results suggest that the electrons are relatively localized and the corresponding energy bands are relatively narrow. The partial DOS of (FeO)₅⁻ and (FeO)₅⁺ clusters is presented in Fig. 7(h) and (l). A similar trend is observed in Fe-d states, and slightly weakening of the O-p states is found by comparing with the (FeO)₅ cluster. Namely, the attachment or deprivation of an extra electron can slightly reduce the depletion through hybridization. This result is further confirmed by the calculation of the total and partial DOS of (FeO)₄ and (FeO)₆, (FeO)₄⁻ and (FeO)₆⁻, (FeO)₄⁺ and (FeO)₆⁺ clusters, as plotted in Fig. S6–S8 (see ESI†).

3.4 Natural population analysis

The natural population analysis (NPA) and natural electron configuration (NEC) have been proved to be powerful tools to represent the localization of charge within the clusters. To investigate reliable charge-transfer information of (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters, the NPA and NEC for the lowest energy (FeO)_n^μ species have been investigated and the results are summarized in Table 6. As shown in Table 6, we can clearly see that the atomic charges of the Fe atom in the (FeO)_n^μ clusters possess positive charges from 0.72 to 7.04e except for (FeO)⁻. This is consistent to the expectation that the charges always transfer from Fe atom to O atom, namely, Fe acts as electron donor in all (FeO)_n^μ clusters. This may be due to the fact that Fe has a strong ability to lose electrons. Moreover an interesting phenomenon appears: within each size, the deviation of natural charges on O atoms between neutral and anionic clusters are less than 1e indicating that the extra electron is partially involved in O atoms. This may be related to the arrangement of the internal charge induced by the extra electron in anionic clusters. The result of NEC in Table 6 for the lowest energy (FeO)_n^μ clusters clearly shows that, the 4s, 3d and 4p orbitals of the Fe atoms behave predominantly as core orbitals, while the 4d, 5p states make only weak contributions. The NEC results of (FeO)₅ illustrate that the valence electron configurations is 4s^0.20–0.423d^6.39–6.624p^0.27–0.394d^0.025p^0–0.01 (for Fe), 2s^1.80–1.822p^4.87–5.143s^0–0.013p^0.01 (for O). Strong spd hybridization deriving from electron transfer from the 3s orbitals of the Fe atoms and the 4s orbital of the O atom to the 3d and 4p orbitals of the Fe atom is observed in (FeO)₅ cluster. This is in accord with the above analysis based on the total and partial DOS.

Table 6 Natural populations of Fe and O atoms, and natural electron configuration (NEC) of Fe and O atoms for the lowest-energy structures of (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters

Clusters	n	Q (Fe)	Q (O)	NEC (Fe)	NEC (O)
(FeO)n	1	0.726	−0.726	4s^0.503d^6.644p^0.13	2s^1.932p^4.773p^0.01
	2	1.706	−1.706	4s^0.333d^6.614p^0.204d^0.01	2s^1.872p^4.973p^0.01
	3	2.663	−2.663	4s^0.31–0.383d^6.46–6.564p^0.24–0.264d^0.01	2s^1.84–1.852p^5.01–5.053s^0.013p^0.01
	4	3.401	−3.401	4s^0.26–0.423d^6.39–6.514p^0.22–0.344d^0.01–0.02	2s^1.82–1.832p^4.96–5.043p^0.01
	5	3.965	−3.965	4s^0.20–0.423d^6.39–6.624p^0.27–0.394d^0.025p^0–0.01	2s^1.80–1.822p^4.87–5.143s^0–0.013p^0.01
	6	4.779	−4.779	4s^0.23–0.373d^6.58–6.854p^0.25–0.514d^0.025p^0–0.01	2s^1.78–1.802p^4.67–5.063s^0–0.013p^0–0.01
	7	5.581	−5.581	4s^0.23–0.363d^6.48–6.674p^0.22–0.494d^0.02–0.045p^0–0.01	2s^1.77–1.802p^4.90–5.053s^0.013p^0.01–0.02
	8	6.123	−6.123	4s^0.23–0.363d^6.34–6.714p^0.31–0.524d^0.02–0.035p^0–0.01	2s^1.75–1.812p^4.84–5.063s^0.013p^0–0.01
(FeO)n^−	1	−0.119	−0.881	4s^1.343d^6.564p^0.25s^0.024d^0.01	2s^1.912p^4.953p^0.01
	2	1.020	−2.020	4s^0.743d^6.434p^0.314d^0.01	2s^1.882p^5.113s^0.013p^0.01
	3	1.867	−2.867	4s^0.36–0.483d^6.61–6.654p^0.27–0.304d^0.01–0.02	2s^1.832p^5.10–5.123p^0.02
	4	2.624	−3.624	4s^0.38–0.473d^6.50–6.604p^0.27–0.404d^0.01–0.02	2s^1.81–1.822p^5.04–5.103p^0.01–0.02
	5	3.210	−4.210	4s^0.21–0.463d^6.44–6.664p^0.30–0.444d^0.02–0.035p^0–0.01	2s^1.79–1.812p^4.95–5.163s^0–0.013p^0–0.02
	6	4.078	−5.078	4s^0.24–0.423d^6.51–6.704p^0.30–0.494d^0.02–0.035p^0–0.01	2s^1.77–1.812p^4.89–5.143s^0–0.013p^0.01–0.02
	7	4.634	−5.634	4s^0.26–0.383d^6.43–6.734p^0.26–0.524d^0.02–0.045p^0–0.01	2s^1.75–1.812p^4.94–5.103s^0.01–0.023p^0–0.01
	8	5.246	−6.246	4s^0.23–0.373d^6.45–6.804p^0.29–0.444d^0.02–0.035p^0–0.01	2s^1.76–1.792p^4.93–5.053s^0.01–0.023p^0–0.01
(FeO)n^+	1	1.415	−0.415	4s^0.273d^6.264p^0.064d^0.01	2s^1.962p^4.443p^0.01
	2	2.687	−1.687	4s^0.193d^6.324p^0.144d^0.01	2s^1.902p^4.923s^0.013p^0.01
	3	3.420	−2.420	4s^0.22–0.263d^6.26–6.544p^0.204d^0.01	2s^1.85–1.862p^4.88–5.013s^0.013p^0.01
	4	4.150	−3.150	4s^0.19–0.353d^6.29–6.464p^0.20–0.344d^0.01–0.02	2s^1.83–1.842p^4.86–5.133s^0.013p^0.01–0.02
	5	4.652	−3.652	4s^0.19–0.373d^6.31–6.564p^0.19–0.364d^0.01–0.02	2s^1.81–1.822p^4.83–5.073s^0.013p^0.01
	6	5.285	−4.258	4s^0.20–0.373d^6.35–6.654p^0.19–0.444d^0.01–0.035p^0–0.01	2s^1.80–1.832p^4.76–5.073s^0–0.013p^0.01–0.02
	7	6.431	−5.431	4s^0.19–0.353d^6.27–6.894p^0.17–0.394d^0.01–0.035p^0–0.01	2s^1.78–1.812p^4.89–5.063s^0.013p^0.01–0.02
	8	7.045	−6.045	4s^0.19–0.373d^6.44–6.584p^0.27–0.404d^0.02–0.035p^0–0.01	2s^1.77–1.812p^4.77–5.063s^0–0.023p^0.01–0.02

---

3.5 Infrared and Raman spectra

In order to gain a deeper insight into the dynamical stabilities of the ferrous oxide clusters, we calculated the vibrational infrared (IR) and Raman spectra of the optimized geometries. The absence of an imaginary frequency in the spectra represents the real nature of the clusters. For diatomic FeO cluster, the calculated results show that there exist a intense peak of IR spectra about 486 km mol⁻¹ at frequency 908 cm⁻¹. This result is in good agreement with existing experimental data 880 cm⁻¹ as well as similar theoretical result 907 cm⁻¹.⁵³ The good agreement between them proves the reliability of our theoretical method. Therefore, we have used it further for more insight into this system and investigated the neutral and charged iron–oxygen clusters. The frequency dependence of the IR and Raman spectra of the most stable (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters are displayed in Fig. S9 and S10 (see ESI†).

It was mentioned above that (FeO)₅ cluster has a larger magnetic moment. There is a need for an in-depth description of the structural information. In view of the intended assignment of the IR and Raman spectra, this is best done in relationship with its charged isomers (Fig. 8). It can be seen from Fig. 8 that the highest intense IR frequency of (FeO)₅ cluster is found at 683 cm⁻¹. It is assigned to the Fe–Fe bond in-plane wagging vibration. The two very close peaks at 643 cm⁻¹ and 652 cm⁻¹ correspond to the similar Fe–O bonds in (FeO)₅ cluster. This IR property is quite different from those of the corresponding anionic and cationic species, in which the strongest peak exists at 632 cm⁻¹ and 644 cm⁻¹, respectively.

Fig. 8 The infrared (a) and Raman (b) spectra of (FeO)₅^0/−/+ clusters.

Raman activity mainly corresponds to the breathing modes and in these modes all the ions in clusters having high symmetry move together. Fig. S10† clearly shows that the neutral and charged (FeO)_n^μ clusters have similar Raman activities and the Raman peaks of the (FeO)_n^μ clusters are evenly distributed in the low frequency region (0–400 cm⁻¹), implying that the Raman activity of the (FeO)_n^μ clusters are stronger in the low frequency band. As for (FeO)₅^μ clusters, the topmost intensity is the breathing mode of Fe atoms in the cluster. In this mode all O atoms remain static. Furthermore, it is worth noting that there are some more breathing modes present in Fig. 8(b), where all O atoms vibrate in the same phase and all Fe atoms are static. The intensities of these breathing modes are much less than the breathing mode of the Fe atoms.

4 Conclusions

We have report a detailed investigation on the structural evolution of the neutral, anionic, and cationic (FeO)_n (n = 1–8) clusters using a combination of the unbiased CALYPSO structure searching method and density-functional theory calculations. Harmonic vibrational analysis has been performed to assure that the optimized geometries are true minima. The binding energies, HOMO–LUMO energy gaps, electronic, and magnetic properties including Raman activities, and infrared intensities are predicted at the PW91/6-311+G* level. The HOMO–LUMO energy gaps show that the (FeO)₅, (FeO)₄⁻ and (FeO)₄⁺ molecules have the largest HOMO–LUMO gap values, confirming their stability. More interestingly, it is found that the magnetic moments of iron oxide clusters display an evident local oscillation of magnetic behavior with increasing cluster size. The calculated total density of states, as well as the partial density of states, clearly indicate that the magnetic moments mainly come from Fe-3d states and that spin polarization is strongly localized on the Fe atoms in iron oxide clusters. These results provide important electronic structure information for small iron oxide clusters. Hopefully, in the near future they can be directly compared with further experimental measurements, which may also be able to address the question of the magnetic properties of these clusters and their dependence on the degrees of oxidation and aggregation.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (no. 11104190, 11304167 and 11274235), 973 Program of China (2014CB660804), Doctoral Education Fund of Education Ministry of China (no. 20100181110086 and 20111223070653), Postdoctoral Science Foundation of China (no. 20110491317 and 2014T70280), Open Project of State Key Laboratory of Superhard Materials (no. 201405), and Young Core Instructor Foundation of Henan Province (no. 2012GGJS-152).

Notes and references

1. H. Q. Wang and H. F. Li, RSC Adv., 2014, 4, 29782–29793.
2. B. Anak, M. Bencharif and F. Rabilloud, RSC Adv., 2014, 4, 13001–13011.
3. X. J. Deng, X. Y. Kong, X. L. Xu, H. G. Xu and W. J. Zheng, RSC Adv., 2014, 4, 25963–25968.
4. A. Albers, S. Demeshko, K. Propper, S. Dechert, E. Bill and F. Meyer, J. Am. Chem. Soc., 2013, 135, 1704–1707.
5. K. M. Xu, T. Huang, H. Wen, Y. R. Liu, Y. B. Gai, W. J. Zheng and W. Huang, RSC Adv., 2013, 3, 24492–24502.
6. K. R. S. Woodcock, T. Vondrak, S. R. Meech and J. M. C. Plane, Phys. Chem. Chem. Phys., 2006, 8, 1812–1821.
7. L. S. Xu, Z. F. Wu, Y. K. Jin, Y. S. Ma and W. X. Huang, Phys. Chem. Chem. Phys., 2013, 15, 12068–12074.
8. J. J. P. Roberts, J. A. Westgard, L. M. Cooper and R. W. Murray, J. Am. Chem. Soc., 2014, 136, 10783–10789.
9. B. Luigjes, S. M. C. Woudenberg, R. Groot, J. D. Meeldijk, H. M. T. Galvis, K. P. Jong, A. P. Philipse and B. H. Erné, J. Phys. Chem. C, 2011, 115, 14598–14605.
10. C. J. Jia, L. D. Sun, F. Luo, X. D. Han, L. J. Heyderman, Z. G. Yan, C. H. Yan, K. Zheng, Z. Zhang, M. Takano, N. Hayashi, M. Eltschka, M. Klaui, U. Rudiger, T. Kasama, L. C. Gontard, R. E. D. Borkowski, G. Tzvetkov and J. Rabe, J. Am. Chem. Soc., 2008, 130, 16968–16977.
11. I. McDonald, G. C. Sloan, A. A. Zijlstra, N. Matsuura, K. E. Kraemer, J. Bernard-Salas and A. J. Markwick, Astrophys. J., Lett., 2010, 717, L92–L97.
12. A. Li, J. M. Liu and B. W. Jiang, Astrophys. J., 2013, 777, 111.
13. S. Toraya-Brown, M. R. Sheen, P. Zhang, L. Chen, J. R. Baird, E. Demdenko, M. J. Turk, P. J. Hoopes, J. R. Conejo-Garcia and S. Fiering, Nanomedicine, 2014, 10, 1273–1285.
14. Iron Oxides: Structure, Properties and Applications, ed. A. I. Martinez, Nova Publishers, Hauppauge, NY, 2012.
15. J. Lin, A. R. O. Raji, K. Nan, Z. Peng, Z. Yan, E. L. G. Samuel, D. Natelson and J. M. Tour, Adv. Funct. Mater., 2014, 24, 2044–2048.
16. P. Baran, R. Boca, I. Chakraborty, J. Giapintzakis, R. Herchel, Q. Huang, J. E. Mcgrady, R. G. Raptis, Y. Sanakis and A. Simopoulos, Inorg. Chem., 2008, 47, 645–655.
17. S. C. Li, Z. J. Li, Z. R. Zhang, B. D. Kay, R. Rousseau and Z. Dohnalek, J. Phys. Chem. C, 2012, 116, 908–916.
18. A. Riedinger, P. Guardia, A. Curcio, M. A. Garcia, R. Cingolani, L. Manna and T. Pellegrino, Nano Lett., 2013, 13, 2399–2406.
19. B. V. Reddy and S. N. Khanna, Phys. Rev. Lett., 2004, 93, 068301.
20. L. S. Wang, H. Wu and S. R. Desai, Phys. Rev. Lett., 1996, 76, 4853–4856.
21. D. N. Shin, Y. Matsuda and E. R. Bernstein, J. Chem. Phys., 2004, 120, 4150–4156.
22. D. N. Shin, Y. Matsuda and E. R. Bernstein, J. Chem. Phys., 2004, 120, 4157–4164.
23. C. Wang, J. Jian, G. Wang, Z. H. Li and M. Zhou, J. Phys. Chem. A, 2014, 118, 4519–4526.
24. G. L. Gutsev, C. A. Weatherford, K. Pradhan and O. Jena, J. Phys. Chem. A, 2010, 114, 9014–9021.
25. J. Lv, Y. C. Wang, L. Zhu and Y. M. Ma, J. Chem. Phys., 2012, 137, 084104.
26. Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
27. Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
28. Y. C. Wang, M. S. Miao, J. Lv, L. Zhu, K. T. Yin, H. Y. Liu and Y. M. Ma, J. Chem. Phys., 2012, 137, 224108.
29. L. Zhu, H. Y. Liu, C. J. Pickard, G. T. Zou and Y. M. Ma, Nat. Chem., 2014, 6, 644–648.
30. S. H. Lu, Y. C. Wang, H. Y. Liu, M. S. Miao and Y. M. Ma, Nat. Commun., 2014, 5, 3666.
31. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. BAkken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 09 Revision C.0, Gaussian, Inc., Wallingford, CT, 2009.
32. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
33. C. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
35. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
36. J. P. Perdew, P. Ziesche and H. Eschrig, Electronic Structure of Solids, Akademie Verlag, Berlin, 1991.
37. A. C. Cheung, N. Lee, A. M. Lyyra, A. J. Merer and A. W. Taylor, J. Mol. Spectrosc., 1982, 95, 213–225.
38. A. J. Merer, Annu. Rev. Phys. Chem., 1989, 40, 407–438.
39. R. J. H. Clark and D. G. Cobbold, Inorg. Chem., 1978, 17, 3169–3174.
40. H. Purdum, P. A. Montano and G. K. Shenoy, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 25, 4412–4417.
41. D. G. Leopold and W. C. Lineberger, J. Chem. Phys., 1986, 85, 51–55.
42. G. L. Gutsev, S. N. Khanna, B. K. Rao and P. Jena, J. Phys. Chem. A, 1999, 103, 5812–5822.
43. J. L. Chen and C. S. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 6558–6561.
44. B. B. Darwent, Natl. Stand. Ref. Data. Ser., 1970, 31, 1–52.
45. S. K. Loh, L. Lian, D. A. Hales and P. B. Armentrout, J. Phys. Chem., 1988, 92, 4009–4012.
46. L. S. Wang, H. Wu and S. R. Desai, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 8028–8031.
47. P. J. Ziemann and A. W. Castleman, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 13480–13486.
48. H. Shiroishi, T. Oda, I. Hamada and N. Fujima, Mol. Simul., 2004, 30, 911–915.
49. B. L. Wang, S. Nagase, J. J. Zhao and G. H. Wang, J. Phys. Chem. C, 2007, 111, 4956–4963.
50. S. Tazibt, S. Bouarab, A. Ziane, J. C. Parlebas and C. Demangeat, J. Phys. B: At., Mol. Opt. Phys., 2010, 43, 165101–165109.
51. N. O. Jones, B. V. Reddy and F. Rasouli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 165411.
52. K. Palotás, A. N. Andriotis and A. Lappas, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075403.
53. G. V. Chertihin, W. Saffel, J. T. Yustein and L. Andrews, J. Phys. Chem., 1996, 100, 5261–5273.

---

Footnote

† Electronic supplementary information (ESI) available: The calculated molecular orbital energy levels, density of states, infrared and Raman spectra, and coordinates of the low-lying structures for (FeO)_n^μ (n = 1–8, μ = 0, ±1) clusters. See DOI: 10.1039/c4ra12259c

---