Hooked on switch: strain-managed cooperative Jahn–Teller effect in Li_0.95Mn_2.05O₄ spinel

Abstract

The crystal structures, phase equilibria and composition ranges of materials that form lithium–manganese spinels have been studied extensively, frequently to optimize specific properties. Here, we report on the Jahn–Teller switching between two tetragonal structures, which is induced by high pressure. Heating the tetragonal phases under high pressure leads to further transformation to the cubic structure. A transformation of the same type was observed upon heating of Li_0.95Mn_2.05O₄ under ambient pressure, however at a milder temperature. The high-pressure high-temperature experiments were performed under pseudo-hydrostatic conditions at pressures of up to 1.87 GPa and temperatures from 303 to 623 K. Furthermore, the axial ratio of tetragonal phases of Li_0.95Mn_2.05O₄ is analyzed. This pressure/temperature switchable material can exhibit a wide range of novel and manipulable properties.

---

Introduction

Cooperative static and dynamic orbital ordering enables the development of oxides to make a switchable material that could be used in certain specific applications.¹ High pressure allows a controlled adjustment of structural parameters, such that they have an influence on the electronic and magnetic properties of materials. Physical properties such as metal–insulator transitions and superconductivity can be involved and can be tuned with pressure.² Recently, it has been shown that pressure can be used to operate a Jahn–Teller-driven magnetic dimensionality switch between two-dimensional and one-dimensional antiferromagnetic coupling.³

Classic examples of the Jahn–Teller switching between two different, closely-related structure types with two distinct molecular distortions of the Jahn–Teller active cations are the Tutton salts of copper, A₂[Cu(H₂O)₆][(S,Se)O₄]₂ (A = K⁺, Rb⁺, Cs⁺, NH⁴⁺, Tl⁺). The propensity for undergoing a phase transition and structural switching depends on the chemical strain induced with the hydrogen-bonding interactions and monovalent cations balance.⁴ Moreover, in the deuterated ammonium copper Tutton salt, the long axis of Jahn–Teller distortion changes direction, which causes a switch between two crystal forms, and the switch-driving agent is the pressure-induced strain.⁵ There are many examples of Jahn–Teller switching in manganese-doped perovskites. Thermally- and electrically-induced switching in the LaGa_1−xMn_xO₃ systems between high-resistance and low-resistance states has been explained in terms of thermo-induced local phase transition, resulting in the oxidation of Mn³⁺ ions and local removal of the Jahn–Teller distortion.⁶ Mn³⁺ ions are Jahn–Teller ions, which cause specific distortions to the crystal lattice. The oxidation of Mn³⁺ to Mn⁴⁺ would result in both the removal of such a distortion and an increase in the number of carriers. Manipulating Jahn–Teller distortions under pressure has been widely reviewed for Cu²⁺ as a central ion.⁷ In coordination systems with diverse coordination atoms, such as CuF₂(H₂O)₂(pyrazine), each trans-coordinated ligand provides an additional degree of freedom to the Jahn–Teller effect. In this type of compound, small perturbations of the metal–ligand environment can be enough to rotate the Jahn–Teller axis and radically modify the material properties. Pressure may act as a switching agent, especially for organic frameworks with relatively high compressibility. Rotation of the Jahn–Teller axis with pressure in the CuF₂(H₂O)₂(pyrazine) structure causes it to switch between a quasi-two-dimensional and a quasi-one-dimensional antiferromagnetic phase.^3,8 Moreover, the Cu(II) citrate dimer reveals a pressure-induced coordination change that leads to piezochromism.⁹

Pressure can also affect lithium–manganese spinels, which are important for energy storage and for purpose-engineered materials. Spinel manganites (such as LiMn₂O₄, Li₄Mn₅O₁₂ and similar materials) are very interesting and complex systems, with interesting correlation between electric transport and magnetic properties and crystal-lattice behaviour. The progenitor of this group of materials, LiMn₂O₄, contains in the unit cell 32 oxide anions, arranged in a cubic close-packed lattice, 8 Li⁺ ions on 1/8 of 64 tetrahedral holes and a 1 : 1 mixture of Mn³⁺ and Mn⁴⁺ ions distributed over 1/2 of 32 octahedral sites. The properties of these materials depend strongly on the composition, in particular, on point defects and on the doping concentration, which induces changes in the relative content of Mn⁴⁺/Mn³⁺ ions.^10–12 Pressure and temperature can be used to obtain lithium–manganese oxide with an orthorhombic structure (Pnma), referred to as the postspinel phase.¹³ The high-pressure postspinel structure comprises an irregular hexagonal 1D channel, which implies the diffusive motion of Li⁺ ions in Li_0.92Mn₂O₄, desirable for positive electrode materials.^14,15 First-principles density functional theory (DFT) calculations show details of the spinel-to-postspinel phase transformation, and provide a kinetic explanation for the stability of the postspinel HP/HT phase under ambient conditions.¹⁶

Deformation of the tetragonally-deformed spinels exposed to high pressure is usually reduced, as manifested by the axial ratio reduction and the atomic positions getting closer to the ideal cubic spinel value. Quite different structural changes are observed for the Jahn–Teller ions in structures when we move away from pure hydrostaticity, and when semihydrostatic or even nonhydrostatic compression is applied. Even a small deviation from hydrostatic conditions can facilitate a pressure-induced phase transition and in turn leads both to new deformation of the nearest neighbourhood of Mn³⁺ ions and a cooperative Jahn–Teller deformation. The transition pressures of LiMn₂O₄ in different pressure-transmitting media were reported to be below 0.5 GPa¹⁷ and 1.2 GPa¹⁸ for silicon oil, 0.2 GPa for boron nitride,¹⁸ 1.2 GPa for NaCl,¹⁸ and 4.36 GPa¹⁹ and 11.0 GPa²⁰ for methanol–ethanol. These results, and survival after the pressure relaxation of the high-pressure artefacts in the samples compressed in nonhydrostatic conditions, indicate that deviatoric stress rather than absolute pressure plays the key role in this phase transition.^20,21

It is also possible to control the Jahn–Teller deformation, and as a result physicochemical properties, of materials with epitaxial strain in thin films.²² The effect of the substrate on the film can be divided into two kinds of strain: the planar strain along the film plane xy and the axial strain along the growth direction z. Since the substrate is typically cubic or pseudocubic, the planar strain is almost isotropic. Epitaxial strain is the reason why the cubic structure of Mn₃O₄ has been observed instead of the tetragonal one in the thin film grown on MgO as a substrate.²³ However, with MgAl₂O₄ as a substrate, the lattice mismatch is minimized and growth of the tetragonal Mn₃O₄ phase has been observed with the c axis elongated in the direction perpendicular to the substrate surface.²⁴ Thus, the Jahn–Teller deformation-type control can be performed not only with temperature and pressure, as we present, but potentially also with the use of epitaxial strain.

In this article we would like to call attention to the interesting effect of reorientation of the cooperative Jahn–Teller effect in a material of particular stoichiometry and obtained in a specific way. We would like to highlight an unusual structural property of Li_0.95Mn_2.05O₄, that is its ability to switch between three types of crystal structure: two of them with the cooperative Jahn–Teller effect of different types of tetragonal deformation, and one cubic structure without a manifested cooperative Jahn–Teller effect.

Experimental

The Li_0.95Mn_2.05O₄ spinel sample was obtained from the appropriate amounts of thoroughly mixed powders of α-Mn₂O₃ and Li₂CO₃ (99.0% Merck) by successive thermal treatment in air at 973 K and, after grinding, at 1073 K for 4 h in air. Finally, the specimen was quenched rapidly in solid CO₂. The precursor (α-Mn₂O₃) was prepared by precipitation of Mn-hydroxide from Mn²⁺ nitrate solution (Mn(NO₃)₂·6H₂O, 99.0% Merck) with sodium hydroxide (98.8% POCH). Washed and dried at room temperature, it was dehydrated for 2 h at 523 K and then successively at 673, 773, and 873 K for 4 h each in air. The crystalline single-phase precursor displayed the bixbyite (Ia3) structure. The tetragonally-distorted spinel structure of the final sample was confirmed by an X-ray diffraction pattern, recorded on a Bruker D8 Advance X-ray diffractometer in the Bragg–Brentano configuration, equipped with a Johansson monochromator (λCu Kα₁ = 1.5406 Å) and using a LynxEye strip detector. Refinement with the Rietveld method was performed for the pattern collected in the angular range 15–120° 2θ using the Jana2006 program.²⁵

TG measurements were run by means of a Setsys 1200 (Setaram) system with a heating rate of 10 K min⁻¹ in air. The chemical composition of the spinel samples was analysed by inductively coupled plasma optical emission spectroscopy (Varian ICP-OES VISTA-MPX).

Li_0.95Mn_2.05O₄ was studied in HP/HT conditions in the pressure range from ambient to 1.87 GPa by means of energy-dispersive X-ray diffraction (EDXRD) at beamline F2.1 at Desy/Hasylab, with a typical collection time of ∼6 min per pattern. The diffraction patterns were recorded using a CANBERRA semiconductor (germanium) detector with resolutions of 153 and 500 eV for energies of 5.9 and 122 keV, respectively (the total average resolution δd/d ≈ 1%), with the diffraction angle fixed at 3.84062°. The sample was mounted on a large-anvil diffraction press, MAX80, in a cylindrical sample container made from hexagonal boron nitride (hBN) inserted into a graphite resistance heater in a cube fabricated from a mixture of boron and epoxy resin. To achieve the quasi-hydrostatic compression conditions, the studied polycrystalline material was mixed (1 : 3) with hexagonal boron nitride. The accuracy of pressure determination was evaluated to be ±0.05 GPa. With increasing temperature we observed a fluctuation in pressure; however, it did not exceed the value of the accuracy of pressure determination. The temperature was measured by the NiCr–Ni thermocouple with a stability of ±2 K.

At a pressure of 1.87 GPa, and in the temperature range 303–623 K, the semi-isobaric measurements were performed. The diffraction from the sodium chloride sample, which was mounted separately in the sample compartment, was used to calibrate the pressure according to Decker EOS.²⁶ To monitor the change in lattice parameters with pressure we fitted diffraction patterns with the Le Bail method. There was no need for special adjustments of experimental patterns for fluorescence because in the analysed energy range there were no fluorescence maxima of any present elements. Diffraction patterns were fitted with the Jana2006 program,²⁵ which enabled refinement with anisotropic strain broadening with meaningful tensor parameters.²⁷ Prior to the Le Bail fitting, XRD patterns were converted into conventional pseudo angle-dispersive data (CuKα₁ radiation). This whole diffraction pattern profile fitting allows determination of the lattice parameters and it works especially well with overlapping of peaks because in this method the intensity is defined on the basis of the multiplicity of the intensities that contribute to a particular peak.

Moreover, the study was performed in high-temperature conditions at ambient pressure by the synchrotron angle-dispersive X-ray diffraction (ADXRD) method. The X-ray diffraction studies at varied temperatures were carried out with a powder diffractometer at the B2 beamline (Hasylab/DESY). The powder sample was mounted in a quartz capillary that rotated during the experiment inside a capillary furnace (STOE). A curved on-site readable imaging plate detector was applied for the data collection. The powder diffraction patterns were recorded in the range 5–60° 2θ. The wavelength was adjusted to 0.70998 Å. For the patterns collected in the high-temperature experiment, the Rietveld refinement was performed using the Jana2006 program.²⁵

Results and discussion

ICP-OES analysis confirmed the nominal cation ratio in the prepared lithium–manganese oxide. The Li/Mn ratio was 0.465 ± 0.004 (the confidence interval of the mean value was calculated for 6 repetitions, standard deviation σ = 0.0043 and statistical confidence P = 95%), whereas for the ‘ideal’ LiMn₂O₄ and Li_0.95Mn_2.05O₄ the Li/Mn ratio is 0.500 and 0.463, respectively. Thermogravimetric analysis (ESI Fig. S1†) indicated that the evident mass loss upon heating occurs only if the temperature exceeds 1150 K, therefore, at the synthesis temperature of 1073 K, thermal dissociation and formation of anionic vacancies can be neglected. Thus, the combination of ICP and thermogravimetric analysis revealed that the chemical composition of the sample agrees well with the nominal composition and is indeed Li_0.95Mn_2.05O₄.

The applied combination of sintering at high temperatures followed by a very rapid quenching process enabled the production of a spinel material that had been impossible to obtain earlier.^28,29 Samples with a Li/Mn ratio smaller than 0.5 are multiphased if they are not quenched after the sintering step.³⁰

For the lithium–manganese oxide of the chosen stoichiometry, the quenching does not preserve the high-temperature crystal structure, but enables the synthesis of a new material of intriguing structure and unusual, hitherto-unknown properties. Mn³⁺ ions exist in the spinel structure of Li_0.95Mn_2.05O₄ in both tetrahedral and octahedral coordination geometries.³¹ The Mn³⁺ cations partially occupy the four-coordinate sites of the spinel structure where removal of the degeneracy of the d⁴ ground state results in flattening of the MnO₄ tetrahedron, as observed in CuCr₂O₄ with Cu²⁺ as a tetrahedrally-coordinated Jahn–Teller ion.³² The local structure deformation, induced by the Jahn–Teller Mn³⁺ ions introduced in the tetrahedral sites, competes with the Jahn–Teller elongation of the Mn³⁺O₆ octahedra, typically observed in manganese-containing spinels (e.g. in Mn₃O₄). However, even the small amount of Mn³⁺ in the tetrahedral sites is able to induce a kind of chemical strain and forces one of two energetically indistinguishable Jahn–Teller deformations on the Mn³⁺O₆ octahedra. Finally, a quite unusual tetragonal spinel of space group I4₁/amd (space group no. 141) and c/a′ < 1 was obtained, as confirmed by the Rietveld refinement of the laboratory ADXRD data (ESI Fig. S3†). Fig. 1 shows the unit cell of the Li_0.95Mn_2.05O₄ spinel with tetrahedra occupied by Li and Mn atoms and the ‘flattened’ octahedra with two short Mn–O distances, practically parallel to the c axis, and four long Mn–O distances almost in the (110) plane (for structural data see ESI Tables S1 and S2†). Although the Le Bail profile fitting and the Rietveld refinement were performed with the I4₁/amd space group, a straightforward illustration of the tetragonal distortion of the spinel structure requires the use of the F4₁/ddm space group as an alternative description of the I4₁/amd space group. We assume a notation for the unit cell parameters in the I4₁/amd space group as a and c, and for the face-centred pseudocubic cell (F4₁/ddm) we express √2a = a′ and c = c′. Our earlier experience with the quenching of the Li_xMn_3−xO₄ lithium-deficient spinels allowed us to choose the nominal stoichiometry of Li_0.95Mn_2.05O₄ as the most promising for the synthesis of the tetragonal spinel with c/a′ < 1, although this tetragonal deformation has been observed in a major phase for samples of compositions between Li_0.94Mn_2.06O₄ and Li_0.97Mn_2.03O₄.³¹

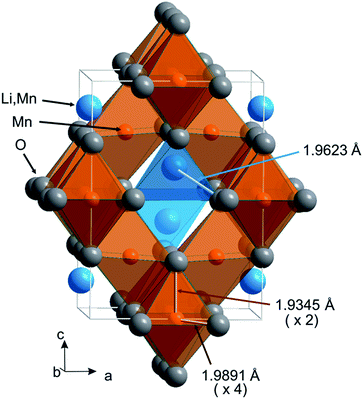Fig. 1 Crystal structure of Li_0.95Mn_2.05O₄ under ambient conditions, space group I4₁/amd, c/a√2 = 0.97809.

It should be stressed that the tetragonal deformation of the spinel structure for this stoichiometry is different from that of the high-temperature tetragonal spinel, observed in situ for LiMn₂O₄ (tetragonal, I4₁/amd c/a′ > 1),³³ and also it does not correspond to the low-temperature structure of LiMn₂O₄ (orthorhombic, Fddd)³⁴ (see ESI, Fig. S2†). Finally, the crystal structure deformation of Li_0.95O_2.05O₄ is also different from that of the single crystal tetragonal spinel (Li_0.91Mn_0.09)Mn₂O₄ synthesized by the flux method (tetragonal, I4₁/amd c/a′ > 1).³⁵

The synchrotron EDXRD patterns were collected at various pressures up to 1.87 GPa, and then for a fixed pressure at various temperatures up to 623 K (ESI Fig. S4†). The Le Bail method enabled refinement of the unit cell parameters (Tables 1 and 2), the profile parameters, and the peak intensities to match the measured powder diffraction patterns collected in each high pressure/high temperature (HP/HT) condition. The Le Bail refinement was successfully used to show the phase transitions in the HP/HT experiments. Models of two tetragonal spinels (I4₁/amd) for c/a′ < 1 and c/a′ > 1 were sufficient to obtain a good fitting of results in the pressure region from 0.15 to 1.87 GPa (representative results are presented in Fig. 3a). The initial models were assumed on the basis of the Rietveld refinement for this sample under ambient conditions for c/a′ < 1 (for the structural data see ESI†) and on the basis of literature data for c/a′ > 1.³³ Moreover, the Le Bail profile fitting of the synchrotron EDXRD patterns collected at temperatures higher than 373 K and under high pressure required input of a model of the cubic spinel phase, with the crystal structure analogous to that of LiMn₂O₄. Representative results of the Le Bail fitting for HP/HT measurements are presented in Fig. 3a(C) and (D) and the obtained unit cell parameters are shown in Table 2.

Table 1 Unit-cell parameters of crystal phases under various pressures and quality parameters of profile refinement with the Le Bail technique

P [GPa]	Tetragonal c/a′ < 1		Tetragonal c/a′ > 1		R p [%]	R wp [%]
	a [Å]	c [Å]	a [Å]	c [Å]
0	5.8911(8)	8.160(2)	—	—	4.66	9.12
0.15	5.8876(5)	8.126(2)	5.746(1)	8.549(3)	4.26	6.10
0.27	5.8840(8)	8.121(2)	5.741(2)	8.569(4)	4.27	6.65
0.46	5.887(1)	8.106(3)	5.734(2)	8.574(3)	3.99	6.17
0.96	5.897(1)	8.066(4)	5.7216(9)	8.591(2)	5.24	7.69
1.39	5.888(1)	8.046(4)	5.7093(7)	8.587(2)	4.65	6.12
1.80	5.876(2)	8.041(6)	5.697(2)	8.586(4)	5.71	7.84

---

Table 2 Unit-cell parameters of crystal phases at a pressure of 1.87 GPa at various temperatures and quality parameters of profile refinement with the Le Bail technique

T [K]	Tetragonal c/a′ < 1		Tetragonal c/a′ > 1		Cubic	R p [%]	R wp [%]
	a [Å]	c [Å]	a [Å]	c [Å]	a [Å]
303	5.876(2)	8.041(6)	5.697(2)	8.586(4)		5.71	7.84
323	5.880(1)	8.056(3)	5.699(2)	8.591(3)		3.51	5.13
373	5.877(1)	8.027(3)	5.715(1)	8.568(4)		5.77	7.43
423	5.896(2)	8.040(4)	5.731(1)	8.555(4)	8.241(2)	4.76	6.36
473			5.727(1)	8.533(5)	8.235(2)	4.49	6.23
523			5.742(1)	8.512(6)	8.242(2)	4.49	6.21
573			5.760(1)	8.469(6)	8.251(2)	4.88	6.54

---

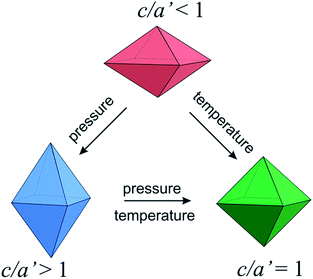
Correlation of Jahn–Teller local deformations in the spinel structure containing ions at degenerate electronic ground states, such as Mn³⁺, leads to the cooperative Jahn–Teller effect. Using pressure and temperature we can change the degree of deformation and switch between two different stages of the Jahn–Teller deformation. It is also possible to transform the tetragonal structure with the cooperative Jahn–Teller effect to the cubic structure with the statistically disordered distortion (Fig. 2). Fig. 3b shows the representative part of the raw EDXRD patterns (corresponding to cubic spinel 311 and 222 lines) for the Li_0.95Mn_2.05O₄ spinel, as a function of pressure up to 1.87 GPa and further at fixed pressure as a function of temperature. Vanishing of the reflections derived from the initial tetragonal phase with c/a′ < 1 is coupled with increasing intensities of the ones corresponding to the new tetragonal phase, of the axial ratio c/a′ > 1 (ESI Fig. S4†). This phase transition was also confirmed by the Le Bail whole pattern profile fitting, with the pseudo angle-dispersive patterns beforehand converted from the energy-dispersive data (Fig. 3a). At a pressure of 1.87 GPa, we found evidence for the coexistence of two tetragonal phases in a ratio of about 1 : 1 (Fig. 3a(B)).

Fig. 2 Schematic diagram of phase transitions in Li_0.95Mn_2.05O₄.

Fig. 3 (a) Le Bail refinement results. For the sake of clarity, not all peaks in the patterns were indexed. Indices in part (A) – tetragonal spinel structure (I4₁/amd) with c/a′ < 1; (B) – tetragonal spinel structures (I4₁/amd) with c/a′ < 1 and c/a′ > 1; (C) – tetragonal spinel structure (I4₁/amd) with c/a′ > 1 and cubic spinel (Fd3̄m); (D) – cubic spinel (Fd3̄m). The vertical bars indicate the positions of Bragg peaks. (b) Representation of the raw energy-dispersive X-ray diffraction profiles of Li_0.95Mn_2.05O₄ as a function of pressure and temperature.

In the Jahn–Teller distorted spinel phase, the ordering of the tetragonally distorted octahedra is caused by the interaction of local distortions through the phonon field, and is a temperature-dependent interaction of electronic properties and phonon branches. With increasing temperature, the correlations of local distortions weaken, and at a critical temperature the phase transition to the distortion-disordered phase takes place. The presence of the tetragonal phase of c/a′ > 1 remains discernible at 573 K, whereas heating to 623 K leads to formation of a pure cubic structure (Fig. 3a(D)). Therefore, the observed phase transitions induce anomalies in the elastic crystalline properties and consequently they induce substantial changes in the electronic structure (change in a splitting of the degenerate energy levels). Also, in the vicinity of the tetragonal-to-cubic phase transition all the crystalline electronic parameters can exhibit appreciable anomalies.

With increasing pressure, the tetragonal phases showed an increasing or decreasing c/a′ ratio for the tetragonal c/a′ > 1 or c/a′ < 1 phases, respectively. The pressure-dependence of the lattice parameter ratio provides quantitative evidence of the reorientation of the Jahn–Teller distortion of Mn³⁺O₆, where Mn³⁺ is located at the centre of this octahedron with each of the Mn³⁺–oxygen bonds directed approximately along the a–b diagonal and the c cell edge of the tetragonal unit cell. Fig. 4 shows that there is a difference between the modes by which strain is accommodated in the high-pressure tetragonal phase (c/a′ > 1) compared to the primary tetragonal phase (c/a′ < 1). An interesting feature is that the axial ratio of the tetragonal phase with c/a′ < 1 decreases only to about 0.967 at ∼1 GPa and does not change significantly on further compression. The axial ratio of the pressure-induced phase (with c/a′ > 1) increases monotonically with pressure, although this tendency is in contradiction to the rule of tetragonally distorted spinels’ response to pressure, according to which pressure diminishes the distortion or even does not affect the axial ratio.^36,37 However, results presented are consistent with the earlier observations for LiMn₂O₄,^20,21 which suggest a specific mechanism for the lithium–manganese samples compressed beyond the limit of hydrostaticity. The c/a′ ratio reached at 2.87 GPa is consistent with that reported for the tetragonal phase obtained by quenching LiMn₂O₄ from 1193 K. Only a slightly smaller c/a′ ratio, 1.062, has been reported for the single crystal obtained by the flux method. This indicates that the elongation of the spinel unit cell obtained in our HP experiment corresponds to those of the known structures of MnO₆ octahedra elongated in the c direction.

Fig. 4 The c/a′ ratio of the lattice parameters for two tetragonal phases: the initial one with c/a′ < 1 (red squares) and the high pressure phase with c/a′ > 1 (blue diamonds).

The observed modulation of the axial ratio with pressure is expected to be of interest in thin layer technology, because a similar modulation of the axial ratio can be obtained in thin layers through an appropriate choice of substrate and layer thickness, and films can be grown with various aspect ratios. The epitaxial stress has been successfully applied in the modification of the physical properties of LaCoO₃. The lattice mismatch in epitaxial thin films of LaCoO₃ on SrTiO₃ produces a tensile strain, making these films one of the few ferromagnetic (FM) insulators known among transition-metal oxides.³⁸

The evolution of the phase composition of the Li_0.95Mn_2.05O₄ spinel with temperature for P = const. = 1.87 GPa is illustrated in Fig. 5. The first temperature-induced phase transition appears at about 423 K and is a transformation of the tetragonal phase with c/a′ < 1 to the cubic phase. This temperature-induced suppression of the cooperative Jahn–Teller effect was also observed in the ADXRD high temperature experiment for Li_0.95Mn_2.05O₄, where Rietveld refinement results reveal 393 K as the temperature of the tetragonal-to-cubic phase transition (Fig. 7). Thus, at a pressure of 1.87 GPa this phase transition is shifted about 30 K in the direction of higher temperature, compared to that observed at ambient pressure.

Fig. 5 The phase composition of the sample at a pressure of 1.87 GPa as a function of temperature obtained from the EDXRD experiment. Red squares: % of the tetragonal phase with c/a′ < 1; blue diamonds: % of the tetragonal phase with c/a′ > 1; green triangles: % of the cubic phase.

The percentage of the second tetragonal phase induced with high pressure, with c/a′ > 1, remains almost unchanged up to 573 K. Finally, at 623 K this phase abruptly disappears. In this temperature region the second phase transition is observed, which could be attributed to statistical disorder of the elongated Mn³⁺ octahedra within the octahedral sublattice of the spinel structure.

The axial ratio, c/a′, remains almost unchanged with increasing temperature for the tetragonal phase of c/a′ < 1 at 1.87 GPa (Fig. 6). However, for the tetragonal phase of c/a′ > 1 the axial ratio decreases gradually from 1.0657 at 303 K to 1.0397 at 573 K. Similar suppression of the cooperative Jahn–Teller effect is manifested in the ADXRD high temperature experiment for the tetragonal phase of c/a′ < 1 (ESI Fig. S5†), which in Fig. 6 can be observed as an increase in the c/a′ ratio. The results of the Rietveld refinement for ADXRD patterns collected at 298, 393 and 413 K are shown in Fig. 7 and in Table 3. The tetragonal-to-cubic phase transition was induced by heating. At about 393 K both tetragonal (c/a′ < 1) and cubic phases were observed, whereas at 413 K only the cubic phase existed. Inflection of the c/a′ ratio as a function of temperature at about 373 K (Fig. 6) gently suggests an additional structural phenomenon. An additional phase transition is possible and can be driven by a charge ordering such as that observed in Fe₃O₄ and in LiMn₂O₄,^34,39 however, to resolve this high resolution measurements are necessary.

Fig. 6 The c/a′ ratio of the lattice parameters for tetragonal phases as a function of temperature: with c/a′ < 1 at 1.87 GPa (red squares); with c/a′ > 1 at 1.87 GPa (blue diamonds); with c/a′ < 1 at ambient pressure (open circles).

Fig. 7 Observed (black) and, calculated (red) profiles from Rietveld refinement of the synchrotron ADXRD patterns obtained for Li_0.95Mn_2.05O₄ at various temperatures at ambient pressure. The vertical bars indicate the positions of Bragg peaks. The lower curves represent the difference between observed and calculated patterns.

Table 3 Unit-cell parameters of crystal phases at ambient pressure at various temperatures and quality parameters of Rietveld refinement

T [K]	Tetragonal c/a′ < 1		Cubic	R p [%]	R wp [%]
	a [Å]	c [Å]	a [Å]
297	5.874(1)	8.1189(15)		5.57	7.11
373	5.873(2)	8.194(3)		5.4	6.84
393	5.850(2)	8.233(3)	8.258(3)	5.33	6.78
413			8.265(1)	5.49	6.98

---

Thus, it is possible to obtain a pressure- and temperature-induced Jahn–Teller switch based on the spinel framework with variable valence metal ions and a precisely fitted synthesis path. This might be a new route to look for new applications of these spinel materials. Further investigations based on the influence of the Jahn–Teller effect on the crystallochemistry of this group of materials is still in progress. These high-pressure and high-temperature phase transformations are important as they provide a potential pathway to obtaining new materials with desirable properties. Furthermore, we can expect that this approach to novel switchable materials is not limited to only one material with a specific stoichiometry.

Conclusions

In the present contribution we have added new information to the knowledge on lithium–manganese spinels by determining the structural properties of Li_0.95Mn_2.05O₄ characterized by its Jahn–Teller instability. Pseudo-hydrostatic compression leads to small perturbations in the Jahn–Teller ion environment and can be sufficient to switch the Jahn–Teller deformation type and radically modify the properties of the spinel material. High pressure application is indicated as an ideal method of achieving such a unique phenomenon. Heating at a pressure of 1.87 GPa transforms both tetragonal phases, c/a′ < 1 and c/a′ > 1, to the cubic phase structure with a suppressed cooperative Jahn–Teller effect. At ambient pressure, heating of the tetragonal Li_0.95Mn_2.05O₄ spinel (c/a′ < 1) also leads to formation of the cubic structure, but at a milder temperature.

Acknowledgements

Some of the research has been carried out at the beamlines F2.1 and B2 of the light source DORIS III, at DESY, a member of the Helmholtz Association (HGF). The research leading to these results has received funding from the European Community’s Seventh Framework Programme (FP7/2007–2013) under grant agreement no. 312284.

Notes and references

1. J. B. Goodenough, Chem. Mater., 2014, 26, 820–829.
2. V. D. Blank and E. I. Estrin, Phase Transitions in Solids Under High Pressure, CRC Press, 2013.
3. S. Ghannadzadeh, J. S. Möller, P. A. Goddard, T. Lancaster, F. Xiao, S. J. Blundell, A. Maisuradze, R. Khasanov, J. L. Manson, S. W. Tozer, D. Graf and J. A. Schlueter, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 241102.
4. C. J. Simmons, H. Stratemeier, M. A. Hitchman and M. J. Riley, Inorg. Chem., 2013, 52, 10481–10499.
5. L. R. Falvello, J. Chem. Soc., Dalton Trans., 1997, 4463–4476.
6. N. Noginova, J. McClure, E. Etheridge, V. I. Gavrilenko and D. Novikov, J. Phys. D: Appl. Phys., 2008, 41, 055411.
7. M. A. Halcrow, Chem. Soc. Rev., 2013, 42, 1784–1795.
8. A. Prescimone, C. Morien, D. Allan, J. A. Schlueter, S. W. Tozer, J. L. Manson, S. Parsons, E. K. Brechin and S. Hill, Angew. Chem., Int. Ed., 2012, 51, 7490–7494.
9. K. W. Galloway, S. A. Moggach, P. Parois, A. R. Lennie, J. E. Warren, E. K. Brechin, R. D. Peacock, R. Valiente, J. González, F. Rodríguez, S. Parsons and M. Murrie, CrystEngComm, 2010, 12, 2516–2519.
10. K. Hoang, J. Mater. Chem. A, 2014, 2, 18271–18280.
11. M. Kopec, J. R. Dygas, F. Krok, A. Mauger, F. Gendron and C. M. Julien, J. Phys. Chem. Solids, 2008, 69, 955–966.
12. D. Liu, W. Zhu, J. Trottier, C. Gagnon, F. Barray, A. Guerfi, A. Mauger, H. Groult, C. M. Julien, J. B. Goodenough and K. Zaghib, RSC Adv., 2014, 4, 154–167.
13. K. Yamaura, Q. Huang, L. Zhang, K. Takada, Y. Baba, T. Nagai, Y. Matsui, K. Kosuda and E. Takayama-Muromachi, J. Am. Chem. Soc., 2006, 128, 9448–9456.
14. Y. Ikedo, J. Sugiyama, O. Ofer, M. Månsson, H. Sakurai, E. Takayama-Muromachi, E. J. Ansaldo, J. H. Brewer and K. H. Chow, J. Phys.: Conf. Ser., 2010, 225, 012017.
15. M. Mamiya, K. Kataoka, J. Akimoto, S. Kikuchi, Y. Terajima and K. Tokiwa, J. Power Sources, 2013, 244, 561–564.
16. C. Ling and F. Mizuno, Chem. Mater., 2013, 25, 3062–3071.
17. A. Paolone, A. Sacchetti, P. Postorino, R. Cantelli, A. Congeduti, G. Rousse and C. Masquelier, Solid State Ionics, 2005, 176, 635–639.
18. P. Piszora, Z. Kristallogr. Suppl., 2007, 26, 387–392.
19. J. Darul, W. Nowicki and P. Piszora, J. Phys. Chem. C, 2012, 116, 17872–17879.
20. Y. Lin, Y. Yang, H. Ma, Y. Cui and W. L. Mao, J. Phys. Chem. C, 2011, 115, 9844–9849.
21. P. Piszora, Solid State Phenom., 2007, 130, 69–72.
22. A. M. Haghiri-Gosnet and J. P. Renard, J. Phys. D: Appl. Phys., 2003, 36, R127.
23. O. Y. Gorbenko, I. E. Graboy, V. A. Amelichev, A. A. Bosak, A. R. Kaul, B. Güttler, V. L. Svetchnikov and H. W. Zandbergen, Solid State Commun., 2002, 124, 15–20.
24. L. Ren, M. Yang, W. Zhou, S. Wu and S. Li, J. Phys. Chem. C, 2014, 118, 243–249.
25. V. Petricek, M. Dusek and L. Palatinus, Jana2006, The crystallographic computing system, Institute of Physics, Praha, Czech Republic, 2006.
26. D. L. Decker, W. A. Bassett, L. Merrill, H. T. Hall and J. D. Barnett, J. Phys. Chem. Ref. Data, 1972, 1, 773–836.
27. P. W. Stephens, J. Appl. Crystallogr., 1999, 32, 281–289.
28. T. R. Hinklin, J. Azurdia, M. Kim, J. C. Marchal, S. Kumar and R. M. Laine, Adv. Mater., 2008, 20, 1373–1375.
29. S. Yeo, S. Guha and S. W. Cheong, J. Phys.: Condens. Matter, 2009, 21, 125402.
30. P. Piszora, J. Alloys Compd., 2005, 401, 34–40.
31. P. Piszora, Chem. Mater., 2006, 18, 4802–4807.
32. B. J. Kennedy and Q. Zhou, J. Solid State Chem., 2008, 181, 2227–2230.
33. R. Kanno, A. Kondo, M. Yonemura, R. Gover, Y. Kawamoto, M. Tabuchi and G. Rousse, J. Power Sources, 1999, 81, 542–546.
34. J. Rodriguez-Carvajal, G. Rousse, C. Masquelier and M. Hervieu, Phys. Rev. Lett., 1998, 81, 4660–4663.
35. H. Björk, H. Dabkowska, J. E. Greedan, T. Gustafsson and J. O. Thomas, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, 57, 331–332.
36. J. Darul, C. Lathe and P. Piszora, J. Phys. Chem. C, 2013, 117, 23487–23494.
37. S. Åsbrink, A. Waśkowska, L. Gerward, J. S. Olsen and E. Talik, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 12651.
38. F. Rivadulla, Z. Bi, E. Bauer, B. Rivas-Murias, J. M. Vila-Fungueiriño and Q. Jia, Chem. Mater., 2013, 25, 55–58.
39. M. S. Senn, J. P. Wright and J. P. Attfield, Nature, 2012, 481, 173–176.

---

Footnote

† Electronic supplementary information (ESI) available: Thermogravimetric curve; comparison of the experimental XRD pattern with the patterns calculated for typical structures of lithium–manganese oxides; results of the Rietveld refinement of the Li_0.95Mn_2.05O₄ pattern collected under ambient conditions; EDXRD patterns obtained in HP/HT experiment; ADXRD patterns obtained at various temperatures under ambient pressure. See DOI: 10.1039/c4ra11533c

---