CDI ragone plot as a functional tool to evaluate desalination performance in capacitive deionization

Abstract

A novel concept to evaluate desalination performance in capacitive deionization (CDI) is proposed called the CDI Ragone plot. The plot can allow for intuitive acquisition of deionization capacity (mg g⁻¹), rate (mg g⁻¹ s⁻¹), and time (s) and thus, will work as a functional tool to evaluate desalination performance in CDI.

---

Capacitive deionization (CDI) is a promising desalination process driven by electrical potential and the consequent double layer formation on the surface of a porous electrode.^1,2 An excess of counter-ions in the double layer leads to a depletion of ions in the region adjacent to the electrode surface; thus, desalinated water can be produced by extracting the solution between the two electrodes. CDI has attracted much attention compared to conventional desalination processes such as thermal distillation and reverse osmosis (RO) because of its potential for an efficient energy use.^3,4 Furthermore, the energy consumed during desalination is simultaneously stored in electrodes because its configuration and principle are similar to an energy storage device. Therefore, the stored energy can be conceptually recovered,^5–8 and a practical energy recovery system^9–11 facilitates low-energy production of fresh water, although it still has a long way to go to realize such an ideal desalination process at this moment.

So far, various attempts have been carried out to achieve an efficient desalination performance. These approaches include synthesizing novel carbon materials,^12–17 modifying carbon electrodes,^18,19 involving Faradaic reactions,^20–22 incorporating ion-exchange membranes or polymers,^23–25 altering operation methods,²⁶ and developing new processes.^27–29 No matter what strategy CDI implements, it is quite important to determine its desalination performance based on an appropriate evaluation method. However, desalination performance has been reported in various ways; thus, CDI requires a standard method to evaluate the desalination performance which could allow for further advancements in this area. Among the various ways, two indicators have most frequently been reported as representing performance, which are the capacity and rate of desalination. The desalination capacity shows the amount of removed ions per mass of electrodes, normally when the performance reaches its equilibrium.¹ On the other hand, the desalination rate indicates the kinetics of desalination expressed as the rate constant¹⁷ or capacity divided by time.^25,29 However, these two parameters have been separately provided at the specific condition, thus facile acquisition of the overall desalination performance is difficult. Therefore, CDI requires a more advanced evaluation method, determining the overall performance which includes the capacity and rate.

In this study, we propose a new concept to evaluate desalination performance in CDI called the CDI Ragone plot. Compared to the conventional Ragone plot for energy storage devices, the CDI Ragone plot evaluates the desalination performance taking into consideration both the capacity and rate, which allows for the intuitive acquisition of the overall desalination performance based on a conventional operating method. Herein we show an evaluation methodology and the implications of the CDI Ragone plot along with the effects of the various parameters, as a functional tool for examining desalination performance in CDI.

Carbon composite electrodes were prepared with MSP-20 (Kansai Coke and Chemicals, Japan), carbon black (Super P, Timcal), and polytetrafluoroethylene (PTFE, Aldrich) binder (86 : 7 : 7 in weight ratio). A mixture containing these components was kneaded with a few milliliters of ethanol until it solidified, and sheet-type electrodes were made by pressing with a roll-pressing machine. The desirable thickness was obtained by adjusting the gap of the two rollers; the thickness was ∼300 μm unless otherwise specified. After the fabrication, the electrodes were dried in a vacuum oven at 120 °C for 12 h. Other carbon electrodes (S-51HF (Norit), YS-2 (Japan EnviroChemicals), CEP21 (Power Carbon Technology, Korea), and MDC¹² (MOF-derived carbon)) were fabricated with the same procedure.

A custom-built CDI cell was used to evaluate desalination performance, in which built-in graphite current collectors were installed. A pair of round-shape carbon electrodes (20 mm in diameter) having a center hole (4 mm in diameter) was placed onto current collectors, and each electrode was covered by anion- and cation-exchange membranes (selemion, AGC ENGINEERING CO., LTD, Japan) with the same geometry as the electrode (membrane-assisted CDI, MCDI). Between the two ion-exchange membranes, a polymer spacer (thickness = 185 μm) was located to allow a feed solution to pass from the outside to the center hole. After the assembly, the CDI cell was pressed and sealed off. A feed solution (2, 10, 50, and 100 mM NaCl) was supplied to the CDI cell with a peristaltic pump (flow rate = 1, 2, and 4 ml min⁻¹) and the effluent conductivity was collected with a flow-type conductivity meter (3574-10C, HORIBA, Japan) which was connected to the outlet. After passing through the conductivity meter, the effluent was disposed (single-pass mode). All experiments were conducted in a temperature chamber at 25 °C.

Desalination performance was evaluated under constant current operation.^1,30 The CDI cell was controlled with a cycler (WBCS3000, WonaTech, Korea); it was charged under various constant currents (1–25 mA) with a cut-off voltage of 1.2 V followed by short-circuiting for many seconds until the outlet conductivity showed a plateau which was close to the initial conductivity. These steps were repeated 3 times to secure the dynamic equilibrium, and the 3^rd cycle was used as a representative profile. The deionization capacity (mg g⁻¹, the mass of NaCl (mg) divided by the mass of both electrodes (g)) was derived from the area below the influent conductivity during the charging step.³¹ The mean deionization rate (mg g⁻¹ s⁻¹) was obtained by dividing the deionization capacity by the duration of charging (s). It should be noted that operating method (e.g., constant current charging–constant current discharging, constant voltage charging–zero voltage discharging, etc.) or CDI without membranes could result in different desalination performances,²⁵ but our focus was to observe the performance obtained only from constant current charging in MCDI. Detailed operating parameters for each experimental condition are provided in Table S1.†

Fig. 1(a) shows a conceptual diagram of the CDI Ragone plot, in which x and y axes represent the deionization capacity and mean deionization rate, respectively. This plot combines two important parameters that represent the desalination performance, which are relevant to the energy and power of energy storage devices in a conventional Ragone plot.³² The most outstanding aspect of the CDI Ragone plot is that it can provide three essential parameters at once: the deionization capacity (x-axis), mean deionization rate (y-axis), and deionization time (dashed lines). More importantly, the overall desalination performance can be evaluated minimizing bias caused by selecting a specific condition. The desalination performance must be evaluated under various current loads to achieve this goal; the lowest and highest current loads could provide the full capacity and maximum rate, respectively. Fig. 1(b) shows representative experimental data, which were converted to draw the CDI Ragone plot. As can be seen, steady conductivity profiles were observed below the initial conductivity (dashed line), showing the typical behavior of constant current operation.³⁰ When operating the CDI cell in this mode, a steady and controlled effluent can be produced depending on the current load; the lower current produces an effluent with a slightly decreased conductivity for a longer time while the higher current produces an effluent with a largely decreased conductivity in a relatively short time. Therefore, a higher mean deionization rate is expected when increasing the current load. On the other hand, the deionization capacity decreases as the current load increases, which could be ascribed to impeded ion transport from the bulk phase to the inside of an electrode and voltage loss because of IR drop. When all of the data points obtained at each current load are plotted, it becomes an arc-shaped line pointing from upper-left to bottom-right in the colored regions in Fig. 1(a). There can be two extreme cases; the one with a high rate but a low capacity (denoted by the blue color) and the one with a high capacity but a low rate (denoted by the red color). The goal of developing a CDI electrode or system will be to shift the plot toward the upper, right region of the plot, which represents the ideal desalination performance (denoted by the green color).

Fig. 1 A conceptual diagram of a CDI Ragone plot (a) and the representative conductivity profiles (b). A CDI Ragone plot consists of the deionization capacity and mean deionization rate, indicating total removed ions during charging and deionization capacity divided by duration of charging, respectively. These two parameters were obtained under constant current charging followed by zero-voltage discharging shown in (b); the area below the influent conductivity (dashed line) refers to the removed ions by the CDI cell. Data points obtained at each current load are located in the CDI Ragone plot, thus becoming a curve representing its experimental condition. The location and shape of a curve represent the desalination performance; two imaginary cases would be a high rate & low capacity (blue color) and a high capacity & low rate (red color). An ideal CDI system would shift a curve toward the upper, right region of the plot (green color).

To confirm the implications of the CDI Ragone plot, prevalent parameters affecting the desalination performance were examined including salt concentration, flow rate, electrode thickness, and types of carbon materials. First, we investigated the effect of salt concentration (2–100 mM NaCl) on the CDI Ragone plot. As shown in Fig. 2(a), a higher salt concentration shifted the plot toward the upper, right region of the plot, indicating increases in both the deionization capacity and mean deionization rate. The capacity increase (a shift to the right region) is mainly because of the compaction of the double layer and the subsequent rise in capacitance.^31,33 In addition, the enhanced rate (a shift to the upper region) can be simply explained by the conductivity increase of the influent solution and the subsequent swift transport of ions from the spacer channel to the electrodes. When comparing the capacity and rate dependent on the salt concentration, more change was observed in the rate than in the capacity; the maximum rate at each highest current load ranged from 0.019 to 0.101 mg g⁻¹ s⁻¹ (a five-fold difference), while a relatively minor difference was observed in the full capacity (17.9 to 23.6 mg g⁻¹) at each lowest current load. In this regard, a higher salt concentration is advantageous because rapid desalination can be achieved compared to a lower salt concentration. However, it should be noted that the charge efficiency¹ (the ratio of removed ions to transferred charge) has been reported to decrease with an increase in salt concentration (see Table S2†).^30,34 From an energetic point of view, a lower charge efficiency is disadvantageous because it implies that more energy is consumed for desalination. Next, the effect of flow rate (1–4 ml min⁻¹) on desalination performance was examined as plotted in Fig. 2(b). The result shows that each plot converges to one point at the lowest current load, indicating a similar deionization capacity and mean deionization rate, while the difference becomes significant as the current load increases. A lower current load allows enough time for ion transport from a bulk phase to an electrode regardless of the flow rate. At a higher current load, however, a higher flow rate could provide more ions in response to an increase in the current load compared to a lower flow rate (see Fig. S2†), thus exhibiting a higher capacity and rate. This is in good agreement with a previous study on flow rate,²⁵ and also extended the previous result by evaluating the performance over various current loads, which is the major advantage of the CDI Ragone plot.

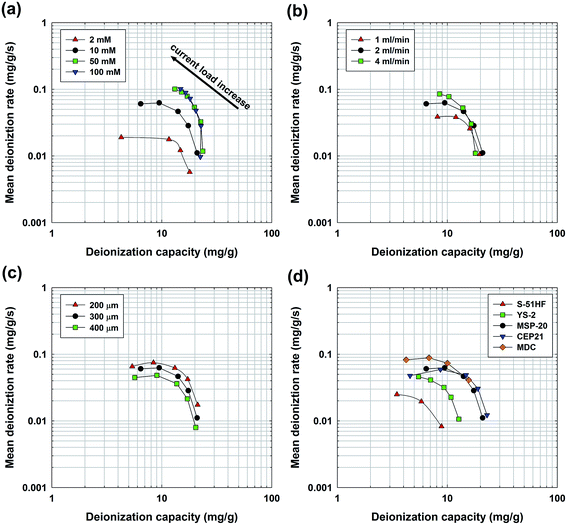Fig. 2 Effect of various parameters on the CDI Ragone plot. Each plot shows the effect of the (a) salt concentration, (b) flow rate, (c) electrode thickness, and (d) type of carbon materials. Each parameter was examined based on the standard operating condition (10 mM NaCl, 2 ml min⁻¹, 300 μm, and MSP-20), and the range of the current load was from 1 to 25 mA but properly adjusted to show the overall performance. Detailed operating parameters for each experimental condition are provided in Table S1.†

Fig. 2(c) shows the desalination performance depending on the variation in electrode thicknesses (200–400 μm), which is extended result of our previous work.³⁵ As can be seen, the plot shifts upward when increasing the electrode thickness, indicating faster desalination, while the full capacity obtained at the lowest current load for each thickness shows a similar value. The result confirms the strong influence of the electrode thickness on the rate of desalination,¹⁴ which is one of the important parameters when designing and optimizing a CDI process. Compared to previous two parameters, however, the variation in the thickness led to different carbon loading on the electrode; a different CDI Ragone plot would come out when it is normalized by another basis (e.g., foot print area, see Fig. 3(a)), so that a careful attention is required to interpret the plot. Lastly, we show a comparison of various carbon materials on the CDI Ragone plot, which is the most frequently used approach by developing novel electrodes.^{12–18,29,36,37} As shown in Fig. 2(d), the CDI Ragone plot enables a comprehensive comparison of electrodes made of various carbon materials at a glance in terms of desalination performance. First, a comparison of microporous activated carbons (S-51HF (▲), YS-2 (■), and MSP-20 (●))³¹ shows the effect of surface area on the deionization capacity and rate. A higher surface area and subsequent capacitance³¹ shifted the plot toward the upper, right side of the CDI Ragone plot, indicating a higher capacity and rate. When comparing MSP-20 (●) and CEP21 (▼), for which CEP21 is relatively hydrophobic (see Fig. S3†), CEP21 exhibited a higher capacity at the lowest current load but its capacity and rate decreased with increasing current load. It can be inferred that hydrophobicity inhibited the transport of ions inside the electrode,³⁸ and this interruption became significant when faster charging was implemented. Therefore, we could deduce from the CDI Ragone plot that carbon which is more hydrophilic (MSP-20) is a better option for rapid desalination. The CDI Ragone plot also could be used to find the role of pore structures on desalination performance. As reported in our previous study,¹² a large pore size could facilitate the rapid transport of ions, thus resulting in rapid desalination. We observed that MDC (◆) is located more in the upper region of the plot than that of the other materials, especially at the higher current load, indicating faster desalination. On the other hand, its capacity is relatively low, indicating a trade-off behavior between capacity and rate as in the case of the ‘high rate & low capacity’ shown in Fig. 1(a). However, similar to the case of the variation in the thickness, a careful attention is required because the activated carbons had different pore structure, especially the MDC. Though the large pore size of MDC could facilitate the performance when it is shown in the mass basis, its low density led to poor performance based on electrode area (see Fig. 3(b)). Therefore, the CDI Ragone plot with various basis including the mass, area, and volume would make more reliable evaluation. In other words, the conventional mass-based normalization for desalination performance needs improvement to be applicable for entire parameters that were discussed above. Among various normalization units (e.g., mg g⁻¹, mg cm⁻², mg cm⁻³), the performance based on electrode volume (mg cm⁻³) could provide more beneficial information for commercialization because overall performance can be determined under restricted volume of the CDI system in practice. However, normalization by electrode volume still makes bias for the electrode thickness; the mass- (Fig. 2(c)) and volume-based (data not shown) CDI Ragone plots are the same in terms of their relative locations (the thinner electrode was located upward), leading to conflicting result compared to the overall performance assessed from the area-based normalization (Fig. 3(a)). Therefore, it is recommended to fix the electrode thickness in order to use volume-based performance, suggesting a standard experimental condition should be made together with a normalization basis in future studies. From the result that was obtained in various parameters, the CDI Ragone plot was found to be a functional tool to investigate and optimize the desalination performance of a system; it could provide overall desalination performance in terms of capacity and rate. Furthermore, the CDI Ragone plot could be used to determine an optimal current load depending on its applications: maximum capacity, rate, and balanced performance between capacity and rate. Comparison between studies would be possible after a standard experimental setup is defined in the future study. More importantly, this study could produce many sequel studies based on various standards (e.g., volume-based capacity or full cycle-based rate), operation methods (e.g., constant voltage), and configurations (e.g., CDI without membranes or flow-electrode CDI).

Fig. 3 CDI Ragone plots normalized by foot print area of electrode (3.02 cm²) for (a) electrode thickness and (b) type of carbon materials. Results of Fig. 2(c) and (d) were converted from mass-based performance (mg g⁻¹ and mg g⁻¹ s⁻¹) to area-based performance (mg cm⁻² and mg cm⁻² s⁻¹). All experiments were carried out under the standard operating condition (10 mM NaCl, 2 ml min⁻¹, 300 μm, and MSP-20), unless otherwise indicated. Detailed operating parameters for each experimental condition are provided in Table S1†.

A novel concept to evaluate desalination performance was proposed, called the CDI Ragone plot. This plot can facilitate the design and optimization of the CDI process depending on its application. From the comparative study on various parameters using the CDI Ragone plot, optimal conditions can be suggested for the best desalination performance in terms of the deionization capacity and rate. In the CDI Ragone plot, a upper, right side shift in the plot is favorable because it indicates a higher deionization capacity and rate. This kind of shift was achieved by increasing the salt concentration and flow rate, and decreasing the electrode thickness. In addition, three carbon electrodes exhibited outstanding desalination performance (mg g⁻¹ and mg g⁻¹ s⁻¹) in different aspects. CEP21 had the highest capacity with a poor rate performance and MDC had the highest rate with a low capacity while MSP-20 was in between the two. However, MDC exhibited the poor desalination performance in the different normalization units (mg cm⁻² and mg cm⁻² s⁻¹), suggesting the necessity of improving the conventional mass-based normalization method. Therefore, a standard experimental condition and normalization basis are required for more reliable evaluation of various parameters and for comparison between studies. Such accomplishment can make the CDI Ragone plot to facilitate designing and optimizing the CDI process, working as a comprehensive guide to evaluate desalination performance.

Acknowledgements

This project is supported by Korea Ministry of Environment as “Converging Technology Project (2014001640002)”. The authors thank Dr Seung Jae Yang and Prof. Chong Rae Park for providing MDC.

Notes and references

1. S. Porada, R. Zhao, A. Van Der Wal, V. Presser and P. M. Biesheuvel, Prog. Mater. Sci., 2013, 58, 1388–1442.
2. M. Noked, A. Soffer and D. Aurbach, J. Solid State Electrochem., 2011, 15, 1563–1578.
3. R. Zhao, S. Porada, P. M. Biesheuvel and A. Van der Wal, Desalination, 2013, 330, 35–41.
4. Y. Oren, Desalination, 2008, 228, 10–29.
5. P. Długołecki and A. Van der Wal, Environ. Sci. Technol., 2013, 47, 4904–4910.
6. Si. Jeon, J.-g. Yeo, S. Yang, J. Choi and D. K. Kim, J. Mater. Chem. A, 2014, 2, 6378–6383.
7. M. A. Anderson, A. L. Cudero and J. Palma, Electrochim. Acta, 2010, 55, 3845–3856.
8. E. García-Quismondo, R. Gómez, F. Vaquero, A. L. Cudero, J. Palma and M. Anderson, Phys. Chem. Chem. Phys., 2013, 15, 7648–7656.
9. A. M. Pernĺa, J. G. Norniella, J. A. Martĺn-Ramos, J. Dĺaz and J. A. Martinez, IEEE Trans. Power Electron., 2012, 27, 3257–3265.
10. A. Pernia, F. J. Alvarez-Gonzalez, M. Prieto, P. Villegas and F. Nuno, IEEE Trans. Power Electron., 2014, 27, 3257–3265.
11. M. Alkuran, M. Orabi and N. Scheinberg, Applied Power Electronic Conference and Exposition, 2008, pp. 1926–1930.
12. S. J. Yang, T. Kim, K. Lee, Y. S. Kim, J. Yoon and C. R. Park, Carbon, 2014, 71, 294–302.
13. Z.-Y. Yang, L.-J. Jin, G.-Q. Lu, Q.-Q. Xiao, Y.-X. Zhang, L. Jing, X.-X. Zhang, Y.-M. Yan and K.-N. Sun, Adv. Funct. Mater., 2014, 24, 3917–3925.
14. S. Porada, L. Borchardt, M. Oschatz, M. Bryjak, J. Atchison, K. Keesman, S. Kaskel, P. M. Biesheuvel and V. Presser, Energy Environ. Sci., 2013, 6, 3700–3712.
15. X. Wen, D. Zhang, L. Shi, T. Yan, H. Wang and J. Zhang, J. Mater. Chem., 2012, 22, 23835–23844.
16. C. Tsouris, R. Mayes, J. Kiggans, K. Sharma, S. Yiacoumi, D. DePaoli and S. Dai, Environ. Sci. Technol., 2011, 45, 10243–10249.
17. H. Li, L. Zou, L. Pan and Z. Sun, Environ. Sci. Technol., 2010, 44, 8692–8697.
18. H. Yin, S. Zhao, J. Wan, H. Tang, L. Chang, L. He, H. Zhao, Y. Gao and Z. Tang, Adv. Mater., 2013, 25, 6270–6276.
19. L. Han, K. G. Karthikeyan, M. A. Anderson, J. J. Wouters and K. B. Gregory, Electrochim. Acta, 2013, 90, 573–581.
20. M. Pasta, C. D. Wessells, Y. Cui and F. La Mantia, Nano Lett., 2012, 12, 839–843.
21. J. Yang, L. Zou, H. Song and Z. Hao, Desalination, 2011, 276, 199–206.
22. J. Lee, S. Kim, C. Kim and J. Yoon, Energy Environ. Sci., 2014, 7, 3683–3689.
23. J.-B. Lee, K.-K. Park, H.-M. Eum and C.-W. Lee, Desalination, 2006, 196, 125–134.
24. Y.-J. Kim and J.-H. Choi, Water Res., 2010, 44, 990–996.
25. R. Zhao, O. Satpradit, H. Rijnaarts, P. M. Biesheuvel and A. Van der Wal, Water Res., 2013, 47, 1941–1952.
26. T. Kim, J. E. Dykstra, S. Porada, A. Van der Wal, J. Yoon and P. M. Biesheuvel, J. Colloid Interface Sci.,  DOI:10.1016/j.jcis.2014.08.041.
27. S.-i. Jeon, H.-r. Park, J.-g. Yeo, S. Yang, C. H. Cho, M. H. Han and D.-K. Kim, Energy Environ. Sci., 2013, 6, 1471–1475.
28. S. Porada, D. Weingarth, H. V. M. Hamelers, M. Bryjak, V. Presser and P. M. Biesheuvel, J. Mater. Chem. A, 2014, 2, 9313–9321.
29. M. E. Suss, T. F. Baumann, W. L. Bourcier, C. M. Spadaccini, K. A. Rose, J. G. Santiago and M. Stadermann, Energy Environ. Sci., 2012, 5, 9511–9519.
30. R. Zhao, P. M. Biesheuvel and A. Van der Wal, Energy Environ. Sci., 2012, 5, 9520–9527.
31. T. Kim and J. Yoon, J. Electroanal. Chem., 2013, 704, 169–174.
32. P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854.
33. A. J. Bard and L. R. Faulkner, Electrochemical methods: fundamentals and applications, Wiley, New York, 1980.
34. P. M. Biesheuvel, S. Porada, M. Levi and M. Bazant, J. Solid State Electrochem., 2014, 18, 1365–1376.
35. T. Kim, H. D. Yoo, S. M. Oh and J. Yoon, Electrochim. Acta, 2014, 139, 374–380.
36. S. Porada, L. Weinstein, R. Dash, A. Van Der Wal, M. Bryjak, Y. Gogotsi and P. M. Biesheuvel, ACS Appl. Mater. Interfaces, 2012, 4, 1194–1199.
37. G. Wang, Q. Dong, Z. Ling, C. Pan, C. Yu and J. Qiu, J. Mater. Chem., 2012, 22, 21819–21823.
38. J. Zhou, W. Xing, S. Zhuo and Y. Zhao, Solid State Sci., 2011, 13, 2000–2006.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra11257a

---