Specific features of electronic structures and nonlinear optical susceptibilities of superhard metallic diamond-like t-B2CN compound
Abstract
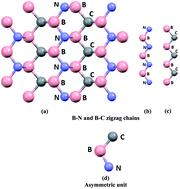
The geometry of diamond-like t-B2CN was relaxed by minimizing the forces acting on each atom using an all-electron full potential linearized augmented plane wave within general gradient approximation (PBE-GGA). Using the relaxed geometry, the electronic band structure's dispersion, total and angular momentum resolved projected density of states, anthropomorphic shape of Fermi surface, electronic charge density distribution, and linear and nonlinear optical responses were performed within the local density approximation (CA-LDA), PBE-GGA, Engel–Vosko generalized gradient approximation (EV-GGA) and the modified Becke–Johnson potential (mBJ). Calculations showed that t-B2CN is metallic with two bands overlapping around the Fermi level. The density of states at the Fermi level N(EF) and the electronic specific heat coefficient (γ) were obtained. The electronic charge density showed that there are only two type of bonds (B–C and B–N). The Fermi surface is formed by two bands; the shape of the Fermi surface consists of empty areas representing holes and shaded areas corresponding to electrons. The linear optical response confirmed that there exists a lossless region between 5.0 eV and 7.5 eV, and the existence of a considerable anisotropy favors enhanced phase matching conditions for the second harmonic generation (SHG). The nonlinear optical susceptibilities exhibited that χ(2)113(ω) is the dominant component, with values of about 5.5 pm V−1 at static limit and 8.8 pm V−1 at λ = 1064 nm. This suggests that the t-B2CN single crystal is a promising nonlinear crystal in comparison with the well-known KTiOPO4 nonlinear optical single crystal.

 Please wait while we load your content...
Please wait while we load your content...