Ligand substitution and electron transfer reactions of trans-(diaqua)(salen)manganese(III) with oxalate: an experimental and computational study†
Akshaya K. Kara,
Achyut N. Acharyab,
V. Rao Mundlapatic,
Guru C. Pradhana,
Himansu S. Biswal*c and
Anadi C. Dash*a
aDepartment of Chemistry Utkal University, Bhubaneswar 751004, India. E-mail: acdash41@gmail.com
bDepartment of Chemistry, College of Engineering and Technology, Bhubaneswar 751003, India
cSchool of Chemical Sciences, National Institute of Science Education and Research (NISER), Institute of Physics Campus, Bhubaneswar 751 005, India. E-mail: himansu@niser.ac.in
First published on 29th October 2014
Abstract
The trans-MnIII(salen)(OH2)2+ undergoes reversible aqua ligand substitution by HOX− (H2salen = N,N′-bis(salicylidene)ethane-1,2-diamine; HOX− = −O–COCO2H) with k1/dm3 mol−1 s−1 (k−1/s−1) = 11.8 ± 0.7 (0.255 ± 0.02), ΔH≠/kJ mol−1 = 54.6 ± 0.8 (64.2 ± 6.7), ΔS≠/J K−1 mol−1 = −41.2 ± 2.6 (−40.8 ± 22.7) at 25.0 °C and I = 0.3 mol dm−3. The low values of the activation enthalpy and nearly the same and negative values of the activation entropy are ascribed to an associative transition state for this interchange process (Ia mechanism). The redox reaction that follows involves several paths and the products are MnII and CO2 identified by ESR spectroscopy and conventional test, respectively. The rate retardation by acrylamide monomer with no perceptible polymerization during the course of the redox reaction supports the involvement of the radical intermediate, C2O4−˙ (= CO2 + CO2−˙) which succeeds in reducing MnIII species much faster than the dimerisation of its congener, CO2−˙ in keeping with the stoichiometry, |[ΔMnIII]/Δ[OX]| = 2. The trans-[MnIII(salen)(OH2)(HOX) and its conjugate base, trans-MnIII(salen)(OH2)(OX)− are virtually inert to intramolecular reduction of the MnIII centre by the bound oxalate species but undergo facile electron transfer by H2OX, HOX− and very slowly by OX2− following the reactivity sequence, kH2OX > kHOX ⋙ kOX and featuring second order kinetics. The rate retardation by the anionic micelles of SDS (sodium dodecyl sulfate) and rate enhancement by N3− provide supportive evidence in favor of the proposed mechanistic pathways. The structure optimization of trans-MnIII(salen)(OH2)(HOX) (A), trans-MnIII(salen)(HOX)2− (B), trans-MnIII(salen)(OH2)(OX)− (C), trans-MnIII(salen)(OH2)(H2OX)+ (E1), and trans-MnIII(salen)(HOX)(H2OX) (E2) {all high spin MnIII(d4)} by Density Functional Theory (DFT) reveals that the structural trans-effect of the unidentately bonded OX2− in C is the strongest and MnIII assumes five coordination with the H2O molecule (displaced from the MnIII centre), hydrogen bonded to the phenoxide oxygen moiety. The computational study highlights different modes of H-bonding in structures A–E. The activation parameters for the redox reactions, A + HOX− and A + H2OX, ΔH≠/kJ mol−1 (ΔS≠/J K−1 mol−1): 42.5 ± 6.2, (−106 ± 20) and 71.7 ± 7.7 (+12 ± 25), respectively, are indicative of different degrees of ordering and reorganization of bonds as expected in the case of a proton coupled electron transfer (PCET) process.
1. Introduction
MnIII complexes with a salen (H2salen = N,N′-bis(salicylidene)ethane-1,2-diamine) motif are models for catalase and superoxide dismutase (SOD) activities.1–4 Many intricate diseases, such as Alzheimer, cancer, multiple sclerosis, heart and brain stokes, are supposed to be related to the superoxide activity and MnIII(salen) complexes have been shown as promising therapeutics.1,3,5 The interaction of bioactive ROS (Reactive Oxygen Species) with the MnIII centre of MnIII(salen) moiety is a primary feature in such processes. MnIII(salen) complexes have been used as catalysts in the epoxidation of olefins, and other organic transformations.6–9 A review of the redox reactions of mononuclear MnIII complexes, essentially of aminopolycarboxylate ligands, appeared several years ago which describes briefly the mechanistic aspects of such reactions.10 Nature's water oxidation catalyst (WOC) responsible for photo-catalyzed O2 evolution from water is a tetra manganese cluster with MnIII–MnIV coupled system which is believed to undergo redox cycling of the oxidation states of the Mn centres.11–13 Recent investigations on the oxidation of oxalate, a ubiquitous moiety in the biological domain, by oxalate oxidase have revealed the importance of the MnIII centre in catalyzing the oxidation of oxalate.14,15 It involves an intermediate MnIII–monooxalate complex in the monodentate form and electron transfer from the bound oxalate species to the MnIII centre is considered to be rate limiting. MnIII(salen) may be used to model this reaction. However, the studies devoted to understand the mechanisms of ligand substitution and redox reactions of MnIII are limited. In view of the importance of oxalate in biology and MnIII(salen) as a suitable oxidant for oxalate oxidation, we, in continuation of our other investigations16,17 of the mechanism of ligand substitution and electron transfer at the MnIII centre, present here a thorough study on trans-MnIII(salen)(OH2)2+ + oxalate system over extended pH and temperature ranges. To the best of our knowledge there is no earlier literature report on such a study, although oxidation of oxalate by higher valent manganese has been the topic of several investigations in the past.18,192 Experimental
2.1 Materials and reagents
MnIII(salen)Cl·H2O was received from our earlier work and synthesized when required and purity checked by elemental analysis and UV-Vis, IR spectra.17 This complex undergoes fast aquation to MnIII(salen)(OH2)2+ when dissolved in water.16,17 The optical spectrum of the diaqua complex in aqueous medium (pH 3) displays λmax, nm (ε max, dm3 mol−1 cm−1): 235(40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240), 279 (18
240), 279 (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120) which agreed well with the previously reported values.17 The GR grade (E. Merck) oxalic acid (H2OX), potassium oxalate, perchloric acid, sodium hydroxide and glacial acetic acid were used as received. All other reagents were of highest grade purity available. Freshly prepared doubly distilled water received from an all glass (borosilicate) distillation set was used to prepare the solutions; the second distillation of water was made through alkaline KMnO4. NaClO4 used for ionic strength adjustment was prepared by mixing requisite amounts of the standardized solutions of NaOH and HClO4. Stock solution of NaClO4 (1 mol dm−3) was prepared from time to time and adjusted to pH 6 and the concentration checked by a combined ion-exchange alkalimetric procedure using Dowex 50W X8 resin in the H+ form. The stock solution of the complex (5 × 10−3 mol dm−3, pH ∼ 5) was protected from light and stored in a refrigerator at ∼20 °C when not in use. It was not allowed to age for more than 24 h.
120) which agreed well with the previously reported values.17 The GR grade (E. Merck) oxalic acid (H2OX), potassium oxalate, perchloric acid, sodium hydroxide and glacial acetic acid were used as received. All other reagents were of highest grade purity available. Freshly prepared doubly distilled water received from an all glass (borosilicate) distillation set was used to prepare the solutions; the second distillation of water was made through alkaline KMnO4. NaClO4 used for ionic strength adjustment was prepared by mixing requisite amounts of the standardized solutions of NaOH and HClO4. Stock solution of NaClO4 (1 mol dm−3) was prepared from time to time and adjusted to pH 6 and the concentration checked by a combined ion-exchange alkalimetric procedure using Dowex 50W X8 resin in the H+ form. The stock solution of the complex (5 × 10−3 mol dm−3, pH ∼ 5) was protected from light and stored in a refrigerator at ∼20 °C when not in use. It was not allowed to age for more than 24 h.
2.2 Physical measurements
A PerkinElmer Lambda25 and a Systronics (India) model 118 UV-visible spectrophotometers with a matched pair of 10 mm quartz cells were used for all absorbance measurements. The IR measurements were made on a PerkinElmer FTIR spectrometer, model Spectrum2 using KBr pellet. Fluorescence measurements were made on a JASCO spectrofluorimeter model FP-8200 using Xe/D2 light sources; band width was set at 10 nm and scan speed was 100 nm min−1. The excitation wavelength (λexct) was set at 265 nm and spectral scans covered 340–500 nm. The intensity of emission at any wavelength was normalized as where
where  denotes intensity at the wavelength maximum in absence of SDS. The ESR measurement was performed on a JEOL (Japan) JES-FA 200 ESR spectrometer at room temperature operating in X-band mode (8.75–9.65 GHz, power 1.08 W, sensitivity 7 × 109 spins/0.1 mT, resolution 2.35 μT). The pH measurements were made with a Systronics (India) pH meter model 335 using a glass–Ag/AgCl, Cl− (3 mol dm−3 NaCl) electrode CL 51. NBS buffers of pH 4.01, 6.86 and 9.20 prepared from KHphthalate, Na2HPO4/KH2PO4, and Na2B4O7·10H2O respectively were used to calibrate the pH meter. The measured pH of the reaction medium was converted to p[H+] (= −log[H+]) established by a calibration curve using dilute HClO4 solutions (1.98 × 10−2 ≤ [H+]/mol dm−3 ≤ 1.00 × 10−5) at the same ionic strength as maintained in the reaction media (I = 0.3 mol dm−3).20
denotes intensity at the wavelength maximum in absence of SDS. The ESR measurement was performed on a JEOL (Japan) JES-FA 200 ESR spectrometer at room temperature operating in X-band mode (8.75–9.65 GHz, power 1.08 W, sensitivity 7 × 109 spins/0.1 mT, resolution 2.35 μT). The pH measurements were made with a Systronics (India) pH meter model 335 using a glass–Ag/AgCl, Cl− (3 mol dm−3 NaCl) electrode CL 51. NBS buffers of pH 4.01, 6.86 and 9.20 prepared from KHphthalate, Na2HPO4/KH2PO4, and Na2B4O7·10H2O respectively were used to calibrate the pH meter. The measured pH of the reaction medium was converted to p[H+] (= −log[H+]) established by a calibration curve using dilute HClO4 solutions (1.98 × 10−2 ≤ [H+]/mol dm−3 ≤ 1.00 × 10−5) at the same ionic strength as maintained in the reaction media (I = 0.3 mol dm−3).20
2.3 Kinetics
The fast kinetics measurements were performed on a KinetAsyst SF-61 SX2 single mixing stopped flow spectrophotometer; the data acquisition and analysis was made using kinetic studio software version 0.94, application version 1.12 (TGK Scientific, U. K). The flow module and the mixing chamber were thermostatted to the desired temperature by circulating water from a refrigerated/heating water bath (Julabo F12-ED). One of the syringes was loaded with the solution of trans-MnIII(salen)(OH2)2+ complex (in situ generated) while the other contained the desired mixture of oxalic acid, HClO4 and NaClO4 such that after mixing the final ionic strength was set at 0.3 mol dm−3. The available pK values of oxalic acid (see later) were used to calculate the ionic composition so as to set the ionic strength at the desired value. Rate measurements were made at 380 nm under pseudo-first order conditions. The absorbance versus time plots were biphasic over extended time scale (see Fig. S1(a and b)†) thus indicating the rapid formation of an intermediate followed by its decay at long time scale. The two processes were treated independently. The initial fast rise of absorbance with time was fitted to eqn (1) to get kfobs and Aeq. Data fitting using the software package (see above) for any individual run was within ±1%. At least 6–10 measurements were made for each run and kfobs could be reproduced within ±5% (σ(kfobs)/kfobs ≤ ± 0.05).
At = C1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kfobst) + Aeq exp(−kfobst) + Aeq
| (1) |
The values of Aeq were dependent on [OX]T for a given [H+] and [complex]T indicating that the formation of the intermediate was equilibrium controlled. A limited number of runs for the slow phase were made by stopped flow spectrophotometry wherever possible. The absorbance–time data for the slow phase of the reaction also studied under pseudo-first order conditions fitted to a single exponential equation with A∞ close to zero (At = C2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ksobst) + A∞) and the corresponding rate constants (ksobs) were calculated. Most rate measurements for the slow reactions were conveniently made by batch sampling technique at 25.0–40.0 °C.17 The concentration of the complex, [MnIII(salen)(OH2)2+] was varied as (0.6–1.22) × 10−4 mol dm−3 and that of [OX]T (= total oxalic acid concentration) in the range 0.0005–0.1 mol dm−3. The ionic strength of the medium was fixed at 0.3 mol dm−3 (NaClO4) unless otherwise quoted. The pH of the reaction mixtures was varied by self buffering due to H2OX/HOX− and HOX−/OX2−. The observed rate constants (ksobs) were calculated by fitting the absorbance (At)–time (t) data to a single exponential equation as mentioned above. A∞ was close to zero for the completion of the reaction which was further verified by simulating the reaction mixture at complete reaction with appropriate solutions made out of MnII acetate, oxalic acid and other components at the same pH (for this the medium was 5% MeOH–water v/v as H2salen was prepared in MeOH). The initial absorbance was in the range 0.4–0.6. For very slow reactions (ksobs ∼ 10−5–10−6 s−1) the rate constants were evaluated by the method of initial rate as described earlier.17 σ(ksobs)/ksobs was generally better than ±2% while the same from the initial rate method was ∼±6%.
exp(−ksobst) + A∞) and the corresponding rate constants (ksobs) were calculated. Most rate measurements for the slow reactions were conveniently made by batch sampling technique at 25.0–40.0 °C.17 The concentration of the complex, [MnIII(salen)(OH2)2+] was varied as (0.6–1.22) × 10−4 mol dm−3 and that of [OX]T (= total oxalic acid concentration) in the range 0.0005–0.1 mol dm−3. The ionic strength of the medium was fixed at 0.3 mol dm−3 (NaClO4) unless otherwise quoted. The pH of the reaction mixtures was varied by self buffering due to H2OX/HOX− and HOX−/OX2−. The observed rate constants (ksobs) were calculated by fitting the absorbance (At)–time (t) data to a single exponential equation as mentioned above. A∞ was close to zero for the completion of the reaction which was further verified by simulating the reaction mixture at complete reaction with appropriate solutions made out of MnII acetate, oxalic acid and other components at the same pH (for this the medium was 5% MeOH–water v/v as H2salen was prepared in MeOH). The initial absorbance was in the range 0.4–0.6. For very slow reactions (ksobs ∼ 10−5–10−6 s−1) the rate constants were evaluated by the method of initial rate as described earlier.17 σ(ksobs)/ksobs was generally better than ±2% while the same from the initial rate method was ∼±6%.
2.4 Initial fast reaction
The initial fast reaction was considered to be the reversible complexation of MnIII(salen)(OH2)2+ with oxalate species. The kfobs values at 20–40 °C are collected in Table S1(a).† In the medium comprising HClO4 and oxalic acid (see Table S1(a)†), [OX]T is partitioned between H2OX and HOX− (pK1 = 1.00–1.03, pK2 = 3.59–3.64 for H2OX at 20–40 °C, I = 0.3 mol dm−3 see Table S1(b)†).21
 | (2) |
However, the concentrations of different oxalate species may be expressed as [HOX−] = f1[OX]T, [H2OX] = f2[OX]T, and [OX2−] = f3[OX]T where f1 = K1[H+]/D, f2 = [H+]2/D, f3 = K1K2/D and D = [H+]2 + K1[H+] + K1K2. The values of [H+], [HOX−] and [H2OX] were computed from the initial analytical values of [HClO4] and [OX]T considering the first stage acid dissociation of H2OX, [H+] = [HClO4] + X, X (= [HOX−]) being the acceptable solution of eqn (3), and [H2OX] = [OX]T − X.
| X2 + ([HClO4] + K1) − K1[OX]T = 0. | (3) |
The kfobs data were fitted to eqn (4) valid for Scheme 1 by a least squares computer program.
| kfobs = (kf1f1+ kf2f2)([OX]T + Q1−1/f1) | (4) |
In eqn (4) Q1 denotes the equilibrium constant for the formation of MnIII(salen)(HOX)(OH2) (eqn (5)).
| Q1 = [MnIII(salen)(HOX)(OH2)]eq/[MnIII(salen)(OH2)2+]eq[HOX−]eq, | (5) |
It turns out that kf2f2 term is statistically insignificant at all temperatures. Thus neglecting kf2f2 term and setting kf1Q1−1 = kf−1 eqn (4) can be rearranged to eqn (6).
| kfobs = kf1f1[OX]T + kf−1 | (6) |
A representative plot at 25 °C (see Fig. 1) bears this fact. As a check the equilibrium absorbance data (Ae) from the stopped flow runs for a constant [complex]T but varying [OX]T and [H+] (see Table S1a†) are used to calculate Q1 from the linear plots of 1/(Ae − A0) versus 1/(f1[OX]T) (see eqn (7)); here A0 and Ac denote the absorbances of MnIII(salen)(OH2)2+ and MnIII(salen)(HOX)(OH2) respectively at the same total concentration of the complex.
| 1/(Ae − A0) = 1/[Q1(Ac − A0) × f1[OX]T] + 1/(Ac − A0). | (7) |
The calculated values of Q1 are 40.1 ± 2.0, 42.6 ± 1.0, 41.2 ± 2.3 and 40.6 ± 2.7 dm3 mol−1 at 20.0°, 25.0°, 30.0° and 40.0 °C respectively which compare well with the values obtained from the kinetic data (see Table S1c,† foot note a). As Q1 shows little variation with temperature its mean value from kinetic and equilibrium measurements (Q1 = 42.0 ± 0.7 dm3 mol−1 at 20–40 °C) is used for all other calculations. A comparison of the rate and activation parameters for the reversible formation of some MnIII complexes is made in Table 1.
| Reaction: R = MnIII(salen) | ka (30 °C) | ΔH≠/kJ mol−1 | ΔS≠/J K−1 mol−1 | Ref. |
|---|---|---|---|---|
| a Units: dm3 mol−1 s−1 (s−1) for the formation (dissociation) reactions. I = 0.3 mol dm−3.b This work.c Ref. 16.d I = 0.2 mol dm−3; hydroquinone (H2Q) and catechol (H2Cat) (ref. 22).e 28 °C; ascorbic acid (H2Asc) (ref. 33).f I = 0.25 mol dm−3 (ref. 36). | ||||
| R(OH2)2+ + HOX− → MnIII(salen)(OH2)(HOX) | 17.5 ± 1.1 | 54.6 ± 0.8 | −41.2 ± 2.6 | b |
| R(OH2)(HOX) → MnIII(salen)(OH2)2+ + HOX− | 0.47 ± 0.07 | 64.2 ± 6.7 | −40.8 ± 22.7 | b |
| R(OH2)2+ + HSO3− → MnIII(salen)(OH2)(HSO3) | (3.0 ± 0.3) × 102 | 42.4 ± 0.2 | −55.3 ± 0.6 | c |
| R(OH2)2+ + SO32− → MnIII(salen)(OH2)(SO3)− | (1.10 ± 0.08) × 103 | 33.0 ± 3.0 | −75 ± 10 | c |
| R(OH2)(OH) + SO32− → R(OH)(SO3)2− | (2.1 ± 0.2) × 103 | 32.4 ± 0.3 | −72.9 ± 0.6 | c |
| R(OH2)(OH) + H2Q → R(OH)(H2Q) | 21.8 ± 0.5 | d | ||
| R(OH2)(OH) + HQ− → R(OH)(HQ)− | (1.4 ± 0.2) × 103 | d | ||
| R(OH2)(OH) + H2Cat → R(OH)(H2Cat) | 1.91 ± 0.41 | d | ||
| R(OH2)(OH) + HCat− → R(OH)(HCat)− | (2.2 ± 0.3) × 102 | d | ||
| R(OH2)2+ + H2Asc → R(OH2)(H2Asc)+ | 1.2 | 72.6 | +2.5 | e |
| MnIII(EDTA)(OH2)− + N3− → MnIII(EDTA)(N3)2− | 0.16 | 57.4 ± 0.9 | −71.3 ± 2.9 | f |
| MnIII(EDTA)(N3)2− → MnIII(EDTA)(OH2)− + N3− | 4.7 × 10−3 | 54.4 ± 0.7 | −110 ± 3 | f |
2.5 Redox reaction
The maxima around 285 and 390 nm (broad) characteristics of the parent complex is lost during the course of the reaction with the development of a maximum at 325 nm (broad). This is in good agreement with the spectrum of the mixture of MnII acetate + salen + H2OX at the same pH and respective concentrations of the reactants, left to equilibration (see Experimental section). The maximum at 325 nm is, however, considerably reduced in intensity at lower pH. Acetate ion/acetic acid at low concentration (∼(1.2–2.4) × 10−4 mol dm−3) originating from Mn(OAc)2 has no effect. The broad 325 nm peak is attributed to MnII(salen)(OH2)(OX/OXH)2−/− in equilibrium with MnII(salen)(OH2)2. The ESR spectrum of the spent reaction mixture displayed 6 line spectrum characteristic of MnII (see Fig. 2) thus establishing the MnIII(salen)/oxalate redox reaction.
 | ||
| Fig. 2 ESR spectrum (X-band) of the product MnII in the reduction of trans-MnIII(salen)(OH2)2+ by oxalate (pH 1.8, ∼27 °C), g = 1.9968. Intensity versus H/mT plot. | ||
The formation of CO2 was qualitatively established by the conventional test as follows. The reaction mixture ([MnIII(salen)(OH2)2+]T = 3 × 10−3 and [OX]T = 0.02 mol dm−3, pH = 3.5, 40 °C) was set aside for 10t1/2 and then treated with a slight excess CaCl2 followed by aqueous NH3 resulting in a white precipitate. This was allowed to coagulate, collected by filtration, air dried and treated with dilute HCl when a colorless gas with effervescence (characteristic of CO2) evolved. Our attempts to perform a quantitative analysis of the unreacted oxalate by KMnO4 titration in acid medium after precipitating it as CaC2O4 from ammoniacal solution was unsuccessful due to the presence of the salen ligand. Based on the identified products we propose the following stoichiometry:
| 2MnIII(salen)(OH2)2+ + OXH− + 3H+ = 2MnII + 2H2salen + 2CO2 + 2H2O. | (8) |
Similar relation can be written for H2OX or OX2−. It may be also noted that under mild acidic condition H2salen undergoes hydrolysis to salicylaldehyde and bis-N-protonated ethylenediamine as the final end products.
The ksobs versus [OX]T plots at [HClO4] = 0.05 mol dm−3 and pH = 3.10 ± 0.09 (see Fig. S3(a and b)†) are distinctly nonlinear. The observed trend shows greater than first-order dependence of ksobs on [OX]T. Further ksobs at constant [OX]T = 0.005 mol dm−3 approaches a low limiting value around pH 5 (∼10−6 s−1, see Fig. S3c†) indicating that OX2− is not an efficient reductant as HOX− and H2OX.
A limited number of runs at 35 °C were made at 5.04 ≤ pH ≤ 6.72, 0.005 ≤ [OX]T mol−1 dm−1−3 ≤ 0.1 in order to establish the redox activity of trans-MnIII(salen))(OH2)(OX)−. Due to the solubility limitation of Na2C2O4 the source of oxalate was K2C2O4 and ionic strength was adjusted by KCl. The presence of chloride under the conditions had no perceptible effect on the absorption spectrum of the di-aqua complex discounting its interference. Under this condition [OX]T = [HOX−] + [OX2−] and the diaqua MnIII complex predominates (∼80%). Here again a nonlinear and greater than first order dependence of ksobs with [OX]T at constant pH (= 5.27 ± 0.07) was observed (Fig. S3d†). Considering these facts Scheme 2 is proposed for the overall reaction for which ksobs (without considering the reaction stoichiometry; kicorr = ki/2, i = 0–7) is given by eqn (9),
 | (9) |
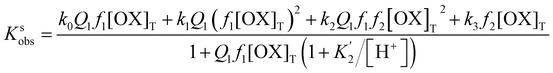 | (10) |
The species, H2OX, will not exist in significant concentrations under the pH conditions 2.9 ≤ pH ≤ 5.08. This amounts to a reasonable choice of neglecting the k2 and k3 terms of eqn (10) to treat the ksobs data at low [OX]T. On this ground eqn (10) reduces to eqn (11):
 | (11) |
The temperature independent value of Q1 (= 42.0 dm3 mol−1) was used, the fraction f1 was calculated as mentioned above and the ksobs data in Tables S3 and S4† were analyzed by eqn (11) using a nonlinear least squares computer program assigning unit weight to each data point. The calculated values of k0, k1 and K′2 are collected in Table 2. The k0 values turned out statistically insignificant. The inclusion of the k2 term in the calculation did not improve the data fitting. A representative plot at 35 °C using a linearized form of eqn (11) (see Fig. 3) clarifies that contributions from k0, k2, and k3 are statistically insignificant.
| Rate constanta | Temp./°C | |||
|---|---|---|---|---|
| a Rate constants (kis) are not corrected for the stoichiometry factor (i.e. kicorr = ki/2).b Calcd from the rate data in Table S2.c Calcd from the rate data in Tables S3 and S4.d Calcd from the temperature dependence of k1 and k2: k = (kBT/h)exp(−ΔH≠/RT + ΔS≠/R). | ||||
| k0/s−1 | 25.0 ± 0.1 | 30.0 ± 0.1 | 35.0 ± 0.1 | 40.0 ± 0.1 |
| 0.05 ± 0.0015b | 0.0045 ± 0.0018b | 0.00002 ± 0.002b | 0.00049 ± 0.0029b | |
| 0.0000 ± 0.0005c | 0.000 ± 0.00027c | 0.000042 ± 0.00025c | 0.00019 ± 0.00092c | |
| k1/dm3 mol−1 s−1 | 0.73 ± 0.12 | 0.87 ± 0.07 | 1.16 ± 0.07 | 1.73 ± 0.24 |
| k2/dm3 mol−1 s−1 | 7.39 ± 1.03 | 10.4 ± 1.2 | 19.6 ± 1.4 | 26.7 ± 4.6 |
| k3/dm3 mol−1 s−1 | 0.00017 ± 0.27 | 0.00093 ± 0.31 | 0.13 ± 0.47 | 0.00013 ± 0.47 |
| 106k4/s−1 | 0.03 ± 14.0 | |||
| k5/dm3 mol−1 s−1 | 0.077 ± 0.047 | |||
| 104 k6/dm3 mol−1 s−1 | 2.94 ± 2.57 | |||
| k7/dm3 mol−1 s−1 | 0.077 ± 0.047 | |||
| k8/dm3 mol−1 s−1 | 1.08 ± 0.09 | |||
| 104K2′/mol dm−3 | 7.14 ± 2.21 | 4.62 ± 0.54 | 2.56 ± 0.31 | 3.52 ± 0.78 |
| Q1/dm3 mol−1 | 42.0 | 42.0 | 42.0 | 42.0 |
| ΔH≠/kJ mol−1d | k1 path, 42.5 ± 6.2 | k2 path, 71.7 ± 7.7 | ||
| ΔS≠/J K−1 mol−1d | −106 ± 20 | +11.7 ± 25.4 | ||
 | ||
| Fig. 3 103ksobs(1 + Q1f1[OX]T(1 + K′2/[H+])/(Q1f1[OX]T) (= Fc/s−1) vs. 103f1[OX]T/mol dm−3 plot at 35 °C. | ||
The ksobs data in Table S2† were then analyzed by eqn (10) using the values of k1, K′2 (see Table 2) and Q1. The calculated values of k0, k2 and k3 are also collected in Table 2. Here again, the k0 and k3 values turned out statistically insignificant.
At 5.04 ≤ pH ≤ 6.72, and 0.0025 ≤ [OX]T/mol dm−3 ≤ 0.1, OX2− and HOX− were considered to be the reducing species. The first step acid dissociation equilibrium of trans-MnIII(salen)(OH2)2+ (pKM ≥ 7.3 (ref. 16 and 22) was also taken in to account. eqn (9) was recast as eqn (12),
 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. On the other hand, the overall stoichiometry 2
1. On the other hand, the overall stoichiometry 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for MnIII/OXT reaction should result if MnIII complex scavenges the radical (C2O4−˙/CO2−˙) at a rate much faster than the rate of its dimerisation. Keeping that in mind we investigated the effect of acrylamide monomer, a good scavenger of the radical, on the kinetics of the reaction under study at 30 °C with [MnIII(salen)(OH2)2+]T = 1.21 × 10−4, [OX]T = 2.5 × 10−3, I = 0.3 mol dm−3 and pH = 3.22. The anticipated polymer formation (through visual inspection) could not be observed. Interestingly the values of ksobs showed a decreasing trend with the increase of [acrylamide]T (104ksobs/s−1 = 1.67 ± 0.02, 1.63 ± 0.02, 1.61 ± 0.02 and 1.57 ± 0.02 at [acrylamide]T(monomer) = 0, 0.01, 0.02, 0.03 mol dm−3 respectively). This indirectly led us to believe that the MnIII complexes compete very successfully and efficiently in scavenging the C2O4−˙ or CO2−˙ generated in the redox process maintaining the stoichiometry (= |Δ[MnIII]|/|Δ[OX]|): 2
1 for MnIII/OXT reaction should result if MnIII complex scavenges the radical (C2O4−˙/CO2−˙) at a rate much faster than the rate of its dimerisation. Keeping that in mind we investigated the effect of acrylamide monomer, a good scavenger of the radical, on the kinetics of the reaction under study at 30 °C with [MnIII(salen)(OH2)2+]T = 1.21 × 10−4, [OX]T = 2.5 × 10−3, I = 0.3 mol dm−3 and pH = 3.22. The anticipated polymer formation (through visual inspection) could not be observed. Interestingly the values of ksobs showed a decreasing trend with the increase of [acrylamide]T (104ksobs/s−1 = 1.67 ± 0.02, 1.63 ± 0.02, 1.61 ± 0.02 and 1.57 ± 0.02 at [acrylamide]T(monomer) = 0, 0.01, 0.02, 0.03 mol dm−3 respectively). This indirectly led us to believe that the MnIII complexes compete very successfully and efficiently in scavenging the C2O4−˙ or CO2−˙ generated in the redox process maintaining the stoichiometry (= |Δ[MnIII]|/|Δ[OX]|): 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and dimerisation of CO2−˙ at high dilution is of little significance; the possible reason may be the role played by the Coulombic repulsion between the anionic radicals in relation to the favorable electrostatic and non covalent interactions (H-bonding) between the radical anion and MnIII(salen)(OH2)2+ and MnIII(salen)(OH2)(OXH).
1, and dimerisation of CO2−˙ at high dilution is of little significance; the possible reason may be the role played by the Coulombic repulsion between the anionic radicals in relation to the favorable electrostatic and non covalent interactions (H-bonding) between the radical anion and MnIII(salen)(OH2)2+ and MnIII(salen)(OH2)(OXH).The rate data (ksobs, 30 °C) at constant [OX]T = 0.006 mol dm−3, pH = 3.97 ± 0.03 and 0.00 ≤ [SDS]T/mol dm−3 ≤ 0.10 are collected in Table S6.† There is no significant effect of [SDS] on the rate constant at [SDS]T ≤ 0.0075 mol dm−3; marked retardation is observed beyond [SDS]T = 0.0075 mol dm−3 and ksobs tends to attain a low limiting value at high [SDS]. This is reconciled with the fact that the diaqua complex and presumably the neutral complex, trans-MnIII(salen)(OH)2(OXH), are partitioned into the micellar pseudo phase of SDS and this protects the MnIII species from electron transfer involving HOX− which on electrostatic ground exists exclusively in the aqueous pseudo phase. The pH condition is such that [OX]T exists in equilibrium in the bulk aqueous phase as HOX− and OX2−. Interestingly there is substantial rate enhancement on increasing [Na+]T by addition of NaClO4 (= 0.01–0.3, see Table S6†) at a fixed [SDS]T = 0.02 which also leads to the decrease of pH. The observed pH perturbation is a clear indication of the prevalence of ion exchange equilibrium involving H+/Na+ between the anionic micellar pseudo phase and the bulk aqueous phase. We consider the participation of the mono cationic MnIII complex in this ion exchange equilibrium along with the equilibrium partitioning of the corresponding neutral HOX complex between the bulk aqueous phase and micellar pseudo phase. Scheme 3 is presented to interpret the rate data. Accordingly,
 | (13) |
| I = 3[Na2OX]T +[NaHOX]T + [NaClO4] + cmc + 0.5(1 − β)[[SDS]T − cmc) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) yz+ = −0.5Z2(I1/2/(1 + I1/2)) + 0.2I yz+ = −0.5Z2(I1/2/(1 + I1/2)) + 0.2I
| (14) |
 | ||
| Scheme 3 MnIII(salen)(OH2)2+ reduction by HOX− in the presence of SDS micelles, R+ = MnIII(salen)(OH2)2+, Dn = [SDS]T − cmc. | ||
The best fit values of Kex, β and cmc turned out as 10.4 ± 0.8, 0.6 and 0.009 (cmc = 0.008 mol dm−3 at 25 °C, in absence of additives)25 respectively while the micellar binding constant Qm for the partitioning of the neutral species, MnIII(salen)(OH2)(HOX), is statistically insignificant (see Tables S6 and S7†).
This trend is explicable in terms of the equilibrium formation of trans-MnIII(salen)(OH2)(N3) competitive with the corresponding HOX− complex followed by the reduction of the azido complex by oxalate species as given below. Accordingly ksobs is given by eqn (15)
 | (15) |
3.1 Results and discussion
The seven coordinate MnIII centre in the transition state does not seem to be unusual considering the seven coordinate complexes, MnIII(EDTA)(OH2)− and MnIII(EDTA)(N3)2− reported by Suwyn and Hamm.36
 | ||
Fig. 4 RI-BP86/def2-TZVPP optimized structures of trans-MnIII(salen)(OH2)(HOX) (A), MnIII(salen)(HOX)2− (B), and MnIII(salen)(OH2)(OX)− (C1, C2), HOX−(OX2−) denotes −O–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)CO2H/−O–C( O)CO2H/−O–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)CO2−. O)CO2−. | ||
Relevant bond distances and bond angles are collected in Table 3. In all these structures, the (N2, O2) square plane around MnIII suffers little distortion while the axial Y–MnIII–X bonds are strongly distorted and also differently for A, B, and C1, C2. For example the Mn–O (38O–COCO2H) bond in A is 0.177 Å shorter than the same in B. Also the Mn–O (43 W) bond for the trans H2O in A is substantially elongated (2.895 Å). The free carboxyl group(s) in both A and B are bridged to the boned carboxylate group(s) through hydrogen bonds with a relatively shorter H-bond length (δ(H-bond)B–A = 0.083 Å) for A. This might be traced to the relatively stronger binding of HOX− to MnIII in A in tune with comparatively shorter Mn–O bond length (38O–COCO2H) in this case. In all such structures MnIII is situated above the partially distorted (N2, O2) square frame of the salen motif. The computed structures of trans-MnIII(salen)(OH2)(HOX) with possible H-bonding of the O–H function of the unbound carboxyl group are depicted in D1–D4 (Fig. 5). It turns out that D1 with a long hydrogen bond (O⋯H bond 2.831 Å) between the phenoxide oxygen and the free carboxyl group is energetically unfavourable; D2 (same as A in Fig. 4) is the most acceptable one.
| A | B | C1 | C2 |
|---|---|---|---|
| Bond distances (Å) | |||
| Mn–O(2 phenoxide) 1.909 | Mn–O(2 phenoxide) 1.908 | Mn–O(2 phenoxide) 1.913 | Mn–O(2 phenoxide) 1.900 |
| Mn–O(3 phenoxide) 1.895 | Mn–O(3 phenoxide) 1.908 | Mn–O(3 phenoxide) 1.921 | Mn–O(3 phenoxide) 1.909 |
| Mn–O(43 W) 2.895 | Mn–O(43 O–COCO2H) 2.257 | Mn–O(42 W) too long | Mn–O(42 W) too long |
| Mn–O(38 O–COCO2H) 2.080 | Mn–O(38 O–COCO2H) 2.257 | Mn–O(38 O–COCO2−) 2.020 | Mn–O(38 O–COCO2−) 2.003 |
| Mn–N(4 imine) 1.992 | Mn–N(4 imine) 2.00 | Mn–N(4 imine) 1.984 | Mn–N(4 imine) 1.993 |
| Mn–N(5 imine) 1.990 | Mn–N(5 imine) 2.00 | Mn–N(5 imine) 1.963 | Mn–N(5 imine) 1.967 |
| O(38)⋯H(42) 1.867 | O(38)⋯H(42) 1.784, O(43)⋯H(49) 1.784 | O(2 phenoxide)⋯H(43 W), 2.081, O(3 phenoxide)⋯H(44 W), 2.116 | O(3 phenoxide)⋯H(44 W) too long, O(2 phenoxide)⋯H(44 W), 2.343, O(41 O–COCO2)⋯H(43 W) 1.815 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Bond angles (degree) | |||
| O(2)–Mn–O(38) 95.1 | O(2)–Mn–O(38) 89.2 | O(2)–Mn–O(38) 96.7 | O(2)–Mn–O(38) 95.9 |
| O(2)–Mn–O(3) 93.7 | O(2)–Mn–O(3) 95.3 | O(2)–Mn–O(3) 93.1 | O(2)–Mn–O(3) 92.5 |
| O(2)–Mn–N(4) 89.6 | O(2)–Mn–N(4) 91.1 | O(2)–Mn–N(4) 89.9 | O(2)–Mn–N(4) 90.5 |
| O(3)–Mn–N(5) 90.8 | O(3)–Mn–N(5) 91.1 | O(3)–Mn–N(5) 90.3 | O(3)–Mn–N(5) 90.3 |
| O(2)–Mn–N(5) 164.8 | O(2)–Mn–N(5) 173.5 | O(2)–Mn–N(5) 166.7 | O(2)–Mn–N(5) 167.5 |
| O(3)–Mn–N(4) 163.9 | O(3)–Mn–N(4) 173.5 | O(3)–Mn–N(4) 159.9 | O(3)–Mn–N(4) 157.3 |
| O(3)–Mn–O(43) 81.6 | O(3)–Mn–O(43) 89.2 | ||
| O(2)–Mn–O(43) 71.0 | O(2)–Mn–O(43) 91.7 | ||
| N(4)–Mn–N(5) 82.3 | N(4)–Mn–N(5) 82.5 | N(4)–Mn–N(5) 82.6 | |
| N(4)–Mn–O(38) 97.1 | N(4)–Mn–O(38) 89.5 | N(4)–Mn–O(38) 96.5 | N(4)–Mn–O(38) 97.6 |
| N(4)–Mn–O(43) 84.6 | N(4)–Mn–O(43) 89.4 | ||
| N(5)–Mn–O(38) 98.7 | N(5)–Mn–O(38) 89.4 | N(5)–Mn–O(38) 95.0 | N(5)–Mn–O(38) 95.2 |
| N(5)–Mn–O(43) 95.3 | N(5)–Mn–O(43) 89.5 | ||
| Mn–O(2)–C(6) 126.1 | Mn–O(2)–C(6) 129.3 | Mn–O(2)–C(6) 129.3 | Mn–O(2)–C(6) 129.8 |
| Mn–O(3)–C(21) 131.2 | Mn–O(3)–C(21) 129.3 | Mn–O(3)–C(21) 130.9 | Mn–O(3)–C(21) 131.2 |
| Mn–N(4)–C(12) 124.7 | Mn–N(4)–C(12) 125.7 | Mn–N(4)–C(12) 126.2 | Mn–N(4)–C(12) 126.1 |
| Mn–N(5)–C(15) 126.6 | Mn–N(5)–C(15) 125.7 | Mn–N(5)–C(15) 127.8 | Mn–N(5)–C(15) 127.8 |
 | ||
| Fig. 5 RI-BP86/def2-TZVPP optimized structures of trans-MnIII(salen)(OH2)(HOX), D1–D4 denote the hydrogen bonded conformational isomers. | ||
Notable is the fact that OX2− coordination to MnIII leads to very strong axial distortion resulting in expulsion of the bound H2O from the MnIII centre (C1, C2). Essentially MnIII in trans-MnIII(salen)(OH2)(OX)− assumes five coordination. Fig. 6 depicts the computed structures of trans-MnIII(salen)(OH2)(H2OX)+ (E1), MnIII(salen)(HOX)(H2OX) (E2), and MnIII(salen)(OX)(H2OX)− (E3). In E1 oxalic acid (H2OX) molecule is bound to MnIII centre by C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O function with long Mn–O bond (2.430 Å); one H-bond between the phenoxide group and the carboxyl proton (H⋯O bond 1.707 Å) of the bound carboxyl group completes a six membered ring structure imparting stability. It may be noted that both the M–O bond lengths trans to each other do not differ significantly although they are assembled differently (H2O–Mn–O
O function with long Mn–O bond (2.430 Å); one H-bond between the phenoxide group and the carboxyl proton (H⋯O bond 1.707 Å) of the bound carboxyl group completes a six membered ring structure imparting stability. It may be noted that both the M–O bond lengths trans to each other do not differ significantly although they are assembled differently (H2O–Mn–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–). In E2 the hydrogen bond length between the phenoxide oxygen and the carboxylic proton decreases to 1.627 Å with elongation of the MnIII–O bond of MnIII–O
C–). In E2 the hydrogen bond length between the phenoxide oxygen and the carboxylic proton decreases to 1.627 Å with elongation of the MnIII–O bond of MnIII–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C– to 3.090 and concurrent compression of the trans-MnIII–O (MnIII–OXH) to 2.068 Å. Interestingly H2OX in E3 is H-bonded to the phenoxide group (O⋯H = 1.465 Å) with a long MnIII–O distance (4.337 Å) of MnIII–O
C– to 3.090 and concurrent compression of the trans-MnIII–O (MnIII–OXH) to 2.068 Å. Interestingly H2OX in E3 is H-bonded to the phenoxide group (O⋯H = 1.465 Å) with a long MnIII–O distance (4.337 Å) of MnIII–O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (no bonding situation) with simultaneous shortening of the trans-Mn–O (1.986 Å) reflecting the strong trans effect of the coordinated OX2−. Although these computationally accessible species, MnIII(salen)(X)(H2OX)+ (X = H2O, HOX− and OX2−) are not experimentally identified in aqueous medium, they provide sufficient insight to understand the reaction mechanism. Thus the computational study shows that there is a possibility of inner sphere reduction of MnIII by HOX− and H2OX in the reactions of MnIII(salen)(OH2)(HOX) with HOX− and H2OX (k1 and k2 paths). The corresponding reactions between trans-MnIII(salen)(OH2)(OX)− and HOX− (k5 path), trans-MnIII(salen)(OH2)(OX) and OX2− (k6 path), and trans-MnIII(salen)(OH2)(HOX) + OX2− (k7 path) in all probability be considered as outer sphere type as coordination of OX2− to MnIII will lead to the displacement of the trans-ligand (C1 and C2) due to the predominant structural trans effect (STE) of OX2−.
C (no bonding situation) with simultaneous shortening of the trans-Mn–O (1.986 Å) reflecting the strong trans effect of the coordinated OX2−. Although these computationally accessible species, MnIII(salen)(X)(H2OX)+ (X = H2O, HOX− and OX2−) are not experimentally identified in aqueous medium, they provide sufficient insight to understand the reaction mechanism. Thus the computational study shows that there is a possibility of inner sphere reduction of MnIII by HOX− and H2OX in the reactions of MnIII(salen)(OH2)(HOX) with HOX− and H2OX (k1 and k2 paths). The corresponding reactions between trans-MnIII(salen)(OH2)(OX)− and HOX− (k5 path), trans-MnIII(salen)(OH2)(OX) and OX2− (k6 path), and trans-MnIII(salen)(OH2)(HOX) + OX2− (k7 path) in all probability be considered as outer sphere type as coordination of OX2− to MnIII will lead to the displacement of the trans-ligand (C1 and C2) due to the predominant structural trans effect (STE) of OX2−.
We observe that the intramolecular electron transfer reactions from the bound oxalate to MnIII centre in trans-MnIII(salen)(OH2)(HOX) (k0) and MnIII(salen)(OH2)(OX)− (k4) are too slow, if at all occur, under the experimental conditions. This is what we observed in an earlier study of the reduction of MnIII by the bound glyoxylate (gem diol form) in trans-MnIII(salen)(OH2)(O2CH(OH)2) (105k0/s−1 = 0.05 ± 0.53 at 45 °C).17 For such complexes the values of their formation equilibrium constant {Q1/mol dm−3 = 33.2–25.0, 42.0, 49.5 (25–40 °C, I/mol dm−3 = 0.3) for CH(OH)2CO2−, HOX− and OX2− respectively} and the pK′ data (−log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K′ = 3.38 ± 0.20 see Table 2) of MnIII(salen)(OH2)(HOX) suggests that the carboxylate ligand binds the MnIII centre in a monodentate fashion; this is further supported on a comparative basis by a value of pK = 2.0 (28 °C, I = 0.3 mol dm−3) for the unbound carboxyl group of bioxalatopentaamminecobalt(III), (NH3)5CoOCOCO2H2+.37 Despite this fact the carboxylate ligand binding results in substantial stabilization of the MnIII state towards intramolecular redox process. The DFT calculations indicate that there is a finite possibility of a 1
K′ = 3.38 ± 0.20 see Table 2) of MnIII(salen)(OH2)(HOX) suggests that the carboxylate ligand binds the MnIII centre in a monodentate fashion; this is further supported on a comparative basis by a value of pK = 2.0 (28 °C, I = 0.3 mol dm−3) for the unbound carboxyl group of bioxalatopentaamminecobalt(III), (NH3)5CoOCOCO2H2+.37 Despite this fact the carboxylate ligand binding results in substantial stabilization of the MnIII state towards intramolecular redox process. The DFT calculations indicate that there is a finite possibility of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 species, MnIII(salen)(H2O)(H2OX)+. We, however, did not observe [H2OX] dependent rate of complexation of MnIII(salen)(OH2)2+. Also the rate constant of reduction of MnIII(salen)(OH2)2+ by H2OX (k3) turned out statistically insignificant. The possible reason for not being able to detect MnIII(salen)(H2O)(H2OX)+ is due to the very low pK1 of oxalic acid (pK1 = 1.0–1.04 at 20–40 °C). Further lowering of the pK1 of the coordinated oxalic acid favours complete H+ dissociation under the experimental conditions and in consequence MnIII(salen)(OH2)(H2OX)+, if formed, gets converted to its HOX analogue. Presumably the experimental identification of MnIII(salen)(OH2)(H2OX)+ in aqueous medium demands still higher [H+] and [H2OX]. However, the acid catalyzed decomposition of MnIII(salen)(OH2)2+ at high [H+] set a limit to our investigation to [H+] ≤ 0.05 mol dm−3.
1 species, MnIII(salen)(H2O)(H2OX)+. We, however, did not observe [H2OX] dependent rate of complexation of MnIII(salen)(OH2)2+. Also the rate constant of reduction of MnIII(salen)(OH2)2+ by H2OX (k3) turned out statistically insignificant. The possible reason for not being able to detect MnIII(salen)(H2O)(H2OX)+ is due to the very low pK1 of oxalic acid (pK1 = 1.0–1.04 at 20–40 °C). Further lowering of the pK1 of the coordinated oxalic acid favours complete H+ dissociation under the experimental conditions and in consequence MnIII(salen)(OH2)(H2OX)+, if formed, gets converted to its HOX analogue. Presumably the experimental identification of MnIII(salen)(OH2)(H2OX)+ in aqueous medium demands still higher [H+] and [H2OX]. However, the acid catalyzed decomposition of MnIII(salen)(OH2)2+ at high [H+] set a limit to our investigation to [H+] ≤ 0.05 mol dm−3.
The predominant reactions are the reduction of MnIII in MnIII(salen)(OH2)(HOX) by HOX− (k1 path) and H2OX (k2 path), H2OX being a better reducing agent than HOX− (k2/k1 ≥ 10 at 25–40 °C). This trend appears surprising as HOX− is a better electron donor than its conjugated acid, H2OX. To account for this difference we suggest that the reaction in the k2 path is preferably an efficient inner-sphere electro-protic reaction involving proton coupled electron transfer, PCET, (Fig. 7) or concerted proton electron transfer, CPET, process as observed in the oxidation of aromatic phenols by MnIII(OH)(dpaq)+ (dpaq = 2-[bis(pyridine-2-ylmethyl)]amino-N-quinolin-8-yl-acetamidate) in MeCN.38
Substantially large differences in the activation enthalpy (ΔΔH≠(k2−k1) = 29.2 ± 9.3 kJ mol−1) and entropy (ΔΔS≠(k2−k1) = +117.5 ± 32.4 J K−1 mol−1) are observed for the two paths. The observed activation enthalpy arises due to (i) the enthalpy changes associated with the pre-equilibria, and (ii) energy demand for the rearrangement of bonds in the activation process. Out of these two contributing factors the later will predominate as the nature of the bond broken and reformed in the equilibrium pre-association are alike (MnIII–O). However, the ΔS≠ term depends on solvation of the reacting species in the initial states and the transition states. In the present case the substantially negative value of the activation entropy for k1 path might indicate the involvement of an ordered transition state. There is likely to be much greater degree of rearrangement of bonds in the k2 path (see Fig. 7) which accounts for the relatively higher values of ΔH≠ and ΔS≠ for this path. A simple calculation of the thermodynamic parameters for the k1 and k2 paths, [X(TS≠2) − X(TS≠1)], where X = G, H, S and TS≠2 and TS≠1 denote the activated states for the electron transfer respectively might clarify this picture. The differential values of the thermodynamic parameters can be expressed as,
G(TS≠2) − G(TS≠1) = −2.303RT[pK1 + log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2/k1] + G0(H+) k2/k1] + G0(H+) |
| H(TS≠2) − H(TS≠1) = ΔH≠(k2) − ΔH≠(k1) − ΔH0(K1) + H0(H+) |
| S(TS≠2) − S(TS≠1) = ΔS≠(k2) − ΔS≠(k1) − T−1ΔH0(K1) + 2.303RpK1 + S0(H+) |
The intramolecular electron transfer for MnIII(salen)(OH2)(OX)− (106k4 = 0.03 ± 14 at 35 °C) is virtually insignificant. The same is also true for the reaction: MnIII(salen)(OH2)2+ + H2OX (k3 = 0.13 ± 0.47 dm3 mol−1 s−1, 35 °C, see Table 2). We attempted to examine the reactions via k0 and k3 paths using SDS as a probe. Our aim was to selectively partition the neutral H2OX moiety along with MnIII(salen)(OH2)2+ and MnIII(salen)(OH2)(HOX) into the anionic micellar pseudo phase and make these reaction paths feasible at a site (i.e. micelle layer) away from the bulk aqueous phase. Our results, however, did not reveal any partitioning of MnIII(salen)(OH2)(HOX) and H2OX into the anionic micelles at the experimental pH (= 3.9). Higher acidity could not be maintained to avoid the competitive pseudo phase ion-exchange equilibrium for (MnIII(salen)(OH2)2+)M/HW+. However, it enabled us to assess the micellar binding of the diaqua complex via ion-exchange equilibrium. The calculated value of the equilibrium constant, Kex (= 10.4 ± 0.8) is marginally higher than the same for the NaM+/HW+ exchange reported earlier (Kex = 1, 2–4) (ref. 39 and 40) and comparable to that of trans-(OH2)CoIII(SO3)+ (Kex = 10 for β = 0.6 at 25 °C).41
We undertook the study of the effect of azide ion (N3−) on the redox reaction as a probe for the reaction mechanism. Under the experimental conditions N3− is not a reductant like HOX−. The value of the binding constant (Q4) for N3− compares well with that of HOX− (Q1). The difference in the values of k1 and k8 (k1/k8 = 1.6 ± 0.3 at 40 °C) is not appreciable. This further suggests that binding of N3− or HOX− to MnIII does not lead to any significant difference in the rate of reduction by HOX− that follows. Hence the study of the effect of N3− validates the fact that trans-(H2O)MnIII(salen)(HOX) is kinetically stable to intramolecular electron transfer,  .
.
4. Conclusion
The electron transfer between trans-MnIII(salen)(OH2)2+ and oxalate species (H2OX, HOX−, OX2−) is preceded by fast and reversible aqua ligand substitution by HOX− resulting in trans-MnIII(salen)(OH2)(HOX). The activation parameters for the formation and dissociation of the HOX complex are in support of associative interchange mechanism (Ia). The trans-MnIII(salen)(OH2)(HOX) and its conjugate base analogue, trans-MnIII(salen)(OH2)(OX)− are kinetically inert to intramolecular reduction of MnIII centre by the bound HOX−/OX2−; the former undergoes facile redox reaction with HOX− and H2OX while the latter by only HOX− under mild acidic condition (2 ≤ pH ≤ 6). Structure optimization by DFT shows that there is a strong structural trans-effect of OX2− in trans-MnIII(salen)(OH2)(OX)− (unlike for its conjugate acid form) resulting in complete expulsion of H2O from the MnIII centre and resulting in a five coordinate species, MnIII(salen)(OX)− with the H2O molecule hydrogen bonded to the phenoxide moiety. The trans-(H2O)MnIII(salen)(HOX), however, assumes a distorted octahedral structure with a long MnIII–OH2 bond. It is possible for the trans-MnIII(salen)(OH2)(HOX) to add HOX/H2OX forming the trans-(HOX)MnIII(salen)(HOX/H2OX)−/0 although such species are not accessible under the experimental conditions. However, the computational study supports the possibility of inner sphere electron transfer processes in the k1 and k2 paths. The computed structure of trans-(HOX)MnIII(salen)(H2OX) with intramolecular hydrogen bond involving the bound phenoxide and H2OX, suggests that the intimate redox step in the k2 path is essentially a proton controlled electron transfer process. The study of the effects of anionic micelles of SDS (sodium dodecyl sulphate) and azide ion provide further support in favor the proposed reaction paths.Acknowledgements
Financial support from the University grants Commission (UGC), New Delhi in terms of a Teacher Fellowship to AKK (Ref. T. F.OU3-007-1/10-11 (ERO)) is acknowledged. AKK thanks the Odisha Education Department and the authority of Sishu Ananta Mahavidyalaya, Khurda, Odisha, India for granting study leave. Authors are thankful to Prof. Gautam K. Lahiri, Indian Institute of Technology, Mumbai for ESR measurement. HSB acknowledges DST-INSPIRE Faculty fellowship award (IFA11-CH-01) for the financial support.References
- Y. G. Abashkin and S. K. Burt, J. Phys. Chem. B, 2004, 108, 2708–2711 CrossRef CAS.
- Y. G. Abashkin and S. K. Burt, Inorg. Chem., 2005, 44, 1425–1432 CrossRef CAS PubMed.
- V. Lanza and G. Vecchio, J. Inorg. Biochem., 2009, 103, 381–388 CrossRef CAS PubMed.
- Y. Noritake, N. Umezawa, N. Kato and T. Higuchi, Inorg. Chem., 2013, 52, 3653–3662 CrossRef CAS PubMed.
- S. Melov, J. Ravenscroft, S. Malik, M. S. Gill, D. W. Walker, P. E. Clayton, D. C. Wallace, B. Malfroy, S. R. Doctrow and G. J. Lithgow, Science, 2000, 289, 1567–1569 CrossRef CAS.
- T. Katsuki, Coord. Chem. Rev., 1995, 140, 189–214 CrossRef CAS.
- M. Lakshmi Kantam and B. Bharathi, Catal. Lett., 1998, 55, 235–237 CrossRef.
- M. Lakshmi Kantam, V. Neeraja, B. Bharathi and C. Venkat Reddy, Catal. Lett., 1999, 62, 67–69 CrossRef.
- B. M. Choudary, M. L. Kantam, B. Bharathi and C. R. Venkat Reddy, J. Mol. Catal. A: Chem., 2001, 168, 69–73 CrossRef CAS.
- S. Gangopadhyay, M. Ali and P. Banerjee, Coord. Chem. Rev., 1994, 135–136, 399–427 CrossRef.
- J. P. McEvoy, J. A. Gascon, V. S. Batista and G. W. Brudvig, Photochem. Photobiol. Sci., 2005, 4, 940–949 CAS.
- T. A. Betley, Y. Surendranath, M. V. Childress, G. E. Alliger, R. Fu, C. C. Cummins and D. G. Nocera, Philos. Trans. R. Soc., B, 2008, 363, 1293–1303 CrossRef CAS PubMed.
- D. R. J. Kolling, N. Cox, M. Gennady Ananyev, J. Ron Pace and G. C. Dismukes, Biophys. J., 2012, 103, 313–322 CrossRef CAS PubMed.
- I. C. Kuan and M. Tien, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 1242–1246 CrossRef CAS.
- M. M. Whittaker, H.-Y. Pan, E. T. Yukl and J. W. Whittaker, J. Biol. Chem., 2007, 282, 7011–7023 CrossRef CAS PubMed.
- A. C. Dash and A. Das, Int. J. Chem. Kinet., 1999, 31, 627–635 CrossRef CAS.
- A. Kar, A. Acharya, G. Pradhan and A. C. Dash, J. Chem. Sci., 2014, 126, 547–559 CrossRef CAS.
- T. J. Jones and R. M. Noyes, J. Phys. Chem., 1983, 87, 4686–4689 CrossRef CAS.
- S. Mukhopadhyay, S. Chaudhuri, R. Das and R. Banerjee, Can. J. Chem., 1993, 71, 2155–2159 CrossRef CAS.
- H. M. Irving, M. G. Miles and L. D. Pettit, Anal. Chim. Acta, 1967, 38, 475–488 CrossRef CAS.
- A. E. Martell and R. M. Smith, in Critical Stability Constants, ed. A. E. Martell and R. M. Smith, Plenum Press, New York, 1977, vol. 3, p. 92 Search PubMed.
- A. Panja, N. Shaikh, M. Ali, P. Vojtíšek and P. Banerjee, Polyhedron, 2003, 22, 1191–1198 CrossRef CAS.
- S. Nayak and A. C. Dash, Transition Met. Chem., 2006, 31, 316–324 CrossRef CAS.
- K. Kovács, B. Vizvári, M. Riedel and J. Tóth, Phys. Chem. Chem. Phys., 2004, 6, 1236–1242 RSC.
- R. H. Ottewill, in Surfactants, ed. T. F. Tadros, Academic Press, London, 1984, p. 8, Table 1 Search PubMed.
- S. Nayak and A. C. Dash, Indian J. Chem., Sect. A: Inorg., Bio-inorg., Phys., Theor. Anal. Chem., 2003, 42, 2427–2438 Search PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354 CrossRef CAS PubMed.
- O. Vahtras, J. Almlöf and M. W. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470 CrossRef CAS.
- I. Salem and A. Gemeay, Transition Met. Chem., 1996, 21, 130–134 CrossRef CAS.
- J. J. Morgan, in Metals in Biological Systems, ed. A. Sigel and H. Sigel, Marcel Dekker Inc., New York, 2000, vol. 37, p. 7, Table 2 Search PubMed.
- D. Lieb, A. Zahl, T. E. Shubina and I. Ivanovic-Burmazovic, J. Am. Chem. Soc., 2010, 132, 7282–7284 CrossRef CAS PubMed.
- M. A. Suwyn and R. E. Hamm, Inorg. Chem., 1967, 6, 2150–2154 CrossRef CAS.
- A. C. Dash and R. K. Nanda, Inorg. Chem., 1974, 13, 655–661 CrossRef CAS.
- G. B. Wijeratne, B. Corzine, V. W. Day and T. A. Jackson, Inorg. Chem., 2014, 53, 7622–7634 CrossRef CAS PubMed.
- L. S. Romsted, in Surfactants in Solutions, ed. K. L. Mittal and B. Lindman, Plenum, New York, 1984, vol. 2, p. 1038, Table 1 (footnote a) Search PubMed.
- C. J. Garnett, A. J. Lambie, W. H. Beck and M. Liler, J. Chem. Soc., Faraday Trans. 1, 1983, 79, 953–964 RSC.
- A. C. Dash and S. S. Mohammed, Indian J. Chem., Sect. A: Inorg., Bio-inorg., Phys., Theor. Anal. Chem., 1991, 30, 653–659 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1(a and b), S2, S3(a–d), S4(a and b), S5; Tables S1(a–c), S(2–8). See DOI: 10.1039/c4ra10324f |
| This journal is © The Royal Society of Chemistry 2014 |







