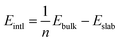Synthesis, structural characterization and computational studies of layered metal phosphonates: [M(HO₃P–C₅H₄N–PO₃H)₂(H₂O)₂]_n [M^II = Co, Zn, Cd]

Abstract

Three novel isomorphous coordination polymers with a general formula [M(HO₃P–C₅H₄N–PO₃H)₂(H₂O)₂]_n [M^II = Co (1), Zn (2) and Cd (3)] have been synthesized and characterized by powder and single-crystal X-ray diffraction, vibrational spectroscopy (IR and Raman) and simultaneous thermal analysis (TG-DTA-MS). Crystal structure analyses of compounds 1–3 have revealed that both phosphonate groups of (pyridin-1-ium-3,5-diyl)diphosphonate ligands serve to extend the metal cations into a strongly undulated grid structure parallel to the (101) plane. The adjacent monolayers are held together via multiple hydrogen bonds and offset face-to-face π–π interactions. The interlayer interaction energy values, estimated using the CRYSTAL code, have revealed that the stabilization energies of compounds 1–3 are quite similar, where 1 is least and 3 most advantageous. Computational studies have been further related to the results of thermal analyses. In the case of compound 1, which has unpaired electrons at the metal centre, the investigation has been supplemented by magnetic measurements. The magnetic properties of 1 (1.7–300 K) have been analyzed assuming that any possible exchange interactions are very weak. The obtained best-fit parameters are: Δ (axial splitting of ⁴T_1g term) = −478 cm⁻¹, λ (spin–orbit coupling) = −103 cm⁻¹, α (orbital reduction factor) = 1.38, and zJ′ (mean-field exchange parameter) = −0.11 cm⁻¹. The negative value of Δ implies that the ground state is the orbital doublet, which cannot be treated within the spin-Hamiltonian approach.

---

Introduction

Coordination polymers¹ are constructed from two fundamental components, namely metal ions or clusters and organic ligands, to obtain one-, two- or three-dimensional structures. However, the ability to predict and control the structural dimensionality of coordination polymers is seriously limited by many structure-directing factors, such as the preferable coordination geometry of the metal ion, the nature of the counter anion, the chemical structure of the ligand, the metal-to-ligand ratio, solvent system, temperature, pH value, and so on.² Among these factors, the judicial selection of a well-designed ligand plays a crucial role for the construction of coordination polymers with desired structures. Generally, the length, shape, conformational freedom, location and orientation of the donor atoms in the organic ligand have a significant influence on the final structures of coordination polymers.

Recently, the diphosphonic acids with a general formula H₂O₃P–Ar–PO₃H₂ (Ar = aryl group) have been proved to be very useful ligands for preparing coordination polymers with fascinating structures³ and interesting gas sorption,⁴ magnetic,⁵ luminescent⁶ and ion exchange⁷ properties. In this work, we chose pyridine-3,5-diyldiphosphonic acid as the organic ligand, based on the following considerations: (i) the phosphonic group possesses three donor O atoms, which depending on the deprotonation rate is capable of binding up to nine metal ions forming a great variety of diverse coordination modes. (ii) The O atoms and OH groups can participate in hydrogen-bonding interactions to increase the dimensionalities of the target products. (iii) The pyridine N atom can also bind metal ions to vary the coordination modes and afford extended and highly-connected frameworks or when it is protonated it can act as a hydrogen bond donor. (iv) The rigidity of the ligand scaffold, imparted by attaching the phosphonic groups directly to the pyridine ring, can result in more predictable structures. (v) The pyridine ring can offer additional aromatic interactions to consolidate the structures. The deprotonated form of pyridine-3,5-diyldiphosphonic acid has previously been reported to form three-dimensional calcium coordination polymer⁸ featuring a unique (4·8²)(4·8⁸·10)(8) topology and discrete cobalt(III) compound.⁹ To the best of our knowledge, two-dimensional coordination polymers based on pyridine-3,5-diyldiphosphonic acid have not been documented to date.

In this paper, we report the syntheses, structural characterization and computational analysis of three new two-dimensional coordination polymers based on pyridine-3,5-diyldiphosphonic acid, namely [M(HO₃P–C₅H₄N–PO₃H)₂(H₂O)₂]_n [M^II = Co (1), Zn (2) and Cd (3)]. In addition, the magnetic properties of 1 have been discussed.

Experimental section

Materials

The starting materials: 3,5-dibromopyridine, diethyl phosphite, triethylamine, tetrakis(triphenylphosphine)palladium(0), cobalt(II) chloride, zinc chloride and cadmium chloride were purchased from Sigma-Aldrich. Toluene, dichloromethane, methanol and concentrated hydrochloric acid (36–38%) were supplied by POCH S.A. All reagents were used as received without further purification.

Synthesis of pyridine-3,5-diyldiphosphonic acid

3,5-Dibromopyridine (3.000 g, 12.7 mmol), diethyl phosphite (3.965 mL, 30.5 mmol), triethylamine (4.251 mL, 30.5 mmol), toluene (10 mL) and tetrakis(triphenylphosphine)palladium were stirred and heated at 85 °C under an argon atmosphere for 24 h, following the reported procedure of Zoń et al.¹⁰ The precipitate of triethylamine hydrobromide, which was formed during the reaction, was filtered off under reduced pressure and washed with toluene (3 × 5 mL). The filtrate was concentrated under reduced pressure to obtain tetraethyl pyridine-3,5-diyldiphosphonate as dark yellow oil. The phosphonate ester was treated with concentrated hydrochloric acid (30 mL) and refluxed for 24 h. After hydrolysis, the reaction mixture was extracted with methylene chloride (2 × 15 mL). The aqueous layer was concentrated under reduced pressure. The residue was dissolved in methanol (30 mL) and left to crystallize at room temperature for 24 h. The white precipitate of pyridine-3,5-diyldiphosphonic acid was collected by filtration under reduced pressure, washed with methanol (3 × 5 mL), dried under reduced pressure and re-crystallized from 1 : 1 water–methanol mixture (30 mL). Yield: 1.426 g (47%). ¹H NMR (300.13 MHz, D₂O): δ 8.93–8.85 (m, 3H, arom. H). ³¹P{¹H} NMR (121.50 MHz, D₂O): δ 3.09 ppm (s).

Preparation of [Co(HO₃P–C₅H₄N–PO₃H)₂(H₂O)₂]_n (1), [Zn(HO₃P–C₅H₄N–PO₃H)₂(H₂O)₂]_n (2) and [Cd(HO₃P–C₅H₄N–PO₃H)₂(H₂O)₂]_n (3)

Pyridine-3,5-diyldiphosphonic acid (30.0 mg, 0.125 mmol) was dissolved in distilled water (2 mL) with heating. Then a solution of cobalt(II) chloride (16.2 mg, 0.125 mmol), zinc chloride (17.0 mg, 0.125 mmol) or cadmium chloride (22.9 mg, 0.125 mmol) in distilled water (1 mL) was added. The resulting mixture was left at room temperature for slow evaporation of the solvent. After five days, pink (in the case of 1) and colourless (in the case of 2 and 3) parallelepiped-shaped crystals were obtained. These crystals were then collected by gravity filtration, washed with distilled water (3 × 0.5 mL) and dried in air. For 1: yield: 11.7 mg (16%). Anal. found (calcd) for C₁₀H₁₆CoN₂O₁₄P₄: C, 20.89 (21.03); H, 2.70 (2.83); N, 4.77 (4.91)%. For 2: yield: 10.0 mg (14%). Anal. found (calcd) for C₁₀H₁₆N₂O₁₄P₄Zn: C, 20.51 (20.80); H, 2.57 (2.80); N, 4.87 (4.85)%. For 3: yield: 11.7 mg (15%). Anal. found (calcd) for C₁₀H₁₆CdN₂O₁₄P₄: C, 19.16 (19.23); H, 2.47 (2.59); N, 4.53 (4.49)%. The phase purity of 1–3 was confirmed by comparison of simulated and experimental powder XRD patterns (Fig. S1–S3†).

Elemental analysis

Standard CHN elemental analyses were measured on an Elementar vario EL III elemental analyzer.

Single-crystal X-ray data collection and structure determination

X-ray intensity data for the crystals 1–3 were collected using graphite monochromatic MoKα radiation on a four-circle κ geometry KUMA KM-4 diffractometer with a two-dimensional area CCD detector. The ω-scan technique with Δω = 1.0° for each image was used for data collection. 930 images for six different runs covering over 99% of the Ewald sphere were performed. One image was used as a standard after every 50 images for monitoring of the crystal stability and the data collection. No correction on the relative intensity variations was necessary. Data collections were made using the CrysAlis CCD program.¹¹ Integration, scaling of the reflections, correction for Lorentz and polarisation effects and absorption corrections were performed using the CrysAlis Red program.¹¹ The structures were solved by the direct methods using SHELXS-97 and refined using SHELXL-97 program.¹² The hydrogen atoms involved in the hydrogen bonds were located in the difference Fourier maps and were refined. The hydrogen atoms bonded to the aromatic carbon atoms were introduced in their geometrical positions. The final difference Fourier maps showed no peaks of chemical significance. Details of the data collection parameters, crystallographic data and final agreement parameters are collected in Table 1. Visualisations of the structures were made with the Diamond 3.1 program.¹³ Selected geometrical parameters are listed in Table 2 and the geometry of hydrogen bonding interactions is collected in Table 3.

Table 1 Crystal data and details of the structure determination for compounds 1–3^a

Compound	1	2	3
a R1 = Σ||Fo| − |Fc||/Σ|Fo|, wR2 = {Σ[w(Fo^2 − Fc^2)^2]/Σ[w(Fo^2)^2]}^1/2.
Formula	C10H16CoN2O14P4	C10H16ZnN2O14P4	C10H16CdN2O14P4
Formula weight (g mol^−1)	571.06	577.50	624.53
Crystal system	Monoclinic	Monoclinic	Monoclinic
Space group	P21/n (no. 14)	P21/n (no. 14)	P21/n (no. 14)
a (Å)	9.151(2)	9.1826(18)	9.331(2)
b (Å)	8.6680(10)	8.6841(17)	8.663(1)
c (Å)	11.631(2)	11.656(2)	11.793(2)
β (°)	95.980(10)	96.31(3)	96.330(10)
V (Å^3)	917.6(3)	923.8(3)	947.5(3)
Z	2	2	2
Dcalc/Dobs (g cm^−3)	2.067/2.06	2.076/2.07	2.189/2.18
F000	578	584	620
μ (mm^−1)	1.366	1.758	1.570
Absorption correction	Numerical, CrysAlis Red	Numerical, CrysAlis Red	Numerical, CrysAlis Red
Tmin/Tmax	0.7722/0.7988	0.6488/0.7816	0.6912/0.7722
Crystal size (mm)	0.25 × 0.21 × 0.18	0.28 × 0.18 × 0.15	0.26 × 0.22 × 0.18
T (K)	295(2)	295(2)	295(2)
Radiation type/wavelength (Å)	Mo Kα/0.71073	Mo Kα/0.71073	Mo Kα/0.71073
θ range (°)	2.70–29.35	2.93–29.20	2.65–29.39
No. of measured reflections	12177	12006	11855
No. of independent reflections	2364	2357	2417
Rint	0.0284	0.0247	0.0988
No. of reflns with I > 2σ(I)	1773	1966	1323
No. of parameters/restraints	157/4	154/4	154/4
R1/wR2 [I > 2σ(I)]^a	0.0258/0.0552	0.0270/0.0666	0.0490/0.0657
R1/wR2 (all data)^a	0.0485/0.0611	0.0378/0.0701	0.1412/0.0836
S	1.006	1.002	1.004
Δρmax/Δρmin (e Å^−3)	+0.36/–0.36	+0.44/–0.32	+0.65/–0.66

---

Table 2 Selected geometric parameters (Å, °) for compounds 1–3^a

Compound	1	2	3	Compound	1	2	3
a Symmetry codes: (i) −1/2 + x, −1/2 − y, 1/2 + z; (ii) 1/2 − x, 1/2 + y, −1/2 − z; (iii) −x, −y, −z.
M–O51^i	2.0507(12)	2.0526(16)	2.220(3)	C5–P5	1.8182(17)	1.821(2)	1.834(4)
M–O31	2.1258(12)	2.1490(15)	2.281(3)	P5–O51	1.4843(12)	1.4848(16)	1.477(3)
M–O1W	2.1717(14)	2.1858(18)	2.340(3)	P5–O52	1.4984(12)	1.5034(14)	1.492(3)
C3–P3	1.8070(16)	1.8104(19)	1.802(4)	P5–O53	1.5805(13)	1.5837(15)	1.569(3)
P3–O31	1.4881(12)	1.4954(14)	1.490(3)	N1–C2	1.340(2)	1.347(3)	1.338(5)
P3–O32	1.5105(11)	1.5136(14)	1.521(3)	N1–C6	1.334(2)	1.336(3)	1.318(5)
P3–O33	1.5671(12)	1.5699(15)	1.564(3)
O31–M–O1W	90.65(5)	90.90(6)	91.49(12)	O31–P3–O33	113.36(7)	113.40(8)	113.41(17)
O51^i–M–O1W	88.80(5)	88.64(6)	87.30(12)	O32–P3–O33	105.55(6)	105.62(8)	105.93(16)
O51^ii–M–O1W	91.20(5)	91.36(6)	92.70(12)	C5–P5–O51	108.89(7)	109.03(9)	109.05(18)
O31^iii–M–O1W	89.35(5)	89.10(6)	88.51(12)	C5–P5–O52	107.32(7)	107.62(9)	108.34(18)
O31–M–O51^i	89.59(5)	89.32(6)	88.74(10)	C5–P5–O53	102.56(7)	102.61(9)	103.1(2)
O31–M–O51^ii	90.41(5)	90.68(6)	91.26(10)	O51–P5–O52	117.62(7)	117.30(9)	116.7(2)
C3–P3–O31	108.73(7)	108.81(8)	108.07(18)	O51–P5–O53	111.05(7)	111.09(9)	110.66(19)
C3–P3–O32	105.52(7)	105.44(8)	106.15(18)	O52–P5–O53	108.29(7)	108.13(9)	108.04(18)
C3–P3–O33	104.71(7)	104.46(8)	104.06(18)	C6–N1–C2	123.13(15)	122.65(17)	123.5(4)
O31–P3–O32	117.94(7)	118.01(8)	118.13(17)

---

Table 3 Hydrogen bond geometry (Å, °) for compounds 1–3^a

Compound	D–H⋯A	d(D–H)	d(H⋯A)	d(D⋯A)	<D–H⋯A
a Symmetry codes: (iv) 1/2 + x, −1/2 − y, 1/2 + z; (v) 3/2 − x, 1/2 + y, −1/2 − z; (vi) 1 − x, −1 − y, −z; (vii) −1 + x, y, z.
Intralayer hydrogen bonds
1	O33–H33⋯O32^ii	0.819(9)	1.764(10)	2.5728(16)	169(2)
2		0.818(10)	1.772(11)	2.579(2)	169(3)
3		0.815(10)	1.807(18)	2.591(4)	161(5)
1	O1W–H2W⋯O32	0.821(9)	2.528(17)	3.1400(18)	132.3(19)
2		0.812(10)	2.49(2)	3.158(2)	140(3)
3		0.820(10)	2.78(5)	3.261(5)	120(5)
Interlayer hydrogen bonds
1	N1–H1N⋯O32^iv	0.815(19)	1.851(19)	2.6648(19)	177(2)
2		0.86	1.80	2.663(2)	177(2)
3		0.86	1.84	2.691(5)	170.5
1	O53–H53⋯O52^v	0.813(9)	1.916(12)	2.6929(17)	159(2)
2		0.809(10)	1.911(13)	2.696(2)	163(3)
3		0.823(10)	1.989(16)	2.801(5)	169(6)
1	O1W–H1W⋯O52^vi	0.834(9)	2.078(11)	2.8929(18)	166(2)
2		0.819(10)	2.078(12)	2.880(2)	166(3)
3		0.825(10)	1.981(14)	2.797(5)	170(5)
1	O1W–H2W⋯O53^vii	0.821(9)	2.474(14)	3.1973(19)	147(2)
2		0.812(10)	2.495(19)	3.189(2)	144(3)
3		0.820(10)	2.37(4)	3.028(5)	137(5)

---

Powder X-ray diffraction data collection

The experimental powder XRD patterns of 1–3 were acquired on a PANalytical X'Pert diffractometer equipped with a Cu Kα radiation source (λ = 1.54182 Å), and operated at 40 kV and 30 mA. The data were collected at room temperature in the range of 2θ = 5–40°. On the other hand, the corresponding simulated powder XRD patterns were generated using Diamond 3.1 software.

Computational details

Computations of the interlayer interaction energy were performed both on the experimental geometries with the X–H distances extended to neutron-normalized values¹⁴ and on the optimized geometries, with the CRYSTAL09 program¹⁵ at the DFT(B3LYP) level of theory.^16–18 The 6-31G** molecular all-electron basis set¹⁹ was used for the purpose of the conducted computations. Only in the case of the cadmium atom a different basis set was applied, namely the one provided by Dou et al.²⁰ Additionally, a second basis set was tested for the zinc atom to check its influence on the final energetic result.²¹ Both Grimme dispersion correction^22,23 and correction for basis set superposition error (BSSE)²⁴ were applied. The evaluation of Coulomb and exchange series was controlled by five thresholds, set arbitrarily to the values of 10⁻⁷, 10⁻⁷, 10⁻⁷, 10⁻⁷, 10⁻¹⁹. The shrinking factor was equal to 4, which refers to 30 k-points in the irreducible Brillouin zone for the monoclinic P2₁/n space group.

Crystal interlayer interactions were evaluated within the supermolecular approach. An additional upper and lower molecular layers were used as ghost function sets to estimate the BSSE. The following interlayer interaction energy (E_intl) calculation formula was applied:^25,26

where E_slab is the energy of a molecular slab extracted from the bulk, while n indicates the slab number per unit cell. Therefore the resulting stabilization energy falls on a part of a slab belonging to the unit cell. CRYSTAL automatically assigns the slab group symmetry and cuts out the repeatable fragment. In this case such a chosen fragment is four times larger than the asymmetric part of the unit cell of the parent crystal structure.

The mentioned geometry optimizations were performed in the CRYSTAL program using the DFT approach and the same functional and basis sets. The unit cell parameters were fixed while the atom positions varied during the optimization.

Vibrational spectroscopy

The FT-IR spectra of 1–3 were recorded on a Bruker Vertex 70v FT-IR spectrometer in the range of 4000–370 cm⁻¹ with a resolution of 2 cm⁻¹ using the KBr pellet technique. The Raman spectra of 1–3 were collected on an Horiba Jobin-Yvon HR800 dispersive Raman spectrometer in the range of 4000–50 cm⁻¹ with a resolution of 2 cm⁻¹ using the He–Ne laser line at 632.8 nm. The Raman spectra were measured in Sol–Gel Nanotechnology Materials Laboratory of Lower Silesian Centre for Advanced Technologies in Wrocław.

Simultaneous thermal analysis

The combined TG-DTA-MS analyses were performed using a simultaneous thermal analyzer NETZSCH STA 449 F3 Jupiter coupled with a quadrupole mass spectrometer QMS 403 C Aëolos. The samples (20.3 mg of 1, 19.5 mg of 2 and 18.4 mg of 3) were placed inside Al₂O₃ crucibles. The measurements were carried out in the temperature range of 35–800 °C with a heating rate of 4 °C min⁻¹ and under dynamic air atmosphere (N₂/O₂ 80 : 20) with a gas flow of 20 mL min⁻¹. The data acquisition and processing were realized using NETZSCH Proteus software.

Magnetic measurements

The magnetic susceptibility measurement for compound 1 (47.0 mg) was carried out in the temperature range of 1.7–300 K using a Quantum Design SQUID magnetometer.

Results and discussion

Solid state organization of compounds 1–3

The single-crystal X-ray diffraction analysis has revealed that compounds 1–3 are isostructural (have the same molecular structure) and isomorphous (have the same space group) and crystallize in the monoclinic P2₁/n space group. The asymmetric unit of 1–3 contains one half of the metal ion, which is located on a special position on the inversion centre at (0, 0, 0), one (pyridin-1-ium-3,5-diyl)diphosphonate monoanion and one coordinated water molecule. The metal ion is six-coordinate with a distorted octahedral geometry. Its coordination environment consists of four phosphonate O-atoms from four (pyridin-1-ium-3,5-diyl)diphosphonate ligands and two O-atoms coming from water molecules (Fig. 1). The M − O bond lengths vary from 2.0507(12) to 2.1717(14) Å for 1, from 2.0526(16) to 2.1858(18) Å for 2 and from 2.220(3) to 2.340(3) Å for 3. The bond angles around the metal ion range from 88.80(5) to 91.20(5)° for 1, from 88.64(6) to 91.36(6)° for 2 and from 87.30(12) to 92.70(12)° for 3.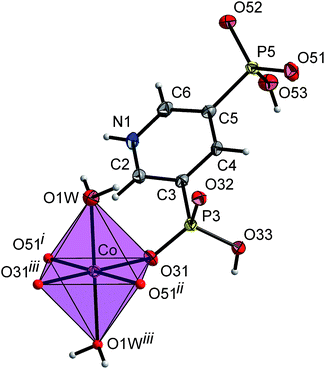

Fig. 1 The asymmetric unit and the coordination polyhedron of compound 1, together with the atom-labelling scheme. The displacement ellipsoids are drawn at the 50% probability level.

Each (pyridin-1-ium-3,5-diyl)diphosphonate moiety acts as η²μ₂ ligand and uses both monodeprotonated phosphonate groups to bind in a monodentate manner to the metal ion, thus creating a monolayer parallel to the (101) plane. The two-dimensional framework is characterized by large R4,8(32) motifs,²⁷ closed between four metal ions, four pyridine rings and eight phosphonate groups (Fig. 2a). The coordination network is strongly undulated and the pyridine rings, to which the phosphonate groups are attached, are tilted at an angle of 66.856(39)° toward the (101) plane. The monolayer is additionally stabilized by phosphonate–phosphonate hydrogen bond, O33–H33⋯O32ⁱⁱ, established between screw-related monoanions. The folding of the layered structure is supported by O1W–H2W⋯O32 hydrogen bond, donated from the water molecule towards the phosphonate O-atom site.

Fig. 2 (a) A view of the (101) monolayer of compound 1. The O–H⋯O hydrogen bonds are shown as dashed lines. The pyridine (C)H atoms are omitted for clarity. (b) A schematic presentation of the two-dimensional 4-connected sql net with (4⁴·6²) topology.

One can consider the metal ions as four-connected nodes (the terminal aqua ligands are disregarded during the simplification process) and the (pyridin-1-ium-3,5-diyl)diphosphonate ligand as two-connected linkers. Therefore, the topology of 1–3 can be presented as a 4-connected sql net with a Schläfli symbol of (4⁴·6²) (Fig. 2b).²⁸

The adjacent monolayers are connected via multiple hydrogen bonds to construct a three-dimensional supramolecular architecture (Fig. 3). One of hydrogen bonds, N1–H1N⋯O32^iv, is established between the protonated N-atom and the phosphonate O-atom site of a glide-related monoanion. The other hydrogen bond, O53–H53⋯O52^v, is formed between monodeprotonated phosphonate groups of screw-related ligands. The aqua ligand donates two water–phosphonate hydrogen bonds, O1W–H1W⋯O52^vi and O1W–H2W⋯O53^vii, which also hold the neighbouring layers together. The three-dimensional network is further supported by offset face-to-face (OFF) interactions, established between inversion-related pyridine rings [for 1: Cg⋯Cg^vi = 4.2844(13) Å (Cg is the ring centroid) and slippage = 2.400 Å, for 2: Cg⋯Cg^vi = 4.2871(13) Å and slippage = 2.400 Å, for 3: Cg⋯Cg^vi = 4.348(3) Å and slippage = 2.440 Å].

Fig. 3 The three-dimensional supramolecular network of compound 1. The terminal aqua ligands and the pyridine (C)H atoms are omitted for clarity.

Computational analysis

The more chemically similar compounds 2 and 3, being closed-shell systems as opposed to the open-shell compound 1, shall be analyzed first. The structures 2 and 3 were successfully optimized to assure reliable X–H bond lengths and directions, which are important to derive sensible interaction energy values (Fig. S4†). To compare the structures and explore the differences resulting from various metal centres, we have calculated the interaction energies (E_intl) between the previously described molecular layers parallel to the (101) plane. The results for both the optimized and not optimized (with the X–H distances extended to neutron-normalized values) cases of 2 and 3 are shown in Table 4. The energies obtained for the optimized crystal structures are more favorable (about 15 kJ mol⁻¹ difference on the average per ASU), but the energy trend is preserved. As expected, the interlayer interaction energy differences between 2 and 3 are almost negligible, being lower than 4 kJ mol⁻¹ per ASU. Among the two, the interactions in 3 seem to be slightly stronger. The strength of the interlayer interactions reflects the presence of noticeable contacts between the molecular slabs, here a number of hydrogen bonds and offset face-to-face interactions. Furthermore, it shows the similarity of the interactions between the molecular surrounding of the metal centre in both cases, what indicates a great similarity of these systems and the metal centre behaviour. Additionally, the Mulliken population analysis provided atomic charge rough estimates. Such charges are naturally basis-set-dependent, however, in the case of zinc there was no difference between the two tested zinc atom models (Table 4). On that basis, one can notice that the cadmium atom is more positive when compared to zinc. It is in agreement with the atom relative polarizabilities, as cadmium is indeed more easily affected and polarized by surrounding atoms.

Table 4 Interlayer interaction energy values, E_intl, and metal atom charges, Q, obtained from Mulliken population analysis calculated in CRYSTAL for 2 and 3

Compound	Eintl (kJ mol^−1)	Q (e)
a Using a literature basis set for the zinc atom^21 different than 6-31G**.b Calculated per the equivalent of ASU.
2	−1112.9/−278.2^b	+0.94
2^a	−1112.8/−278.2^b	+0.94
2-opt	−1174.8/−293.7^b	+0.95
2-opt^a	−1174.7/−293.7^b	+0.95
3	−1138.9/−284.7^b	+1.30
3-opt	−1190.2/−297.6^b	+1.30

---

The compound 1, being an open-shell system, was much more difficult to be analyzed computationally due to the convergence problems. The obtained atomic charge of cobalt was equal to +0.88e, what makes it the least positive metal centre compared to 2 and 3. Nevertheless, the estimated interlayer interaction energy on the basis of partial results amounted to about −275 kJ mol⁻¹ per ASU for the unoptimized case, which makes it very much comparable to the other two structures.

Spectroscopic characterization of compounds 1–3

The complementary IR and Raman spectra of 1–3 are shown in Fig. S5–S7.† The spectra are very similar to each other in the entire measuring range because the connectivity patterns are the same in all three compounds. A series of intense bands, observed in IR spectra at 1180–930 cm⁻¹, is associated with the stretching vibrations of the tetrahedral CPO₃ group. The corresponding PO₃ deformation vibrations are found in the region 555–415 cm⁻¹. The O–H⋯O and N–H⋯O hydrogen bonds give rise to a medium absorption at 3555–2280 cm⁻¹. The band above 3550 cm⁻¹ is due to the O–H stretching vibrations of the coordinated water molecule. The broad band at 3335–3265 cm⁻¹ is related to the N–H stretching vibration of the protonated pyridine ring. The corresponding N–H deformation vibration gives a strong band around 1265 cm⁻¹. The overlapping bands in the region 2855–2280 cm⁻¹ are connected with the O–H stretching vibrations of the phosphonate groups. The aromatic C–H stretching vibrations give rise to two bands at 3090–3055 cm⁻¹. The ring C=C and C=N stretching vibrations result in bands of medium-to-strong intensity in the region 1625–1560 cm⁻¹ and 1400–1360 cm⁻¹. Strong bands, observed at 855–815 cm⁻¹, are characteristic for C–H out-of-plane deformation vibrations. The out-of-plane ring deformation vibrations occur around 690 cm⁻¹. Additionally, a very strong band due to the C–H in-plane deformation vibrations is observed in the Raman spectra near 1030 cm⁻¹. The positions and intensities of all observed vibrational modes together with their tentative assignments are given in Table S2.†

Thermal stability of compounds 1–3

The simultaneous TG-DTA curves of 1–3 are shown in Fig. S8–S10.† Compounds 1–3 exhibit almost the same thermal decomposition process, and display two distinct weight loss stages. The first weight loss, corresponding to an endothermic peak with maximum at 232.0 °C for compound 1 (at 235.4 °C for 2, at 237.0 °C for 3) and giving rise to the peak at m/z = 18, is attributed to the release of two coordinated water molecules (1: found, 6.40 wt%; calcd, 6.31 wt%; 2: found, 6.25 wt%; calcd, 6.24 wt%; 3: found, 6.74 wt%; calcd, 5.77 wt%). The second weight loss of 46.40 wt% for 1 (in the case of 2: of 33.75 wt%; in the case of 3: of 40.66 wt%), observed in the temperature range from 250 to 800 °C, is accompanied by an exothermic peak centered at 605.5 °C (for 2: at 611.0 °C; for 3: at 629.5 °C). Accordingly, this stage is assigned to the gradual oxidative decomposition of the organic ligand followed by the carbon dioxide and nitrogen dioxide evolvement, as it was suggested by the MS peaks at m/z values of 44 and 46, respectively.

Magnetic properties of compound 1

The magnetic susceptibility of 1 (Fig. 4) shows the Curie–Weiss behavior above the temperature ca. 200 K with a Weiss constant Θ = −9.3 K and a magnetic moment of 5.06μ_B. The moment is larger than the value of 3.87μ_B expected for the spin-only value of an ion with S = 3/2 and g = 2.0, but is close to the value expected for independent spin and orbital moments {L = 3, S = 3/2; μ_LS = [L(L + 1) + 4S(S + 1)]^1/2 = 5.20μ_B}, so a considerable orbital contribution to the magnetic moment may be anticipated. Spin–orbit coupling may also account for the large value of Θ, regardless of a weak or absent exchange coupling.²⁹ The effective magnetic moment slowly decreases from 5.02μ_B at 300 K to 4.80μ_B at 120 K, and then more quickly to 3.80μ_B at 1.7 K, suggesting weak antiferromagnetic exchange interactions between metal ions. It is difficult to find an obvious exchange path in the case of 1. The bridges created by the (pyridin-1-ium-3,5-diyl)diphosphonate ligand along the (101) plane are very long [Co–OPO–CCC–OPO–Co, d(Co⋯Co) = 8.893 Å]. The shortest metal–-metal distances (8.246 Å) are observed in the (1̄01) plane but the possible exchange path is through the long Co–O1W–H1W⋯O52–P5–O51–Co pathway with the medium-weak hydrogen bond [d(D⋯A) = 2.893 Å]. These structural features allow us to consider the magnetic behavior of 1 as due to the simple mononuclear entity.

Fig. 4 Temperature dependence of magnetic susceptibility, χ, (◊) and effective magnetic moment, μ_eff, (Δ) of 1. The solid lines correspond to the best fit parameters. The inset shows the low temperature region of μ_eff (T), the broken line is fitted without taking into account exchange interactions.

An analysis of magnetic behaviour of six-coordinated Co^II high-spin complexes is a challenging task. In the octahedral ligand-field the magnetic moment of the ground ⁴T_1g term experiences a large contribution of orbital angular momentum, making impossible to apply a convenient spin Hamiltonian formalism. An axial deformation of the octahedral ligand environment splits the ⁴T_1g term into ⁴A_1g and ⁴E_g terms, and only when the orbital singlet is the lowest and the ⁴E_g orbital doublet is thermally inaccessible, the spin Hamiltonian may be employed.³⁰

The Hamiltonian involving the spin–orbit coupling of the ⁴T_1g ground term of the high-spin octahedral Co^II ions, an axial deformation of the octahedron, and the Zeeman effect, can be written as:³¹

Ĥ = −αλL̂Ŝ + Δ[L̂_z² − (1/3)L(L + 1)] + β(−αL̂ + g_eŜ)B. (1)

The first term accounts for the spin–orbit coupling, where λ is the spin–orbit coupling parameter and α is an orbital reduction factor defined as α = Ak. The value of the A parameter varies between 1 and 3/2 within the confines of the strong and weak field cases, the k parameter considers the covalency of the metal–ligand bonds (0 ≤ k ≤ 1). In order to simplify the calculations drawn upon eqn (1) the isomorphism between T₁ orbital triplet and P term (L = 1, M_L = 0, ±1) has been taken into account. Matrix elements of L̂ within T₁ and P satisfy the relationship ‖T‖ = −α||P||. The second element of eqn (1) corresponds to an axial distortion of the ⁴T_1g term, Δ being the energy difference between ⁴A_1g and ⁴E_g terms (Δ > 0 with the singlet lying below the doublet). The last element describes the Zeeman effect, g_e = 2.0023. The true symmetry of the metal environment in 1 is lower than axial. In this case the Hamiltonian (eqn (1)) should be completed with the term represented a rhombic distortion E(L̂_x² − L̂_y²); furthermore the α and λ could be considered as anisotropic parameters. In order to avoid overparametrization these elements are usually treated as isotropic in the case of an analysis of powder samples.

As an analytical expression to describe the magnetic susceptibility through the Hamiltonian of eqn (1) cannot be derived, the effective spin model published by Lloret³¹ has been applied. In line with this approach each of the Co^II ions possesses the effective spin S_eff = 1/2, related to the real spin (S = 3/2) by S = (5/3)S_eff, with a Lande factor of the ground doublet g₀. In order to take into account the population of the excited levels, the temperature-dependent G(T) functional has been introduced in place of g₀. It was determined empirically as a function of T, λ, Δ and α. Good results are achieved when magnetic interactions are weak in comparison to the spin–orbit coupling |J/λ| < 0.1. The magnetic susceptibility calculated with the Hamiltonian (eqn (1)) below 10 K slightly differs from the experiment (see the inset in Fig. 4), and the temperature variation of the effective magnetic moment suggests that weak intermolecular antiferromagnetic interactions are the principal cause of this discrepancy. A better fit is obtained by considering a weak antiferromagnetic coupling through a molecular field approximation, χ = χ_zfs/(1 − zJ′χ_zfs/Ng²β²). A very good agreement between the simulated and experimental data (Fig. 4) was achieved with α = 1.38, Δ = −478 cm⁻¹, λ = −103 cm⁻¹, and zJ′ = −0.11 cm⁻¹, R = Σ[(χT)_exp − (χT)_calc]²/Σ[(χT)_exp]² = 1.7 × 10⁻⁵ (76 points). It is worth noting that the susceptibility could be fit with a positive Δ value, but the α parameter always was larger than 3/2. A negative value of the axial deformation Δ implies the orbital doublet ⁴E_g as the ground term.

Antiferromagnetic interactions in 1 are very week, therefore the levels energies are a result of superimposed ligand field and spin–orbit effects, splitting the ⁴T_1g ground term into six Kramers doublets. Substitution the μ_eff (T) best fit parameters α, Δ and λ into the Hamiltonian (eqn (1)) with B = 0 gives the overall splitting equal to 847 cm⁻¹, while the first excited level is located 147 cm⁻¹ above the ground. It is evident that below 30 K the filling of the excited levels may be completely ignored. It means that the field dependent magnetization can be calculated with the aid of the Brillouin's function. Putting the effective S_eff = 1/2 for the ground level we obtain (with α = 1.37) the Lande factor g = (10 + 2α)/3 = 4.25.³¹ The magnetization measured at 1.72 K and calculated for various external fields is drawn in Fig. 5 as a solid line and fits the experimental data pretty well.

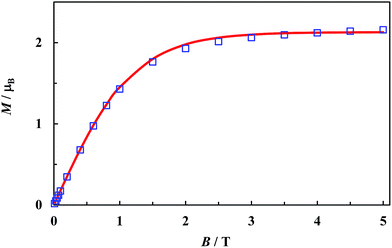Fig. 5 Magnetization as a function of magnetic induction of 1. The solid line – Brillouin's function calculated with S_eff = 1/2, g = 4.25.

The Co^II environment in 1 can be considered as the tetragonally elongated octahedron [d_axial (Co⋯O) = 2.172 Å and the average d_equatorial (Co⋯O) = 2.088 Å]. In this situation the crystal-field theory predicts the ⁴E_g orbital doublet as the ground state,³² which fully agrees with the results of the analysis of magnetic data. Tetragonally elongated Co^II complexes are less common than the compressed, but it certainly can be concluded, that the α, Δ and λ parameters are within the ranges of those reported for high-spin complexes.^33–36 The measured effective moment at 1.71 K (3.80μ_B) is close to the calculated moment 3.68μ_B of the lowest Kramers doublet (S_eff = 1/2, g = 4.25), which further validates the model with the virtually isolated metal ions.

Conclusions

The first examples of two-dimensional coordination polymers based on pyridine-3,5-diyldiphosphonic acid have been synthesized under mild conditions and precisely characterized. Compounds 1–3 are isomorphous with the same layer topology, in which the metal ions are extended along the (101) plane. Neighbouring layers are assembled into three-dimensional network via multiple hydrogen-bonding and π–π interactions. The interlayer interaction energies of compounds 1–3 are similar and relatively strong mainly due to the well-developed hydrogen-bonds. It seems though that the molecular slabs in compound 3 are slightly better stabilized in the crystal lattice than those in compounds 1 and 2. This judgment is consistent with the results of thermal analyses, which also indicate that the compound 3 is thermodynamically slightly more stable than its analogues (1 and 2). Additionally, the derived Mulliken atom charges for the examined metal centres show that the cadmium atom is most positively charged, what is in agreement with the relative polarizabilities of cobalt, zinc and cadmium. The investigation of magnetic properties of 1 reveals paramagnetic behaviour with very weak antiferromagnetic interactions between high-spin cobalt ions.

Acknowledgements

This work was financed by the National Science Centre (grant no. 2011/01/N/ST5/05639). MW and VVA also gratefully acknowledge the instrumental grant no. 6221/IA/119/2012 from Polish Ministry of Science and Higher Education, which supported the Integrated Departmental Laboratory for Engineering and Research of Advanced Materials, where the measurements of the IR spectra were performed. Calculations have been carried out using resources provided by Wrocław Centre for Networking and Supercomputing (http://wcss.pl, grant no. 285).

Notes and references

1. S. R. Batten, N. R. Champness, X.-M. Chen, J. Garcia-Martinez, S. Kitagawa, L. Öhrström, M. O'Keeffe, M. P. Suh and J. Reedijk, Pure Appl. Chem., 2013, 85, 1715.
2. P. DeBurgomaster, W. Ouellette, H. Liu, C. J. O'Connor and J. Zubieta, CrystEngComm, 2010, 12, 446.
3. P. O. Adelani and T. E. Albrecht-Schmitt, Cryst. Growth Des., 2011, 11, 4227.
4. R. Vaidhyanathan, J. Liang, S. S. Iremonger and G. K. H. Shimizu, Supramol. Chem., 2011, 23, 278.
5. D.-K. Cao, S. Gao and L.-M. Zheng, J. Solid State Chem., 2004, 177, 2311.
6. P. O. Adelani, A. G. Pliver and T. E. Albrecht-Schmitt, Cryst. Growth Des., 2011, 11, 1966.
7. P. O. Adelani and T. E. Albrecht-Schmitt, Angew. Chem., Int. Ed., 2010, 49, 8909.
8. M. Wilk, J. Janczak and V. Videnova-Adrabinska, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2012, 68, m41.
9. F. Lakadamyali, A. Reynal, M. Kato, J. R. Durrant and E. Reisner, Chem.–Eur. J., 2012, 18, 15464.
10. J. Zoń, V. Videnova-Adrabinska, J. Janczak, M. Wilk, A. Samoć, R. Gancarz and M. Samoć, CrystEngComm, 2011, 13, 3474.
11. CrysAlis CCD and CrysAlis RED, v. 1.171.33.42, Oxford Diffraction Poland, Wrocław, Poland, 2009.
12. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112.
13. K. Brandenburg and H. Putz, Diamond v. 3.1, Crystal Impact GbR, Bonn, Germany, 2008.
14. F. H. Allen and I. J. Bruno, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 380.
15. R. Dovesi, V. R. Saunders, R. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco and M. Llunell, CRYSTAL09 User's Manual, University of Torino, Torino, Italy, 2009.
16. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
17. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
18. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
19. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
20. Y. Dou, R. G. Egdell, D. S. L. Law, N. M. Harrison and B. G. Searle, J. Phys.: Condens. Matter, 1998, 10, 8447.
21. J. E. Jaffe and A. C. Hess, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 7903.
22. S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211.
23. B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, CrystEngComm, 2008, 10, 405.
24. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
25. K. N. Jarzembska, M. Kubsik, R. Kamiński, K. Woźniak and P. M. Dominiak, Cryst. Growth Des., 2012, 12, 2508.
26. M. Wilk, K. N. Jarzembska, J. Janczak, J. Hoffmann and V. Videnova-Adrabinska, J. Mol. Struct., 2014, 1074, 240.
27. V. Videnova-Adrabinska, Coord. Chem. Rev., 2007, 251, 1987.
28. V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576.
29. M. Kurmoo, Chem. Soc. Rev., 2009, 38, 1353.
30. R. Boča, Struct. Bonding, 2006, 117, 1.
31. F. Lloret, M. Julve, J. Cano, R. Ruiz-García and E. Pardo, Inorg. Chim. Acta, 2008, 361, 3432.
32. J. Titiš and R. Boča, Inorg. Chem., 2011, 50, 11838.
33. G. De Munno, M. Julve, F. Lloret, J. Faus and A. Caneschi, J. Chem. Soc., Dalton Trans., 1994, 1175.
34. O. Fabelo, J. Pasán, F. Lloret, M. Julve and C. Ruiz-Pérez, CrystEngComm, 2007, 9, 815.
35. O. Fabelo, L. Cańadillas-Delgado, J. Pasán, F. S. Delgado, F. Lloret, J. Cano, M. Julve and C. Ruiz-Pérez, Inorg. Chem., 2009, 48, 11342.
36. J. Carranza, J. Sletten, F. Lloret and M. Julve, Inorg. Chim. Acta, 2011, 371, 13.

---

Footnote

† Electronic supplementary information (ESI) available: Powder X-ray diffraction patterns, optimized atomic coordinates, FT-IR and Raman spectra, TG-DTA curves. CCDC 1018369–1018371. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4ra10257f

---