Dispersive liquid–liquid microextraction for preconcentration and determination of phenytoin in real samples using response surface methodology-high performance liquid chromatography
Eslam Pourbasheer*a,
Samira Sadafia,
Mohammad Reza Ganjalibc and
Maryam Abbasghorbanid
aDepartment of Chemistry, Payame Noor University (PNU), P. O. Box 19395-3697, Tehran, Iran. E-mail: pourbasheer@ut.ac.ir; Tel: +98 45 33515003
bCenter of Excellence in Electrochemistry, Faculty of Chemistry, University of Tehran, P. O. Box 14155-6455, Tehran, Iran
cBiosensor Research Center, Endocrinology and Metabolism Molecular-Cellular Sciences Institute, Tehran University of Medical Sciences, Tehran, Iran
dGas Division, Research Institute of Petroleum Industry, P. O. Box 14665-137, Tehran, Iran
First published on 12th November 2014
Abstract
In the present study, dispersive liquid–liquid microextraction (DLLME) was developed for preconcentration and determination of phenytoin in real samples by high performance liquid chromatography (HPLC). Several experimental variables were investigated such as the extraction solvent, disperser solvent, salt effect, extraction time, centrifuge time, centrifuge speed and sample volume. Firstly, an orthogonal array design (OAD) was applied to choose the significant variables. Then, the significant factors were optimized using the central composite design (CCD). The variables were optimized with the aid of the response surface methodology. Chloroform and ethanol were selected as extraction and dispersive solvents, respectively. In this method, a linear range of 0.01–24 μg mL−1 and the relative standard deviation from 1.7 to 12.35% were obtained for water samples. Also, for urine samples, the linear range of 0.2–24 μg mL−1 and the relative standard deviation from 1.41 to 9.3% were obtained. The limit of detection (LOD) and limit of quantitative (LOQ) were 0.94 and 2.84 and also, 1.63 and 4.94 μg mL−1 for water and urine samples respectively.
1. Introduction
Phenytoin (PHT) is a phenylated hydantoin derivative used as an anti-epileptic to treat seizure disorders.1 Blitz synthesized PHT in 1908.2 PHT has a structure similar to phenobarbital. PHT became accessible in 1938 after the discovery of its antiseizure efficacy by Merritt and Putnam.3 This drug is bound significantly to plasma proteins (about 90%) and metabolized in the liver.Many analytical methods have been reported for the analysis of PHT and its metabolites4,5 and PHT in combination with other antiepileptic drugs in plasma. Frequently published methods were included; high performance liquid chromatography,6–8 thin layer chromatography,9 gas chromatography,10 fluorescence polarization immunoassay,11 and spectrophotometry.12 The extraction of PHT has been described by many publications which include solid-phase extraction (SPE)5,7,8 and liquid–liquid extraction (LLE)13 which LLE is one of the oldest methods of preconcentration and matrix isolation. The disadvantage of LLE is time-consuming, and it requires large amounts of organic solvent. The SPE uses much less solvent than LLE but this method is relatively expensive. Supercritical fluid extraction (SFE) also is expensive.14 Solid-phase microextraction (SPME) is a solvent free process developed by Arthur and Pawliszyn,15 that includes simultaneous extraction and preconcentration of analytes from aqueous samples. The disadvantages are: (a) SPME is expensive (b) its fiber is fragile (c) has limited lifetime.16 Liquid-phase microextraction (LPME) is method developed by He and Lee in 1997.17,18 LPME was developed as a solvent-minimized sample pretreatment procedure and the benefits of this approach are inexpensive, little solvent is used.19 The disadvantage are included: fast stirring would tend to format air bubble,14 extraction is time-consuming, and equilibrium could not be attained after a long time in most cases.20
Dispersive liquid–liquid microextraction (DLLME) is an analytical technique among extraction, the method newly discovered by Assadi and co-workers.13 In DLLME extracting solvent mixture and dispersive solvent quickly is injected by syringe to the water sample solution. Therefore it can be seen that the extraction solvent is distributed to form tiny droplets within the aqueous sample solution. After extraction, phase separation is performed by centrifuges. In the final stage the enriched analyte in the sedimented phase is removed from the centrifuge and injected into the instrument.
The benefits of DLLME are its easily of operation, high enrichment factor, high extraction recovery. In this method minimal volume of extraction solvents is used. Large surface area of the droplets of solvent extracted and aqueous samples will lead to a rapid equilibrium.21
In the present study, the dispersive liquid–liquid microextraction was used for preconcentration and determination of phenytoin in real samples using response surface method and high performance liquid chromatography.
2. Experimental
2.1 Chemicals and reagents
Phenytoin was obtained from Merck. Carbon tetrachloride, chloroform, 1,2-dichlorobenzene, 1,2-dichloroethane, as extraction solvent and acetone, acetonitrile, methanol and ethanol as dispersive solvents were obtained from Merck. The stock solutions of phenytoin were prepared by dissolving in methanol. Working solutions were prepared by dilution of standard stock solution with methanol. High-purity deionized water was applied for all the experiments.2.2 Instrumentation
Chromatographic measurements were performed using a HPLC system equipped with series UV detector model 2550 set at 254 nm, and model 3207 manual injector with a 20 μL sample loop. A centrifuge Hettich made in Germany with power of 6000 (rpm) was used for centrifuging. The pH meter of Metrohm 744 model, made in Switzerland was applied to adjust the mobile phase. A 100.0 μL microsyringe (Hamilton) was used for injection.2.3 Chromatographic conditions
Analytes were separated on NUCLEOSIL 100-5, C18 column (125 mm × 4.6 mm internal diameter) under isocratic condition with a mobile phase consist of 30% acetonitrile and 70% acetate buffer solution (0.02 M, pH 4.6). The flow rate of mobile phase was 1.0 mL min−1 and the UV detection wavelength was set at 254 nm. The analytical column and precolumn were kept at 25 ± 2 °C.2.4 Dispersive liquid–liquid microextraction procedure
The 5.66 mL of working standard solution was placed in a 10 mL of glass centrifuge tube with conical bottom. According to the optimized conditions, a mixture of 157 μL chloroform (extraction solvent) and 1.37 mL of ethanol (disperser solvent) was quickly injected into the sample solution using a 100 μL syringe. A cloudy solution (water, ethanol and chloroform) was formed in a test tube (the cloudy state was stable for a long time). Then the mixture was centrifuged for 3 min at 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm. Accordingly, the dispersed fine particles of extraction phase were sedimented in the bottom of conical test tube. The sedimented phase was withdrawn by a 100 μL microsyringe (Hamilton) and was transferred to conical bottom tube, and then the solvent evaporated and was dissolved in methanol (the methanol volume was equal to the evaporated solvent volume). Finally, it was injected into the HPLC instrument for analysis.
000 rpm. Accordingly, the dispersed fine particles of extraction phase were sedimented in the bottom of conical test tube. The sedimented phase was withdrawn by a 100 μL microsyringe (Hamilton) and was transferred to conical bottom tube, and then the solvent evaporated and was dissolved in methanol (the methanol volume was equal to the evaporated solvent volume). Finally, it was injected into the HPLC instrument for analysis.
In this work, the urine samples were collected from healthy volunteer in our lab, who was not receiving any pharmaceutical treatment at the time of sampling and the samples were centrifuged for 3 min at 2000 rpm. Then, supernatants were decanted into a clean glass tube and filtered through a 0.2 μm filter. The 0.5 mL of filtration products was diluted to 10 mL. Also, the water sample was provided from our laboratory and filtered through a 0.2 μm filter and applied for extraction as same as the urine sample.
2.5 Calculation of enrichment factor and recovery
The enrichment factor (EF) was defined as the ratio between the analyte concentration in the sedimented phase (Csed) and the initial concentration of analyte (C0) within the sample:
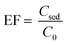 | (1) |
The Csed was estimated from calibration graph of direct injection of PHT standard solution in the chloroform at the range of 1–55 μg mL−1.
Also, for evaluation of the extraction, the extraction recovery ER (%) was calculated as the following:
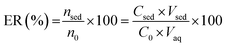 | (2) |
3. Results and discussion
3.1 Selection of extraction solvent
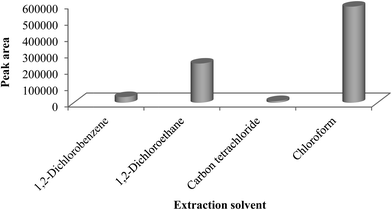
The selection of the solvent is important for the DLLME process. In DLLME, the extractor solvent should has the following properties: (a) it should have more density than the water, (b) immiscibility with aqueous phase, (c) suitable chromatography behavior.22 In this experiment, some solvents such as 1,2-dichlorobenzene, carbon tetrachloride, 1,2-dichloroethane and chloroform were studied as extraction solvent and acetone, acetonitrile, methanol and ethanol were considered as disperser solvents. The effect of these solvents on the extraction efficiency of DLLME was investigated using 1 mL of dispersive solvents and 100 μL of extraction solvents. Evaluation of carbon tetrachloride with ethanol showed a cloudy solution was formed, but the formed, organic phase after centrifugation was not clear. 1,2-dichlorobenzene with ethanol were examined that the result showed cloudy solution was not formed. 1,2-dichloroethane with ethanol was evaluated and cloudy solution was formed, however the organic phase was very little. Finally, the investigations of chloroform with ethanol showed that the very good cloudy solution was formed using the chloroform as extraction solvent. The results showed that the extraction response (peak area) of chloroform was excellent, and then was selected as extraction solvent for subsequent experiments. The results are shown in Fig. 1.3.2 Selection of disperser solvent
Miscibility of dispersive solvent in both aqueous phase (sample solution) and organic phase (extracting solvent) is a significant factor to select a dispersive solvent.23 Thereby, acetone, acetonitrile, methanol and ethanol are selected for this purpose and effect of these solvents on the proficiency of DLLME was evaluated using 1 mL of each above mentioned disperser solvents and 100 μL of extraction solvents. Results showed that the highest yield was obtained by ethanol. Finally, ethanol was chosen as the disperser solvent.3.3 Optimization of DLLME
| Factor | Symbol | Low level | High level |
|---|---|---|---|
| Extraction solvent | A | 100 | 200 |
| Dispersive solvent | B | 0.5 | 1.5 |
| Extraction time | C | 1 | 10 |
| Centrifuge time | D | 3 | 10 |
| Centrifuge speed | E | 2000 | 4000 |
| Salt effect | F | 0.5 | 2 |
| Sample volume | G | 3 | 6 |
| Run | Block | A | B | C | D | E | F | G | Peak area |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Block 1 | 200 | 0.5 | 10 | 3 | 4000 | 0.5 | 6 | 707![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 610 |
| 2 | Block 1 | 100 | 0.5 | 1 | 3 | 2000 | 0.5 | 3 | 713![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 026 026 |
| 3 | Block 1 | 100 | 0.5 | 1 | 10 | 4000 | 2 | 6 | 995![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 742 742 |
| 4 | Block 1 | 100 | 1.5 | 10 | 10 | 4000 | 0.5 | 3 | 686![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 692 692 |
| 5 | Block 1 | 200 | 1.5 | 1 | 3 | 4000 | 2 | 3 | 337![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 543 543 |
| 6 | Block 1 | 200 | 1.5 | 1 | 10 | 2000 | 0.5 | 6 | 1.02 × 106 |
| 7 | Block 1 | 200 | 0.5 | 10 | 10 | 2000 | 2 | 3 | 519![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863 863 |
| 8 | Block 1 | 100 | 1.5 | 10 | 3 | 2000 | 2 | 6 | 1.39 × 106 |
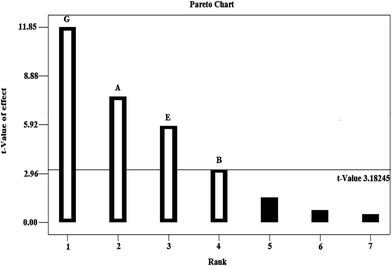
In this study, analysis of variance (ANOVA) was used to identify significant factors. According to the ANOVA table, the model F-value of 60.75 implies that the model is significant. The “Prob > F” values less than 0.050 indicates model terms are significant and values greater than 0.1 indicate the model terms are not significant. In this case A, B, E, G were significant model terms. Also, the results were shown in Pareto chart (Fig. 2). Pareto chart shows that the disperser solvent volume (chloroform), extraction solvent volume (ethanol), sample volume and centrifuge speed are the most actuarial significant effects on the dependent variables at the p < 0.05 level. As can be seen in Fig. 2, the salt effect (F), extraction time (C) and centrifuge time (D) were not significant.
A central composite design combines a two-level factorial design with plus points (star points) and at least wiseone point at the center of the experimental zone to achieve the properties such as: rotatability or orthogonality, in order to fit quadratic polynomials. In addition to describing the linear effects of factors on the response, CCD explains the interaction and quadratic effects of the variables.
In this work to reduce the number of experiments from central composite design, small central composite design was used. Small composite design is minimal point designs and they are very sensitive to outliers. With this method, alpha value 1.68 was obtained. Replicates of factorial points, center points in each factorial block replicates of axial (star) points and center points in each axial block was equal to 1, 4, 1, 3 respectively. In this study, four variables were investigated such as solvent extraction (A), solvent dispersive (B), centrifuged speed (C) and sample volume (D). Thus, 23 experiments were designed by CCD. The experiments were randomized and were divided into two blocks. The factor levels are shown in Table 3.
| Factor | Symbol | Level | ||||
|---|---|---|---|---|---|---|
| −α | −1 | 0 | +1 | +α | ||
| Extraction solvent | A | 66 | 100 | 150 | 200 | 234 |
| Dispersive solvent | B | 0.2 | 0.5 | 1 | 1.5 | 1.8 |
| Centrifuged speed | C | 1318 | 2000 | 3000 | 4000 | 4682 |
| Sample volume | D | 2 | 3 | 4.5 | 6 | 7 |
The ANOVA data to evaluate the significance of the model equation and for response surface quadratic model are shown in Table 4. The model F-value of 4.94 implies the model is significant. Values of “Prob > F” less than 0.050 indicate model terms are significant. In this case D, BD, A2 are significant model terms. Values greater than 0.100 indicate the model terms are not significant. The second-order equation can quantitatively describe the relationship between the responses and independent variables. This model is shown in eqn (3) which includes: four main effects and six two-factor interaction effects and four curvature effects.
Peak area = +1.124 × 106 + 1.196 × 105(A) + 1.178 × 105(B) + 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 475.17(C) + 2.517 × 105(D) + 1.495 × 105(AB) − 75 475.17(C) + 2.517 × 105(D) + 1.495 × 105(AB) − 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 952.5(AC) + 1.517 × 105(AD) + 98 952.5(AC) + 1.517 × 105(AD) + 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 890.75(BC) + 2.942 × 105(BD) + 1.138 × 105(CD) − 1.848 × 105(A2) − 47 890.75(BC) + 2.942 × 105(BD) + 1.138 × 105(CD) − 1.848 × 105(A2) − 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 454.90(B2) + 19 454.90(B2) + 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 994.96(C2) − 38 994.96(C2) − 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 261.80(D2) 261.80(D2)
| (3) |
| Sourcea | Sum of squaresb | d.f.c | Mean squared | F-valuee | p-value Prob > Ff | Significance |
|---|---|---|---|---|---|---|
| a Source of variation.b Sum of the squared differences between the average values and the overall mean.c Degrees of freedom.d Sum of squares divided by d.f.e Test for comparing term variance with residual (error) variance.f Probability of seeing the observed F-value if the null hypothesis is true.g Consists of terms used to estimate experimental error.h Variation of the data around the fitted model.i Variation in the response in replicated design points.j Totals of all information corrected for the mean. | ||||||
| Model | 1.69 × 1012 | 14 | 1.21 × 1011 | 4.94 | 0.0205 | Significant |
| A | 8.10 × 1010 | 1 | 8.10 × 1010 | 3.31 | 0.1116 | |
| B | 7.85 × 1010 | 1 | 7.85 × 1010 | 3.21 | 0.1163 | |
| C | 1.19 × 1010 | 1 | 1.19 × 1010 | 0.49 | 0.5085 | |
| D | 3.58 × 1011 | 1 | 3.58 × 1011 | 14.66 | 0.0065 | |
| AB | 7.41 × 1010 | 1 | 7.41 × 1010 | 3.03 | 0.1253 | |
| AC | 4.62 × 1010 | 1 | 4.62 × 1010 | 1.89 | 0.2118 | |
| AD | 7.63 × 1010 | 1 | 7.63 × 1010 | 3.12 | 0.1206 | |
| BC | 7.82 × 1010 | 1 | 7.82 × 1010 | 3.2 | 0.1168 | |
| BD | 2.87 × 1011 | 1 | 2.87 × 1011 | 11.73 | 0.0111 | |
| CD | 1.04 × 1011 | 1 | 1.04 × 1011 | 4.24 | 0.0785 | |
| A2 | 5.38 × 1011 | 1 | 5.38 × 1011 | 21.99 | 0.0022 | |
| B2 | 3.55 × 1010 | 1 | 3.55 × 1010 | 1.45 | 0.2676 | |
| C2 | 6.30 × 109 | 1 | 6.30 × 109 | 0.26 | 0.6274 | |
| D2 | 2.31 × 1010 | 1 | 2.31 × 1010 | 0.94 | 0.3639 | |
| Residualg | 1.71 × 1011 | 7 | 2.45 × 1010 | |||
| Lack of fith | 7.98 × 1010 | 2 | 3.99 × 1010 | 2.18 | 0.2082 | Not significant |
| Pure errori | 9.14 × 1010 | 5 | 1.83 × 1010 | |||
| CorTotalj | 1.86 × 1012 | 22 | ||||
The “lack of fit F-value” of 2.18 implies the lack of fit is not significant relative to the pure error. The quality of fit of the polynomial model equation was evaluated by the coefficient of determination (R2, adjusted-R2 and “adequate precision”). R2 is a measure by the model and equal to 0.908. The adjusted-R2 is regulated for the number of terms in the model. It decreases as the number of terms in the model increases, if those additional terms do not add value to the model and its value was equal to 0.724.“Adeq Precision” measures the signal to noise ratio. A ratio greater than 4 is desirable. The ratio of 8.367 indicates an adequate signal. This model can be used to navigate the design space.
Graphs obtained from the model are shown in Fig. 3. In Fig. 3a it is clear that, when the volume of extraction solvent (chloroform) increased from 100 to 200 μL, the peak area increased. In the other hand, by increasing the volume of extraction solvent, the volume of sedimented phase increases and the recovery of extraction increases which cause to have high peak area value.
 | ||
| Fig. 3 Effect of each factor on the extraction efficiency: (a) extraction solvent, (b) dispersive solvent, (c) sample volume from central composite design. | ||
In Fig. 3b, by increasing the volume of disperser (ethanol) from 0.5 to 1.5 mL, dispersion of extraction solvent (chloroform) occurred properly and cloudy solution is formed completely, therefore the peak area is increased.
As can be seen in Fig. 3c, the sample volume is increased from 3 to 6 mL, and with increasing the sample volume at a fixed concentration of the phenytoin, the peak area increased. In fact, by increasing the sample volume at constant concentration of the drug, the amount of drug will increase and in high sample volume, the better cloudy solution will form. Therefore peak area will increase.
Fig. 4 shows the interaction diagrams. An interaction occurs when the response is different, depending on the settings of two factors. The plots make it easy to exegesis two factor interactions. If appear two non-parallel lines in the diagram, show that the effect of one factor depends on the level of the other. Fig. 4a shows that there is not significant interaction between the volume of extractor and sample volume. Fig. 4b and c shows the interaction of extractor–disperser and disperser–sample volume.
 | ||
| Fig. 5 Three-dimensional response surface for: (a) extractor–sample volume, (b) extractor–disperser, (c) disperser–sample volume. | ||
According to the overall results of optimization study, the following experimental conditions are chosen: volume of chloroform: 157 μL; volume of ethanol: 1.37 mL; sample volume: 5.66 mL; centrifugation speed: 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm; extraction time: 3 min. The observed experimental enrichment factor under the above conditions was 16.93.
000 rpm; extraction time: 3 min. The observed experimental enrichment factor under the above conditions was 16.93.
| Samples | Concentration (μg mL−1) | Recoverya (%) | LODb (μg mL−1) | LOQc (μg mL−1) | rd | RSDe |
|---|---|---|---|---|---|---|
| a Mean recovery for three determination.b Limit of detection.c Limit of quantitative.d Correlation coefficients.e Relative standard deviation (n = 3); calculated as [(standard deviation of analytical response/mean of analytical response) × 100]. | ||||||
| Water sample | 0.4 | 90.55 | 0.94 | 2.84 | 0.9991 | 12.35% |
| 3 | 99.00 | 5.48% | ||||
| 21 | 98.33 | 1.7% | ||||
| Urine sample | 0.4 | 73.87 | 1.63 | 4.94 | 0.9990 | 9.3% |
| 3 | 120.66 | 2.43% | ||||
| 21 | 101.45 | 1.41% | ||||
4. Conclusion
In the present study, the dispersive liquid–liquid microextraction was applied for preconcentration and determination of phenytoin in real samples using response surface method-high performance liquid chromatography. Firstly, an orthogonal array design was applied to choose the significant variables. Then, the significant factors were optimized by using a central composite design. The variables were optimized with the aid of the response surface methodology. Experiments showed that ethanol and chloroform are the most suitable as disperser and extractor solvents respectively. Using experimental design reduced the number of tests, resulting in saving time and experimental costs. The proposed method was used for determination of phenytoin in urine and water samples and good statistical results were obtained.References
- B. Gurley, M. Marx and K. Olsen, J. Chromatogr. B: Biomed. Sci. Appl., 1995, 670, 358 CrossRef CAS.
- M. Bialer, Adv. Drug Delivery Rev., 2012, 64, 887 CrossRef CAS PubMed.
- H. H. Merritt and T. J. Putnam, Epilepsia, 1945, 3, 51 CrossRef PubMed.
- A. Bereczki, A. Tolokán, G. Horvai, V. Horváth, F. Lanza, A. J. Hall and B. Sellergren, J. Chromatogr. A, 2001, 930, 31 CrossRef CAS.
- F. Guan, C. E. Uboh, L. R. Soma, E. K. Birks, D. Teleis, J. A. Rudy, A. O. Watson and D. S. Tsang, J. Chromatogr. B: Biomed. Sci. Appl., 2000, 746, 209 CrossRef CAS.
- L. Budakova, H. Brozmanova, M. Grundmann and J. Fischer, J. Sep. Sci., 2008, 31, 1 CrossRef CAS PubMed.
- F. Bugamelli, C. Sabbioni, R. Mandrioli, E. Kenndler, F. Albani and M. A. Raggi, Anal. Chim. Acta, 2002, 472, 1 CrossRef CAS.
- T. A. C. Vermeij and P. M. Edelbroek, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2007, 857, 40 CrossRef CAS PubMed.
- G. Rao and D. Mclennon, J. Chromatogr. A, 1977, 137, 231 CrossRef CAS.
- C. Basheer, H. K. Lee and J. PObbard, J. Chromatogr. A, 2002, 968, 191 CrossRef CAS.
- M. Lu-Steffes, G. Pittluck, M. Jolley, H. Panas, D. Olive, C. Wang, D. Nystrom, C. Keegan, T. Davis and S. Stroupe, Clin. Chem., 1982, 28, 2278 CAS.
- Z. Rezaei, B. Hemmateenejad, S. Khabnadideh and M. Gorgin, Talanta, 2005, 65, 21 CAS.
- M. Rezaee, Y. Assadi, M. R. Milani Hosseini, E. Aghaee, F. Ahmadi and S. Berijani, J. Chromatogr. A, 2006, 1116, 1 CrossRef CAS PubMed.
- G. Shen and H. K. Lee, Anal. Chem., 2002, 74, 648 CrossRef CAS.
- C. L. Arthur and J. Pawliszyn, Anal. Chem., 1990, 62, 2145 CrossRef CAS.
- J. Wu, H. L. Lord, J. Pawliszyn and H. Kataoka, J. Microcolumn Sep., 2000, 12, 255 CrossRef CAS.
- Y. He and H. Lee, Anal. Chem., 1997, 69, 4634 CrossRef CAS.
- Y. Wang, Y. C. Kwok, Y. He and H. K. Lee, Anal. Chem., 1998, 70, 4610 CrossRef CAS.
- S. Pedersen-Bjergaard and K. E. Rasmussen, Anal. Chem., 1999, 71, 2650 CrossRef CAS.
- A. Sarafraz-Yazdi and A. Amiri, TrAC, Trends Anal. Chem., 2010, 29, 1 CrossRef CAS PubMed.
- A. N. Anthemidis and K. I. G. Ioannou, Talanta, 2009, 79, 86 CrossRef CAS PubMed.
- A. Daneshfar, T. Khezeli and H. Lotfi, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2009, 877, 456 CrossRef CAS PubMed.
- Y. Li, G. Wei, J. Hu, X. Liu, X. Zhao and X. Wang, Anal. Chim. Acta, 2008, 615, 96 CrossRef CAS PubMed.
- D. Nagaraju and S. D. Huang, J. Chromatogr. A, 2007, 1161, 89 CrossRef CAS PubMed.
- V. Gunaraj and N. Murugan, J. Mater. Process. Technol., 1999, 88, 266 CrossRef.
| This journal is © The Royal Society of Chemistry 2014 |