Nanoscale phase stability in Li ion battery anode materials

Abstract

A thermodynamic model was developed in particular for nanocrystalline partially ionic solids, which represent a group of Li ion battery anode materials. The lithium compounds were used as examples to demonstrate the model applications in studies of phase stability and phase transformation behavior in the nanoscale anode system. The peritectic and eutectic transformations were described systematically concerning the reaction temperatures and liquid concentrations at various equilibria, in which the grain size effects on the equilibrium, stability and transformation of Li-containing phases were quantified. To verify the model predictions, a series of experiments were performed using the nanocrystalline Li–Si system as sample materials. The experimental finding confirmed the model calculations, based on which the correlation of phase stability, temperature, grain size and critical grain size was proposed.

---

1 Introduction

As compared with conventional polycrystalline materials, distinctly different phase transformation behavior has been discovered in a variety of nanocrystalline materials such as Ni–Ti,¹ Fe–Mn,² Ti–Al,³ Sm–Co,⁴ Mo–Si,⁵ Cd–Se⁶ and Li–C.⁷ As the most representative microstructure characteristic, the interface (e.g. grain boundary and phase boundary) plays a significant role in the thermodynamic properties hence the phase stability of the nanocrystalline materials.⁸ Therefore, the conventional thermodynamic models in which the effect of interface on the fundamental functions is neglected can not accurately describe the thermodynamic properties of the nanocrystalline materials.

Early work was performed by Jiang et al.⁹ to quantify the size-dependence of solid–liquid interface energy and apply the model to describe the melting behavior of metallic nanoparticles.^10,11 Since the concept “nanothermodynamics” was proposed by Hill in 2001,¹² in the last decade some thermodynamic models have been developed for nanomaterials, focusing on the nanograin growth behavior of metals^13–15 or solid-state phase transformations in nanoscale alloy systems.^16–18 However, the “nanothermodynamic” models that describe solid–liquid or solid–gas phase transformations in nanocrystalline bulk materials, especially in nanocrystalline partially ionic solids, have been rarely reported in the literature so far. The partially ionic solids are a special group of crystalline compounds in which the ionic and covalent bonds coexist.¹⁹ They are common in the compounds formed for instance by metal and semiconductor elements²⁰ or by lithium and non-metallic elements.²¹ The phase stability of the partially ionic lithium compounds is closely related to the intercalation/deintercalation behavior of Li ion, and hence the electrochemical properties of Li ion battery anodes.

Because of the greatly increased volume fraction of the interface that provides fast transport path for the Li ions²² and the excess volume at interface that allows additional storage of Li ions and generates favorable accommodation strain in the process of charging and discharging,²³ particularly, the nanocrystalline structure provides a more homogeneous volume expansion for Li ion,²⁴ the nanocrystalline anode materials have attracted increasing attention in the development of candidates for high performance Li ion batteries.²⁵ Accordingly, the nanoscale phase stability and phase transformation characteristics of the partially ionic lithium compounds are especially important.

Based on the above background, in this paper our attention is concentrated on the development of a thermodynamic model in particular for the nanocrystalline partially ionic solids. The Li–Si compounds were used as examples to demonstrate the applications of the model in studies of phase stability and phase transformation behavior, as well as their grain size dependence, in the nanocrystalline partially ionic solids. Moreover, a series of experiments were performed to verify the model predictions. The structure of the paper is: Section 2 describes the development of the thermodynamic model, where the grain size effects on the thermodynamic properties of the nanocrystalline partially ionic solids are quantified; Section 3 demonstrates the applications of the model in calculations of the equilibrium, stability and transformation of phases, with the peritectic and eutectic reactions as examples; Section 4 shows the comparisons between the experimental results and model predictions using the nanocrystalline Li₂₂Si₅ solid as the starting material.

2 Thermodynamic model for nanocrystalline partially ionic solids

In the nanocrystalline bulk materials, with the decrease in grain size the volume fraction of grain boundaries increases. The nanograin boundary can be assumed as a “dilated crystal”^26,27 having an expanded unit cell in which the nearest-neighbor separation between atoms is larger than the equilibrium interatomic distance in the grain interior. As a result, the pressure in the nanograin boundary region is generated. Apply the isothermal equation of state for partially ionic solids²⁸ and take the temperature effect on the universal equation of state²⁹ into consideration, the pressure in the nanograin boundary region is expressed as:

P = −E₀(C′a*e^−a*/l′ + Z′/X²)/(3X²V₀) + α₀B₀(T − T_R) (1)

where X = r/r₀ = (V/V₀)^1/3, r is the nearest-neighbor atomic distance in the grain boundary region, r₀ is the interatomic distance at the equilibrium state, V and V₀ are the atomic volumes in the grain boundary region and in the crystal at the equilibrium state, respectively. T is the temperature, α₀ and B₀ are the zero-pressure bulk expansion coefficient and bulk modulus at the reference temperature T_R, respectively. E₀ is the cohesive energy of atoms at the equilibrium state, which includes both the ionic and covalent contributions.¹⁹ Z′ is the normalized Coulomb energy.³⁰ C′ is the normalized well depth formulated as:

C′ = (Z′ − 1)/E*(a^*₀) (2)

Here, E*(a*) is the universal energy function that describes the partially covalent character of the bond and also the repulsion between the atomic cores at a distance r, which has the expression as:³⁰

E*(a*) = −(1 + a*)exp(−a*) (3)

a* is the scaled length:

a* = (X − r^′₀/r₀)/l′ (4)

a^*₀ = l′Z′/(Z′ − 1 − Z′l′) (5)

r^′₀ is the value of r for which E*(a*) has a minimum:

r^′₀ = r₀(1 − a^*₀l′) (6)

The normalized scaling length l′ is:³⁰

l′ = [E₀/(d²E(r)/dr²)_r0]^1/2/r₀ (7)

From the above equations, the parameter l′ can be obtained, i.e. by second differentiating the pressure in the grain boundary region (eqn (1)) with respect to r at r₀:

2Γ(l′)² = (1 − Z′) + 2Z′l′ − 2Z′(l′)² (8)

then combining with differentiating the bulk modulus with respect to pressure at P = 0:

B^′₀ = 1 − Z′/Γ + [4(Γ + Z′)l′ − Z′]/[6Γ(l′)²] (9)

where Γ = 9B₀V₀/2E₀. Then parameters of Z′, r^′₀, a^*₀ and C′ are calculated by eqn (2), (5) and (6). Thus the pressure in the grain boundary region, as a function of the interatomic distance in the grain boundary region and temperature, is obtained.

The Grüneisen parameter of the “dilated crystal” at the grain boundary can be derived, as suggested by Wagner:²⁷

γ = −1 − 0.5V (∂²P/∂V² – 10P/9V²)/(∂P/∂V + 2P/3V) (10)

Thus, the thermodynamic properties in the grain boundary region, i.e. the enthalpy H_b, entropy S_b and Gibbs free energy G_b, can be calculated:²⁶

H_b = E + PV (11)

S_b = C_Vγ ln(V/V₀) (12)

G_b = H_b + C_V (T − T_R) − T[S_b + C_V ln(T − T_R)] (13)

The subscript b denotes the grain boundary. In eqn (11), E is the cohesive energy of atoms in the grain boundary region:³⁰

E = E₀ (C′ E* (a*) − Z′/X) (14)

C_V is the specific heat capacity at constant volume, and is calculated by introducing the Debye temperature Θ, as described in our previous work:¹⁴

where R is the gas constant.

The thermodynamic properties of the whole partially ionic solid bulk are attributed to the contributions of atoms in the grain boundary regions and in the grain interiors, respectively. The atomic fraction at grain boundaries, x_b, is thus introduced as a function of the grain size d:

x_b = 1/{V/V₀[4d³/(3h(2d − h)²) − 1] + 1} (16)

where h is the thickness of the grain boundary.

The fundamental thermodynamic functions of the whole partially ionic solid bulk are thus expressed as:

H(T,d) = x_bH_b + (1 − x_b)H_i (17)

S(T,d) = x_bS_b + (1 − x_b)S_i (18)

G(T,d) = x_bG_b + (1 − x_b)G_i (19)

The subscript i denotes the grain interior. The thermodynamic properties of crystals in the grain interiors are considered unaffected by the grain size and can be obtained from some database, e.g. SGTE.³¹

As described above, because the arrangement of grain boundary atoms and hence the interatomic distance and energy state are affected by the grain size, the thermodynamic properties in the grain boundary region are dependent on the grain size in addition to the temperature. For the conventional partially ionic solids with coarse grain sizes, e.g. larger than submicron scale, the effects of grain boundaries and grain size on the thermodynamic properties are generally ignored. In contrast, in the nanocrystalline partially ionic solids with an obviously increased volume fraction of grain boundaries with the decrease of grain size on the nanoscale, both the thermodynamic characteristics and grain boundary atomic fraction are affected by the grain size. As indicated by eqn (16), when the grain size is decreased to below a critical value, there will be a sharp increase in the atomic fraction of grain boundaries. As a result, the phase destabilization or phase transformation may occur at a critical grain size in the nanocrystalline partially ionic solids.

3 Model applications in equilibrium and transformation of phases

The thermodynamics of the nanocrystalline partially ionic solid at a given composition is quantified by the model described in Section 2. Based on the principle of Gibbs free energy minimization, the phase equilibria of solid–solid, solid–liquid and solid–gas states can be calculated using the model with the nanoscale effect introduced. Theoretically, the phase transformation behavior of solid ↔ solid, solid ↔ liquid and solid ↔ gas can be predicted quantitatively, where the effect of grain size on the phase stability of nanocrystalline solid is evaluated by the model calculations.

In this section, the equilibria and phase transformations of solid and liquid phases will be calculated as examples to demonstrate the model applications. The Li–Si compounds with stoichiometric compositions, as typical partially ionic solids, are used as sample materials.

3.1 Calculation of thermodynamic properties of nanocrystalline Li–Si solids

The thermodynamic properties are calculated for the nanocrystalline Li–Si solids with stoichiometric compositions, such as Li₂₂Si₅, Li₁₃Si₄, Li₇Si₃ and Li₁₂Si₇, which exist in the Li–Si phase diagram. The input for the model calculations include mainly the parameters at the equilibrium state, i.e. the interatomic distance r₀, bulk modulus B₀, cohesive energy E₀, bulk thermal expansion coefficient α₀ and Debye temperature Θ₀. The sources and the access to obtain these parameters are described as below.

The interatomic distance r₀ is calculated by r₀ = (3V₀/4π)^1/3, where V₀ is the atomic volume in a perfect crystal at the equilibrium state. The bulk modulus B₀ is obtained by the first principles calculation.³² The cohesive energy E₀ is obtained from literature.³³ The Debye temperature Θ₀ is calculated by the equation Θ₀ = (48π⁵)^1/6k(ν)(ħ/k_B)(r₀B₀/M)^1/2,³⁴ where,

ν is the Poisson's ratio.³⁵ The thermal expansion coefficient α₀ is obtained by α₀ = 3λ₀, λ₀ is the linear expansion coefficient, and can be calculated by the Ruffa model.^36,37

From the above accesses, the input parameters of the proposed thermodynamic model for the nanocrystalline partially ionic solids can be obtained. As an example, the input to calculate the thermodynamic properties of the nanocrystalline Li₂₂Si₅ and Li₁₃Si₄ solids are listed in the Table 1.

Table 1 Input parameters for model calculations of thermodynamic properties for the nanocrystalline Li₂₂Si₅ and Li₁₃Si₄ solids

	r0 (nm)	B0 (GPa)	E0 (10^−19 J per atom)	Θ0 (K)	α0 (10^−6 K^−1)
Li22Si5	1.538	34.89	3.7648	491	70.43
Li13Si4	1.558	38.68	4.0896	694	62.99

---

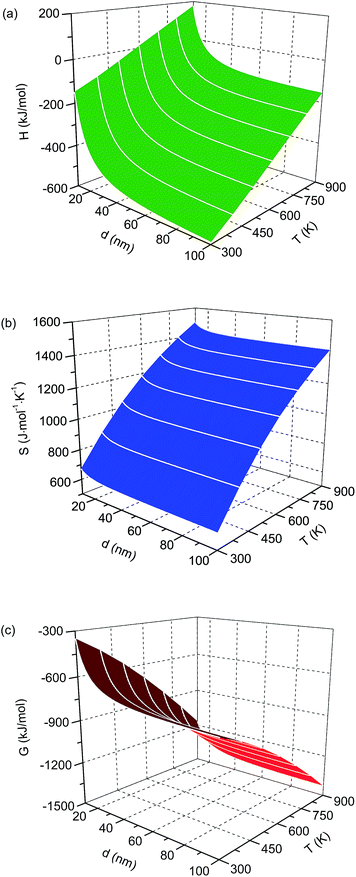
The calculated enthalpy, entropy and Gibbs free energy of the nanocrystalline Li₂₂Si₅ solid are shown in Fig. 1, as functions of temperature and grain size. The thermodynamic properties exhibit a rapid increase with the decrease of grain size when below a critical value, e.g. ∼20 nm for Li₂₂Si₅.

Fig. 1 Calculated thermodynamic properties of nanocrystalline Li₂₂Si₅ solid, as functions of temperature and grain size: (a) enthalpy; (b) entropy; (c) Gibbs free energy. The solid curves denote isothermal lines at a temperature interval of 100 K.

3.2 Prediction of peritectic reaction and solid–liquid transformation

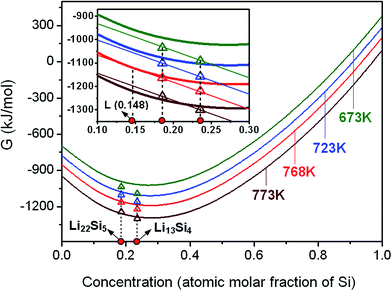
The Gibbs free energies of the nanocrystalline Li–Si solids, as a function of temperature and grain size, are used as dominant variables to evaluate the phase stabilities at equilibrium state, and also criteria for the occurrence of phase transformations.

Take the nanocrystalline Li₂₂Si₅ solid as an initial material, with increasing the temperature while the liquid phase appears, the three-phase equilibrium Li₂₂Si₅ ↔ L + Li₁₃Si₄ is reached, which corresponds to the peritectic reaction balance. For the Li₂₂Si₅ solid with a certain grain size, the equilibrium of Li₂₂Si₅ solid, liquid and Li₁₃Si₄ solid, as well as the peritectic reaction temperature, is one and only, which can be obtained by the common tangent principle. The intersection between the common tangent and curve of Gibbs free energy of the liquid phase determines the liquid composition at the peritectic equilibrium. As shown in Fig. 2, the nanocrystalline Li₂₂Si₅ with a mean grain size d = 25 nm will reach peritectic equilibrium at T_p (25 nm) = 768 K, leading to the formation of Li₁₃Si₄ solid and liquid with a concentration of 0.148 at% Si. It is seen that the peritectic transformation temperature of the nanocrystalline Li₂₂Si₅ solid decreases obviously as compared with that of the conventional polycrystalline solid (T_p = 901 K).

Fig. 2 Calculations of liquid concentration and temperature of peritectic equilibrium Li₂₂Si₅ ↔ L + Li₁₃Si₄ at a given grain size (d = 25 nm). The curves represent liquid phase at different concentrations and temperatures, and triangles represent Li₂₂Si₅ and Li₁₃Si₄ solids at different temperatures. The inset denotes local enlargement to determine peritectic equilibrium based on common tangent principle.

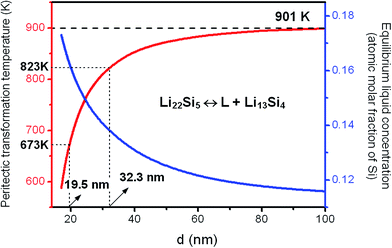
Apply the model, the liquid concentration at peritectic equilibrium and the peritectic transformation temperature can be calculated as a function of grain size, as shown in Fig. 3. It can be seen that with grain sizes larger than 80 nm the peritectic transformation temperature is increasingly close to that of the conventional polycrystalline Li₂₂Si₅ solid. However, with decreasing the grain size, the peritectic transformation temperature decreases while the liquid concentration at the peritectic equilibrium increases. Therefore, in the nanoscale Li–Si phase diagram, the two-phase areas, i.e. “liquid + Li₁₃Si₄ solid” and “Li₂₂Si₅ solid + Li₁₃Si₄ solid”, will become smaller with the decrease in grain size.

Fig. 3 Calculated liquid concentration at peritectic equilibrium and peritectic transformation temperature as a function of grain size.

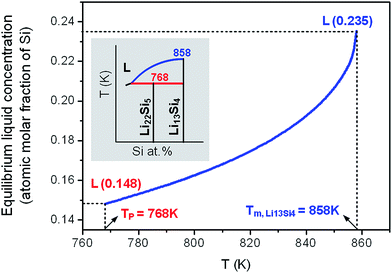
For the initial nanocrystalline Li₂₂Si₅ solid, at temperatures above the peritectic equilibrium temperature, the liquid and Li₁₃Si₄ solid will coexist instead of the Li₂₂Si₅ solid. To evaluate this phase equilibrium where the solid has a constant stoichiometric composition, the liquid concentration as a function of temperature (i.e. the liquidus) is calculated using the model, with the nanocrystalline Li₂₂Si₅ solid of a certain grain size as the starting material. As shown in Fig. 4, when the temperature is higher than the peritectic transformation temperature as T_P = 768 K (d = 25 nm), the liquid concentration at the solid–liquid equilibrium Li₁₃Si₄ ↔ L increases with the temperature, till the melting point of Li₁₃Si₄ solid at T_m,Li13Si4 = 858 K (d = 25 nm). Accordingly, in the nanoscale Li–Si phase diagram, as the local area shown in the inset of Fig. 4, the liquidus moves downwards and rightwards as compared with the conventional binary diagram.

Fig. 4 Calculated liquid concentration at solid–liquid equilibrium from the start of peritectic transformation to the melting point of Li₁₃Si₄ solid, with the nanocrystalline Li₂₂Si₅ solid (d = 25 nm) as the starting material. The inset shows local phase diagram of Li₂₂Si₅ ↔ L + Li₁₃Si₄ and Li₁₃Si₄ ↔ L equlibria.

3.3 Prediction of eutectic reaction and solid–liquid transformation

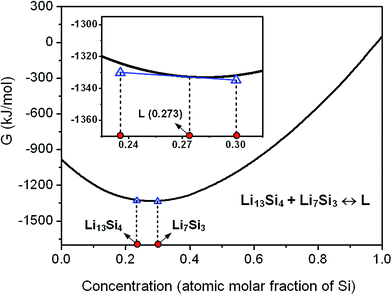
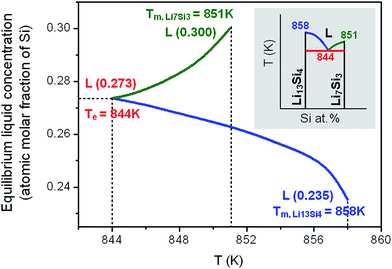
In the case that the initial solid is composed of two phases as Li₁₃Si₄ and Li₇Si₃, with the increase of temperature, the equilibrium Li₁₃Si₄ + Li₇Si₃ ↔ L will be attained and the eutectic transformation can occur. Fig. 5 shows the model prediction on the eutectic reaction based on the calculations of Gibbs free energies of Li₁₃Si₄, Li₇Si₃ and liquid phases. With an initial grain size d = 25 nm, the eutectic reaction temperature is predicted as T_e = 844 K, and the liquid concentration at the eutectic equilibrium is calculated as 0.273 at% Si. As compared with the eutectic transformation temperature of the conventional polycrystalline solid (T_e = 982 K), the eutectic reaction temperature decreases greatly in the nanocrystalline material.

Fig. 5 Prediction of eutectic reaction Li₁₃Si₄ + Li₇Si₃ ↔ L for initial solid with a given grain size (d = 25 nm). The inset denotes local enlargement to determine liquid concentration at the eutectic equilibrium.

When the temperature is higher than the eutectic transformation temperature, the two phases of “liquid + Li₁₃Si₄ solid” or “liquid + Li₇Si₃ solid” may form, depending on the composition of the initial solid. The liquid concentration at the solid–liquid equilibrium is calculated for the initial solid with a given grain size (d = 25 nm), as shown in Fig. 6. In contrast to the equilibrium Li₁₃Si₄ ↔ L resulting from the peritectic reaction (see Fig. 4, where the liquid concentration increases with the temperature), the liquid concentration at the equilibrium Li₁₃Si₄ ↔ L which is generated from the eutectic reaction decreases with the temperature, till the melting point of Li₁₃Si₄ at T_m,Li13Si4 = 858 K. For the equilibrium Li₇Si₃ ↔ L, the liquid concentration increases with the temperature till the melting point of Li₇Si₃ at T_m,Li7Si3 = 851 K. From the calculation results, it is clear that in the nanoscale Li–Si system, for the phase equilibria related to the eutectic reaction Li₁₃Si₄ + Li₇Si₃ ↔ L, as the local phase diagram shown in the inset of Fig. 6, the liquid area expands and the two-phase areas (liquid–solid and solid–solid) shrink, as compared with the conventional binary phase diagram.

Fig. 6 Calculated liquid concentration at solid–liquid equilibrium from the start of eutectic transformation to the melting points of solids, for initial solid with a given grain size (d = 25 nm). The inset shows local phase diagram of Li₁₃Si₄ + Li₇Si₃ ↔ L, Li₁₃Si₄ ↔ L and Li₇Si₃ ↔ L equlibria.

As demonstrated by the above examples of model applications, in principle any phase equilibrium or phase transformation that contains nanocrystalline partially ionic solid can be evaluated by the model. For an anode system in the Li ion battery such as Li–Si, based on the calculated results of the three-phase (peritectic and eutectic reactions) and two-phase (solid and liquid) equilibria, the phase diagram on the nanoscale can be developed. Thus the characteristics of phase transformation temperature and equilibrium liquid concentration can be obtained for any nanoscale Li–Si anode systems. However, it should be noted that the transformation from amorphous to crystalline, which may occur in Li–Si alloys under electrochemical condition, is not taken into account in the model. Therefore, the present model describes the thermodynamic phase stability rather than the electrochemical behavior.

4 Experimental verification of the model

To verify the model predictions, a series of experiments were performed using the nanocrystalline Li₂₂Si₅ bulk material as an example of the anode system. Firstly, a dense nano-grained Li₂₂Si₅ bulk sample was prepared as the starting material. Lithium slices and silicon powder both with 99.99% purity were used as raw materials, with a 2.0 wt% excess of lithium to compensate for the loss due to its high chemical activity. The raw materials were mixed and compressed in a die made of tungsten carbide. The die was put in a spark plasma sintering (SPS) system with the vacuum degree higher than 10⁻³ Pa, in which an alloy ingot with a single phase Li₂₂Si₅ was prepared. Then in the glove box the ingot was crushed into powder and milled with a ball-to-powder weight ratio of 60 : 1 at a constant rotation rate of 500 rpm for 16 h. From this procedure, the fine amorphous powder was obtained, and was immediately fed in the die and put in the SPS system to be densified. To obtain the nanocrystalline Li₂₂Si₅ bulk material from the amorphous powder by the concurrent crystallization and densification processes, the sintering parameters were optimized as an external pressure of 300 MPa, a final sintering temperature of 200 °C, a heating rate of 50 °C min⁻¹ and no isothermal holding before rapid cooling to the room temperature.

The as-prepared nanocrystalline Li₂₂Si₅ bulk material was measured to have a nearly full relative density (99.9%). The annealed counterparts were used as samples to examine the phase equilibria and phase transformation behavior.

4.1 Experimental results of thermodynamic properties and comparison with model calculations

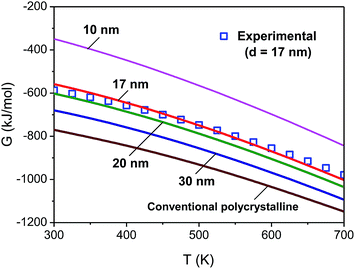
The phase constitution and mean grain size of the as-prepared nanocrystalline Li₂₂Si₅ bulk sample were detected by the X-ray diffraction (XRD). It is found that the Li₂₂Si₅ with a cubic crystal structure is clearly the dominant phase, with a little lithium oxide present. The mean grain size is estimated as about 17 nm using the modified Scherrer formula.³⁸

The measured specific heat capacity at constant pressure of the as-prepared nanocrystalline Li₂₂Si₅ solid is shown in Fig. 7, and compared with that of the conventional polycrystalline counterpart. The specific heat capacity is used to obtain the enthalpy, entropy and Gibbs free energy based on the known thermodynamic equations.³⁹ The Gibbs free energy as a function of temperature obtained from the experimental result (for the sample with mean grain size of 17 nm) is compared with the model calculations at different grain sizes, as shown in Fig. 8. It is seen that the calculated Gibbs free energy is consistent with the function obtained from experimental result, and its changing tendency with the grain size is reasonable.

Fig. 7 Experimental measurements of the specific heat capacity at constant pressure for the as-prepared nanocrystalline Li₂₂Si₅ solid, and comparison with that of the conventional polycrystalline counterpart.

Fig. 8 Comparison of Gibbs free energy between model calculation and function obtained from experimental result for Li₂₂Si₅ sample with mean grain size d = 17 nm. The solid lines and squares represent model calculations and experimental, respectively.

4.2 Experimental results of phase transformation and comparison with model predictions

The as-prepared nanocrystalline Li₂₂Si₅ bulk sample was divided into several parts, which were annealed separately at different temperatures in a vacuum furnace. The phase constitutions of the annealed samples were examined by XRD, and were used to reflect the phase transformation behavior in experiments. The change of phase constitution with the annealing temperature is shown in Fig. 9. It is observed that the sample annealed at 573 K has the same phase constitution as that in the as-prepared nanocrystalline Li₂₂Si₅ solid (marked as 298 K), i.e. no phase transformation occurs. The mean grain size of the 573 K-annealed sample is estimated as 19.6 nm by the modified Scherrer formula based on its XRD pattern. The representative grain size distribution is in a range of 18.1–24.9 nm, which is obtained from the typical diffraction peaks of the matrix phase in the XRD pattern (Fig. 9). As predicted by the model calculations, to have the peritectic transformation at 573 K, the critical grain size is 16.6 nm (Fig. 3). Therefore, the 573 K-annealing experiment confirms the model prediction that the phase transformation does not take place when the grain size is larger than the critical value.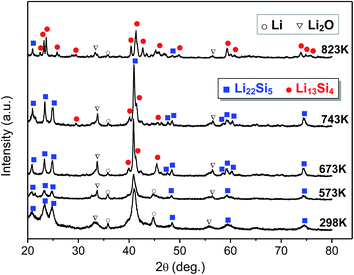

Fig. 9 Experimental results of change in phase constitution with the annealing temperature, with the as-prepared nanocrystalline Li₂₂Si₅ sample as the starting material.

In the 673 K-annealed sample, as shown in Fig. 9, with the Li₂₂Si₅ as the dominant phase, the Li₁₃Si₄ phase with a monoclinic crystal structure appears in a small amount, which indicates the occurrence of the peritectic transformation. In this sample, the mean grain size of Li₂₂Si₅ phase is about 24.4 nm, and the representative grain size distribution is 18.8–30.0 nm. As calculated by the model, the critical grain size for the peritectic transformation at 673 K is 19.5 nm (Fig. 3). It implies that grains larger than 19.5 nm will keep the Li₂₂Si₅ phase, while the peritectic transformation takes place preferentially in those grains smaller than the critical value. Consequently, the Li₂₂Si₅ and Li₁₃Si₄ phases coexist in the sample and the former predominates, as found in the experiment. The 743 K-annealed sample has a similar phase constitution as the sample annealed at 673 K, but the amount of Li₁₃Si₄ phase increases (Fig. 9).

For the sample annealed at 823 K, the Li₁₃Si₄ becomes the dominant phase with a small amount of Li₂₂Si₅ phase coexisting (Fig. 9). The mean grain size of Li₁₃Si₄ phase is about 31.2 nm, and the representative grain size distribution is 22.1–35.1 nm. The critical grain size for the peritectic transformation at 823 K is predicted as 32.3 nm by the model (Fig. 3). Since the mean grain size is smaller than the critical value, moreover, as observed from the grain size distribution, most grains are smaller than the critical size, thus instead of Li₂₂Si₅ the Li₁₃Si₄ phase predominates in the 823 K-annealed sample as product of the peritectic transformation. Therefore, the experimental result proves the model calculation on the grain-size-dependence of the phase transformation.

As a summary of the above analyses on the phase transformation and the effects of temperature and grain size, the change of phase constitution with the mean grain size and its correlation with the critical grain size (calculated by the model) are shown in Fig. 10. It can be seen clearly that in the nanocrystalline Li₂₂Si₅ solid, the peritectic transformation can occur at temperatures much lower (e.g. 673 K) than that in the conventional polycrystalline material (901 K). In the heating process, at a certain temperature the peritectic transformation Li₂₂Si₅ → L + Li₁₃Si₄ may occur firstly in the grains that are smaller than the critical size that corresponds to the minimum of the Gibbs free energy in the multiphase system. With the increase of temperature, both the mean grain size and the critical grain size increase, moreover, the absolute grain size distribution becomes broader. In the case that most of the grain sizes are smaller than the critical value, even at the relatively lower temperature, the peritectic transformation can be accomplished, leading to the formation of Li₁₃Si₄ as the dominant phase in the anode system.

Fig. 10 Correlation of phase constitution, critical grain size and mean grain size at a certain temperature. The symbols “○” and “△” represent the mean grain size from experiments and the critical value for peritectic transformation calculated by the model, and the filled rectangle represents the grain size distribution of the matrix phase, obtained from XRD data of the main diffraction peaks.

5 Summary and conclusions

The nanoscale phase stability in the anode system is crucial to the functional properties and operational reliability of the Li ion battery. In the present paper, we concentrate our attention on quantitative description of the phase stability and phase transformation mechanism in the nanocrystalline Li ion battery anode materials. The following conclusions are obtained from modeling and experimental studies.

Introduce both the ionic and covalent contributions to the cohesive energy of atoms and grain size effect on the structure and energy state of interface, a model was developed to describe systematic thermodynamic properties and hence the multiphase equilibrium and phase stability of nanocrystalline partially ionic solids. Applied to Li–Si compounds, the model calculations appealed that with the decrease of grain size on the nanoscale, both the peritectic and eutectic reaction temperatures decrease, while the liquid concentration at equilibrium may increase or decrease depending on the initial composition. The changes in transformation temperature and equilibrium concentration result in expansion of liquid area and shrinkage of liquid–solid and solid–solid areas in the nanoscale phase diagram. Experimental results with the nanograined Li₂₂Si₅ bulk sample as the starting material confirmed the model predictions on the phase transformation characteristics of the nanocrystalline partially ionic solids, and supported the effect of grain size on the phase stability in the nanoscale anode system. It was proposed that the equilibrium, stability and transformation of phases in the nanocrystalline Li alloy system are determined by the correlation of temperature, grain size and critical grain size. When the grain size is smaller than the critical value, phase transformations may occur at clearly lower temperatures as compared to those in the conventional polycrystalline anode materials.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (51174009, 51371012), German Research Foundation (DFG, SO 1075/1-2) and the Beijing “Great Wall Scholars” program (CIT&TCD20130314).

References

1. T. Waitz and H. P. Karnthaler, Acta Mater., 2004, 52, 5461.
2. B. Efros, V. Pilyugin, A. Patselov, S. Gladkovskii, N. Efros, L. Loladze and V. Varyukhin, Mater. Sci. Eng., A, 2009, 503, 114.
3. N. Forouzanmehr, F. Karimzadeh and M. H. Enayati, J. Alloys Compd., 2009, 471, 93.
4. Z. X. Zhang, X. Y. Song and W. W. Xu, Acta Mater., 2011, 59, 1808.
5. P. C. Kang and Z. D. Yin, Nanotechnology, 2004, 15, 851.
6. M. Grunwald and C. Dellago, Nano Lett., 2009, 9, 2099.
7. J. T. He, X. Y. Song, W. W. Xu, Y. Y. Zhou, M. Seyring and M. Rettenmayr, Mater. Lett., 2013, 94, 176.
8. K. Thornton, J. Agren and P. W. Voorhees, Acta Mater., 2003, 51, 5675.
9. Q. Jiang, H. X. Shi and M. Zhao, Acta Mater., 1999, 47, 2109.
10. Q. Jiang, Z. Zhang and J. C. Li, Acta Mater., 2000, 48, 4791.
11. Q. Jiang, D. S. Zhao and M. Zhao, Acta Mater., 2001, 49, 3143.
12. T. L. Hill, Nano Lett., 2001, 1, 111.
13. R. Kirchheim, Acta Mater., 2002, 50, 413.
14. X. Y. Song, J. X. Zhang, L. M. Li, K. Y. Yang and G. Q. Liu, Acta Mater., 2006, 54, 5541.
15. Z. Chen, F. Liu, H. F. Wang, W. Yang, G. C. Yang and Y. H. Zhou, Acta Mater., 2009, 57, 1466.
16. Y. Zheng and C. H. Woo, Appl. Phys. A, 2009, 97, 617.
17. W. W. Xu, X. Y. Song, N. D. Lu and C. Huang, Acta Mater., 2010, 58, 396.
18. D. Amram, L. Klinger and E. Rabkin, Acta Mater., 2013, 61, 5130.
19. H. Schlosser, J. Ferrante and J. R. Smith, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 9696.
20. Y. Imai, Y. Mori, S. Nakamura and K. I. Takarabe, J. Alloys Compd., 2013, 558, 179.
21. H. Miyaoka, W. Ishida, T. Ichikawa and Y. Kojima, J. Alloys Compd., 2011, 509, 719.
22. L. Ji, Z. Lin, M. Alcoutlabi and X. Zhang, Energy Environ. Sci., 2011, 4, 2682.
23. S. M. Mukhopadhyay, Nanoscale Multifunctional Materials: Science & Applications, John Wiley & Sons, Hoboken, 2011.
24. M. Wagemaker, F. M. Mulder and A. Van der Ven, Adv. Mater., 2009, 21, 2703.
25. A. Shukla and T. Kumar, Curr. Sci., 2008, 94, 314.
26. H. J. Fecht, Phys. Rev. Lett., 1990, 65, 610.
27. M. Wagner, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 635.
28. H. Schlosser and J. Ferrante, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 6646.
29. P. Vinet, J. R. Smith, J. Ferrante and J. H. Rose, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 1945.
30. H. Schlosser and J. Ferrante, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1073.
31. A. T. Dinsdale, Calphad, 1991, 15, 317.
32. V. L. Chevrier, J. W. Zwanziger and J. R. Dahn, Can. J. Phys., 2009, 87, 625.
33. Z. W. Cui, F. Gao, Z. H. Cui and J. M. Qu, J. Power Sources, 2012, 207, 150.
34. X. M. Tao, Y. F. Ouyang, H. S. Liu, F. J. Zeng, Y. P. Feng and Z. P. Jin, Phys. B, 2007, 399, 27.
35. J. Moon, K. Cho and M. Cho, Int. J. Precis. Eng. Manuf., 2012, 13, 1191.
36. A. R. Ruffa, J. Mater. Sci., 1980, 15, 2258.
37. A. R. Ruffa, J. Mater. Sci., 1980, 15, 2268.
38. A. W. Burton, K. Ong, T. Rea and I. Y. Chan, Microporous Mesoporous Mater., 2009, 117, 75.
39. R. T. Dehoff, Thermodynamics in Materials Science, Taylor & Francis, Boca Ratom, 2nd edn, 2006.

---