Features of the potential energy surface for the SiO + OH → SiO₂ + H reaction: relationship to oxygen isotopic partitioning during gas phase SiO₂ formation

Abstract

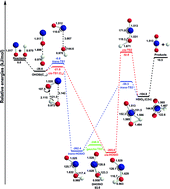
The SiOOH potential energy surface has become central to the understanding of recent experiments (Science 2013, 342, 463) by Chakraborty associated with nebular meteorite formation. The entrance complex, transition states, and exit complex for the title reaction SiO + OH→ SiO₂ + H have been studied using the CCSD(T) method with correlation consistent basis sets as large as cc-pV(Q+d)Z. Reported here are characteristics of the reactants, products, six transition states, and four intermediate complexes for this reaction. These show four previously undiscovered stationary point geometries. The entrance complex OH⋯OSi is predicted to lie 28.6 kJ mol⁻¹ below the separated reactants. The classical barriers cis-TS1 and trans-TS1 are predicted to lie 21.8 kJ mol⁻¹ and 6.8 kJ mol⁻¹, respectively, below the reactants. The exit complex HSiO₂ is bound by 115.3 kJ mol⁻¹ relative to the separated products. After zero-point vibrational energy corrections, the reaction energy is predicted to be −1.4 kJ mol⁻¹. Vibrational frequencies of the stationary points are reported and compared with the limited available experimental results. The SiOOH potential surface is found to be very different from that for COOH, contrary to the analogy drawn by Chakraborty. Notwithstanding, the assumption of Chakraborty appears justified, because all the stationary points for the SiO + OH reaction have lower relative energies than known for the analogous carbon system.

---

1. Introduction

Molecular SiO has been detected in young protoplanetary nebulae and other astronomical sources,^1–3 and is found to react with OH in the early nebula.^4,5 Recently, in order to study the mass-independent oxygen isotopic partitioning during gas-phase SiO₂ formation in solar nebula, Chakraborty, Yanchulova, and Thiemens⁶ reported experiments designed to measure the oxygen isotopic compositions of solid SiO₂ generated by gas phase reactions under controlled experimental conditions. Chakraborty et al. concluded that the source of the observed mass-independent oxygen isotopic partitioning may be the reaction SiO + OH → SiO₂ + H, valence isoelectronic to the familiar reaction CO + OH → CO₂ + H, observed in atmosphere.^7,8

In 1996, Chagger, et al.⁹ studied silica formation from hexamethyldisiloxane oxidation by means of a CH₄–N₂/air opposed diffusion flame technique, and the reaction mechanism involved the reaction noted above, SiO + OH → SiO₂ + H. These authors also listed the available reaction enthalpy and rate constant. In 2009, the kinetics of the reaction SiO + OH → SiO₂ + H were investigated by Martin, Blitz and Plane¹⁰ using the pulsed laser photolysis of a Si atom precursor in the presence of O₂, followed by time-resolved non-resonant laser-induced fluorescence. They measured the rate constant to be (5.7 ± 2.0) × 10⁻¹² cm³ per molecule per second at 293 K and 4–20 Torr.

Theoretically, in 1995, Zachariah and Tsang¹¹ predicted features of the potential energy surface for the reaction SiO + OH → SiO₂ + H with the MP4/6-311(2df,p)//MP2/6-31(d) method. Recently, Martin, Blitz and Plane¹⁰ obtained a potential energy profile of this reaction using CBS-Q single point energies at geometries optimized with the B3LYP/6-311+G(2d,p) method. As Martin et al. discussed, the low pressure limiting rate coefficient at room temperature (SiO + OH → HOSiO → SiO₂ + H) obtained by Zachariah and Tsang¹¹ is 15 times smaller than their experimental determination and Rice–Ramsperger–Kassel–Markus (RRKM) fit; while it is 10 times larger than their estimate for the cis-HOSiO → SiO₂ + H pathway. It is well known that deduced rate constants depend strongly on the quality of the potential energy surface adopted.¹² Although the research of ref. 10 and 11 is very valuable, higher level theoretical studies are now possible and appropriate. In the present study, we will adopt very high level theoretical methods up to CCSD(T)/cc-pV(Q+d)Z to predict a more complete potential energy surface, which will give new possible pathways and more reliable activation energies for the SiO + OH → SiO₂ + H reaction. We hope that the newer results will provide a solid base for the future kinetic studies.

2. Theoretical methods

The CCSD(T) method with large basis sets has recently been used to study the potential energy surfaces of F + H₂O, Cl + H₂O, and I + H₂O,^13–15 and those results are in good agreement with the limited available experimental findings. In the present work, we use the same CCSD(T) method with correlation consistent basis sets up to cc-pV(Q+d)Z to study the stationary points on the potential energy surface for the SiO + OH → SiO₂ + H reaction.

In our research, coupled cluster computations were carried out to explore the stationary points on the SiO + OH → SiO₂ + H potential energy surface, including the reactants, products, transition states, and intermediate complexes. All geometries are fully optimized using single and double excitation coupled-cluster theory with perturbative triple excitations CCSD(T).^16,17 The Dunning correlation-consistent cc-pVnZ (n = D, T, Q) basis sets were adopted for the hydrogen and oxygen atoms,¹⁸ while the cc-pV(n+d)Z (n = D, T, Q) basis sets¹⁹ were utilized for the silicon atom. With the coupled-cluster methods, the 1s-like molecular orbital for oxygen is frozen, while the 1s2s2p-like molecular orbitals for silicon are frozen. Harmonic vibrational frequencies predicted at the same level were used to evaluate the zero point vibrational energies (ZPVE) and for the characterization of the stationary points. All open-shell Hartree–Fock computations were unrestricted (UHF), and the coupled cluster methods adopted were also unrestricted, UCCSD(T). All coupled cluster computations were carried out using the CFOUR program.²⁰

3. Results and discussion

The potential surface for the SiO + OH → SiO₂ + H reaction is sketched qualitatively in Fig. 1. Our optimized bond distances for the reactants (SiO and OH) are 1.517 Å and 0.970 Å, compared to experiment, 1.510 Å and 0.970 Å.²¹ For product (SiO₂), although no experimental geometry for the gas phase molecule is available, our theoretical (1.513 Å) Si–O bond length is fair agreement with the CCSD(T)/aug-cc-pVTZ result (1.525 Å) of Kostko, Ahmed, and Metz.²² They obtained the Si–O bond distance via the computation of a series of single-point energies. Darling and Schlegel²³ earlier reported an MP2/6-31G(d) theoretical Si–O distance of 1.542 Å.

Fig. 1 Stationary points on the SiO + OH potential energy surface without zero-point vibrational energy (ZPVE) corrections at the CCSD(T)/cc-pV(Q+d)Z level of theory. In each structure the Si atom is represented by a blue sphere.

Fig. 1 shows that there are two possible pathways for the SiO + OH → SiO₂ + H reaction, and for each pathway there is more than one transition state. However, the two pathways share same entrance complex and exit complex. The entrance complex OH⋯OSi is of linear geometry with C_∞v symmetry, which was not reported in previous theoretical studies.^10,11 This complex is predicted to lie 28.6 kJ mol⁻¹ below the separated reactants (SiO + OH) at the CCSD(T)/cc-pV(Q+d)Z level of theory.

For the valence isoelectronic HO + CO → H + CO₂ reaction, Ma, Li, and Guo in 2012 reported two entrance complexes.²⁴ Beside the OHCO complex on the cis pathway, there is another linear complex OH⋯CO on the trans pathway. It may be noted that the electronegativity of silicon is less than that of carbon, and a generic Si⋯H interaction may be weaker than the comparable C–H interaction. The greater importance of polarization functions (d orbitals) for silicon may also be pertinent here. In fact, we have attempted to optimize the OHSiO structure analogous to OHCO, but it has at least two imaginary vibrational frequencies, and it eventually collapses to the OHOSi complex seen on the left of Fig. 1. The predicted OH⋯OSi distance for our single entrance complex is 1.90 Å, which lies in the typical range of hydrogen bonding distances. It is significantly shorter than the analogous OH⋯OC distance (2.30 Å) predicted via the CCSD(T)-F12b/aug-cc-pVTZ method by Xie, Li, Xie, and Guo.²⁵ The exit complex HSiO₂ (Fig. 1) for the SiO + OH→ SiO₂ + H reaction is predicted to be a planar structure with C_2v symmetry, lying 10.5 − (−104.8) = 115.3 kJ mol⁻¹ below the products SiO₂ + H. This exit complex was reported by Martin, Blitz, and Plane to lie below separated SiO₂ + H by 96.1 kJ mol⁻¹,¹⁰ but no such a complex was reported in Zachariah and Tsang's paper.¹¹ The Si–O and H–Si bond lengths for C_2v symmetrical HSiO₂ are 1.565 and 1.467 Å, respectively, which are not inconsistent with the B3LYP/6-311+G(2d,p) optimized results (1.523 Å for Si–O and 1.481 Å for H–Si) of Plane and coworkers.¹⁰

From the entrance complex to the exit complex, there are two pathways. The first pathway (red in Fig. 1) proceeds via a cis-HOSiO intermediate, and the other pathway (blue in Fig. 1) involves a trans-HOSiO intermediate. The cis and trans isomers have similar bond distances, bond angles, and relative energies. The cis isomer lies below the reactants by 265.0 kJ mol⁻¹, with the trans isomer is lower than reactants by 262.4 kJ mol⁻¹.

Between the entrance complex and the cis or trans intermediates, there are transition states, i.e., cis-TS1 and trans-TS1, which were not reported before.^10,11 Each of these has one imaginary vibrational frequency, namely, 81i cm⁻¹ ((Q+d)Z) for cis-TS1 and 123i cm⁻¹ for trans-TS1. Structures cis-TS1 and trans-TS1 are predicted to lie 21.8 kJ mol⁻¹ and 6.8 kJ mol⁻¹, respectively, below the reactants at the CCSD(T)/cc-pV(Q+d)Z level of theory. These two transition states are very different in geometry, although the nonbonded OSi⋯O distances in the two structures are comparable (∼3.0 Å). Specifically, trans-TS1 has a chain structure, while the cis transition state has a cyclic structure, with an O⋯H hydrogen bond facilitated by the cis geometry. Accordingly, the cis isomer has a lower energy than the trans-TS1, by 15.0 kJ mol⁻¹. Compared with the unique entrance complex OHOSi, the barriers of these two transition states are [(−6.8) − (−28.6)] = 21.8 (trans) and [(−21.8) − (−28.6)] = 6.8 (cis) kJ mol⁻¹, respectively. After zero-point vibrational energy corrections, the barriers (with respect to the entrance complex) for trans-TS1 and cis-TS1 decrease to [(−5.0) − (−22.3)] = 17.3 and [(−16.1) − (−22.3)] = 6.2 kJ mol⁻¹ (Fig. 2).

Fig. 2 Stationary points on the SiO + OH potential energy surface after zero-point vibrational energy (ZPVE) corrections.

From the cis and trans intermediates to the unique exit complex (HSiO₂), there are corresponding cis and trans transition states, i.e., cis-TS2 and trans-TS2. Each of these is predicted to display one imaginary vibrational frequency, i.e., 1271i cm⁻¹ for cis-TS2 and 1179i cm⁻¹ for trans-TS2 with the cc-pV(Q+d)Z basis sets. The corresponding normal modes reveal Si–O bond formation and O–H bond breaking as the reaction proceeds toward products SiO₂ + H. Since the cis-TS2 and trans-TS2 transition states have rather different geometries, they are predicted to have divergent relative energies, 33 kJ mol⁻¹ for cis-TS2 and −60 kJ mol⁻¹ for trans-TS2. The latter prediction is consistent with the previous theoretical value of 63 kJ mol⁻¹ by Martin, Blitz and Plane.¹⁰ The former prediction is comparable to the theoretical value of 22 kJ mol⁻¹,¹⁰ (note that 12.13 in Fig. 10 of ref. 10 may be a typographical error for 22.13 if their ESI data are correct).

The isomerization between the two intermediates (trans-HOSiO to cis-HOSiO) involves two transition states (trans-TS3 and gauche-TS3, both green in Fig. 1), which are neither on cis nor on trans reaction pathway. The barrier of trans-TS3 is much higher than that of gauche-TS3. This is because the trans-TS3 (C_s symmetry) structure is confined to the plane, and the isomerization is by way of the Si–O–H angle change in the plane. In contrast, gauche-TS3 (C₁ symmetry) is through the lower energy internal-rotation around the Si–O single bond. The barrier for gauche-TS3 (13.5 kJ mol⁻¹ from trans-HOSiO side) is in good agreement with the barrier of 11.8 kJ mol⁻¹ from Martin, Blitz and Plane,¹⁰ and with the 10 kJ mol⁻¹ reported by Zachariah and Tsang.¹¹ The trans-TS3 transition state was not mentioned in previous theoretical studies.^10,11

The theoretical relative energies (ΔE) with respect to the reactants (OH + SiO), harmonic vibrational frequencies (cm⁻¹), and the zero-point vibrational energies (kJ mol⁻¹) for the stationary points on the SiO + OH→ SiO₂ + H potential energy surface are reported in Table 1. It is noted that the predicted results for SiO₂, SiO, and OH are in good agreement with the experimental vibrational frequencies.^21,26

Table 1 Relative energies (ΔE) with respect to the reactants (OH + SiO), harmonic vibrational frequencies (cm⁻¹) and zero-point vibrational energies (kJ mol⁻¹) of the stationary points for the SiO + OH → SiO₂ + H reaction at the CCSD(T)/cc-pV(Q+d)Z levels of theory. The available experimental results are also listed for comparison

	ΔE (kJ mol^−1)	ZPVE (kJ mol^−1)	Vibrational frequencies (cm^−1)
			ω1	ω2	ω3	ω4	ω5	ω6	ω7
a Fundamental frequencies.^26b Harmonic vibrational frequencies.^21
OHOSi	−28.6	36.12	3641	1244	459	459	163	37	37
cis-TS1	−21.8	35.51	3706	1226	477	361	165	81i
cis-HOSiO	−265.0	44.15	3831	1201	893	772	389	294
cis-TS2	32.8	17.91	1395	957	285	282	75	1271i
HSiO2	−104.8	32.78	2323	1028	895	567	364	304
trans-HOSiO	−262.4	44.28	3875	1218	860	789	353	307
trans-TS1	−6.8	31.68	3742	1235	171	101	47	123i
trans-TS2	−59.5	28.28	1883	1302	893	350	299	1179i
gauche-TS3	−248.9	41.31	3897	1207	868	621	314	384i
trans-TS3	−6.2	31.68	3748	1235	185	87	42	96i
SiO		7.40	1237
OH		22.43	3750
SiO + OH	0.0	29.83
SiO2		17.95	1436	989	288	288
SiO2 + H	10.5	17.95
Experiment
SiO2^a		17.78	1416	1010	273	273
SiO^b		7.43	1242
OH^b		22.36	3738

---

A sketch of the CCSD(T) potential energy surface after zero-point vibrational energy (ZPVE) corrections is presented in Fig. 2. Relative to the reactants (SiO + OH), the energies for the intermediate complexes and transition states, except for cis-TS2 and trans-TS2, slightly increase, compared with those values without ZPVE corrections.

The SiO + OH → SiO₂ + H reaction is predicted to be endothermic by 10.5 kJ mol⁻¹ at the CCSD(T)/cc-pV(Q+d)Z level of theory without ZVPE corrections. After the ZPVE corrections, the SiO + OH endothermicity with the cc-pV(D+d)Z, cc-pV(T+d)Z, and cc-pV(Q+d)Z basis sets is predicted to be 39.4, 4.8, and −1.4 kJ mol⁻¹, respectively. The best predicted reaction energy with ZPVE correction (−1.4 kJ mol⁻¹ with the cc-pV(Q+d)Z basis set) is smaller in magnitude than the previous (exothermic) theoretical values of −7 kJ mol⁻¹ derived from their theoretical heats of formation at 298.15 K by Zachariah and Tsang¹¹ and −6.6 kJ mol⁻¹ (CBS-Q) by Martin, Blitz and Plane.¹⁰ Our theoretical reaction energy (−1.4 kJ mol⁻¹) is somewhat different from the experimental value (−24.9 kJ mol⁻¹ at 0 K, and −26.0 kJ mol⁻¹ at 298.15 K) derived from the NIST heats of formation.²⁷ However, there is another experimental reaction enthalpy −0.4 kJ mol⁻¹ at 298.15 K reported by Chagger et al.,⁹ who adopted different heat of formation of −279.9 ± 17 kJ mol⁻¹ for SiO₂ reported by that of Hildenbrand et al. in 1994.²⁸ It is notable that there is a significant uncertainty in the heat of formation of SiO₂, so this comparison with experimental data may not be entirely helpful. Actually Hildenbrand and Lau also report a heat of formation for a HOSiO species,²⁸ which is far from all theoretical values.

For this reaction, there are two possible pathways. One pathway may be called the cis pathway (red in Fig. 1), i.e., SiO + OH (reactants) → entrance complex → cis-TS1 → cis-HOSiO (intermediate) → cis-TS2 → exit complex → SiO₂ + H (products). In this pathway the highest barrier is 32.8 kJ mol⁻¹ (cis-TS2). Another pathway may be called trans pathway (blue in Fig. 1), i.e., SiO + OH (reactants) → entrance complex → trans-TS1 → trans-HOSiO (intermediate) → trans-TS2 → exit complex → SiO₂ + H (products). In this pathway the highest barrier is −6.8 kcal mol⁻¹ (the trans-TS1 structure). Clearly, the trans pathway is more favorable than the cis pathway. However, with the aid of the transition states between cis and trans intermediates (green in Fig. 1), we can have a slightly more complicated pathway with even lower barrier. That is, SiO + OH (reactants) → entrance complex → cis-TS1 → cis-HOSiO (intermediate) → gauche-TS3 → trans-HOSiO (intermediate) → trans-TS2 → exit complex → SiO₂ + H (products). In this cis–trans combination pathway, the highest lying transition state lies −21.8 kJ mol⁻¹ (cis-TS1) without ZPVE or −16.1 kJ mol⁻¹ with ZPVE.

4. Concluding remarks

Finally, we turn to the 2013 paper by Chakraborty, Yanchulova, and Thiemens.⁶ We begin by quoting them rather carefully in this regard: “a vibrationally excited transition state (COOH)* has been predicted for the CO + OH → CO₂ + H reaction, and the existence of a vibrationally excited intermediate was demonstrated. A similar intermediate state (SiOOH)* for the SiO + OH→ SiO₂ + H is feasible, and it is via this excited state that the observed mass-independent effect would be generated.”

Compared with the previous theoretical PES of ref. 10 and 11, we have found some new stationary points, i.e., the entrance complex OHOSi, trans-TS1, cis-TS1, and trans-TS3. We suggest that both cis and trans pathway proceed via the exit complex HSiO₂. The transition state cis-TS2 does not directly connect to the products because there is no barrier (lower than 115.3 kJ mol⁻¹) from the products to the exit complex. Based on our more complete and reliable PES, we suggest a possible pathway through cis-TS1 (−21.8 kJ mol⁻¹) and trans-TS2 (−59.5 kJ mol⁻¹).

In Fig. 3, we have redrawn (to match our Fig. 2 as closely as possible) the reliable energetics of the OH + CO system predicted by Li, Wang, Jiang, Ma, Dawes, Xie, Bowman, and Guo.²⁹ One sees very quickly that SiOOH and COOH potential surfaces differ in many respects. First, the endothermic SiO + OH → SiO₂ + H reaction is barrierless. Other than the products and reactants, the highest lying stationary point, cis-TS1, lies 16.1 kJ mol⁻¹ below the reactants. For the exothermic CO + OH → CO₂ + H, there is a barrier (cis-TS2) lying 10.1 kJ mol⁻¹ above the reactants. Secondly, the trans and cis HOSiO minima lie much lower (−248.0 and −250.7 kJ mol⁻¹) than the analogous equilibrium structures of trans and cis HOCO (−123.8 and −116.4 kJ mol⁻¹). One should also note that the HCO₂ minimum is separated by a barrier from products CO₂ + H, while the HSiO₂ equilibrium goes directly uphill to products SiO₂ + H. Another way of saying this is that SiO₂ + H reacts without a barrier, while the CO₂ + H reaction faces a significant (58.2 kJ mol⁻¹) barrier, consistent with the remarkable stability of CO₂.

Fig. 3 The CO + OH reaction pathways analogous to our SiO + OH system. Redrawn from Fig. 1 of Bowman, Guo, and coworkers.²⁹

Despite the major differences between the COOH and SiOOH energy landscapes, the assumption of Chakraborty, Yanchulova, and Thiemens⁶ seems to be justified. Indeed the transition states and intermediates of the SiO + OH system are all more accessible energetically than those for the CO + OH system.

Acknowledgements

Yanjun Hao acknowledges financial support from the China Scholarships Council (CSC). This research was supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Chemical Sciences Division, Fundamental Interactions Branch.

References

1. V. Bujarrabal, J. Alcolea, R. Soria-Ruiz, P. Planesas, D. Teyssier, J. Cernicharo, L. Decin, C. Dominik, K. Justtanont, A. de Koter, A. P. Marston, G. Melnick, K. M. Menten, D. A. Neufeld, H. Olofsson, M. Schmidt, F. L. Schöier, R. Szczerba and L. B. F. M. Waters, Astron. Astrophys., 2012, 537, A8.
2. S.-H. Cho and J. Kim, Astron. J., 2012, 144, 129.
3. L.-A. Nyman, P. J. Hall and H. Olofsson, Astron. Astrophys., Suppl. Ser., 1998, 127, 185–200.
4. C. Walsh, T. J. Millar and H. Nomura, Astrophys. J., 2010, 722, 1607–1623.
5. G. J. MacPherson and A. Boss, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 19152–19158.
6. S. Chakraborty, P. Yanchulova and M. H. Thiemens, Science, 2013, 342, 463–466.
7. T. Röckmann, C. A. M. Brenninkmeijer, G. Saueressig, P. Bergamaschi, J. N. Crowley, H. Fischer and P. J. Crutzen, Science, 1998, 24, 544–546.
8. A. K. Huff and M. H. Thiemens, Geophys. Res. Lett., 1998, 25, 3509–3512.
9. H. K. Chagger, D. Hainsworth, P. M. Patterson, M. Pourkashanian and A. Williams, 26th Symposium (International) on Combustion, 1996, vol. 26, pp. 1859–1865.
10. J. C. Gómez Martin, M. A. Blitz and J. M. C. Plane, Phys. Chem. Chem. Phys., 2009, 11, 10945–10954.
11. M. R. Zachariah and W. Tsang, J. Phys. Chem., 1995, 99, 5308–5318.
12. Reaction Rate Constant Computations: Theories and Applications, ed. K. Han and T. Chu, Royal Society of Chemistry, London, 2014.
13. G. Li, L. Zhou, Q.-S. Li, Y. Xie and H. F. Schaefer, Phys. Chem. Chem. Phys., 2012, 14, 10891–10895.
14. Y. Guo, M. Zhang, Y. Xie and H. F. Schaefer, J. Chem. Phys., 2013, 139, 041101.
15. Y. Hao, J. Gu, Y. Guo, M. Zhang, Y. Xie and H. F. Schaefer, Phys. Chem. Chem. Phys., 2014, 16, 2641–2646.
16. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
17. R. J. Bartlett, J. D. Watts, S. A. Kucharski and J. Noga, Chem. Phys. Lett., 1990, 165, 513–522.
18. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
19. T. H. Dunning Jr, K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244–9253.
20. CFOUR, a quantum chemical program package written by J. F. Stanton, J. Gauss, M. E. Harding and P. G. Szalay, with contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, L. Cheng, O. Christiansen, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. A. Matthews, T. Metzroth, D. P. O'Neill, D. R. Price, E. Prochnow, K. Ruud, F. Schiffmann, W. Schwalbach, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang and J. D. Watts, with the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jorgensen and J. Olsen), and ECP routines by A. V. Mitin and C. van Wullen, 2010.
21. K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure Constant of Diatomic Molecules, van Nostrand Reinhold, New York, 1979.
22. O. Kostko, M. Ahmed and R. B. Metz, J. Phys. Chem. A, 2009, 113, 1225–1230.
23. C. L. Darling and H. B. Schlegel, J. Phys. Chem., 1993, 97, 8207–8211.
24. J. Y. Ma, J. Li and H. Guo, J. Phys. Chem. Lett., 2012, 3, 2482–2486.
25. C. Xie, J. Li, D. Xie and H. Guo, J. Chem. Phys., 2012, 137, 024308.
26. L. Andrews and M. Mccluskey, J. Mol. Spectrosc., 1992, 154, 223–225.
27. M. W. Chase, NIST-JANAF Thermochemical Tables, J. Phys. Chem. Ref. Data, 4th edn, 1998, pp. 959–1951, Monograph 9.
28. D. L. Hildenbrand and K. H. Lau, J. Chem. Phys., 1994, 101, 6076–6079.
29. J. Li, Y. Wang, B. Jiang, J. Ma, R. Dawes, D. Xie, J. Bowman and H. Guo, J. Chem. Phys., 2012, 136, 041103.

---