X-ray induced fragmentation of size-selected salt cluster-ions stored in an ion trap

Abstract

A method for spectroscopic characterization of free ionic clusters and nanoparticles utilizing X-ray synchrotron radiation is presented. We demonstrate that size-selected ammonium bisulphate cluster ions, NH₄⁺(NH₄HSO₄)_n, captured in a linear ion trap, exhibit well-defined core-level absorption edges in the reconstructed fragment-ion abundance spectra. In addition to the specific photo-fragmentation pathways observed at the N1s-, O1s- and S2p-edges, dissociation also occurs as a consequence of clusters colliding with helium present as buffer gas in the ion trap. Separate off-beam experiments were conducted to establish the activation kinetics of these collision induced dissociation processes. Furthermore, it is demonstrated that the electrons released upon photoionization of background helium are too few in number to produce multiply charged cluster ions, and thereby induce fragmentation of the salt clusters, to any significant degree. The mechanisms for photon absorption and subsequent cluster fragmentation are analysed and discussed. In addition to its inherent element specificity, the method holds promise for cluster structure elucidation resulting from the sensitivity of the near edge absorption structure to the local chemical environment of the excited atom.

---

Introduction

Gas-phase clusters constitute the logical bridge between the gaseous and condensed phases, and the study of cluster properties as a function of size provides fundamental insight of importance to chemistry and physics.¹ Mass spectrometry has been invaluable for cluster research, because it allows for sensitive and unequivocal identification of the clusters according to their mass-to-charge ratio. Both initially neutral and inherently charged clusters can be studied; the large selection of mass spectrometric instrumentation available allows for ion formation, manipulation, reaction and characterization of a wide range of cluster types. With the advent of high-pressure ion sources² and ion flow tubes,³ starting from the 1960s, it became possible to study ion–molecule reactions leading to association, and thereby also cluster formation, in a more systematic manner than previously. In due course, this historical development resulted in the production of a substantial amount of thermochemical data on the binding of monomer units in ionic molecular clusters.^4–6 A complementary approach to studying cluster thermochemistry by association is collisional induced dissociation (CID); although it should be pointed out that the latter is a kinetic rather than an equilibrium thermodynamic method.^7–9

Besides photoionization and electron impact/chemical ionization, charged clusters are conveniently formed using common ionization techniques like fast atom bombardment,¹⁰ electrospray ionization (ESI),^11–13 matrix-assisted laser desorption/secondary ion mass spectrometry,^14–16 and by laser desorption/ionization in association with supersonic expansion.^17,18 In addition, a range of more specialized experimental techniques can also be used for this purpose.¹⁹

The chemical reactivity of ionic clusters has been a research field with abundant activity,²⁰ including also the particular relevance of metal clusters to catalysis.^21,22 The structure of ionic clusters can be inferred from ion mobility measurements,^23,24 by electron diffraction,^25,26 and from energies by consideration of the variation in cluster abundance with size (magic numbers).^27–31 With the exception of laser induced fluorescence,³² it is challenging to perform absorption spectroscopy for ionic clusters present in a mass spectrometer because of the low target density. However, the mass spectrometric method offers an alternative approach, namely to study cluster dissociation as a function of wavelength, sometimes termed “action spectroscopy”, in the infrared region (by multiphoton absorption or single photon absorption using noble gas atom “tagging”),^33–37 in the ultraviolet/visible region,^38–41 and in the X-ray region using both linearly^42,43 and circularly^44,45 polarized radiation. Insight into the electronic properties, including magnetism, has also been obtained by electron photodetachment.⁴⁶ The interpretation of structural and spectroscopic data of clusters has been greatly facilitated by the use of computational quantum chemistry.^47–49

The fine structure of the X-ray absorption spectra provides unique insights into the electronic structure of molecular systems; core electron binding energies are particularly sensitive to the local chemical environments (chemical shift). Efforts in X-ray action spectroscopy of ionic clusters have been focused on atomic clusters, and we are not aware of any studies of this kind for molecular clusters. While the interest in metal clusters has been focused on catalysis, electron delocalization and magnetic properties, molecular clusters typically display localized electronic structures. Clusters held together by hydrogen bonds are especially fascinating, and it would be valuable to establish an X-ray spectroscopic method to study hydrogen bonding and protolysis within clusters of this kind, in particular for a better understanding of atmospheric water nucleation and hydrogen bonding in biological molecules.

In an effort to develop an experimental approach for this purpose, we build on an existing method for protein- and peptide-ion characterization in which a commercial ion-trap mass spectrometer equipped with an electrospray ion source is combined with a tuneable source of synchrotron radiation. As a test system we have selected the cationic ammonium bisulphate clusters, NH₄⁺(NH₄HSO₄)_n, hereafter abbreviated by A⁺(AS)_n. These clusters are relatively easy to produce in good abundance by electrospray, and are directly relevant for nucleation of tropospheric particles. Observations suggest that sulphuric acid and ammonia play key roles in the first nucleation steps due to a combination of their gaseous nature and their strong bonding to water.^50–56

Our long-term goal is to establish the detailed interaction mechanisms between ammonia/amines, sulphuric acid and water molecules and elucidate the structures of clusters formed among these species. In the present context, we will limit ourselves to present our first experimental findings, and to discuss the nature of the processes involved in ion activation leading to cluster fragmentation, including the interaction with the helium contained in the ion trap.

Results

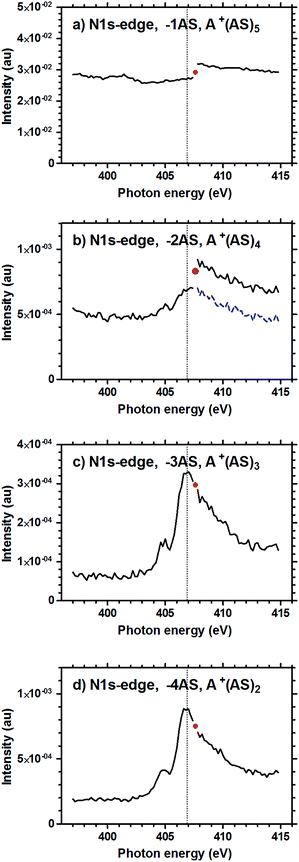
In the experiments, size selected A⁺(AS)₆ clusters were stored in the mass spectrometer ion-trap and exposed to X-rays for 550 ms, after which the resulting fragments and remaining parent ions were detected (please refer to the section Experimental methods for details). The measurements showed that dissociation generally results in the formation of smaller A⁺(AS)_n (n < 6) clusters. Small amounts of H⁺(AS)_n fragments were also detected, but with abundances one order of magnitude lower than the abundances of the corresponding A⁺(AS)_n fragments. The ESI contains a mass spectrum showing the cluster distribution resulting from electrospray ionization, i.e., before size selection (Fig. S1†); there is also a mass spectrum showing the detected ions after a size selected cluster A⁺(AS)₆ has been exposed to X-rays (Fig. S2†). Peaks in the abundance spectra corresponding to the loss of 1–4 AS units were normalized to the reactant ion intensity, and are given as functions of photon energy in Fig. 1–3 below.

Fig. 1 Relative intensity of fragmentation peaks corresponding to the loss of 1 AS unit (panel a), 2 AS units (panel b), 3 AS units (panel c) and 4 AS units (panel d) from the A⁺(AS)₆ cluster ion in the energy region of the oxygen-1s absorption edge. Original measurement in black (data points lost for 534.2–535.4 eV); completing measurement in red. The vertical dotted line is included to guide the eye.

Fig. 2 Relative intensity of fragmentation peaks corresponding to the loss of 1 AS unit (panel a), 2 AS units (panel b), 3 AS units (panel c) and 4 AS units (panel d) from the A⁺(AS)₆ cluster ion in the energy region of the nitrogen-1s absorption edge. Original measurement in black (a single data point lost at 407.6 eV); completing measurement shown as a red dot. The dashed blue line in panel b is a copy of the solid line translated downwards. The vertical dotted line is included to guide the eye.

Fig. 3 Relative intensity of fragmentation peaks corresponding to the loss 1 AS unit (panel a), 2 AS units (panel b), 3 AS units (panel c) and 4 AS units (panel d) from the A⁺(AS)₆ cluster ion in the energy region of the sulphur-2p absorption edge. The vertical dotted line is included to guide the eye.

Fig. 1 shows the result of the measurement on the A⁺(AS)₆ clusters in the photon energy range of 525–550 eV, corresponding to the oxygen-1s (O1s) absorption. Some data points were lost during the original measurement (see the Experimental methods section); this is observed as gaps in the black curves. An additional measurement, shown in red, was performed immediately afterwards in order to complete the set. The curves for A⁺(AS)₃ and A⁺(AS)₂ (panels c and d) corresponding to the loss of 3 and 4 AS units, respectively, display distinct adsorption edges similar to a molecular O1s photoabsorption spectrum. The two peak shapes are equal within experimental uncertainty. However, the curve for A⁺(AS)₅ (panel a) resulting from the loss of a single AS unit is almost featureless, and the signal is orders of magnitude stronger than the others. On these grounds it seems unlikely that the ion fragmentation process in which only one AS unit is lost is the result of a specific excitation process involving the O1s electrons. The nature of this process will be further discussed below. For all intents and purposes the same points can also be made for the spectrum reproduced in Fig. 1b for A⁺(AS)₄, although the signal is one order of magnitude weaker than that of A⁺(AS)₅. The disjointed nature of the completing measurements for A⁺(AS)₅ and A⁺(AS)₄ shown in red colour is interesting. The completing measurement was performed immediately after the original measurement; for Fig. 1a and b, the signal levels of the completing measurement (red curves) correspond to the high-energy ends of the original measurement (black curves). This indicates that the slow decrease in intensity of these two fragment signals during data acquisition is dependent upon other factors than photon energy. Such factors could be He pressure and temperature, suggesting that these processes are background induced rather than X-ray induced. In contrast, the perfect overlap of the completing measurement and the original measurement in Fig. 1c and d should be noted.

The reconstructed spectra corresponding to the measurement for photon energies in the range 396–415 eV, corresponding to the nitrogen-1s (N1s) absorption, are reported in Fig. 2. Also in this case data were lost for a narrow photon energy range, and one data point was re-measured immediately after the first scan; the corresponding data point is shown as a red dot. Just like in the O1s experiment of Fig. 1, distinct absorption edges were obtained for the fragments A⁺(AS)₃ and A⁺(AS)₂ (Fig. 2c and d). Also for this energy range the spectrum for A⁺(AS)₅ lacks fine structure, as seen in Fig. 2a. However, there is a jump in the detected intensity of the A⁺(AS)₅ fragment occurring at the point of data loss. This shift in intensity is not observed in Fig. 2c or d. Interestingly, some structure can be seen for A⁺(AS)₄ (from the loss of 2 AS units), in Fig. 2b. An absorption edge can be identified, likely superimposed on a signal due to a pressure/temperature dependent process. Aligning the fragmentation curve after the jump to the curve before the jump (shown as a dashed blue line in Fig. 2b) clearly reproduces the shape of the absorption edges as seen in Fig. 2c and d.

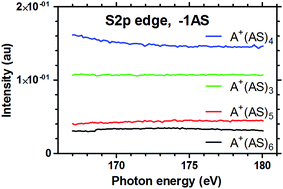
Fig. 3 shows the results of the fragmentation of A⁺(AS)₆ in the photon energy range 167–180 eV, corresponding to sulphur-2p (S2p) absorption. Again, we can see the same general trends as observed for the O1s and N1s energy ranges: distinct absorption edges for A⁺(AS)₃ and A⁺(AS)₂ (Fig. 3c and d) and an essentially featureless spectrum for A⁺(AS)₅ (Fig. 3a). The fragment A⁺(AS)₄ (Fig. 3b) can here be seen to contain the absorption edge just like A⁺(AS)₃ and A⁺(AS)₂ although there is more noise in the signal.

During the measurement sessions it became evident that the loss of AS, and to a minor degree the loss of 2AS, could be due to a He pressure dependent process, most likely due to CID. Helium is present at a pressure of approximately 10⁻³ mbar, and is necessary for trapping and stabilization of the ion trajectories within the linear quadrupole ion trap. The low mass of helium only allows for relatively little energy transfer and we envisage a slow heating process due to subsequent collisions between the trapped clusters and helium, leading to dissociation as follows:

Separate experiments were performed for each of the clusters A⁺(AS)_n with n = 1–6 to investigate the kinetics of dissociation in the absence of X-rays; the results are shown in Fig. 4. It is seen that at a fixed He pressure the decay of the ion is exponential (linear in the semi-logarithmic plot), indicating in all cases a quasi-unimolecular process, in accordance with a collision induced process. It is noteworthy that the dissociation rate varies with the cluster size, with the smallest sizes (n = 1 and 2) giving rise to the slowest dissociation. However, the dissociation rate does not increase monotonically with cluster size, as is evident from Fig. 4.

Fig. 4 Relative intensity of the parent ions A⁺(AS)_n (with n = 1–6) for different ion-trap storage times. Cluster size n is also indicated next to the data series for clarity. Note the semi-logarithmic scale.

It should be mentioned that in the measurements there was an isobaric overlap of the ions by the doubly charged ions of twice the mass, for instance, the ion A₂²⁺(AS)₁₂ overlapped A⁺(AS)₆ in the mass spectra. This is detected by the formation of fragment clusters larger than the nominal parent ion, e.g., A⁺(AS)₈, A⁺(AS)₉, A⁺(AS)₁₀. Fortunately, the presence of the overlapping ions can be detected also by changes in the isotopic pattern of the ion we wish to study, and this fact can be used to separate the two. Generally, the presence of doubly charged clusters was greater for the larger clusters. For most sizes, the overlapping ion was no more than 10% of the detected parent ion intensity; the maximum value was 35% and was observed for n = 4. Nevertheless, a comparison of the data in Fig. 4 before and after compensating for the isobaric overlap showed that the effect on the results was very small. The overlapping ions were also not found to influence the results of the X-ray experiments.

The exponential decrease with time of the populations of all six different cluster sizes presented in Fig. 4 gives a strong hint about the heating mechanism in the cluster–helium collisions and the relative stability of the clusters. The exponential decrease of concentrations is observed also for short times, which means that the clusters equilibrate to a stationary energy distribution rapidly compared with the time scale of the decay, and that the distribution is maintained during the whole ten seconds of the experiment for the surviving clusters. The energy distribution is different for each cluster. The equilibration time can be estimated as follows: the helium–cluster collision frequency is the product of the helium atoms thermal speed (1400 m s⁻¹); the density of helium at 10⁻³ mbar (2.4 × 10¹⁹ m⁻³); and the cluster–helium collision cross section, for which we will use the geometric value, 27 × 10⁻²⁰ × n^2/3 m². This gives the collision frequency ν = 9000 n^2/3 s⁻¹. This neglects to take into account the motion of the ions in the trap, which would raise the frequency.

For the average energy transfer in a single collision between a helium atom and a cluster at temperatures T_He and T, respectively, we will use the value −2k_B(T − T_He), corresponding to an average heating for T < T_He. For the heat capacity of the cluster, C, we assume that only the six frustrated rotational and translational degrees of freedom of each of the n ion pairs and the ammonium ion are thermally active. The intramolecular vibrations are considered too high in frequency to be excited under the present conditions. In the high-temperature limit of the harmonic model, this gives a heat capacity of C = (6(n + 1) − 6)k_B = 6nk_B after subtracting the contributions from the rotational and translational degrees of freedom of the whole cluster. Thus, we get a cooling rate of 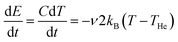, or K s⁻¹, where ν is the gas–cluster collision frequency calculated above. Thus the difference in cluster and gas temperature decreases exponentially with the time constant 0.33 n^1/3 ms. After n^1/3 ms the difference is reduced to 5% of the initial value. Thus the time needed to reach a stationary energy distribution is considerably shorter than any measurement time, even if allowing for liberal corrections to this estimate.

The translational energy of the ions is not equilibrated to the trap temperature and the stationary state internal energy distribution is consequently not thermal at 300 K. It is therefore not possible to extract absolute activation energies from the measured decay rate coefficients. It is possible to find the activation energies relative to an effective temperature using an Arrhenius expression for the decay rate coefficient:

E_a/k_BT_e = ln(Ω/k_n), (2)

where E_a is the activation energy, T_e the effective temperature, k_n the measured rate coefficient and Ω the Arrhenius frequency factor. Using Ω = n^2/3 10¹⁶ s⁻¹, T_e = 300 K and k_n values between 6.27 × 10⁻⁴ and 2.48 × 10⁻¹ s⁻¹ one gets activation energies between 1.0 and 1.2 eV (96–116 kJ mol⁻¹).

The hypothesis that CID is the main physical process behind the featureless −1AS loss signals of Fig. 1–3 is substantiated by the data gathered in Fig. 5. It shows the relative signals for the measurements of −1AS obtained in the presence of X-ray irradiation for each of the clusters A⁺(AS)_n with n = 3–6 (the data for A⁺(AS)₆ in Fig. 5 is identical to the data in Fig. 3a). For all measurements it is clear that the relative signal varies during the long measurement periods, for some clusters extending to 10 h. For each single measurement point the cluster ions are trapped for a period of 600 ms (irradiated for 550 ms), which in comparison with Fig. 4 is short, indicating that the CID should be most important for −1AS, but that also some −2AS should be observed. However, the relative amount of −1AS for each cluster size in Fig. 5 should be roughly proportional to the slope of the curves in Fig. 4, and this is clearly the case.

Fig. 5 Relative intensity of the fragmentation peaks corresponding to loss of a single AS unit loss from the clusters A⁺(AS)₆, A⁺(AS)₅, A⁺(AS)₄ and A⁺(AS)₃ in the energy region of the S2p absorption edge.

We have also considered other background processes besides CID that may cause unspecific dissociation. The helium in the trap will be ionized in a non-resonant process:

He + hν → He⁺ + e⁻ (3)

While, in principle, the recombination energy (or, equivalently, the first ionization energy) of He⁺ of I_He = 24.6 eV is sufficient for exothermic charge transfer to occur according to e.g.:⁵⁷

He⁺ + A⁺(AS)_n → He + A(AS)_n²⁺ → A⁺(AS)_n−1 + AS⁺ (4)

we consider it unlikely that the cross section of the first step of Reaction (4) would be of considerable significance since the trapped ions will have insufficient translational energy to overcome the barrier due to the Coulomb repulsion between the reactant ions.⁵⁸ However, the electrons formed by photoionization of helium are energetic and constitute a possible source for further ionization of the target ions by electron impact, eventually producing short-lived doubly charged species that may fragment to give A⁺(AS)_x ions. This will be discussed in the following.

Photoionization of target ions takes place at a rate of η^p_i = ϕ_pσ^p_i(E)N_i, where ϕ_p is the photon flux, N_i is the number of ions in the part of the trap that is illuminated by the X-rays and σ^p_i(E) is the cross section of ionization of target ions at the photon energy E. A similar expression may be formed for the rate of photoionization of helium, η^p_He = ϕ_pσ^p_He(E)N_He, where the subscripted quantities are defined in a completely analogous manner as for the target ions. The photoelectrons emitted from helium have a kinetic energy E − I_He, and at a sufficiently high pressure of helium, these photoelectrons may compete with X-ray photons with respect to ionizing the target ions. Factors that favor electron-impact ionization are the possibility that the cross-section for electron-impact ionization may be significantly larger than that for photon-induced ionization, i.e., σ^e_i(E − I_He) ≫ σ^p_i(E), and that the number of target ions exposed to photoelectrons may be much larger than the number of ions exposed to photons. The first item is difficult to assess due to lack of data on absolute cross sections of either kind. The necessary information is however available for helium and with the photon energy used for ionization at the S2p edge (165 eV) as an example, the ratio σ^e_He(E − I_He)/σ^p_He(E) is near 270.^59,60

The difference in effective sample volume between the two ionization processes must be considered along with the difference between electron and photon fluxes. This may be done in terms of a simple analytical model that is based on an idealized geometry of the ion trap as a cylinder of radius R_t and containing constant ion and helium number densities ρ_i and ρ_He = p_He/k_BT such that ρ_i ≪ ρ_He. The sample is exposed to a rather narrow beam of X-rays such that the beam is co-centric with the trap and has a radius R_p < R_t. An additional, simplifying assumption is that helium photoelectrons are emitted in a radial direction, i.e., normal to the axial direction of the trap, which is a good approximation in the case of unpolarized photons. While the full derivation of the model is given as ESI,† we will make use of the resulting tight upper bound to the ratio of electron-impact to photo-ionization rates of the target ions, given by

At the relevant experimental conditions: a helium pressure of 10⁻³ mbar at 300 K, corresponding to ρ_He = 2.4 × 10¹⁹ m⁻³; a photon energy of 165 eV, such that σ^p_He = 0.123 Mb = 0.123 × 10⁻²² m²;⁵⁹ and a trap diameter of 2 mm, we get η^e_i/η^p_i = 3 × 10⁻⁷ × σ^e_i(E − I_He)/σ^p_i(E). Assuming a value for σ^e_i(E − I_He)/σ^p_i(E) of 1000, which is more than thrice the value for helium, electron impact accounts for only 0.03% of all target ionization events.

After having discussed how the spectra are influenced by cluster ionization and fragmentation due to collisions and photoelectrons, we will now return to discuss the X-ray absorption at the core–shell edges. The profiles observed for the −3AS and −4AS spectra displayed in Fig. 1–3 are characteristic for the resonant X-ray absorption spectra in the vicinity of core–shell absorption edges (K-edges for nitrogen and oxygen and L-edge for sulphur). In the −3AS and −4AS spectra for nitrogen and oxygen a pre-edge feature is clearly observed. The excitation of a core electron by the absorption of an X-ray photon is a well-documented process from X-ray absorption spectroscopy of neutral species.⁶¹ Briefly, in the case of a singly charged cluster-ion, the core electron is excited either to a low-lying, initially empty orbital, or it is ionized to the continuum. In either case, the core hole will be filled by a valence electron within a few femtoseconds, either accompanied by the emission of an energetic Auger electron or accompanied by X-ray emission. Since the branching ratio between Auger and X-ray emission is strongly in favour of the former in the currently studied energy range, the resulting species will be either doubly- or triply-charged and very likely dissociate by a Coulomb-explosion process. As a matter of fact, we find that among the “clean” X-ray induced spectra (−4AS, −3AS and to some extent −2AS), the one corresponding to the smallest ionic fragment, A⁺(AS)₂, is the most abundant. This finding is consistent with a Coulomb-explosion process, which is expected to lead to small singly charged fragments. Unfortunately, due to restrictions on the lower m/z limit imposed by the experimental setup, we were not able to probe the mass range corresponding to the smallest species, A⁺ and A⁺(AS)₁.

As stated above, in addition to the above processes, we have also considered a flux dependent baseline in the resonant X-ray induced fragmentation, which was found to be insignificant.

Experimental method

The experiments were performed at the SOLEIL synchrotron radiation facility (France) at the soft X-ray PLEIADES beamline⁶² dedicated to the ultrahigh resolution studies of isolated species, from atoms,⁶³ molecules,⁶⁴ and ions,⁶⁵ to clusters⁶⁶ and nanoparticles. We used a linear ion-trap mass spectrometer (LTQ XL, Thermo Electron, San Jose, CA, USA) connected to the beamline. We used the same general scheme of coupling the beamline and the mass spectrometer as described in earlier publications,⁶⁷ but with some improvements.

Ammonium bisulphate cluster ions A⁺(AS)_n were produced using an electrospray ionization probe (HESI II, Thermo Scientific), by spraying a 17 mM solution of ammonium sulphate in water/methanol 1 : 1. The ion source was at a temperature of approximately 30 °C and operated at 4.5 kV (100 μA current) with a flow rate of 10 μL min⁻¹. The capillary temperature is tuned according to a trade-off between ion intensity and preserving the larger clusters; it was set to 275 °C. All the ion optics parameters were tuned automatically to maximize the cluster ion signal. The ions were transferred to the linear, cylindrical ion trap of length 30 mm and diameter 2 mm, where a single cluster size was selected and all other ions expelled. The mass spectrometer was tuned in CID mode with the collision energy tuned to zero. The m/z width for the selection of a single ion was set to 15 Th (Da per elementary charge). The mass spectrometer low mass cut off is determined by the instrument specific activation parameter, Q, which was adjusted to 0.18 in order to observe the lighter clusters. Normal scan rate was used. The instrument maintained a pressure of approximately 10⁻³ mbar of helium in the ion trap in order to collisionally slow down the stored ions as they enter the ion trap.⁶⁸

For the X-ray measurements, ion clusters of size n = 6 were stored in the ion trap for 600 ms. The activation trigger of the LTQ was connected to the input of a digital delay generator (DG645 from Stanford Research Systems, Sunnyvale, CA, USA); the output of the delay generator was connected to a photon shutter on the beamline.⁶⁹ The delay generator opened the shutter for 550 ms. Hence, after 550 ms irradiation, the ions were stored for an additional 50 ms before detection. This procedure has proven useful to strongly reduce the background noise coming from the parasitic ionization of the background gases in the vacuum manifold containing the ion trap. Indeed, the photon energy range of the present study is above the ionization energy of helium. For each photon energy, data were accumulated for two minutes on the selected ion and then averaged; this corresponds to approximately 220 individual tandem mass spectra. Subsequently, the photon energy was incremented and the procedure repeated.

The fragment-specific photoabsorption spectra were recorded over three ranges of photon energies: 167–180 eV (with an energy step of 0.15 eV), 397–415 eV (0.20 eV step), and 525–549 eV (0.20 eV step), corresponding to the S2p-, the N1s- and the O1s absorption edges, respectively. In the S2p and N1s measurements, the photon beam was monochromatized by means of a gold-coated silicon diffraction plane grating with 400 lines per mm, varied line spacing and varied groove depth. With the exit slit set to 400 μm and 200 μm, this provided photon bandwidths of 0.12 eV and 0.22 eV around the S2p edge and the N1s edge, respectively. For the O1s edge measurements a diffraction grating with 2400 lines per mm was used instead, providing an approximate bandwidth of 0.28 eV with an exit slit of 400 μm. The photon beam cross section area at the sample was 3.7 × 10⁻⁸ m² with the 200 μm exit slit and 5.9 × 10⁻⁸ m² with the 400 μm exit slit.

Synchrotron beam loss occurred at certain points during the allotted measurement time, mainly due to local thunderstorms. This resulted in some measurements being lost or unusable; however, completing measurements were collected immediately after the completion of the original experimental run.

When exploring the time-dependency of the collision induced fragmentation processes occurring in the trap in the absence of X-rays, the ions were stored in the ion-trap for a defined duration of time. Ammonium bisulphate clusters with n = 2–6 were selected and stored for 100, 250, 500, 750, 1000, 2000, 3500, 5000, 7000 and 10 000 ms. In each measurement, data was accumulated for 5 minutes.

The mass spectrometric abundances were normalized to the reactant ion intensity. Corrections for variations in photon flux were deemed unnecessary for the current purposes.

Reagents

Ammonium sulphate: 99.5%, Sigma-Aldrich, Saint-Quentin-Fallavier, France. Methanol: Chromasolv, Sigma-Aldrich, Saint-Quentin-Fallavier, France. Water was purified using a Milli-Q system (Millipore, Saint-Quentin en Yvelines, France).

Conclusions

Based on our experimental results and the theoretical considerations presented above a clear picture concerning the X-ray induced fragmentation of small cluster-ions has emerged, with the following characteristics:

(i) Resonant X-ray induced dissociation (RXID)—the process of primary interest in this context—is observed to take place, as is evident from the spectra reconstructed from the photon energy dependent variation in the abundances of fragment ions. These spectra, recorded around the N1s-, the O1s- and the S2p absorption edges, display similar characteristics to X-ray photoabsorption spectra. As a result of the X-ray absorption, small fragment ions are formed, typical for Coulomb explosion of doubly and triply charged clusters.

(ii) Considerable fragmentation is also observed to take place resulting from collisional activation by the background carrier gas (helium), as probed in separate off-line experiments. This fragmentation is showed to result in an exponential decay of cluster abundances. It is a rather slow process (on the time scale of the irradiation period) with sequential loss of monomer (here: AS) units; it has a major influence on the appearance of the fragment ion spectrum due to inducing abundant loss of a single monomer unit, and, to a smaller extent, two monomer units. For the smaller fragments (loss of 3 or 4 AS) this process can be neglected, and the corresponding fragment ion spectra can be considered to be results of X-ray induced processes only.

Careful analysis indicates that the electrons generated by the photoionization of background helium are only a minor source of fragment ions formed in the experiments described here. We also have observed that flux dependent baseline in the resonant X-ray induced fragmentation is insignificant.

On this basis we conclude that we have established a novel experimental protocol for X-ray absorption spectroscopy of molecular cluster ions that is ripe for being developed into a general-purpose method for detailed structure analysis of small clusters. In this respect, the sensitivity of the core electron resonant excitation and ionization energies and spectral profiles to the chemical environment is the key factor. In particular, for clusters of relevance to nucleation processes in the atmosphere, this could become an ideal tool for probing delicate details of hydrogen bond patterns and intramolecular protolysis within such clusters.

Acknowledgements

The experiments were performed at the PLEIADES beamline at SOLEIL Synchrotron facility (France), during beamtime allocated under proposals number 20120182 and 20130120. We are grateful to E. Robert for technical assistance and to the SOLEIL staff for stable operation of the equipment and storage ring during the experiments. T.J., M.R., and J.N. are grateful to the EU through the CALIPSO program for travel support, while E.U., G.M., K.H., K.B., and O.B. are grateful to Professor Hanna Vehkamäki and the Nordforsk network NICITA for travel support. GS acknowledge support from the Brazilian funding agency CAPES (8683-11-5) for scholarship grant. This work was supported by the Norwegian Research Council by the Grants no. 205512/F20, Nano-solvation in Hydrogen-Bonded Clusters; and no. 179568/V30, to the Centre of Theoretical and Computational Chemistry through their Centre of Excellence program. This work was supported by the Agence Nationale de la Recherche Scientifique, France, under the project ANR-08-BLAN-0065. CM and MP acknowledge the COST action CM1204 – XUV/X-ray light and fast ions for ultrafast chemistry (XLIC).

References

1. A. W. Castleman and K. H. Bowen, J. Chem. Phys., 1996, 100, 12911–12944.
2. F. H. Field, J. L. Franklin and M. S. B. Munson, J. Am. Chem. Soc., 1963, 85, 3575–3583.
3. E. E. Ferguson, F. C. Fehsenfeld and A. L. Schmeltekopf, in Advances in Atomic and Molecular Physics, ed. D. R. Bates and E. Immanuel, Academic Press, 1969, vol. 5, pp. 1–56.
4. A. W. Castleman and R. G. Keesee, Chem. Rev., 1986, 86, 589–618.
5. P. Kebarle, Int. J. Mass Spectrom., 2000, 200, 313–330.
6. M. Meot-Ner, Chem. Rev., 2005, 105, 213–284.
7. T. F. Magnera, D. E. David and J. Michl, Chem. Phys. Lett., 1991, 182, 363–370.
8. N. F. Dalleska, K. Honma and P. B. Armentrout, J. Am. Chem. Soc., 1993, 115, 12125–12131.
9. P. B. Armentrout, Annu. Rev. Phys. Chem., 2001, 52, 423–461.
10. G. Puzo and J. C. Prome, Org. Mass Spectrom., 1985, 20, 288–291.
11. B. Ganem, Y. T. Li and J. D. Henion, J. Am. Chem. Soc., 1991, 113, 7818–7819.
12. C. Y. Hao, R. E. March, T. R. Croley, J. C. Smith and S. P. Rafferty, J. Mass Spectrom., 2001, 36, 79–96.
13. D. X. Zhang, L. M. Wu, K. J. Koch and R. G. Cooks, Eur. Mass Spectrom., 1999, 5, 353–361.
14. R. G. Orth, H. T. Jonkman and J. Michl, J. Am. Chem. Soc., 1981, 103, 1564–1565.
15. M. Karas and R. Kruger, Chem. Rev., 2003, 103, 427–439.
16. J. Cveticanin, V. Koteski, J. Belosevic-Cavor, A. Radosavljevic, Z. Kacarevic-Popovic, D. Trpkov, D. Acimovic, Z. R. Miladinovic, M. Cindric and O. Neskovic, Vacuum, 2013, 89, 47–52.
17. T. G. Dietz, M. A. Duncan, D. E. Powers and R. E. Smalley, J. Chem. Phys., 1981, 74, 6511–6512.
18. M. Dey and J. Grotemeyer, Eur. Mass Spectrom., 1995, 1, 95–103.
19. W. A. de Heer, Rev. Mod. Phys., 1993, 65, 611–676.
20. G. Niedner-Schatteburg and V. E. Bondybey, Chem. Rev., 2000, 100, 4059–4086.
21. M. E. Geusic, M. D. Morse and R. E. Smalley, J. Chem. Phys., 1985, 82, 590–591.
22. T. F. Magnera, D. E. David and J. Michl, J. Am. Chem. Soc., 1987, 109, 936–938.
23. J. T. Moseley, R. M. Snuggs, D. W. Martin and E. W. Mcdaniel, Phys. Rev., 1969, 178, 240–248.
24. D. E. Clemmer and M. F. Jarrold, J. Mass Spectrom., 1997, 32, 577–592.
25. M. Maier-Borst, D. B. Cameron, M. Rokni and J. H. Parks, Phys. Rev. A, 1999, 59, R3162–R3165.
26. T. Rapps, R. Ahlrichs, E. Waldt, M. M. Kappes and D. Schooss, Angew. Chem., Int. Ed., 2013, 52, 6102–6105.
27. S. S. Lin, Rev. Sci. Instrum., 1973, 44, 516–517.
28. J. Q. Searcy and J. B. Fenn, J. Chem. Phys., 1974, 61, 5282–5288.
29. J. L. Kassner and D. E. Hagen, J. Chem. Phys., 1976, 64, 1860–1861.
30. B. K. Teo and N. J. A. Sloane, Inorg. Chem., 1985, 24, 4545–4558.
31. K. Hansen, P. U. Andersson and E. Uggerud, J. Chem. Phys., 2009, 131, 124303.
32. L. F. Dimauro, M. Heaven and T. A. Miller, Chem. Phys. Lett., 1984, 104, 526–532.
33. R. L. Woodin, D. S. Bomse and J. L. Beauchamp, J. Am. Chem. Soc., 1978, 100, 3248–3250.
34. M. Okumura, L. I. Yeh and Y. T. Lee, J. Chem. Phys., 1985, 83, 3705–3706.
35. P. Ayotte, G. H. Weddle, J. Kim and M. A. Johnson, Chem. Phys., 1998, 239, 485–491.
36. L. I. Yeh, M. Okumura, J. D. Myers, J. M. Price and Y. T. Lee, J. Chem. Phys., 1989, 91, 7319–7330.
37. K. R. Asmis and D. M. Neumark, Acc. Chem. Res., 2012, 45, 43–52.
38. R. C. Dunbar and B. B. Hutchins, J. Am. Chem. Soc., 1974, 96, 3816–3820.
39. W. A. Deheer, K. Selby, V. Kresin, J. Masui, M. Vollmer, A. Chatelain and W. D. Knight, Phys. Rev. Lett., 1987, 59, 1805–1808.
40. J. Tiggesbäumker, L. Köller, H. O. Lutz and K. H. Meiwes-Broer, Chem. Phys. Lett., 1992, 190, 42–47.
41. M. Schmidt and H. Haberland, Eur. Phys. J. D, 1999, 6, 109–118.
42. K. Hirsch, J. T. Lau, P. Klar, A. Langenberg, J. Probst, J. Rittmann, M. Vogel, V. Zamudio-Bayer, T. Möller and B. von Issendorff, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154029.
43. S. Krummacher, M. Biermann, M. Neeb, A. Liebsch and W. Eberhardt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 8424–8429.
44. S. Peredkov, A. Savci, S. Peters, M. Neeb, W. Eberhardt, H. Kampschulte, J. Meyer, M. Tombers, B. Hofferberth, F. Menges and G. Niedner-Schatteburg, J. Electron Spectrosc. Relat. Phenom., 2011, 184, 113–118.
45. S. Peredkov, M. Neeb, W. Eberhardt, J. Meyer, M. Tombers, H. Kampschulte and G. Niedner-Schatteburg, Phys. Rev. Lett., 2011, 107, 233401.
46. G. Ganteför and W. Eberhardt, Phys. Rev. Lett., 1996, 76, 4975–4978.
47. T. P. Martin, Phys. Rep., 1983, 95, 167–199.
48. K. Laasonen and M. L. Klein, J. Chem. Phys., 1994, 98, 10079–10083.
49. F. Weigend and R. Ahlrichs, Philos. Trans. R. Soc., A, 2010, 368, 1245–1263.
50. T. Kurtén, L. Torpo, M. R. Sundberg, V. M. Kerminen, H. Vehkamäki and M. Kulmala, Atmos. Chem. Phys., 2007, 7, 2765–2773.
51. IPCC, in Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, ed. S. Solomon, D. Qin, M. Manning, Z. Chen, M. Marquis, K. B. Averyt, M. Tignor and H. L. Miller, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2007.
52. J. Merikanto, D. V. Spracklen, G. W. Mann, S. J. Pickering and K. S. Carslaw, Atmos. Chem. Phys., 2009, 9, 8601–8616.
53. M. Kulmala, Science, 2003, 302, 1000–1001.
54. J. Almeida, S. Schobesberger, A. Kürten, I. K. Ortega, O. Kupiainen-Määttä, A. P. Praplan, A. Adamov, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, N. M. Donahue, A. Downard, E. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, H. Henschel, T. Jokinen, H. Junninen, M. Kajos, J. Kangasluoma, H. Keskinen, A. Kupc, T. Kurtén, A. N. Kvashin, A. Laaksonen, K. Lehtipalo, M. Leiminger, J. Leppä, V. Loukonen, V. Makhmutov, S. Mathot, M. J. McGrath, T. Nieminen, T. Olenius, A. Onnela, T. Petäjä, F. Riccobono, I. Riipinen, M. Rissanen, L. Rondo, T. Ruuskanen, F. D. Santos, N. Sarnela, S. Schallhart, R. Schnitzhofer, J. H. Seinfeld, M. Simon, M. Sipilä, Y. Stozhkov, F. Stratmann, A. Tome, J. Tröstl, G. Tsagkogeorgas, P. Vaattovaara, Y. Viisanen, A. Virtanen, A. Vrtala, P. E. Wagner, E. Weingartner, H. Wex, C. Williamson, D. Wimmer, P. L. Ye, T. Yli-Juuti, K. S. Carslaw, M. Kulmala, J. Curtius, U. Baltensperger, D. R. Worsnop, H. Vehkamäki and J. Kirkby, Nature, 2013, 502, 359–363.
55. B. R. Bzdek, J. W. DePalma, D. P. Ridge, J. Laskin and M. V. Johnston, J. Am. Chem. Soc., 2013, 135, 3276–3285.
56. K. D. Froyd and E. R. Lovejoy, J. Phys. Chem. A, 2012, 116, 5886–5899.
57. Note: The B3LYP/6-31G(d) (second) vertical ionization energy of A(AS)⁺ is calculated to be 0.50 hartrees.
58. Note: Even at our highest photon energy, the recoil energy departed to He⁺ is only about twice the thermal kinetic energy. The low kinetic energy prevents He⁺ from approaching the positively charged target ions at a distance that makes electron capture efficient. Combined with the low abundance of He⁺ in the trap, this makes Reaction (4) of little importance.
59. G. V. Marr and J. B. West, At. Data Nucl. Data Tables, 1976, 18, 497–508.
60. A. A. Sorokin, I. L. Beigman, S. V. Bobashev, M. Richter and L. A. Vainshtein, J. Phys. B: At., Mol. Opt. Phys., 2004, 37, 3215–3226.
61. J. Stöhr, NEXAFS Spectroscopy, Springer Verlag, Berlin, 1992.
62. O. Travnikova, J. C. Liu, A. Lindblad, C. Nicolas, J. Söderstrom, V. Kimberg, F. Gel'mukhanov and C. Miron, Phys. Rev. Lett., 2010, 105, 233001.
63. J. Söderström, A. Lindblad, A. N. Grum-Grzhimailo, O. Travnikova, C. Nicolas, S. Svensson and C. Miron, New J. Phys., 2011, 13, 073014.
64. C. Miron, C. Nicolas, O. Travnikova, P. Morin, Y. P. Sun, F. Gel'mukhanov, N. Kosugi and V. Kimberg, Nat. Phys., 2012, 8, 135–138.
65. C. Blancard, P. Cosse, G. Faussurier, J. M. Bizau, D. Cubaynes, N. El Hassan, S. Guilbaud, M. M. Al Shorman, E. Robert, X. J. Liu, C. Nicolas and C. Miron, Phys. Rev. A, 2012, 85, 043408.
66. M. Patanen, C. Nicolas, X. J. Liu, O. Travnikova and C. Miron, Phys. Chem. Chem. Phys., 2013, 15, 10112–10117.
67. A. R. Milosavljevic, F. Canon, C. Nicolas, C. Miron, L. Nahon and A. Giuliani, J. Phys. Chem. Lett., 2012, 3, 1191–1196.
68. J. C. Schwartz, M. W. Senko and J. E. P. Syka, J. Am. Soc. Mass Spectrom., 2002, 13, 659–669.
69. A. R. Milosavljevic, C. Nicolas, J. F. Gil, F. Canon, M. Refregiers, L. Nahon and A. Giuliani, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 279, 34–36.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra09787d

---