Effect of hydration on the stability and tautomerisms of different isomers of uracil†
Abstract
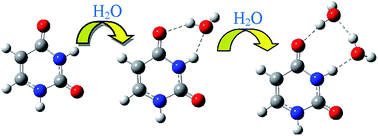
Thermodynamic and structural properties of isolated, hydrated and solvated forms of twelve isomers of uracil were studied theoretically. It was found that the di-keto tautomer is the most stable isomer in gas and aqueous phases and in hydrated forms. Internal proton transfers and O–H rotations in uracil were studied employing B3LYP and MP2 methods in a gas phase. Activation energies (Ea) and Gibbs free energies (ΔG#) of the isomerization processes were calculated. The calculated activation energies of the proton transfer reactions were in the range of 110–180 kJ mol−1 and the energy barriers of internal O–H rotations were generally smaller than 40 kJ mol−1. The high energy barriers of the proton transfers indicate that proton transfers are hard to achieve. Therefore, the catalytic effects of one, two and three water molecules on the proton transfer processes in the hydrated isomers of uracil were investigated. The calculations showed that water molecules lower the energy barriers of the proton transfer reactions and catalyze the tautomerism processes in uracil.

 Please wait while we load your content...
Please wait while we load your content...