Adsorption of CO, SO₂, HCN, NH₃, and H₂CO on zigzag GaP nanotubes: a QM/MM study

Abstract

The interactions of the single-walled zigzag (5, 0), (6, 0), and (7, 0) GaP nanotubes (GaPNTs) with CO, SO₂, HCN, NH₃, and H₂CO molecules are theoretically studied at the ONIOM(B3LYP/6-31G(d):UFF) level. A pyrene-like ring of the nanotube is chosen as an adsorption site in the high layer of the ONIOM calculations for the adsorption of a single molecule. Binding energy, Gibbs free energy change, density of states, and Mulliken charge transfer are computed to analyze the nature of the binding between GaPNT and the adsorbate molecule. The bindings of CO and H₂CO towards GaPNTs are weaker than those of NH₃, SO₂, and HCN molecules. The strongest adsorption is found to be with NH₃. The dispersion corrected functional (wB97XD) has been introduced to compare the results with those of the B3LYP functional.

---

1. Introduction

Since the discovery of carbon nanotubes (CNTs) by Iijima,¹ efforts are being made for its development as materials such that it can be used as gas storage elements, as sensors in nanoelectronics, and as bio-compatible agents in medicine.² The adsorptions of NO₂ and NH₃ gases on CNTs at room temperature have been found to change the conductivity of the nanotubes largely.³ Molecules like O₂ and SO₂ also interact with CNTs strongly.^4,5 First-principles calculations on the interactions of NO₂, O₂, NH₃, N₂, H₂O, and Ar with CNTs have been carried out by Zhao et al.⁶ Over the years, there is a strong zeal to improve the sensitivities of CNTs towards toxic gases like CO, H₂S, and H₂CO using different strategies. A substitutional doping with Si atom has been found to be very effective in increasing the reactivity of CNTs towards toxic gases.^7,8 Silicon carbide nanotubes (SiCNTs) and nanowires, synthesized in various shapes and structures are often used as an alternate to CNTs. It has been established^9–12 that SiCNTs are excellent sensors for detecting small molecules like NO, CO, CO₂, HCN, and NO₂. Phenol gets adsorbed on (8, 0) SiCNT preferentially through OH–Si interaction rather than π–π interaction between the phenol ring and the hexagon of SiCNT.¹³ The armchair nanotubes of germanium carbide (GeCNT), whose elements belong to the same group 14, have been found to be semiconducting in nature with a wide spectrum of band gaps.¹⁴ Recently, electron transport properties and adsorption sensitivities of zigzag GeCNT towards N₂, CO, SO₂, HCN, NH₃, and H₂CO molecules have also been theoretically studied.^15,16

In addition to the nanotubes of group 14, attention has been drawn to the nanotubes formed by group 13 and 15, namely, boron nitride nanotubes (BNNTs). The BNNTs are found to be less toxic compared to CNTs, and they also exhibit electronic properties independent of the diameter and chirality. It has been theoretically¹⁷ revealed that at the ambient conditions, boron-rich BNNT can capture CO₂ initiated through the barrier-less physisorption process. A DFT study¹⁸ shows that the pristine and cobalt doped BNNTs interact with CO₂ more strongly compared to CNTs, and hence can be used as a better absorber. Xiao et al.¹⁹ have performed ONIOM calculations to show that NO and NO₂ can be used successfully to heal the N-vacancy in BNNT.

Gallium phosphide being isovalent with BN has been found to be useful for light emission devices in the visible range.²⁰ GaP nanowires and nitrogen doped nanobelts have been prepared in recent years.^21–25 Gallium phosphide nanotubes (GaPNTs) with a zinc blend structure have been synthesized and characterized by Wu et al.²⁶ The structures of (10, 0) and (6, 6) GaPNTs are optimized from DFT calculations by Mirzaei and Mirzaei.²⁷ These authors have also calculated NMR properties of (6, 0) and (4, 4) GaPNTs, including isotropic and anisotropic chemical shielding parameters.²⁸ Effects of tubular diameters on the electronic and structural properties of GaPNTs have been investigated theoretically.²⁹ All electron based DFT calculations with GGA (PBE) exchange correlation functional are carried out³⁰ to optimize the geometries of alkali and transition metal doped single walled GaPNT (10, 0). Srivastava et al.³¹ have studied the stabilities and electronic properties of zigzag GaPNTs by ab initio based DFT calculations. These authors have also used a two-probe model for (4, 0) GaPNT to explore its transport properties. In this article, we report the adsorption sensitivities of several toxic molecules such as CO, HCN, SO₂, NH₃, and H₂CO on (n, 0) GaPNTs (n = 5–7) using DFT based ONIOM calculations. Adsorption energy, Gibbs free energy change, and charge transfer from nanotube to the adsorbate molecule are calculated in each interaction.

2. Computational details

Three semiconducting zigzag (5, 0), (6, 0), and (7, 0) GaPNTs are considered in the present study. Preliminary calculations have been carried out on perfect GaPNTs with PBE³² functional in DFT using SIESTA-3.1 code³³ to get their appropriate input geometries for the actual QM/MM calculations of the nanotube–adsorbate complex. Adsorptions of small molecules towards (n, 0) GaPNTs are studied here by adopting a two-layered ONIOM approach.^34,35 Although the ONIOM method is not efficient to handle truly delocalized properties like band structure, several successful studies have been performed to obtain accurate results for large complex molecular systems in different chemical problems, including thermochemistry, homogeneous catalysis, stereoselectivity in organic synthesis, structure and enzymatic reaction mechanism.³⁶ Geometries of nanotube–adsorbate complexes are optimized for various orientations of the axis of the adsorbate molecule. We have explored different adsorption sites such as (i) top of the P/Ga atom, (ii) top of the center of the Ga–P bond, and (iii) top of the center of the Ga–P hexagon. In the two-layer ONIOM calculation, the DFT method of the hybrid density functional, B3LYP^37–39 with 6-31G(d) basis set for all atoms is employed for the high layer, while for the low layer a molecular mechanics method with Universal Force Field (UFF)⁴⁰ is used. It is difficult to give a preference to molecular mechanics over the semiempirical method like PM6 for the low layer in the ONIOM calculations. The calculations with PM6 are computationally much more demanding than the UFF based calculations. Due to the problem of the SCF convergence in the PM6 method, the ONIOM optimization and frequency analysis could not be successfully carried out for some of the GaPNT–adsorbate complexes. Again in view of the cost-efficiency, the lower level description by UFF is found to be attractive. The ONIOM methodology as implemented in Gaussian 03 (ref. 41) uses such a QM/MM approach. The energy of a given system in a two-layer ONIOM approach is given by

E [ONIOM] = E_real [MM] + E_model [QM] − E_model [MM],

where ‘real’ refers to the real system containing all atoms and ‘model’ represents the high layer. Electronic embedding has been incorporated in the ONIOM calculation so as to provide a better description of the electrostatic interaction between the QM and MM region and allows the QM wavefunctions to be polarized. During the geometry optimization no symmetry constraint was imposed. For all the models, the SCF convergence limit was set to 10⁻⁶ a.u. on energy and electron density. All stationary points on the potential energy surfaces were confirmed from the harmonic vibrational frequency analysis of the involved species using ONIOM approach. During the optimization of the single-molecule adsorbed complexes, the high layer of the ONIOM method is modeled as a pyrene-like system located on the GaP nanotube surface. It may be pointed out that the pyrene-like fragment of GaP nanotube as the high-layer in the ONIOM method is adequate because of the absence of π-delocalization as in CNTs. The buckling effect is known in the GaPNT due to the presence of mixture of sp² and sp³ hybridization.³⁰ However, a similar ONIOM modeling has already been successfully implemented to predict the binding energies of SWCNTs with different adsorbing species even though there exists a π-delocalization.^36,42–45 To validate the pyrene model selected for high-layer ONIOM calculations, the structural parameters such as bond length, bond angle, deformation of six-membered ring, and electronic properties like band gap have been compared with the fully relaxed GaPNTs by DFT calculations.³¹ Zero-point energy (ZPE) corrected electronic energies are used to compute the adsorption energy (E_a) for the GaPNT–adsorbate complexes.

E_a = E [ONIOM]_{GaPNT–adsorbate} − E [B3LYP/6-31G(d)]_adsorbate − E [ONIOM]_GaPNT

A negative value of E_a signifies a favorable adsorption. Adsorption energies are computed without using counterpoise (CP) corrections to the basis set superposition error (BSSE) as these cannot be done in the ONIOM approach. Moreover, it was previously shown that CP corrections do not improve energies and the uncorrected results are in better agreement with the experimental data.^46,47 In order to check the thermodynamic spontaneity of the process, Gibbs free energy changes (ΔG_a) due to molecular adsorption are calculated from the following expression:

ΔG_a = G(GaPNT–adsorbate) − G(GaPNT) − G(adsorbate)

where G(GaPNT–adsorbate), G(GaPNT), and G(adsorbate) are the corresponding free energies. Thermal energy corrections were employed in calculating the free energy of each structure at 298.15 K and 1 atm. The ideal gas, rigid rotor, and harmonic oscillator approximations were respectively used for the translational, rotational, and vibrational contributions to the free energy.⁴⁸ Mulliken charge transfer (Q_T) from the nanotube to the adsorbate molecule due to the adsorption process has been estimated at the same level of theory. The effect of dispersion interaction has been investigated by extending our computations from hybrid functional (B3LYP) to the meta-hybrid functional (wB97XD)⁴⁹ for the high-layer modeling in the ONIOM calculations.

3. Results and discussion

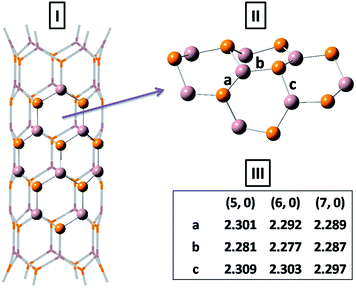
Fig. 1 shows the most stable structure of the perfect (6, 0) GaP nanotube optimized at the ONIOM (B3LYP/6-31G(d):UFF) level. Three typical Ga–P bonds (labeled as ‘a’, ‘b’, and ‘c’) within this high layer are not exactly the same. The average Ga–P bond length is very close to the previously reported value of 2.28 Å by Mirzaei and Mirzaei.²⁷ In accordance with the earlier calculations³¹ on (n, 0) GaPNTs (3 ≤ n ≤ 16) at the PBE/DZP level of theory, the present QM/MM study also shows that after optimization the more electronegative P atoms move outward radially, while the more electropositive Ga atoms shift inward of the curved hexagonal layer. A different hybridization of Ga and P results in the buckling of the tube surface and the degree of buckling reduces with the chirality. Each of CO, HCN, SO₂, NH₃, and H₂CO is allowed to be adsorbed on the pyrene-like ring of the nanotube. The relaxed high-layer structures optimized at the B3LYP/6-31G(d) level of theory for the adsorption of all five molecules on (5, 0) GaPNT are shown in Fig. 2.

Fig. 1 Highlighted atoms of the representative perfect GaP nanotube used in the high layer of the ONIOM calculation. The pyrene-like structure is used for the adsorption of a single adsorbate molecule. (Color codes: Ga – pink, P – yellow.)

Fig. 2 Optimized high-layer structures for the adsorption of single molecule on the (5, 0) GaPNT surface.

In the CO adsorbed complex, carbon binds relatively strongly with Ga keeping the oxygen atom away from the nanotube. The CO molecule is positioned on top of the Ga atom of the hexagonal layer. Ga–C–O is almost linear with an average bond angle of about 177° and the neighboring Ga–P bonds relax marginally. In the most stable SO₂ adsorbed complex of GaPNT, the sulphur atom is strongly bonded to the central P atom of the pyrene ring, while the two O atoms are attached to the two adjacent Ga atoms. A slight difference in the bond distances of the two Ga–O bonds may be due to the choice of the model in the high layer. The P–S and Ga–O interaction distances increase slowly with the increase in the diameter of the nanotube. The adsorption of SO₂ is expected to be stronger for (5, 0) GaPNT. Due to strong adsorption, the neighboring Ga–P bonds elongate by 0.14–0.18 Å for all the GaPNTs studied here.

The adsorption of HCN on GaPNT is reasonably strong. The N atom of HCN is oriented towards the central Ga of the pyrene ring. In the HCN adsorbed complex, Ga–N–C–H remains almost collinear for all three chiralities and the neighboring Ga–P bonds relax by about 0.03–0.04 Å due to this adsorption. The ammonia molecule gets adsorbed to the GaP nanotube very strongly. The N atom is bonded directly to the central Ga atom with an average Ga–N distance of 2.18 Å. Three symmetrical H atoms are oriented above the pyrene ring of the nanotube in a staggered conformation with respect to three Ga–P bonds, which make 94–98° with Ga–N.

When H₂CO is adsorbed on the GaP nanotube, C=O is oriented parallel to the Ga–P bond making a four-membered ring in the most stable configuration and the reaction is similar to a [2 + 2] cycloaddition. The C atom of the formaldehyde molecule is bonded to the P atom in the middle of the pyrene ring, while the O atom is attached to Ga. The C–O bond (labeled as ‘b’) in the adsorbed nanotube is elongated by about 0.16 Å, while the H–C–H bond angle is reduced to 109° due to the change in the hybridization. The elongation of the surrounding Ga–P bonds due to adsorption of H₂CO is 0.07–0.12 Å. For all three chiralities, a second most stable configuration of H₂CO-adsorbed nanotube has been predicted, in which C and O atoms of H₂CO are bonded to Ga and P atoms of the nanotube, respectively, making a similar type of [2 + 2] cycloaddition. The energy of this second complex is calculated to be 83–92 kJ mol⁻¹ higher than the most stable one.

Table 2 displays the computed adsorption energies (E_a) and Gibbs free energy changes (ΔG_a) for the adsorption of one adsorbate molecule on (n, 0) GaPNTs (n = 5–7) at the ONIOM (B3LYP/6-31G(d):UFF) level of theory. Looking at the magnitude of the adsorption energies, it is predicted that the strongest adsorption occurs with the NH₃ molecule. The GaP nanotube of smaller chirality is found to be susceptible to stronger adsorption of these small molecules. However, the calculated ΔG_a values at T = 298.15 K for the adsorption of SO₂ and NH₃ are largely negative, while for the adsorption of CO and H₂CO on (n, 0) GaPNTs, these are positive, implying that these adsorption processes are not thermodynamically favorable. In case of the adsorption of HCN, ΔG_a for (5, 0) GaPNT is only −2.8 kJ mol⁻¹, while for (6, 0) and (7, 0) nanotubes these are 1.3 and 6.8 kJ mol⁻¹, respectively. We searched for any possible transition structure during the adsorption of all five small molecules, but found none. Therefore, it is expected that none of the adsorption processes studied here require crossing a barrier. The negative value of ΔG_a signifies the exergonic adsorption process, and hence is a measure of thermodynamic spontaneity. Electronic interaction energies are always negative, but ΔH − TΔS determines the course of the reaction. Thus, the positive free energy changes in case of CO and H₂CO indicate that the adsorptions may not occur under the conditions for which the calculations were made. However, the actual experimental conditions will dictate the spontaneity of the adsorption processes.

Table 1 Some important bond lengths of the most stable adsorbed complexes for the adsorption of small gas molecules on (n, 0) GaPNTs (n = 5–7) computed at the ONIOM(B3LYP/6-31G(d):UFF) level of theory^b

Adsorbate molecule	Bonds^a	Bond length (Å)
		(5, 0) GaPNT	(6, 0) GaPNT	(7, 0) GaPNT
a Fig. 2.b Values in parentheses are results obtained using wB97XD functional.
CO	a	2.719	2.807	2.905
		(2.465)	(2.575)	(2.675)
	b	1.134	1.134	1.135
		(1.129)	(1.130)	(1.130)
SO2	a	2.238	2.242	2.244
		(2.186)	(2.186)	(2.185)
	b	1.588	1.585	1.582
		(1.571)	(1.572)	(1.571)
	c	2.007	2.008	2.016
		(2.004)	(2.002)	(2.017)
	d	1.569	1.568	1.567
		(1.560)	(1.559)	(1.557)
	e	2.035	2.035	2.044
		(2.005)	(2.008)	(2.017)
HCN	a	2.200	2.215	2.245
		(2.162)	(2.167)	(2.187)
NH3	a	2.150	2.157	2.171
		(2.120)	(2.123)	(2.136)
H2CO	a	1.926	1.928	1.935
		(1.906)	(1.904)	(1.910)
	b	1.370	1.369	1.364
		(1.373)	(1.373)	(1.370)
	c	1.980	1.983	1.991
		(1.935)	(1.933)	(1.936)

---

Table 2 Calculated adsorption energy (E_a) and Gibbs free energy change (ΔG_a) for the adsorption of gas molecules on (n, 0) GaPNTs (n = 5–7) at the ONIOM(B3LYP/6-31G(d):UFF) level of theory. All the values are in kJ mol⁻¹

Adsorbate molecule	(5, 0) GaPNT		(6, 0) GaPNT		(7, 0) GaPNT
	Ea	ΔGa	Ea	ΔGa	Ea	ΔGa
CO	−28.5	6.2	−25.6	8.8	−21.9	12.1
SO2	−81.4	−25.0	−77.2	−21.0	−67.3	−12.3
HCN	−42.3	−2.8	−38.2	1.3	−32.9	6.8
NH3	−98.6	−62.6	−97.2	−57.8	−87.9	−48.2
H2CO	−14.9	33.3	−11.9	36.6	−4.7	42.8

---

We have extended our ONIOM calculations on the adsorptions of all five molecules on (5, 0) GaPNT using TZVP basis sets to explore the improvement of their adsorption energies, if any. A full geometry optimization calculation has been carried out at the ONIOM(B3LYP/TZVP:UFF) level. The comparative results are shown in ESI Fig. S1,† which indicate that B3LYP/TZVP calculations overestimate the interaction energy by 22–28 kJ mol⁻¹.

Fig. 3 displays the density of states (DOS) spectra of the bare and adsorbed (5, 0) GaPNT, while the remaining two sets of DOS spectra for (6, 0) and (7, 0) nanotubes are shown in ESI Fig. S2 and S3.† Each DOS spectrum is convoluted with a Gaussian FWHM of 0.3 eV and the zero energy is set to HOMO. In general, the computed HOMO–LUMO gap (E_g) of (n, 0) GaPNT gradually increases with the diameter of the tube (Table 3). This is in accordance with the results obtained by Srivastava et al.³¹ based on band structure analysis using the k-point sampling method. As a result of the adsorption of one adsorbate molecule, E_g is increased by 0.06–0.24 eV. Only in case of the adsorption of SO₂ on (7, 0) GaPNT, the computed E_g is reduced by 0.13 eV. The HOMO peak looks similar for all single molecule adsorptions except SO₂. The band splitting in the upper part of the valence band and in the lower part of the conduction band are noticeable due to the stronger adsorption of the sulphur dioxide molecule on (5, 0) GaPNT. The density around HOMO is also changed for NH₃ indicating its larger influence on the electronic structure of the nanotube. However, the signature of the DOS spectra varies with the diameter of the tube, but in each case the overall spectra of SO₂ and NH₃ adsorbed complexes are different compared to those of the corresponding bare nanotube.

Fig. 3 DOS spectra of the adsorbed (5, 0) GaPNT complexes.

Table 3 Computed HOMO–LUMO energy gap E_g (eV) and Mulliken charge transfer (Q_T) for the most stable (n, 0) GaPNT (n = 5–7) adsorbate complexes at the ONIOM(B3LYP/6-31G(d):UFF) level of theory

Adsorbate molecule	(5, 0) GaPNT		(6, 0) GaPNT		(7, 0) GaPNT
	Eg	QT	Eg	QT	Eg	QT
CO	2.14	0.14	2.20	0.13	2.57	0.12
SO2	2.15	−0.31	2.20	−0.31	2.38	−0.31
HCN	2.23	0.17	2.28	0.17	2.68	0.16
NH3	2.21	0.24	2.27	0.24	2.69	0.25
H2CO	2.32	−0.34	2.39	−0.34	2.54	−0.34
Pure nanotube	2.08		2.15		2.51

---

The extent of charge transfer (Q_T) between GaPNT and the adsorbate molecule is calculated from the Mulliken analysis and the computed values for all three GaP nanotubes are given in Table 3. The negative value of Q_T implies that the electron is transferred from the nanotube to the adsorbate molecule. SO₂ and H₂CO molecules after being adsorbed withdraw about 0.31e and 0.34e charges, respectively from the GaP nanotube. For the adsorption of other three molecules, viz. CO, HCN, and NH₃, the nanotube as a whole accumulates some amount of electronic charges. The amount of charge transfer does not vary much with the size of the tube.

When the dispersion interactions are included through the wB97XD functional, the important interaction bond distances of the adsorbed complexes shorten. This has been shown in Table 1 by comparing these bond distances from the ONIOM calculations using B3LYP and wB97XD functionals, respectively. ESI Tables S1 and S2† display other results of the calculations, which include such dispersion interactions. However, Q_T values computed using wB97XD functional do not change much. As depicted in Fig. 4, despite having an excellent matching of Q_T, the calculated adsorption energies using B3LYP hybrid functional are overestimated by as much as 41 kJ mol⁻¹. This overestimation is reflected in the large reduction of E_g.⁴⁵ The computed E_g values of different adsorbing species obtained by employing both B3LYP and wB97XD functionals are shown in Fig. 5. The relative values for different adsorbate molecules in two different functional are comparable.

Fig. 4 Comparison of (a) adsorption energy (E_a) and (b) Mulliken charge transfer (Q_T) computed with B3LYP and wB97XD functionals.

Fig. 5 Comparison of the HOMO–LUMO gap (E_g) computed with B3LYP and wB97XD functional.

4. Conclusion

Adsorptions of small molecules, viz. CO, SO₂, HCN, NH₃, and H₂CO, on (n, 0) GaPNTs (n = 5–7) have been investigated by carrying out ONIOM calculations at the B3LYP/6-31G(d):UFF level. All the adsorption processes are found to be exothermic in nature and their energy profiles do not possess any energy barrier as no transition structure has been obtained. In general, bindings of NH₃, SO₂, and HCN towards GaP nanotubes are predicted to be stronger than either CO or H₂CO molecules. The smaller nanotubes are more reactive to these adsorbate molecules. The changes in the DOS pattern of the adsorbed GaPNTs help in analyzing the extent of binding between the nanotube and the adsorbate molecule. The HOMO–LUMO gap of the GaP nanotube generally increases upon the adsorption of small molecule. The adsorption of SO₂ on (7, 0) GaPNT is an exception for which the gap decreases by about 0.13 eV. Mulliken charge analyses predict that the adsorptions of SO₂ and H₂CO result in charge transfer from GaPNT to the adsorbate molecule. In the adsorption of other molecules, the charge is transferred in the opposite direction. The adsorption energies computed at the ONIOM(B3LYP/6-31G(d):UFF) level of theory are always overestimated compared to ONIOM(wB97XD/6-31G(d):UFF) calculations. The dispersive energy dominates for the adsorption of gas molecules on to the GaPNT surface. However, in the latter case, the HOMO–LUMO energy gaps are larger than those obtained with pure and hybrid density functional. Of all the GaPNTs studied here, the E_g of (5, 0) GaPNT increases by about 11.5% upon the adsorption of H₂CO molecule.

References

1. S. Iijima, Nature, 1991, 354, 56.
2. M. S. Dresselhaus, G. Dresselhaus and P. Avouris, Carbon Nanotubes: Synthesis, Structure, Properties and Applications, Springer, Berlin, 2000.
3. J. Kong, N. R. Franklin, C. W. Zhou, M. G. Chapline, S. Peng, K. J. Cho and H. J. Dai, Science, 2000, 287, 622.
4. P. G. Collins, K. Bradley, M. Ishigami and A. Zettl, Science, 2000, 287, 1801.
5. A. Goldoni, R. Larciprete, L. Petaccia and S. Lizzit, J. Am. Chem. Soc., 2003, 125, 11329.
6. J. Zhao, A. Buldum, J. Han and J. P. Lu, Nanotechnology, 2002, 13, 195.
7. G. Guo, F. Wang, H. Sun and D. Zhang, Int. J. Quantum Chem., 2008, 108, 203.
8. H. Jiang, D. Zhang and R. Wang, Nanotechnology, 2009, 20, 145501.
9. R. Q. Wu, M. Yang, Y. H. Lu, Y. P. Feng, Z. G. Huang and Q. Y. Wu, J. Phys. Chem. C, 2008, 112, 15985.
10. G. H. Gao and H. S. Kang, J. Chem. Theory Comput., 2008, 4, 1690.
11. G. H. Gao, S. H. Pank and H. S. Kang, Chem. Phys., 2009, 355, 50.
12. J. X. Zhao and Y. H. Ding, J. Chem. Theory Comput., 2009, 5, 1099.
13. J. X. Zhao, B. Gao, Q. H. Cai, X. G. Wang and X. Z. Wang, Theor. Chem. Acc., 2011, 129, 85.
14. S. J. Rathi and A. K. Ray, Nanotechnology, 2008, 19, 335706.
15. P. N. Samanta and K. K. Das, J. Phys. Chem. C, 2012, 117, 515.
16. P. N. Samanta and K. K. Das, Chem. Phys. Lett., 2013, 577, 107.
17. H. Choi, Y. C. Park, Y.-H. Kim and Y. S. Lee, J. Am. Chem. Soc., 2011, 133, 2084.
18. E. N. C. Paura, W. F. Da Cunha, J. B. L. Martins, G. M. E Silva, L. F. Roncaratti and R. Gargano, RSC Adv., 2014, 4, 28249.
19. B. Xiao, X.-F. Yu and Y.-H. Ding, RSC Adv., 2014, 4, 22688.
20. Y. H. Kim, Y. W. Jun, B. H. Jun, S. M. Lee and J. Cheon, J. Am. Chem. Soc., 2002, 124, 13656.
21. C. Tang, S. Fan, M. L. de la Chapelle, H. Dang and P. Li, Adv. Mater., 2000, 12, 1346.
22. S. Gao, Y. Xie, J. Lu, G. Du, W. He, D. Cui, B. Huang and M. Jiang, Inorg. Chem., 2002, 41, 1850.
23. W. S. Shi, Y. F. Zheng, N. Wang, C. S. Lee and S. T. Lee, Adv. Mater., 2001, 13, 591.
24. H. W. Seo, S. Y. Bae, J. Park, H. Yang, M. Kang and S. Kim, Chem. Commun., 2002, 2564.
25. H. W. Seo, S. Y. Bae, J. Park, H. Yang, M. Kang and S. Kim, Appl. Phys. Lett., 2003, 82, 3752.
26. Q. Wu, Z. Hu, C. Liu, X. Wang, Y. Chen and Y. Lu, J. Phys. Chem. B, 2005, 109, 19719.
27. M. Mirzaei and M. Mirzaei, Phys. E, 2011, 43, 1343.
28. M. Mirzaei and M. Mirzaei, Monatsh. Chem., 2011, 142, 111.
29. M. Mirzaei, M. Yousefi and M. Meskinfam, Solid State Sci., 2012, 14, 801.
30. C. Kamal, A. Chakrabarti, A. Banerjee and S. K. Deb, Phys. E, 2013, 54, 273.
31. A. Srivastava, S. K. Jain and P. S. Khare, J. Mol. Model., 2014, 20, 2171.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
33. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
34. S. Daprich, I. Komáromi, K. S. Byun, K. Morokuma and M. J. Frisch, J. Mol. Struct.: THEOCHEM, 1999, 462, 1.
35. T. Vreven, K. S. Byun, I. Komáromi, S. Daprich, J. A. Montgomery Jr, K. Morokuma and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 815.
36. K. Morokuma, Bull. Korean Chem. Soc., 2003, 24, 797.
37. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
38. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
39. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
40. A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024.
41. M. J. Frischet al., GAUSSIAN 03 revision E.01, Gaussian, Inc., Wallingford, CT, 2004.
42. A. Ricca and J. A. Drocco, Chem. Phys. Lett., 2002, 362, 217.
43. R. Wanbayor and V. Ruangpornvisuti, Carbon, 2008, 46, 12.
44. X. Lu, F. Tian, X. Xu, N. Wang and Q. Zhang, J. Am. Chem. Soc., 2003, 125, 10459.
45. S. Osuna, J. Morera, M. Cases, K. Morokuma and M. Sola, J. Phys. Chem. A, 2009, 113, 9721.
46. J. R. Alvarez-Idaboy and A. Galano, Theor. Chem. Acc., 2010, 126, 75.
47. L. M. Mentel and E. J. Baerends, J. Chem. Theory Comput., 2014, 10, 252.
48. W. J. Hehre, L. Radom, P. V. R. Schleyer and J. A. Pople, Ab initio molecular orbital theory, Wiley, New York, 1986, pp. 226–261.
49. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra09706h

---