Dual-frequency microwave-driven resonant excitations of skyrmions in nanoscale magnets

Abstract

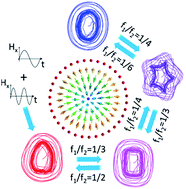
Since the first prediction of their existence in magnetic materials, skyrmions have been intensively investigated both theoretically and experimentally. However, it remains a challenge to manipulate skyrmions and to understand their dynamics. We study nonlinear dynamics of coupled skyrmions in Co/Ru/Co nanodisks by micromagnetic simulations and show that resonant excitation can be controlled in nanoscale magnets by a dual-frequency microwave field. Two coupled resonant modes, clockwise (CW) and counterclockwise (CCW) rotation modes, are found. Polygon-like resonant excitation is observed and modulated from triangle-like to heptagon-like dynamics by a microwave field with a commensurate frequency ratio. The quasiperiodic behavior of the excitation is related to an incommensurate ratio. We also present numerical solutions of the extended Thiele’s equation for skyrmions and obtain a good agreement between the solutions and the micromagnetic simulation results. This work contributes to the understanding of skyrmion dynamics and supplies a new route to manipulating skyrmions in nanoscale magnets using resonant excitation.

---

1 Introduction

Nanoscale magnets have attracted much attention in recent years due to their unique magnetic properties which are sensitive to the geometrical parameters of the magnets.^1–4 For example, scaling a magnet down from the bulk to a nanofilm will lead to a strong shape anisotropy. As the geometric size scales down further, many peculiar properties will emerge, such as a single-domain state from a multidomain one, topological spin textures and so on.^1,5–7 Among them, topological spin textures are especially intriguing due to their potential applications in high-density data storage, microwave devices and spintronics, because of their nanoscale size, non-volatility and high speed operation.^8–10

Skyrmions as one type of topological spin texture have recently been observed experimentally in chiral-lattice magnets,^11–17 and are also predicted to exist in coupled ordinary magnets.^18–20 Skyrmions are envisioned as promising candidates for applications in spintronics and magnetic storage,^8,21,22 due to their small size, high structural stability, low threshold current density to drive their motion, and intriguing magnetoelectric effects.^12,22–24 Therefore, besides spin-polarized currents,^25–27 searching for other methods to efficiently manipulate skyrmions at the nanoscale and understanding the dynamics of skyrmions, particularly at resonant excitations, are important subjects for practical applications.

Many research works on the resonant excitation of a vortex with a topological spin texture have been carried out in recent years, showing that the vortex core can be switched even with low power consumption, and nanostructural magnets with topological spin textures have potential applications in microwave sources and resonators.^9,10,28–30 However, the resonant excitation of skyrmions have seldom been reported. In our recent work, a skyrmion under resonant excitation has shown dual-frequency flower-like dynamics when driven by a single-frequency microwave field, which is ascribed to its nonlocal deformation of the topological density distribution.³¹ It is therefore curious and worthwhile to investigate skyrmion motion in a dual-frequency microwave driving field, which is of great importance for further understanding the behaviors under resonant excitation, and may supply a more facile way to manipulate skyrmions for their application.

In this work, we present an approach for manipulating topological resonant excitations of coupled skyrmions in nanoscale magnets by a dual-frequency microwave field. We find two resonant modes with opposite directions of rotation in a single-frequency microwave field. The two modes have dynamically coupled phases under the dual-frequency field, which have not been discovered before. By modulating the commensurate ratio of the dual-frequencies, we obtain a polygon-like resonant excitation and are able to controllably change it. Quasiperiodic behavior is observed when the frequency ratio is incommensurate. Numerical solutions of the extended Thiele’s equation are in best agreement with the micromagnetic simulation results and verify that the effective mass is vital to the polygon-like resonant excitation of the skyrmions as well as the value of the frequency and the frequency ratio of the external field. We also show that the perpendicular coupling between two skyrmions has a great effect on the skyrmion dynamics.

2 Methods

The resonant excitation of coupled skyrmions in Co/Ru/Co nanodisks was studied by means of the three-dimensional object oriented micromagnetic framework (OOMMF) code.³² The material parameters of the hexagonal-close-packed (hcp) cobalt that was chosen include the saturation magnetization M_s = 1.4 × 10⁶ A m⁻¹, the exchange stiffness A_ex = 3 × 10⁻¹¹ J m⁻¹ and the uniaxial anisotropy constant K_u = 5.2 × 10⁵ J m⁻³ with a direction perpendicular to the nanodisk plane. The interfacial coupling constant of the adjacent surfaces was −5 × 10⁻⁵ J m⁻² according to ref. 33. The dimensionless damping α was 0.02. The radius R of the Co/Ru/Co nanodisk was 100 nm. The thickness L of the Co was 18 nm, while that of the Ru was 2 nm. The cell size was 2 × 2 × 2 nm³, which is smaller than the exchange length of cobalt (about 4.94 nm). The method of obtaining the static coupled skyrmions was the same as in our previous work.¹⁸ Different initial magnetic states (vortex-like, in-plane-like, and out-of-plane-like initial states) were used to obtain the most stable state. An in-plane microwave field was applied to the static coupled skyrmions in the x-direction to activate the resonant excitation of the coupled skyrmions. The frequency of the external field was equal to or close to the eigenfrequency of the system. The waveforms of the microwave fields were H sin(2πft) with frequencies of 1 GHz or 5 GHz, and H₁ sin(2πf₁t) + H₂ sin(2πf₂t) with f₁/f₂ of 1/2, 1/3, 1/4, 1/5, 1/6 or the golden ratio.

3 Results and discussion

3.1 Effective mass

The deformation of a skyrmion at resonance will be large and nonlocal because of its smooth global spin texture. To consider the nonlocal nature of the large deformation, we use a guiding center (the center of the topological density) to depict its dynamics.³⁴ Considering that the local magnetization S(x,t) depends not only on the guiding center’s position R(t) but also on its velocity Ṙ(t),³⁵ we can get:

S(x,t) = S(x − R(t), Ṙ(t)). (1)

Then we are able to obtain the extended Thiele’s equation for the guiding center:where G is the gyrovector, ê_i is the unit coordinate vector (i(j) = x, y), the coefficient μ is a function of the structural and magnetic parameters,^36,37 H is an external magnetic field, R_j (double dot) is the acceleration of the guiding center and M is the effective mass tensor with elements:where γ is the gyromagnetic ratio and n is the unit vector of the local magnetization. The potential energy of the guiding centers is:where k, d = |R_t − R_b|, and U_Sky–Sky(d) are the stiffness coefficient, the distance between two guiding centers, and the magnetostatic coupling between two skyrmions, respectively. For a skyrmion with a nonlocal deformation, the effective mass, which is related to the time derivative of the topological density q̇,³⁵ has to be used to comprehend the dynamical behavior of the skyrmion.

3.2 Results of the micromagnetic simulations

The resonant excitations of the two coupled skyrmions are stimulated by a microwave magnetic field as shown in Fig. 1. The field is 100 Oe in amplitude and is applied along the +x direction on the top nanolayer as shown in Fig. 1a. The trajectories of the guiding center for the top nanolayer in the field H sin(2πft) with frequencies of 1 GHz and 5 GHz are shown in Fig. 1b and c, respectively. The frequencies of the external field are chosen to be the eigenfrequencies of a hexagonal trajectory for the gyrotropic motion of the coupled skyrmions.¹⁸ Both of the resonant orbits are approximately circular, and the radius of 30.5 nm in Fig. 1b is much larger than that of 3.3 nm in Fig. 1c. We find that the directions of their circulations are opposite, clockwise (CW) for the lower frequency mode and counterclockwise (CCW) for the higher frequency mode. Compared with the resonant excitation of vortices,^30,38 the rotation of skyrmions depends not only on their polarities, but also strongly on the frequency of the microwave field due to their global spin textures. Mochizuki³⁹ has studied the microwave absorption spectra of a two-dimensional model, in which a skyrmion crystal is stabilized by the Dzyaloshinsky–Moriya interaction (DMI). It transpired that for twofold spin-wave modes, with a small microwave magnetic field, the frequency difference between the two modes is small. However, we find that with the effective mass, eqn (3), the two resonant excitation modes, far from being degenerate, exhibit a large frequency difference. When a dual-frequency microwave field H₁ sin(2πf₁t) + H₂ sin(2πf₂t) with f₁ = 1 GHz and f₂ = 5 GHz is applied, the resonant trajectory of excitation is a hypocycloid, reminiscent of a hexagon instead of a circle as shown in Fig. 1d. Circular, elliptical or even stadium-like orbits are common, while a hexagon is unusual in the resonant excitation of vortices.^37,38 Interestingly, comparing the trajectory of the guiding center in the dual-frequency field with the sum trajectory of that in the two single-frequency field, one can observe differences in amplitude and phase (about 12 degrees), which indicate that two excitation modes are coupled with each other. The inset of Fig. 1d shows that the dynamical phase difference remained unchanged when the contribution of the higher-frequency mode was increased.

Fig. 1 (a) A sketch of two coupled skyrmions with opposite chiralities in a Co/Ru/Co nanodisk. (b), (c) and (d) are the trajectories of the skyrmion on the top nanolayer in single-frequency fields of 1 GHz (b), 5 GHz (c), and a dual-frequency field with ratios f₁/f₂ of 1/5 and H₁/H₂ of 5/1 (d), respectively. The orange dotted line and the pink dotted line in the inset are the sum of the orbits at 1 GHz and 5 GHz with amplitude ratios of 5/1 and 1/1, respectively. The curved arrows represent the senses of rotation. The numbers in (d) label the cusps of the hexagon during two periods. The amplitude of H₁ is 100 Oe.

To comprehend the striking features of the hexagonal resonant excitation, Fig. 2a shows the time evolution of the topological density in one period for the steady orbits in Fig. 1b–d. All the topological density distributions display a large nonlocal deformation, unlike the very small and local deformations in vortex cores or in the narrow walls of bubbles.^35,40 Clearly, this global deformation rotates like a rigid body, suggesting that the effective mass associated with the deformation of the topological density shall be included to describe the dynamics of the coupled skyrmions. The direction of rotation for the lower-frequency mode is CW, while that for the higher-frequency one is CCW, which is consistent with the results in Fig. 1b–d. When the dual-frequency microwave magnetic field is applied, the direction of rotation is CW and the distribution of the topological density is similar to that of the lower-frequency mode with a slight difference, indicating that the hexagon is a superposition of the CW and CCW modes with the CW mode dominating.

Fig. 2 (a) The variation of the topological density for the top nanolayer in one period under the different in-plane microwave magnetic fields. (b) The time dependence of R_x, R_y, the total (E_tot), uniaxial anisotropic (E_an) and demagnetization (E_dem) energies in two periods for the hexagonal steady orbit in Fig. 1d. The dots correspond to the cusps of the hexagon.

In order to elucidate the contribution of the competition between the different energies to stabilize the hexagonal trajectory, Fig. 2b shows the energies of the skyrmions as a function of time. The dots correspond to the six cusps of the hexagon labeled in Fig. 1d. Obviously, R_x, R_y and the energies vary periodically with time and the periods are about 1 ns. The uniaxial anisotropic (E_an) and demagnetization (E_dem) energies constitute the most part of the total energy. Interestingly, the variation in the E_tot is almost one order smaller than that of both the E_an and E_dem, suggesting that competition between the E_an and E_dem plays a substantial role in determining the stable hexagonal trajectory. At each cusp, the E_dem is located at a valley and the E_an is located at a peak, whereas the E_dem reaches a maximum and the E_an reaches a minimum between two cusps. The above analysis is also applicable to other types of polygonal trajectories.

We have demonstrated that resonant excitation can be used to transform the rotational trajectory of skyrmions from an approximate circle to a hexagon by switching from a single-frequency microwave field to a dual-frequency one. Here we further show in Fig. 3 that tuning the frequency ratio of the dual-frequency microwave field is also beneficial for the controllability of skyrmion dynamics. The frequency f₁ is chosen to be 1.15 GHz, which is the eigenfrequency of a circular trajectory for the gyrotropic motion of coupled skyrmions. In a microwave field with the eigenfrequency, the dynamics of the skyrmion will exhibit a strong resonant excitation. Based on the strong resonant excitation, polygon-like trajectories can be obtained by tuning the frequency ratio of the dual-frequency field. The frequency ratio f₁/f₂ is 1/2, 1/3, 1/4 and 1/6, whereas the amplitude ratio is 2/1, 3/1, 4/1, and 6/1 in Fig. 3a–d, respectively. The figures show that the steady orbit of the topological resonant excitation is indeed able to be transformed from hexagons to other polygons such as triangles, quadrangles, pentagons, and heptagons. Such controllability of the resonant excitation at the nanoscale by means of a dual-frequency microwave field would be useful for the manipulation of skyrmions and the design of microwave devices.

Fig. 3 Transformation of the topological resonant trajectory of the guiding center in different microwave magnetic fields with the waveform H₁ sin(2πf₁t) + H₂ sin(2πf₂t). (a), (b), (c), (d) f₁ is chosen to be 1.15 GHz and the ratio of f₁/f₂ is 1/2, 1/3 1/4 and 1/6, respectively. The corresponding ratio of H₁/H₂ is 2/1, 3/1, 4/1, and 6/1, respectively. The amplitude H₁ is 50 Oe.

In Fig. 4, the resonant excitation of the skyrmion shows quasiperiodic behavior when an incommensurate frequency ratio (i.e. the golden ratio ) of the microwave magnetic field is chosen. Considering that it is not possible to use a true irrational number in simulations, here we used a rational number with a precision up to 16 significant decimal digits for the golden ratio and checked that the result is insensitive to the number of digits if the decimal digits go higher than 10. The trajectories of the resonant excitations in a single-frequency (rational number) microwave field are periodic circles. After introducing a microwave field with an irrational-number frequency, the system began to display quasiperiodicity. With the increase of the amplitude ratio H₁/H₂, the trajectories became more uncertain due to an increasing effect of the irrational-number frequency. The nonlinear dynamical behavior was also found in a Josephson-junction system under two ac sources, when the frequency ratio was a golden ratio.⁴¹

Fig. 4 The quasiperiodic behavior of the resonant excitation of a skyrmion in a microwave magnetic field with the frequency f₁ = 1.15 GHz and f₁/f₂ = 1/golden ratio. (a), (b), (c), (d) The corresponding amplitude ratio H₁/H₂ is 2/1, golden ratio, 1/2, and 1/3, respectively. The amplitude H₁ is 50 Oe.

We have to point out that coupling between two skyrmions also plays a crucial role in the stability and controllability of the coupled skyrmion dynamics, as illustrated in eqn (2) and (4). Fig. 5 shows the influence of coupling on the trajectories and on the topological density distributions of skyrmions. Firstly, two guiding centers are driven apart by an external constant magnetic field along the +x direction to ±30 nm for the top and bottom skyrmions, respectively, as labeled by the dark diamonds in Fig. 5a. The guiding centers of the two skyrmions move in opposite directions due to different chiralities and are finally decoupled. Then a dual-frequency microwave magnetic field (f₁/f₂ = 1/5 and H₁/H₂ = 5/1) replacing the constant field drives the two skyrmions to rotate. During 0–0.6 ns, the two guiding centers of the skyrmions remain at a diagonal position from each other but with the same CCW direction of rotation. The trajectories are quadrangles other than hexagons, and are quite complex and unstable as shown in Fig. 5a. The topological density distributions of points A and B labeled in Fig. 5a also show complicated patterns and large deformations in Fig. 5c. When getting close to each other at 0.6 ns due to a damping effect, the guiding centers of the skyrmions are coupled. Consequently, their senses of rotation change from CCW to CW, and hexagonal trajectories are revived, as shown in Fig. 5b. Compared with the topological density distributions at the initial time, those of the coupled skyrmions shown in Fig. 5d start to take a shape similar to the stable ones previously shown in Fig. 2a, and rotate as a relatively rigid body from point C to D (labeled in Fig. 5b). A change in the direction of rotation indicates that the skyrmion dynamics depend not only on their polarities, but also on the eigenfrequencies of the circulation, which is distinguished from the vortex. The results also indicate that the coupling between skyrmions can be used to manipulate the topological density distribution, thus having an influence on the effective mass and on the dynamics of the system.

Fig. 5 (a) and (b) The trajectories of the guiding centers of two skyrmions at 0–0.6 ns and 0.6–40 ns, respectively, after replacing an applied constant magnetic field with the dual-frequency microwave field. The dark diamonds in (a) show the positions of the two guiding centers at 0 ns. (c) and (d) The topological density distributions of points A (0.035 ns on the top nanolayer), B (0.035 ns on the bottom nanolayer), C (1.008 ns on the top nanolayer) and D (1.216 ns on the top nanolayer) labeled in (a) and (b), respectively. The white stars in (c) and (d) represent the positions of the guiding center.

3.3 Numerical solutions to the extended Thiele’s equation

To understand the polygon-like resonant excitation of coupled skyrmions under a dual-frequency microwave field, numerical solutions to eqn (2) were obtained by the Runge–Kutta method for different frequency ratios, as shown in Fig. 6. Because the two skyrmions move almost synchronously, we can use an effective potential energy to replace the total potential energy of one skyrmion. Eqn (2) with a dissipation term considered for the dynamics of skyrmions in the top nanodisk can be rewritten as follows:where K is the effective stiffness coefficient and D is the damping parameter.³⁶ Here, for numerical solutions to eqn (5) and (6), D = 5.59 × 10⁻¹⁴ J s m⁻², G = 4πM_sL/γ = 1.8 × 10⁻¹² J s m⁻² and μ = πμ₀RLM_sξ = 1.0 × 10⁻¹⁴ kg m² (A⁻¹ s⁻²) with ξ ≈ 0.93 for the skyrmions in this work.³⁶ Values for K (0.013 J m⁻²) and M (7.08 × 10⁻²³ kg) are calculated under zero field according to the eigenfrequencies of nearly 0.96 and 4.98 GHz for a hexagonal trajectory of gyrotropic motion and 1.15 GHz for a circular one.^18,40

Fig. 6 Numerical solutions to eqn (5) and (6) for skyrmions driven by a dual-frequency field H_x = H₁ sin(2πf₁t) + H₂ sin(2πf₂t). The values of f₁, the frequency ratio f₁/f₂ and the corresponding H₁/H₂ are (a) 1.15 GHz, 1/2 and 2/1, (b) 1.15 GHz, 1/3 and 3/1, (c) 1.15 GHz, 1/4 and 4/1, (d) 1.15 GHz, 1/6 and 6/1, (e) 1.15 GHz, 1/4.4 and 4.4/1, (f) 2.00 GHz, 1/4 and 4/1, respectively.

A polygon-like resonant excitation can be driven by a dual-frequency field H_x = H₁ sin(2πf₁t) + H₂ sin(2πf₂t) with f₁ being 1.15 GHz (one of the eigenfrequencies of the skyrmions) and f₂ being an integral multiple of f₁, as shown in Fig. 6a–d. The polygonal trajectories from the numerical solution are in best agreement with those from micromagnetic simulations (Fig. 3). When f₂ is a non-integral multiple of f₁, a polygon-like orbit cannot be obtained. As an example, Fig. 6e illustrates the resonant excitation of a skyrmion in a field with f₁/f₂ being 1/4.4, which gives a different result from the polygon-like resonance, indicating that the resonant dynamics of skyrmions is sensitive to the frequency ratio of the dual-frequency field.

Actually, not only the frequency ratio, but also the value of the frequency is of great importance to the dynamics of skyrmions. The dynamics of skyrmions will show neither a strong resonance, nor a polygon-like trajectory, if the frequency of the external field is not equal nor close to the eigenfrequency of the skyrmions. To confirm this, Fig. 6f demonstrates the trajectory of a skyrmion in a field with a frequency f₁ of 2.00 GHz, which is far away from the eigenfrequency of the skyrmion. In this case, though a dual-frequency field is applied, the dynamics of the skyrmion do not show polygon-like behavior.

To clarify the importance of the effective mass to the polygon-like dynamics of skyrmions, Fig. 7 shows the numerical solutions to eqn (5) and (6) with and without the effective mass term. The parameters of eqn (5) and (6) used in Fig. 7 are the same as those used in Fig. 6. An external field with f₁ of 1.00 GHz (one of the eigenfrequencies of the coupled skyrmions), f₁/f₂ of 1/5 and H₁/H₂ of 5/1 is applied on the system. Fig. 7a demonstrates the steady orbit of the numerical solution as the effective mass is considered. A hexagonal trajectory is obtained, which agrees well with the results of Fig. 1d from the micromagnetic simulation. However, when the effective mass term is not considered, the result is totally different and an approximately circular trajectory is obtained as shown in Fig. 7b. The results indicate that the effective mass is vital to the polygon-like trajectory.

Fig. 7 Numerical solutions to eqn (5) and (6) for a skyrmion driven by a dual-frequency field H_x = H₁ sin(2πf₁t) + H₂ sin(2πf₂t) with f₁ being 1.00 GHz (a) with and (b) without considering the effective mass term. The frequency ratio f₁/f₂ is 1/5, and the amplitude ratio H₁/H₂ is 5/1. Only steady trajectories are shown here.

From Fig. 6 and 7, the factors governing the polygon-like excitations of skyrmions can be listed as follows: (1) the frequency f₁ of the external field has to be equal or close to the eigenfrequency of the skyrmion. (2) A dual-frequency field with an integer frequency ratio f₂/f₁ is necessary. (3) The effective mass of the skyrmion associated with the time derivative of the topological density is important to the polygon-like resonant excitation.

Note that twofold spin-wave mode excitations under a small microwave field are theoretically anticipated while only a low-frequency mode has been experimentally observed. A high-frequency mode may be mixed with a helical mode or indistinguishable from a breathing mode due to their similar resonance frequencies.^22,39,42 Compared with the spin-wave modes, the two modes of topological resonant excitation in the present work have higher frequencies and a larger frequency difference. Moreover, there is no evidence of a conical mode for the Co/Ru/Co nanodisks. Therefore, we expect that the topological resonant modes are to be found in experiments and may contribute to the understanding of the collective excitation in skyrmions.

4 Conclusions

In conclusion, we have numerically studied the resonant excitation of two coupled skyrmions in Co/Ru/Co nanodisks by micromagnetic simulations. The Thiele’s equation of guiding centers incorporating an effective mass term is used to comprehend two coupled resonant modes of the skyrmions with nonlocal deformation. Rotational trajectories have been controllably transformed from circular to different polygonal shapes by tuning the commensurate frequency ratio of a dual-frequency microwave field with f₁ chosen to be the eigenfrequency of the skyrmions. Quasiperiodic behavior of the skyrmion dynamics is observed when the frequency ratio is incommensurate. A numerical solution to the extended Thiele’s equation clarifies the importance of the value of f₁, the frequency ratio f₁/f₂ of a dual-frequency field and the effective mass to the polygon-like resonant excitations of the skyrmions. We have also shown that the coupling between two skyrmions has an obvious effect on their dynamics. These findings contribute to a better understanding of skyrmion dynamics and may open a new avenue to the manipulation of spin textures in nanoscale magnets by a dual-frequency microwave field.

Acknowledgements

We appreciate helpful discussions with Prof. Peter F. de Chatel. The work is supported by the National Basic Research Program (no. 2010CB934603) of China, Ministry of Science and Technology China and the National Natural Science Foundation of China under Grant no. 51331006.

References

1. I. K. Schuller, S. Kim and C. Leighton, J. Magn. Magn. Mater., 1999, 200, 571–582.
2. M. R. Fitzsimmons, S. D. Bader, J. A. Borchers, G. P. Felcher, J. K. Furdyna, A. Hoffmann, J. B. Kortright, I. K. Schuller, T. C. Schulthess, S. K. Sinha, M. F. Toney, D. Weller and S. Wolf, J. Magn. Magn. Mater., 2004, 271, 103–146.
3. J. Fu, J. Zhang, Y. Peng, J. Zhao, G. Tan, N. J. Mellors, E. Xie and W. Han, Nanoscale, 2012, 4, 3932–3936.
4. M. S. Salem, P. Sergelius, R. M. Corona, J. Escrig, D. Görlitz and K. Nielsch, Nanoscale, 2013, 5, 3941–3947.
5. S.-B. Choe, Y. Acremann, A. Scholl, A. Bauer, A. Doran, J. Stöhr and H. A. Padmore, Science, 2004, 304, 420–422.
6. J. P. Park, P. Eames, D. M. Engebretson, J. Berezovsky and P. A. Crowell, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 020403.
7. C. Phatak, A. K. Petford-Long and O. Heinonen, Phys. Rev. Lett., 2012, 108, 067205.
8. H. Jung, K.-S. Lee, D.-E. Jeong, Y.-S. Choi, Y.-S. Yu, D.-S. Han, A. Vogel, L. Bocklage, G. Meier, M.-Y. Im, P. Fischer and S.-K. Kim, Sci. Rep., 2011, 1, 59.
9. A. Dussaux, B. Georges, J. Grollier, V. Cros, A. V. Khvalkovskiy, A. Fukushima, M. Konoto, H. Kubota, K. Yakushiji, S. Yuasa, K. A. Zvezdin, K. Ando and A. Fert, Nat. Commun., 2010, 1, 8.
10. V. S. Pribiag, I. N. Krivorotov, G. D. Fuchs, P. M. Braganca, O. Ozatay, J. C. Sankey, D. C. Ralph and R. A. Buhrman, Nat. Phys., 2007, 3, 498–503.
11. S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii and P. Böni, Science, 2009, 323, 915–919.
12. X. Z. Yu, Y. Onose, N. Kanazawa, J. H. Park, J. H. Han, Y. Matsui, N. Nagaosa and Y. Tokura, Nature, 2010, 465, 901–904.
13. X. Z. Yu, N. Kanazawa, Y. Onose, K. Kimoto, W. Z. Zhang, S. Ishiwata, Y. Matsui and Y. Tokura, Nat. Mater., 2011, 10, 106–109.
14. T. Adams, S. Mühlbauer, C. Pfleiderer, F. Jonietz, A. Bauer, A. Neubauer, R. Georgii, P. Böni, U. Keiderling, K. Everschor, M. Garst and A. Rosch, Phys. Rev. Lett., 2011, 107, 217206.
15. S. Heinze, K. von Bergmann, M. Menzel, J. Brede, A. Kubetzka, R. Wiesendanger, G. Bihlmayer and S. Blügel, Nat. Phys., 2011, 7, 713–718.
16. I. Raičević, D. Popović, C. Panagopoulos, L. Benfatto, M. B. Silva Neto, E. S. Choi and T. Sasagawa, Phys. Rev. Lett., 2011, 106, 227206.
17. S. Seki, X. Z. Yu, S. Ishiwata and Y. Tokura, Science, 2012, 336, 198–201.
18. Y. Y. Dai, H. Wang, P. Tao, T. Yang, W. J. Ren and Z. D. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 054403.
19. L. Sun, R. X. Cao, B. F. Miao, Z. Feng, B. You, D. Wu, W. Zhang, A. Hu and H. F. Ding, Phys. Rev. Lett., 2013, 110, 167201.
20. J. Li, A. Tan, K. W. Moon, A. Doran, M. A. Marcus, A. T. Young, E. Arenholz, S. Ma, R. F. Yang, C. Hwang and Z. Q. Qiu, Nat. Commun., 2014, 5, 4704.
21. C. Pfleiderer and A. Rosch, Nature, 2010, 465, 880–881.
22. Y. Okamura, F. Kagawa, M. Mochizuki, M. Kubota, S. Seki, S. Ishiwata, M. Kawasaki, Y. Onose and Y. Tokura, Nat. Commun., 2013, 4, 2391.
23. F. Jonietz, S. Mühlbauer, C. Pfleiderer, A. Neubauer, W. Münzer, A. Bauer, T. Adams, R. Georgii, P. Böni, R. A. Duine, K. Everschor, M. Garst and A. Rosch, Science, 2010, 330, 1648–1651.
24. X. Z. Yu, N. Kanazawa, W. Z. Zhang, T. Nagai, T. Hara, K. Kimoto, Y. Matsui, Y. Onose and Y. Tokura, Nat. Commun., 2012, 3, 988.
25. J. Iwasaki, M. Mochizuki and N. Nagaosa, Nat. Commun., 2013, 4, 1463.
26. J. Iwasaki, M. Mochizuki and N. Nagaosa, Nat. Nanotechnol., 2013, 8, 742–747.
27. Y. Zhou and M. Ezawa, Nat. Commun., 2014, 5, 4652.
28. B. Van Waeyenberge, A. Puzic, H. Stoll, K. W. Chou, T. Tyliszczak, R. Hertel, M. Fähnle, H. Brückl, K. Rott, G. Reiss, I. Neudecker, D. Weiss, C. H. Back and G. Schütz, Nature, 2006, 444, 461–464.
29. K. Yamada, S. Kasai, Y. Nakatani, K. Kobayashi, H. Kohno, A. Thiaville and T. Ono, Nat. Mater., 2007, 6, 269–273.
30. S.-K. Kim, K.-S. Lee, Y.-S. Yu and Y.-S. Choi, Appl. Phys. Lett., 2008, 92, 022509.
31. Y. Dai, H. Wang, T. Yang, W. Ren and Z. Zhang, Sci. Rep., 2014, 4, 6135.
32. M. J. Donahue and D. G. Porter, OOMMF User’s Guide, Version 1.2a5, 2012.
33. P. J. H. Bloemen, H. W. van Kesteren, H. J. M. Swagten and W. J. M. de Jonge, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 13505–13514.
34. N. Papanicolaou and T. N. Tomaras, Nucl. Phys. B, 1991, 360, 425–462.
35. G. M. Wysin, F. G. Mertens, A. R. Völkel and A. R. Bishop, in Nonlinear Coherent Structures in Physics and Biology, ed. K. H. Spatschek and F. G. Mertens, Plenum Press, New York, 1993.
36. K. Yu. Guslienko, Appl. Phys. Lett., 2006, 89, 022510.
37. K.-S. Lee and S.-K. Kim, Appl. Phys. Lett., 2007, 91, 132511.
38. S. Kasai, Y. Nakatani, K. Kobayashi, H. Kohno and T. Ono, Phys. Rev. Lett., 2006, 97, 107204.
39. M. Mochizuki, Phys. Rev. Lett., 2012, 108, 017601.
40. I. Makhfudz, B. Krüger and O. Tchernyshyov, Phys. Rev. Lett., 2012, 109, 217201.
41. D.-R. He, W. J. Yeh and Y. H. Kao, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 172–178.
42. Y. Onose, Y. Okamura, S. Seki, S. Ishiwata and Y. Tokura, Phys. Rev. Lett., 2012, 109, 037603.

---