Magneto-electric/dielectric and fluorescence effects in multiferroic xBaTiO3–(1 − x)ZnFe2O4 nanostructures
Kuldeep Chand Verma*a,
S. K. Tripathia and
R. K. Kotnalab
aCentre of Advanced Study in Physics, Department of Physics, Panjab University, Chandigarh 160 014, India. E-mail: kuldeep0309@yahoo.co.in; dkuldeep.physics@gmail.com; Tel: +91 9418941286
bNational Physical Laboratory, New Delhi 110012, India
First published on 27th October 2014
Abstract
Multiferroic composites of xBaTiO3–(1 − x)ZnFe2O4 (BTZF) [x = 0.25 (BTZF2575), 0.35 (BTZF3565), 0.45 (BTZF4555), 0.50 (BTZF5050) and 0.75 (BTZF7525)] nanostructure have been synthesized by a sol–gel method. Different types of nanostructural shapes and sizes have been obtained by the effect of ionic radii, surface energy and poly vinyl alcohol, which enhances the magneto-electric/dielectric interaction between BT/ZF phases. The crystalline phases of BTZF composite are confirmed by X-ray diffraction, and nanostructural dimensions and shape by transmission electron microscopy. The improvement in magnetization of BTZF is dependent upon the size and shape of the nanostructure, stoichiometric ratio and strength of occupation of cations at octahedral and tetrahedral sites. The chemical states of Fe in BTZF are analyzed by X-ray photoelectron spectroscopy. The ferroelectric property is explained by the nano size effect, 1D nanostructure shape, lattice distortion and epitaxial strain between two phases. The magnetoelectric coefficient is measured at room temperature under an applied dc magnetizing field and show different types of behavior in each sample. The magnetocapacitance is measured and explained on the basis of Maxwell–Wagner space charge and magnetoresistance, and relates to theoretical investigation, which proves that the enhancement not only depends on the size/shape of nanostructure but also the strain-induced phase transition where out-of-plane polarization appears in the composite. The photoemission of BTZF is observed by fluorescence spectroscopy.
1. Introduction
Multiferroic (MF) magnetoelectric (ME) nanostructural composites aimed at understanding new physics – such as product properties, dynamic coupling between electric and magnetic dipole moments,1 and microwave damping2 – have attracted significance for use in magnetoelectronic and spintronic devices.3–5 The ME coupling in MF composites is strain mediated from electrical order in one phase to magnetic order in the other, creating the desired ME phenomena.6 The spin-current-based multiferroicity of an MF composite is an interfacing ME coupling: interfacing ferromagnetic (FM) with ferroelectric (FE) triggers in the FM low-energy (coherent magnonic) excitations near the interface, which builds up a spatially inhomogeneous, spin-current-carrying surface magnetic order within the spin-diffusion length (on the order of nm).7 These ME couplings contribute as: (i) quasistatic screening spins, which follow adiabatically the direction of local magnetic moments, yielding a linear ME effect; (ii) deviations from adiabaticity give rise to an exponential spiral spin density which goes along with an emergent electric response associated with the intrinsic spin current of the spiral.8 In a comparison of an ME nanostructural composite with its bulk form, the FE and FM phases could be tuned and controlled at room temperature.9 In these composite, the two different phases can be combined at the atomic level, and thus interface losses could be reduced significantly, which results in an epitaxial or superlattice structure resides stress/strain.10The ME coupling manifests itself by electric properties on an applied magnetic field, called direct ME effect, and is usually quantified in terms of the polarization and voltage coefficients. This polarization defines the change δP by an applied magnetic field δH as the magnetic-field control of electric polarization, which is termed the dynamic ME coefficient: αE = ∂P/∂H.11 The associated output voltage δV induced by δH affects the dielectric properties of ME as well; additional important information on the degree of ME coupling is provided by the magnetodielectric coefficients. This can be easily evaluated by measuring the dependence of capacitance C on magnetic-field intensity is so called magnetocapacitance (MC).11,12 The MC effect can be understood on the basis of Maxwell–Wagner space charge effect at the interface of composite and electrode or grain boundaries,13 and magnetoresistance (MR).
Recently, perovskite based MF composites such as BaTiO3–CoFe2O4,3,13 BaTiO3/Fe,6 ZnFe2O4–BaTiO3,12 BiFeO3–CoFe2O4,14 CoFe2O4–PbTiO3,15 LaCaMnO3/BiFeO3,16 Pb(Zr0.52Ti0.48)O3–La0.65Sr0.35MnO3,17 FeGaB/Pb(La,Sn,Zr,Ti)O3,18 BaTiO3–Ni0.7Zn0.3Fe2O4,19 Ba0.8Ca0.2TiO3–Ni0.2Cu0.3Zn0.5Fe2O4 (ref. 20) etc. have been widely investigated. Among them, the perovskite BaTiO3 (BT) is a well-known21 room-temperature ferroelectric that is tetragonal with a = b = 3.99 Å and c = 4.03 Å. At higher temperatures it is cubic and thus not ferroelectric, but on cooling it becomes tetragonal below the Curie temperature of 410 K,22 orthorhombic below 290 K and rhombohedral below 190 K. It is given in a recent report23 that the polycrystalline tetragonal BT nanostructure has enhanced polarization due to its twin structure in which stress residing near grain boundaries can easily control depolarization field and long range interactions. The nanostructural ZnFe2O4 (ZF) involves the redistribution of Fe3+ to tetrahedral and Zn2+ to octahedral interstices. This cationic rearrangement leads to the formation of two (A) and (B) magnetic sublattices, which are then responsible for the enhanced magnetization displayed when compared with bulk ZF.24,25 In order to obtain a high ME response in MF composites, the ferrite phase should be highly magnetostrictive possessing high resistivity, which is possible in the ZF nanostructure.
In comparison with nanoparticles and thin films, one dimensional (1D) nanostructures (nanorods, nanowires etc.) have special physical properties.26 This is due to their anisotropic property and unique size effect. Glinchuk et al.27 pointed out that ferroic nanorods or nanowires will show giant ME effects as their radii decrease, and then induce an abnormal increase in the dielectric tunability and dramatic phase transition. Moreover, M. Q. Cai et al.28 used first-principles calculations for the enhancement of spontaneous polarization as the polarization is induced along the length direction of the wire, by which the tension induced by the nanowire surface curvature counteracts the near-surface depolarization effect.
In this paper we have synthesized MF composites xBaTiO3–(1 − x)ZnFe2O4 (BTZF) [x = 0.25 (BTZF2575), 0.35 (BTZF3565), 0.45 (BTZF4555), 0.50 (BTZF5050) and 0.75 (BTZF7525)] nanostructures by a sol–gel method using poly vinyl alcohol (PVA) as surfactant. The structural, microstructural, ferroelectric, ferromagnetic, ME coefficient, magnetodielectric and fluorescence properties have been investigated.
2. Experimental details
2.1 Preparation of BTZF nanostructures
For the synthesis of BTZF2575, BTZF3565, BTZF4555, BTZF5050 and BTZF7525 nanostructures, a typical simple chemical process, i.e., sol–gel using PVA as surfactant was used. The precursor solution was prepared from barium acetate, tetra-n-butyl orthotitanate, zinc acetate and ferric chloride with desired molar concentrations. In this method, ethanol and acetic acid were mixed in the ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The tetra-n-butyl orthotitanate was added to it and stirred for 2 h using a magnetic stirrer and denoted as solution A. Barium acetate, zinc acetate and ferric chloride were dissolved in distilled water separately to give a clear solution denoted as solution B. The final solution M was prepared by mixing A and B dropwise and stirring for another 3 h. This precursor solution M was added to a PVA solution in the molar ratio of M
1. The tetra-n-butyl orthotitanate was added to it and stirred for 2 h using a magnetic stirrer and denoted as solution A. Barium acetate, zinc acetate and ferric chloride were dissolved in distilled water separately to give a clear solution denoted as solution B. The final solution M was prepared by mixing A and B dropwise and stirring for another 3 h. This precursor solution M was added to a PVA solution in the molar ratio of M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PVA, 5
PVA, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The solution was dried at 250 °C and annealed at 700 °C for 2 h to crystallize.
2. The solution was dried at 250 °C and annealed at 700 °C for 2 h to crystallize.
2.2 Characterization
Atomic absorption spectroscopy analysis was used to check the composition of Ba, Ti, Zn and Fe content in BTZF using a Perkin-Elmer system and both experimental and theoretical values of composition are well matched in each FE BT and FM ZF composite. The crystalline structure was analyzed by X-ray diffraction (XRD) by using an X’Pert PRO PANalytical system and microstructure by transmission electron microscopy (TEM) using a HITACHI H-7500. For electrical measurements, the BTZF crystalline powder was pressed into pellets of thickness ∼0.5 mm by the cold isostatic pressing method with a pressure of 5 bar for 10 min and then sintered at 1000 °C for 5 h. Polarization under the influence of an applied electric field was measured using a Radiant Technologies FE test system. Magnetization of BTZF was measured at room temperature using a Lakeshore 7304 vibrating sample magnetometer. X-ray photoelectron spectroscopy (XPS) was performed using a Perkin-Elmer model 1257 equipped with a non-monochromatized Al Kα X-ray source. The ME coupling coefficient was measured by the dynamic field method used a system built in-house. A buffer and high-pass filter circuit to reduce the background voltage noise were employed in the measurement set-up to detect the induced ME voltage across the sample thickness. The room temperature magnetodielectric performed on BTZF samples at frequency of 1 kHz by change in relative dielectric permittivity as a function of an applied magnetic field strength was measured by combining a Wayne Kerr 6500B Precision Impedance analyzer with the Lakeshore 7304. The photoemission is shown by fluorescence spectrum of BTZF was recorded using an Edinburgh FLSP920 spectrofluorophotometer at room temperature.3. Result and discussion
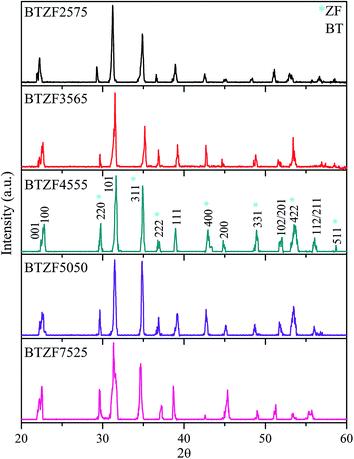
Fig. 1 shows the XRD patterns of all samples of BTZF composites measured at room temperature. The pattern confirms the existence of two phases, namely perovskite and spinel together corresponding to BT and ZF, respectively. The polycrystalline BT with tetragonal phase at diffraction angles 2θ = 21.74, 22.66, 31.71, 39.27, 44.73, 51.75 and 56.01 correspond to (001), (100), (101), (111), (200), (102/201) and (112/211) respectively, observed. The reflections 001/100 and 102/201 are the splitting of cubic into tetragonal phase. Meanwhile, 2θ = 29.69, 35.27, 36.84, 42.78, 48.73, 53.45 and 58.67° correspond to (220), (311), (222), (400), (331), (422) and (511), respectively, indicates the cubic spinel phase of ZF. Using the CHEKCELL lattice constant refinement program, the lattice parameters of both phases are summarized in Table 1. The distortion ratio c/a of tetragonal BT is 1.0494, 1.0087, 1.0076, 1.0089 and 1.0097, respectively, calculated for BTZF2575, BTZF3565, BTZF4555, BTZF5050 and BTZF7525 composite. The distortion, c/a when compared with pure BT (c/a ∼ 1.01),21 75%BT in BTZF has slightly smaller value of c/a and decreases with decreasing BT to 45%BT. The smaller c/a value of the BT phase in the composite than in the pure BT ceramic suggests the diffusion of Fe3+ or Zn2+ into the BT lattice from the ZF phase. BaTiO3 is known to enable substitution of different sizes of ions including Fe3+ and Zn2+ and the doping/substitution site depends on the size of the ions.29 The ionic radii of Fe3+ (0.69 Å) and Zn2+ (0.88 Å) are more comparable to the ionic radius of Ti4+ (0.745 Å) than Ba2+ (1.49 Å) and therefore, Fe3+ and Zn2+ substitution will occur at the Ti-site.30 Meanwhile, substitution of Fe3+ can result in a decrease of BT lattice parameters because of its smaller radius than Ti4+.18 Zn2+ substitution, on the other hand, can increase the BT lattice parameters due to it having a larger ionic radius than Ti4+. Therefore, with 25%BT in BTZF, the large value of lattice distortion occurs because Zn2+ is reach and has a larger ionic radius than both Fe3+ and Ti4+. Moreover, substitution of Zn2+ and Fe3+ at Ti4+ sites will cause the formation of oxygen vacancies to maintain the electroneutrality30 and these oxygen vacancies contribute to the increase of the lattice parameters.| BTZF | Lattice constant | Multiferroic properties | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BT | ZF | BTZF | |||||||||||
| a (Å) | c (Å) | a (Å) | d (nm) | l (nm) | Ms (emu g−1) | Mr (emu g−1) | Hc (Oe) | Ps (μC cm−2) | Pr (μC cm−2) | Ec (kV cm−1) | αE (mV cm−1 Oe−1) | MC (%) | |
| 2575 | 4.0013 | 4.1992 | 8.448 | 6 | >100 | 0.19 | 0.056 | 1068 | 69.61 | 18.44 | 13.79 | 122.9 | 2.84 |
| 3565 | 3.992 | 4.0274 | 8.438 | 33 | 103 | 15.41 | 3.19 | 319 | 41.95 | 5.47 | 1.78 | 30.5 | 1.24 |
| 4555 | 3.992 | 4.0222 | 8.432 | 54 | 120 | 8.71 | 1.38 | 255 | 26.31 | 5.36 | 3.61 | 29.2 | 0.78 |
| 5050 | 3.995 | 4.0304 | 8.422 | 59 | 141 | 0.15 | 0.038 | 249 | 31.66 | 6.41 | 12.81 | 51.7 | 1.42 |
| 7525 | 3.999 | 4.0378 | 8.351 | 84 | — | 0.25 | 0.047 | 116 | 26.10 | 12.51 | 12.93 | 43.9 | 1.12 |
Fig. 2(a and b) show the TEM images (left) and HRTEM images (right) of BTZF nanostructural composites measured at different magnifications because the shape and size of nanostructure (nanoparticles, nanowires and nanorods) in each sample is quite different hence creates difficulty in visualizing clear pictures of the shape and size at same magnification for each sample. The BTZF2575 composite forms nanowire-like structures of average diameter (d) 6 nm and length of greater than 100 nm. But with increasing BT concentration the dimensions along the long side decrease and the diameter shows an increment, i.e., the formation of nanorod-like structures. The average value of d is 33, 54 and 59, and l is 103, 120 and 141 nm, respectively, measured for BTZF3565, BTZF4555 and BTZF5050 nanorods. However, the BTZF7525 composite forms nanoparticles of cubic shape and the average value of d is 84 nm. The mechanism of the formation of nanoparticles, nanorods and nanowires is explained in the next paragraph. It has been also observed in the TEM images that there are random distribution of dark and bright borders, which may be the formation of FE BT and FM ZF phases alternatively into a single nanocrystal, as is clearly shown by the HRTEM images in the right panels of Fig. 2(a and b). Large regions of periodically ordered material are no longer observed, indicating random filling of phases. This type of behavior imagining the two phases in a single crystal is described recently by Sreenivasulu et al.31 The planes with interplanar spacing d ∼ 0.28 nm of the most intense peak (101) of BT in the XRD pattern is observed in all HRTEM images and d ∼ 0.25 of the most intense peak (311) of ZF is also seen. In BTZF2575, the most frequent lattice fringes are oriented parallel to the major axis of the nanowires. The high crystallinity of the particles is evident from the selected area electron diffraction (SAED) patterns shown in the insets of the HRTEM images and show that all the composites are of polycrystalline phase.
The formation of different types of nanostructural (nanoparticles, nanorods and nanowires) formations is explained on the basis of ionic radii, surface energy and PVA acting as surfactant, as well as orientation during the growth process of large aggregates of metal ions. The variation in the size of grains is due to different ionic radii of metal ions and their stoichiometric ratio is different in each BTZF composite. The variation in the shape of BTZF nanostructures is explained on the basis of the surface energy of Zn2+ ions, which is higher and forms agglomerations during chemical reaction with OH− ions.32 The Zn2+ ions in OH− medium normally take the form of divalent metal ions and their solubility increases with appropriate concentration and temperature. During heating, the surfactant PVA helps in synthesizing nanostructures. Under heat treatment of PVA, there exist two sites, namely hydrophobic (Hb) and hydrophilic (Hp), of PVA and they form clusters. The Hb sites keep the materials separate due to their repulsive forces which slow down the rate of reaction, whereas Hp sites keep the metal intact and retard the growth process. Therefore, higher concentrations of Zn2+ ions form large agglomerations with OH− and when this product reacts with PVA, the Hp site gives the orientation to grow continuously in the confined reverse micelle process, causing formation of nanorods and nanowires. Moreover, the Ostwald ripening theory32 is also responsible for this type of crystal growth process.
Fig. 3(a–e) shows the FM behavior of BTZF composites by measuring magnetization versus applied magnetizing field (M–Hdc) hysteresis at room temperature. The values of saturation magnetization (Ms) are 0.19, 15.41, 8.71, 0.15 and 0.25 emu g−1, values of remanent magnetization (Mr) are 0.056, 3.19, 1.38, 0.038 and 0.047 emu g−1, and values of coercive field (Hc) are 1068, 319, 255, 249 and 116 Oe, measured for BTZF2575, BTZF3565, BTZF4555, BTZF5050 and BTZF7525 composites, respectively, and are also given in Table 1. These values of ferromagnetism showed an improvement over reported work on BT based MF composites.12,19,20,33–35 The variation of observed ferromagnetism with BT concentration in BTZF is shown in Fig. 3(f). The value of magnetization is slightly varied with 25, 50 and 75% of ZF concentration in BTZF but increases abruptly with 55 and 65% of ZF. This type of behavior is explained on the basis of size and shape of nanostructure, and stoichiometric ratio of the MF BTZF composite. The slight variation in ferromagnetism is the general behavior and depends upon the size of nanograins.32 The shape of nanostructure is also responsible for improvement in Ms since the nanostructure is increased in the strength of magnetic exchange interaction by surface spins contributed by their large surface to volume ratio and involves a similar behavior given by Callsen et al.36 for nonmagnetic organic molecules on the FM surface using theoretical first principle calculations. In the BTZF nanostructures, the nonmagnetic nano boundaries between nanograins are present instead of organic molecules. It is demonstrated that the possibility of a hybrid nano boundary–FM interface acts as a local embedded surface spin based magnetic unit due to a magnetic hardening of BT in the composite and exhibits spin-filter functionality with sharp spin split molecular-like electronic features at the nano boundary site. This surface spin induced local magnetic hardening leads to exchange interactions and therefore a larger magnetic anisotropic energy results in a stable magnetization axis. This type of magnetism by surfaces and interfaces of nonmagnetic nano boundaries is also described by Neeleshwar et al.37 for Ge quantum dots. As discussed above, it is concluded that the orbital momentum induced at the surface conduction electrons is crucial to understand the observed giant anisotropy.
The abrupt increment of Ms in BTZF3565 and BTZF4555 (Fig. 3(f)) composites is also seen in various ferrites and MF systems based on ZF.25,38 Generally in ZF, the magnetic properties are strongly dependent on the strength of occupation of various cations at octahedral and tetrahedral sites. It is well known that in nanostructural ZF, the antiferromagnetic ordering temperature is much higher (TN = 450 K)25 and can be raised by increasing the Fe3+ occupation at the tetrahedral sites through mechanical activation. This increase of magnetization originates in the stronger inter sub-lattice (A–B) superexchange interaction as compared to intra sub-lattice (A–A and B–B) interactions. At lower ZF concentration, A–A and B–B interactions are dominant. But with higher concentrations, i.e., 50–60% ZF in BTZF, Fe3+ occupies Ti4+ B sites of perovskite via oxygen vacancy and hence stronger superexchange A–B interactions occur, which results in an abrupt increment in magnetization. With sufficient higher concentration, 75% of ZF, weakening of the A–B exchange interaction occurs and the parallel orientation of the magnetic moments in B-site is altered so that they compensate each other only partially, which leads to a progressive decrease of saturation magnetization.
In order to find the contribution of Fe on ferromagnetism of BTZF composites, the XPS spectra are given in Fig. 4, measured at room temperature for Fe 2p states in the binding energy region 700–727 eV. It was reported39 that Fe 2p photoelectron peaks from oxidized iron are associated with satellite peaks, which is important for identifying the chemical states. The Fe2+ and Fe3+ 2p3/2 peaks always show satellite peaks at 6 eV and 8 eV above the principal peaks at 709.5 eV and 711.2 eV, respectively.39 In Fig. 4, the satellite peaks were found in the energy region of 6–8 eV above the 2p3/2 principal peak. It indicates that in this BTZF MF system Fe coexists in both Fe2+ and Fe3+ states. When Fe3+ ions coexist with Fe2+ in ZF, the Fe3+ distorts the lattice structure more than the Fe2+ ion due to the effects of charge and ionic size.40 The difference in energy between the Fe 2p3/2 and 2p1/2 peaks resulting from spin–orbit coupling is ∼13.5 eV, which is very close to the reported value of Fe 2p.39 The peaks related to 2p3/2 are 710.16, 709.83, 710.07, 710.05 and 710.16 eV, and 2p1/2 are 723.67, 723.34, 723.59, 723.37 and 723.92 eV, respectively, observed for BTZF2575, BTZF3565, BTZF4555, BTZF5050 and BTZF7525 composites. These results suggest that the Fe ions have mixed valence state of 2+ and 3+ and must be contributing ferromagnetism via oxygen vacancies.
The insets of Fig. 3(a–e) show the polarization versus electric field (P–E) hysteresis curves at room temperature on poled samples of BTZF composites with 50 Hz being the frequency of polarization. The values of spontaneous polarization, Ps = 69.61, 41.95, 26.31, 31.66 and 26.18 μC cm−2, remanent polarization, Pr = 18.44, 5.47, 5.36, 6.41 and 12.51 μC cm−2, and coercive field, Ec = 13.79, 1.78, 3.61, 12.81 and 12.93 kV cm−1, respectively, measured for BTZF2575, BTZF3565, BTZF4555, BTZF5050 and BTZF7525 composite and are also given in Table 1. These values of polarization show improvement over reported work on BT based MF composites.12,20,33,41,13,17 The values of Pr are plotted in Fig. 3(f) with varying BT concentration and show an abrupt decrement for BT > 0.25 and again enhanced for BT ≥ 0.5. This improvement and increment in the value of Pr is dependent upon different factors, i.e., nanosize, 1D nanostructural formation, lattice distortion and epitaxial strain23,28 and the resulting mechanism is described by the following arguments: the suggestion by Lu et al.42 also applies to the BTZF nanostructural composite which is associated with multidomains, the ZF certainly induced modifications of the FE properties of BT, which might change the depolarization field including change in interfacial strain via magnetostriction effect. However, the stability of ferroelectricity in nanoscale BT is proposed by Spanier et al.43 on the basis of polarization-induced surface charges. Incomplete screening of surface charges by nanostructures results in a depolarization field that opposes the bulk polarization, thereby suppressing ferroelectricity. When the nanostructural formation occurs in the forms of rods and wire, the capacitive contribution is eliminated between the tip and the length so that the resulting map exhibits only the contribution from the surface charges associated with a local electric polarization. Moreover, the BTZF nanostructure is synthesized by a sol–gel based chemical process where there may be the possibility of the presence of OH ions on the surfaces. These molecular adsorbate OH ions can compensate the surface polarization charges, providing a mechanism for reducing the depolarizing fields.43 In the BTZF nanostructure exist both Fe2+/Fe3+ ions (Fig. 4), which creates the possibility that each Fe2+ with its surrounding Fe3+ will form a dipole with strong local polarization. Under an external electric field, the hopping of electrons between Fe2+ and Fe3+, which is equivalent to the reversal of the dipole, contributes to the large polarization and involves a similar behavior observed in nano MF YFeO3.44 Furthermore, the jumping of electrons in Fe2+/Fe3+ dipoles is also a switching process of the dipole, which contributes to magnetocapacitance effect (Fig. 6) due to the jumping becoming easier in a magnetic field.44
The ME coupling coefficient was determined as a function of dc magnetic field using the equation:11
 | (1) |
 | ||
| Fig. 5 ME voltage coefficient (αE) with Hdc (0–6 kOe) under the influence of Hac = 5 Oe and frequency of 1093 Hz of BTZF nanostructures. | ||
The origin of ME coupling of BTZF composites is the coupling of FE and FM degrees of freedom due to the influence of the FE matrix on the exchange coupling constant via screening of the intragrain and intergrain Coulomb interactions. Therefore, a possible mechanism for ME coupling of this FE/FM (BTZF) interface is based on screening effects.51 The spin-polarized charge density formed in the FM in the vicinity of the FM/FE interface52 acts with a torque on the magnetic moments in the FM, resulting in a noncollinear magnetic ordering.53 Hence, electric polarization emerges that couples the FM to the FE part. Additionally, the FE polarization (and electric field) stems actually from the FE surface, which triggers the spin spiral in a FM. The latter carries a spin current with an associated Aharonov–Casher effect and/or Dzyaloshinkii–Moriya (DM) interaction.54 In this sense the ME coupling is caused by an emergent inverse DM interaction at MF interfaces.7
Recently, MF composites have been reported with MC or magnetodielectric (MD) effects,11,12 where for composites with inhomogeneous structures in the interfacial layers for different resistivity and other electric structures, the MR value could be calculated with a simple equivalent circuit of two parallel RC elements in series. MR depends upon core-based and the interfacial (nanograins boundaries) of the MF composite.12 For an MF composite under an external magnetic field, the magnetostriction in the magnetic phase produces stresses transferred in the FE phase, resulting in an electric polarization via the ME effect.12 As a result, the dielectric behavior is modified. The MC/MD is the change in dielectric constant (ε), [ε(H) − ε(0)]/ε(0), where ε(H) and ε(0) denote the dielectric constants at applied magnetic field H and zero field, respectively. Fig. 6 shows the change in the real part of the relative dielectric permittivity of the nanostructural BTZF composites at 1 kHz as a function of magnetic field Hdc and measured at room temperature. Clearly, the capacitance decreases with increasing applied magnetic field (negative value of MC) and a similar behavior is also observed by Anjum et al.55 for their MF system. The value of MC at Hdc = 3 kOe is 2.84, 1.24, 0.78, 1.42 and 1.12%, respectively, calculated for BTZF2575, BTZF3565, BTZF4555, BTZF5050 and BTZF7525 composites.
 | ||
| Fig. 6 MD responses of the BTZF nanostructures under the influence of Hdc (0–6 kOe) at 1 kHz of frequency. | ||
Pertsev et al.11 gives theoretical calculations of strain-mediated MC of BaTiO3 film deposited on FM substrate showing a similar behavior to that observed in the present BTZF nanostructure where ME coupling is mediated via lattice strain. It has been observed for BT films that the lattice mismatch Sεαα(um = −1%) ≅ 43 and Sεαα = (um = +1%) ≅ −58, where Sεαβ = Sεαβ(um) of the out-of-plane permittivity ε33 as a function of the initial biaxial strain um. In the present case, BT has tetragonal phase with higher tetragonal distortion and ZF shows cubic phase. Therefore, these values of Sεαα may be improved for different types of nanostructural formations of BTZF.56
For this strain-mediated ME effect in a MF composite, the coefficient can be calculated as
 | (2) |
Indeed, when the magnetic field is not parallel to the composite interface, the demagnetising field eventually makes dm3αβ smaller than the piezomagnetic coupling where the internal magnetic field is equal to the applied one. Consider BTZF as a parallel plate capacitor, where only the out-of plane composite permittivity ε33 is important. Introducing the strain sensitivities Sεαβ of the permittivity ε33 via the relation δεαβ = ∂ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε33/∂uαβ, the resulting product is obtained as:
ε33/∂uαβ, the resulting product is obtained as:
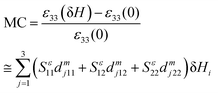 | (3) |
This eqn (3) is valid for weak fields δH ≪ H that do not change the initial piezomagnetic coefficients and strain sensitivity significantly. Therefore, sensitivities Sεαβ can be calculated using the non-linear thermodynamic theory57,58 by neglecting the in-plane lattice strain.11 When the composite stabilizes in the tetragonal c phase (P1 = P2 = 0, P3 ≠ 0) the strain-mediated MC appears to be significant and there is no direct proportionality between the MC and the ME voltage coefficient. Therefore, it gives a contrast between the MC and ME voltage coefficient which may become negligible at P3 = 0 in the conventional parallel plate capacitor geometry of BTZF nanostructures where BT and ZF are distributed randomly, separated by a buffer layer of nano grain boundaries.
In the case of aa phase (|P1| = |P2|, P3 = 0) forming an isotropic biaxial strain (u11 = u22 = um, u12 = 0), the measuring magnetic field δH does not induce shear strain u12 in the composite9 and is sufficient to calculate the strain mediated MC using (3).
Therefore, to evaluate the MC of an ME composite, we need to know only the longitudinal piezomagnetic coefficient characterizing the deformation uS11 induced along the field direction and the transverse coefficient governing the deformation uS⊥ in the direction orthogonal to δH. Considering dm‖ and dm⊥, we obtain
 | (4) |
Fig. 7 shows the fluorescence spectra of BTZF nanostructures measured at room temperature. Absorption bands corresponding to green centred at 555.48 and 563.33 nm, and red at 646.42 and 674.84 nm are observed. The green luminescence is distinctly enhanced in BTZF 2575, 7525 and 5050 nanostructures. However, the emission intensity is enhanced for BTZF7525. The generation of oxygen vacancies in the lattice lead to the shrinking of the lattice.59,60 The distortion of the local asymmetry along B-sites of BT increases, and the transition probabilities that govern various intra-shell transitions giving rise to both green and red emission are increased.59 As a whole, the enhanced luminescence is conjectured to result from the distortion of the local asymmetry and oxygen vacancies generated by Fe3+ ion incorporation in the Ti4+ lattices.60 The absorption bands, i.e., 279.57, 340.78 and 352.58 nm lie in the UV emission region, which is related to near band emission attributed to free-exciton recombination.61
 | ||
| Fig. 7 Fluorescence spectra of BTZF 2575 (black), 3565 (red), 4555 (dark cyan), 5050 (violet) and 7525 (pink) nanostructure measured at room temperature. | ||
4. Conclusion
The MF BTZF composites were synthesized by a sol–gel process at 700 °C 2 h−1 using PVA as surfactant, resulting in nanorods, nanowires and nanoparticle type nanostructural formations, which have enhanced ME coefficient and MC response. The XRD results show coexistence of polycrystalline phases, i.e., tetragonal and spinel, respectively, for BT and ZF. The tetragonal distortion of the BT phase depends upon the size and concentration of composite ions, and oxygen vacancies. The nanostructures of BTZF2575 form nanowires while BTZF3565, BTZF4555 and BTZF5050 are nanorods and BTZF7525 form nanoparticles. The mechanism in the formation of nanoparticles, nanorods and nanowires is explained on the basis of ionic radii, surface energy, PVA and Ostwald ripening process. The XPS analysis results show mixed valence state of 2+ and 3+ of Fe in each BTZF sample. The values of Ms = 0.19, 15.41, 8.71, 0.15 and 0.25 emu g−1, Ps = 69.61, 41.95, 26.31, 31.66 and 26.18 μC cm−2, αE (at Hdc = 3 kOe) = 122.9, 30.5, 29.2, 51.7 and 43.9 mV cm−1 Oe−1, and MC (at 1 kHz frequency and Hdc = 3 kOe) = 2.84, 1.24, 0.78, 1.42 and 1.12% were measured for BTZF2575, BTZF3565, BTZF4555, BTZF5050 and BTZF7525 nanostructural composites, respectively. The enhancement in ME and MD is possible by strain-mediated magnetocapacitance and exists on the basis of nonlinear thermodynamic theory can be exploited in magnetic-field-controlled ferroelectric capacitors, namely magnetovaractors implemented in electronic oscillators, where the oscillation frequency is tuned by a dc magnetic field remotely (via the change of capacitance) in contrast to conventional voltage-controlled oscillators.References
- W. Eerenstein, M. Wiora, J. L. Prieto, J. J. Scott and N. D. Mathur, Nat. Mater., 2007, 6, 348 CrossRef CAS PubMed.
- C. Brosseau, V. Castel and M. Potel, J. Appl. Phys., 2010, 108, 024306 CrossRef PubMed.
- Y. Shen, J. Sun, L. Li, Y. Yao, C. Zhou, R. Su and Y. Yang, J. Mater. Chem. C, 2014, 2, 2545 RSC.
- J. Wu and J. Wang, J. Appl. Phys., 2009, 105, 124107 CrossRef PubMed.
- J. Wu and J. Wang, Electrochem. Solid-State Lett., 2009, 12(10), G61 CrossRef CAS PubMed.
- A. Sukhov, P. P. Horley, C. L. Jia and J. Berakdar, J. Appl. Phys., 2013, 113, 013908 CrossRef PubMed.
- C. L. Jia, T. L. Wei, C. J. Jiang, D. S. Xue, A. Sukhov and J. Berakdar, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 054423 CrossRef.
- M. Mostovoy, Phys. Rev. Lett., 2006, 96, 067601 CrossRef.
- Y. Wang, J. Hu, Y. Lin and C. W. Nan, NPG Asia Mater., 2010, 2(2), 61 CrossRef.
- M. H. Frey and D. A. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 3158 CrossRef CAS.
- N. A. Pertsev, S. Prokhorenko and B. Dkhil, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 134111 CrossRef.
- M. Lorenz, M. Ziese, G. Wagner, J. Lenzner, C. Kranert, K. Brachwitz and M. Grundmann, CrystEngComm, 2012, 14, 6477 RSC.
- J. S. Andrew, J. D. Starr and M. A. K. Budi, Scr. Mater., 2014, 74, 38 CrossRef CAS PubMed.
- F. Yan, G. Chen, L. Lu, P. Finkel and J. E. Spanier, Appl. Phys. Lett., 2013, 103, 024906 Search PubMed.
- C. Y. Tsai, H. R. Chen, F. C. Chang, H. H. Kuo, H. M. Cheng, W. C. Tsai, Y. H. Chu, C. H. Lai and W. F. Hsieh, J. Appl. Phys., 2014, 115, 134317 CrossRef PubMed.
- D. Yi, J. Liu, S. Okamoto, S. Jagannatha, Y. C. Chen, P. Yu, Y. H. Chu, E. Arenholz and R. Ramesh, Phys. Rev. Lett., 2013, 111, 127601 CrossRef.
- X. Lv, C. Cheng, Y. Yiao, M. Tang, Z. Tang, H. Cai, Y. Zhou and R. Li, Mater. Lett., 2013, 100, 7 CrossRef CAS PubMed.
- Z. Zhou, X. Y. Zhang, T. F. Xie, T. X. Nan, Y. Gao, X. Yang, X. J. Sun and D. Z. Sun, Appl. Phys. Lett., 2014, 104, 012905 CrossRef PubMed.
- R. F. Zhang, C. Y. Deng, L. Ren, Z. Li and J. P. Zhou, Mater. Res. Bull., 2013, 48, 4100 CrossRef CAS PubMed.
- K. Sadhana, S. R. Murthy, S. Jie, Y. Xie, Y. Liu, Q. Zhan and R. W. Li, J. Appl. Phys., 2013, 113, 17C731 CrossRef PubMed.
- H. F. Kay and P. Vousden, Philos. Mag., 1949, 40, 1019 CAS.
- A. M. Bratkovsky and A. P. Levanyuk, Phys. Rev. Lett., 2005, 94, 107601 CrossRef CAS.
- K. C. Verma, J. Kaur, N. S. Negi and R. K. Kotnala, Solid State Commun., 2014, 178, 11 CrossRef CAS PubMed.
- K. C. Verma, V. P. Singh, M. Ram, J. Shah and R. K. Kotnala, J. Magn. Magn. Mater., 2011, 323, 3271 CrossRef CAS PubMed.
- M. Atif, S. K. Hasanain and M. Nadeem, Solid State Commun., 2006, 138, 416 CrossRef CAS PubMed.
- B. Liu, B. Hu and Z. Du, Chem. Comm., 2011, 47, 8166 RSC.
- M. Glinchuk, E. Eliseev, A. Morozovska and R. Blinc, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 024106 CrossRef.
- M. Q. Cai, Y. Zheng, B. Wang and G. W. Yang, Appl. Phys. Lett., 2009, 95, 232901 CrossRef PubMed.
- D. Ghosh, H. Han, J. C. Nino, G. Subhash and J. L. Jones, J. Am. Ceram. Soc., 2012, 95, 2504 CrossRef CAS PubMed.
- M. T. Buscaglia, V. Buscaglia, M. Viviani and P. Nanni, J. Am. Ceram. Soc., 2001, 84(2), 376 CrossRef CAS PubMed.
- G. Sreenivasulu, M. Popov, F. A. Chavez, S. L. Hamilton, P. R. Lehto and G. Srinivasan, Appl. Phys. Lett., 2014, 104, 052901 CrossRef PubMed.
- R. K. Kotnala, V. Gupta and K. C. Verma, Curr. Appl. Phys., 2014, 14, 749 CrossRef PubMed.
- G. Sreenivasulu, M. Popov, F. A. Chavez, S. L. Hamilton, P. R. Lehto and G. Srinivasan, Appl. Phys. Lett., 2014, 104, 052901 CrossRef PubMed.
- M. Lorenz, V. Lazenka, P. Schwinkendorf, F. Bern, M. Ziese, H. Modarresi, A. Volodin, M. J. V. Bael, K. Temst, A. Vantomme and M. Grundmann, J. Phys. D: Appl. Phys., 2014, 47, 135303 CrossRef.
- K. C. Verma, V. Gupta, J. Kaur and R. K. Kotnala, J. Alloys Compd., 2013, 578, 5 CrossRef CAS PubMed.
- M. Callsen, V. Caciuc, N. Kiselev, N. Atodiresei and S. Blugel, Phys. Rev. Lett., 2013, 111, 106805 CrossRef.
- S. Neeleshwar, C. L. Chen, C. B. Tsai, Y. Y. Chen and C. C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 201307 CrossRef.
- S. K. Upadhyay and V. R. Reddy, J. Appl. Phys., 2013, 113, 114107 CrossRef PubMed.
- J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-ray Photoelectron Spectroscopy Physical Electronics, reissue edn., 1995 Search PubMed.
- S. Y. Seo, C. H. Kwak, Y. B. Lee and S. H. Kim, J. Korean Phys. Soc., 2008, 52, 805 CrossRef CAS.
- C. X. Li, B. Yang, S. T. Zhang, D. Q. Liu, R. Zhang, Y. Sun and W. W. Cao, J. Alloys Compd., 2014, 590, 346 CrossRef CAS PubMed.
- X. Lu, Y. Kim, S. Goetze, X. Li, S. Dong, P. Werner, M. Alexe and D. Hesse, Nano Lett., 2011, 11, 3202 CrossRef CAS PubMed.
- J. E. Spanier, A. M. Kolpak, J. J. Urban, I. Grinberg, L. Ouyang, W. S. Yun, A. M. Rappe and H. Park, Nano Lett., 2006, 6, 735 CrossRef CAS PubMed.
- Z. X. Cheng, H. Shen, J. Y. Xu, P. Liu, S. J. Zhang, J. L. Wang, X. L. Wang and S. X. Dou, J. Appl. Phys., 2012, 111, 034103 CrossRef PubMed.
- J. Ma, J. Hu, Z. Li and C. W. Nan, Adv. Mater., 2011, 23, 1062 CrossRef CAS PubMed.
- V. G. Bary’achtar, V. A. L’vov and D. A. Jablonskii, JETP Lett., 1983, 37, 673 Search PubMed.
- E. V. Ramana, F. Fiqueiras, M. P. F. Graca and M. A. Valente, Dalton Trans., 2014, 43, 9934 RSC.
- R. C. Kambale, K. M. Song and N. Hur, Curr. Appl. Phys., 2013, 13, 562 CrossRef PubMed.
- M. Liu, O. J. Lou, S. Li, X. Xing, G. Yang and N. X. Sun, J. Appl. Phys., 2011, 109, 07D913 Search PubMed.
- E. A. Eliseev, A. N. Morozovska, M. D. Glinchuk and R. Blinc, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165433 CrossRef.
- O. G. Udalov, N. M. Chtchelkatchev and I. S. Beloborodov, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 174203 CrossRef.
- L. Chotorlishvili, R. Khomeriki, A. Sukhov, S. Ruffo and J. Berakdar, Phys. Rev. Lett., 2013, 111, 117202 CrossRef CAS.
- N. Sedlmayr, V. K. Dugaev and J. Berakdar, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 174422 CrossRef.
- H. Katsura, N. Nagaosa and A. V. Balatsky, Phys. Rev. Lett., 2005, 95, 057205 CrossRef.
- G. Anjum, S. Mollah, D. K. Shukla and R. Kumar, Mater. Lett., 2010, 64, 2003 CrossRef CAS PubMed.
- H. Zheng, J. Wang, S. E. Lofland, Z. Ma, L. M. Ardabili, T. Zhao, L. S. Riba, S. R. Shinde, S. B. Ogale, F. Bai, D. Viehland, Y. Jia, D. G. Schlom, M. Wuttig, A. Roytburd and R. Ramesh, Science, 2004, 303, 661 CrossRef CAS PubMed.
- N. A. Pertsev, A. G. Zembilgotov and A. K. Tagantsev, Phys. Rev. Lett., 1998, 80, 1988 CrossRef CAS.
- A. G. Zembilgotov, N. A. Pertsev, U. Bottger and R. Waser, Appl. Phys. Lett., 2005, 86, 052903 CrossRef PubMed.
- X. Chen, Z. Liu, Q. Sun, M. Ye and F. Wang, Opt. Commun., 2011, 284, 2046 CrossRef CAS PubMed.
- Q. Sun, X. Chen, Z. Liu, F. Wang, Z. Jiang and C. Wang, J. Alloys Compd., 2011, 509, 5336 CrossRef CAS PubMed.
- X. Li, Y. Hou, Q. Zhao and L. Wang, J. Colloid Interface Sci., 2011, 358, 102 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |