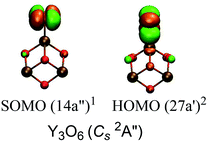Structural evolution, sequential oxidation and chemical bonding in tri-yttrium oxide clusters: Y₃O_x⁻ and Y₃O_x (x = 0–6)

Abstract

We report a systematic and comprehensive investigation on the electronic structures and chemical bonding of a series of tri-yttrium oxide clusters, Y₃O_x^−/0 (x = 0–6), using density functional theory (DFT) calculations. The generalized Koopmans' theorem was applied to predict the vertical detachment energies (VDEs) and simulate the photoelectron spectra (PES) for Y₃O_x⁻ (x = 0–6) clusters. A trend of sequential oxidation is observed from Y₃O⁻ to Y₃O₆⁻. All of these clusters tend to form structures with a capped oxygen atom. For Y₃O_x^−/0 (x = 2–4), the O atoms prefer the bridging sites of Y₃O^−/0, whereas the fifth O atoms for Y₃O₅^−/0 are bonded to the terminal sites. In particular, the ground states of Y₃O₆^−/0 are found to be interesting species, which may be viewed as molecular models for dioxygen activation by Y₃O₄^−/0. σ- and π-aromaticity is found in Y₃⁻ by the molecular orbital analysis and Adaptive Natural Density Partitioning (AdNDP) analysis. Molecular orbital analyses are performed to analyze the chemical bonding in the tri-yttrium oxide clusters and to elucidate their electronic and structural evolution.

---

1. Introduction

Yttrium oxides have important applications in the field of catalysts, fireproofing, electrode materials, and magnetic materials,^1–11 and they are especially used as doping agents for catalyst supports and catalysts.^8–11 For instance, yttria-doped alumina is more thermally stable than bare alumina and can be used as a catalyst support for the thermo-catalytic cracking process.^8,9 Furthermore, homonuclear yttrium oxide clusters and heteronuclear aluminum-doped yttrium oxide clusters have exhibited different catalytic performances in redox reactions with N₂O/CO. The yttrium oxide cluster doped with aluminum (YAlO₃⁺˙) was proven to bring about efficient CO oxidation, and the reaction pattern of YAlO₃⁺˙ is considerably different from that of Y₂O₃⁺˙ as a result of the doping effects.¹⁰ As a first step in developing a comprehensive understanding of complex catalytic processes on early transition-metal oxides, we are interested in systematically studying the electronic structure and chemical bonding of isolated transition-metal oxide clusters.

Yttrium oxide clusters have been studied both experimentally^10,12–14 and theoretically.^{10,11,15–18} The photoionization spectra of yttrium clusters Y_n and Y_nO (n = 2–31) have been recorded by Knickelbein, and a steep non-monotonic decrease of ionization potentials (IPs) was discovered up to about ten atoms, followed by a more gradual decline.¹² Wu and Wang¹³ reported the photoelectron spectrum and electronic structures of YO_n⁻ (n = 1–5). Pramann and co-workers¹⁴ obtained the photoelectron spectrum of Y_nO_m (n = 2–10, m = 1–3), in which a shifting of the threshold energies to higher binding energies was observed with the increase of cluster size n. Recently, attentions have also been focused on the theoretical studies of yttrium oxide clusters. For example, the structural and electronic properties of Y₃O and Y₄O were studied by Gu et al., where the structures of Y₃O and Y₄O were found to be pyramidal and bi-pyramidal, respectively, and the calculated electron affinities and ionization potentials were in good agreement with the available experimental data.^15,16 In addition, Yang and co-workers investigated the structural, electronic, and magnetic properties of Y_nO (n = 2–14).¹⁷ The calculated ionization potentials and electron affinities were in good agreement with the experimental results, implying that the ground states of these clusters are reliable to better understand yttrium oxide clusters and materials. Very recently, Rahane et al.¹⁸ reported a DFT study on the structural and electronic properties of (Y₂O₃)_n^0/±1 (n = 1–10) clusters and found that the charge transfer from the Y atoms to the oxygen atoms increases with the increase in cluster size. To the best of our knowledge, there are still very few investigations on tri-yttrium oxide clusters.

We have been interested in developing cluster models to characterize metal cluster species in the gas phase and to provide fundamental mechanistic insights for catalysts,^19–24 as well as novel all-metal aromaticity.²⁵ In the previous studies, all-metal aromaticity was first reported using Al₄²⁻ as an example with double σ- and π-aromaticity.²⁶ New computational evidence has been presented about triple (σ-, π- and δ-) aromaticity in the lowest D_3h (¹A^′₁) singlet state of Hf₃.²⁷ Nowadays, a few review articles concerning all-transition-metal aromaticity/antiaromaticity have been published.^28–35 For example Boldyrev et al.²⁸ performed the adaptive natural density partitioning (AdNDP) method to state the aromaticity for the Sc₃⁻ (D_3h ¹A^′₁) cluster. σ- and π-aromaticity represents a mode of chemical bonding and may play an important role in multinuclear transition metal compounds.

In this work, we focus on exploring the geometric and electronic structures of early transition metal clusters and their oxide clusters. DFT calculations are employed to elucidate the electronic structure and chemical bonding of Y₃O_x^−/0 (x = 0–6). In particular, the ground states of Y₃O₆^−/0 are found to be interesting species, which may be viewed as molecular models for dioxygen activation by Y₃O₄^−/0. A sequential oxidation is observed in the Y₃O_x⁻ (x = 0–6) clusters as a function of x. The AdNDP method is performed to analyze the aromaticity of Y₃⁻ cluster, indicating that the Y₃⁻ possesses σ- and π-aromaticity.

2. Computational methods

The theoretical calculations were performed at the DFT level using the BP86 functional.^36,37 The global minimum searches were performed using analytical gradients with the Stuttgart relativistic small core basis set and effective core potential^38,39 augmented with two f-type and one g-type polarization function for yttrium [ζ(f) = 0.144, 0.546; ζ(g) = 0.249] as recommended by Martin and Sundermann⁴⁰ and the aug-cc-pVTZ basis set^41,42 for oxygen. Scalar relativistic effects, that is, the mass velocity and Darwin effects, were taken into account via the quasi-relativistic pseudo-potentials. Vibrational frequency calculations were performed to verify the nature of the stationary points. The vertical electron detachment energies (VDEs) were calculated using the generalized Koopmans' theorem by adding a correction term to the eigen values of the anion.⁴³ The correction term was calculated as δE = E₁ − E₂ − ε_HOMO, where E₁ and E₂ are the total energies of the anion and neutral ion, respectively, in their ground states at the anion equilibrium geometry, and ε_HOMO corresponds to the eigen value of the highest occupied molecular orbital (HOMO) of the anion. The relative energies of the low-lying structures were further evaluated via single-point calculations at the coupled cluster [CCSD(T)]^44–48 level with the Y/Stuttgart + 2f1g/O/aug-cc-pVTZ basis sets at the BP86 geometries. For open-shell systems, the UCCSD(T) approach was used, where a restricted open-shell Hartree–Fock (ROHF) calculation was initially performed and the spin constraint was relaxed in the correlation treatment. In addition, more accurate optimizations in CCSD(T) were carried out for certain close-lying structures with the Y/Stuttgart + 2f1g/O/aug-cc-pVTZ basis sets. All the DFT calculations were performed with the Gaussian 09 software package,⁴⁹ and the CCSD(T) calculations were done using the MOLPRO 2010.1 package.⁵⁰ Three-dimensional contours of the molecular orbitals were visualized using the VMD software.⁵¹ Different exchange–correlation functionals were tested for accuracy and consistency. The BP86 functional showed superior results in terms of electron binding energies and structures for yttrium oxide clusters. The previous studies on yttrium oxide clusters^52,53 also indicated that BP86 calculations can give good consistency with the experimental results and better overall performance in predicting the molecular properties. Therefore, we used the results with the BP86 functional for our discussion.

The adaptive natural density partitioning (AdNDP) method has been recently developed by Boldyrev et al.²⁸ The principles of the method have been described elsewhere.⁵⁴ The AdNDP analysis for the ground state of Y₃⁻ cluster was performed using DFT at the BP86/lanl2dz level. The results of the AdNDP analysis were visualized using the MOLEKEL 5.4 software.⁵⁵

3. Theoretical results

The optimized ground states and low-lying isomers (within ∼0.40 eV) at the BP86 level for the anionic Y₃O_x⁻ and neutral Y₃O_x (x = 0–6) are presented in Fig. 1–7, respectively. More optimized geometries at higher energies are given as ESI (Fig. S1–S7†). In the following discussion, O_t, O_b and O_c represent the terminal, bridging and capped oxygen atoms, respectively.

3.1 Y₃⁻ and Y₃

For the tri-yttrium clusters, four possible atomic arrangements: linear (C_∞v or D_∞h), equilateral triangle (D_3h), isosceles triangle (C_2v), or completely distorted triangle (C_s) were considered. The ground states and the selected low-lying isomers (within ∼0.40 eV) of the tri-yttrium clusters (Y₃⁻ and Y₃) are listed in Fig. 1. Our theoretical results clearly show that the global minimum of Y₃⁻ is a D_3h (¹A^′₁) structure (Fig. 1a), which is in accordance with the previous study by Chi et al.³¹ The corresponding triplet (D_3h, ³A^′′₂) (Fig. 1b) and (D_3h, ³A^′₁) (Fig. 1c) are 0.27 eV and 0.34 eV higher in energy, respectively. The low-lying isomer (Fig. 1d) with a C_2v (³A₂) symmetry is 0.34 eV higher above the ground state.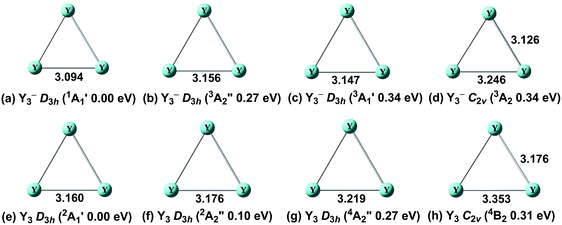

Fig. 1 Optimized global minima and selected low-lying structures (within ∼0.40 eV) for Y₃^−/0 clusters at the BP86 level. The bond lengths are in angstroms.

For the neutral Y₃, the ground state is revealed to be D_3h (²A^′₁) (Fig. 1e). The Y–Y bond is slightly longer (∼0.08 Å) compared to that of the anion (Fig. 1a). In the work by Dai et al.,⁵⁶ the structure (D_3h, ²A′′) (Fig. 1f) was predicted to be the ground state of Y₃ using the complete active space multiconfiguration self-consistent field (CAS-MCSCF) method. However, it was 0.10 eV higher in energy above the D_3h (²A^′₁) state in our calculation. The corresponding quartet (D_3h, ⁴A^′′₂) (Fig. 1g) is 0.27 eV higher in energy at the BP86 level. Similar to the anion, there also exists a C_2v (⁴B₂) structure, which is 0.31 eV above the ground state. The single-point CCSD(T) (Table SI†) were also carried out, and the results are in agreement with that of our BP86 calculations instead of that of the previous study.⁵⁶ Further theoretical calculations with more sophisticated methods may be necessary to resolve the true ground state of Y₃.

3.2 Oxygen-deficient clusters: Y₃O_x^−/0 (x = 0–4)

3.2.1 Y₃O⁻ and Y₃O. The optimized ground states and selected low-lying isomers within ∼0.40 eV for Y₃O⁻ and Y₃O are presented in Fig. 2. The potential energy surfaces for Y₃O⁻ are rather flat with several closely low-lying isomers near the global minimum. The ground state of Y₃O⁻ is closed-shell with C_3v symmetry (Fig. 2a). It can be viewed as a pyramid, in which the oxygen atom overtop the plane of tri-yttrium equilateral triangle by 1.092 Å and the bond lengths of Y–O_c and Y–Y are 2.157 Å and 3.142 Å, respectively. The similar corresponding triplet isomer is relaxed to C_s structure (Fig. 2c) and was pointed as the global minimum by Gu et al.,¹⁵ whereas it is revealed to be 0.07 eV higher above the ground state in our calculation at the BP86 level. The second low-lying isomer C_2v (³B₁) (Fig. 2b) is 0.05 eV above the ground state with a bridging oxygen atom, in which the distances between Y atom and O atoms are 2.002 Å and can be defined as Y–O single bonds.⁵⁷ To further confirm the ground state of Y₃O⁻, CCSD(T) calculations were performed for these close-lying isomers (within ∼0.20 eV). The results show that the isomer (C_3v, ¹A₁) (Fig. 2a) is the global minimum and is 0.02 eV more stable than the (C_2v, ³B₁) structure (Fig. 2b) under CCSD(T) optimizations. Other selected low-lying isomers (Fig. 2d–g) are at least 0.20 eV higher at the BP86 level.

Fig. 2 Optimized global minima and selected low-lying structures (within ∼0.40 eV) for Y₃O^−/0 clusters at the BP86 level. The bond lengths are in angstroms.

The neutral ground state (C_3v, ²A₁) (Fig. 2h) is totally conformed to the result of Yang et al.,¹⁷ which resembles that of Y₃O⁻, except for a slightly lengthened Y–Y bond (by 0.061 Å) and shortened Y–O bond (by 0.016 Å). The low-lying isomer (Fig. 2i) with C_2v symmetry is a quartet (⁴B₁), and 0.25 eV above the ground state.

3.2.2 Y₃O₂⁻ and Y₃O₂. To search for the most stable structure of Y₃O₂^−/0, various structural possibilities with different spin multiplicities are taken into consideration. The potential energy surfaces for Y₃O₂⁻ and Y₃O₂ are both rather flat. The selected optimized structures of Y₃O₂⁻ and Y₃O₂, along with their relative energies, are given in Fig. 3. The ground state of Y₃O₂⁻ is a closed-shell (¹A′) C_s (Fig. 3a) configuration with a capped and a bridging O atom. The similar (C_s, ³A′′) (Fig. 3c) and (C_s, ³A′) (Fig. 3d) isomers in atomic connectivity are 0.18 eV and 0.20 eV higher in energy, respectively. A low-lying (C_s, ¹A′) (Fig. 3b) isomer is located 0.02 eV above the ground state, which possesses two bridging oxygen atoms and its corresponding triplet state (C_2v, ³A₂) (Fig. 3e) is 0.21 eV above the ground state. As for the different structures shown in Fig. 2 (within ∼0.20 eV), further theoretical calculations at the CCSD(T) level are performed to resolve the true global minimum, as reported in Table SI.† The CCSD(T) results show that the isomer (C_s, ¹A′) (Fig. 3a) is the ground state, and the other isomers are at least 0.25 eV higher in energy.

Fig. 3 Optimized global minima and selected low-lying structures (within ∼0.40 eV) for Y₃O₂^−/0 clusters at the BP86 level. The bond lengths are in angstroms.

The global minimum (C_s, ²A′) (Fig. 3h) for the neutral Y₃O₂ is similar to that of Y₃O₂⁻. The capped oxygen atom is closer to the yttrium atoms at the bottom compared to Y₃O₂⁻. Three low-lying isomers are found within 0.20 eV at the BP86 level. Similar to the anion, single-point CCSD(T) calculations are performed for these isomers, showing that isomer (C_s, ²A′) (Fig. 3h) is the ground state. It is lower by at least 0.31 eV in energy than the others, as shown in Table SI.†

3.2.3 Y₃O₃⁻ and Y₃O₃. The low-lying isomers for Y₃O₃⁻ are given in Fig. 4. The ground state (Fig. 4a) is a triplet C_s (³A′′) (Fig. 4a) structure and it can be regarded as adding a bridging O atom on the basis of Y₃O₂⁻. The corresponding singlet state C_s (¹A′) (Fig. 4c) is located 0.32 eV above the ground state. The isomer (C_3v, ³A₁) (Fig. 4b) with three bridging oxygen atoms is only 0.02 eV higher in energy. The Y–O distance is 2.031 Å, which can be assigned as a single bond.⁵⁷ The relative energies for these BP86 geometries (within ∼0.20 eV) are further calculated using single point CCSD(T) calculations. The results of the CCSD(T) calculations (Table SI†) are in line with those of the DFT calculations, and the isomer (C_s, ³A′′) (Fig. 4a) is the most stable structure.

Fig. 4 Optimized global minima and selected low-lying structures (within ∼0.40 eV) for Y₃O₃^−/0 clusters at the BP86 level. The bond lengths are in angstroms.

Similar to the anion, the ground state of neutral Y₃O₃ has a capped and two bridging O atoms, as shown in Fig. 4d (C_s, ²A′′). However, the distance between the topmost yttrium atom and the capped oxygen atom is shortened (∼0.216 Å). The structure (C_s, ²A′) (Fig. 4f) was similar to (C_s, ²A′′) (Fig. 4d) in geometrical configuration, which is 0.12 eV less stable. The second low-lying isomer (C_s, ²A′) (Fig. 4e) with three bridging O atoms is only 0.04 eV higher in energy at the BP86 level, which is viewed as the global minimum by Yang et al.⁵⁸ The corresponding quartet state (D_3h, ⁴A^′₁) (Fig. 4g) is 0.16 eV above the ground state. As for these low-lying isomers, single-point CCSD(T) are calculated using the BP86 results. The isomer in Fig. 4d is the most stable structure among the above-mentioned four isomers. The other isomers are more than 0.12 eV higher in energy, as given in ESI (Table SI†).

3.2.4 Y₃O₄⁻ and Y₃O₄. We carried out an extensive structural search for the ground states on the potential energy surfaces of Y₃O₄^−/0 clusters. Three low-lying isomers for Y₃O₄⁻ clusters within ∼0.40 eV are found in our calculation. As shown in Fig. 5a–c, they all can be regarded as umbellate clusters with three bridging O atoms and a capped O atom. Single-point CCSD(T) calculations are performed using the BP86 geometries for these three anionic isomers. The results reveal that the ground state is closed shell with C_3v (¹A₁) symmetry (Fig. 5a), whereas the corresponding triplet isomers (Fig. 5b and c) are 0.18 eV and 0.25 eV higher in energy.

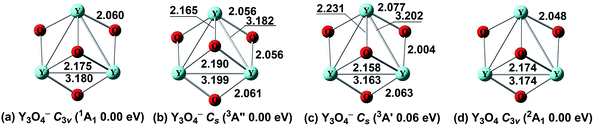Fig. 5 Optimized global minima and selected low-lying structures (within ∼0.40 eV) for Y₃O₄^−/0 clusters at the BP86 level. The bond lengths are in angstroms.

The ground state of Y₃O₄ is predicted to be ²A₁ with C_3v symmetry (Fig. 5d), which is in agreement with a previous report.⁵⁹ It is similar to the ground state of Y₃O₄⁻ cluster in terms of atomic connectivity, except that all the corresponding bond distances become a little shorter. The nearest low-lying isomer (Fig. S5e†) with a terminal and two bridging O atoms is located 0.52 eV above the ground state.

3.3 Stoichiometric clusters: Y₃O₅^−/0

The ground state for Y₃O₅⁻ is C_s (¹A′) (Fig. 6a), in which three Y atoms transfer a total of ten electrons to the oxygen atoms. In the ground state of Y₃O₅⁻ anionic cluster, the Y–O_t bond distance is 1.926 Å which can be assigned as a typical Y=O double bond.⁵⁷ The length of the Y–O_c bond connecting the top Y atom increases to 2.486 Å, compared with 2.175 Å in the ground state of Y₃O₄⁻ (Fig. 5d). A higher symmetry C_2v (¹A₁) structure is about 0.57 eV above the ground state, as shown in Fig. S6a.†

Fig. 6 Optimized global minima and selected low-lying structures (within ∼0.40 eV) for Y₃O₅^−/0 clusters at the BP86 level. The bond lengths are in angstroms.

The ground state of Y₃O₅ is predicted to be ²A′′ with C_s symmetry (Fig. 6b). The Y–O_t bond length is 2.155 Å and about 0.229 Å longer compared to that of the anion (Fig. 6a). Nevertheless, the length of the Y–O_c bond connecting the top Y atom becomes a slightly shorter (∼0.177 Å). Other isomers, shown in Fig. 6c and d, are 0.11 eV and 0.21 eV higher, respectively. The results of the single-point CCSD(T) calculations with the BP86 geometries within 0.20 eV indicate that the isomer (C_s, ²A′′) (Fig. 6b) is the ground state and the isomer in Fig. 6c is 0.19 eV above the ground state.

3.4 Oxygen-rich clusters: Y₃O₆^−/0

We started the structural search for the oxygen-rich clusters Y₃O₆^−/0 by adding one oxygen atom (terminal, capped or bridging oxygen atom) from the structures of Y₃O₅^−/0 clusters. The ground state of Y₃O₆⁻ is the C_s (¹A′) (Fig. 7a) structure, which can be viewed as replacing the terminal oxygen in the ground state of Y₃O₅⁻ (C_s, ¹A′) (Fig. 6a) by an O₂ unit. The calculated O–O bond length of the O₂ unit in the ground state of Y₃O₆⁻ (Fig. 7a) is 1.492 Å, which is close to that of the free peroxide anion O₂²⁻ (1.540 Å calculated at the same level). The triplet state isomers (Fig. 7b and e) with an O₂ unit are 0.06 eV and 0.27 eV higher in energy. The third low-lying isomer C_s (³A′′) (Fig. 7c) with two terminal oxygen atoms is 0.19 eV higher in energy. Single-point CCSD(T) calculations are performed for the low-lying isomers, revealing that isomer (C_s ¹A′) (Fig. 7a) is the global minimum, and is about 0.60 eV lower in energy than isomer (C_s, ³A′′) (Fig. 7b).

Fig. 7 Optimized global minima and selected low-lying structures (within ∼0.40 eV) for Y₃O₆^−/0 clusters at the BP86 level. The bond lengths are in angstroms.

The neutral ground state C_s (²A′′) (Fig. 7g) shows similar structural characteristics relative to its anion, except that the distance of the O₂ unit is shortened. The bond length is 1.353 Å for the O₂ unit, which is assigned as a superoxide (O₂⁻˙) unit (1.361 Å calculated at the same level). The alternative optimized neutral structures are at least 0.72 eV above the ground state (Fig. S7, ESI†).

4. Discussion

4.1 Interpretation of the simulated photoelectron spectra and molecular orbital analyses

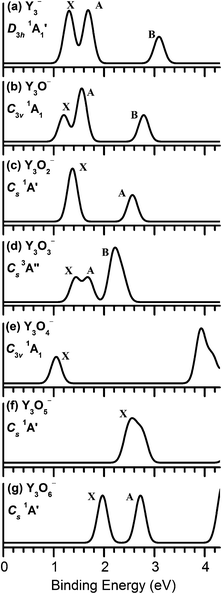
We calculated the vertical detachment energies (VDEs) of Y₃O_x⁻ (x = 0–6) on the basis of the identified anionic ground-state structures using the generalized Koopmans' theorem. The calculated VDEs and the simulated PES spectra for the global minima are collected in Table 1 and Fig. 8, respectively. Other VDEs for the selected low-lying isomers are listed in Fig. S8.† All the simulations were done by fitting the distribution of the calculated VDEs with unit-area Gaussian functions of 0.10 eV width. In the single-particle picture, photodetachment involves the removal of electrons from the occupied molecular orbitals (MOs) of an anion. The final states are the ground and excited states of the corresponding neutral. Within the one-electron formalism, each occupied MO for a closed-shell anion will generate a single PES band with the associated vibrational structures governed by the Franck–Condon principle. However, Y₃O₃⁻ is open-shell with two single unpaired electrons in their lowest-energy structures. In these cases, detachment from a fully occupied MO would result in two detachment channels because of the removal of either the spin-down (α) or the spin-up (β) electrons, giving rise to doublet (D) and quartet (Q) final states, respectively, as given in Table 1. In the following investigation, we will attempt to qualitatively account the simulated PES features using molecular orbital analyses. Considering the complicated nature of the electronic structures of these systems, many of the assignments should be tentatively considered.

Table 1 Theoretical vertical detachment energies (VDEs) of global minima Y₃O_x⁻ (x = 0–6) clusters (all energies are in eV)

	Theory^a
	Feature^b	MO	VDE
a The labels α and β denote majority and minority spins, whereas D and Q denote doublet and quartet Y3O3 final states upon photodetachment, respectively.b The labels denote the peaks in the simulated PES.
Y3^−, (D3h ^1A′)	X	4a^′1	1.29
		2a^′′2	1.32
	A	4e	1.68
			1.68
	B	3a^′1	3.09
Y3O^−, (C3v ^1A1)	X	7a1	1.20
	A	6e	1.56
			1.56
	B	6a1	2.79
Y3O2^−, (Cs ^1A′)	X	17a′	1.37
		8a′′	1.38
	A	16a′	2.56
Y3O3^−, (Cs ^3A′′)	X	18a′ (α)	1.43 (D)
	A	12a′′ (α)	1.69 (D)
	B	17a′ (α); [17a′ (β)]	2.37 (D); [2.19 (Q)]
Y3O4^−, (C3v ^1A1)	X	11a1	1.05
	A	10e	3.92
			3.92
Y3O5^−, (Cs ^1A′)	X	24a′	2.47
		13a′′	2.60
		23a′	2.77
Y3O6^−, (Cs ^1A′)	X	14a′′	1.97

---

Fig. 8 The simulated photoelectron spectra for the global minima of Y₃O_x⁻ (x = 0–6). The simulations are done by fitting the distribution of the calculated vertical detachment energies with unit-area Gaussian functions of 0.10 eV width.

4.1.1 Metal cluster: Y₃⁻. The global minimum of Y₃⁻ is a D_3h (¹A^′₁) (Fig. 1a) structure in our calculation. Its valence electronic configuration is …(3a^′₁)²(4e′)⁴(2a^′′₂)²(4a^′₁)², as shown in Fig. 9a. The band X in the simulated PES can be assigned to the electron detachment transition from the MO 4a^′₁ and 2a^′′₂, and the VDEs are 1.29 eV for 4a^′₁, 1.32 eV for 2a^′′₂. However, when an electron is removed from Y₃⁻, the ground state of Y₃ would still maintain the equilateral triangular structure. As shown in Fig. 9a, 4a^′₁ is a bonding orbital, thus the detachment from 4a^′₁ makes the Y–Y bond length increase from 3.094 Å to 3.160 Å (Fig. 1a and e). The band A is calculated to be about 1.68 eV, which can be assigned to the electron detachment transition from the degenerate orbital HOMO−2 (4e′). The HOMO−3 (3a^′₁) is a bonding MO mainly composed of s orbitals from the three Y atoms. Its corresponding VDE is 3.09 eV, which is relatively high.

Fig. 9 Pictures of the valence molecular orbitals for the ground states of the Y₃O_x⁻ (x = 0–6) clusters.

4.1.2 Oxygen-deficient clusters: Y₃O_x⁻ (x = 1–4). As mentioned earlier, our DFT calculations and further CCSD(T) optimizations indicate that the isomer C_3v (¹A₁) (Fig. 2a) is the lowest-energy structure of Y₃O⁻. It can be regarded as adding a capped oxygen atom based on the ground state of Y₃⁻ (Fig. 1a). Its valence electronic configuration is …(6a₁)²(6e)⁴(7a₁)², as shown in Fig. 9b. The calculated VDE (1.20 eV) for the first detachment channel from the 7a₁ MO is in excellent agreement with the experimental measurement of 1.25 eV (ref. 14). The corresponding bonding MO 7a₁ primarily consists of d orbitals from the three Y atoms. Two sharper features (X, A) are displayed at lower binding energies, which coincides with the experimental spectrum,¹⁴ and the second detachment channel is from 6e MOs (Fig. 9b) with a calculated VDE of 1.56 eV. For the low-lying isomer (Fig. 2b), which is the powerful competitor for the ground state of Y₃O⁻ in the CCSD(T) optimization level, the simulated photoelectron spectra (Fig. S8a†) displays only one detachment channel (within 2.00 eV), which is distinct from the experimental spectrum.¹⁴

For Y₃O₂⁻, the ground state of Y₃O₂⁻ is a closed-shell (¹A′) C_s (Fig. 3a) configuration with a capped and a bridging O atom. The calculated first VDE for the lowest energy structure C_s (¹A′) (Fig. 3a) is 1.37 eV at the BP86 level, which is close to that of 1.60 eV, measured by experiment,¹⁴ and the second VDE (1.38 eV) is only 0.01 eV higher than the first VDE. Its valence electronic configuration shown in Fig. 9c is …(16a′)²(8a′′)²(17a′)². Therefore, photodetachment from HOMO (17a′) and HOMO−1 (8a′′) orbitals yield the first PES band X (Fig. 7c). It is only about 0.17 eV higher than that (1.20 eV) of Y₃O⁻ because of the nonbonding (17a′) orbital.

The ground state of Y₃O₃⁻ is an open shell C_s (³A′′) structure, which can be viewed as adding a bridging O atom on the basis of Y₃O₂⁻. Its valence electronic configuration is …(17a′)²(12a′′)¹(18a′)¹. The first detachment channel for the Y₃O₃⁻ (C_s, ³A′′) ground state is derived from the orbital 18a′ (α) with the calculated VDE of 1.43 eV, which is in good consistency with the previous experimental value (1.52 eV).¹⁴ Fig. 9d presents the molecular orbitals of Y₃O₃⁻. The HOMO 18a′ consists of a Y 5s character, which makes the first VDE to slightly increase, in contrast to Y₃O⁻ and Y₃O₂⁻. The second detachment channel is from 12a′′ (α) with the calculated VDE of 1.69 eV, and the band B is yielded by detaching the electron from the fully occupied 17a′ (α, β) orbital with different VDEs of 2.37 eV and 2.19 eV, respectively.

In the Y₃O₄⁻ anion, the results of the single-point CCSD(T) calculations manifest that the isomer with a capped and three bridging O atoms is the global minimum. Its valence electron configuration is …(17a₁)²(10e)⁴(18a₁)². The calculated VDE for the band X is 1.05 eV. In Fig. 9e, the HOMO mainly consists of Y 5s character, which is contributed equally by each of the three Y atoms. Similar to the study by Wu,⁵⁹ each Y atom possesses three valence electrons, and three Y atoms will lose a total of eight electrons to form the Y₃O₄⁻ cluster. The orbital analysis indicates that the rest of the 5s electrons are distributed by the three yttrium atoms.

4.1.3 Stoichiometric cluster: Y₃O₅⁻. The ground state for Y₃O₅⁻ is a closed-shell structure with C_s (¹A′) symmetry (Fig. 6a) and it appears as a terminal O atom based on Y₃O₄⁻. In the stoichiometric Y₃O₅⁻ cluster, all the Y atoms possess the maximum +3 oxidation state, each of which is chemically saturated, and the O atoms possess a −2 oxidation state. The valence electron configuration of Y₃O₅⁻ is …(23a′)²(13a′′)²(24a′)². The large VDE value (2.47 eV) observed in our PES spectrum is consistent with the fact that Y₃O₅⁻ should be a relatively stable molecule. In Y₃O₅⁻, all the 4d or 5s electrons are transferred from Y to O, and the increase for the first VDE of Y₃O₅⁻ is mainly on account of the terminal O 2p features.

4.1.4 Oxygen-rich clusters: Y₃O₆⁻. The ground state of Y₃O₆⁻ is C_s (¹A′), which can be viewed as the replacement of a terminal O atom in Y₃O₅⁻ by an O₂ unit. The O₂ unit can be viewed as a peroxide anion O₂²⁻ with a 1.492 Å O–O bond. We can primarily estimate that the addition of two electrons into the π* orbital lengthens the O–O bond. The valence electron configuration of anionic Y₃O₆⁻ is …(26a′)²(27a′)²(14a′′)². The calculated VDE for the band X is 1.97 eV, corresponding to the detachment of the p electrons on the HOMO, which is a π* orbital of the O₂ unit. Thus, the detachment from the 14a′′ orbital results in the significant decrease of the O_t–O_t distance in the neutral cluster (Fig. 7g).

4.2 Structural evolution and Sequential oxidation of Y₃O_x⁻ (x = 1–6)

The current study shows that the ground states of all Y₃O_x⁻ (x = 1–6) clusters are the structures with a capped oxygen atom. Starting from the Y₃⁻ triangle structure, the ground state of Y₃O⁻ is found to be a pyramid, in which the capped oxygen atom is above the plane of the tri-yttrium equilateral triangle. The next three oxygen atoms successively take up the bridging sites until Y₃O₄⁻, which is based on a six-membered Y₃O₃ ring, adds a capped oxygen atom. On the basis of the ground state of Y₃O₄⁻, the subsequently added oxygen atom is shown to occupy the terminal site, forming Y₃O₅⁻, and the ground state of Y₃O₆⁻ can be viewed as replacing a terminal O atom in Y₃O₅⁻ by an O₂ unit. In Fig. 10, the trend of electron affinities (EAs) is consistent with that of the first VDEs until Y₃O₄, which indicates the corresponding anionic and neutral clusters Y₃O_x^−/0 (x = 1–4), possess the similar geometric configurations.

Fig. 10 The first vertical detachment energies and electron affinities for the ground states Y₃O_x⁻ (x = 1–6) clusters as a function of O content.

Fig. 10 displays the trend of the first VDEs for Y₃O_x⁻ (x = 1–6). The first VDEs of the Y₃O_x⁻ (x = 1–4) oxide clusters are all above 1.0 eV, 1.20 eV for Y₃O⁻, 1.37 eV for Y₃O₂⁻, 1.43 eV for Y₃O₃⁻, and 1.05 eV for Y₃O₄⁻. For Y₃O₅⁻, the first VDE increases to 2.47 eV, while the first VDE for Y₃O₆⁻ decreases to 1.97 eV. Y has an electron configuration of 4d¹5s², and the bare tri-yttrium anion Y₃⁻ has 10 valence electrons. The Y-derived valence electrons sequentially transfer to the added oxygen atoms with increasing x. The values of the first VDEs for Y₃O_x⁻ (x = 1–4) slightly change as a function of O content. The higher binding energy for Y₃O₅⁻ can be explained by the nature of the HOMO (24a′) (Fig. 9f), which is primarily the terminal oxygen atom 2p-based orbital. The first VDE for Y₃O₆⁻ decreases compared with that for Y₃O₅⁻ because of the electrons derived from π* molecular orbital. The trend of VDEs in Y₃O_x⁻ (x = 1–6) is consistent with the previous studies of metal oxide clusters,^23,60–64 suggesting the sequential oxidation of the metal oxides clusters.

4.3 All-metal aromaticity of Y₃⁻

4.3.1 The molecular orbital analysis. The global minimum of Y₃⁻ is a D_3h (¹A^′₁) structure (Fig. 1a). Earlier, Feixas³² reported that Y₃⁻ has σ- and π-aromaticity with the nucleus-independent chemical shifts (NICS) values. To further understand the electronic structure and chemical bonding in the Y₃⁻ cluster, a detailed molecular orbital (MO) analysis was carried out, as shown in Fig. 9a. The full-filled 3a^′₁ and 4e′ are a set of completely bonding and partially bonding/antibonding MO and should not significantly contribute to the net aromaticity in the Y₃⁻ cluster. The fully occupied 2a^′′₂ MO is made up of the 4d orbitals of Y atoms, and is of π-aromatic character. The 4a^′₁ MO is completely delocalized σ bonding and is primarily composed of the 4d orbital of each Y atom, which is responsible for the d-orbital σ-aromatic character according to the (4n + 2) Hückel rule for σ aromaticity.⁶⁵ Thus, the Y₃⁻ D_3h (¹A^′₁) can be considered as a case of d-orbital σ- and π-aromaticity, which is very similar to the Sc₃⁻ cluster.²⁸

4.3.2 AdNDP analysis. To further verify the aromaticity of Y₃⁻, AdNDP analysis is used to determine the ways of its chemical bonding. The AdNDP program can obtain the electronic structure in terms of the n-center two-electron (nc-2e) bonds. It reveals both localized Lewis bonding and delocalized bonding elements (nc-2e objects, n ≥ 3), which are associated with the concepts of aromaticity and antiaromaticity.⁵⁴ There are 10 valence electrons in Y₃⁻, which form 5 valence electronic pairs. According to the AdNDP analysis (Fig. 11), these pairs are revealed as follows: three 2c–2e Y–Y σ-bonds between two yttrium atoms with ON = 1.99|e|, a completely delocalized 3c–2e d-orbital π-bond with ON = 2.00|e| and a 3c–2e d-orbital σ-bond with ON = 2.00|e|, in which ON represents the occupied number. Therefore, the Y₃⁻ cluster has a double (σ- and π-) aromaticity via the AdNDP analysis.

Fig. 11 Chemical-bonding elements revealed by the AdNDP analysis of the Y₃⁻ cluster. The ONs are reported at the BP86/lanl2dz level of theory.

4.4 Y₃O₄^−/0 as reduced molecular models for dioxygen activation: Y₃O₄^−/0 + O₂ → Y₃O₆^−/0

As mentioned earlier, the ground states of Y₃O₆ (Fig. 7g) and Y₃O₆⁻ (Fig. 7a) clusters can be viewed as addition of a superoxide O₂⁻˙ and peroxide O₂²⁻ units on Y₃O₄ and Y₃O₄⁻ clusters, respectively. The observation of O₂ units in Y₃O₆ and Y₃O₆⁻ provides us with an excellent opportunity to study the activation of O₂ by the Y₃O₄ and Y₃O₄⁻ clusters. The energies of the O₂ addition reactions are evaluated at the BP86 level:

Y₃O₄ (C_3v, ²A₁) + O₂ → Y₃O₆ (C_s, ²A′′) − 2.97 eV (1)

Y₃O₄⁻ (C_3v, ¹A₁) + O₂ → Y₃O₆⁻ (C_s, ¹A′) − 3.25 eV (2)

Eqn (1) and (2) can be viewed as the reactions of O₂ with the ground states of Y₃O₄ and Y₃O₄⁻, respectively. Our calculation yielded the O₂ chemisorption energy of −2.97 eV in Y₃O₄ and −3.25 eV in Y₃O₄⁻. Similar to our previous studies of metal oxide clusters,^22,66–68 molecular orbitals in the O-rich systems are analyzed to obtain further insight into the nature of the chemical bonding. The orbitals of Y₃O₆ are illustrated in Fig. 12. The singly occupied MO is one of the two π* orbitals of the bound O₂ unit, and the HOMO are the doubly occupied π* orbital of O₂ that is singly occupied in free O₂. The O–O distance (1.353 Å) in Y₃O₆ (Fig. 6g) is longer than that in free O₂ and is close to that in the superoxide O₂⁻˙ unit. It shows that the rest of the 5s electrons of Y₃O₄ may be readily transferred to the π* orbitals of an approaching O₂ molecule, making Y₃O₄ a reductive agent for O₂ activation. Analogously, the O–O distance (1.492 Å) in Y₃O₆⁻ (Fig. 7a) is close to that in the peroxide O₂²⁻ unit and the extra two 5s electrons of Y₃O₄⁻ may be transferred to the π* orbitals of an approaching O₂ molecule. Therefore, the Y₃O₆ and Y₃O₆⁻ clusters can be considered to be the oxidation products for the activation of O₂ through electron transfer between the reduced metal site and dioxygen at the metal oxide surface.

Fig. 12 Molecular orbital pictures of the two highest-energy occupied orbitals of Y₃O₆.

5. Conclusion

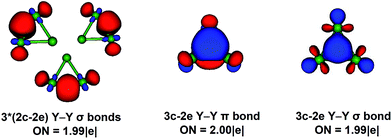
We report a systematic photoelectron spectroscopy and density functional study of a series of tri-nuclear yttrium oxide clusters: Y₃O_x⁻ and Y₃O_x (x = 0–6). Extensive DFT calculations are performed at the BP86 level to locate the ground states for the Y₃O_x^−/0 (x = 0–6) cluster. The ground states for Y₃⁻ and Y₃ are D_3h (¹A′) and D_3h (²A^′₁) structures, respectively. The tri-yttrium oxide clusters Y₃O_x^−/0 (x = 1–6) all have a capped oxygen atom. Starting from Y₃O⁻, the successive addition of the bridging oxygen atoms, yield the ground states of Y₃O₂⁻, Y₃O₃⁻ and Y₃O₄⁻. Nevertheless, the next added oxygen atom is found to be a terminal one in the Y₃O₅⁻ cluster and the oxygen-rich cluster Y₃O₆⁻ is found to have an O₂ unit. The neutral species have similar structures with their corresponding anionic clusters. As for the oxygen-rich clusters Y₃O₆⁻ and Y₃O_6, O₂²⁻ and O₂⁻˙ units are found, which can be viewed as Y₃O₄⁻ and Y₃O₄ that are oxidized by O₂, respectively. Molecular orbital analyses are carried out to elucidate the chemical bonding of these clusters and provide insights into the sequential oxidation from Y₃O⁻ to Y₃O₆⁻. The molecular orbital analysis presents that Y₃⁻ (D_3h, ¹A^′₁) possesses σ- and π-aromaticity. The AdNDP analysis reveals that one 3c–2e σ-bond and one 3c–2e π-bond completely delocalized over the three yttrium atoms, which further proves the characteristic of aromaticity in the Y₃⁻ cluster.

Acknowledgements

We gratefully acknowledge supports from the National Natural Science Foundation of China (21071031, 21301030, 21371034 and 21373048), and the Natural Science Foundation of Fujian Province for Distinguished Young Investigator Grant (2013J06004).

Reference

1. D. Kima, S. Jeonga, J. Moona and S. H. Cho, J. Colloid Interface Sci., 2006, 297, 589.
2. P. V. A. Padmanabhan, S. Ramanathan, K. P. Sreekumar, R. U. Satpute, T. R. G. Kutty, M. R. Gonal and L. M. Gantayet, Mater. Chem. Phys., 2007, 106, 416.
3. A. M. Pires, O. A. Serra and M. R. Davolos, J. Lumin., 2005, 113, 174.
4. W. J. Song, J. S. Li, T. B. Zhang, H. C. Kou and X. Y. Xue, J. Power Sources, 2014, 245, 808.
5. Y. Chen, J. Bunch, C. Jin, C. H. Yang and F. L. Chen, J. Power Sources, 2012, 204, 40.
6. V. Singh, V. K. Rai, B. Voss, M. Haase, R. P. S. Chakradhar, D. T. Naidu and S. H. Kim, Spectrochim. Acta, Part A, 2013, 109, 206.
7. A. M. Pires, O. A. Serra and M. R. Davolos, J. Alloys Compd., 2004, 374, 181.
8. N. Al-Yassir and R. L. V. Mao, Can. J. Chem., 2008, 86, 146.
9. N. Al-Yassir and R. L. V. Mao, Appl. Catal., A, 2007, 317, 275.
10. J. B. Ma, Z. C. Wang, M. Schlangen, S. G. He and H. Schwarz, Angew. Chem., Int. Ed., 2013, 52, 1226.
11. V. V. Lavrov, V. Blagojevic, G. K. Koyanagi, G. Orlova and D. K. Bohme, J. Phys. Chem. A, 2004, 108, 5610.
12. M. Knickelbein, Chem. Phys., 1995, 102, 1.
13. H. B. Wu and L. S. Wang, J. Phys. Chem. A, 1998, 102, 9129.
14. A. Pramann, Y. Nakamura and A. Nakajima, J. Phys. Chem. A, 2001, 105, 7534.
15. G. Gu, B. Dai, X. Ding and J. Yang, Eur. Phys. J. D, 2004, 29, 27.
16. B. Dai, K. Deng and J. Yang, Chem. Phys. Lett., 2002, 364, 188.
17. Z. Yang and S. J. Xiong, J. Chem. Phys., 2008, 129, 124308.
18. A. B. Rahane, P. A. Murkute, M. D. Deshpande and V. Kumar, J. Phys. Chem. A, 2013, 117, 5542.
19. H. J. Zhai, X. Huang, T. Waters, X. B. Wang, R. A. J. O'Hair, A. G. Wedd and L. S. Wang, J. Phys. Chem. A, 2005, 109, 10512.
20. H. J. Zhai, X. Huang, L. F. Cui, X. Li, J. Li and L. S. Wang, J. Phys. Chem. A, 2005, 109, 6019.
21. H. J. Zhai, B. Wang, X. Huang and L. S. Wang, J. Phys. Chem. A, 2009, 113, 9804.
22. B. Wang, W. J. Chen, B. C. Zhao, Y. F. Zhang and X. Huang, J. Phys. Chem. A, 2010, 114, 1964.
23. W. J. Chen, H. J. Zhai, Y. F. Zhang, X. Huang and L. S. Wang, J. Phys. Chem. A, 2010, 114, 5958.
24. Q. Zhou, W. C. Gong, L. Xie, C. G. Zheng, W. Zhang, B. Wang, Y. F. Zhang and X. Huang, Spectrochim. Acta, Part A, 2014, 117, 651.
25. B. Wang, H. J. Zhai, X. Huang and L. S. Wang, J. Phys. Chem. A, 2008, 112, 10962.
26. P. W. Fowler, R. W. A. Havenith and E. Steiner, Chem. Phys. Lett., 2002, 359, 530.
27. B. B. Averkiev and A. I. Boldyrev, J. Phys. Chem. A, 2007, 111, 12864.
28. T. R. Galeev and A. I. Boldyrev, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2011, 107, 124.
29. A. E. Kuznetsov, J. D. Corbett, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2001, 40, 3369.
30. Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, J. Chem. Theory Comput., 2013, 9, 4789.
31. X. X. Chi and Y. Liu, Int. J. Quantum Chem., 2007, 107, 1886.
32. F. Feixas, E. Matito, M. Duran, J. Poater and M. Sol, Theor. Chem. Acc., 2011, 128, 419.
33. A. E. Kuznetsov, K. A. Birch, A. I. Boldyrev, X. Li, H. J. Zhai and L. S. Wang, Science, 2003, 300, 622.
34. H. J. Zhai, W. J. Chen, X. Huang and L. S. Wang, RSC Adv., 2012, 2, 2707.
35. X. Huang, H. J. Zhai, B. Kiran and L. S. Wang, Angew. Chem., Int. Ed., 2005, 44, 7251.
36. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
37. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822.
38. W. Küchle, M. Dolg, H. Stoll and H. Preuss, Pseudopotentials of the Stuttgart/Dresden group 1998, revision, August 11, 1998, http://www.theochem.uni-stuttgart.de/pseudopotentiale.
39. D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123.
40. J. M. L. Martin and A. Sundermann, J. Chem. Phys., 2001, 114, 3408.
41. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
42. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
43. D. J. Tozer and N. C. Handy, J. Chem. Phys., 1998, 109, 10180.
44. G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910.
45. G. E. Scuseria, C. L. Janssen and H. F. Schaefer III, J. Chem. Phys., 1988, 89, 7382.
46. K. Raghavachari and G. W. Trucks, Chem. Phys. Lett., 1989, 157, 479.
47. J. D. Watts, J. Gauss and R. J. Bartlett, J. Chem. Phys., 1993, 98, 8718.
48. R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291.
49. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylow, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford CT, 2009.
50. H. J. Werner, P. J. Knowles, F. R. Manby, M. Schütz, P. Celani, G. Knizia, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. HamPel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. KöPPl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and A. Wolf, MOLPRO, version 2010.1, a package of ab initio programs, http://www.molpro.net.
51. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33.
52. L. Andrews, M. F. Zhou and G. V. Chertihin, J. Phys. Chem. A, 1999, 103, 6525.
53. Y. Gong, C. F. Ding and M. F. Zhou, J. Phys. Chem. A, 2009, 113, 8569.
54. D. Yu. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207.
55. U. Varetto, Molekel5.4, Swiss National Supercomputing Centre, Manno, Switzerland, 2009.
56. D. Dai and K. Balasubramanian, J. Chem. Phys., 1993, 98, 7098.
57. Y. X. Zhao, X. L. Ding, Y. P. Ma, Z. C. Wang and S. G. He, Theor. Chem. Acc., 2010, 127, 449.
58. Z. Yang and S. J. Xiong, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 245101.
59. L. Wu, C. Zhang, S. A. Krasnokutski and D. S. Yang, J. Chem. Phys., 2012, 137, 084312.
60. H. Wu, X. Li, X. B. Wang, C. F. Ding and L. S. Wang, J. Chem. Phys., 1998, 109, 449.
61. L. S. Wang, H. Wu and S. R. Desai, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 53, 8028.
62. L. S. Wang, H. Wu and S. R. Desai, Phys. Rev. Lett., 1996, 76, 4853.
63. S. J. Lin, X. H. Zhang, L. Xu, B. Wang, Y. F. Zhang and X. Huang, J. Phys. Chem. A, 2013, 117, 3093.
64. L. F. Wang, L. Xie, H. L. Fang, Y. F. Li, X. B. Zhang, B. Wang, Y. F. Zhang and X. Huang, Spectrochim. Acta, Part A, 2014, 131, 446.
65. A. P. Sergeeva, B. B. Averkiev and A. I. Boldyrev, Struct. Bonding, 2010, 136, 275.
66. H. J. Zhai, X. H. Zhang, W. J. Chen, X. Huang and L. S. Wang, J. Am. Chem. Soc., 2011, 133, 3085.
67. X. Huang, H. J. Zhai, T. Waters, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2006, 45, 657.
68. S. J. Lin, W. C. Gong, L. F. Wang, W. B. Liu, B. C. Zhao, B. Wang, Y. F. Zhang and X. Huang, Theor. Chem. Acc., 2014, 133, 1435.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra09202c

---