Suppressing phase retraction and coalescence of co-continuous polymer blends: effect of nanoparticles and particle network
Abstract
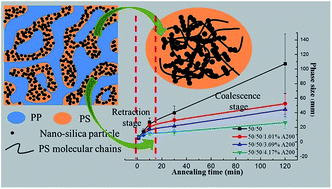
The morphologies of polymer blends generated during processing are usually unstable and morphology coarsening often occurs in the melt state, so suppressing the morphology coarsening is crucial to obtain polymer blends with tailored and stable structure and properties. Here, we report the morphology coarsening behavior of a co-continuous polypropylene/polystyrene (PP/PS) blend, with and without nano-silica particles, subjected to quiescent annealing in the melt state. The filled nano-silica particles were controlled to selectively distribute in the PS phase and formed a rheological particle network at a concentration of 8 wt% relative to the mass of the PS phase. A significant coarsening, which can be divided into two stages with different coarsening rates, was observed for the pure blend. Real-time monitoring of the coarsening process showed that the morphology coarsening process proceeded via retraction of elongated domains first and then coalescence of the retracted domains. The filled nano-silica particles were found to be able to suppress the coarsening process, which was demonstrated to be achieved by slowing down the retraction process of elongated domains. It was also found that the suppression effect of nano-silica particles heavily depended on the particle concentration and when a particle network formed, the suppression effect was more prominent. A stabilization mechanism, based on the phase deformation being closely related to the movement of polymer molecular chains, was proposed to expound the role of the introduced particles. When a particle network structure was formed, the movement of polymer molecular chains was significantly retarded and the corresponding phase deformation became difficult, leading to suppressed retraction process of the elongated domains and the whole phase coarsening phenomenon.

 Please wait while we load your content...
Please wait while we load your content...