Interstitial hydrogen in Laves phases – local electronic structure modifications from first-principles
Abstract
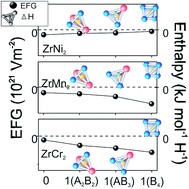
Understanding the microscopic aspect of the hydride formation process provides an insight into the experimentally observed properties of prospective hydrogen storage materials. In this paper, we have studied the local structural and electronic modifications induced by hydrogen absorption in cubic C15 Laves phases AB2 (A = Zr; B = Cr, Mn, Ni), as well as the stability of the formed hydrides, by means of density functional theory (DFT). To address the effect of hydrogen absorbed in one of three tetrahedral sites (96g, 32e, and 8b) on the electronic structure of its surrounding atoms, we have calculated the electric field gradient (EFG) on the position of Cr, Mn, and Ni in pure and hydrogenated compounds. EFG is associated with the hydrogen site-preference, and formation enthalpies of ZrB2H hydrides are used to examine their formation feasibility. Obtained enthalpies reveal that ZrMn2H and ZrNi2H are both unstable regardless of the occupied site, and the only attainable hydride is ZrCr2H, with comparable occupational probability of sites 96g and 32e. EFG results indicate that a hydrogen distribution within the crystal depends on the level of induced electronic structure modifications; i.e., the hydrogen site-preference is governed by the condition of minimal divergence of the electronic charge from its initial distribution.

 Please wait while we load your content...
Please wait while we load your content...