Internal friction characteristic and analysis of in-plane natural frequency of trilayer complexes formed from graphenes and boron nitride nanosheets
Jianhui Yuanab and
K. M. Liew*bc
aSchool of Physics and Electronic Science, Changsha University of Science and technology, Changsha 410114, China
bDepartment of Architecture and Civil Engineering, City University of Hong Kong, Kowloon, Hong Kong SAR. E-mail: kmliew@cityu.edu.hk; Tel: +852 3442 7601
cCity University of Hong Kong Shenzhen Research Institute Building, Shenzhen Hi-Tech Industrial Park, Nanshan District, Shenzhen, China
First published on 3rd September 2014
Abstract
The internal friction and in-plane natural frequency of a trilayer complex formed by a monolayer graphene sandwiched in the bilayer of boron nitride nanosheets (BN/G/BN) and graphenes (G/G/G) are studied by using molecular dynamics. The investigation shows that the internal friction coefficients for BN/G/BN (∼0.025) are significantly higher than that of G/G/G (∼0.015). The coefficients for both G/G/G and BN/G/BN increased with external pressure. The speed of increase is divided into quick increase, slow increase and saturation stage. The internal friction coefficients for G/G/G and BN/G/BN follow the simple microscopic theory of Amontons laws only when the external pressure exceeds 170 nN. These findings are expected to help enhance the understanding of the mechanism of nano-tribology and provide an effective micro-control method of internal friction. Subsequent analysis shows that the in-plane natural frequency of mid-layer graphene in BN/G/BN is significantly higher than in G/G/G and both increase as the external pressure increases. Moreover, the natural frequency of mid-layer graphene in trilayer complexes, especially in BN/G/BN, is extremely sensitive to external pressure loads.
1. Introduction
The graphite, with a layered structure, is widely used in lubricated systems because the weak interaction between layers leads to low friction and wear during relative sliding. It is one of the very important solid lubricants. Graphite and molybdenum disulfide are typical low friction materials, while mica is not.1 These materials are used as solid lubricants in an artificial satellite in which liquid lubricants, such as hydrocarbons, are not used because of the high vacuum environment. Few additives are mixed into automotive lubricants in order to generate a solid lubricant film in the sliding contact area because of the heat and shear, which often undergo tribochemical reactions. Graphene, which consists of a single or several layers of graphite, has attracted broad interest because of its unique electronic, thermal and mechanical properties2–5 and may prove to be an important material for electronics and micro- or nano-electromechanical systems (M/NEMS) in the future.6–9 For graphene to become a material of interest for M/NEMS, its interfacial and mechanical properties will play an important role in determining the overall system performance. As a model material, an in-depth investigation leading to an improved understanding of mechanical and interfacial behavior of graphene would advance the knowledge of the mechanistic origins of friction and potentially lead to its application in future M/NEMS devices.Friction is one of the most familiar physical phenomena and has been investigated since long because of its importance in various types of machinery and in many systems in science. In the last two decades atomic scale friction has attracted considerable attention for understanding the fundamental mechanisms of macroscopic friction and in many fields related to high precision engineering such as nanomachines.10 In the application process of graphene, the frictional behavior is a factor that affects its performance. Therefore, the research on the friction characteristics of graphene has considerable practical significance. However, for a long time, people's understanding of friction has been very limited as it has been limited to macro level and little is known about the microscopic mechanism of macroscopic friction. To understand the mechanisms underlying its friction behavior, people's understanding of friction has gradually become deeper into molecular, atomic levels until tools, such as atomic force microscope (AFM)11 and friction force microscope (FFM),12 are available. Because the AFM and FFM studies cannot provide direct evidence of in the changes taking place at the interface buried between the probe and the graphene, molecular dynamics (MD) simulations have been introduced to explain the observed behaviors. As a result, a new academic subject nano-tribology has come into existence. For now, FFM and AFM have been successfully applied for the investigation of frictional surfaces of diamond and graphite, and provide an objective and direct image for people to understand the friction at atomic scale.13–15 Along with the deeper understanding of the friction, theoretical research on nano-tribology has made great progress; the harmonic oscillator model of nano-tribology has been popularly approved.16 On the basis of the concept of the harmonic oscillator model, using MD and the approximate method in which the relaxation energies between the harmonic oscillators are equal to the potential barriers between the maximum and minimum potential energy in the process of interfacial sliding, the friction on the atomic scale has been investigated in literature.17,18 The results are in good agreement with the experiment. Matsushita et al.19 and Zaidi et al.20 investigated the atomic scale friction between clean graphite surfaces and behavior of graphite in friction under various environments by MD. Neitola et al.21 investigated the nanoscale friction between two graphite layers placed in contact using ab initio methods. Recent measurements have revealed a novel trend in which the frictional resistance to sliding is smaller on bilayer graphene than on single layer graphene.22,23 This trend has been confirmed through another set of experiments that included up to four layers of graphene and other layered materials.4,24,25 The latter experimental measurements are explain by a puckering effect in which a wrinkle in front of the FFM tip that resists sliding is more dominant with fewer layers.
In the research on vibration properties, Murmu and Pradhan26 employed the nonlocal elasticity theory for the analysis of the vibration of rectangular single layered graphene sheets (SLGS) embedded in an elastic medium. They have used both Winkler-type and Pasternak-type models for simulating the interaction of graphene sheets with a surrounding elastic medium. They reported that the natural frequencies of SLGS are strongly dependent on the small-scale coefficients. Pradhan and Phadikar27 investigated the vibration of the embedded multilayered graphene sheets (MLGSs) based on the nonlocal elasticity theory. They showed that the small-scale effect is quite important and needs to be included in the continuum model of graphene sheet. Murmu and Pradhan28 studied the free in-plane vibration of nanoplates by nonlocal continuum model and obtained the explicit relations of natural frequencies through direct separation of variables. Recently, graphene has been extensively considered for designing nanoresonators that can exhibit a high-frequency dynamic range29,30 with favorable high Q factors.31,32 The high-frequency dynamics of graphene is attributed to its excellent mechanical properties such as Young's modulus of approximately 1 TPa;33,34 it is noted that a resonant frequency is linearly proportional to the square root of Young's modulus when a device operates in harmonic oscillation.35,36 Until recently, most research works30,31,37 have focused on harmonic oscillation of a graphene resonator.
Many theoretical and experimental studies on mono- or bi-layer graphenes and boron nitride nanosheets (BNNSs) have examined the structures of nanosheets and some of the conclusions have been useful in engineering applications.38–40 However, the study on their trilayer systems still seems insufficient. Because of their possible applications in nano-electronic devices, it has also been the subject of several recent studies. The trilayer graphene system exhibits stacking-dependent electronic properties under the influence of a perpendicular electric field, with the semiconducting ABC stacked trilayer showing a large tunable gap relative to the metallic ABA stacked trilayer.41,42 While monolayer graphene retains its gapless feature in the presence of a perpendicular electric field, a BN/graphene/BN trilayer system shows stacking-dependent energy gap tunability.43,44 However, internal friction and in-plane vibration properties of the trilayer graphene and BN/graphene/BN systems do not appear to have been covered in extant research.
To take full advantage of the structural performance of multilayer architecture in any environment, we have studied structural stability and elastic properties of monolayer and bilayer carbon nanotube, graphene and BN nanotubes (nanosheet) by using MD simulation.45–49 In this study, we further investigate the trilayer architecture based on these studies. This paper mainly studies the hybrid trilayer system monolayer graphene inserted into the bilayer graphene and BNNSs (G/G/G and BN/G/BN). Their interlaminar interaction, internal friction and interlayer in-plane natural frequency in trilayer G/G/G and BN/G/BN nanosheets are investigated by calculating and analysing their system energies and electron density after deformation under different conditions. The differences between G/G/G and BN/G/BN are compared and some useful observations and conclusions are obtained. These results can provide some important information for the proper utilization of trilayer nanosheets under various practical conditions.
2. Computational model and method
The structural model for graphenes and BNNSs was set up according to atomic space coordinates. The nanosheets in this study can be achieved using 20 and 10 repeat basic units in length and width. The corresponding sizes were 4.1188 and 2.4600 nm, as shown in Fig. (1)a1. The trilayer BN/G/BN and G/G/G complex nanosheets were constructed through the parallel setting of a monolayer graphene sandwiched between bilayer BNNSs and graphenes with different interlayer distances. Dangling bonds existed at the atoms around the borders of the nanosheets, which were considered to be more active. A few hydrogen atoms were used as an auto-update link of the boundary of the nanosheets to achieve electron saturation, as shown in Fig. (1)a2 and b2. The original structure optimization, system energies and deformation electron density were calculated and analyzed using the universal force field (UFF)50 and the density functional theory (DFT) method. | ||
| Fig. 1 Geometric models of monolayer graphene and BNNS (a1, b1), trilayer BN/G/BN and G/G/G (a2, b2) (unit: nm). | ||
The UFF, a molecular mechanics force field, is where the force field parameters are estimated using general rules based only on the element, its hybridization and its connectivity. The potential energy of the UFF is expressed as the sum of bonded and non-bonded interactions:
| E@ = ER + Eθ + Eτ + Eω + Ev + Eel. | (1) |
The bonded interactions include bond stretching ER, the bending angle Eθ, the dihedral angle torsion Eτ and the inversion terms Eω, whereas non-bonded interactions include the van der Waals interaction Eν and the electrostatic interaction Eel. The UFF includes a parameter generator that calculates the force field parameters by combining the atomic parameters. Thus, the force field parameters for any combination of force field types can be generated as required. For further details, including the generator equations, see the literature.50–52
3. Results and discussion
3.1 Interlaminar interaction among trilayer nanosheets
This article mainly describes the friction forces caused by the electron interaction between atomic layers, regardless of the phonons interactions. The interaction energy is applied to the interaction among nanosheets, and its calculation method is as follows:
 | (2) |
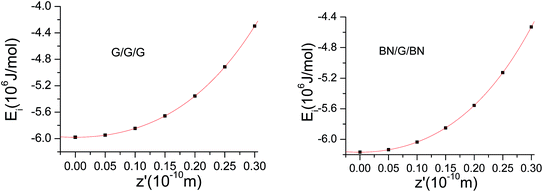
In the formula, Ei represents the interaction energy, E@ represents the total energy of the system, En represents the single point energy of each layer of the nanosheet,  represents the sum of the single point energy of all the nanosheets in the trilayer system. The results of the computer simulation for single-point energies of graphene and BNNS in BN/G/BN and G/G/G are shown in Table 1. The interlayer distances for trilayer nanosheets are gradually reduced from 0.347 to 0.317 nm for BN/G/BN and 0.341 to 0.311 nm for G/G/G along the direction of the surface normal in steps of 0.05 Å. The interaction energies at each step length are calculated during the procedure of the still compression (Fig. 2).
represents the sum of the single point energy of all the nanosheets in the trilayer system. The results of the computer simulation for single-point energies of graphene and BNNS in BN/G/BN and G/G/G are shown in Table 1. The interlayer distances for trilayer nanosheets are gradually reduced from 0.347 to 0.317 nm for BN/G/BN and 0.341 to 0.311 nm for G/G/G along the direction of the surface normal in steps of 0.05 Å. The interaction energies at each step length are calculated during the procedure of the still compression (Fig. 2).
| Complex | BN/G/BN | G/G/G | ||
|---|---|---|---|---|
| Location | Up (down) layer | Mid-layer | Up (down) layer | Mid-layer |
| En | 5.20149 | 7.26364 | 7.26019 | 7.26178 |
| Env | 4.24088 | 5.84545 | 5.80947 | 5.85349 |
The normal pressure (FN) at different interlayer distances can be obtained according to the differential operation of the interaction energy (Ei) with respect to the interlayer distances (z):
| FN = −∂Ei(z)/∂z = ∂Ei(z′)/∂z′ | (3) |
| z′ (Ǻ) | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 |
|---|---|---|---|---|---|---|
| G/G/G | 21.25271 | 47.20411 | 80.06473 | 121.5035 | 173.6097 | 238.9905 |
| BN/G/BN | 20.9615 | 46.36965 | 78.33133 | 118.3702 | 168.375 | 230.6791 |
3.2 Friction phenomenon among trilayer nanosheets
To examine the internal friction in the trilayer nanosheets, the mid-layer graphenes in G/G/G and BN/G/BN are applied to slide along the x direction in its plane. The loading scheme is as follows. At different lengths of compression along the normal direction of the surface from 0.05 Ǻ to 0.30 Ǻ in steps of 0.05 Å, the slide distances are designed from 0 to 0.4 nm for G/G/G and 0 to 0.46 nm for BN/G/BN at an incremental displacement step of 0.2 Å. The interaction energies at each step length are calculated during the procedure of the sliding. In addition, the periodical boundary conditions are applied to x and y coordinates to avoid the potential energy at different positions along the sliding path that exhibits a global gradually increasing trend when the sliding distance becomes larger, which is due to the increase in surface energy, while the periodic variation because of periodically changing neighboring atomic distances between layers can still be preserved. As a result, this concludes that the periodic variation of the sliding distance cannot be too large. According to the method described in (ref. 17), the potential energy at different positions along the sliding path can be calculated from the following formula:| U(x,FN) = Ei(x,z(x,FN)) + AFN(x) − Umin(x,FN) | (4) |
As shown in Fig. 4(A), the potential energies exhibit periodic variations with the sliding distance of mid-layer graphenes along x direction. This is because the neighboring atomic distances at all the levels between mid-layer graphene and up-down layer nanosheets change periodically with the sliding. From Fig. 4(A), it is easy to see that the potential energies at all sliding distances uniformly increase with the increase in the normal pressure, but the law of periodic change in the potential energies with sliding distance remains almost unchanged. This is because the neighboring atomic distances at all levels between mid-layer graphene and up-down layer nanosheets uniformly decrease with the normal pressure, the potential repulsion between the atoms increases and the system energy uniformly increases as pressure. However, the distance between neighbouring atoms at all levels between mid-layer graphene and up-down layer nanosheets have similar trends under different magnitudes of pressure with the sliding of mid-layer graphene. To know the effect of frictional coefficients in different pressure, the potential energies for the length of compression as a function of the sliding distances are calculated, as shown in Fig. 4(B). The calculated curves are basically similar to that of Fig. 4(A). For simplicity, x larger than 2.2 Ǻ is not shown in Fig. 4(B). In the process of the relative sliding, the system has to overcome the potential barriers between the interfaces. On the basis of the harmonic oscillator model, the numerical potential barrier equals to the work performed by overcoming the friction. The friction force can be determined by the following formula:
| f(x,FN) = ∂U(x,FN)/∂x | (5) |
| ΔUmax(FN) = Umax(FN) − Umin(FN) | (6) |
ΔUmax = ΔAf = ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ·Δx ·Δx
| (7) |
![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) is the average force of friction, Δx is the distance between maximum and minimum potential energy positions on the sliding path. Finally, an average coefficient of friction under the normal pressure is obtained by the average force of friction:
is the average force of friction, Δx is the distance between maximum and minimum potential energy positions on the sliding path. Finally, an average coefficient of friction under the normal pressure is obtained by the average force of friction:
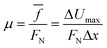 | (8) |
According to the formula, when the mid-layer graphenes in G/G/G and BN/G/BN slide along the x direction in the plane, the internal friction coefficients under different pressures are calculated, as shown in Fig. 5.
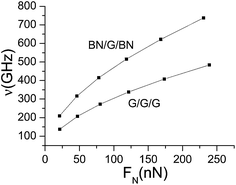
Fig. 5 shows that the internal friction coefficients for G/G/G are from 0.014 to 0.0156, and for BN/G/BN they are from 0.023 to 0.0255. The coefficients for BN/G/BN are always significantly higher than that for G/G/G. In general, a large internal friction coefficient can make the system work more steadily; thus, the results indicate that structural stability of the trilayer BN/G/BN should be higher than that of the G/G/G. To understand the differences between G/G/G and BN/G/BN, the deformation electron density and its isoline structure are further calculated and analyzed by DFT. Fig. 6 shows the deformation electron density and its section isoline by simulating G/G/G and BN/G/BN model with interlayer compression and midlayer sliding distances of 0.15 and o.4 Ǻ, respectively. The electron density is similar to the online equivalent and it gradually becomes smaller on the vertical isolines from the inside outward. The isoline intervals reflect the local electronic conditions in which the greater the interval, the weaker is the localization and the more are the free electrons, and vice versa. As shown in Fig. 6(a1) and (b1), the outer-layer electrons for BNNSs are obviously partial to the N atom in the B–N bond. However, for graphenes, the electrons are more concentrated at the center of the C–C bond. The outer-layer electrons are the main cause of the covalent bond. If the outer-layer electrons spend most of their time within the nuclei of the two atoms, then the covalent bond is placed in the bonding orbital in this case the distribution of the electron density is less at either end and large in the middle. In contrast, if the electrons spend most of their time outside the nuclei of the two atoms, then the covalent bond is placed in the antibonding orbital in this case the distribution of the electron density is large at both ends and less in the middle. This is because in the bonding orbital electron density between the nuclei increases, whereas in the antibonding orbital it decreases. Placing an electron in the bonding orbital stabilizes the molecule because it remains in between the two nuclei. Conversely, placing electrons in the antibonding orbital causes a decrease in stability.53 The deformation of the electron density plot in Fig. 6 shows that each layer of graphenes in G/G/G has a good bonding electronic distribution, which is less at each end and large in the middle. The electrons are mainly uniformly distributed along the atoms in rings on the plane and there are fewer electrons in the out-plane (see Fig. 6(a2)), resulting in weak interaction between up-down neighboring nanosheets for G/G/G. However, the situation for BN/G/BN is rather different. Because the different types of atoms exists between up-down nanosheets and the polar covalent bond exists in the B–N bond, electronegativity becomes a dominant factor. The electronic localization of the inner layer may be weakened, a few s electrons become p electrons because of the excitation and partial electronic delocalization of the outer shell, which results in an increase in electron mobility. Consequently, there are more electrons between up-down neighboring nanosheets (see Fig. 6(b2)), showing a long range attraction between up-down neighboring nanosheets. Clearly, the resistance in BN/G/BN should be greater than that in G/G/G when mid-layer graphene is drawn out of trilayer nanosheets along its plane, naturally resulting in the higher internal friction coefficients in BN/G/BN. Moreover, this also explains, more intuitively, that the structural stability of the trilayer BN/G/BN is higher than that of the G/G/G from another angle.
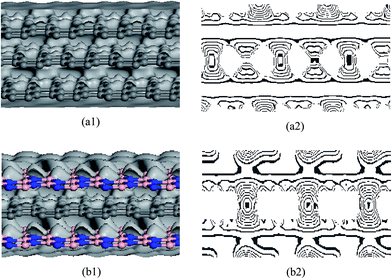 | ||
| Fig. 6 Deformation electron density (left) and isoline structure (right) on cross section of G/G/G (a1, a2) and BN/G/BN (b1, b2) with the compressed interlayer distances of 0.15 Å. | ||
It can be further concluded from Fig. 5 that the coefficients for both G/G/G and BN/G/BN increase with the pressure. The growth rate can be divided into three stages. The pressure for relatively quick increases is in the less than 50 nN range, that for slow increase is in the range of 50 to170 nN and the saturation phenomenon on the variation of friction coefficients with pressure occurs in the greater than 170 nN range, i.e., the friction coefficients are basically constant following the simple microscopic theory of Amontons laws.54 Because the friction coefficients of the graphenes are related to surface structure, roughness and environment, the experimental results are not a constant value. Values are in a range of 0.006 to 0.45.55–57 The calculated results in this paper are obviously within the range of the experiment datum.
3.3 In-plane natural frequency of mid-layer graphenes in trilayer nanosheets
As seen in Fig. 4, with the normal pressure on trilayer nanosheets, a periodic potential obviously emerges along the x direction. It is natural to create a restoring force nearby the minimum potential energy (equilibrium position). By fitting the curve around the equilibrium position, it can be found that the restoring force has a good linear correlation with displacement to equilibrium position. As we all know, graphene possesses an ultrahigh intrinsic strength and stiffness; thus, the mid-layer graphene in trilayer nanosheets can be approximately considered to be entirely rigid. Therefore, if the thermal effect is neglected, the equation of free vibration on the mid-layer graphenes along x direction can be expressed as:| Mẍ + kx = 0 | (9) |
| k = ∂2U(x,FN)/∂x2 | (10) |
The second order polynomial is used to fit the computing data of potential energy to sliding displacement near the minimum potential energy in Fig. 4, and then the equivalent elastic coefficients k at different lengths of compression are calculated (Fig. 7).
According to the general resonance theory, the natural frequency can be calculated as follows:
 | (11) |
On the basis of the formula, combined with the results in Table 2, the natural frequency under different normal pressures can be obtained, as shown in Fig. 8.
It can be seen from Fig. 8 that the natural frequency of mid-layer graphene in its plane direction increases with the increase in normal pressure. The natural frequency in BN/G/BN is significantly higher than in G/G/G, and both of them increase with the pressure. Through data fitting, the function relation between the normal pressure and the natural frequency can be obtained as follows:
| ν = 93.54397 + 2.44859FN − 0.00346FN2 for G/G/G | (12) |
| ν = 141.09183 + 3.83886FN − 0.00552FN2 for BN/G/BN | (13) |
Eqn (12) and (13) show that the change of natural frequency is of the order of GHz and the external normal pressure is of the order of nN and, therefore, the in-plane natural frequency for mid-layer graphene in trilayer nanosheets is extremely sensitive to external pressure loads, especially for mid-layer graphene in BN/G/BN. This feature indicates a huge application foreground in micro/nano force sensor.
4. Conclusion
By calculating the interlaminar interaction of trilayer coupled structures under different external normal pressures and their potential energies at different relative sliding positions of the mid-layer graphene, the internal friction and natural frequency in trilayer nanosheets G/G/G and BN/G/BN are examined. The results indicate that the internal friction coefficients for G/G/G and BN/G/BN are about 0.015 and 0.025, respectively. The internal friction coefficients for BN/G/BN is significantly higher than that for G/G/G. The coefficients for both G/G/G and BN/G/BN increase with the increase in pressure at the three growth rates. The pressure for relatively quick increase occurs in less than 50 nN range and that for slow increase is in the range of 50 to 170 nN and the saturation phenomenon for the friction coefficients to the pressure occurs in the greater than 170 nN range, i.e., the friction coefficients vary little with the pressure change, following simple microscopic theory of Amontons laws. These results are useful for understanding the mechanism of nano-tribology and provide an effective micro-control method of internal friction.Further analysis indicates that the in-plane natural frequency of mid-layer graphene in trilayer complexes increases with the increase in external normal pressure and the natural frequency in BN/G/BN is significantly higher than in G/G/G. It is found that the in-plane natural frequency is extremely sensitive to external pressure loads, especially for mid-layer graphene in BN/G/BN. Compared with traditional materials, graphene in BN/G/BN may potentially be a new sensing element in micro/nano force sensors, which have promising application prospects in future M/NEMS.
Acknowledgements
The work described in this paper was supported by grants from the Research Grants Council of the Hong Kong Special Administrative Region, China (Project no. 9042047, CityU 11208914) and National Natural Science Foundation of China (Grant no. 51378448). The work was also supported by Hunan Provincial Natural Science Foundation of China (Project no. 14JJ2076), Scientific Research Fund of Hunan Provincial Education Department, China (Project no. 12A001), the Construct Program of the Key Discipline in Hunan Province and Aid Program for Science and the Technology Innovative Research Team in Higher Educational Institutions of Hunan Province, China.References
- F. P. Bowden, The friction and lubrication of solids. [1], Clarendon Press, 1958 Search PubMed.
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef CAS.
- A. A. Balandin, S. Ghosh, W. Z. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902–907 CrossRef CAS PubMed.
- C. Lee, Q. Y. Li, W. Kalb, X. Z. Liu, H. Berger, R. W. Carpick and J. Hone, Science, 2010, 328, 76–80 CrossRef CAS PubMed.
- J. Li, Z. H. Zhang, G. Kwong, W. Tian, Z. Q. Fan and X. Q. Deng, Carbon, 2013, 61, 284–293 CrossRef CAS PubMed.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- A. K. Geim, Science, 2009, 324, 1530–1534 CrossRef CAS PubMed.
- Z. H. Zhang, X. Q. Deng, X. Q. Tan, M. Qiu and J. B. Pan, Appl. Phys. Lett., 2010, 97, 183105 CrossRef PubMed.
- N. N. Klimov, S. Jung, S. Z. Zhu, T. Li, C. A. Wright, S. D. Solares, D. B. Newell, N. B. Zhitenev and J. A. Stroscio, Science, 2012, 336, 1557–1561 CrossRef CAS PubMed.
- G. Gudehus, Mech. Cohesive-Frict. Mater., 1998, 3, 365 CrossRef.
- G. Binning, H. Rohrer, C. Gerber and E. Weibel, Phys. Rev. Lett., 1982, 49, 57–61 CrossRef CAS.
- G. Binnig, C. F. Quate and C. Gerber, Phys. Rev. Lett., 1986, 56, 930–933 CrossRef.
- C. M. Mate, G. M. McClelland, R. Erlandsson and S. Chiang, Phys. Rev. Lett., 1987, 59, 1942–1945 CrossRef CAS.
- A. Smolyanitsky, S. Z. Zhu, Z. Deng, T. Li and R. J. Cannara, RSC Adv., 2014, 4, 26721–26728 RSC.
- Z. Deng, A. Smolyanitsky, Q. Y. Li, X. Q. Feng and R. J. Cannara, Nat. Mater., 2012, 11, 1032–1037 CAS.
- M. Weiss and F. J. Elmer, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 7539–7549 CrossRef CAS.
- W. Zhong and D. Tomanek, Phys. Rev. Lett., 1990, 64, 3054–3057 CrossRef CAS.
- D. Tomanek, W. Zhong and H. Thomas, Europhys. Lett., 1991, 15, 887–892 CrossRef CAS.
- K. Matsushita, H. Matsukawa and N. Sasaki, Solid State Commun., 2005, 136, 51–55 CrossRef CAS PubMed.
- H. Zaidi, D. Paulmier, A. Jeanmaire and H. Nery, Surf. Sci., 1991, 251, 778–781 CrossRef.
- R. Neitola, H. Ruuska and T. A. Pakkanen, J. Phys. Chem. B, 2005, 109, 10348–10354 CrossRef CAS PubMed.
- T. Filleter, J. L. McChesney, A. Bostwick, E. Rotenberg, K. V. Emtsev, T. Seyller, K. Horn and R. Bennewitz, Phys. Rev. Lett., 2009, 102, 086102 CrossRef CAS.
- T. Filleter and R. Bennewitz, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155412 CrossRef.
- C. Lee, X. D. Wei, Q. Y. Li, R. Carpick, J. W. Kysar and J. Hone, Phys. Status Solidi B, 2009, 246, 2562–2567 CrossRef CAS.
- Z. Deng, N. N. Klimov, S. D. Solares, T. Li, H. Xu and R. J. Cannara, Langmuir, 2013, 29, 235–243 CrossRef CAS PubMed.
- T. Murmu and S. C. Pradhan, J. Appl. Phys., 2009, 105, 064319 CrossRef PubMed.
- S. C. Pradhan and J. K. Phadikar, Phys. Lett. A, 2009, 373, 1062–1069 CrossRef CAS PubMed.
- T. Murmu and S. C. Pradhan, Physica E, 2009, 41, 1628–1633 CrossRef CAS PubMed.
- J. S. Bunch, A. M. van der Zande, S. S. Verbridge, I. W. Frank, D. M. Tanenbaum, J. M. Parpia, H. G. Craighead and P. L. McEuen, Science, 2007, 315, 490–493 CrossRef CAS PubMed.
- D. Garcia-Sanchez, A. M. van der Zande, A. S. Paulo, B. Lassagne, P. L. McEuen and A. Bachtold, Nano Lett., 2008, 8, 1399–1403 CrossRef CAS PubMed.
- R. A. Barton, B. Ilic, A. M. van der Zande, W. S. Whitney, P. L. McEuen, J. M. Parpia and H. G. Craighead, Nano Lett., 2011, 11, 1232–1236 CrossRef CAS PubMed.
- A. Eichler, J. Moser, J. Chaste, M. Zdrojek, I. Wilson-Rae and A. Bachtold, Nat. Nanotechnol., 2011, 6, 339–342 CrossRef CAS PubMed.
- J. W. Jiang, J. S. Wang and B. W. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 113405 CrossRef.
- O. Hod and G. E. Scuseria, Nano Lett., 2009, 9, 2619–2622 CrossRef CAS PubMed.
- K. Eom, H. S. Park, D. S. Yoon and T. Kwon, Phys. Rep., 2011, 503, 115–163 CrossRef CAS PubMed.
- M. Poot and H. S. J. van der Zant, Phys. Rep., 2012, 511, 273–335 CrossRef PubMed.
- A. M. van der Zande, R. A. Barton, J. S. Alden, C. S. Ruiz-Vargas, W. S. Whitney, P. H. Q. Pham, J. Park, J. M. Parpia, H. G. Craighead and P. L. McEuen, Nano Lett., 2010, 10, 4869–4873 CrossRef CAS PubMed.
- F. Scarpa, S. Adhikari and R. Chowdhury, Phys. Lett. A, 2010, 374, 2053–2057 CrossRef CAS PubMed.
- Y. M. Shi, C. Hamsen, X. T. Jia, K. K. Kim, A. Reina, M. Hofmann, A. L. Hsu, K. Zhang, H. N. Li, Z. Y. Juang, M. S. Dresselhaus, L. J. Li and J. Kong, Nano Lett., 2010, 10, 4134–4139 CrossRef CAS PubMed.
- Z. H. Zhang, C. Guo, D. J. Kwong, J. Li, X. Q. Deng and Z. Q. Fan, Adv. Funct. Mater., 2013, 23, 2765–2774 CrossRef CAS.
- W. Bao, L. Jing, J. Velasco, Y. Lee, G. Liu, D. Tran, B. Standley, M. Aykol, S. B. Cronin, D. Smirnov, M. Koshino, E. McCann, M. Bockrath and C. N. Lau, Nat. Phys., 2011, 7, 948–952 CrossRef CAS.
- F. Zhang, B. Sahu, H. K. Min and A. H. MacDonald, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 035409 CrossRef.
- R. G. Quhe, J. X. Zheng, G. F. Luo, Q. H. Liu, R. Qin, J. Zhou, D. P. Yu, S. Nagase, W. N. Mei, Z. X. Gao and J. Lu, NPG Asia Mater., 2012, 4, E6 CrossRef.
- J. Slawinska, I. Zasada, P. Kosinski and Z. Klusek, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 085431 CrossRef.
- J. H. Yuan, J. X. Liao, C. H. Yang and X. H. Shi, Curr. Nanosci., 2013, 9, 324–329 CrossRef CAS.
- J. H. Yuan and K. M. Liew, J. Nanosci. Nanotechnol., 2012, 12, 2617–2624 CrossRef CAS PubMed.
- J. H. Yuan and K. M. Liew, Carbon, 2011, 49, 677–683 CrossRef CAS PubMed.
- K. M. Liew and J. H. Yuan, Nanotechnology, 2011, 22, 085701 CrossRef CAS PubMed.
- J. H. Yuan and K. M. Liew, J. Phys. Chem. C, 2011, 115, 431–435 CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- C. J. Casewit, K. S. Colwell and A. K. Rappe, J. Am. Chem. Soc., 1992, 114, 10035–10046 CrossRef CAS.
- L. Boldrin, F. Scarpa, R. Chowdhury and S. Adhikari, Nanotechnology, 2011, 22, 505702 CrossRef CAS PubMed.
- D. W. Smith, J. Chem. Educ., 2000, 77, 780–784 CrossRef CAS.
- M. H. Muser, L. Wenning and M. O. Robbins, Phys. Rev. Lett., 2001, 86, 1295–1298 CrossRef CAS.
- J. A. Ruan and B. Bhushan, J. Appl. Phys., 1994, 76, 8117–8120 CrossRef CAS PubMed.
- J. Sugishita and S. Fujiyoshi, Wear, 1981, 68, 7–20 CrossRef CAS.
- H. Zaidi, E. Csapo, H. Nery, D. Paulmier and T. Mathia, Surf. Coat. Technol., 1993, 62, 388–392 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |