DOI:
10.1039/C4RA08915D
(Paper)
RSC Adv., 2014,
4, 52770-52784
Dielectric studies of a nano-crystalline CaCu2.90Zn0.10Ti4O12 electro-ceramic by one pot glycine assisted synthesis from inexpensive TiO2 for energy storage capacitors
Received
19th August 2014
, Accepted 13th October 2014
First published on 14th October 2014
Abstract
A facile way for the synthesis of nano-crystalline CaCu2.90Zn0.10Ti4O12 (CCZTO) using a solution combustion technique based on the glycine–nitrate process with inexpensive solid TiO2 powder as the raw material is introduced in this manuscript, for the first time. The precursor powder was calcined between 200 °C and 850 °C for 3 h in air. Phase formation, crystalline nature, morphology and chemical purity of the fabricated CCZTO were investigated with TG/DTA, FT-IR, FT-Raman, XRD, SAED patterns, SEM, TEM, EDX and XPS analyses, respectively. The XRD results indicated that all sintered samples had a major CaCu3Ti4O12 structure with some amount of CaTiO3 and CuO. The bright-field TEM micrographs revealed that the particle size was in the range of 15–50 nm, which was in good agreement with the average crystallite size obtained from XRD. SEM micrographs of the sintered CCZTO ceramics showed the average grain sizes were in the range of 800 nm–7 μm. EDX and XPS studies confirmed the stoichiometry and purity of the ceramics. The nature of the relaxation behavior of the ceramics was rationalized using impedance and modulus spectroscopy. The activation energies calculated from the grain-boundary relaxation time constant were found to be in the range of 0.79–0.52 eV, which confirmed the Maxwell–Wagner type of relaxation present in the ceramic. Our inexpensive novel solution chemistry based method for CCZTO_16h gives a high dielectric constant (799) and low dielectric loss (0.091) at 100 Hz at room temperature, which has potential significance for cost-effective technological applications in microelectronic devices.
1. Introduction
“Nano-materials” possessing 1–100 nm particle sizes, have unique chemical, physical, optical, mechanical and dielectric properties. Multifunctional materials are in demand for future nanotechnology. In the development of device miniaturization and high-density data storage systems, it is highly desirable to integrate multifunctionality into a single material. The perovskite nano-materials form the building blocks for new bottom up approaches, due to their intrinsic size-dependent properties and their resulting applications. In recent years, the study of newer types of nano-sized dielectric materials and their isomorphs has been of great interest. The requirement for new, innovative and easily obtainable dielectric materials that produce high dielectric permittivity with very low dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) has always received great attention, due to their potential application in miniaturizing electronic devices.
δ) has always received great attention, due to their potential application in miniaturizing electronic devices.
The CaCu3Ti4O12 (CCTO) perovskite has attracted much interest due to its high dielectric constant (>104), which is almost frequency independent up to 106 Hz, and shows good thermal stability over the temperature range, 100–600 K.1,2 The obstacle for using this material in the miniaturization of electronic devices is the high dielectric loss. The continuous miniaturization of advanced electronic devices will require dielectric layers of multi-layer ceramic capacitors thinner than 500 nm in the near future. Therefore, fine calcium copper titanate (CCTO) nanoparticles smaller than 100 nm are eagerly desired. CCTO complex perovskite structure is very flexible, i.e. its dielectric constant (εr) and dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) is highly dependent on the various cationic substitutions, such as La at Ca and Cr, and Hf at the Ti site,3–6 The cationic substitutions at the Cu site and its concentration in CCTO ceramic affect the dielectric properties, because Cu ion is one of the most effective intergranular dopants for barrier layer capacitors and can act as an acceptor ion.7 The presence of Cu+/Cu2+ ratios and their correlation with oxygen vacancies had great influence on the dielectric properties of polycrystalline CCTO via the internal barrier layer capacitance (IBLC) mechanism, because the IBLC is a widely accepted mechanism at the present stage which is responsible for the high εr. The substitution of Zn, Mn and Mg at the Cu-site enhanced the dielectric properties of CCTO without changing its crystal structure, reported earlier by solid-state routes.8–12 The dielectric properties are also modified by using synthesis routes13,14 and processing conditions such as sintering temperature,15,16 sintering time,17 cooling rate and partial pressure of sintering atmosphere.18 The electrical properties of CCTO are highly dependent on the processing routes. An appropriate method of synthesis is still required for the fabrication of nano-crystalline CCTO having the desirable features for miniaturizing the electronic devices. CCTO ceramic is generally synthesized by a solid-state reaction method at high temperatures for a long sintering time. This route suffers from the disadvantage of the presence of a secondary phase, because of limited atomic diffusion through micrometer sized molecules.19–21 On the other hand, the wet chemical routes provide atomic level mixing of individual metal ions, and result in the formation of nano-crystalline materials at much lower sintering temperatures and a shorter duration than the solid state methods. There are many wet chemical routes, such as sol–gel, co-precipitation, precursor solution technique, hydrothermal process, microwave heating, pyrolysis routes and flame synthesis,22–28 which have already been reported for the synthesis of CCTO ceramics. However, in these chemical methods, Ti is used as Ti(OR)4, which is very costly and difficult to handle by maintaining pH. Among many powder wet synthetic techniques, combustion synthesis (CS) has been of particular interest recently; it can produce various industrially useful materials with some unique properties at a low cost. Combustion synthesis involves a self-sustained reaction in a homogeneous solution of different oxidizers (e.g., metal nitrates) and fuels (e.g., citric acid, urea, glycine etc.). It has been successfully used in the synthesis of perovskite materials.29
δ) is highly dependent on the various cationic substitutions, such as La at Ca and Cr, and Hf at the Ti site,3–6 The cationic substitutions at the Cu site and its concentration in CCTO ceramic affect the dielectric properties, because Cu ion is one of the most effective intergranular dopants for barrier layer capacitors and can act as an acceptor ion.7 The presence of Cu+/Cu2+ ratios and their correlation with oxygen vacancies had great influence on the dielectric properties of polycrystalline CCTO via the internal barrier layer capacitance (IBLC) mechanism, because the IBLC is a widely accepted mechanism at the present stage which is responsible for the high εr. The substitution of Zn, Mn and Mg at the Cu-site enhanced the dielectric properties of CCTO without changing its crystal structure, reported earlier by solid-state routes.8–12 The dielectric properties are also modified by using synthesis routes13,14 and processing conditions such as sintering temperature,15,16 sintering time,17 cooling rate and partial pressure of sintering atmosphere.18 The electrical properties of CCTO are highly dependent on the processing routes. An appropriate method of synthesis is still required for the fabrication of nano-crystalline CCTO having the desirable features for miniaturizing the electronic devices. CCTO ceramic is generally synthesized by a solid-state reaction method at high temperatures for a long sintering time. This route suffers from the disadvantage of the presence of a secondary phase, because of limited atomic diffusion through micrometer sized molecules.19–21 On the other hand, the wet chemical routes provide atomic level mixing of individual metal ions, and result in the formation of nano-crystalline materials at much lower sintering temperatures and a shorter duration than the solid state methods. There are many wet chemical routes, such as sol–gel, co-precipitation, precursor solution technique, hydrothermal process, microwave heating, pyrolysis routes and flame synthesis,22–28 which have already been reported for the synthesis of CCTO ceramics. However, in these chemical methods, Ti is used as Ti(OR)4, which is very costly and difficult to handle by maintaining pH. Among many powder wet synthetic techniques, combustion synthesis (CS) has been of particular interest recently; it can produce various industrially useful materials with some unique properties at a low cost. Combustion synthesis involves a self-sustained reaction in a homogeneous solution of different oxidizers (e.g., metal nitrates) and fuels (e.g., citric acid, urea, glycine etc.). It has been successfully used in the synthesis of perovskite materials.29
Here in, we report the facile synthesis and systematic investigation of nano-crystalline CaCu2.90Zn0.10Ti4O12 ceramic by a glycine–nitrate solution-combustion process, applying inexpensive and stable solid TiO2 powder as the Titanium source, which is converted into titanium oxy-nitrate in our lab. To the best of our knowledge, not much work has been reported on the synthesis of CCTO ceramic using inexpensive solid TiO2 as a raw material and systematically varying the sintering condition. Our method is different from other chemical methods where an alkoxide, oxynitrate, or chloride of titanium is used, which are very expensive. In this method, the cheap raw material, solid TiO2, is used. It is converted into TiO(NO3)2, and other metal ions were taken in solution form. This is one of the biggest advantages over the other wet chemical methods. This method is useful for obtaining a homogeneous and fine precursor powder, and also provides a novel technique for processing ceramic materials. These advantages could be achieved because the mixing process is performed in a solution state, as nitrate solutions of metal ions, along with inexpensive TiO(NO3)2. The ceramics obtained by this route were characterized by TG/DTA, IR/RAMAN, XRD, SEM, EDX, XPS and TEM techniques, along with measurement of their dielectric properties and impedance analysis.
2. Experimental
2.1. Synthesis of materials
The nano-crystalline CaCu2.90Zn0.10Ti4O12 electro-ceramic was synthesized using solution combustion synthesis through various different steps. Analytical grade chemicals, Ca(NO3)2·4H2O (99.5%, Qualigens), Cu(NO3)2·3H2O (99.5%, Merck), Zn(NO3)2 (99.5%, Merck), TiO2 (99.5%, Merck) and glycine (99.5%, Merck) having a purity of 99.5% or better were used as starting materials. Standard aqueous solutions of Ca2+, Cu2+, Zn2+ and glycine were prepared in doubly distilled water. In order to avoid the use of water insoluble TiO2 and cost-bearing titanium isopropoxide, Ti(OR)4, the TiO2 was dissolved in H2SO4 and converted to titanium oxysulphate TiO(SO4) (eqn (1)). The solution was then diluted with the addition of distilled water in an ice bath. Ammonium hydroxide (NH4OH) was added to the chilled solution, wherein a white precipitate of titanium oxyhydrate solid (eqn (2)) was formed. The precipitate was washed repeatedly to make it sulphate-free. Then, the washed white precipitate was dissolved in dilute nitric acid (HNO3), which was then changed to titanium oxynitrate solution (eqn (3)), which is as good as Ti(OR)4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 for the synthesis of CCZTO.
30 for the synthesis of CCZTO.| | |
TiO2 + H2SO4→ TiO(SO4) + H2O
| (1) |
| | |
TiO(SO4) + 2NH4OH → TiO(OH)2 + (NH4)2SO4
| (2) |
| | |
TiO(OH)2 + 2HNO3 → TiO(NO3)2 + 2H2O
| (3) |
A schematic flow chart of the process is shown in Fig. 1 to convert solid TiO2 into TiO(NO3)2. The concentrations of the Ti4+ metal ions in their respective stock solutions were determined gravimetrically. The stoichiometric amounts of standard aqueous solutions of Ca2+, Cu2+, Zn2+, and Ti4+ as TiO(NO3)2 for the synthesis of CCZTO were mixed in a beaker along with aqueous glycine (equivalent to metal ions). The resulting solutions were heated on a hot plate with a magnetic stirrer at 70–80 °C to evaporate the water, and until self-ignition took place. The process of ignition occurred in air at room temperature, and burnt under self-propagating combustion, which exhausted a large amount of gases and produced the fluffy mass of CCZTO ceramic powder. In this method, the mixing process was performed in solution as a nitrate solution. The technique involves the mixing of solutions of a metal precursor and an organic poly-functional acid possessing at least one hydroxyl and one carboxylic acid group, such as citric, glycine, tartaric and glycerol, which results in complexation of the metal by the poly-carboxylic acid. Glycine, as a complexing agent, can form a complex with cations at both the carboxylic end and the amino group end and provide the fuel for the ignition step. The ignition step increased the temperature to form a very fine crystalline precursor powder at a very low temperature.31 The foamy product of CCZTO was collected and calcined in air from 200 to 850 °C for 3 h in an electrical furnace. The calcined powder at 850 °C with 2 wt% polyvinyl alcohol (PVA) was pressed into cylindrical pellets using a hydraulic press. The PVA binder was burnt out at 350 °C for 2 h. Finally, the pellets of CCZTO were sintered in air at 950 °C for 8, 12, 16 and 20 h, hereafter abbreviated as CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h, respectively. A schematic diagram of the synthesis processes is displayed in Fig. 2.
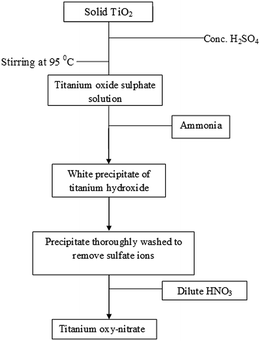 |
| | Fig. 1 A schematic flow chart of the process to convert solid TiO2 into TiO(NO3)2. | |
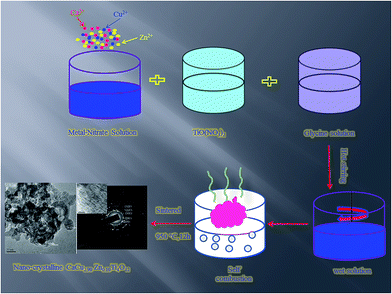 |
| | Fig. 2 A schematic diagram of the synthesis processes of nano-crystalline CaCu2.90Zn0.10Ti4O12. | |
2.2. Structural and microstructural characterization
Differential thermal analysis (DTA) and thermo gravimetric analysis (TGA) of precursor powder was performed in an air atmosphere using a TGA/DTA Analyser, Perkin-Elmer, USA. The crystalline phase of the sintered samples was identified using an X-ray Diffractometer (Rich-Siefert, ID-3000) employing Cu Kα radiation. Microstructural examination of the fractured surfaces of the sintered ceramics was investigated using a scanning electron microscope (SEM, Model JEOL JSM5410). The energy dispersive X-ray analyser (EDX, model Kevex, Sigma KS3) was used for elemental analysis. The particle size was examined using a high resolution transmission electron microscope (HRTEM, FEI Tecnai F30). X-ray photoelectron spectroscopy (XPS) analysis of CCZTO_20h was performed using a Thermo Fisher K-Alpha in wide scan survey mode and high-energy resolution with Al Kα (1486.6 eV).
2.3. Infrared and Raman spectroscopy
The infrared spectra (FT-IR) were measured using circular pellets, made from a mixture of KBr (potassium bromate) and the powder of each sample. The infrared spectra (FT-IR) were recorded in the 400–4000 cm−1 range with a Varian 3100 FTIR instrument. The Raman spectroscopy, of the powder samples, was carried out in a T64000, Jobin Yvon SPEX spectrometer using an Ar back-scattering geometry, between 100 and 1000 cm−1.
2.4. Dielectric and electrical measurements
The dielectric and electrical data of the CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h ceramics were collected using an impedance analyzer (Hioki 3522-50 LCR HiTESTER, Japan) over a frequency range of 102–106 Hz, and in the temperature range of 300–550 K.
3. Results and discussion
The ideal temperature for the glycine gel decomposition was determined by the thermo-gravimetric analysis (TGA) and differential-thermal analysis (DTA). Simultaneous TGA/DTA characterization was carried out on CaCu2.90Zn0.10Ti4O12 ceramic of dried precursor powder with a heating rate of 10 °C min−1 in static air from room temperature (RT) to 1000 °C (Fig. 3). The TG curve shows two stages of weight loss. The first one occurred in the temperature range from RT to 185 °C, while the second one occurred from 250 to 450 °C. A third stage occurred from 450 to 745 °C, with no further weight loss observed in the temperature range of 745 to 1000 °C. The first stage of weight loss was related to the elimination of residual water and the dehydration of hydrated water present in the precursor powder. The second, larger stage of weight loss may be due to the combustion of organic components and excess glycine present in the precursor powders, along with the formation of the intermediate compound, CaCu2.9Zn0.10O4. On the DTA curve, a more intensive exothermic peak was observed between 150 and 450 °C, indicating that the thermal events were associated with the burnout of organic species involved in the precursor powder. The second weight loss was related to an exothermic reaction of the oxidation of glycine and formation of intermediate CaCu2.90Zn0.10O4. In the third case, a very small step up curve formed between 714 and 866 °C on the TG curve, indicating an increase in weight due to the addition reaction, because the final product CaCu2.90Zn0.10Ti4O12 formed after 800 °C by the combination of the intermediate compound CaCu2.90Zn0.10O4 with TiO2 to give the final product at higher temperature. The absence of peaks in the DTA curve beyond 800 °C also supported the findings of TG analysis, confirming that the final product formed around 800 °C. The chemical reactions involved in the formation of the CaCu2.90Zn0.10Ti4O12 ceramic are given in three steps as shown in the following equations:| | |
TiO(NO3)2(aq) + 2C2H5NO2(aq) + 2NH4NO3(aq) + O2 → TiO2(s) + 3N2(g) + 4CO2(g) + 9H2O(g)
| (4) |
| | |
CaCO3 + 2.9CuO + 0.10ZnO → CaCu2.9Zn0.10O4 + CO2
| (5) |
| | |
CaCu2.9Zn0.10O4 + 4TiO2 → CaCu2.9Zn0.10Ti4O12
| (6) |
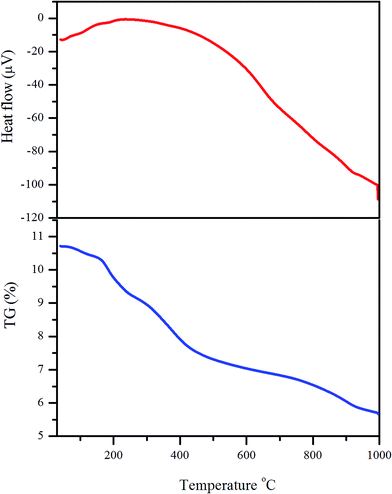 |
| | Fig. 3 TG/DTA curves for the precursor powder of CaCu2.90Zn0.10Ti4O12. | |
The results of the thermal studies showed that CaCu2.90Zn0.10Ti4O12 ceramic synthesized by the solution combustion route involved a lower sintering temperature and shorter sintering duration to get a good electro-ceramic.
The FT-IR spectra of the CCZTO precursor powder calcined at 200–850 °C for 3 h in air are shown in Fig. 4. It can be seen from the spectrum of the precursor calcined at 200 °C that a strong and broad absorption band appeared in the region of 2647–3600 cm−1, centered at 3203 cm−1, originating from the O–H vibration of the weakly-bound water and C–H vibration of alkyl groups in the precursors. The peak at 1636 cm−1 corresponded to the bending mode of H2O.32 In addition, a sharp absorption peak prevailed around 1382 cm−1, due to C–H rock. The absorption peaks at 1192 and 1120 cm−1 were assigned to C–N stretch. The absorption peak in the lower wave number 577 cm−1 was marked by an νM–O stretch, where M = Ti or Cu. Typical bands characteristic of oxygen–metal bonds were observed in the 450–640 cm−1 region. The infrared spectrum of the samples calcined at 200, 400, 600 and 800 °C showed broad peaks at wave numbers 3203, 3312, 3367, 3277 and 3422 cm−1, due to O–H stretch, while reduction of the broadness was observed with increasing calcination temperatures. All four spectra from 200 to 800 °C showed peaks at 1636 cm−1 corresponding to the bending mode of H2O, 1382 cm−1 due to C–H rock, 1192 and 1120 cm−1 assigned to C–N stretch, along with an absorption peak in the lower wave number of 577 cm−1, which was marked by νM–O stretch. The phase formation of CCZTO was further confirmed by FT-IR, which is shown in Fig. 5(e) for the powder calcined at 850 °C. The absorption peaks at wave numbers 3277, 1636 and 1382 cm−1 completely vanished for the sample at 850 °C. The absorption peak at 473 cm−1 was due to the νTi–O–Ti vibrational mode.33 The Ca–O was observed at 606 cm−1.34 There were absorption bands in the region from 380–700 cm−1, arising from the mixed vibrations of the CuO4 and TiO6 groups prevailing in the CCTO structure.35 This is considered to be stiffening of the network and structural rearrangement, which lead to the perovskite phase formation. A higher calcination temperature is required to increase the crystallinity of the CCTO phase further.
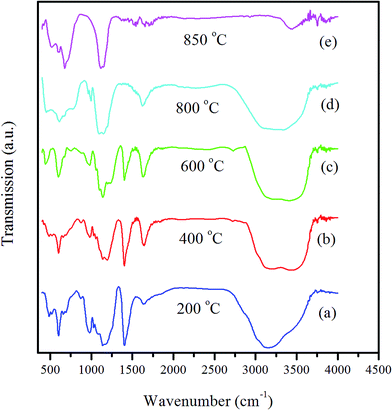 |
| | Fig. 4 FT-IR spectra of CaCu2.90Zn0.10Ti4O12 precursor powders heat treated from 200 to 850 °C for 3 h. | |
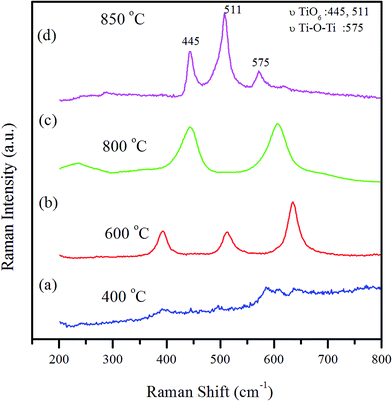 |
| | Fig. 5 Raman Spectra of CaCu2.90Zn0.10Ti4O12 precursor powders heat treated from 400 to 850 °C for 3 h. | |
In order to observe the effect of the phonon vibration on the formation of the structure of CCZTO, Raman spectra were measured. Raman scattering spectra of the CCZTO precursor powders thermally treated from 400 to 850 °C for 3 h in air are shown in Fig. 5. The sample heated at 400 °C showed a very low intensity peak at 395 and 575 cm−1. The intensities of the peak increased with an increase in the sintering duration. The samples heated at 600 and 800 °C show the Raman activation modes at 395, 511, 638 and 445, 610 cm−1, respectively. According to the literature,36 all the modes associated to titanium oxide (anatase phase) showed very intense bands at 720, 638, 515, 395, 196 and 143 cm−1. They correspond to the Raman active normal modes of representations A1g, 2B1g, and 3Eg of the space group D4h.37 The modes at 610 cm−1 of the sample heated at 800 °C can be the dislocated modes of the presence of the CaTiO3 phase. Three strong peaks observed in the wave region of 400–600 cm−1 were the characteristic bands of the CCTO phase, which could be detected in the spectra of the sample thermally treated at 850 °C for 3 h. We can point out three evident peaks, all of them associated with the CCTO phase: 445, 511, and 575 cm−1. These agree with other reported results for CCTO.38 Powders heat treated at 800 °C for 3 h presented a relevant peak at 445 cm−1, typical of the CCTO phase, but the general spectra was significantly poorer than that of the powder heat treated at 850 °C for 3 h. The Raman lines at peaks of 445 and 511 cm−1 were associated with the Ag symmetry (TiO6, rotation-like) and the peak at 575 cm−1 with Fg symmetry (O–Ti–O, antitensing). Although a high degree of structural disorder at short range was noted in the powders heat treated at low temperatures, the spectra showed Raman active modes. A wide Raman active mode of the CCZTO powders heat treated at 800 °C confirmed no structural organization at long range, but structural order at short range. Nevertheless, the Raman spectra obtained from the CCZTO powder thermally treated at 800 °C evidenced Raman active modes associated to the rutile phase of (610 cm−1). It was observed that a raise in temperature promoted the increase of structural order, as demonstrated by the appearance of well-defined Raman peaks (see powders treated at 800 and 850 °C).
XRD patterns of CaCu2.90Zn0.10Ti4O12 sintered at 950 °C with different sintering durations (8, 12, 16 and 20 h) are shown in Fig. 6. All patterns were matched well with the major CCTO peaks based in the Powder Diffraction File database (#75-2188). However, two minor peaks found in the pattern were identified as the CuO and CaTiO3 phase, appearing for all CCTO pellets regardless of the sintering time. The content of CCZTO was almost constant with an increase in the sintering duration from 8 to 20 h. Even when the sintering duration reached 20 h, the peak for CuO was still present. This indicates that the sintering duration has little effect on the purity of CCTO, between 8 and 20 h. As expected, the pure CCTO phase can only be obtained when the ratio of calcium, copper and titanium is very close to the stoichiometric one. It was also reported that the phase composition (single or multi-phased material) of the CCTO powder is mostly controlled by the Ti content.39,40 The authors believed that the secondary phases occur when the sol–gel process ion diffusing displacement is shortened. These ceramics show distinct peaks of (220), (400), (422) and (440) orientations and confirm the polycrystalline characteristics of the ceramics. The lattice parameters and unit cell volume, determined using the least square refinement method, are given in Table 1, which were in close agreement with the results reported earlier.41 From the line broadening of the main peaks, the average crystallite size of the ceramics was estimated using the Debye Scherrer formula:42
| |
D = kλ/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ
| (7) |
where
λ is the wavelength of the X-ray,
k is a constant taken as 0.89,
θ is the diffraction angle and
β is the full width at half maxima (FWHM). The average crystallite size derived from the XRD data and particle size from TEM analysis are given in
Table 1.
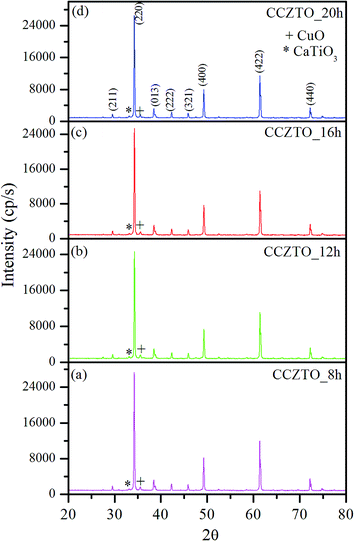 |
| | Fig. 6 X-ray powder diffraction patterns of (a) CCZTO_8h, (b) CCZTO_12h, (c) CCZTO_16h, and (d) CCZTO_20h sintered at 950 °C. | |
Table 1 Lattice parameter, unit cell volume, average crystallite size and particle size obtained from XRD and TEM for CaCu2.90Zn0.10Ti4O12 at various sintering times
| Duration of time |
Lattice parameter (Å) |
Lattice volume (Å3) |
Crystallite size from XRD (nm) |
Particle size from TEM (nm) |
| 8 h |
7.382 |
402.411 |
39.75 |
— |
| 12 h |
7.386 |
403.049 |
40.40 |
— |
| 16 h |
7.387 |
403.210 |
41.20 |
— |
| 20 h |
7.388 |
403.292 |
46.81 |
30 ± 15 |
The variations of lattice parameter with sintering time are shown in Fig. 7. It can be observed in the figure that the lattice parameter increased with an increase in the sintering time. The change in unit cell parameter with time of annealing was due to an increase in density. During the heat treatment, each crystallite gets enough dwelling time to become properly crystallized.43 It was clearly observed that the average crystallite size increased with an increase in sintering duration, confirmed by the TEM analysis. This is mainly due to overgrown grains, resulting from the destruction of the grain boundaries at higher sintering times. These data clearly show that increasing sintering time is responsible for increasing crystallite size for CaCu2.90Zn0.10Ti4O12 ceramic.
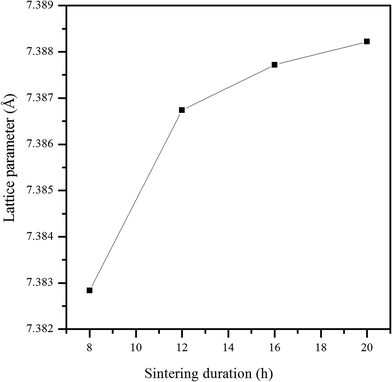 |
| | Fig. 7 Variation of lattice parameter with the change of sintering time for CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h sintered at 950 °C. | |
The TEM images of the CCZTO powders calcined at 200, 400, 600 and 850 °C for 3 h and sintered at 950 °C for 20 h are shown in Fig. 8. It can be clearly seen from the TEM bright-field images that all of the samples consisted of nano-crystalline CCZTO particles. After sintering at 950 °C for 20 h, bulk CCZTO ceramic with different microstructure was obtained. The average particle size increased as a function of the calcination temperature (T), and the average diameter was equal to 50 ± 15 nm, 10 ± 5 nm, 20 ± 5 nm, 25 ± 5 nm and 30 ± 15 nm for T = 200, 400, 600 and 850 °C for 3 h, and 950 °C for 20 h, respectively. As expected, the sample sintered at 950 °C for 20 h consisted of nanoparticles with the largest particle sizes. The average crystallite size obtained using the Debye Scherrer formula was in nearly good agreement with the particle size obtained by TEM (T = 950 °C). The morphology of the images showed that few particles appeared in spherical shape; however, some elongated particles were also present, as shown in the TEM images. Some moderately agglomerated particles, as well as separate particles were present in the images. Agglomeration is understood in terms of an increase in size with annealing temperature; hence some degree of agglomeration at higher annealing temperatures is unavoidable. The particles of the calcined samples had a high degree of agglomeration caused by mutual influence between particles which arises from forces such as van der Walls forces, capillary forces and electrostatic forces. Furthermore, the presence of water molecules and hydroxyl groups in powder calcined at high temperatures partially affects the agglomeration of particles.
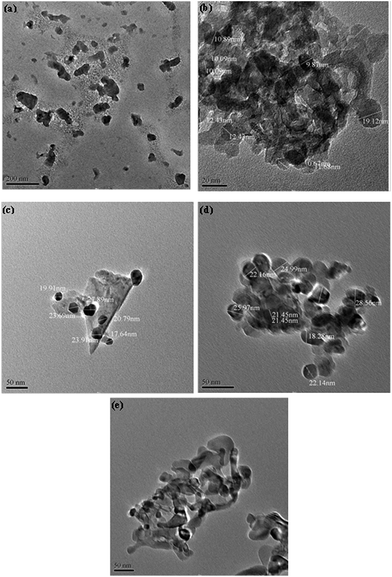 |
| | Fig. 8 HR-TEM images of the calcined CaCu2.90Zn0.10Ti4O12 powder at (a) 200, (b) 400, (c) 600, and (d) 850 °C for 3 h, and (e) sintered at 950 °C for 20 h. | |
The indexed selected area electron diffraction (SAED) pattern and the inset in Fig. 9 show the interatomic distance between two lattices of the CCZTO ceramics sintered at different temperatures. SAED pattern images of CCZTO nano-crystals calcined at different temperatures were characterized by diffraction rings with discrete spots. The sharp circular distinct ring patterns manifesting the crystallinity of the individual nanoparticles and the SAED rings, being discrete spots and not continuous, suggest not only the complex polycrystalline nature but also a preferential orientation of the synthesized CCZTO nanoparticles. The SAED pattern of the sample calcined at 200 °C was completely amorphous, while the samples calcined at 400, 600 and 850 °C showed crystallinity. Electron diffraction patterns of the particles with higher calcination temperatures contained more intense spots, as shown in the 850 °C and sintered sample 950 °C, indicating the larger particle size of highly crystalline structure, compared to the low temperature calcined samples. The indexed electron diffraction patterns also supported the cubic structure. Clear lattice fringes were observed in all the samples in the inset, indicating the defect-free nature of the sample with a high degree of crystallinity, except for the sample calcined at 200 °C. The interplanar d-spacings (hkl) measured from the selected-area electron diffraction patterns were in good agreement with the values of the XRD patterns. The lattice spacings were equal to 0.31, 0.33, 0.16 and 0.26 nm, corresponding to the (211), (211), (422) and (220) planes of the cubic phase of CCZTO nanoparticles, which is in agreement with the XRD data. The interplanar d-spacing did not depend on the calcination temperature, but depended on the orientation of the imaged crystals.
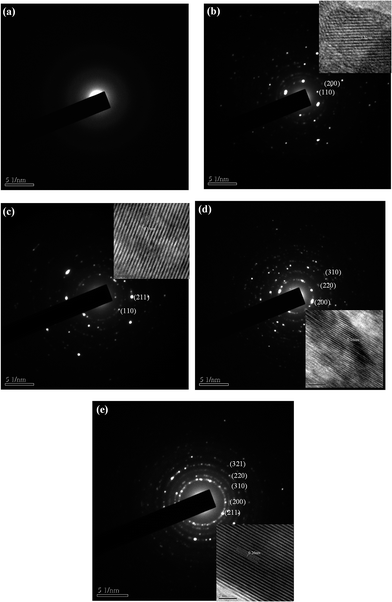 |
| | Fig. 9 Indexed SAED patterns of the calcined CaCu2.90Zn0.10Ti4O12 powder at (a) 200, (b) 400, (c) 600, and (d) 850 °C for 3 h, and (e) sintered at 950 °C for 20 h. The inset shows the interatomic distance between two lattices. | |
The SEM images of the surface microstructures of the ceramics sintered at various sintering times are shown in Fig. 10. As shown in Fig. 10, the microstructures of CaCu2.9Zn0.10Ti4O12 changed significantly with changes in sintering duration. All the SEM images of CCZTO showed a bimodal distribution of grains, with small grains of several micrometres distributed among the larger grains of several tens of micrometres. A similar structure was also observed in the CCTO ceramics sintered at low temperatures.44 The grain sizes of the specimen sintered at 950 °C with different durations were found to be in the ranges of 800 nm–2.5 μm, 2–4 μm, 3–5 μm and 4–7 μm for the ceramics sintered at 8, 12, 16 and 20 h, respectively. It can be seen that the grain size increased with an increase of sintering time, and correspondingly, the grain boundary was reduced. Increasing the sintering time significantly promoted the grain growth and microstructural densification.
 |
| | Fig. 10 SEM images of (a) CCZTO_8h, (b) CCZTO_12h, (c) CCZTO_16h, and (d) CCZTO_20h ceramics sintered at 950 °C. | |
Energy dispersive X-ray spectra (EDX) of CCZTO ceramic sintered at 950 °C for 8, 12, 16 and 20 h are shown in Fig. 11. Analyses of the result clearly showed the presence of Ca, Cu, Zn, O and Ti as per stoichiometric ratio in the CCZTO ceramics, with an extra peak of Pt at 2.15 keV. Pt coating was performed by ion beam sputtering for increasing the conductivity, which was necessary to avoid charging of samples. The EDX results confirmed the purity of the materials. Quantitative analysis, which gave the atomic percentages of the various elements, is shown in Table 2.
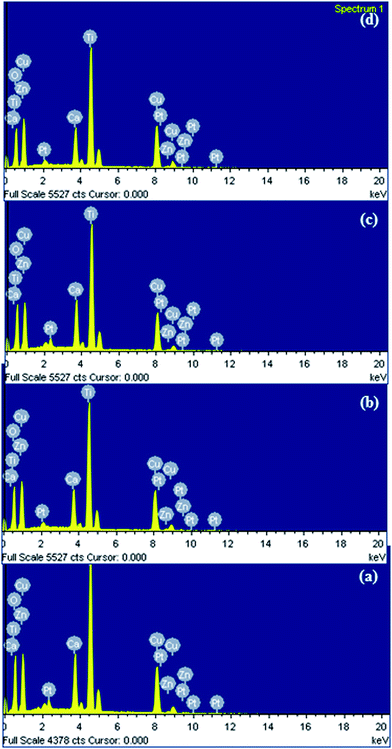 |
| | Fig. 11 Energy dispersive X-ray spectra of (a) CCZTO_8h, (b) CCZTO_12h, (c) CCZTO_16h, and (d) CCZTO_20h ceramics sintered at 950 °C. | |
Table 2 Atomic percentages of the elements for CaCu2.90Zn0.10Ti4O12 (CCZTO) sintered at 950 °C for 8, 12, 16, and 20 h
| Sintering durations |
Atomic % of elements |
| Ca |
Cu |
Zn |
Ti |
O |
| 8 h |
3.67 |
10.01 |
0.31 |
12.92 |
73.10 |
| 12 h |
3.33 |
11.14 |
0.46 |
13.41 |
71.66 |
| 16 h |
3.94 |
9.82 |
0.24 |
12.93 |
73.08 |
| 20 h |
3.43 |
12.03 |
0.52 |
13.64 |
70.38 |
XPS analysis was carried out to investigate the quantitative analysis of the elements, and the oxidation states of polyvalent ions in the ceramic CaCu2.90Zn0.10Ti4O12 sintered at 950 °C for 20 h. The core level XPS survey spectra of CCZTO, Ca 2p, Cu 2p, Ti 2p and Zn 2p regions are presented in Fig. 12(a–e). Low-energy electron charge compensation of the C 1s peak at 284.6 eV was used to eliminate the effect of a positive charge on sample surfaces during XPS analysis. From all XPS spectra, it was clear that only peaks corresponding to Ca, Cu, O, Zn and Ti were present and proved the compositional purity of the samples. From Fig. 12(b), the presence of calcium in the +2 oxidation state in the ceramic was clear, revealed not only from the binding energy (349 eV) of Ca 2p level, but also from the shape and symmetry of the peak. In the ceramic, copper and zinc were in the +2 oxidation state, while titanium was in the +4 oxidation state. The presence of copper in the +2 oxidation state was evidenced from the binding energy of the Cu 2p spectra, with peaks at 933.8 and 953.7 eV, which correspond to Cu 2p3/2 and Cu 2p1/2, respectively. The large peak at 933.8 eV represented the existence of Cu2+ in CCZTO, which should be the valence state of the Cu in CCTO.45 Fig. 12(d) shows the spectrum of the Zn 2p3/2 region, in which zinc occurred in the state Zn2+ in the spectrum, corresponding to line at 1021.8 eV.46 Fig. 12(e) displays the XPS spectrum of the Ti 2p regions, which showed two prominent peaks with positions at 458.3 and 463.8 eV, corresponding to the Ti 2p doublet, namely Ti 2p3/2 and Ti 2p1/2, respectively. Appearance of Ti 2p3/2 at 458.4 eV confirmed that Ti remained in the +4 oxidation state within our CCZTO ceramic. For our CCZTO ceramic, Zn 2p3/2 peak position was located in the energy range corresponding to the +2 oxidation state, thus we may conclude that Zn substituted Cu, which remains in the +2 oxidation state.
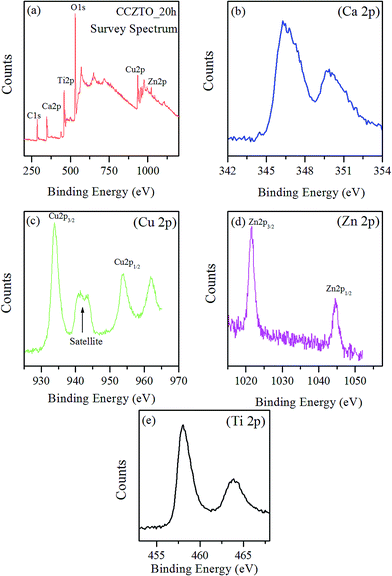 |
| | Fig. 12 X-ray photoelectron core-level spectra of (a) survey spectrum (b) Ca 2p, (c) Cu 2p, (d) Ti 2p, and (e) Zn 2p for CCZTO_20 h sintered at 950 °C. | |
The temperature dependence of the dielectric constant (εr) of the CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h ceramic at different frequencies, 0.1, 1 and 10 kHz, are shown in Fig. 13. The values of εr for the CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h ceramic at RT were found to be 306, 467, 799 and 945, respectively, at 100 Hz. It is noted that ceramics usually have a low dielectric constant, due to low sintering temperatures, or in the case of polyphased CCTO material, the presence of the second or third phase (CaTiO3 and CuO) in ceramics reported earlier.39 It is also inferred that εr increases with increasing sintering duration. This is due to the fact that the longer sintering duration produces more oxygen vacancies in the CCZTO ceramics, and resulting in a higher dielectric constant. It can be seen from all the figures that the dielectric constant (εr) exhibited a step like increase from a low value to a giant value at temperatures above 400 K, which was prominent in the low frequency region, and diminished with an increase in the frequency. At above room temperature, a broad dielectric peak appeared between 400 and 525 K, which also shifted with higher temperature and decreased in amplitude with an increase in frequency. This showed a ferroelectric relaxor behavior present in these ceramic.47
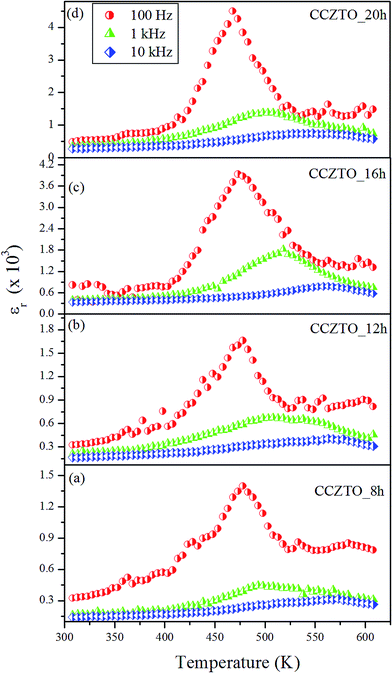 |
| | Fig. 13 Variation of dielectric constant (εr) versus temperature of the (a) CCZTO_8h, (b) CCZTO_12h, (c) CCZTO_16h, and (d) CCZTO_20h ceramics sintered at 950 °C at 0.1, 1 and 10 kHz. | |
The plots of dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) at different frequencies, 0.1, 1 and 10 kHz, as a function of the temperature for CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics are presented in Fig. 14. The values of tan
δ) at different frequencies, 0.1, 1 and 10 kHz, as a function of the temperature for CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics are presented in Fig. 14. The values of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for the ceramics CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h at RT, at 100 Hz were found to be 0.06, 0.072, 0.091 and 0.112, respectively. More importantly, it was also found that the dielectric loss increased with an increase in sintering duration. It was also observed that the loss tangent (tan
δ for the ceramics CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h at RT, at 100 Hz were found to be 0.06, 0.072, 0.091 and 0.112, respectively. More importantly, it was also found that the dielectric loss increased with an increase in sintering duration. It was also observed that the loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) was nearly constant at 10 kHz, but increased with a decrease in frequency, and also showed an anomaly at higher temperatures in CCZTO_8h. It was clearly seen that the tan
δ) was nearly constant at 10 kHz, but increased with a decrease in frequency, and also showed an anomaly at higher temperatures in CCZTO_8h. It was clearly seen that the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ increased with increase in temperature, and increased sharply beyond 425 K. This is characteristic of a relaxor behavior, which is usually characterized by diffuse phase transition and strong relaxational dispersion in the dielectric loss (tan
δ increased with increase in temperature, and increased sharply beyond 425 K. This is characteristic of a relaxor behavior, which is usually characterized by diffuse phase transition and strong relaxational dispersion in the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ), indicating thermal-activated relaxation.
δ), indicating thermal-activated relaxation.
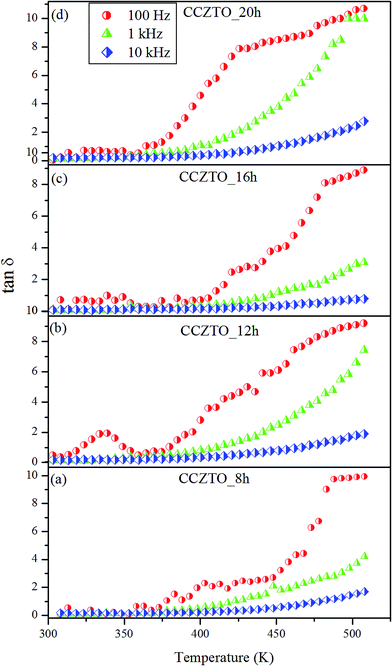 |
| | Fig. 14 Variation of dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) versus temperature of the (a) CCZTO_8h, (b) CCZTO_12h, (c) CCZTO_16h, and (d) CCZTO_20h ceramics sintered at 950 °C at 0.1, 1 and 10 kHz. δ) versus temperature of the (a) CCZTO_8h, (b) CCZTO_12h, (c) CCZTO_16h, and (d) CCZTO_20h ceramics sintered at 950 °C at 0.1, 1 and 10 kHz. | |
The plots of dielectric constant (εr) and dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for the CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h ceramics as a function of frequency at 500 K are shown in Fig. 15(a and b). Dielectric permittivity for CCZTO ceramics increased rapidly in the lower frequency ranges (1 kHz to 100 Hz), and decreased slowly in the frequency range of 103–105 Hz. As frequency increased, the dielectric constant drastically decreased. The increment of the dielectric constant as frequency decreased could possibly be due to interfacial polarization. The charge carriers may be blocked at the electrode interface under the influence of an electric field. It has been reported that CaCu3Ti4O12 ceramics consist of insulating grain boundaries and semiconducting grains. The charge carriers accumulated at the interface between semiconducting grains and insulating grain boundaries resulted in an increase in the dielectric constant. It is seen from Fig. 15(b) that the dielectric loss for all the CCZTO ceramics was higher at low frequencies, up to 104 Hz, then almost constant from the frequency range of 104–105 Hz. It is also indicated from the figure that the dielectric loss for all the ceramics showed dielectric relaxation behavior in the low frequency range. The low frequency relaxation may be due to space charge polarization, which arises when two phases of grain–grain boundaries of different electrical conductivities are in contact.48
δ) for the CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h ceramics as a function of frequency at 500 K are shown in Fig. 15(a and b). Dielectric permittivity for CCZTO ceramics increased rapidly in the lower frequency ranges (1 kHz to 100 Hz), and decreased slowly in the frequency range of 103–105 Hz. As frequency increased, the dielectric constant drastically decreased. The increment of the dielectric constant as frequency decreased could possibly be due to interfacial polarization. The charge carriers may be blocked at the electrode interface under the influence of an electric field. It has been reported that CaCu3Ti4O12 ceramics consist of insulating grain boundaries and semiconducting grains. The charge carriers accumulated at the interface between semiconducting grains and insulating grain boundaries resulted in an increase in the dielectric constant. It is seen from Fig. 15(b) that the dielectric loss for all the CCZTO ceramics was higher at low frequencies, up to 104 Hz, then almost constant from the frequency range of 104–105 Hz. It is also indicated from the figure that the dielectric loss for all the ceramics showed dielectric relaxation behavior in the low frequency range. The low frequency relaxation may be due to space charge polarization, which arises when two phases of grain–grain boundaries of different electrical conductivities are in contact.48
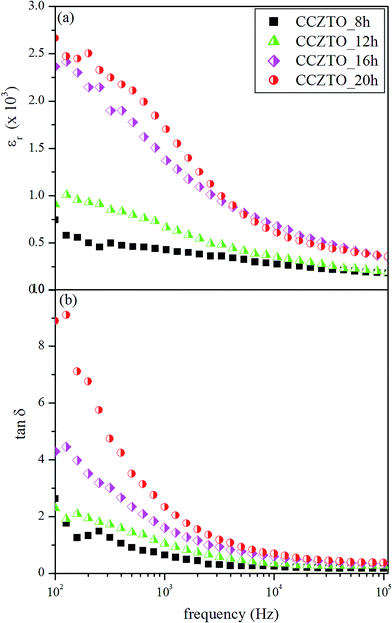 |
| | Fig. 15 Variations of (a) dielectric constant (εr) and (b) dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) versus frequency at 500 K for the CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics. δ) versus frequency at 500 K for the CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics. | |
The AC conductivity (σAC) dependence on frequency at a few selected temperatures is shown in Fig. 16 for the CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h ceramics. A similar type of conductivity behavior was observed in all the ceramics. The conductivities showed a dispersion pattern, which shifted toward higher frequency with an increase in temperature. At low frequency, the conductivities showed a flat response, corresponding to the σDC part of the conductivity. It was clear that the flat region constituting σDC conductivity increased with increasing temperature. It was concluded that the conductivity increased with an increase in the sintering temperature. This suggested that oxygen vacancies are created during the sintering process of the ceramic due to the slight loss of oxygen occurring during sintering, in accordance with the reaction:
| |
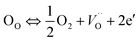 | (8) |
where all the above species are written according to the Kröger–Vink notation of defects.
38 The electrons released in the above reaction may be captured by Cu
2+, leading to the formation of Cu
+. This leads to hopping of electrons among the two different valence states, which increases the conductivity of the grains.
49 The conductivity dispersion in solids is described using Jonscher's law:
σAC =
σDC +
Aωn, where
σDC is the DC bulk conductivity,
A is the temperature-dependent constant determining the magnitude of dispersion at high temperatures, and
n is the power law exponential term representing the degree of interaction between mobile ions, which varies between 0 and 1. For
n = 0, the electrical conduction is frequency independent, while the conduction for
n > 0 is frequency dependent. The exponent
n can be calculated as a function of temperature by plotting ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAC vs.
σAC vs. ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f
f, giving a straight line with a slope equal to exponent
n. The values of
n for all the ceramics were calculated from
Fig. 16, and were found to be in the range of 0.97–0.84, 0.91–0.78, 0.87–0.69 and 0.83–0.63 in the temperature range from 408 to 488 K. It is observed that the value of
n decreases with increase in temperature. This type of behavior is only observed in the crystalline oxide materials.
50
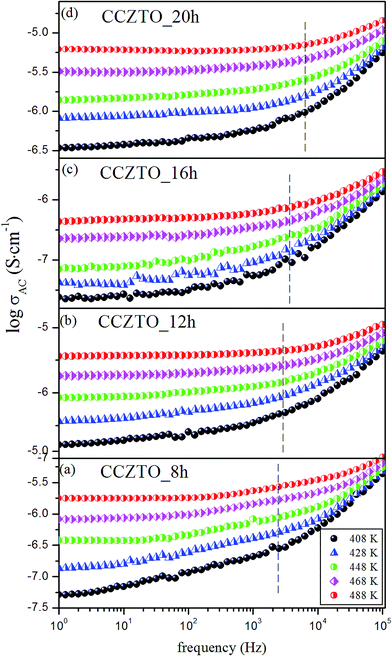 |
| | Fig. 16 Frequency dependence of AC conductivity (σAC) at a few selected temperatures for the (a) CCZTO_8h, (b) CCZTO_12h, (c) CCZTO_16h, and (d) CCZTO_20h ceramics. | |
Impedance (Z*) and modulus spectroscopy (M*) are powerful techniques used to analyze the contributions of grains, grain-boundaries and electrode specimen interface, which greatly influence the electrical properties in electro-ceramics. The complex impedance plot can produce two semi-circles, depending upon the electrical properties of the material. The first semicircle, at low frequency, represents the resistance of the grain boundary, while the second at high frequency corresponds to the resistance of grain or bulk properties.51,52 To see the clear grain boundary contribution, selected higher temperature (428 K) for impedance was analyzed. The typical complex impedance plots were obtained at 428 K temperature over a range of frequencies (100 Hz–1 MHz), as shown in Fig. 17. The non-zero intercept of the arc passing through the origin on the Z′ axis gives the resistance of the grain (Rg) in the high frequency range, which is not shown here due to the limited frequency range and temperature tested, while that of another arc in the lower frequency range gives the resistance of the grain boundary (Rgb) and electrode effect (Rel). The grain semicircular arc at high frequency has been suppressed due to the high resistance of the grain boundary, which is usually observed for internal barrier layer capacitance (IBLC), as is characteristic of the semiconducting grain with an insulating grain boundary corresponding to the grain. The impedance spectrum clearly demonstrated the presence of a semicircular arc due to the grain boundary. It was shown that the resistance of the ceramics decreased with increasing sintering duration. The impedance can be calculated from the following equations:
| |
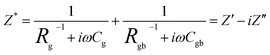 | (9) |
where
| |
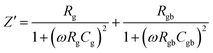 | (10) |
and
| |
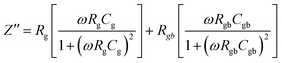 | (11) |
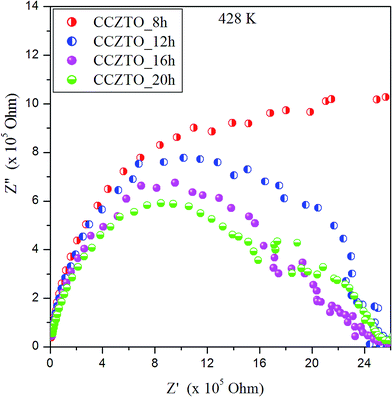 |
| | Fig. 17 Impedance plane plots of Z′′ vs. Z′ at 428 K for the CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics. | |
The calculated resistances of the grain-boundaries (Rgb) for the CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h ceramics were found to be 2.83 × 106, 2.69 × 106, 2.47 × 106 and 2.07 × 106 Ω, respectively. The resistance of the grain-boundaries decreased with increasing sintering duration, resulting in an increase in AC conductivity.
The variation of the imaginary part of the impedance Z′′ with frequency at a few selected temperatures is shown in Fig. 18 for the CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h ceramics. All the ceramics clearly demonstrated relaxation peaks at all measured temperatures. The peaks were suppressed, and slightly shifted to the high frequency region with an increase in temperature, confirming the existence of a temperature-dependent dielectric relaxation. The asymmetric broadening of the peaks suggested the presence of electrical processes in the material with a distribution of relaxation time. The relaxation behavior arose due to immobile species or electrons at low temperatures, and defects or vacancies at higher temperatures. The dispersion of curves in the low frequency region at different temperatures was very clear, and appeared to merge at higher frequencies, irrespective of the temperature. This behavior was apparently due to the presence of the space charge polarization effects at lower frequencies, which were definitely eliminated at higher frequencies.
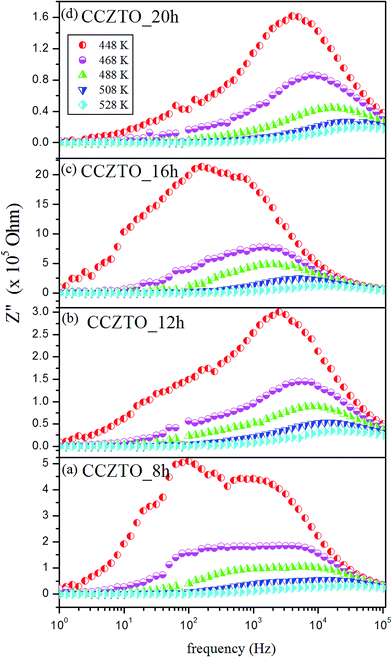 |
| | Fig. 18 Impedance plane plots Z′′ vs. frequency at selected temperatures for the (a) CCZTO_8h, (b) CCZTO_12h, (c) CCZTO_16h, and (d) CCZTO_20h ceramics. | |
The impedance data was also used to evaluate the relaxation time of the electrical phenomena in the CCZTO ceramics using the relation τ = 1/ω = 1/2πf, where f is the relaxation frequency. The nature of the variation of relaxation time (τgb) of the grain boundary with the reciprocal of temperature (1/T) is shown in Fig. 19 for the CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics. The activation energy in the relaxation process was determined by the temperature dependent relaxation time constant τgb which obeys the Arrhenius law by the following equations:
| |
τgb = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ea/kT) exp(Ea/kT)
| (12) |
where
Ea is the activation energy involved in the dielectric relaxation process,
τ0 is the pre-exponential factor,
k is Boltzmann constant, and
T is the absolute temperature. The grain boundary activation energy was evaluated from the slope of ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τgb
τgb against 1/
T curve, and was found to be 0.79 eV, 0.77 eV, 0.62 eV and 0.52 eV, respectively, for the CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics. The values of
Ea decreased with increasing duration, which was due to the semi-conducting nature coming from the grains, which increases with the thinning of the insulating grain boundary. These values also agreed with the value reported earlier for the Maxwell–Wagner relaxation arising from the interfacial polarization for CCTO ceramics, which confirmed the temperature dependence of dielectric properties.
53,54
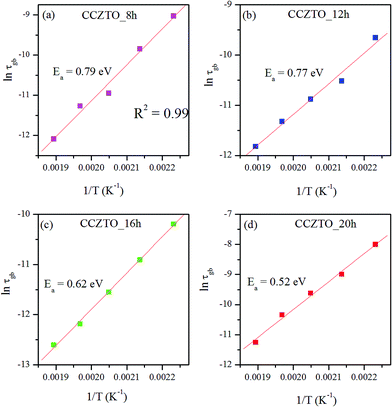 |
| | Fig. 19 Variation of relaxation time (τgb) with inverse of temperature (1/T) for (a) CCZTO_8h, (b) CCZTO_12h, (c) CCZTO_16h, and (d) CCZTO_20h ceramics. | |
In order to investigate the relaxation mechanism of the ceramic, the representative electrical modulus of CCZTO_20h has been introduced due to its special advantage of suppressing the electrode polarization effect. The electrical modulus can be calculated from the following equation:
| | |
M* = M′ + iM′′ = iωC0Z*(ω) = ε′/(ε′2+ε′′2) + i ε′′/ (ε′2+ε′′2)
| (14) |
where M′, M′′ and,
ε′,
ε′′ are the real and imaginary parts of the electric modulus and dielectric constants, respectively and
C0 represents the vacuum capacitance of the sample holder and the electrode arrangement. The real and imaginary parts of the modulus at different temperatures are calculated using
eqn (14). The variation of real (M′) and imaginary (M′′) parts of the electric modulus as a function of frequency in the temperature range 448–528 K have been depicted in
Fig. 20(a and b), respectively. M′ shows a constant value at higher frequencies while at lower frequencies it approaches to zero for all temperatures. But shows dispersion in the intermediate frequencies which increases as temperature increases. While M′′ exhibits a single broad relaxation peak centered in the dispersion region of M′ in the temperature range. The broad nature of the peak is consequence of distribution of relaxation time which shifts towards higher frequencies as temperature increases, confirms the relaxation phenomenon is thermally activated and the frequency region under the curve determines the region in which charge carriers are mobile on long distances. The region where the peak occurs indicating the transition from the long range to short range mobility with increase in frequency as the region below the peak maximum determine the range in which carriers are mobile overlong distance and above the peak they are confined to potential barriers, being mobile over short distances.
55 This type of behavior suggests the existence of a temperature dependent hoping type mechanism of charge transport. The complex electric modulus spectra (M′
vs. M′′) have been carried out in selected temperature range 448–488 K as presented in
Fig. 20(c). One semicircle in
Fig. 20(c) can be observed for all the temperatures with very smaller shift towards higher M′′ values. This behavior could be related to the decrease in modulus resistance with the increase of temperature in good agreement with the literature.
56,57
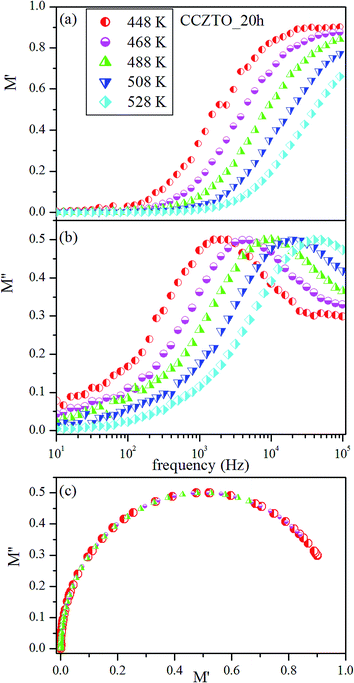 |
| | Fig. 20 (a) Variation of real part of M′ and (b) imaginary part of M′′ with frequency at different temperatures. (c) Cole–Cole plots between M′ and M′′ for CCZTO_20h ceramics at different temperatures. | |
The Cole–Cole plot in the modulus formalism justifies a poly-dispersive nature for the dielectric relaxation at low frequencies. The relaxation processes cannot be described in the whole frequency and temperature ranges using the electric modulus formalism. To confirm the relaxation time is temperature dependent or not which may obey the ideal Debye type or non-ideal Debye type behavior, for this context, scaling of modulus plots was proposed and found to be excellent technique to reveal the relaxation mechanism in the measured frequencies and temperature range. Therefore, we plotted the representative CCZTO_20h, Z′′ and M′′ data in scaled co-ordinates i.e. Z′′/Z′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax, and M′′/M′′max vs. log
f/fmax, and M′′/M′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax, respectively shown in Fig. 21(a and b), where fmax is the peak frequency. In the Fig. 21(a) the complete data of Z′′ does not collapse into one master curve rather gives a peak at the same point and hence the scaling behavior of Z′′ clearly demonstrates that in CCZTO_20h ceramic the relaxation mechanism is temperature dependent indicating M
f/fmax, respectively shown in Fig. 21(a and b), where fmax is the peak frequency. In the Fig. 21(a) the complete data of Z′′ does not collapse into one master curve rather gives a peak at the same point and hence the scaling behavior of Z′′ clearly demonstrates that in CCZTO_20h ceramic the relaxation mechanism is temperature dependent indicating M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W type relaxation. Fig. 21(b) represents the (M′′/M′′max vs. log
W type relaxation. Fig. 21(b) represents the (M′′/M′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax) normalized behavior of electric modulus. The imaginary part of modulus (M′′) is scaled by its maximum value while frequency is scaled by the peak frequency (fmax). All curves shows peak maxima at the same frequency which indicated that the same type of relaxation behavior is observed as shown in Fig. 21(a). In ideal system, the peak maximum of Z′′ and M′′ is found at the same frequency, and the shape of the peaks is identical with that predicted by Debye theory.58 To understand the Debye behavior of the CCZTO, Inset of Fig. 21(b) show the representative plot of Z′′/Z′′max vs. log
f/fmax) normalized behavior of electric modulus. The imaginary part of modulus (M′′) is scaled by its maximum value while frequency is scaled by the peak frequency (fmax). All curves shows peak maxima at the same frequency which indicated that the same type of relaxation behavior is observed as shown in Fig. 21(a). In ideal system, the peak maximum of Z′′ and M′′ is found at the same frequency, and the shape of the peaks is identical with that predicted by Debye theory.58 To understand the Debye behavior of the CCZTO, Inset of Fig. 21(b) show the representative plot of Z′′/Z′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax, and M′′/M′′max vs. log
f/fmax, and M′′/M′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax for the CCZTO_20h at 448 K. It is observed that the Z′′max and M′′max occur at the same frequency which represents a similar distribution of relaxation times of two dielectric functions (impedance and modulus) τZ = τM. However, the Z′′/Z′′max and M′′/M′′max peaks do not perfectly overlap and an evidence of M
f/fmax for the CCZTO_20h at 448 K. It is observed that the Z′′max and M′′max occur at the same frequency which represents a similar distribution of relaxation times of two dielectric functions (impedance and modulus) τZ = τM. However, the Z′′/Z′′max and M′′/M′′max peaks do not perfectly overlap and an evidence of M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W type relaxations present in these ceramics.
W type relaxations present in these ceramics.
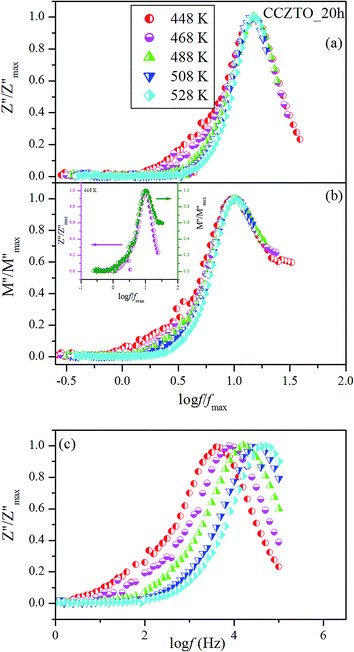 |
| | Fig. 21 (a) Normalized imaginary part of impedance (Z′′), (b) normalized imaginary part of modulus (M′′) vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax at different temperature: Inset show the representative plot of Z′′/Z′′max vs. log f/fmax at different temperature: Inset show the representative plot of Z′′/Z′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax, and M′′/M′′max vs. log f/fmax, and M′′/M′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax for the CCZTO_20h at 448 K. (c) Master curves of normalized functions of impedance Z′′/Z′′max vs. log f/fmax for the CCZTO_20h at 448 K. (c) Master curves of normalized functions of impedance Z′′/Z′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f of CCZTO_20h ceramics. f of CCZTO_20h ceramics. | |
In the above discussion, the dielectric relaxation has been analyzed in the formalisms of modulus M* where localized movement of carriers is dominant. In the case of long range movement, the resistive and conductive behaviors are analyzed by Z* and Y*(1/Z*). The plot of Z′′ versus frequency is able to distinguish whether the short range or long range movement of charge carries is dominant in a relaxation process. The separation of peak frequencies between Z′′ indicates that the relaxation process is dominated by the short range movement of charge carriers and arises from non-ideal Debye-like behavior, while the frequencies coincidence suggests that long rang movement of charge carriers is dominant. The normalized plots of max Z′′/Z′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f for CCZTO_20h is shown in Fig. 21(c). The slight mismatch in peak frequency of normalized Z′′ are associated with the movement of oxygen vacancies indicates the occurrence of localized movement of oxygen vacancies which confirmed our previous argument that the relaxation mechanism is temperature dependent follows non ideal Debye-type or M
f for CCZTO_20h is shown in Fig. 21(c). The slight mismatch in peak frequency of normalized Z′′ are associated with the movement of oxygen vacancies indicates the occurrence of localized movement of oxygen vacancies which confirmed our previous argument that the relaxation mechanism is temperature dependent follows non ideal Debye-type or M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W type relaxation behavior.
W type relaxation behavior.
4. Conclusion
We have synthesized nano-crystalline CaCu2.90Zn0.10Ti4O12 powder at a relatively low temperature with a short calcining time by using a glycine–nitrate solution-combustion process, applying inexpensive and stable solid TiO2 powder as the Titanium source instead of quite expensive alkoxide, oxynitrate, or chloride of titanium. CCZTO phase formations were confirmed by XRD. The particle sizes of the ceramic were found to be in the nano size range, 15–50 nm. The grain size varied from 800 nm to 7 μm, as measured by FE-SEM. EDX and XPS studies confirmed the stoichiometry and purity of the CCZTO ceramics. From the dielectric measurements, both dielectric constant and loss tangent increased with an increase in sintering time. CCZTO_16h gives the high dielectric constant εr (799) and low dielectric loss (0.091) at 100 Hz at room temperature. The impedance analyses of CCZTO ceramics showed a high dielectric constant, which was associated with the major contributions of the grain boundaries at higher sintering times and temperatures. Impedance analysis of this ceramic confirmed the presence of Maxwell-Wagner type relaxation, which is temperature dependent, and normalized impedance (Z′′) also confirmed the MW type relaxation. The activation energy value was found to be in the range of 0.79–0.52 eV, which is decreased with increasing sintering duration, suggesting that the electrical conduction in this ceramic is mainly due to the mobility of the ionized oxygen defects.
Acknowledgements
This work was supported by the 2010 Research Fund of University of Ulsan in Republic of Korea.
References
- M. A. Subramanian, D. Li, N. Duan, B. A. Reisner and A. W. Sleight, J. Solid State Chem., 2000, 151, 323 CrossRef CAS.
- A. P. Ramirez, M. A. Subramanian, M. Gardel, G. Blumberg, D. Li, T. Vogt and S. M. Shapiro, J. Solid State Chem., 2000, 115, 217 CrossRef CAS.
- B. Cheng, Y. H. Lin, J. Yuan, J. Cai, C. W. Nan, X. Xiao and H. Jinliang, J. Appl. Phys., 2009, 106, 034111 CrossRef PubMed.
- L. Feng, X. Tang, Y. Yan, X. Chen, Z. Jiao and G. Cao, Phys. Status Solidi A, 2006, 203, R22 CrossRef CAS.
- Q. Zheng, H. Fan and C. Long, J. Alloys Compd., 2012, 511, 90 CrossRef CAS PubMed.
- M. A. de la Rubia, P. Leret, A. del Campo, R. E. Alonso, A. R. López-Garcia, J. F. Fernández and J. de Frutos, J. Eur. Ceram. Soc., 2012, 32, 1691 CrossRef CAS PubMed.
- L. Singh, U. S. Rai, K. D. Mandal and A. K. Rai, Appl. Phys. A: Mater. Sci. Process., 2012, 112, 891 CrossRef.
- L. Singh, U. S. Rai, K. D. Mandal and M. Yashpal, J. Adv. Dielectr., 2012, 02, 1250007 CrossRef.
- S. D. Hutagalung, L. Y. Ooi and Z. A. Ahmad, J. Alloys Compd., 2009, 476, 477 CrossRef CAS PubMed.
- J. Cai, Y. H. Lin, B. Cheng, C. W. Nan, J. He, Y. Wu and X. Chen, Appl. Phys. Lett., 2007, 91, 252905 CrossRef PubMed.
- M. Li, X. L. Chen, D. F. Zhang, W. Y. Wang and W. J. Wang, Sens. Actuators, B, 2010, 147, 447 CrossRef CAS PubMed.
- L. Ni and X. M. Chen, Solid State Commun., 2009, 149, 379 CrossRef CAS PubMed.
- L. Singh, U. S. Rai, K. D. Mandal and N. B. Singh, Prog. Cryst. Growth Charact. Mater., 2014, 60, 15 CrossRef CAS PubMed.
- S. Jin, H. Xia, Y. Zhang, J. Guo and J. Xu, Mater. Lett., 2007, 61, 1404 CrossRef CAS PubMed.
- R. Aoyagi, M. Iwata and M. Maeda, Ferroelectrics, 2007, 356, 90 CrossRef CAS.
- B. Shri Prakash and K. B. R. Varma, Phys. B, 2006, 382, 312 CrossRef PubMed.
- L. Singh, U. S. Rai, A. K. Rai and K. D. Mandal, Electron. Mater. Lett., 2013, 9, 107 CrossRef CAS.
- T. B. Adams, D. C. Sinclair and A. R. West, J. Am. Ceram. Soc., 2006, 89, 3129 CrossRef CAS PubMed.
- D. C. Sinclair, T. B. Adams, F. D. Morrison and A. R. West, Appl. Phys. Lett., 2002, 80, 2153 CrossRef CAS PubMed.
- J. Liu, C. G. Duan, W. N. Mei, R. W. Smith and J. R. Hardy, J. Appl. Phys., 2005, 98, 093703 CrossRef PubMed.
- W. Li and R. Schwartz, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 012104 CrossRef.
- J. Liu, R. W. Smith and W. N. Mei, Chem. Mater., 2007, 19, 6020 CrossRef CAS.
- P. Jha, P. Arora and A. K. Ganguli, Mater. Lett., 2003, 57, 2443 CrossRef CAS.
- C. Masingboon, P. Thongbai, S. Maensiri, T. Yamwong and S. Seraphin, Mater. Chem. Phys., 2008, 109, 262 CrossRef CAS PubMed.
- H. Yu, H. Liu, D. Luo and M. Cao, J. Mater. Process. Technol., 2008, 208, 145 CrossRef CAS PubMed.
- L. Liu, H. Fan, P. Fang and X. Chen, Mater. Res. Bull., 2008, 43, 1800 CrossRef CAS PubMed.
- B. Barbier, C. Combettes, S. Guillemet-Fritsch, T. Chartier, F. Rossignol, A. Rumeau, T. Lebey and E. Dutarde, J. Eur. Ceram. Soc., 2009, 29, 731 CrossRef CAS PubMed.
- W. L. Li, Y. Zhao, Q. G. Chi, Z. G. Zhang and W. D. Fei, RSC Adv., 2012, 2, 6073 RSC.
- L. Singh, U. S. Rai, K. D. Mandal, B. C. Sin, H. Lee, H. Chung and Y. Lee, Mater. Charact., 2014, 96, 54 CrossRef CAS PubMed.
- A. K. Rai, K. N. Rao, L. Vinoth Kumar and K. D. Mandal, J. Alloys Compd., 2009, 475, 316 CrossRef CAS PubMed.
- L. A. Chick, L. R. Pederson, G. D. Maupin, J. L. Bates, L. E. Thomas and G. J. Exarhos, Mater. Lett., 1990, 10, 6 CrossRef CAS.
- P. Thomas, K. Dwarakanath, K. B. R. Varma and T. R. N. Kutty, J. Therm. Anal. Calorim., 2009, 95, 267 CrossRef CAS.
- A. F. L. Almeida, R. S. Oliveira, J. C. Goes, J. M. Sasaki, A. G. Filho, J. M. Filho and A. S. B. Sombra, Mater. Sci. Eng., B, 2002, 96, 275 CrossRef.
- X. S. Shajan and C. Mahadevan, Cryst. Res. Technol., 2005, 40, 598 CrossRef CAS.
- P. Thomas, K. Dwarakanath, K. B. R. Varma and T. R. N. Kutty, J. Phys. Chem. Solids, 2008, 69, 2594 CrossRef CAS PubMed.
- L. C. Kretly, A. F. L. Almeida, R. S. de Oliveira, J. M. Sasaki and A. S. B. Sombra, Microw. Opt. Tech. Lett., 2003, 39, 145 CrossRef.
- B. Swain, Adv. Mater. Processes, 1989, 134, 76 Search PubMed.
- A. F. L. Almeida, P. B. A. Fechine, M. P. F. Graça, M. A. Valente and A. S. B. Sombra, J. Mater. Sci.: Mater. Electron., 2008, 20, 163 CrossRef.
- S. G. Fritsch, T. Lebey, M. Boulos and B. Durand, J. Eur. Ceram. Soc., 2006, 26, 1245 CrossRef PubMed.
- R. Schmidt, S. Pandey, P. Fiorenzad and D. C. Sinclair, RSC Adv., 2013, 3, 14580 RSC.
- T. Li, Z. Chen, Y. Su, L. Su and J. Zhang, J. Mater. Sci., 2009, 44, 6149 CrossRef CAS PubMed.
- B. D. Culity and S. R. Stock, Elements of X-ray Diffraction, Prentice Hall, 3rd edn, 2001, vol. 1, p. 7 Search PubMed.
- D. Kaur and S. B. Narang, Ceram.-Silik., 2010, 54, 108 CAS.
- S. F. Shao, J. L. Zhang, P. Zheng, W. L. Zhong and C. L. Wang, J. Appl. Phys., 2006, 99, 084106 CrossRef PubMed.
- G. Deng, N. Xanthopoulos and P. Muralt, Appl. Phys. Lett., 2008, 92, 172909 CrossRef PubMed.
- X. F. Sun, S. G. Wang, X. M. Zhang, J. P. Chen, X. M. Li, B. Y. Gao and Y. Ma, J. Colloid Interface Sci., 2009, 335, 11 CrossRef CAS PubMed.
- M. Veith, S. Ren, M. Wittmar and H. Bolz, J. Solid State Chem., 2009, 182, 2930 CrossRef CAS PubMed.
- P. R. Bueno, W. C. Ribeiro, M. A. Ramírez, J. A. Varela and E. Longo, Appl. Phys. Lett., 2007, 90, 142912 CrossRef PubMed.
- F. Moura, E. C. Aguiar, E. Longo, J. A. Varela and A. Z. Simões, J. Alloys Compd., 2011, 509, 3817 CrossRef CAS PubMed.
- A. Sen, U. N. Maiti, R. Thapa and K. K. Chattopadhyay, Appl. Phys. A: Mater. Sci. Process., 2011, 104, 1105 CrossRef CAS.
- L. Ramajo, M. Reboredo and M. Castro, Composites, Part A, 2005, 36, 1267 CrossRef PubMed.
- L. Ni and X. M. Chen, Appl. Phys. Lett., 2007, 91, 122905 CrossRef PubMed.
- L. Singh, U. S. Rai, A. K. Rai and K. D. Mandal, J. Adv. Ceram., 2013, 2, 119 CrossRef CAS PubMed.
- C. Mu, H. Zhang, Y. He and P. Liu, Phys. B, 2010, 405, 386 CrossRef CAS PubMed.
- L. Singh, U. S. Rai, K. D. Mandal, B. C. Sin, S. I. Lee and Y. Lee, Ceram. Int., 2014, 40, 10073 CrossRef CAS PubMed.
- L. Singh, U. S. Rai and K. D. Mandal, J. Alloys Compd., 2013, 555, 176 CrossRef CAS PubMed.
- S. I. R. Costa, M. Li, J. R. Frade and D. C. Sinclair, RSC Adv., 2013, 3, 7030 RSC.
- R. J. Grant, M. D. Ingram and A. R. West, Electrochim. Acta, 1977, 22, 729 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) has always received great attention, due to their potential application in miniaturizing electronic devices.
δ) has always received great attention, due to their potential application in miniaturizing electronic devices.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) is highly dependent on the various cationic substitutions, such as La at Ca and Cr, and Hf at the Ti site,3–6 The cationic substitutions at the Cu site and its concentration in CCTO ceramic affect the dielectric properties, because Cu ion is one of the most effective intergranular dopants for barrier layer capacitors and can act as an acceptor ion.7 The presence of Cu+/Cu2+ ratios and their correlation with oxygen vacancies had great influence on the dielectric properties of polycrystalline CCTO via the internal barrier layer capacitance (IBLC) mechanism, because the IBLC is a widely accepted mechanism at the present stage which is responsible for the high εr. The substitution of Zn, Mn and Mg at the Cu-site enhanced the dielectric properties of CCTO without changing its crystal structure, reported earlier by solid-state routes.8–12 The dielectric properties are also modified by using synthesis routes13,14 and processing conditions such as sintering temperature,15,16 sintering time,17 cooling rate and partial pressure of sintering atmosphere.18 The electrical properties of CCTO are highly dependent on the processing routes. An appropriate method of synthesis is still required for the fabrication of nano-crystalline CCTO having the desirable features for miniaturizing the electronic devices. CCTO ceramic is generally synthesized by a solid-state reaction method at high temperatures for a long sintering time. This route suffers from the disadvantage of the presence of a secondary phase, because of limited atomic diffusion through micrometer sized molecules.19–21 On the other hand, the wet chemical routes provide atomic level mixing of individual metal ions, and result in the formation of nano-crystalline materials at much lower sintering temperatures and a shorter duration than the solid state methods. There are many wet chemical routes, such as sol–gel, co-precipitation, precursor solution technique, hydrothermal process, microwave heating, pyrolysis routes and flame synthesis,22–28 which have already been reported for the synthesis of CCTO ceramics. However, in these chemical methods, Ti is used as Ti(OR)4, which is very costly and difficult to handle by maintaining pH. Among many powder wet synthetic techniques, combustion synthesis (CS) has been of particular interest recently; it can produce various industrially useful materials with some unique properties at a low cost. Combustion synthesis involves a self-sustained reaction in a homogeneous solution of different oxidizers (e.g., metal nitrates) and fuels (e.g., citric acid, urea, glycine etc.). It has been successfully used in the synthesis of perovskite materials.29
δ) is highly dependent on the various cationic substitutions, such as La at Ca and Cr, and Hf at the Ti site,3–6 The cationic substitutions at the Cu site and its concentration in CCTO ceramic affect the dielectric properties, because Cu ion is one of the most effective intergranular dopants for barrier layer capacitors and can act as an acceptor ion.7 The presence of Cu+/Cu2+ ratios and their correlation with oxygen vacancies had great influence on the dielectric properties of polycrystalline CCTO via the internal barrier layer capacitance (IBLC) mechanism, because the IBLC is a widely accepted mechanism at the present stage which is responsible for the high εr. The substitution of Zn, Mn and Mg at the Cu-site enhanced the dielectric properties of CCTO without changing its crystal structure, reported earlier by solid-state routes.8–12 The dielectric properties are also modified by using synthesis routes13,14 and processing conditions such as sintering temperature,15,16 sintering time,17 cooling rate and partial pressure of sintering atmosphere.18 The electrical properties of CCTO are highly dependent on the processing routes. An appropriate method of synthesis is still required for the fabrication of nano-crystalline CCTO having the desirable features for miniaturizing the electronic devices. CCTO ceramic is generally synthesized by a solid-state reaction method at high temperatures for a long sintering time. This route suffers from the disadvantage of the presence of a secondary phase, because of limited atomic diffusion through micrometer sized molecules.19–21 On the other hand, the wet chemical routes provide atomic level mixing of individual metal ions, and result in the formation of nano-crystalline materials at much lower sintering temperatures and a shorter duration than the solid state methods. There are many wet chemical routes, such as sol–gel, co-precipitation, precursor solution technique, hydrothermal process, microwave heating, pyrolysis routes and flame synthesis,22–28 which have already been reported for the synthesis of CCTO ceramics. However, in these chemical methods, Ti is used as Ti(OR)4, which is very costly and difficult to handle by maintaining pH. Among many powder wet synthetic techniques, combustion synthesis (CS) has been of particular interest recently; it can produce various industrially useful materials with some unique properties at a low cost. Combustion synthesis involves a self-sustained reaction in a homogeneous solution of different oxidizers (e.g., metal nitrates) and fuels (e.g., citric acid, urea, glycine etc.). It has been successfully used in the synthesis of perovskite materials.29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 for the synthesis of CCZTO.
30 for the synthesis of CCZTO.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ







![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) at different frequencies, 0.1, 1 and 10 kHz, as a function of the temperature for CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics are presented in Fig. 14. The values of tan
δ) at different frequencies, 0.1, 1 and 10 kHz, as a function of the temperature for CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics are presented in Fig. 14. The values of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for the ceramics CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h at RT, at 100 Hz were found to be 0.06, 0.072, 0.091 and 0.112, respectively. More importantly, it was also found that the dielectric loss increased with an increase in sintering duration. It was also observed that the loss tangent (tan
δ for the ceramics CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h at RT, at 100 Hz were found to be 0.06, 0.072, 0.091 and 0.112, respectively. More importantly, it was also found that the dielectric loss increased with an increase in sintering duration. It was also observed that the loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) was nearly constant at 10 kHz, but increased with a decrease in frequency, and also showed an anomaly at higher temperatures in CCZTO_8h. It was clearly seen that the tan
δ) was nearly constant at 10 kHz, but increased with a decrease in frequency, and also showed an anomaly at higher temperatures in CCZTO_8h. It was clearly seen that the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ increased with increase in temperature, and increased sharply beyond 425 K. This is characteristic of a relaxor behavior, which is usually characterized by diffuse phase transition and strong relaxational dispersion in the dielectric loss (tan
δ increased with increase in temperature, and increased sharply beyond 425 K. This is characteristic of a relaxor behavior, which is usually characterized by diffuse phase transition and strong relaxational dispersion in the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ), indicating thermal-activated relaxation.
δ), indicating thermal-activated relaxation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) versus temperature of the (a) CCZTO_8h, (b) CCZTO_12h, (c) CCZTO_16h, and (d) CCZTO_20h ceramics sintered at 950 °C at 0.1, 1 and 10 kHz.
δ) versus temperature of the (a) CCZTO_8h, (b) CCZTO_12h, (c) CCZTO_16h, and (d) CCZTO_20h ceramics sintered at 950 °C at 0.1, 1 and 10 kHz.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for the CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h ceramics as a function of frequency at 500 K are shown in Fig. 15(a and b). Dielectric permittivity for CCZTO ceramics increased rapidly in the lower frequency ranges (1 kHz to 100 Hz), and decreased slowly in the frequency range of 103–105 Hz. As frequency increased, the dielectric constant drastically decreased. The increment of the dielectric constant as frequency decreased could possibly be due to interfacial polarization. The charge carriers may be blocked at the electrode interface under the influence of an electric field. It has been reported that CaCu3Ti4O12 ceramics consist of insulating grain boundaries and semiconducting grains. The charge carriers accumulated at the interface between semiconducting grains and insulating grain boundaries resulted in an increase in the dielectric constant. It is seen from Fig. 15(b) that the dielectric loss for all the CCZTO ceramics was higher at low frequencies, up to 104 Hz, then almost constant from the frequency range of 104–105 Hz. It is also indicated from the figure that the dielectric loss for all the ceramics showed dielectric relaxation behavior in the low frequency range. The low frequency relaxation may be due to space charge polarization, which arises when two phases of grain–grain boundaries of different electrical conductivities are in contact.48
δ) for the CCZTO_8h, CCZTO_12h, CCZTO_16h and CCZTO_20h ceramics as a function of frequency at 500 K are shown in Fig. 15(a and b). Dielectric permittivity for CCZTO ceramics increased rapidly in the lower frequency ranges (1 kHz to 100 Hz), and decreased slowly in the frequency range of 103–105 Hz. As frequency increased, the dielectric constant drastically decreased. The increment of the dielectric constant as frequency decreased could possibly be due to interfacial polarization. The charge carriers may be blocked at the electrode interface under the influence of an electric field. It has been reported that CaCu3Ti4O12 ceramics consist of insulating grain boundaries and semiconducting grains. The charge carriers accumulated at the interface between semiconducting grains and insulating grain boundaries resulted in an increase in the dielectric constant. It is seen from Fig. 15(b) that the dielectric loss for all the CCZTO ceramics was higher at low frequencies, up to 104 Hz, then almost constant from the frequency range of 104–105 Hz. It is also indicated from the figure that the dielectric loss for all the ceramics showed dielectric relaxation behavior in the low frequency range. The low frequency relaxation may be due to space charge polarization, which arises when two phases of grain–grain boundaries of different electrical conductivities are in contact.48
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) versus frequency at 500 K for the CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics.
δ) versus frequency at 500 K for the CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics.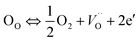
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAC vs. ln
σAC vs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f, giving a straight line with a slope equal to exponent n. The values of n for all the ceramics were calculated from Fig. 16, and were found to be in the range of 0.97–0.84, 0.91–0.78, 0.87–0.69 and 0.83–0.63 in the temperature range from 408 to 488 K. It is observed that the value of n decreases with increase in temperature. This type of behavior is only observed in the crystalline oxide materials.50
f, giving a straight line with a slope equal to exponent n. The values of n for all the ceramics were calculated from Fig. 16, and were found to be in the range of 0.97–0.84, 0.91–0.78, 0.87–0.69 and 0.83–0.63 in the temperature range from 408 to 488 K. It is observed that the value of n decreases with increase in temperature. This type of behavior is only observed in the crystalline oxide materials.50

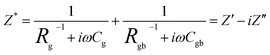
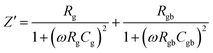
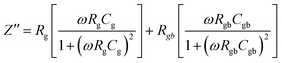


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ea/kT)
exp(Ea/kT)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τgb against 1/T curve, and was found to be 0.79 eV, 0.77 eV, 0.62 eV and 0.52 eV, respectively, for the CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics. The values of Ea decreased with increasing duration, which was due to the semi-conducting nature coming from the grains, which increases with the thinning of the insulating grain boundary. These values also agreed with the value reported earlier for the Maxwell–Wagner relaxation arising from the interfacial polarization for CCTO ceramics, which confirmed the temperature dependence of dielectric properties.53,54
τgb against 1/T curve, and was found to be 0.79 eV, 0.77 eV, 0.62 eV and 0.52 eV, respectively, for the CCZTO_8h, CCZTO_12h, CCZTO_16h, and CCZTO_20h ceramics. The values of Ea decreased with increasing duration, which was due to the semi-conducting nature coming from the grains, which increases with the thinning of the insulating grain boundary. These values also agreed with the value reported earlier for the Maxwell–Wagner relaxation arising from the interfacial polarization for CCTO ceramics, which confirmed the temperature dependence of dielectric properties.53,54

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax, and M′′/M′′max vs. log
f/fmax, and M′′/M′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax, respectively shown in Fig. 21(a and b), where fmax is the peak frequency. In the Fig. 21(a) the complete data of Z′′ does not collapse into one master curve rather gives a peak at the same point and hence the scaling behavior of Z′′ clearly demonstrates that in CCZTO_20h ceramic the relaxation mechanism is temperature dependent indicating M
f/fmax, respectively shown in Fig. 21(a and b), where fmax is the peak frequency. In the Fig. 21(a) the complete data of Z′′ does not collapse into one master curve rather gives a peak at the same point and hence the scaling behavior of Z′′ clearly demonstrates that in CCZTO_20h ceramic the relaxation mechanism is temperature dependent indicating M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W type relaxation. Fig. 21(b) represents the (M′′/M′′max vs. log
W type relaxation. Fig. 21(b) represents the (M′′/M′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax) normalized behavior of electric modulus. The imaginary part of modulus (M′′) is scaled by its maximum value while frequency is scaled by the peak frequency (fmax). All curves shows peak maxima at the same frequency which indicated that the same type of relaxation behavior is observed as shown in Fig. 21(a). In ideal system, the peak maximum of Z′′ and M′′ is found at the same frequency, and the shape of the peaks is identical with that predicted by Debye theory.58 To understand the Debye behavior of the CCZTO, Inset of Fig. 21(b) show the representative plot of Z′′/Z′′max vs. log
f/fmax) normalized behavior of electric modulus. The imaginary part of modulus (M′′) is scaled by its maximum value while frequency is scaled by the peak frequency (fmax). All curves shows peak maxima at the same frequency which indicated that the same type of relaxation behavior is observed as shown in Fig. 21(a). In ideal system, the peak maximum of Z′′ and M′′ is found at the same frequency, and the shape of the peaks is identical with that predicted by Debye theory.58 To understand the Debye behavior of the CCZTO, Inset of Fig. 21(b) show the representative plot of Z′′/Z′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax, and M′′/M′′max vs. log
f/fmax, and M′′/M′′max vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/fmax for the CCZTO_20h at 448 K. It is observed that the Z′′max and M′′max occur at the same frequency which represents a similar distribution of relaxation times of two dielectric functions (impedance and modulus) τZ = τM. However, the Z′′/Z′′max and M′′/M′′max peaks do not perfectly overlap and an evidence of M
f/fmax for the CCZTO_20h at 448 K. It is observed that the Z′′max and M′′max occur at the same frequency which represents a similar distribution of relaxation times of two dielectric functions (impedance and modulus) τZ = τM. However, the Z′′/Z′′max and M′′/M′′max peaks do not perfectly overlap and an evidence of M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W type relaxations present in these ceramics.
W type relaxations present in these ceramics.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f for CCZTO_20h is shown in Fig. 21(c). The slight mismatch in peak frequency of normalized Z′′ are associated with the movement of oxygen vacancies indicates the occurrence of localized movement of oxygen vacancies which confirmed our previous argument that the relaxation mechanism is temperature dependent follows non ideal Debye-type or M
f for CCZTO_20h is shown in Fig. 21(c). The slight mismatch in peak frequency of normalized Z′′ are associated with the movement of oxygen vacancies indicates the occurrence of localized movement of oxygen vacancies which confirmed our previous argument that the relaxation mechanism is temperature dependent follows non ideal Debye-type or M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W type relaxation behavior.
W type relaxation behavior.





