Reduction potential predictions of some aromatic nitrogen-containing molecules†
Rajeev S. Assary*ab,
Fikile R. Brushettac and
Larry A. Curtissab
aJoint Center for Energy Storage Research, Argonne National Laboratories, Argonne, IL 60439, USA. E-mail: assary@anl.gov; Fax: +1-630-252-9555; Tel: +1-630-252-3536
bMaterials Science Division, Argonne National Laboratory, Argonne, IL 60439, USA
cDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 20th October 2014
Abstract
Accurate quantum chemical methods offer a reliable alternative to time-consuming experimental evaluations for obtaining a priori electrochemical knowledge of a large number of redox active molecules. In this contribution, quantum chemical calculations are performed to investigate the redox behavior of quinoxalines, a promising family of active materials for non-aqueous flow batteries, as a function of substituent group. The reduction potentials of 40 quinoxaline derivatives with a range of electron-donating and electron-withdrawing groups are computed. Calculations indicate the addition of electron-donating groups, particularly alkyl groups, can significantly lower the reduction potential albeit with a concomitant decrease in oxidative stability. A simple descriptor is derived for computing reduction potentials of quinoxaline derivatives from the LUMO energies of the neutral molecules without time-consuming free energy calculations. The relationship was validated for a broader set of aromatic nitrogen-containing molecules including pyrazine, phenazine, bipyridine, pyridine, pyrimidine, pyridazine, and quinoline, suggesting that it is a good starting point for large high-throughput computations to screen reduction windows of novel molecules.
1. Introduction
Fundamental breakthroughs are required in electrochemical systems such as advanced metal-intercalation, metal/air, metal/sulfur, and redox flow batteries to improve electrical energy storage for transportation and stationary needs.1–7 A redox flow battery (RFB) is an electrochemical device that stores energy in flowable solutions, or suspensions, of electroactive materials, which are housed in external tanks and pumped to a power-generating electroreactor.8,9 As compared to enclosed rechargeable batteries, RFBs may offer a number of advantages in terms of cost, performance, and flexibility including decoupled power and energy, long operating lifetimes, simplified manufacturing, and improved safety.Recently, the use of redox active organic molecules for energy storage has garnered significant interest due to their high intrinsic capacities, tunable properties via molecular design, and potentially low costs.9–16 For example, Aziz et al.13 and Narayanan et al.14 have reported the use of quinone derivatives in acidic aqueous RFBs. Under non-aqueous conditions, molecules such as anthraquinone,13,17,18 quinoxaline,11 and thiophene19,20 have been investigated for energy storage applications. Moreover, a number of high-potential redox shuttles have been developed for overcharge protection in lithium-ion batteries.21 Recently, Brushett et al. demonstrated an all-organic non-aqueous redox flow (NRF) battery based on quinoxaline derivatives and 2,5-di-tert-butyl-1,4-bis(2-methoxyethoxy)benzene (DBBB, also referred to as ANL RS2).11
There are a large number of redox active organic molecules (e.g., aromatics containing N, S, and O atoms) that may be considered for use in NRF batteries. Consequently, the identification of optimal redox couples via experimentation is a daunting task and rapid screening of redox properties via reliable computational methods represents a powerful means of down selecting candidates with minimal investment. Indeed, employing accurate quantum chemical methods may enable screening of thousands of molecules for desired electrochemical window, solubility, and stability. Quantum chemical studies to understand the electrochemical windows of select chemical families such as hydrocarbons,22 quinones23–28 and isoindoles29,30 are available in the literature. These studies provide a basic understanding of the electrochemical windows that can be used as a first level of screening to narrow down a large molecular set. Similar ‘genome’-scale approaches were found to be efficient for materials discovery in battery31,32 and photovoltaic applications.33
Herein, we use computations based on density functional theory (DFT) to investigate reduction potentials of quinoxaline and a number of its derivatives (40 molecules) as negative electrolyte materials for NRF batteries (Scheme S1†).11 First, we modeled the impact of electron-donating and electron-withdrawing substituent groups on the reduction potentials of quinoxaline molecules. Second, we used the data generated to derive an empirical relationship that connects reduction potentials with energies of lowest unoccupied molecular orbitals (LUMOs). Third, we extended this relationship to other aromatic nitrogen-containing molecules (40 molecules) including pyrazine, phenazine, and bipyridine derivatives. These simple descriptors may be used in high-throughput computational screening of thousands of organic molecules to down select candidates with promising reduction properties for RFB application.
2. Methods
2.1 Computational details
All calculations presented in the paper are performed using the Gaussian 09 software.34 The B3LYP/6-31+G(d) level of theory is used to compute the structure and energetics of all species in the gas phase. The same level of theory was used to calculate zero point energies, free energy corrections (298 K, 1 atm pressure) and solvation energies. The SMD35 model was used to compute the solvation free energy by a single point energy calculation on the gas-phase optimized geometry using water as the dielectric medium.35 We find that this is an effective approximation for computing free energies of redox active species in solution, and this level of theory is reasonably accurate for the computation of reduction potentials (see Table S1A of the ESI† for the benchmarking of the accuracy of density functional methods). We have optimized selected systems using the SMD solvent (water dielectric medium) model to include the solvation effects in determining the geometry and energy. For this study, changing the dielectric medium to acetone, dimethyl sulfoxide, or methanol did not significantly impact the computed redox potentials of quinoxaline derivatives (see Table S1B of the ESI†). The Gibbs free energy of molecule ‘M’ in the solution is computed as the sum of the free energy in the gas phase (Ggas) and the solvation free energy (ΔGsolv).Using the thermodynamic cycle shown Scheme 1, solution-phase free energy change for reduction or oxidation process (ΔGredox) can be computed as:
| ΔGredox = ΔGgas + ΔΔGsolv | (1) |
| ΔΔG = ΔGsolv(M−) − ΔGsolv(M) | (2) |
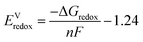 | (3) |
Additionally it should be noted that the binding of a second electron to the mono-anion in the gas phase is thermodynamically uphill (negative electron affinity), while inclusion of solvation contributions favors the binding of the second electron. The negative electron affinities result in less accurate reduction potential, but in cases where experimental values are available agreement is reasonable. It has been found that finite basis sets can give reasonable results in comparison to gas-phase experimental results for gas-phase temporary anions with negative electron affinities due to a cancellation of errors.49 In general, quantum chemical calculations can be used to compute the redox potentials of a material of interest with reasonable accuracy.28,48,50,51
3. Results and discussion
3.1 The impact of substituent groups on calculated redox potentials and specific energy
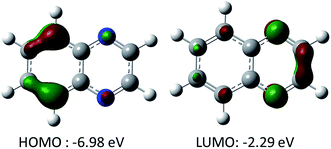
As quinoxalines are predominantly under investigation for negative active species, our focus will be to determine how to most effectively lower the reduction potential without significantly increasing the molecular weight (thus lowering the charge storage capacity). Fig. 1 shows the computed highest occupied molecular orbital (HOMO) and LUMO for unsubstituted quinoxaline. The HOMO is located in the benzene ring, while the LUMO is located in the pyrazine ring of the quinoxaline. Note that the computed oxidation potential of unsubstituted quinoxaline is 5.26 V due to the stability of HOMO orbital, consistent with the oxidative stability of benzene. From the computed LUMO of quinoxaline, it is clear that the nitrogen-containing ring is responsible for the electron affinity of quinoxaline and, therefore, the reduction potential of quinoxaline and its derivatives can be most effectively altered by substitution on this ring.To explore the effect of substitutions on reduction potential, oxidation potential, and specific energy (normalized to a common reference), 40 quinoxaline derivatives are investigated (Fig. 2).
The set of entries can be partitioned into the following substituent groups: alkyl groups (electron donating, entries 2–25), alkoxy groups (electron donating, entries 25–29), amino and hydroxyl groups (electron donating, entries 30–34), and phenyl, chloro, acetyl, and ester groups (electron withdrawing, entries 35–40). Based on the HOMO and LUMO characteristics of unsubstituted quinoxaline (Fig. 1), the introduction of electron-donating groups in the nitrogen ring increases the electron density and, hence, decreases the electron affinity and reduction potential. Where possible, the computed reduction potentials of quinoxaline derivatives are compared to experimentally obtained values to determine model accuracy and validate trends. It is important to note that, in this study, explicit effects of salts, impurities, concentration, and electrode materials are not considered, which may be significant for comparison with experiments.
Ames et al. reported the quinoxaline reduction at −1.8 V vs. SCE (ca. 1.5 V vs. Li/Li+) in 0.1 M TEAP in dimethylformamide.52 Similarly, Barqawi and Atfah reported −1.62 V vs. SCE (ca. 1.7 V vs. Li/Li+) in 0.1 M TBAPF6 in acetonitrile.53 The computed reduction potential of quinoxaline is 1.55 V vs. Li/Li+ (Table 1, entry 1) which is reasonably consistent with the experiments indicating the reliability of the computational methods used here. The computed potentials of alkyl-substituted quinoxalines (entries 2 to 25) clearly show a lowering in the reduction potentials. The most effective positions for methyl/alkyl substitutions are positions 2 and 3 of the quinoxaline. Among alkyl-substituted quinoxalines, entries 3, 11, 12, 13, 14 and 15 appear the most promising candidates in terms of the electrochemical window, with minimal substitutions (important for maximizing molecular capacity) compared to entries 16, 17, 21, 22, 23, 24. From quinoxaline (entry 1) to 2,3,5,6,7,8-hexamethylquinoxaline (entry 25), a decrease of reduction potential by 0.41 V for the first reduction event is computed, which is the maximum decrease computed for alkyl substitutions among our data set. The computed potential in the second electron transfer process of that same species 25 is 0.51 V less than that of quinoxaline. However, concomitant with the decrease in reduction potential is a decrease in the oxidative stability of almost 1 V as compared to quinoxaline (5.26 V). This may be acceptable as the negative electrolyte would not be expected to reach those potentials. The introduction of alkoxy groups (entries 27 to 29) in either position 2 or 3 of quinoxaline shows less impact on redox potentials as compared to alkyl groups. Further, the introduction of other electron-donating groups such as amino (entries 30 and 32) or dimethylamino groups (entries 31 and 33) also results in a decrease of the redox potential, albeit less effective than the addition of alkyl groups.
| Entries (as shown in Fig. 2) | Electron affinity | Potential vs. Li/Li+ (V) | ||||
|---|---|---|---|---|---|---|
| (−ve of LUMO) | ERed1 computed from eqn (3) | Predicted reduction potential = (0.69 × EA)a | Error functiona | |||
| EA (eV) | ERed1 | ERed2 | EOx1 | *ERed1 | δE = (*ERed1 − ERed1) | |
| a Details of predicted first reduction potentials and error function are shown in Section 3.2. | ||||||
| 1 | 2.29 | 1.55 (1.52 (ref. 52)) | 1.00 | 5.26 | 1.58 | 0.03 |
| 2 | 2.10 | 1.44 | 0.89 | 5.14 | 1.45 | 0.01 |
| 3 | 1.94 | 1.34 (1.45 (ref. 52)) | 0.83 | 5.06 | 1.34 | 0.00 |
| 4 | 2.21 | 1.49 | 0.91 | 4.90 | 1.53 | 0.04 |
| 5 | 2.21 | 1.53 | 0.89 | 4.97 | 1.53 | 0.00 |
| 6 | 2.10 | 1.44 | 0.85 | 4.74 | 1.45 | 0.01 |
| 7 | 2.15 | 1.44 | 0.93 | 4.63 | 1.48 | 0.04 |
| 8 | 2.12 | 1.43 | 0.84 | 4.71 | 1.46 | 0.03 |
| 9 | 2.08 | 1.45 | 0.81 | 4.89 | 1.44 | −0.01 |
| 10 | 2.14 | 1.48 | 0.88 | 4.70 | 1.48 | 0.00 |
| 11 | 2.08 | 1.36 | 0.85 | 5.06 | 1.44 | 0.08 |
| 12 | 1.84 | 1.3 | 0.77 | 4.86 | 1.27 | −0.03 |
| 13 | 1.89 | 1.29 | 0.73 | 4.76 | 1.30 | 0.01 |
| 14 | 1.98 | 1.33 | 0.76 | 4.91 | 1.37 | 0.04 |
| 15 | 2.05 | 1.31 | 0.85 | 5.03 | 1.42 | 0.11 |
| 16 | 1.92 | 1.25 | 0.69 | 4.66 | 1.32 | 0.07 |
| 17 | 1.82 | 1.18 | 0.63 | 4.57 | 1.25 | 0.07 |
| 18 | 1.95 | 1.36 | 0.74 | 5.01 | 1.35 | −0.01 |
| 19 | 1.90 | 1.24 | 0.67 | 4.91 | 1.31 | 0.07 |
| 20 | 1.89 | 1.31 | 0.75 | 4.83 | 1.31 | 0.00 |
| 21 | 1.79 | 1.25 | 0.69 | 4.77 | 1.24 | −0.01 |
| 22 | 1.83 | 1.21 | 0.66 | 4.79 | 1.26 | 0.05 |
| 23 | 1.86 | 1.2 | 0.66 | 4.69 | 1.28 | 0.08 |
| 24 | 1.87 | 1.19 | 0.63 | 4.69 | 1.29 | 0.10 |
| 25 | 1.64 | 1.14 | 0.49 | 4.27 | 1.13 | −0.01 |
| 26 | 2.00 | 1.36 | 0.86 | 5.06 | 1.38 | 0.02 |
| 27 | 1.83 | 1.46 | 0.87 | 4.73 | 1.27 | −0.19 |
| 28 | 2.10 | 1.43 | 0.89 | 5.15 | 1.45 | 0.02 |
| 29 | 1.98 | 1.65 | 0.93 | 5.16 | 1.36 | −0.29 |
| 30 | 1.91 | 1.28 | 0.75 | 4.40 | 1.32 | 0.04 |
| 31 | 1.79 | 1.24 | 0.75 | 4.06 | 1.23 | −0.01 |
| 32 | 1.58 | 1.03 | 0.59 | 4.06 | 1.09 | 0.06 |
| 33 | 1.52 | 1.18 | 0.63 | 4.57 | 1.05 | −0.13 |
| 34 | 1.96 | 1.31 | 0.77 | 4.96 | 1.35 | 0.04 |
| 35 | 2.23 | 1.55 (1.77 (ref. 52)) | 1.09 | 4.73 | 1.54 | −0.01 |
| 36 | 2.70 | 1.78 | 1.35 | 5.58 | 1.86 | 0.08 |
| 37 | 2.82 | 2.08 | 1.62 | 5.48 | 1.95 | −0.13 |
| 38 | 2.68 | 2.01 | 1.53 | 5.46 | 1.85 | −0.16 |
| 39 | 2.65 | 2.15 | 1.67 | 5.61 | 1.83 | −0.32 |
| 40 | 2.82 | 2.07 | 1.60 | 5.29 | 1.95 | −0.12 |
Electron-withdrawing groups increase the electron affinity and hence increase the redox potential (entries 36 to 40). For instance, the computed reduction potential of 2,3-dicholoroquinoxaline (entry 36) is 0.23 V higher than that of unsubstituted quinoxaline. Similarly, functional groups such as carboxyl (entry 37), ester (entries 38 and 39), and acetoxy (entry 40) increase the reduction potential by ∼0.5 V for both the first and second electron reduction process. Note that chloro-substituted quinoxaline (entry 36) is not stable upon the second reduction, where detachment of C–Cl bond occurs. The C–Cl bond length increases from 1.75 Å (neutral) to 1.79 Å (singly reduced) and subsequently to 1.96 Å (doubly reduced) suggesting that decomposition is likely during the reduction process. For substituents that contain C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group (acetyl group), major structural changes occur in the C
O group (acetyl group), major structural changes occur in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group rather than the quinoxaline ring resulting in different redox characteristics from the quinoxaline or its methylated counterparts.
O group rather than the quinoxaline ring resulting in different redox characteristics from the quinoxaline or its methylated counterparts.
Using 4 V vs. Li/Li+ as a common reference point (redox potential of DBBB-based positive electrolyte), a high-level specific energy calculation was performed for each of the 40 quinoxaline derivatives and then normalized to unsubstituted quinoxaline (Q, entry 1 in Table 2). For this particular data set, none of the voltage changes offset the increase in molecular weight, meaning that the specific energy of all the substituted quinoxaline derivatives was lower than that of the unsubstituted quinoxaline. However, it is important to note that these candidates represent only a small subset of the possible quinoxaline derivatives and that the addition of substituent groups can impart other favorable properties (e.g., solubility, diffusivity, viscosity) beyond modifying reduction potential.
| Entries | Specific energy evaluation | |||||
|---|---|---|---|---|---|---|
| Molecular weight | Number of electrons | Mol. cap. = MC (A h kg−1) | Average redox voltage (V) | Specific energy (SE) (vs. DBBB) (W h kg−1) | Normalized specific energy vs. quinoxaline (Q) | |
| MW (g mol−1) | n | MC = nF/(3.6 × MW) | V = (ERed1 + ERed2)/n | SE = MC(4 − V) | SE[i]/SE[Q] | |
| 1 (Q) | 130.15 | 2 | 411.86 | 1.28 | 1122.31 | 1.00 |
| 2 | 144.17 | 2 | 371.80 | 1.17 | 1054.06 | 0.94 |
| 3 | 158.2 | 2 | 338.83 | 1.09 | 987.69 | 0.88 |
| 4 | 144.17 | 2 | 371.80 | 1.20 | 1041.05 | 0.93 |
| 5 | 144.17 | 2 | 371.80 | 1.21 | 1037.33 | 0.92 |
| 6 | 158.2 | 2 | 338.83 | 1.15 | 967.36 | 0.86 |
| 7 | 158.2 | 2 | 338.83 | 1.19 | 953.81 | 0.85 |
| 8 | 158.2 | 2 | 338.83 | 1.14 | 970.75 | 0.86 |
| 9 | 158.2 | 2 | 338.83 | 1.13 | 972.44 | 0.87 |
| 10 | 158.2 | 2 | 338.83 | 1.18 | 955.50 | 0.85 |
| 11 | 172.33 | 2 | 311.05 | 1.12 | 895.82 | 0.80 |
| 12 | 172.33 | 2 | 311.05 | 1.04 | 922.26 | 0.82 |
| 13 | 172.33 | 2 | 311.05 | 1.01 | 930.03 | 0.83 |
| 14 | 214.31 | 2 | 250.12 | 1.05 | 739.10 | 0.66 |
| 15 | 186.25 | 2 | 287.80 | 1.04 | 851.89 | 0.76 |
| 16 | 242.36 | 2 | 221.17 | 0.97 | 670.15 | 0.60 |
| 17 | 256.39 | 2 | 209.07 | 0.91 | 647.07 | 0.58 |
| 18 | 184.24 | 2 | 290.94 | 1.05 | 858.28 | 0.76 |
| 19 | 212.29 | 2 | 252.50 | 0.94 | 772.65 | 0.69 |
| 20 | 214.31 | 2 | 250.12 | 1.03 | 742.85 | 0.66 |
| 21 | 228.33 | 2 | 234.76 | 0.97 | 711.33 | 0.63 |
| 22 | 242.26 | 2 | 221.26 | 0.94 | 678.17 | 0.60 |
| 23 | 256.39 | 2 | 209.07 | 0.93 | 641.84 | 0.57 |
| 24 | 270.41 | 2 | 198.23 | 0.91 | 612.53 | 0.55 |
| 25 | 214.31 | 2 | 250.12 | 0.82 | 796.63 | 0.71 |
| 26 | 160.17 | 2 | 334.66 | 1.11 | 967.18 | 0.86 |
| 27 | 190.2 | 2 | 281.82 | 1.17 | 798.97 | 0.71 |
| 28 | 145.14 | 2 | 369.32 | 1.16 | 1048.87 | 0.93 |
| 29 | 160.13 | 2 | 334.75 | 1.29 | 907.16 | 0.81 |
| 30 | 145.16 | 2 | 369.27 | 1.02 | 1102.27 | 0.98 |
| 31 | 173.21 | 2 | 309.47 | 1.00 | 929.95 | 0.83 |
| 32 | 160.18 | 2 | 334.64 | 0.81 | 1067.51 | 0.95 |
| 33 | 216.28 | 2 | 247.84 | 0.91 | 767.07 | 0.68 |
| 34 | 162.15 | 2 | 330.58 | 1.04 | 978.51 | 0.87 |
| 35 | 282.34 | 2 | 189.85 | 1.32 | 508.80 | 0.45 |
| 36 | 199.34 | 2 | 268.90 | 1.57 | 654.78 | 0.58 |
| 37 | 174.16 | 2 | 307.78 | 1.85 | 661.73 | 0.59 |
| 38 | 188.18 | 2 | 284.85 | 1.77 | 635.21 | 0.57 |
| 39 | 246.22 | 2 | 217.70 | 1.91 | 455.00 | 0.41 |
| 40 | 172.18 | 2 | 311.32 | 1.84 | 674.01 | 0.60 |
3.2 A descriptor for reduction potential evaluation for quinoxaline derivatives
Data presented in Table 1 represent a small fraction of the possible quinoxaline derivatives that may be utilized as charge storage species. However, though faster than manual synthesis and experimentation, mapping thousands of redox candidates via free energy calculations is time-consuming and limits throughput. Developing simple high-level descriptors to predict redox windows can significantly accelerate the innovation process. Indeed, similar approaches have been successfully employed for the high-throughput calculation of battery and photovoltaic materials.13,32,33 Thus linking the reduction potential evaluation presented in the previous section to a larger set of quinoxaline derivatives requires simple descriptors to predict reduction potential. Using the first reduction potential data of quinoxaline derivatives (entries 1 to 40 shown in Table 1), it is possible to derive a simple descriptor that enables the prediction of first reduction potentials of novel quinoxaline derivatives. According to the Nernst relation (eqn (3)), the computed reduction potential (Ered1n) of a quinoxaline derivative n (denoted entry n) is directly proportional to the free energy change associated with the reduction process (ΔGred1n), which, in turn, is proportional to the electron affinity (EA) of the molecule. The electron affinity (EA) of the molecule is directly proportional to the LUMO energy (εLUMO) of the molecule (eqn (4)):| ΔGred1n = k1EA | (4) |
| EA = k2εLUMO | (5) |
Using eqn (3) and (4), the reduction potential (Ered1n) can be written using the following equations:
| Ered1n = −k1k2 × εLUMO | (6) |
| Ered1n = −Kn × εLUMO | (7) |
As part of the data set developed for the 40 quinoxaline derivatives shown in Table 1, we have computed the Kn (for n = 1 to 40) values using the computed reduction potentials and energy of the LUMO. The computed average value of Kn is 0.69. Therefore, upon computing the LUMO energy of the neutral molecule, the prediction of the first reduction potential of a novel quinoxaline derivative can be made using the following relationship:
| Ered1novel = −0.69 × εLUMO | (8) |
To show this comparison more effectively, we have computed the error function (δE), a difference between the predicted reduction potentials (*ERed1) using eqn (8) and the computed reduction potentials (ERed1) from eqn (3) (Nernst equation), and the values are shown in Table 1. The predicted reduction potentials are consistent with that of the computed reduction potentials as shown in Table 1 and Fig. S1† and the average deviation between computed vs. predicted reduction potentials is 0.07 V. The greatest advantage of predicted potential over the computed one is the simplicity of the former, where only a single point energy evaluation of the neutral species is essential, while the latter requires more computationally intensive free energy evaluations of the neutral species and anions in solution. We note that by using scaled LUMO energies it is possible to predict the electron affinity of organic molecules with reasonable accuracy,54 unless the LUMO of the molecule is poorly defined by the level of theory.55 Additionally, the redox window is one of the desired properties required for screening. Other descriptors for solubility and stability are required for screening and to narrow down the candidates. This will be a subject for further investigation.
3.3 Validation of reduction potential descriptors for other nitrogen-containing species
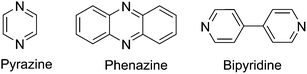
In the previous section, we have successfully developed and tested a descriptive relationship for evaluating reduction potentials of quinoxaline derivatives using the computed LUMO energy of neutral species. To assess the broad applicability of this descriptive relationship for predicting reduction potential of other nitrogen containing molecules, we have chosen selected base molecules such as pyrazine, phenazine, and bipyridine. The structures of base molecules are shown in Fig. 3 and schematics of all the derivatives of the base molecules are shown in Fig. S2a–c.† The computed LUMO energies (eV), predicted first reduction potentials (*ERed1) using eqn (8), and computed reduction potentials (ERed1) using eqn (3) for these 40 molecules are presented in Table 3. The computed first reduction potentials of pyrazine, phenazine, and bipyridine are in good agreement (±0.1 V) with experimental studies56–58 (Table 3), indicating the accuracy of the computation methods. From Table 3, it is shown that the predicted reduction potentials are in good agreement with the computed reduction potentials (from thermodynamic cycle).| Entriesa | Molecular species | LUMO (eV) | Reduction potentials (V vs. Li/Li+) | |
|---|---|---|---|---|
| Predicted | Computed | |||
| *ERed1 | ERed1 | |||
| a Schematics of all the structures are given in Fig. S2. | ||||
| 41 | Pyrazine (P) | −1.83 | 1.07 | 1.10 (1.12 (ref. 56)) |
| 42 | 2-Methyl P | −1.62 | 0.95 | 0.97 |
| 43 | 2,3-Dimethyl P | −1.44 | 0.84 | 0.82 |
| 44 | 2,5-Dimethyl P | −1.45 | 0.85 | 1.01 |
| 45 | 2,6-Dimetyl P | −1.50 | 0.88 | 0.96 |
| 46 | 2,3,5-Trimethyl P | −1.27 | 0.74 | 0.84 |
| 47 | 2,3,5,6-Tetramethyl P | −1.12 | 0.65 | 0.69 |
| 48 | 2-Methoxy P | −1.58 | 0.92 | 1.02 |
| 49 | 2,3-Dimethoxy P | −1.13 | 0.66 | 0.69 |
| 50 | 2,5-Dimethoxy P | −1.53 | 0.89 | 1.02 |
| 51 | 2,6-Dimethoxy P | −1.24 | 0.72 | 0.75 |
| 52 | 2,3,5,6-Tetramethoxy P | −0.81 | 0.47 | 0.66 |
| 53 | Phenazine (Ph) | −2.75 | 1.90 | 2.01 (2.04 (ref. 57)) |
| 54 | 1-Methyl Ph | −2.69 | 1.85 | 1.96 |
| 55 | 2-Methyl Ph | −2.85 | 1.97 | 1.98 |
| 56 | 1,2-Dimethyl Ph | −2.62 | 1.81 | 1.95 |
| 57 | 1,3-Dimethyl Ph | −2.58 | 1.78 | 1.88 |
| 58 | 1,4-Dimethyl Ph | −2.62 | 1.81 | 1.91 |
| 59 | 1,2,3-Trimethyl Ph | −2.53 | 1.74 | 1.86 |
| 60 | 1,2,3,4-Tetramethyl Ph | −2.45 | 1.69 | 1.99 |
| 61 | 2,3-Dimethyl Ph | −2.57 | 1.77 | 1.91 |
| 62 | 1-Chloro Ph | −2.95 | 2.04 | 2.13 |
| 63 | 2-Chloro Ph | −2.95 | 2.04 | 2.11 |
| 64 | 1,2,8,9-Tetramethyl Ph | −2.49 | 1.72 | 1.84 |
| 65 | 1,4,6,9-Tetramethyl Ph | −2.43 | 1.67 | 1.74 |
| 66 | 1,2,7,8-Tetramethyl Ph | −2.46 | 1.70 | 1.81 |
| 67 | 1,2,6,7-Tetramethyl Ph | −2.45 | 1.69 | 1.78 |
| 68 | 2,3,7,8-Tetramethyl Ph | −2.40 | 1.65 | 1.8 |
| 69 | 1,2,3,4,6,7,8,9-Octamethyl Ph | −2.18 | 1.51 | 1.57 |
| 60 | 1-tert-Butyl Ph | −2.68 | 1.85 | 1.9 |
| 71 | 2-tert-Butyl Ph | −2.67 | 1.84 | 1.96 |
| 72 | Bipyridine (B) | −2.02 | 1.18 | 1.31 (1.19 (ref. 58)) |
| 73 | 2-Methyl B | −1.94 | 1.13 | 1.27 |
| 74 | 2,3-Dimethyl B | −1.62 | 0.94 | 1.00 |
| 75 | 2,5-Dimethyl B | −1.70 | 0.99 | 1.05 |
| 76 | 2,6-Dimethyl B | −1.87 | 1.09 | 1.21 |
| 77 | 2,3,5,6-Tetramethyl B | −1.17 | 0.69 | 0.70 |
| 78 | 2,2′-Dimethyl B | −1.86 | 1.09 | 1.21 |
| 79 | 2,2′,6,6′-Tetramethyl B | −1.72 | 1.00 | 1.15 |
| 80 | 2,2′,3,3′,5,5′,6,6′-Octamethyl B | −0.63 | 0.37 | 0.32 |
To show this comparison more effectively, the predicted reduction potentials versus the computed reduction potentials for all derivatives from Table 3 are shown in Fig. 4. The linearity of the data points with a regression coefficient of ca. 0.98 indicates that the relationship is promising and can be useful for a fast first-tier screening procedure for quinoxaline, pyrazine, phenazine, and bipyridine families. To further show the application of this descriptive relationship (eqn (8)), in Fig. 5 we show the computed vs. predicted reduction potentials of 9 different aromatic nitrogen families. These are quinoxaline, pyrazine, phenazine, bipyridine pyridine, pyrimidine, pyridazine, quinoline and isoquinoline. The predicted reduction potentials using eqn (8) are in good agreement with the computed reduction potentials for all molecules, indicating that the relationship can be used for the fast first-tier screening procedure for aromatic nitrogen-containing molecules provided the LUMO energy can be computed at the B3LYP/6-31+G(d) level of theory.
 | ||
| Fig. 4 Computed reduction potentials using eqn (3) vs. the predicted reduction potentials using eqn (8) for pyrazine, phenazine, and bipyridine derivatives (from Table 3). | ||
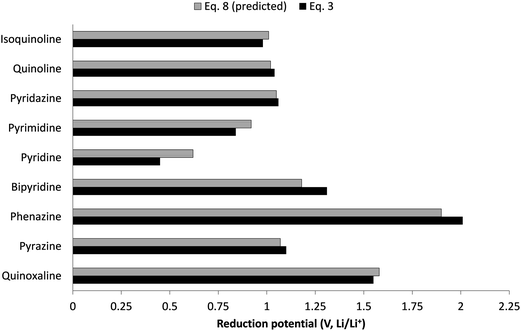 | ||
| Fig. 5 Comparison of computed reduction potentials (using eqn (3)) vs. the predicted reduction potentials (using eqn (8)) for various aromatic nitrogen-containing molecules. The data associated with this figure are presented in Table S2.† | ||
4. Conclusions
Here, we investigated the application of quantum chemical methods for the computation of quinoxaline reduction potentials and for the development of a simple descriptor that enables reduction potential predictions of nitrogen-containing aromatics without computationally demanding free energy simulations. First, quantum chemical calculations were performed on 40 quinoxaline derivatives to determine the impact of substituent groups, both electron-withdrawing and electron-donating, on reduction potentials. The calculations indicate the addition of electron-donating groups, particularly alkyl groups, can lower the reduction potential of quinoxalines albeit with concomitant decreases in oxidative stability. It should be noted that the benefits of lower reduction potentials must be balanced with the increase in molecular weights which together impact specific energy. Based on this computational study, we derived a descriptor for computing reduction potentials of novel quinoxaline derivatives without time-consuming free energy and solvation calculations. Finally, we validated this descriptive relationship for select aromatic nitrogen-containing molecules: pyrazine, phenazine, bipyridine pyridine, pyrimidine, pyridazine, quinoline, and isoquinoline. We anticipate that these simple descriptors may be used in high-throughput computational screening of thousands of organic molecules to down select candidates with promising reduction properties for RFB application.Acknowledgements
This work was supported as part of the Joint Center for Energy Storage Research, an Energy Innovation Hub funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences. We gratefully acknowledge the computing resources provided on “Blues”, a 320-node computing cluster operated by the Laboratory Computing Resource Center at Argonne National Laboratory. Use of the Center for Nanoscale Materials was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract no. DE-AC02-06CH11357.References
- B. Dunn, H. Kamath and J. M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2011, 11, 19–29 CrossRef PubMed.
- D. Rastler, Electricity Energy Storage Options: A white paper Primer on Applications, Costs and Benefits, EPRI Technical Update 1020676, 2010 Search PubMed.
- J. Eyer and G. Gorey, Energy Storage for the Electricity Grid: benefits and Market Potential Assessment Guide, Sandia Report SAND2010-0815, 2010 Search PubMed.
- Z. G. Yang, J. L. Zhang, M. C. W. Kintner-Meyer, X. C. Lu, D. W. Choi, J. P. Lemmon and J. Liu, Chem. Rev., 2011, 111, 3577–3613 CrossRef CAS PubMed.
- P. Poizot and F. Dolhem, Energy Environ. Sci., 2011, 4, 2003–2019 CAS.
- M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- M. Skyllas-Kazacos, M. H. Chakrabarti, S. A. Hajimolana, F. S. Mjalli and M. Saleem, J. Electrochem. Soc., 2011, 158, R55–R79 CrossRef CAS PubMed.
- W. Wang, Q. T. Luo, B. Li, X. L. Wei, L. Y. Li and Z. G. Yang, Adv. Funct. Mater., 2013, 23, 970–986 CrossRef CAS.
- Z. Song and H. Zhou, Energy Environ. Sci., 2013, 6, 2280–2301 CAS.
- F. R. Brushett, J. T. Vaughey and A. N. Jansen, Adv. Energy Mater., 2013, 2, 1390–1396 CrossRef.
- S. Renault, S. Gottis, A.-L. Barres, M. Courty, O. Chauvet, F. Dolhem and P. Poizot, Energy Environ. Sci., 2013, 6, 2124–2133 CAS.
- B. Huskinson, M. P. Marshak, C. Suh, S. Er, M. R. Gerhardt, C. J. Galvin, X. Chen, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Nature, 2014, 505, 195–198 CrossRef CAS PubMed.
- B. Yang, L. Hoober-Burkhardt, F. Wang, G. S. Prakash and S. Narayanan, J. Electrochem. Soc., 2014, 161, A1371–A1380 CrossRef CAS PubMed.
- X. Wei, L. Cosimbescu, W. Xu, J. Z. Hu, M. Vijayakumar, J. Feng, M. Y. Hu, X. Deng, J. Xiao, J. Liu, V. Sprenkle and W. Wang, Adv. Energy Mater., 2014, 1400678 Search PubMed.
- Z. Li, S. Li, S. Liu, K. Huang, D. Fang, F. Wang and S. Peng, Electrochem. Solid-State Lett., 2011, 14, A171–A173 CrossRef CAS PubMed.
- B. Huskinson, S. Nawar, M. R. Gerhardt and M. J. Aziz, ECS Trans., 2013, 53, 101–105 CrossRef CAS PubMed.
- W. Wang, W. Xu, L. Cosimbescu, D. Choi, L. Li and Z. Yang, Chem. Commun., 2012, 48, 6669–6671 RSC.
- J. C. Henderson, Y. Kiya, G. R. Hutchison and H. c. D. Abruna, J. Phys. Chem. C, 2008, 112, 3989–3997 CAS.
- W. D. Zhou, K. Hernandez-Burgos, S. E. Burkhardt, H. L. Qian and H. D. Abruna, J. Phys. Chem. C, 2013, 117, 6022–6032 CAS.
- Z. Chen, Y. Qin and K. Amine, Electrochim. Acta, 2009, 54, 5605–5613 CrossRef CAS PubMed.
- D. Méndez-Hernández, P. Tarakeshwar, D. Gust, T. Moore, A. Moore and V. Mujica, J. Mol. Model., 2013, 19, 2845–2848 CrossRef PubMed.
- J. R. T. Johnsson Wass, E. Ahlberg, I. Panas and D. J. Schiffrin, J. Phys. Chem. A, 2006, 110, 2005–2020 CrossRef CAS PubMed.
- M. Namazian and M. L. Coote, J. Phys. Chem. A, 2007, 111, 7227–7232 CrossRef CAS PubMed.
- M. Namazian, H. A. Almodarresieh, M. R. Noorbala and H. R. Zare, Chem. Phys. Lett., 2004, 396, 424–428 CrossRef CAS PubMed.
- K. S. Raymond, A. K. Grafton and R. A. Wheeler, J. Phys. Chem. B, 1997, 101, 623–631 CrossRef CAS.
- K. Hernández-Burgos, S. E. Burkhardt, G. G. Rodríguez-Calero, R. G. Hennig and H. D. Abruña, J. Phys. Chem. C, 2014, 118, 6046–6051 Search PubMed.
- J. E. Bachman, L. A. Curtiss and R. S. Assary, J. Phys. Chem. A, 2014, 118, 8852–8860 CrossRef CAS PubMed.
- C. Karlsson, E. Jamstorp, M. Stromme and M. Sjodin, J. Phys. Chem. C, 2012, 116, 3793–3801 CAS.
- C. Karlsson, A. Gogoll, M. Stromme and M. Sjodin, J. Phys. Chem. C, 2013, 117, 894–901 CAS.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef PubMed.
- J. Hachmann, R. Olivares-Amaya, A. Jinich, A. L. Appleton, M. A. Blood-Forsythe, L. s. R. Seress, C. Roman-Salgado, K. Trepte, S. Atahan-Evrenk and S. l. Er, Energy Environ. Sci., 2014, 7, 698–704 CAS.
- G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- A. V. Marenich, J. Ho, M. L. Coote, C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2014, 16, 15068–15106 RSC.
- J. J. Guerard and J. S. Arey, J. Chem. Theory Comput., 2013, 9, 5046–5058 CrossRef CAS.
- R. S. Assary, L. A. Curtiss and J. S. Moore, J. Phys. Chem. C, 2014, 118, 11545–11558 CAS.
- A. A. Isse and A. Gennaro, J. Phys. Chem. B, 2010, 114, 7894–7899 CrossRef CAS PubMed.
- S. Bhattacharyya, M. T. Stankovich, D. G. Truhlar and J. Gao, J. Phys. Chem. A, 2007, 111, 5729–5742 CrossRef CAS PubMed.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2006, 110, 16066–16081 CrossRef CAS PubMed.
- J. Moens, P. Geerlings and G. Roos, Chem.–Eur. J., 2007, 13, 8174–8184 CrossRef CAS PubMed.
- O. Borodin, W. Behl and T. R. Jow, J. Phys. Chem. C, 2013, 117, 8661–8682 CAS.
- J. M. Vollmer, L. A. Curtiss, D. R. Vissers and K. Amine, J. Electrochem. Soc., 2004, 151, A178–A183 CrossRef CAS PubMed.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2006, 111, 408–422 CrossRef PubMed.
- L. Xing, O. Borodin, G. D. Smith and W. Li, J. Phys. Chem. A, 2011, 115, 13896–13905 CrossRef CAS PubMed.
- R. L. Wang, C. Buhrmester and J. R. Dahn, J. Electrochem. Soc., 2006, 153, A445–A449 CrossRef CAS PubMed.
- R. S. Assary, L. A. Curtiss, P. C. Redfern, Z. Zhang and K. Amine, J. Phys. Chem. C, 2011, 115, 12216–12223 CAS.
- A. Z. Szarka, L. A. Curtiss and J. R. Miller, Chem. Phys., 1999, 246, 147–155 CrossRef CAS.
- S. E. Burkhardt, M. A. Lowe, S. Conte, W. D. Zhou, H. L. Qian, G. G. Rodriguez-Calero, J. Gao, R. G. Hennig and H. D. Abruna, Energy Environ. Sci., 2012, 5, 7176–7187 CAS.
- L. Xing and O. Borodin, Phys. Chem. Chem. Phys., 2012, 14, 12838–12843 RSC.
- J. R. Ames, M. A. Houghtaling and D. L. Terrian, Electrochim. Acta, 1992, 37, 1433–1436 CrossRef CAS.
- K. R. Barqawi and M. A. Atfah, Electrochim. Acta, 1987, 32, 597–599 CrossRef CAS.
- G. Zhang and C. B. Musgrave, J. Phys. Chem. A, 2007, 111, 1554–1561 CrossRef CAS PubMed.
- R. Stowasser and R. Hoffmann, J. Am. Chem. Soc., 1999, 121, 3414–3420 CrossRef CAS.
- S. O. Yaman, E. Esenturk, C. Kayran and A. M. Onal, Z. Naturforsch., B: J. Chem. Sci., 2002, 57, 92–98 CAS.
- D. T. Sawyer and R. Y. Komai, Anal. Chem., 1972, 44, 715–721 CrossRef CAS PubMed.
- C. V. Krishnan, C. Creutz, H. A. Schwarz and N. Sutin, J. Am. Chem. Soc., 1983, 105, 5617–5623 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: An example of all-organic redox flow battery (Scheme S1), computed reduction potentials of quinoxaline using various levels of theory (Table S1A), computed reduction potentials in various dielectric mediums (Table S1B), comparison of computed vs. predicted reduction potential of various aromatic nitrogen-containing molecules (Table S2), computed reduction potentials vs. the predicted reduction potentials for quinoxaline derivatives (Fig. S1), and selected pyrazine (Fig. S2a), phenazine (Fig. S2b), and bipyridine molecules (Fig. S2c) are present. See DOI: 10.1039/c4ra08563a |
| This journal is © The Royal Society of Chemistry 2014 |