View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C4RA08222B (Paper) RSC Adv., 2014, 4, 44394-44407

First analysis of the Herzberg (C1Σ+ → A1Π) band system in the less-abundant 13C17O isotopologue

Rafał Hakalla*
Materials Spectroscopy Laboratory, Department of Experimental Physics, Faculty of Mathematics and Natural Science, University of Rzeszów, ul. Prof. S. Pigonia 1, 35-959 Rzeszów, Poland. E-mail: hakalla@ur.edu.pl

Received 24th June 2014 , Accepted 19th August 2014

First published on 19th August 2014

Abstract

This work presents high-resolution emission spectra measurements of the Herzberg band system, which has not been observed and analysed in the 13C17O isotopologue so far. Bands C → A (0,1), (0,2) and (0,3) were recorded in a region at 22[thin space (1/6-em)]950–26[thin space (1/6-em)]050 cm−1 using high-accuracy dispersive optical spectroscopy. The 13C17O molecules were formed and excited in a stainless steel hollow-cathode lamp with two anodes. All 224 rovibrational spectra lines, up to Jmax = 30, were precisely measured with an accuracy of about 0.0030 cm−1 and rotationally analysed. In this work the following have been determined in 13C17O for the first time: the merged rotational constants of the C1Σ+(ν = 0) Rydberg state and the individual rotational constants of the A1Π(ν = 3) state, as well as the rotational and vibrational equilibrium constants for the C1Σ+ state, the band origins of the C → A system, the isotope shifts, and the ΔGC1/2 vibrational quantum. The combined analysis of the Herzberg bands obtained now and the Ångström (B1Σ+ → A1Π) system analysed earlier (R. Hakalla et al., J. Phys. Chem. A, 2013, 117, 12299 and R. Hakalla et al., J. Mol. Spectrosc., 2012, 272, 11) yielded a precisely relative characteristic of the C1Σ+(ν = 0) and B1Σ+(ν = 0 and 1) Rydberg states in the 13C17O molecule, among others νCB00, νCB01 vibrational quanta. Also, many molecular constant values of the C1Σ+ state in the 12C16O, 12C17O, 13C16O, 12C18O, and 13C18O isotopologues were determined, which have not been published so far, as well as the RKR turning points, Franck–Condon factors, relative intensities, r-centroids for the Herzberg band system and the main, isotopically invariant parameters of the C1Σ+ state in the CO molecule within the Born–Oppenheimer approximation. In the A1Π(ν = 3) state of the 13C17O molecule, extensive, multi-state rotational perturbations were found, which were analysed and substantiated in detail. The vibrational level ν = 0 of the C1Σ+ state was analysed, paying special attention to possible irregularities, and no noticeable perturbations were found in it up to the observed Jmax.

1. Introduction

Carbon monoxide is one of the most important molecules in astronomy, because it is readily detectable and chemically stable as well as being the second, after H2, most abundant molecular constituent in star-forming clouds and the main gas-phase reservoir of interstellar carbon. The presence of the CO molecule was discovered in planets, solar and stellar atmospheres, interstellar space, comet tails, supernova remnants as well as in the spectra of diverse cosmic objects. A large CO abundance gives a detectable signal for even rarer isotopologues. Spectroscopic research into CO and its lesser-abundant isotopologues is fully justified because of its special significance as the main tracer of gas properties, structure and kinematics in a wide variety of astrophysical environments.1–11 They control much of the chemistry in the gas phase and are the precursors to more complex molecules.12–15 The CO molecule is also highly relevant in research into Earth's atmosphere. Its concentrations in different layers of the troposphere, stratosphere, and mesosphere vary strongly. Because of short atmospheric lifetime (about 2 months), changes in sources and sinks in the environment are reflected in atmospheric concentrations faster than other molecules.16,17

Research on lesser-abundant isotopologues of CO, such as 13C17O, are more and more appreciated and extensively discussed because of their unique application possibilities, such as partial elimination of a serious optical problem called ‘depth effects’ in the ISM method18 or more precise determination of the [12C]/[13C] ratio in outer space than on the basis of the ordinary 12C16O or even 12C18O isotopologues, which in turn leads to determination of the primary/secondary nuclear processing ratio of the stars.18 The first observation of interstellar 13C17O was made by Bensch et al.18 towards the ρ-Ophiuchi molecular cloud. In laboratory conditions its recording and analysis were made several times,9,17,19–26 recently by Hakalla et al.27,28

Highly excited electronic states of CO now belong to one of the main trends in the research into this molecule.19,27–45 A special area of interest are the states lying in the region of dissociation energy, among others – the (npσ) C1Σ+ Rydberg state. This state, since its discovery by Hopfield and Birge,46 has been observed and analysed in the following transitions: the Hopfield–Birge (C1Σ+ → X1Σ+),30,31,47–56 as well as recently discovered C1Σ+ → d3Δi57 and C1Σ+ → B1Σ+.52,58,59 However, the most comprehensive and complete information about the C1Σ+ state comes from the Herzberg (C1Σ+ → A1Π) band system,40,54–56,60–70 whose spectrum is situated in the VIS range. This system was precisely analysed for most isotopologues of CO, that is: 12C16O, 13C16O, 12C18O, 14C16O, 13C18O, and 14C18O, but it remained unknown in the 13C17O molecule up to now. The only information concerning the upper state of this system in 13C17O is a preliminary analysis of the C1Σ+(ν = 1) vibrational level on the basis the C → X transition.31 Therefore, I have decided to make the first recording of the Herzberg band system in 13C17O. A complete analysis of the experimental material enabled me to receive the first piece of information about the energetic structure parameters of the C1Σ+ → A1Π transition, as well as about the C1Σ+(ν = 0) and A1Π(ν = 3) states in the isotopologue under consideration.

2. Experiment

The experimental methods have been described in ref. 28, therefore, only details that are relevant for the current results are presented in this section.

The source of spectra of the Herzberg (C1Σ+ → A1Π) band system in 13C17O was a water-cooled, hollow-cathode lamp with two anodes.71 At first it was filled with a mixture of acetylene 13C2D2 (99.98% purity of 13C) and helium under pressure of about 6 and 1 Torr, respectively. Next, I passed an electric current through the mixture in order to obtain a sufficient amount of deposit of 13C on the electrodes. This process lasted for about 100 h. In the next stage, the lamp was evacuated and molecular oxygen was let into this space including 70% of the 17O2 isotope, as non-flowing gas under pressure of about 2 Torr. Finally, the electrodes were powered by direct current of the following parameters: 2 × 670 V and 2 × 36 mA. These experimental conditions had been previously tested several times and chosen as optimal to fulfil the aim of this work. In this way, the Herzberg system in the 13C17O isotopologue was recorded for the first time, in particular (0,1), (0,2), and (0,3) bands of the C → A transition.

Measurement equipment that is used to record the Herzberg band system in the 13C17O molecule has been recently constructed in our laboratory. It uses a high accuracy dispersive optical spectroscopy72–76 (see also Fig. 1 of ref. 28). The molecular spectra were observed in the 6th order for (0,1) and (0,2) bands, as well as in the 5th order for (0,3) band of the C1Σ+ → A1Π transition. The reciprocal dispersion was in a range of 0.07–0.11 nm mm−1, and theoretical resolving power was approximately 273[thin space (1/6-em)]600 for (0,1) and (0,2) bands, as well as 228[thin space (1/6-em)]000 for the (0,3) band. As a calibration spectrum, an atomic spectrum of thorium was used,77 which was produced in the water-cooled, hollow-cathode tube with the cathode lined with thin Th foil, from a few overlapping orders.

The peak positions of spectral lines were calculated by means of a least-squares procedure assuming a Gaussian line-shape for each spectral contour (30 points per line), with an uncertainty of the peak position for a single line of approximately 0.1–0.2 μm. In order to calculate the wavenumbers of the CO molecule, the 7th-, 4th-, and 5th-order interpolation polynomials were used and the typical standard deviation of the least-squares fit for the 25–35 calibration lines was approximately 1.7 × 10−3 cm−1, 1.6 × 10−3 cm−1, and 1.7 × 10−3 cm−1 for the (0,1), (0,2), and (0,3) bands, respectively.

Intense and single lines of the CO molecule had a spectral width of about 0.15 cm−1. Their maximum signal-to-noise ratio was about 60[thin space (1/6-em)]:[thin space (1/6-em)]1, 65[thin space (1/6-em)]:[thin space (1/6-em)]1, and 55[thin space (1/6-em)]:[thin space (1/6-em)]1 for the (0,1), (0,2), and (0,3) bands, respectively. The most intense lines produce the count rates of about 7000 photons per s, 8000 photons per s, and 6000 photons per s for the (0,1), (0,2), and (0,3) bands, respectively.

Accuracy of the measurements of the 13C17O strong and single lines amounted to about 0.0030 cm−1. Some of the weaker and blended lines were measured with lower accuracy, which amounted to about 0.0060 cm−1. Summary of the observation and analyses of the C1Σ+ → A1Π system in the 13C17O isotopologue is given in Table 1.

Table 1 Summary of observation and analyses of the C1Σ+ → A1Π system in the 13C17O isotopologue
Band Remarks Band heada nb Jmax fc (σ × 103)d
a In cm−1, 1σ in parentheses.b Total number of observed lines.c Number of degrees of freedom of the fit for the individual band-by-band analysis using the linear least-squares method proposed by Curl and Dane78 and Watson.79d Standard deviation of the fit (in cm−1) for the individual band-by-band analysis using the linear least-squares method proposed by Curl and Dane78 and Watson.79
(0,1) First analysis 25[thin space (1/6-em)]721.2184 (8) 77 26 22 1.25
(0,2) First analysis 24[thin space (1/6-em)]324.5528 (15) 78 30 19 1.64
(0,3) First analysis 22[thin space (1/6-em)]958.6704 (1) 69 25 18 1.08

In this experiment altogether 224 spectral emission lines were recorded that belong to the Herzberg band system in 13C17O. Their wavenumbers are presented in Table 2. A high quality, expanded view of these bands together with their rotational assignments are provided in Fig. 1–3.

Table 2 Observed wavenumbers (in cm−1) and their rotational assignments of the Herzberg (C1Σ+ → A1Π) band system in the 13C17O isotopologuea
J P11ee(J) Q11ef(J) R11ee(J)
a Values in parentheses denote observed minus calculated values in units of the last quoted digit. Asterisks denote the less accurate lines not used in the evaluation of individual rotational constants of the C1Σ+ and A1Π states.
(0,1) band
1 25[thin space (1/6-em)]725.8655 * 25[thin space (1/6-em)]729.4075 (0) 25[thin space (1/6-em)]736.7235 (0)
2 25[thin space (1/6-em)]723.6738 (–3) 25[thin space (1/6-em)]730.7075 (0) 25[thin space (1/6-em)]741.7706 (2)
3 25[thin space (1/6-em)]722.1800 (–5) 25[thin space (1/6-em)]732.7651 (0) 25[thin space (1/6-em)]747.5149 (5)
4 25[thin space (1/6-em)]721.3674 (–1) 25[thin space (1/6-em)]735.5791 (0) 25[thin space (1/6-em)]753.9381 (1)
5 25[thin space (1/6-em)]721.2184 (–8) 25[thin space (1/6-em)]739.0904 (0) 25[thin space (1/6-em)]761.0261 (8)
6 25[thin space (1/6-em)]721.7609 (7) 25[thin space (1/6-em)]743.2781 (0) 25[thin space (1/6-em)]768.7996 (–7)
7 25[thin space (1/6-em)]722.9069 (3) 25[thin space (1/6-em)]748.1045 (0) 25[thin space (1/6-em)]777.1785 (–4)
8 25[thin space (1/6-em)]724.7457 (1) 25[thin space (1/6-em)]753.6045 (0) 25[thin space (1/6-em)]786.2481 (–1)
9 25[thin space (1/6-em)]727.2543 (3) 25[thin space (1/6-em)]759.7540 (0) 25[thin space (1/6-em)]795.9843 (–3)
10 25[thin space (1/6-em)]730.4327 (–11) 25[thin space (1/6-em)]766.5608 (0) 25[thin space (1/6-em)]806.3911 (12)
11 25[thin space (1/6-em)]734.2899 (–7) 25[thin space (1/6-em)]774.0345 (0) 25[thin space (1/6-em)]817.4703 (8)
12 25[thin space (1/6-em)]738.8083 (6) 25[thin space (1/6-em)]782.1732 (0) 25[thin space (1/6-em)]829.2058 (–5)
13 25[thin space (1/6-em)]744.0098 (3) 25[thin space (1/6-em)]790.9934 (0) 25[thin space (1/6-em)]841.6242 (–3)
14 25[thin space (1/6-em)]749.8744 (–1) 25[thin space (1/6-em)]800.4757 (0) 25[thin space (1/6-em)]854.7023 (1)
15 25[thin space (1/6-em)]756.4304 (3) 25[thin space (1/6-em)]810.6398 (0) 25[thin space (1/6-em)]868.4664 (–3)
16 25[thin space (1/6-em)]763.6543 (11) 25[thin space (1/6-em)]821.4665 (0) 25[thin space (1/6-em)]882.8936 (–11)
17 25[thin space (1/6-em)]771.5625 (5) 25[thin space (1/6-em)]832.9707 (0) 25[thin space (1/6-em)]898.0035 (–4)
18 25[thin space (1/6-em)]780.1409 (2) 25[thin space (1/6-em)]845.1476 (0) 25[thin space (1/6-em)]913.7783 (–1)
19 25[thin space (1/6-em)]789.4081 (–7) 25[thin space (1/6-em)]858.0132 (0) 25[thin space (1/6-em)]930.2382 (8)
20 25[thin space (1/6-em)]799.3539 (–7) 25[thin space (1/6-em)]871.5368 (0) 25[thin space (1/6-em)]947.3698 (8)
21 25[thin space (1/6-em)]809.9405 (–4) 25[thin space (1/6-em)]885.7593 (0) 25[thin space (1/6-em)]965.1359 (4)
22 25[thin space (1/6-em)]821.2283 (14) 25[thin space (1/6-em)]900.6472 (0) 25[thin space (1/6-em)]983.5947 (–14)
23 25[thin space (1/6-em)]833.2159 (–2) 25[thin space (1/6-em)]916.2223 (0) 26[thin space (1/6-em)]002.7541 (2)
24 25[thin space (1/6-em)]845.9040 (–24) 25[thin space (1/6-em)]932.4561 (0) 26[thin space (1/6-em)]022.6088 (23)
25 25[thin space (1/6-em)]859.2706 (17) 25[thin space (1/6-em)]949.4114 (0) 26[thin space (1/6-em)]043.1232 (–17)
26 25[thin space (1/6-em)]873.3247 (0) 25[thin space (1/6-em)]967.0644 (0)    
 
(0,2) band
1 24[thin space (1/6-em)]329.0005 * 24[thin space (1/6-em)]332.6019 (0) 24[thin space (1/6-em)]339.8588 (0)
2 24[thin space (1/6-em)]326.8040 (–2) 24[thin space (1/6-em)]334.0366 (0) 24[thin space (1/6-em)]344.9010 (2)
3 24[thin space (1/6-em)]325.3431 (1) 24[thin space (1/6-em)]336.1890 (0) 24[thin space (1/6-em)]350.6772 (–1)
4 24[thin space (1/6-em)]324.5803 (4) 24[thin space (1/6-em)]339.0526 (0) 24[thin space (1/6-em)]357.1506 (–4)
5 24[thin space (1/6-em)]324.5528 (–15) 24[thin space (1/6-em)]342.6406 (0) 24[thin space (1/6-em)]364.3597 (15)
6 24[thin space (1/6-em)]325.2242 (1) 24[thin space (1/6-em)]346.9687 (0) 24[thin space (1/6-em)]372.2646 (–2)
7 24[thin space (1/6-em)]326.6361 (–10) 24[thin space (1/6-em)]352.0892 (0) 24[thin space (1/6-em)]380.9111 (9)
8 24[thin space (1/6-em)]328.7408 (–10) 24[thin space (1/6-em)]357.5260 (0) 24[thin space (1/6-em)]390.2462 (10)
9 24[thin space (1/6-em)]331.5832 (–5) 24[thin space (1/6-em)]364.0934 (0) 24[thin space (1/6-em)]400.3157 (5)
10 24[thin space (1/6-em)]335.1340 (7) 24[thin space (1/6-em)]371.2617 (0) 24[thin space (1/6-em)]411.0897 (–7)
11 24[thin space (1/6-em)]339.4130 (6) 24[thin space (1/6-em)]379.1658 (0) 24[thin space (1/6-em)]422.5917 (–6)
12 24[thin space (1/6-em)]344.4085 (–4) 24[thin space (1/6-em)]387.7637 (0) 24[thin space (1/6-em)]434.8089 (5)
13 24[thin space (1/6-em)]350.1225 (–19) 24[thin space (1/6-em)]397.0884 (0) 24[thin space (1/6-em)]447.7421 (19)
14 24[thin space (1/6-em)]356.5664 (15) 24[thin space (1/6-em)]407.1397 (0) 24[thin space (1/6-em)]461.3921 (–14)
15 24[thin space (1/6-em)]363.7283 (23) 24[thin space (1/6-em)]417.9027 (0) 24[thin space (1/6-em)]475.7611 (–23)
16 24[thin space (1/6-em)]371.6039 (–3) 24[thin space (1/6-em)]429.3919 (0) 24[thin space (1/6-em)]490.8466 (3)
17 24[thin space (1/6-em)]380.2221 (–10) 24[thin space (1/6-em)]441.6017 (0) 24[thin space (1/6-em)]506.6664 (9)
18 24[thin space (1/6-em)]389.5645 (–2) 24[thin space (1/6-em)]454.5307 (0) 24[thin space (1/6-em)]523.2030 (3)
19 24[thin space (1/6-em)]399.6452 (18) 24[thin space (1/6-em)]468.1977 (0) 24[thin space (1/6-em)]540.4704 (–17)
20 24[thin space (1/6-em)]410.4760 (15) 24[thin space (1/6-em)]482.5763 (0) 24[thin space (1/6-em)]558.4872 (–15)
21 24[thin space (1/6-em)]422.0568 (–12) 24[thin space (1/6-em)]497.7064 (0) 24[thin space (1/6-em)]577.2534 (12)
22 24[thin space (1/6-em)]434.4693 (–12) 24[thin space (1/6-em)]513.5773 (0) 24[thin space (1/6-em)]596.8401 (12)
23 24[thin space (1/6-em)]447.8874 (0) 24[thin space (1/6-em)]530.2069 (0)    
24 24[thin space (1/6-em)]463.6597 (0) 24[thin space (1/6-em)]547.6119 (0)    
25 24[thin space (1/6-em)]472.9260 (0) 24[thin space (1/6-em)]565.8989 (0)    
26 24[thin space (1/6-em)]489.1007 (0) 24[thin space (1/6-em)]585.3910 (0)    
27 24[thin space (1/6-em)]505.0891 (0)        
28 24[thin space (1/6-em)]522.8370 (0)        
29 24[thin space (1/6-em)]540.6194 (0)        
30 24[thin space (1/6-em)]559.1643 (0)        
 
(0,3) band
1 22[thin space (1/6-em)]962.7250 * 22[thin space (1/6-em)]966.2885 (0) 22[thin space (1/6-em)]973.5829 (0)
2 22[thin space (1/6-em)]960.6167 (1) 22[thin space (1/6-em)]967.8074 (0) 22[thin space (1/6-em)]978.7127 (–2)
3 22[thin space (1/6-em)]959.2675 (1) 22[thin space (1/6-em)]970.0817 (0) 22[thin space (1/6-em)]984.6012 (–1)
4 22[thin space (1/6-em)]958.6704 (–1) 22[thin space (1/6-em)]973.1184 (0) 22[thin space (1/6-em)]991.2411 (2)
5 22[thin space (1/6-em)]958.8342 (–7) 22[thin space (1/6-em)]976.9160 (0) 22[thin space (1/6-em)]998.6414 (6)
6 22[thin space (1/6-em)]959.7551 (0) 22[thin space (1/6-em)]981.4756 (0) 23[thin space (1/6-em)]006.7951 (0)
7 22[thin space (1/6-em)]961.4636 (0) 22[thin space (1/6-em)]986.7994 (0) 23[thin space (1/6-em)]015.7291 *
8 22[thin space (1/6-em)]963.9146 (7) 22[thin space (1/6-em)]992.8806 (0) 23[thin space (1/6-em)]025.4156 (–8)
9 22[thin space (1/6-em)]967.1513 (7) 22[thin space (1/6-em)]999.7251 (0) 23[thin space (1/6-em)]035.8804 (–8)
10 22[thin space (1/6-em)]971.1433 (–7) 23[thin space (1/6-em)]007.3378 (0) 23047.1008 (8)
11 22[thin space (1/6-em)]975.8988 (8) 23[thin space (1/6-em)]015.7291 (0) 23[thin space (1/6-em)]059.0760 (–8)
12 22[thin space (1/6-em)]981.4405 (–1) 23[thin space (1/6-em)]024.9156 (0) 23[thin space (1/6-em)]071.8392 (1)
13 22[thin space (1/6-em)]987.7428 (0) 23[thin space (1/6-em)]034.9604 (0) 23[thin space (1/6-em)]085.3575 (–1)
14 22[thin space (1/6-em)]994.8781 (8) 23[thin space (1/6-em)]046.3929 (0) 23[thin space (1/6-em)]099.7042 (–8)
15 23[thin space (1/6-em)]002.9034 (–14) 23[thin space (1/6-em)]055.4444 (0) 23[thin space (1/6-em)]114.9428 (13)
16 23[thin space (1/6-em)]012.1705 (–14) 23[thin space (1/6-em)]068.2595 (0) 23[thin space (1/6-em)]131.4147 (13)
17 23[thin space (1/6-em)]016.9919 (7) 23[thin space (1/6-em)]081.3794 (0) 23[thin space (1/6-em)]143.4324 (–7)
18 23[thin space (1/6-em)]029.0170 (4) 23[thin space (1/6-em)]096.4837 (0) 23[thin space (1/6-em)]162.6539 (–5)
19 23[thin space (1/6-em)]040.2729 (–9) 23[thin space (1/6-em)]109.9910 (0) 23[thin space (1/6-em)]181.1036 (10)
20 23[thin space (1/6-em)]052.0410 (12) 23[thin space (1/6-em)]122.2876 (0) 23[thin space (1/6-em)]200.0531 (–12)
21 23[thin space (1/6-em)]064.4702 (–4) 23[thin space (1/6-em)]139.9343 (0) 23[thin space (1/6-em)]219.6659 (4)
22 23[thin space (1/6-em)]077.6547 (2) 23[thin space (1/6-em)]156.8946 (0) 23[thin space (1/6-em)]240.0240 (–1)
23 23[thin space (1/6-em)]091.5662 (0)        
24 23[thin space (1/6-em)]106.2391 (0)        
25 23[thin space (1/6-em)]121.6477 (0)        


image file: c4ra08222b-f1.tif
Fig. 1 The emission spectrum of carbon monoxide showing the first observation and rotational interpretation of the C1Σ+ → A1Π (0,1) transition in the 13C17O isotopologue, on an expanded scale. Due to relatively high intensity of the Th calibration lines, their peaks are marked with broken lines. The positions of the band-head region of the less intense C1Σ+ → A1Π(0,1) transition of 13C16O was indicated at 25[thin space (1/6-em)]706 cm−1. See Section 3 for further information.

image file: c4ra08222b-f2.tif
Fig. 2 The emission spectrum of carbon monoxide showing the first observation and rotational interpretation of the C1Σ+ → A1Π (0,2) transition in the 13C17O isotopologue, on an expanded scale. Due to relatively high intensity of the Th calibration lines, their peaks are marked with broken lines. See Section 3 for further information.

image file: c4ra08222b-f3.tif
Fig. 3 The emission spectrum of carbon monoxide showing the first observation and rotational interpretation of the C1Σ+ → A1Π (0,3) transition in the 13C17O isotopologue, on an expanded scale. Due to relatively high intensity of the Th calibration lines, their peaks are marked with broken lines. See Section 3 for further information.

3. Description of the spectra

The three most intense (0,1), (0,2) and (0,3) bands belonging to the C1Σ+ → A1Π system in 13C17O were recorded in the region 22[thin space (1/6-em)]950–26[thin space (1/6-em)]050 cm−1. It is the first observation of this system in the 13C17O isotopologue as there was a misprint in the work by Hakalla et al.27 (Fig. 2 and 3), where the band heads C → A(0,2) and C → A(0,3), which appeared there as belonging to the 13C17O, in fact belong the 13C16O molecule.

Preliminary interpretation of the bands, that is, identification of branches and J-numbering of the lines were carried out with the use of the previous information concerning the lower state of the Herzberg system, that is, the A1Π(ν′′ = 1, 2) state27,28 as well as by means of well – known spectroscopic methods.

A rotational interpretation of the molecular spectra of the 13C17O molecule is very complicated because of the fact that they are accompanied by analogous spectra of the 13C16O molecule of intensity 30[thin space (1/6-em)]:[thin space (1/6-em)]70 in comparison to the spectra that are being studied, which can be well seen, for example, in Fig. 1. It resulted from the application of a gas in the spectral lamp, including 70% of the 17O2 isotope. Additionally, despite the application of carbon of high spectral purity, that is 99.98% of 13C in the experiment, impurities appeared in the spectrum caused by the lines belonging to the 12C16O and 12C17O molecules, which had an impact on the weaker lines of the spectrum studied. The impact of those impurities was taken into account in the interpretation process on the basis of the previous data concerning the C → A system in the 12C16O68 and 13C16O63 molecules. Detailed data concerning the B → A(1,0) band in 13C17O obtained from ref. 27 allowed us to eliminate its influence on the interpretation and spectrum analysis belonging to the C → A(0,2) transition.

4. Analyses and calculations

A reduction of the 13C17O Herzberg spectral lines to the rovibronic molecular parameters was carried out in a few stages using the well-known theoretical model, in which both states participating in the studied transition are represented by the proper Hamiltonians; for the upper C1Σ+ state:
 
〈H〉 = T′v + B′vJ(J + 1) − D′vJ2(J + 1)2 + …, (1)

and for both Λ-components of the A1Π lower state:

 
〈H〉 = T′′v + B′′v[J(J + 1) − 1] − D′′v[J(J + 1) − 1]2 + …, (2)
where expressions T′v and T′′v denote the rotation-less energies for the C1Σ+ and A1Π states, respectively, calculated with regard to the lowest rovibrational level of the X1Σ+ ground state. Considering the precision of obtained wavenumbers of the lines and the observed Jmax value of the rotational quantum number in the spectra, only Bν and Dν for the C1Σ+ and A1Π states, as well as the ν0(ν′, ν′′) = T′v − T′′v band origins were statistically significant in reproducing the experimental wavenumbers.

In order to calculate individual rotational constants Bν and Dν of the C1Σ+(ν = 0) state, the linear least-squares method was used in the version proposed by Curl and Dane78 and Watson79 by an individual band-by-band analysis. This method is an efficient means to separate molecular information concerning the upper C1Σ+(ν′ = 0) state, which is considered to be regular in all analysed isotopologues,30 from that which concerns the strongly perturbed state of A1Π(ν′′ = 1, 2)27,28 and A1Π(ν′′ = 3) (this work). These constants are gathered in Table 4. With the use of the constants, the following have been calculated: ν0(0,1), ν0(0,2), and ν0(0,3) band origins of the C → A transition and effective rotational constants of the A1Π(ν′′ = 3) state in the 13C17O molecule, using the least-squares method. The results are presented in Tables 3 and 4, respectively.

Table 3 Band origins and isotope shifts of the C1Σ+ → A1Π transition in 13C17Oa,b
Band Band origin Isotope shiftc
a In cm−1.b Uncertainties in parentheses represent one standard deviation in units of the last quoted digit.c Calculated as ν0(12C16O) – ν0(13C17O) experimental values. The ν0(12C16O) were taken from ref. 68.
(0,1) 25[thin space (1/6-em)]727.9077 (62) –40.621 (25)
(0,2) 24[thin space (1/6-em)]330.4469 (46) –88.738 (22)
(0,3) 22[thin space (1/6-em)]964.1402 (68) –135.194 (17)

Table 4 Individual and merged molecular constants (in cm−1) for the C1Σ+ and A1Π states of 13C17Oa
State ν Bν Dν × 106 Description
a Uncertainties in parentheses represent one standard deviation in units of the last quoted digit.b The estimated variance and the number of degrees of freedom of the merging were σM2 = 0.43 and fM = 4, respectively.
C1Σ+ 0 1.809707 (15) 5.528 (17) From C → A (0,1)
1.809738 (23) 5.566 (33) From C → A (0,2)
1.809703 (16) 5.520 (23) From C → A (0,3)
1.8097113 (93) 5.532 (12) Merged valueb
A1Π 3 1.43134 (30) 6.17 (47) From C → A (0,3)

Finally, the molecular constants obtained from the individual fit of the C → A(0,1), (0,2), and (0,3) bands, were used as the input data for the merge fit procedure proposed by Albritton et al.80 and Coxon,81 giving the final rotational constants for the observed C1Σ+(ν = 0) Rydberg state in the 13C17O isotopologue. The estimated variance and the number of degrees of freedom of the merging were σM2 = 0.43 and fM = 4, respectively. The results are highlighted in Table 4.

In the next step, combination differences between corresponding lines of two bands belonging to the Herzberg (this work) and Ångström27,28 systems were calculated: CA(0,1)–BA(0,1), CA(0,2)–BA(0,2), and CA(0,1)–BA(1,1) with a common lower vibronic level, in accordance with the formula introduced by Jenkins and McKellar:82

 
image file: c4ra08222b-t1.tif (3)
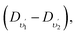where symbols used in the equation are commonly known. By plotting these combination differences against J(J + 1) a straight line is expected for a negligibly small difference image file: c4ra08222b-t2.tif and this condition is fulfilled quite good in the studied C–A system.

Thanks to this procedure, it was possible to precisely determine νCB00 and νCB01 parameters of the rovibronic structure differences of the C1Σ+(ν = 0) and B1Σ+(ν = 0 and 1) states in 13C17O. Within this calculation, the ΔBCB00 and ΔBCB01 rotational parameters differences were also obtained. The final values of νCB00 and ΔBCB00 parameters were calculated by means of a weighted arithmetic mean. All the results are collected in Table 5. A relative analysis of the Herzberg and Ångström band systems carried out in this way allowed for both elimination of the perturbation effect of the A1Π(ν = 1 and 2) state, as well as verification of the regularity of the C1Σ+(ν = 0) and B1Σ+(ν = 0 and 1) states. The Jenkins and McKellar functions of the Herzberg C1Σ+(ν = 0) → A1Π(ν = 1, 2) band system relative to the Ångström B1Σ+(ν = 0, 1) → A1Π(ν = 1, 2) transition in the 13C17O isotopologue are illustrated in Fig. 4.

Table 5 Molecular constants (in cm−1) of the C1Σ+(ν = 0) relative to the B1Σ+(ν = 0 and 1) vibrational levels in the CO moleculea
Quantum 13C17O 12C16O 13C16O
Experimentalb Calculated Calculated Calculated
a Uncertainties in parentheses represent one standard deviation in units of the last quoted digit.b Calculated by means of the rovibronic combination differences of the recorded lines of the Herzberg bands system obtained in this work and the respective lines of the Ångström system from ref. 27 and 28, on the basis of the formulae introduced by Jenkins and McKellar,82 in accordance with the description given in Section 4.c Calculated on the basis of values of band origins obtained in this work and given by Hakalla et al.,28 as a weighted arithmetic mean of the differences (ν0)CA01–(ν0)BA01 and (ν0)CA02–(ν0)BA02.d Calculated on the basis of values of band origins obtained in this work and given by Hakalla et al.,27 as the difference (ν0)CA01–(ν0)BA11.e Calculated on the basis of the difference of values of the merged molecular constants obtained in this work and by Hakalla et al.27,28 for the C1Σ+(ν = 0) and B1Σ+(ν = 0 and 1) levels, respectively.f The νCB10 quantum was calculated on the basis of the difference of values (σC–X10–σB–X00) given by Amiot et al.52g The νCB10 quantum was calculated on the basis of the difference of values (σC–X10–σB–X00) given by Tilford et al.51
νCB00 5001.80086 (12) 5001.792 (6)c    
νCB01 2990.8355 (30) 2990.877 (24)d    
νCB10     7149.438 (78)f 7101.64g
    7149.38e 5064.33g
νCB11     5067.276 (78)f  
    5067.12e  
ΔBCB00 × 103 −3.4805 (41) −3.483 (15)e    
ΔBCB01 × 102 1.989 (26) 1.9484 (32)e    


image file: c4ra08222b-f4.tif
Fig. 4 The Jenkins and McKellar functions82 of the Herzberg C1Σ+(ν = 0) → A1Π(ν = 1, 2) band system relative to the Ångström B1Σ+(ν = 0, 1) → A1Π (ν = 1, 2) transition in the 13C17O isotopologue. The small graphs have been included to precisely present the regions of J's origins.

At the next stage of molecular parameters' calculations, the rotational equilibrium constants for the C1Σ+ state were determined in the 13C17O molecule for the first time. It was carried out by means of the weighted least-squares method using the merged rotational constants obtained in this work for the C1Σ+(ν = 0) state and the individual rotational constants published by Cacciani et al.31 for the C1Σ+(ν = 1) state. The results are given in Table 6. Because only two vibrational levels of the C1Σ+ state are known for 13C17O, the constants were determined from a fit of the data in which the amount of data equals the number of determined parameters. In that case standard deviations of equilibrium parameters were calculated by means of the Gauss error propagation method.

Table 6 Vibrational quanta and equilibrium molecular constants for the C1Σ+ state in the CO moleculea
Constant Isotopologue
12C16O 12C17O 13C16O 12C18O 13C17O 13C18O
a In cm−1. Uncertainties in parentheses represent one standard deviation in units of the last quoted digit. Values given in braces were constrained during the calculation. Values calculated within this work are given in bold.b Calculated on the basis of TC1 and TC0 values given by Amiot et al.52c Calculated on the basis of TC1 and TC0 values given by Ubachs et al.50d Calculated on the basis of TC1 and TC0 values given by Haridass et al.40e Obtained on the basis of all values of the ΔGC1/2 vibrational quanta for the CO isotopologues, given in this table.f After Tilford and Simmons.51g After Kępa.68h Evaluated from the 12C16O parameters given by Kępa68 using Dunham's isotopic relationships.i Evaluated from the 12C16O parameters given by Tilford and Simmons51 using Dunham's isotopic relationships.j Calculated on the basis of the values of individual rotational constants given by Amiot et al.52 for the C1Σ+ state.k Calculated on the basis of the values of individual rotational constants given by Ubachs et al.50 for the C1Σ+ state.l After Kępa.63m Evaluated from the 12C16O parameters calculated in this work on the basis of the data provided by Amiot et al.,52 using Dunham's isotopic relationships.n Evaluated from the 12C16O parameters calculated in this work on the basis of the data provided by Ubachs et al.,50 using Dunham's isotopic relationships.o Calculated on the basis of the values of individual rotational constants given by Roncin et al.58 and Cacciani et al.31 for the C1Σ+, ν = 0, and 1 vibrational level, respectively.p Calculated on the basis of the values of individual rotational constants given by Kępa67 and Cacciani et al.31 for the C1Σ+, ν = 0 and 1 vibrational level, respectively.
ΔGC1/2 2146.529 (80)b 2120.20 (48)c 2099.40 (3)c 2095.43 (16)c   2046.95 (3)d
ωe 2173.6 (15)e   2125.1 (15)e 2121.0 (10)e 2096.8 (14)e 2071.4 (14)e
2175.92f          
2119.23 (16)g          
ωexe 13.45 (76)e   12.85 (72)e 12.80 (51)e 12.51 (70)e 12.21 (69)e
14.76f          
36.353 (79)g          
Be 1.95321 (53)k   1.86760 (11)k 1.86080 (32)k 1.81848 (39) 1.77504 (11)p
1.953276 (76)j   1.86716m 1.86004m 1.81770m 1.773932m
1.95436 (38)g       1.81820l  
1.95381 (36)l       1.81773i  
1.9533f       1.81871h  
αe × 102 1.954 (10)k   1.820 (20)k 1.860 (29)k 1.754 (55) 1.7052 (86)p
1.979 (15)j   1.850m 1.839m 1.856h 1.7128m
2.067 (41)g       1.760i  
2.005 (39)l       1.776n  
1.96f          
De × 106 6.1501 (51)k   5.6346 (62)k 6.64 (26)o 5.471 (49) 5.2431 (44)p
6.75 (35)j   5.6198n 5.58n 5.326n 5.0726n
        5.85m  
βe × 107 1.47 (10)k   {1.31}n {1.30}n {1.23}n {1.1554}n

In order to determine the vibrational equilibrium constants for the C1Σ+ Rydberg state in the 13C17O isotopologue, the values ΔGC1/2 vibrational quanta of the C1Σ+ state were determined using TC1 and TC0 values for 12C16O,52 12C17O,50 13C16O,50 12C18O,50 and 13C18O40 as well as using the weighted least-squares method. The vibrational equilibrium constants of the C1Σ+ state for 12C16O, 13C16O, 12C18O, and 13C18O were also calculated. The determination in this work of the vibrational equilibrium constants for the ordinary 12C16O molecule deserves special attention, because they aspire to solve the problem of incompatibility between the values given by Tilford et al.47,51 and by Kępa.62,68 Table 6 presents finally results.

The rotational and vibrational equilibrium constants allowed for determining parameters of the potential curve of the C1Σ+ Rydberg state in the 13C17O molecule: the RKR turning points, Y00 Dunham's factor, zero point energy and the re equilibrium inter-nuclear distance. These results are gathered in Table 7. Also, the Franck–Condon factors, relative intensities, and r-centroids for the Herzberg band system in the lesser-abundant 13C17O isotopologue were calculated, additionally using the rotational and vibrational equilibrium constants of the A1Π state calculated by Hakalla et al.27 The results are presented in Table 8.

Table 7 Vibrational levels and RKR turning points for the C1Σ+ Rydberg state of 13C17Oa
  Y00 0.5745
a G(ν) and Y00 are in cm−1; re, rmin, and rmax values are in Å.b The value of the C1Σ+ zero-point energy in the 13C17O isotopologue.c Extrapolated for the experimentally unobserved C1Σ+(ν = 2) vibrational level of the 13C17O isotopologue on the basis of rovibrational equilibrium constants listed in Table 6.
  re 1.121 71 (12)
ν = 0 G(ν) + Y00 1045.2725b
rmin 1.07765
rmax 1.17134
ν = 1 G(ν) + Y00 3117.0525
rmin 1.04858
rmax 1.21164
ν = 2c G(ν) + Y00 5163.8125
rmin 1.02999
rmax 1.24158

Table 8 Franck–Condon factors, relative intensities, and r-centroids for the Herzberg (C1Σ+ → A1Π) band system in the 13C17O isotopologuea
C1Σ+ (ν), A1Π (ν) 0 1 2b
a The values given one below the other denote – in the following order: Franck–Condon factors, relative intensities (in image file: c4ra08222b-t5.tif scaled to 10), and r-centroids (in Å) for each band.b Extrapolated for the experimentally unobserved C1Σ+(ν = 2) vibrational level in the 13C17O isotopologue on the basis of rovibrational equilibrium constants listed in Table 6.c Extrapolated for the experimentally unobserved A1Π(ν = 4) vibrational level in the 13C17O isotopologue on the basis of rovibrational equilibrium constants given by Hakalla et al.27
0 8.1321 × 10−2 0.2217 0.2852
3.4477 10.0000 10.0000
1.1833 1.2104 1.2377
1 0.1803 0.1810 2.2038 × 10−2
7.8652 7.7679 0.7376
1.1643 1.1906 1.2136
2 0.2183 3.6493 × 10−2 5.0347 × 10−2
10.0000 1.5369 1.6064
1.1461 1.1709 1.2015
3 0.1926 3.6515 × 10−3 0.1156
9.2294 0.1615 3.5132
1.1285 1.1590 1.1814
4c 0.1384 5.7538 × 10−2 5.8338 × 10−2
6.9187 2.6620 1.8281
1.1115 1.1380 1.1632

5. Isotopic dependences of the C1Σ+ Rydberg state of natural CO isotopologues

Carbon and oxygen have two: 12C, 13C and three: 16O, 17O, 18O natural and stable isotopes, respectively. Thus, these two elements make up six stable isotopologues of the CO molecule, from which the least-abundant is the 13C17O isotopologue. For example, all isotopologues, important for research into the Earth's atmosphere, have the following natural abundance: 98.7% (12C16O), 1.1% (13C16O), 0.2% (12C18O), 0.04% (12C17O), 0.0023% (13C18O), and 0.0004% (13C17O).17

Although the C1Σ+(ν = 0) state was observed in almost all natural isotopologues of CO, 13C17O and 14C17O still remained an exception. The experimental values of the rotational and vibrational equilibrium constants of the C1Σ+ Rydberg state have been so far known only for the ordinary 12C16O molecule.51,63,68

In order to study the reduced mass relationship of the ωe vibrational equilibrium constant for the C1Σ+ state of CO, values ωe were used that were calculated in this work for both the 13C17O, as well as for 12C16O, 13C16O, 12C18O, and 13C18O isotopologues, using methods described in Section 4. The results of the calculations are provided in Table 9.

Table 9 Rotational and vibrational equilibrium constants (in cm−1) used to calculate the isotopically invariant parameters of the C1Σ+ Rydberg state in the CO moleculea,b
  Isotopologue
a 1σ in parentheses.b For more details see Table 6 and text.
Constant 12C16O 13C16O 12C18O 13C17O 13C18O
ωe 2173.6 (15) 2125.1 (15) 2121.0 (10) 2096.8 (14) 2071.4 (14)
Be 1.953276 (76) 1.86760 (11) 1.86080 (32) 1.81848 (39) 1.77504 (11)

Using considerably extended data, we checked isotopic dependence of the ωe constant of the C1Σ+ state through plotting a graph of all known values of this quantity in a function of a μ−1/2 argument, which is graphically illustrated in Fig. 5. The linear graph suggests that for the model of isotopic dependence of the Ykl Dunham parameter,83 the following equation can be used:

 
image file: c4ra08222b-t3.tif(4)
where Ukl is an isotopically invariant parameter (Dunham coefficient), and μ is the reduced mass of the CO molecule. Conditions of using this formula have been discussed in detail in ref. 38.


image file: c4ra08222b-f5.tif
Fig. 5 Experimental values of the reduced mass dependence of ωe = f(μ−1/2) and Be = f(μ−1) equilibrium constants of the C1Σ+ Rydberg state in the carbon monoxide molecule. Corresponding values (see Table 9) were calculated for the 12C16O, 13C16O, 12C18O, 13C17O and 13C18O isotopologues. The regression lines in both graphs were plotted by means of the weighted linear least-square method. Standard deviation is impossible to show because of a relatively large scale of the plot.

Using eqn (4) in the form of image file: c4ra08222b-t4.tif and values of the ωe equilibrium constants for the C1Σ+ state, provided in Table 9, the experimental value of the U10 isotopically invariant parameter was calculated. The calculations were performed by means of the weighted linear least-square method. The result is highlighted in Table 10.

Table 10 Isotopically invariant parameters (in cm−1) for the C1Σ+ Rydberg state in the CO moleculea
Molecule State Isotopically invariant parameterb
a 1σ in parentheses.b The values were calculated for the strictly fulfilled the Born–Oppenheimer approximation (see description in Section 5).
CO C1Σ+ U10 5691.35 (45)
    U01 13.39749 (59)

Next, in order to study the reduced mass relationship of the Be rotational equilibrium constant for the C1Σ+ state of CO, Be values were used that were determined in this work for both 13C17O by means of the method described in Section 4, as well as for 12C16O, 13C16O, 12C18O, and 13C18O with the same method but on the basis of individual rotational constants B0 and B1 given for 12C16O,52 13C16O,50 12C18O,50 and 13C18O.31,40 The results of these calculations are given in Tables 6 and 9.

Using eqn (4), the isotopic dependence of the Be rotational molecular constant of the C1Σ+ state in a function of μ−1 argument was checked (see Fig. 5). A linear graph Be = f(μ−1) allows for the use of the eqn (4) in the form of Y01 = μ−1U01. The U01 isotopically invariant parameter was calculated by means of the weighted linear least-square method. The value obtained in this way is presented in Table 10.

If there is a breakdown of the Born–Oppenheimer approximation then instead of eqn (4), we should use the formula describing the Dunham coefficients in the following form:84

 
image file: c4ra08222b-t6.tif(5)
where MA, MB are the atomic masses, me is the electron mass, and ΔAkl, ΔBkl are dimensionless isotopically invariant coefficients. Unfortunately, an attempt to determine the Δ01 and Δ10 coefficients from eqn (5) on the basis of the U10 and U01 isotopically invariant parameters for the C1Σ+ state of CO did not give satisfactory results. Precision and isotopic variation of the calculated values ωe and Be are still not enough to determine possible, small deviations from the Born–Oppenheimer approximation. I believe that higher precision of determining the wavenumbers, maybe in the range of the fifth decimal place, will allow for a calculation of the Born–Oppenheimer approximation breakdown in the CO molecule in future analyses.

6. Irregularities inside the Herzberg band system in the 13C17O isotopologue

6.1. Perturbations of the A1Π(ν = 3) state in 13C17O

The most comprehensive observations and analyses of extensive and multi-state perturbations of the A1Π state in CO have been so far carried out in the ordinary 12C16O molecule,10,85–93 as it has been described in ref. 27. An improved analysis of the ν = 0 and 1 levels of this state in the 12C16O molecule has been recently presented by Niu et al.94 There is far less information on perturbations appearing in this state in the natural CO isotopologues,41,60,95–98 especially in the least-abundant 13C17O.27,28 The A1Π(ν = 3) vibrational level in 13C17O has not been studied so far.

The analysis of perturbations which appear in the A1Π(ν = 3) state of the 13C17O molecule, done in this work, was carried out in the aspect of confrontation of the perturbations observed and predicted from analyses of possibilities of interactions between the A1Π(ν = 3) state and nearby lying states in the region 70[thin space (1/6-em)]000–74[thin space (1/6-em)]000 cm−1.

To locate perturbations of the A1Π(ν = 3) state in the 13C17O isotopologue, the graph of functions fQ(J) with image file: c4ra08222b-t7.tif and gQ(J) with image file: c4ra08222b-t8.tif was used, which were introduced by Gerö99 and Kovács.100 They were plotted for respective lines of the branches of the C → A(0,3) band. The results are presented in Fig. 6 and 7. The non-linear function graph clearly indicates the location of the sought irregularities. Detailed description of the properties and applications of the fx and gx functions, where x = Q and image file: c4ra08222b-t9.tif was presented in my previous work.28


image file: c4ra08222b-f6.tif
Fig. 6 Rotational perturbations of the A1Π(ν = 3) state in the 13C17O isotopologue illustrated by the fx(J) functions of Kovács,100 where x = Q and image file: c4ra08222b-t12.tif. The graphs were plotted for the C1Σ+ → A1Π (0,3) transition. Uncertainties of single measurements are negligibly small in the scales used in these graphs.

image file: c4ra08222b-f7.tif
Fig. 7 Rotational perturbations of the of the A1Π(ν = 3) state in the 13C17O isotopologue illustrated by the gx(J) functions of Kovács,100 where x = Q and image file: c4ra08222b-t13.tif. The graphs were plotted for the C1Σ+ → A1Π (0,3) transition. Uncertainties of single measurements are negligibly small in the scales used in these graphs.

The predicted perturbations for both Λ-components of the A1Π(ν = 3; J = 0–45) state in 13C17O were determined by means of the rovibronic term-crossing diagram for this state and the nearby lying I1Σ−(ν = 4, 5), D1Δ(ν = 3, 4), e3Σ−(ν = 5, 6), a′3Σ+(ν = 13), a3Πr(ν = 14) and d3Δi(ν = 8, 9) states, and also by means of the parity selection rules.101 The above calculations were performed by means of molecular constants for the A1Π state determined in this work and those given by Field87 and Kittrell et al.102 for the 12C16O molecule and recalculated to the 13C17O molecule by means of standard isotopic relations83 for I1Σ−, e3Σ−, a′3Σ+, a3Πr, and d3Δi, as well as for D1Δ, respectively. The results are given in Fig. 8.


image file: c4ra08222b-f8.tif
Fig. 8 Rovibronic term crossing diagram for the perturbed A1Π(ν = 3) state in 13C17O isotopologue together with I1Σ−(ν = 4, 5), D1Δ(ν = 3, 4), e3Σ−(ν = 5, 6), a′3Σ+(ν = 13), a3Πr(ν = 14) and d3Δi(ν = 8, 9) perturbing states. Places marked with circles indicate regions for which the strongest perturbations are expected.

The identification of the perturbing state was made through analyses of correlations between the irregularities of experimental functions fQ(J) with image file: c4ra08222b-t10.tif and gQ(J) with image file: c4ra08222b-t11.tif (Fig. 6 and 7) and the predicted maxima of perturbations resulting from the rovibronic term-crossing diagram (Fig. 8) as well as the selection rules for perturbations.101 In Table 11 complete information was gathered on the places of perturbations and states responsible for them, which appear in the A1Π(ν = 3) level of the 13C17O molecule.

Table 11 Observed and predicted perturbations of the A1Π(ν = 3) vibrational level in 13C17Oa
Maximum of perturbation (J) of the Λ–doubling component Perturbing state
f e Triplet component Vibrational level
Observed Calculated Observed Calculated
a Asterisks indicates regions experimentally unverified.
* 9 * 9 F(3) d3Δi (ν = 8)
14–15 13 * 13 F(2)
18–20 17 16–17 17 F(1)
14–15 14     F(1) a′3Σ+ (ν = 13)
    16–17 17 F(2)
18–20 20     F(3)
* 34–35 * 34–35   D1Δ (ν = 4)
* 41–42       I1Σ − (ν = 5)
* 40 * 40   a3Πr (ν = 14)
* 44 * 44  
* 48 * 48  

The perturbations occurrence in the rotational structure of the observed bands can also be directly exhibited by a plot of the differences between the observed and calculated term values [T(ν, J)obs − T(ν, J)calc] versus the rotational quantum number J. Such a graph for the A1Π(ν = 3) state of the 13C17O molecule is presented in Fig. 9. As one can see, more or less discontinuities occur at different J values for A1Π(ν = 3) state. It is a characteristic phenomenon in the regions where perturbations occur.


image file: c4ra08222b-f9.tif
Fig. 9 Differences between the observed [T(ν, J)obs] and calculated [T(ν, J)calc] term values of the A1Π(ν = 3) vibrational level in the 13C17O isotopologue. See Table 11 and Section 6 for more details relevant to identification of the states responsible for the observed perturbations.

6.2. Regularity of the C1Σ+(ν = 0) Rydberg state in the 13C17O isotopologue

Studies on highly excited electron states of the CO molecule, carried out in the last two decades, and based on detailed analysis of the observed transitions C1Σ+(ν = 0) → X1Σ+,30,48,50 c3Π(ν = 0) → X1Σ+,30 and k3Π → X1Σ+[thin space (1/6-em)]30,103 in 12C16O molecule showed that the C1Σ+(ν = 0) Rydberg state lies closely both to the k3Π(ν = 1,2) as well as the c3Π(ν = 0) states and it should cross these states at low and higher J, respectively.30,50 Therefore, the C1Σ+(ν = 0) state should be irregular.

The Jenkins and McKellar functions of the Herzberg C1Σ+(ν = 0) → A1Π(ν = 1, 2) band system relative to the Ångström B1Σ+(ν = 0, 1) → A1Π(ν = 1, 2) transitions in the 13C17O isotopologue, presented in Fig. 4, completely eliminate the impact of the common A1Π (ν = 1, 2) lower rovibronic state. Therefore, a detailed analysis of the regular and linear course of these functions allows us to state precisely and unambiguously that in the observed spectrum regions and within experimental error limits, the observed C1Σ+(ν = 0) i B1Σ+(ν = 0 and 1) levels in the 13C17O isotopologue are completely regular and without rotational perturbations up to the observed Jmax, just as it is in the ordinary 12C16O molecule.30,50 Thus, an interaction between the C1Σ+(ν = 0) state and the k3Π and c3Π states in the 13C17O isotopologue, if it exists at all, is so weak that one cannot observe it within measuring error limits. At the same time, as Ubachs et al.19,50 conclude, the C1Σ+(ν = 0) state is not affected by accidental predissociation.

7. Discussion and conclusions

The first observations and analyses of the Herzberg (C1Σ+ → A1Π) band system in the natural and stable least-abundant 13C17O isotopologue enabled us to calculate the set of molecular constants both for the upper and lower state of this system as well as to present an outline of the first comprehensive characteristics of the C1Σ+ Rydberg state.

A careful investigation of the Kovács functions' course (see Fig. 6 and 7) and the [T(ν, J)obs − T(ν, J)calc] differences (see Fig. 9) for the A1Π(ν = 3) state in 13C17O, allowed for precise identification of all places of perturbations and states responsible for them. The results of these observations and analyses are given in Table 11. In Fig. 9 in the region J = 9–20 clearly multistate perturbations overlap deriving from the d3Δi(ν = 8) and a′3Σ+(ν = 13) states giving maximum deviations of the terms by almost 3 cm−1 for J = 17 (e-component) and causing an uncharacteristic course of rotational perturbation for J = 18–20 (f-component). Far weaker perturbations for J = 9 (e- and f-components) and J = 13 (e-component) are denoted in Table 11 as “experimentally unverified” because they are not distinguished from the impact of successive perturbations, closely lying to them. Therefore, we cannot state explicitly that they exist.

The difference of values between the νCB00 and νCB01 vibrational quanta should result in the value of vibrational distance between the ν = 0 and ν = 1 levels of the B1Σ+ electronic state, that is, the ΔGB1/2 vibrational quantum. The value calculated in this way for 13C17O on the basis of the data from Table 5 for the C → A system equals 2010.9654 (31) cm−1 and it remains consistent with the value of 2010.9622 (69) cm−1 calculated by Hakalla et al.27 on the basis of the analysis of 1 → ν′′ (ref. 27) and 0 → ν′′(ref. 28) progressions of the B → A band system.

During the process of determining experimental values of the νCB00 and νCB01 vibrational quanta for the 13C17O isotopologue, also the values of the ΔBCB00 = BC0 − BB0 and ΔBCB01 = BC0 − BB1 rotational quanta were calculated. They are presented in Table 5. These values equal −3.4805(41) × 10−3cm−1 and 1.989(26) × 10−2 cm−1, respectively. The results are consistent with the values calculated on the basis of direct difference of the merged rotational constants BC0 (this work) and BB0[thin space (1/6-em)]28 as well as BC0 (this work) and BB1,27 which equal −3.483(15) × 10−3 cm−1 and 1.9484(32) × 10−2 cm−1, respectively. This consistency confirms high quality of the calculations performed in this work.

As a result of the analyses carried out in this work, both vibrational and rotational equilibrium constants of the C1Σ+ state for 12C16O, 13C16O, 12C18O, 13C17O and 13C18O isotopologues were determined, which are given in Table 6. For many years an important problem has not been solved in the ordinary 12C16O molecule, that is, a considerable inconsistency between the values of the vibrational equilibrium constants ωe and ωexe, given by Tilford et al.,47,51 and those given by Kępa.62,68 The results presented in this work, that is ωe = 2173.6(15) cm−1 and ωexe = 13.45(76) cm−1 allow for the final solution of this problem in favour of the values given by Tilford et al.,47,51 which are consistent with the presented one within two standard deviations.

At the current stage of the research, it is still not possible to determine the ΔGC1/2 vibrational quantum for the C1Σ+ state in 13C17O by means of rovibrational combination differences104 because of the lack of observed transitions in this molecule from the C1Σ+(ν = 1) state to the A1Π state or from the C1Σ+(ν = 0) state to the X1Σ+ ground state. That is why I decided to assess this value on the basis of the determined vibrational equilibrium constants given in Table 6 and using the formula ΔGC1/2 = ωe − 2ωexe.104 The result is ΔGC1/2 = 2071.8 (28) cm−1 for the 13C17O isotopologue.

Conclusions

Presented high-quality measurements and analyses, as well as the precise results for the Herzberg (C1Σ+ → A1Π) band system, which has not been so far studied in 13C17O, allowed us to considerably extend the spectroscopic and quantum-mechanical information on the C1Σ+ Rydberg state and on the strongly perturbed A1Π state in the CO molecule.

Acknowledgements

I express my gratitude for the financial support of the European Regional Development Fund and the Polish state budget in the frame of the Carpathian Regional Operational Program (RPO WP) for the period 2007–2013 via the funding of the Centre for Innovation and Transfer of Natural Science and Engineering Knowledge of the University of Rzeszów. I express my deepest gratitude to Professor Mirosław Zachwieja and Professor Ryszard Kępa, as well as to Dr. Wojciech Szajna for their invaluable assistance with this research and its publication.

Notes and references

  1. E. Bayet, M. Gerin, T. G. Phillips and A. Contursi, Astron. Astrophys., 2006, 460, 467 CrossRef CAS.
  2. T. M. Dame, D. Hartmann and P. Thaddeus, Astrophys. J., 2001, 547, 792 CrossRef CAS.
  3. T. R. Greve, F. Bertoldi and I. Smail, et al., Mon. Not. R. Astron. Soc., 2005, 359, 1165 CrossRef CAS PubMed.
  4. P. J. Huggins, R. Bachiller, P. Planesas, T. Forveille and P. Cox, Astrophys. J., 2005, 160, 272 CAS.
  5. J. C. Bennett, C. S. Jamieson and R. I. Kaiser, Phys. Chem. Chem. Phys., 2010, 12, 4032 RSC.
  6. J. Najita, J. S. Carr and R. D. Mathieu, Astrophys. J., 2003, 589, 931 CrossRef CAS.
  7. G. Narayanan, M. H. Heyer and C. Brunt, et al., Astrophys. J., 2008, 177, 341 CAS.
  8. T. Oka, M. Nagai, K. Kamegai, K. Tanaka and N. Kuboi, Publ. Astron. Soc. Jpn., 2007, 59, 15 CAS.
  9. R. Visser, E. F. van Dishoeck and J. H. Black, Astron. Astrophys., 2009, 503, 323 CrossRef CAS PubMed.
  10. D. C. Morton and L. Noreau, Astrophys. J., Suppl. Ser., 1994, 95, 301 CrossRef CAS.
  11. N. Neininger, M. Guélin, H. Ungerechts, R. Lucas and R. Wielebinski, Nature, 1998, 395, 871 CrossRef CAS PubMed.
  12. T. L. Wilson and R. T. Rood, Annu. Rev. Astron. Astrophys., 1994, 32, 191 CrossRef CAS.
  13. N. Prantzos, O. Aubert and J. Audouze, Astron. Astrophys., 1996, 309, 760 CAS.
  14. T. L. Wilson and F. Matteucci, Annu. Rev. Astron. Astrophys., 1992, 4, 1 CrossRef.
  15. M. A. Frerking, W. D. Langer and R. W. Wilson, Astrophys. J., 1982, 262, 590 CrossRef CAS.
  16. M. A. K. Khalil, EOS, Transactions of the American Geophysical Union, 1995, 76, 353 Search PubMed.
  17. B. Sumpf, J. P. Burrows, A. Kissel, H.-D. Kronfeldt, O. Kurtz, I. Meusel, J. Orphal and S. Voigt, J. Mol. Spectrosc., 1998, 190, 226 CrossRef CAS.
  18. F. Bensch, I. Pak, J. G. A. Wouterloot, G. Klapper and G. Winnewisser, Astrophys. J., 2001, 562, L185 CrossRef CAS.
  19. W. Ubachs, I. Velchev and P. Cacciani, J. Chem. Phys., 2000, 113, 547 CrossRef CAS PubMed.
  20. G. Guelachvili, J. Mol. Spectrosc., 1979, 75, 251 CrossRef CAS.
  21. C. Puzzarini, L. Dore and G. Cazzoli, J. Mol. Spectrosc., 2003, 217, 19 CrossRef CAS.
  22. M. Winnewisser, B. P. Winnewisser and G. Winnewisser, Mol. Astrophys. ser. C, 1985, 157, 375 CAS.
  23. G. Winnewisser, B. S. Dumesh, I. Pak, L. A. Surin, F. Lewen, D. A. Roth and F. S. Rusin, J. Mol. Spectrosc., 1998, 192, 243 CrossRef CAS.
  24. G. Klapper, L. Surin, F. Lewen, H. S. P. Müller, I. Pak and G. Winnewisser, Astrophys. J., 2003, 582, 262 CrossRef CAS.
  25. D. Goorvitch, Astrophys. J., Suppl. Ser., 1994, 95, 535 CrossRef CAS.
  26. G. Guelachvili, D. de Villeneuve, R. Farrenq, W. Urban and J. Verges, J. Mol. Spectrosc., 1983, 98, 64 CrossRef CAS.
  27. R. Hakalla, W. Szajna and M. Zachwieja, J. Phys. Chem. A, 2013, 117, 12299 CrossRef CAS PubMed.
  28. R. Hakalla and M. Zachwieja, J. Mol. Spectrosc., 2012, 272, 11 CrossRef CAS PubMed.
  29. P. Cacciani, F. Brandi, J. P. Sprengers, A. Johansson, A. L'Huillier, C.-G. Wahlström and W. Ubachs, Chem. Phys., 2002, 282, 63 CrossRef CAS.
  30. J. Baker and F. Launay, Chem. Phys. Lett., 2005, 415, 296 CrossRef CAS PubMed.
  31. P. Cacciani, F. Brandi, I. Velchev, C. Lyngå, C.-G. Wahlström and W. Ubachs, Eur. Phys. J. D, 2001, 15, 47 CrossRef CAS.
  32. M. Eidelsberg, F. Launay, K. Ito, T. Matsui, P. C. Hinnen, E. Reinhold, W. Ubachs and K. P. Huber, J. Chem. Phys., 2004, 121, 292 CrossRef CAS PubMed.
  33. M. Eidelsberg, Y. Sheffer, S. R. Federman, J. L. Lemaire, J. H. Fillion, F. Rostas and J. Ruiz, Astrophys. J., 2006, 647, 1543 CrossRef CAS.
  34. G. D. Dickenson, A. C. Nortje, C. M. Steenkamp, E. G. Rohwer and A. du Plessis, Astrophys. J., 2010, 714, L268 CrossRef CAS.
  35. R. Hakalla, W. Szajna, M. Zachwieja and R. Kępa, Acta Phys. Pol., A, 2012, 122, 674 CAS.
  36. R. Hakalla, W. Szajna and M. Zachwieja, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 215102 CrossRef.
  37. R. Kępa, M. Ostrowska-Kopeć, I. Piotrowska, M. Zachwieja, R. Hakalla, W. Szajna and P. Kolek, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 045101 CrossRef.
  38. R. Hakalla, M. Zachwieja and W. Szajna, J. Quant. Spectrosc. Radiat. Transfer, 2014, 140, 7 CrossRef CAS PubMed.
  39. M. Drabbels, J. Heinze, J. J. ter Meulen and W. L. Meerts, J. Chem. Phys., 1993, 99, 5701 CrossRef CAS PubMed.
  40. C. Haridass, S. P. Reddy and A. C. LeFloch, J. Mol. Spectrosc., 1994, 168, 429 CrossRef CAS.
  41. C. V. V. Prasad and S. P. Reddy, J. Mol. Spectrosc., 1985, 130, 62 CrossRef.
  42. N. de Oliveira, D. Joyeux, D. Phalippou, J. C. Rodier, F. Polack, M. Vervloet and L. Nahon, Rev. Sci. Instrum., 2009, 80, 043101 CrossRef CAS PubMed.
  43. N. de Oliveira, M. Roudjane, D. Joyeux, D. Phalippou, J.-C. Rodier and L. Nahon, Nat. Photonics, 2011, 5, 149 CrossRef CAS.
  44. H. Lefebvre-Brion, H. P. Liebermann and G. J. Vázquez, J. Chem. Phys., 2010, 132, 024311 CrossRef CAS PubMed.
  45. H. Lefebvre-Brion and M. Eidelsberg, J. Mol. Spectrosc., 2012, 271, 59 CrossRef CAS PubMed.
  46. J. J. Hopfield and R. T. Birge, Phys. Rev., 1927, 29, 922 CAS.
  47. S. G. Tilford and J. T. Vanderslice, J. Mol. Spectrosc., 1968, 26, 419 CrossRef CAS.
  48. M. Eidelsberg and F. Rostas, Astron. Astrophys., 1990, 235, 472 CAS.
  49. M. Eidelsberg, J. J. Benayoun, Y. Viala and F. Rostas, Astron. Astrophys., Suppl. Ser., 1991, 90, 23 Search PubMed.
  50. W. Ubachs, P. C. Hinnen, P. Hansen, S. Stolte, W. Hogervorst and P. Cacciani, J. Mol. Spectrosc., 1995, 174, 388 CrossRef CAS.
  51. S. G. Tilford and J. D. Simmons, J. Phys. Chem. Ref. Data, 1972, 1, 147 CrossRef CAS PubMed.
  52. C. Amiot, J.-Y. Roncin and J. Verges, J. Phys. B: At. Mol. Phys., 1986, 19, L19 CrossRef CAS.
  53. P. J. H. Tjossem and K. C. Smyth, J. Chem. Phys., 1989, 91, 2041 CrossRef CAS PubMed.
  54. K. Tsnkiyama, M. Tsnkakoshi and T. Kasnya, J. Appl. Phys., 1990, B50, 23 CrossRef.
  55. A. Le Floch, J. Mol. Spectrosc., 1992, 155, 177 CrossRef CAS.
  56. M. Drabbels, W. L. Meerts and J. J. ter Meulen, J. Chem. Phys., 1993, 99, 2352 CrossRef CAS PubMed.
  57. R. Kępa, Chem. Phys., 1986, 110, 123 CrossRef.
  58. J.-Y. Roncin, A. Ross and E. Boursey, J. Mol. Spectrosc., 1993, 162, 353 CrossRef CAS.
  59. H. Hasegawa and K. Tsukiyama, Appl. Phys. B: Lasers Opt., 1996, 63, 311 Search PubMed.
  60. C. V. V. Prasad, S. P. Reddy and M. Sandys-Wunsch, J. Mol. Spectrosc., 1985, 114, 436 CrossRef CAS.
  61. R. K. Asundi, R. K. Dhumwad and A. B. Patwardhan, J. Mol. Spectrosc., 1970, 34, 528 CrossRef CAS.
  62. R. Kępa, Acta Phys. Pol., 1969, A36, 1109 Search PubMed.
  63. R. Kępa, Acta Phys. Acad. Sci. Hung., 1978, 45, 133 CrossRef.
  64. J. D. Janjić, L. J. Čonkić, D. S. Pešić, R. Kepa and M. Rytel, J. Mol. Spectrosc., 1978, 72, 297 CrossRef.
  65. R. Kępa, Acta Phys. Pol., 1982, A62, 467 Search PubMed.
  66. R. Kępa, Chem. Phys., 1986, 110, 123 CrossRef.
  67. R. Kępa, Can. J. Phys., 1988, 66, 1012 CrossRef.
  68. R. Kępa, J. Mol. Spectrosc., 1989, 135, 119 CrossRef.
  69. R. Kępa, A. Para, M. Rytel and J. Janjić, Acta Phys. Hung., 1990, 68, 205 Search PubMed.
  70. R. Kępa, M. Jarosz, A. Kocan, I. Piotrowska-Domagała and K. Porada, Acta Phys. Hung. New Ser.: Heavy Ion Phys., 1998, 8, 207 Search PubMed.
  71. R. A. Bacis, J. Phys. E: Sci. Instrum., 1976, 9, 1081 CrossRef CAS.
  72. W. Szajna and M. Zachwieja, Eur. Phys. J. D, 2009, 55, 549 CrossRef CAS.
  73. W. Szajna and M. Zachwieja, J. Mol. Spectrosc., 2010, 260, 130 CrossRef CAS PubMed.
  74. W. Szajna, M. Zachwieja, R. Hakalla and R. Kępa, Acta Phys. Pol., A, 2011, 120, 417 CAS.
  75. W. Szajna and M. Zachwieja, J. Mol. Spectrosc., 2011, 269, 56 CrossRef CAS PubMed.
  76. M. Zachwieja, W. Szajna and R. Hakalla, J. Mol. Spectrosc., 2012, 275, 53 CrossRef CAS PubMed.
  77. B. A. Palmer and R. Engleman, Atlas of the Thorium Spectrum, Los Alamos National Laboratory, Los Alamos NM, 1983, unpublished Search PubMed.
  78. R. F. Curl and C. B. Dane, J. Mol. Spectrosc., 1988, 128, 406 CrossRef CAS.
  79. J. K. G. Watson, J. Mol. Spectrosc., 1989, 138, 302 CrossRef CAS.
  80. D. L. Albritton, A. L. Schmeltekopf and R. N. Zare, J. Mol. Spectrosc., 1977, 67, 132 CrossRef CAS.
  81. J. A. Coxon, J. Mol. Spectrosc., 1978, 72, 252 CrossRef CAS.
  82. F. A. Jenkins and A. McKellar, Phys. Rev., 1932, 42, 464 CrossRef CAS.
  83. J. L. Dunham, Phys. Rev., 1932, 41, 721 CrossRef CAS.
  84. J. K. G. Watson, J. Mol. Spectrosc., 1980, 80, 411 CrossRef CAS.
  85. P. H. Krupenie, The Band Spectrum of Carbon Monoxide, National Bureau of Standards, Washington, DC, 1966 Search PubMed.
  86. J. D. Simmons, A. M. Bass and S. G. Tilford, Astrophys. J., 1969, 155, 345 CrossRef CAS.
  87. R. W. Field, PhD thesis, Harvard University, Cambridge, MA, 1971.
  88. R. W. Field, B. G. Wicke, J. D. Simmons and S. G. Tilford, J. Mol. Spectrosc., 1972, 44, 383 CrossRef CAS.
  89. A. C. Le Floch, F. Launay, J. Rostas, R. W. Field, C. M. Brown and K. Yoshino, J. Mol. Spectrosc., 1987, 121, 337 CrossRef CAS.
  90. A. C. Le Floch, PhD thesis, University Paris-Sud, Orsay, France, 1989.
  91. A. C. Le Floch, J. Mol. Spectrosc., 1992, 155, 177 CrossRef CAS.
  92. M. Drabbels, J. J. ter Meulen and W. L. Meerts, Chem. Phys. Lett., 1997, 267, 127 CrossRef CAS.
  93. M. Majumder, N. Sathyamurthy, H. Lefebvre-Brion and G. J. Vázquez, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 185101 CrossRef.
  94. M. L. Niu, E. J. Salumbides, D. Zhao, N. de Oliveira, D. Joyeux, L. Nahon, R. W. Field and W. Ubachs, Mol. Phys., 2013, 111, 2163 CrossRef CAS.
  95. L. M. Beaty, V. D. Brown, K. P. Huber and A. C. Le Floch, Astrophys. J., Suppl. Ser., 1997, 109, 269 CrossRef CAS.
  96. L. Gavilan, J. L. Lemaire, M. Eidelsberg, S. R. Federman, G. Stark, A. N. Heays, J. H. Fillion, J. R. Lyons and N. de Oliveira, J. Phys. Chem. A, 2013, 117, 9644 CrossRef CAS PubMed.
  97. A. Du Plessis, E. G. Rohwer and C. M. Steenkamp, Astrophys. J., Suppl. Ser., 2006, 165, 432 CrossRef CAS.
  98. R. Kępa, M. Ostrowska-Kopeć and I. Piotrowska, J. Mol. Spectrosc., 2011, 266, 104 CrossRef PubMed.
  99. L. Gerö, Z. Phys., 1935, 93, 669 CrossRef.
  100. I. Kovács, Rotational Structure In the Spectra of Diatomic Molecules, Akadémai Kiadó, Budapest, London, Hilger, 1969 Search PubMed.
  101. H. Lefebvre-Brion and R. W. Field, Perturbation in the Spectra of Diatomic Molecules, Academic Press, Orlando, 1986 Search PubMed.
  102. C. Kittrell and B. A. Garetz, Spectrochim. Acta, Part A, 1989, 45, 31 CrossRef.
  103. J. Baker and F. Launay, J. Mol. Spectrosc., 1994, 165, 75 CrossRef CAS.
  104. G. Herzberg, Molecular Spectra and Molecular Structure. I. Spectra of Diatomic Molecules, Van Nostrand: Princeton, NJ, 1950 Search PubMed.
This journal is © The Royal Society of Chemistry 2014
Click here to see how this site uses Cookies. View our privacy policy here.