A computational study on the mechanism and kinetics of the reaction between CH3CH2S and OH†
Tianlei Zhang*a,
Rui Wanga,
Liting Zhoua,
Zhiyin Wanga,
Qiong Xua,
Suotian Mina and
Wenliang Wang*b
aSchool of Chemical & Environment Science, Shaanxi University of Technology, Hanzhong, Shaanxi 723001, China. E-mail: ztianlei88@163.com; Fax: +86-0916-2641083; Tel: +86-0916-2641083
bKey Laboratory for Macromolecular Science of Shaanxi Province, School of Chemistry & Chemical Engineering, Shaanxi Normal University, Xi'an, Shaanxi 710062, China. E-mail: wlwang@snnu.edu.cn
First published on 13th November 2014
Abstract
The reaction mechanism of CH3CH2S with OH radicals is studied at the CBS-QB3 level of theory. Five substitution processes and eleven addition–elimination channels are identified for the title reaction. The calculated results indicate that addition–elimination channels CH3CHS + H2O, CH2CH2 + HSOH, CH3CHSO + H2 and CH3CH2SH + O are dominant. Other channels may be negligible due to the high barrier heights. Rate constants and branching ratios are estimated by means of the conventional transition state theory with zero curvature tunnelling over the temperature range of 200–3000 K. The calculation shows that the overall rate constant in the temperature of 200–3000 K is mainly dependent on the channels CH3CHS + H2O, CH2CH2 + HSOH and CH3CH2SH + O. The three-parameter expression for the total rate constant is fitted to be ktotal = 7.42 × 10−21T2.63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−772.43/T) cm3 molecule−1 s−1 between 200–3000 K.
exp(−772.43/T) cm3 molecule−1 s−1 between 200–3000 K.
1. Introduction
CH3CH2S, CH3S, CH2SH, CH2S and HCS and other sulfur-containing small organic molecules released from fuel combustion and the oxidation of sulfur, have become one of the major pollution sources of the atmospheric environment.1–3 These sulfur-containing compounds have been widely studied because of their negative effects on the Earth's environment.4–8 CH3CH2S is a typical representative of sulfur-containing small organic molecules, which is the main product of laser photolysis of C2H5SSC2H5 or C2H5SH and also an important reaction intermediate.9–11 Although this sulfur-contained small molecules shows a very low level in Earth's atmosphere, but it have a significant impact on climate change and acid rain formation. Therefore, the stability of this sulfur-contained small molecule, its reactivity with atmospheric free radicals and how to eliminate its effect on air pollution has attracted wide attention. OH are one of the most important atmospheric oxidant.12,13 Outer shells of OH have unpaired electron, it always tends to get electronics, with high activity, and thus the role of atmospheric trace constituents from strong oxidants, for many important compounds, reaction with OH is their degradation rate-determining step.14–16The reaction of sulfur-contained small molecules with OH radical is one of the most important degradation processes in the atmosphere.17–19 Zhang et al.20 investigated the mechanism of the reaction of C2H5S with HO2 at the CCSD(T)/aug-cc-pVDZ//B3LYP/6-311G(2d,p) method. They obtained both hydrogen abstraction and addition–elimination reaction pathways on the singlet and triplet potential surfaces. Cao et al.21 theoretically investigated the reaction mechanism of CH3SCH2CH3 with OH at the CCSD(T)/6-311++G(d,p)//MP2/6-31+G(2d,p). They measured The CVT/SCT rate constants of hydrogen abstraction channels over the temperature range of 200–900 K. However, the reaction of CH3CH2S with OH has not been reported so far to the best of our knowledge.
The objective of the present study on the reaction of C2H5S with OH is to exploit its possible reaction pathways, to shed light on the reaction mechanism, to provide new insight into the new sink of aliphatic thiols in the atmosphere, and fundamental foundations for preventing and eliminating air pollutions from aliphatic thiols. So in this paper, the reaction mechanism of CH3CH2S with OH radical is studied. Then based on the obtained mechanism information, the rate constants of the major channel are calculated.
2. Computational method
The quantum chemistry calculations reported in this work were carried out with Gaussian 09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 program packages. We used the B3LYP/CBSB7 and UB3LYP/CBSB7
22 program packages. We used the B3LYP/CBSB7 and UB3LYP/CBSB7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23,24 method to optimize and characterize the closed-shell and open-shell stationary points respectively. At this level of theory, we also calculated the harmonic vibrational frequencies to verify the nature of the corresponding stationary points (minima or transition state), to provide the zero-point vibrational energy (ZPE) and to determine the thermodynamic contributions to the enthalpy and free energy. Moreover, to ensure that the transition states were connected to the desired reactants and products, we performed intrinsic reaction coordinate (IRC)25–28 calculations. In order to obtain more accurate relative energies, based on the optimized geometries, we performed single-point CBS-QB3
23,24 method to optimize and characterize the closed-shell and open-shell stationary points respectively. At this level of theory, we also calculated the harmonic vibrational frequencies to verify the nature of the corresponding stationary points (minima or transition state), to provide the zero-point vibrational energy (ZPE) and to determine the thermodynamic contributions to the enthalpy and free energy. Moreover, to ensure that the transition states were connected to the desired reactants and products, we performed intrinsic reaction coordinate (IRC)25–28 calculations. In order to obtain more accurate relative energies, based on the optimized geometries, we performed single-point CBS-QB3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29,30 and CCSD(T)/aug-cc-pVTZ31 for closed-shell and performed single-point UCBS-QB3 and UCCSD(T)/aug-cc-pVTZ calculations for open-shell stationary points. Finally, the kinetic properties of the system were calculated using conventional transition state theory (TST)32–34 in the VKLab35–37 program coupled with the steady state approximation.
29,30 and CCSD(T)/aug-cc-pVTZ31 for closed-shell and performed single-point UCBS-QB3 and UCCSD(T)/aug-cc-pVTZ calculations for open-shell stationary points. Finally, the kinetic properties of the system were calculated using conventional transition state theory (TST)32–34 in the VKLab35–37 program coupled with the steady state approximation.
These calculations made use of the energies obtained at the CBS-QB3 level of theory and the partition functions computed at the B3LYP/CBSB7 level of theory. The tunnelling correction to the rate constants was computed using the zero-order approximation of a vibrationally adiabatic potential energy surface (PES) with zero curvature. In this case, the unsymmetrical Eckart potential energy barrier was used to approximate the potential energy curve.
3. Results and discussion
The values 〈S2〉 of all the species involving the C2H5S + OH reaction were shown in Table S1.† As illustrated in Table S1,† after spin annihilation for the singlet, doublet and triplet species, the values of 〈S2〉 were respectively nearly 0.0000, 0.7500, and 2.0000 at the B3LYP/CBSB7 level of theory, so the spin contamination is not severe. All optimized geometries of the reactants, complexes, transition states, and products involving the nucleophilic substitution reaction and addition–elimination channels at the B3LYP/CBSB7 level of theory along with the available experimental38–42 values were displayed in Fig. 1, 3 and 5. For the species (OH, 1CH3CHS, H2O, 1CH2CH2S, 1CH2S, CH3, CH3OH, CH4, CH2CH2 and H2), the mean absolute deviations of bond lengths and bond angles between the calculated values at the B3LYP/CBSB7 level of theory and the corresponding experiment ones are 0.006 Å and 0.06°, respectively. So the calculated bond lengths and angles at the B3LYP/CBSB7 level of theory are acceptable. Besides, experimental data is not available with which to judge the accuracy of our results, therefore Table S2† lists the relative energies (ΔE), enthalpies (ΔH(298)), and free energies (ΔG(298)) to the reactants (C2H5S + OH) at the CBS-QB3 level as well as the heats of formation for every channel evaluated by CCSD(T)/aug-cc-pVTZ//B3LYP/CBSB7 calculations. By comparing the reaction enthalpy results obtained with CCSD(T)/aug-cc-pVTZ//B3LYP/CBSB7 and CBS-QB3, energetic results agree to 1–2 kcal mol−1. Therefore, the CBS-QB3 level of theory was able to describe the title reaction reliably. So potential energy profile of nucleophilic substitution reaction and addition–elimination channels for the reaction of CH3CH2S with OH at the CBS-QB3 level of theory were presented in Fig. 2, 4 and 6. | ||
| Fig. 2 Schematic energy diagram for the singlet and triplet nucleophilic substitution reaction of C2H5S + OH at the CBS-QB3 level of theory. | ||
3.1. Reaction mechanism
Five substitution processes (R1–R5) and eleven addition–elimination channels (R6–R16) were modeled for the title reaction, which were listed in Scheme S1–S3,† as well as Fig. 2, 4 and 6, where “IM” and “IMF” denote post-reactant complex and pre-product complex of the corresponding reaction pathway, respectively. For simplicity, the singlet and triplet species are signed 1 and 3 as superscription.Singlet channels of Channel R1 and R2 proceeded by the oxygen atom of OH radical respectively attacking to the carbon atom of α-CH2 and β-CH3, simultaneously C(1)–C(2) bond breaking. The corresponding transition state was TS1 and TS2, respectively. In TS1, the breaking C(1)–C(2) bond shown in Fig. 1 was elongated by 0.686 Å compared with that in CH3CH2S, while the forming O–C(2) bond was 0.630 Å longer than that in SCH2OH. In TS2, the breaking C(1)–C(2) bond is elongated by 0.359 Å compared with that in CH3CH2S, while the forming O–C(2) bond is 0.495 Å longer than that in CH3OH. The barrier height of Channel R1 and R2 was 24.78 and 18.23 kcal mol−1, respectively.
Similar with singlet Channel R1, the triplet oxygen-to-(α)carbon nucleophilic substitution channel (R3) is also located to produce SCH2OH + CH3. The barrier height of Channel R3 is 31.95 kcal mol−1, which is higher by 7.17 kcal mol−1 than that of the singlet channel R1, showing that the formation of SCH2OH + CH3 mainly take from Channel R1. The triplet oxygen-to-(β) carbon nucleophilic substitution channel (R4) is located to produce CH3OH + 3CH2S with the energy barrier of 33.34 kcal mol−1. Compared with the barrier of singlet oxygen-to-(β) carbon nucleophilic substitution channel (R2), the barrier height of Channel R4 is higher by 15.11 kcal mol−1, indicating that oxygen-to-(β) carbon nucleophilic substitution reaction mainly occurs on the singlet potential energy surface.
Differently from singlet nucleophilic substitution reaction that oxygen-to-sulfur nucleophilic substitution could not taken place due to the stability of 1CH3CH2SOH, the triplet oxygen-to-sulfur nucleophilic substitution channel (R5) is located to produce CH3 + CH2SOH. The barrier height of Channel R5 was 30.02 kcal mol−1. This was lower by 1.93–3.32 kcal mol−1 than that of triplet Channels R3 and R4, but it was higher by 5.24–11.29 kcal mol−1 than that of singlet Channels R1 and R2. From above mechanism elucidation, it can be concluded that triplet nucleophilic substitution mechanisms are more unfeasible than the singlet because of the higher barrier heights. The nucleophilic substitution reaction of C2H5S + OH should mainly occur on the singlet PES. Moreover, singlet oxygen-to-(β) carbon nucleophilic substitution channel (R2) is most favorable nucleophilic substitution channel.
3.1.2.1 The channel of H2O formation. Five hydrogen atoms of the CH3CH2S are distributed into the two groups, which are, H atom in α-CH2 (α-position carbon atom adjacent to the sulfur atom) and β-CH3 (carbon atom stands away from the sulfur atom). Thus, two possible reaction of hydrogen abstraction from CH3CH2S by OH radical are investigated on both singlet and triplet potential energy surface (singlet channels (R6 and R7) and triplet channels (R8 and R9)). Moreover, similar with the reaction between CH3SCH2CH3 and OH,43 each reaction can occur in more than one pathway due to the effect of sulfur atom of CH3CH2S.
Before the transition state and the products, singlet channels R6 and R7 (shown in Fig. 4) begin with the 1CH3CH2SOH intermediate, whose structure is loose with the O atom of OH and the S atom of CH3CH2S separation of 1.699 Å. The relative energy of 1CH3CH2SOH to the reactants (CH3CH2S + OH) is −69.82 kcal mol−1 at the CBS-QB3 level of theory. For channel R6, starting from 1CH3CH2SOH, products (CH3CHS + H2O) were obtained via transition state TS6a, TS6b, which were labeled as Path R6a and R6b, respectively. Transition state TS6a, and TS6b differentiated mainly from each other in the relative orientation of the hydrogen atoms of OH radical. Such geometrical discrepancy may leads that TS6b was only lower by 0.12 kcal mol−1 than that of TS6a.
For channel R7, beginning with 1CH3CH2SOH, products (CH2CH2S + H2O) can be obtained via TS7a and TS7b, respectively. The difference between TS7a and TS7b mainly lies in dihedral angle ∠HO(4)H(7)C(2) (in Fig. 3). Hydrogen atom of the OH radical is directed toward the sulfur atom in TS7a (∠HO(4)H(7)C(2) = 109.8°), while it is stays away from the sulfur atom in TS7b (∠HO(4)H(7)C(2) = −92.6°). The imaginary frequencies of TS7a and TS7b are 1602i cm−1 and 1490i cm−1, respectively. The relative energy of TS7a and TS7b to the reactants (CH3CH2S + OH) is respectively −2.04 and −2.40 kcal mol−1, which is higher by 15.60–15.84 kcal mol−1 than that of TS6a (−17.88 kcal mol−1) and TS6b (−18.00 kcal mol−1), indicating that, for singlet H-abstraction channels, Channel R6 is easily to occur for the lower barrier heights compared to channel R7.
Similar to the singlet H-abstraction processes (Channels R6 and R7), the corresponding triplet α-CH2 site and β-CH3 site H-abstraction reaction were found beginning with the formation of intermediate 3CH3CH2SOH before the transition state and the products. From the geometrical point of view as depicted in Fig. 3, the bond distance between the O atom of OH and the S atom of CH3CH2S in 3CH3CH2SOH complex is stretched by 0.419 Å compared with the corresponding bond distance in 1CH3CH2SOH. Such discrepancy may lead that the relative energy of 3CH3CH2SOH to the reactants (CH3CH2S + OH) is higher by 59.5 kcal mol−1 than that of 1CH3CH2SOH to the reactants (CH3CH2S + OH). Starting from 3CH3CH2SOH complex, triplet α-CH2 site and β-CH3 site H-abstraction reaction occurs via Channel R8 (TS8a, TS8b) and Channel R9 (TS9a, TS9b and TS9c), respectively. Compared with the corresponding transition states in singlet H-abstraction processes (Channels R6 and R7), triplet transition states shown in Fig. 3 were different in two respects. First, there is not the formation of S–O bond in triplet transition states. Second, the C–H–O bond angle in triplet transition state is less bent (e.g., ∠O(4)H(5)C(1) 134.7° in TS6a vs. 160.3° in TS8a; ∠O(4)H(7)C(2) 154.4° in TS7a vs. 173.4° in TS9a). It is shown in Fig. 4 that the relative energy of TS8a and TS8b in Channel R8 is lower by 1.23–5.91 kcal mol−1 than that of the TS9a, TS9b and TS9c in Channel R9. This indicates that triplet α-CH2 H-abstraction reaction (Channel R8) is easily to take place than triplet β-CH3 site H-abstraction reaction (Channel R9). However, compared with singlet α-CH2 H-abstraction reaction (Channel R6), the relative energy of TS8a and TS8b in Channel R8 is higher by 16.70–17.34 kcal mol−1 than that of the TS6a, and TS6b in Channel R1.
 | ||
| Fig. 4 Schematic energy diagram for the singlet (a) and triplet (b) channels of H2O formation in the addition–elimination reaction of C2H5S + OH at the CBS-QB3 level of theory. | ||
According to the discussed above, for the activity of hydrogen abstraction, the singlet channels are stronger than triplet channel, and for the activity of hydrogen abstraction of the singlet channel, the α-carbon atom is stronger than β-carbon atom (the order is: α-CH2 (R6) > β-CH3 (R7) > α-CH3 (R8) > β-CH3 (R9)). Atomic Mulliken charge of α-carbon atom (α-CH3, 0.0464e) is more electropositive than that of β-CH3 (0.1231e), which leads to the C–H bond of α-position weaker than that of β-position. On the other hand, the stability orders of the product radicals, 1CH3CHS > 1CH2CH2S > 3CH3CHS > 3CH2CH2S, produced by R6, R7, R8 and R9, respectively, is in consistent with the activity order of hydrogen abstraction. This is possibly because the substituent at the unpaired electron position influences on the stability of the above-mentioned radicals.
3.1.2.2 The channels of CH4 formation. As described above that 1CH3CH2SOH was much more stable than 3CH3CH2SOH, all the addition–elimination channels R10–R16 were taken into account beginning with pre-reactant complex 1CH3CH2SOH. Similar with the reaction between CH3 and C2H5OH,44 Channels R10 and R11 in Fig. 6 have been considered that the C atom of CH3 respectively abstracts the hydrogen atom from C(1) and O(4) sites in 1CH3CH2SOH with the H3C⋯H–X bond (where X denotes HCSOH and CH2SO) in their transition states. For Channel R10, as shown in Fig. 5, one of the two H atoms of the CH2 group in 1CH3CH2SOH can migrate toward the C atom in the CH3 group to produce CH4 + HCSOH via TS10. The breaking C(1)–C(2) bond was elongated from 1.523 Å in 1CH3CH2SOH to 2.198 Å in TS10. The barrier height of R10 was 79.09 kcal mol−1. Channel R11 leads to the formation of CH4 + CH2SO via TS11. The product CH2SO can be further formed to cyclic geometry (c-CH2SO) via transition state TS11-1 with the barrier height of 52.11 kcal mol−1. The breaking O–H bond in TS11 was 1.216 Å much longer than the corresponding value in 1CH3CH2SOH. The forward potential barrier of Channel R11 at the CBS-QB3 level was 74.52 kcal mol−1, which was lower by 4.57 kcal mol−1 than that of Channel R10. The higher C–H dissociation energy (C–H, 473.0 kJ mol−1; O–H, 436.0 kJ mol−1) of CH2SOH moiety may be responsible for the higher barrier of Channel 10.
 | ||
| Fig. 6 Schematic energy diagram for the singlet addition–elimination reaction of C2H5S + OH at the CBS-QB3 level of theory. | ||
3.1.2.3 The channels of C2H4 formation. For Channel R12, our result presented in Fig. 5 shows that HOSH elimination from 1CH3CH2SOH occurs via a four-centered (H(9)–S(3)–C(2)–C(1)) transition state TS12 with C1 symmetry. The dihedral angle of the H atom in the four centered-ring H(9)-S(3)-C(2)-C(1) is −0.5°. The breaking C–H and C–S bonds in TS12 are 0.333 and 0.552 Å longer than those in 1CH3CH2SOH. TS12 lies below the reactants C2H5S + OH by 13.28 kcal mol−1 at the CBS-QB3 level, which is respectively lower by 22.55 kcal mol−1 and 17.98 kcal mol−1 than the corresponding values of TS10 and TS11. This indicates that HOSH elimination (Channel R12) is much favorable than the C atom of CH3 respectively abstracts the hydrogen atom from C(1) and O(4) sites in 1CH3CH2SOH (Channels R10 and R11) kinetically.
3.1.2.4 The channels of H2 formation. As shown in Fig. 5, Channels R13 and R14 are the C–H cleavage and the H2-elimination reactions. Differently from Channel R13 that the H atom of the OH group and one of the two H atoms from the CH2 group in 1CH3CH2SOH form H2 via HHO(4)S(3)C(1) five-member-ring transition state TS13, in Channel R14, two H atoms each from the CH3 and OH groups in 1CH3CH2SOH, form a HHO(4)S(3)C(1)C(2) six-member-ring transition state TS14, resulting in H2 elimination to produce H2, CH2
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 and SO. Comparing the two H2-elimination processes in Channels R13 and R14, we see that TS14 is about 11.58 kcal mol−1 higher than TS13. The difference may be ascribed to the fact that a strong stereo repulsion force from the CH3 group exists and additional C(1)–S(3) bond breaking in TS14.
CH2 and SO. Comparing the two H2-elimination processes in Channels R13 and R14, we see that TS14 is about 11.58 kcal mol−1 higher than TS13. The difference may be ascribed to the fact that a strong stereo repulsion force from the CH3 group exists and additional C(1)–S(3) bond breaking in TS14.
3.1.2.5 The channels of CH3CH2SH and CH3OH formation. As shown in Fig. 5, we also calculated other reaction channels consisting CH3CH2SH + O (Channel R15) and CH3OH + CH2S (Channel R16) channels. Channel R16 may be negligible for the high relative energy (9.45–34.13 kcal mol−1) of TS16 to the transition states TS10–TS15. Such energy discrepancy is possibly due to the two bonds (S(3)–O(4) and C(1)–C(2)) cleavage, which makes the Channel R16 much harder. For Channel 15, starting from 1CH3CH2SOH complex, the isomerization process (1CH3CH2SOH → TS15 → CH3CH2SHO) takes place by the S atom abstracts hydrogen atom from OH site in 1CH3CH2SOH. This reaction channel includes the O(4)–H(10) dissociation and S(3)–H(O(4)) bond formation. The O(4)–H(10), and S(3)–H(O(4)) bond lengths in TS15 is 1.479 and 1.394 Å, respectively. The transition states TS15 show three-member-ring structures (H(10)–O(4)–S(3)) and has a barrier of 58.02 kcal mol−1, which is only higher by 1.48 kcal mol−1 than that of Channel 12. This indicates that Channel R15 also occurs easily.
In summary, addition–elimination channels R6, R12, R13 and R15 are the major channels. Other channels may be negligible due to the high barrier heights. Furthermore, the lowest barrier for the channel CH3CHS + H2O is ∼ 5 kcal mol−1 lower than that of the addition–elimination channel CH2CH2 + HSOH, which is similar with the reactions of ethanol45 (the lowest energy channel is the H2O-formation reaction).
3.2. Rate constant calculation for major channels
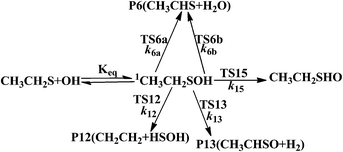
The rate constant calculations of the selected channels were shown in Scheme 1, where “TS” and “Keq” denote the transition state and equilibrium constant of the corresponding reaction pathway, respectively. k denotes the rate constant of the corresponding reaction pathway. We neglect the rate constant calculation of channel R1–R5, R7–R11, R14 and R16 because of their high barriers. Reaction channels R6, R12, R13 and R15 all began with the formation of a prereactive complex before progressing through the transition state, which is depicted in eqn (1).
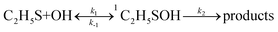 | (1) |
Assuming that the prereactive complex 1C2H5SOH was in equilibrium with the reactants and was at steady state, the overall rate constant was expressed as.
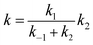 | (2) |
If k2 « k−1, the rate constant was rewritten as
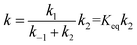 | (3) |
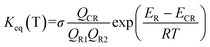 | (4) |
The various Q values denoted the partition functions of the intermediates, reactants C2H5S and OH. ER, ECR are the total energies of the reactants and the post-reactant complex CR; σ is the symmetry number.
In the rate constant calculation, the overall rate constant ktotal are calculated within the temperature range of 200–3000 K, which was given by ktotal = Keq × (k6a + k6b + k12 + k13 + k15). Fig. 7 and Table S3† lists the temperature dependence of kR6(kR1 = Keq × (k6a + k6b)), kR12(kR12 = Keq × k12), k13(k13 = Keq × k13), k15 (kR15 = Keq × k15) and ktotal within the temperature range of 200–3000 K. In the calculated temperature range, kR6, kR12, k13, k15 and ktotal all decrease slowly at low temperature, and increase at high temperature range. Such as, as the temperature increases, ktotal decreases slowly in the temperature range of 200–298 K (k298total/k200total = 0.88), and increases within the temperature range of 298–3000 K (k3000total/k295total = 13.1). The branching ratios of channel R6, R12, R13 and R15 are described in Fig. 8 and Table S4.† It can be seen in Fig. 8 and Table S4† that the overall rate constant in the temperature of 200–3000 K is main dependent on the R6, R12 and R15. At 200 K, the contribution of R1(k6ktotal), R12(k15/ktotal) and R15((k15/ktotal)) to the total rate constant is 50.0%, 25.0%, 18.0%, respectively. As the temperature increases, R6 and R12 become significant (k6/ktotal, 66.0%, k12/ktotal, 28.0%, k15/ktotal, 5.0% at 3000 K). The contribution of R13 to the overall rate constant over the temperature of 200–3000 K is small within 7%.
For kinetic modeling applications, the calculated TST rate constant k6, k12, k13, k15 and ktotal in the temperature range of 200–3000 K have been fitted to the three-parameter expressions (unit in cm3 molecule−1 s−1):
k6 = 2.77 × 10−21T2.71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−751.02/T) exp(−751.02/T) |
k12 = 3.00 × 10−21T2.60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−714.11/T) exp(−714.11/T) |
k13 = 7.13 × 10−22T2.35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1054.81/T) exp(−1054.81/T) |
k15 = 4.97 × 10−20T2.02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−711.46/T) exp(−711.46/T) |
ktotal = 7.42 × 10−21T2.63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−772.43/T) exp(−772.43/T) |
4. Conclusions
Theoretical method CBS-QB3 is applied to study the reaction mechanism of CH3CH2S with OH. The rate constants of major channels are evaluated over the temperature range of 200–3000 K. The main conclusions are summarized as follows:(1) Two mechanisms are investigated for the title reaction, namely, substitution and addition–elimination. Addition–elimination channels CH3CHS + H2O, CH2CH2 + HSOH, CH3CHSO + H2 and CH3CH2SH + O are the major channels.
(2) The overall rate constant in the temperature of 200–3000 K is main dependent on the channels CH3CHS + H2O, CH2CH2 + HSOH and CH3CH2SH + O. The contribution of channel CH3CHSO + H2 to the overall rate constant over the calculated temperature is small within 7%.
Acknowledgements
The project was supported by the National Natural Science Foundation of China (21473108), Education department of shaanxi provincial government research project (14JK1154), the Funds of Research Programs of Shaanxi University of Technology (SLGQD13(2)-3, SLGQD13(2)-4).References
- K. Torén, S. Hagberg and H. Westberg, Am. J. Ind. Med., 1996, 29, 111–122 CrossRef.
- S. Aloisio, Chem. Phys., 2006, 326, 335–343 CrossRef CAS PubMed.
- I. Barnes, J. Hjorth and N. Mihalopoulos, Chem. Rev., 2006, 106, 940–975 CrossRef CAS PubMed.
- N. González-García, À. González-Lafont and J. M. Lluch, J. Comput. Chem., 2005, 26, 569–583 CrossRef PubMed.
- K. Wang, L. Du and M. Ge, J. Environ. Sci., 2009, 21, 137–141 CrossRef CAS.
- A. M. El-Nahas, T. Uchimaru, M. Sugie, K. Tokuhashi and A. Sekiya, J. Mol. Struct.: THEOCHEM, 2005, 722, 9–19 CrossRef CAS PubMed.
- J. Jee and F.-M. Tao, J. Phys. Chem. A, 2006, 110, 7682–7689 CrossRef CAS PubMed.
- B. P. Lomans, C. van der Drift, A. Pol and H. J. M. Op den Camp, CMLS, Cell. Mol. Life Sci., 2002, 59, 575–588 CrossRef CAS.
- Z. X. Ma, C. L. Liao, H. M. Yin, C. Y. Ng, S.-W. Chiu, N. Ling Ma and W.-K. Li, Chem. Phys. Lett., 1993, 213, 250–256 CrossRef CAS.
- Y. S. Cheung, C. W. Hsu and C. Y. Ng, J. Electron Spectrosc. Relat. Phenom., 1998, 97, 115–120 CrossRef CAS.
- C.-Y. Ng, Annu. Rev. Phys. Chem., 2002, 53, 101–140 CrossRef CAS PubMed.
- M. B. Williams, P. Campuzano-Jost, A. J. Hynes and A. J. Pounds, J. Phys. Chem. A, 2009, 113, 6697–6709 CrossRef CAS PubMed.
- A. Cruz-Torres and A. Galano, J. Phys. Chem. A, 2007, 111, 1523–1529 CrossRef CAS PubMed.
- A. Galano, J. Phys. Chem. A, 2006, 110, 9153–9160 CrossRef CAS PubMed.
- C. Zavala-Oseguera, J. R. Alvarez-Idaboy, G. Merino and A. Galano, J. Phys. Chem. A, 2009, 113, 13913–13920 CrossRef CAS PubMed.
- R. Crehuet, J. M. Anglada and J. M. Bofill, Chem.–Eur. J., 2001, 7, 2227–2235 CrossRef CAS.
- E. Baboukas, J. Sciare and N. Mihalopoulos, Atmos. Environ., 2002, 36, 5131–5139 CrossRef CAS.
- L. Zhu, J. M. Nicovich and P. H. Wine, J. Phys. Chem. A, 2005, 109, 3903–3911 CrossRef CAS PubMed.
- B. Kirchner and M. Reiher, J. Am. Chem. Soc., 2002, 124, 6206–6215 CrossRef CAS PubMed.
- Y. Zhang, W. Zhang, T. Zhang, W. Tian and W. Wang, Comput. Theor. Chem., 2012, 994, 65–72 CrossRef CAS PubMed.
- J. Cao, W. Wang, Y. Zhang, W. Wang, T. Zhang, J. Lv and C. Li, Theor. Chem. Acc., 2011, 129, 771–780 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, revision A.01, Gaussian, Inc., Wallingford, 2004 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- M. Page and J. W. McIver, J. Chem. Phys., 1988, 88, 922–935 CrossRef CAS PubMed.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS PubMed.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822–2827 CrossRef CAS PubMed.
- B. Sirjean, E. Dames, H. Wang and W. Tsang, J. Phys. Chem. A, 2012, 116, 319–332 CrossRef CAS PubMed.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975 CrossRef CAS PubMed.
- B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 1979, 70, 1593–1598 CrossRef CAS PubMed.
- B. C. Garrett and D. G. Truhlar, J. Am. Chem. Soc., 1979, 101, 4534–4548 CrossRef CAS.
- B. C. Garrett, D. G. Truhlar, R. S. Grev and A. W. Magnuson, J. Phys. Chem., 1980, 84, 1730–1748 CrossRef CAS.
- S. W. Zhang and N. T. Truong, VKLab version 1.0, University of Utah, Salt Lake City, 2001 Search PubMed.
- C.-M. Gong, Z.-R. Li and X.-Y. Li, Energy Fuels, 2012, 26, 2811–2820 CrossRef CAS.
- W. T. Duncan, R. L. Bell and T. N. Truong, J. Comput. Chem., 1998, 19, 1039–1052 CrossRef CAS.
- A. R. Hoy and P. R. Bunker, J. Mol. Spectrosc., 1979, 74, 1–8 CrossRef CAS.
- K. Okiye, C. Hirose, D. G. Lister and J. Sheridan, Chem. Phys. Lett., 1974, 24, 111–113 CrossRef CAS.
- D. J. Clouthier, G. Huang, A. G. Adam and A. J. Merer, J. Chem. Phys., 1994, 101, 7300–7310 CrossRef CAS PubMed.
- P. Venkateswarlu and W. Gordy, J. Chem. Phys., 1955, 23, 1200–1202 CrossRef CAS PubMed.
- E. Herbst, J. K. Messer, F. C. De Lucia and P. Helminger, J. Mol. Spectrosc., 1984, 108, 42–57 CrossRef CAS.
- J. Cao, W. Wang, Y. Zhang, W. Wang, T. Zhang, J. Lv and C. Li, Theor. Chem. Acc., 2011, 129, 771–780 CrossRef CAS.
- Z. F. Xu, J. Park and M. C. Lin, J. Chem. Phys., 2004, 120, 6593–6599 CrossRef CAS PubMed.
- J. Park, R. S. Zhu and M. C. Lin, J. Chem. Phys., 2002, 117, 3224–3231 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra07780f |
| This journal is © The Royal Society of Chemistry 2014 |