Fragmentation of typical sulfonamide drugs via heterolytic bond cleavage and stepwise rearrangement

Abstract

Although many experiments have been carried out to elucidate the fragmentation of typical sulfonamide drugs, little effort has been devoted to understanding the reaction process theoretically. Herein, the characteristic fragmentation pathways were investigated by performing density functional theory calculations. Employing sulfamethoxazole as a representative sulfonamide, the structure of the molecular ion was initially examined. The site of protonation was found to be located at the nitrogen atom of the isoxazole ring, which could facilitate energy minimization by forming a hydrogen bond. The fragment ion A at m/z 156 was then recognized as the result of heterolytic S–N bond cleavage with the energy requirement of 50.25 kcal mol⁻¹. This result could be supported by analyzing the S–N bond nature and by the energy comparison of different reaction pathways. Formation of the fragment ion B at m/z 108 was attributed to a stepwise rearrangement reaction. Heterolytic C–S bond cleavage was the rate-limiting step of the overall reaction, with an energy barrier of 31.93 kcal mol⁻¹. This is in good agreement with the Fukui function and spin density analysis. The fragment ion C(T) at m/z 92 was also obtained from the heterolytic C–S bond cleavage of A, with the energy requirement of 29.98 kcal mol⁻¹. The results in this work suggested that formation of the fragment ions B and C(T) were competitive reactions with the major difference being the degree of the heterolytic C–S bond cleavage.

---

1. Introduction

Sulfonamides (Fig. 1), as a class of antimicrobial pharmaceuticals, are extensively used for the treatment of bacterial infections in both livestock production and human therapy.¹ Disposal of hospital waste and improper management of animal manure may lead to the introduction of sulfonamides into the environment.^2–4 The presence of such drug residues is of particular concern due to their potential pathogenicity and, to a lesser extent, the possibility of transferring antibiotic resistance genes to pathogenic bacteria of humans.⁵ In addition, various chemical or biochemical treatments could transform the sulfonamides to many other unknown substances, which might possess hazard potential for both humans and the environment. Consequently, it is of great significance to find an appropriate method to detect and characterize the sulfonamide drugs and their transformation products.

Fig. 1 Schematic diagram of the characteristic fragment ions of typical sulfonamide drugs.

Electrospray ionization (ESI) mass spectrometry (MS) combined with high performance liquid chromatography (HPLC) has been widely accepted as the preferred tool for routine quantitative and qualitative determination of sulfonamide drugs and their transformation products.^6,7 Identification of the components of a sample can be achieved by matching the retention time in chromatographic separation and by tandem mass spectrometry (MS/MS). Particularly for the characterization of unknown products, accurate interpretation of the fragmentation pathways plays a critical role in elucidating their structural information.⁸ Therefore, much attention has been focused on understanding and then further summarizing different fragmentation mechanisms.^9,10

It has been well established that the sulfonamide drugs follow characteristic fragmentation pathways⁹ to produce the typical fragment ions A at m/z 156, B at m/z 108, and C(T) at m/z 92 (Fig. 1 and S1†). In general, formation of the fragment ions A and C(T) has been attributed to direct bond cleavage, while the fragment ion B was believed to be obtained from the rearrangement of fragment ion A.^9,11 This was considered to be the critical evidence for identifying the p-aminophenylsulfonyl structure (A) of the analytes. Despite the considerable experimental progress made in recent years, only little effort has been devoted to the theoretical investigation of this fragmentation pattern.¹¹

In this work, we performed density functional theory (DFT) calculations to study the characteristic fragmentation pathways of typical sulfonamide drugs. Much literature has proved that DFT calculation can be a reliable and complementary approach in the elucidation of fragmentation patterns and identification of unknown compounds.^10,12 As a proof-of-concept work, sulfamethoxazole (SMX) was employed as a representative substrate for sulfonamide drugs because it is one of the most frequently detected antibiotics in occurrence surveys of the environment.^13,14 It is anticipated that this work could not only help in gaining a deep insight into the structural features of sulfonamides but also become useful predictive evidence in future applications.

2. Computational details

The DFT calculation was performed in Gaussian 09 (B.01) software¹⁵ at the B3LYP level of theory with the 6-31+G(d,p) basis set, and was conducted in gas phase to simulate the condition in MS.^10,12 The geometry was fully optimized with the default convergence criteria. The vibrational frequency was then calculated to determine the nature of the stationary point and the zero-point energy (ZPE). Each transition state was verified on the desired reaction path by performing an intrinsic reaction coordinate analysis. The energy (E_ZPE) discussed in this work is the sum of electronic and zero-point energy. In addition, the structure of the stationary point was further confirmed to be an electronic minimum by wavefunction stability analysis. Unless otherwise noted, the singlet spin state proved to be reasonable for even-electron structures. However, in some cases, the optimized geometry in the triplet spin state (labeled by (T)), rather than that in the singlet spin state, was the most stable structure. The Cartesian coordinates and the E_ZPE values of all the optimized structures can be found in the ESI.†

The quantum theory of atoms in molecules analysis was implemented in the Multiwfn software¹⁶ (Version 3.2) by analyzing the wavefunction obtained from the optimization. The topology graphs with the bond critical point (BCP) and the bond path were then plotted. The corresponding parameters including electron density (ρ in a.u.), Laplacian of electron density (∇²ρ in a.u.), local kinetic energy density (G in a.u.), local potential energy density (V in a.u.), electron localization function (ELF), reduced density gradient (RDG = 1/(2(3π²)^1/3)|∇ρ|/ρ^4/3), and the second Hessian eigenvalue (λ₂) were calculated at the BCP. The two-dimensional (2D) diagrams of the ∇²ρ and the ELF were also calculated and plotted by using the Multiwfn software, while the RDG isosurface and the three-dimensional (3D) diagrams of the Fukui function were calculated by Multiwfn and constructed with Gaussview.

3. Results and discussion

3.1. Formation of the molecular ion

In principle, the molecular ion of SMX should be present as the protonated form in positive mode ESI. The sites of protonation were studied to determine the structure of the molecular ion due to its pronounced effect on the subsequent fragmentation in the MS/MS experiments.¹² Fig. 2 shows five possible conformations, which can be divided into two categories: species protonated at the nitrogen atoms such as NP1, NP2, and NP3, and those at the oxygen atoms such as OP1 and OP2. In this work, all these structures were optimized in DFT calculations. To facilitate the comparison, their energy values are reported in Fig. 2 by using NP3 as the reference (i.e. zero point of energy level).

Fig. 2 The energy values (kcal mol⁻¹) of all five conformations of protonated SMX and the corresponding transition states; and plot of RDG versus sign(λ₂)ρ with the corresponding isosurface (RDG = 0.3 a.u.) for the hydrogen bond (O⋯H–N).

NP1 was the species protonated at the nitrogen atom of the aniline moiety. It has been postulated to exist in aqueous media,⁷ but still needs to be examined here in the gas phase (MS condition). Fig. 2 shows that NP1 has the highest energy (25.16 kcal mol⁻¹) of all five conformations. Moreover, due to the additional proton on the amino group, the S–N bond cleavage of NP1 should give the divalent cation instead of the fragment ion A. Therefore, NP1 is unlikely to be a reasonable structure for the molecular ion. On the contrary, NP3 was the most energetically stable structure, which could explain the formation of the fragment ion A easily by means of the cleavage of its S–N bond.⁸ In light of recent work,¹⁷ the proton located at the nitrogen atom of the isoxazole ring was believed to be an important stabilizer in the NP3 structure by forming a hydrogen bond between the nitrogen and oxygen atoms. In this work, NP3 was proposed to be the most probable structure for the molecular ion. NP2, with the second lowest energy (11.50 kcal mol⁻¹) of the five conformations, has the largest structural change relative to its neutral form. This is attributed to the great lengthening of S–N bond to 2.173 Å, resulting from the protonation at the central nitrogen atom. This suggested that NP2 might be the precursor of the fragment ion A if it was not already dissociated into two parts. Hence, NP2 was also a possible structure for the molecular ion.

OP1 and OP2 were species protonated at the two oxygen atoms of the sulfonyl moiety, thus could not produce the fragment ion A by breaking the S–N bond directly. However, they have comparable energies (20.86 kcal mol⁻¹ for OP1 and 20.31 kcal mol⁻¹ for OP2) and can transform to each other by passing through a transition state TSP2, suggesting a possible equilibrium between them. The energy barriers were 32.92 and 33.47 kcal mol⁻¹ starting from OP1 and OP2, respectively. The imaginary frequency at 1833.10i cm⁻¹ was an oscillatory motion of the hydrogen atom between the two oxygen atoms. OP1 could be further transformed to the most stable structure NP3 by passing through the transition state TSP1. Due to its negative energy barrier, this reaction was considered to be spontaneous, while its inverse process with the energy barrier of 19.69 kcal mol⁻¹ should be unfavorable. The imaginary frequency at 84.73i cm⁻¹ was a torsional vibration of the hydrogen atom around the oxygen atom, resulting in the formal migration of hydrogen atom to the nitrogen atom of the isoxazole ring. It is thus inferred that OP1 and OP2 (if they were present) would be in equilibrium with each other and could be transformed irreversibly to NP3 via a proton transfer reaction.

On the basis of the above discussion, NP3 was believed to be the most reasonable structure for the molecular ion. To support this result, topology analysis was performed for NP3.¹⁸ Fig. S2a† shows a BCP and a bond path between the hydrogen and oxygen atoms, indicating an intramolecular hydrogen bond (O⋯H–N). As displayed in Table 1, the low ρ and the positive ∇²ρ at this BCP suggested a closed-shell interaction, and were exactly in the range (i.e. ρ = 0.002–0.035 a.u. and ∇²ρ = 0.024–0.139 a.u.) of criteria indicative of hydrogen bond.¹⁹ This result could be confirmed by the ratio of |V(b)|/G(b) < 1.²⁰ The hydrogen bond energy was calculated by the relationship E = V/2 as 6.35 kcal mol⁻¹.²¹ We then performed a visualization approach for the noncovalent interaction.²² The spike at the bottom of Fig. 2 corresponded to sign(λ₂)ρ (i.e. sign(λ₂) is the sign of λ₂) of approximately −0.0249 a.u., which is consistent with the result of topology analysis and could indicate an attractive interaction. The RDG isosurface at 0.3 a.u. was created and exactly localized between the hydrogen and oxygen atoms. All above results in combination with the ELF value near zero confirmed the existence of the hydrogen bond, which was believed to play a critical role in decreasing the energy level of NP3.

Table 1 Bond length (L in Å); and energy (E in kcal mol⁻¹) of hydrogen bond^a, heterolytic^b and homolytic^c cleavage of the S–N bond; and values of ρ, ∇²ρ, |V|/G, ELF

Parameters	Bond
	O⋯H–N in NP3	S–N in NP2	S–N in NP3
L	2.0002	2.1732	1.7978
E	6.3514^a	21.934^b	50.251^b
		39.977^c	62.197^c
ρ	0.0249	0.0832	0.1779
∇^2ρ	0.0890	0.0795	−0.2883
|V|/G	0.9527	1.4793	2.9269
ELF	0.0760	0.5869	0.8119

---

3.2. Formation of the fragment ion A

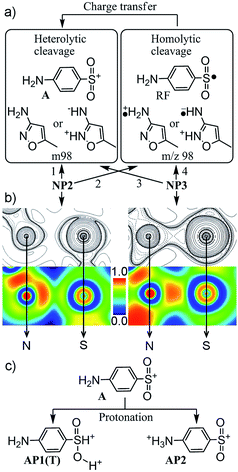
As shown in Fig. 1, formation of the fragment ion A was recognized as a facile cleavage of the S–N bond in the MS/MS experiments, and thus could be analyzed by comparing lengths of this bond between the structures of the protonated and the neutral species.¹² As discussed above, there is a remarkable lengthening of the S–N bond (2.173 Å) of NP2 in comparison with that (1.726 Å) of its neutral form. For the other four conformations, an elongation of the S–N bond resulting from protonation could be also observed in NP3 (1.798 Å), while the S–N bond lengths of NP1, OP1, and OP2 were shortened to 1.694 Å, 1.649 Å, and 1.659 Å, respectively. The result was in agreement with the aforementioned conclusion that only NP2 and NP3 were reasonable structures for the molecular ion.

Fig. 3a depicts the two possible pathways for the formation of the fragment ion A from NP2 and NP3. In most cases, collision-induced dissociation in the ESI-MS was believed to generate the fragment ion A via heterolytic cleavage of the S–N bond. As an alternative, we also proposed an indirect pathway involving the homolytic cleavage of the S–N bond and a subsequent charge transfer process. This is possible on the basis of recent observations of odd-electron dissociations under ESI conditions.^10,23 In particular, sulfonamides have been assumed to be favorable precursors in the formation of radical fragments (RF) because of the stabilization of radical species with the aniline structure.¹⁰

Fig. 3 (a) Schematic diagram of the heterolytic cleavage of the S–N bonds of NP2 (1) and NP3 (3), and the homolytic cleavage of the S–N bonds of NP2 (2) and NP3 (4); and (b) 2D contour line diagram of the ∇²ρ (solid and dashed lines represent the positive and negative regions, respectively) and 2D color-filled diagram of the ELF of the S–N bonds of NP2 and NP3; and (c) schematic diagram of the protonation of A.

The energy changes of all possible pathways were then listed in Table 1. In line with the results regarding the lengthening of the S–N bond, its cleavage was much easier for NP2 than for NP3. NP2 requires the lowest energy (21.93 kcal mol⁻¹) for the heterolytic cleavage of the S–N bond, while NP3 requires the energy of 50.25 kcal mol⁻¹. This reminded us to examine the mutual transformation of NP2 and NP3, because the Curtin–Hammett principle was also applied in MS.²⁴ However, no transition state structure was found for such a reaction. This could be easily understood by considering the large structural difference between NP2 and NP3 (Fig. S3†). Hence, the main pathway for the formation of the fragment ion A is the heterolytic S–N bond cleavage of NP3, since which was the major component of the molecular ion. It is worth noting that heterolytic cleavage always required less energy than homolytic cleavage for both NP2 and NP3. The previous work also showed that the presence of a substantial energy barrier should be considered in the charge transfer process.¹⁰ Moreover, no previous study has detected a radical fragment ion at m/z 98 in the fragmentation of SMX. Therefore, it is reasonable to deduce that the indirect pathway proposed here could be omitted in this work.

Topology analysis was then performed for NP2.¹⁸ As shown in Fig. S2,† the BCPs and the bond paths were found for the S–N bonds of both NP2 and NP3. Particularly for NP2, the low ρ and the positive ∇²ρ at the BCP (Table 1) indicated a closed-shell interaction. The ratio of |V(b)|/G(b) between 1 and 2 suggested that the bond nature was an intermediate type between closed-shell and shared interactions.²⁰ These results were supported by the ELF value of 0.59 corresponding to a free electron gas behavior.²⁵ Hence, the S–N bond of NP2 was deduced to be ionic and electrostatic-dominated bonding. This could explain the low energy requirement for the S–N bond cleavage of NP2, and suggested that NP2 might already be a complex of two fragments (A and m98). It is clear from Fig. 3b that, the ∇²ρ is positive (charge depletion) in the bonding range, and the ELF area is separated into two parts with high ELF values close to the nitrogen nucleus and low ELF values in the intersection region. By contrast, all parameters (Table 1) of the S–N bond of NP3 exhibit the covalent character (i.e. ∇²ρ < 0, |V(b)|/G(b) > 2, and ELF = 0.81).^18,20,25 This was also verified in Fig. 3b by the charge concentration (negative value) of ∇²ρ and the existence of a disynaptic valence basin (high ELF) between the sulfur and nitrogen atoms. Consequently, NP3 was further confirmed to be the most reasonable molecular ion. If NP2 was also present, it should be a minor component of the molecular ion and only discussed in the formation of the fragment ion A.

Note that the fragment ion A was also believed to be the precursor of the fragment ions B and C(T). As displayed in Fig. 3c, protonation of the fragment ion A was assumed to occur in the MS/MS experiments at the nitrogen atom of the aniline ring and the oxygen atom of the sulfonyl moiety. AP2 was neglected in the following discussion because the additional proton on the amino group was not beneficial to the formation of the target fragment ions (B and C(T)). Consequently, only A and AP1(T) were considered in the further fragmentation.

3.3. Formation of the fragment ion B

In contrast to the simple bond cleavage, the fragment ion B was believed to have originated from structural rearrangement during the fragmentation.^9,11 The molecular ion and the dissociation intermediates A and AP1(T) were proposed to be potential precursors, whose rearrangement processes were subsequently attempted to be modeled. The potential energy profiles are given in Fig. 4, in which the reported energy values were normalized by using the reactants as the zero-points.

Fig. 4 The potential energy profiles (kcal mol⁻¹) of the rearrangement reactions from (a) NP3, (b) AP1(T), and (c) A to produce B (isovalue of spin density = 0.02); and (d) the Fukui function (isovalue = 0.005) governing nucleophilic attack of NP3, AP1(T), A, and P11(T).

Direct rearrangement. On the basis of the preliminary result, we investigated the direct rearrangement from the molecular ion NP3 to the fragment ion B. The potential energy profile of the reaction is shown in Fig. 4a, in which the transition state structures in both singlet (TSD) and triplet (TSD(T)) spin state are indicated. The energy barriers were 55.45 kcal mol⁻¹ for TSD and 59.87 kcal mol⁻¹ for TSD(T), respectively. The imaginary frequencies of both TSD at 396.15i cm⁻¹ and TSD(T) at 48.34i cm⁻¹ corresponded to the simultaneous cleavage of the C–S bond and formation of a C–O bond. The major difference of the two transition state structures is the larger extension of the C–S bond (1.740 Å) of NP3 to that (2.709 Å) of TSD(T) than that (2.030 Å) of TSD. It should be mentioned here that the wavefunction of TSD was not stable. Consequently, TSD(T) seems more reasonable to represent the transition state of the reaction. By passing through TSD(T), NP3 could be transformed to the rearranged structure ReNP3. The reaction has a relatively high energy barrier of 59.87 kcal mol⁻¹ and is exothermic by only 2.99 kcal mol⁻¹, indicating that the direct rearrangement seems to be unfavorable. Moreover, formation of the fragment ion B requires an additional 19.32 kcal mol⁻¹ by breaking the S–O bond of ReNP3. All these results suggested that this direct rearrangement could not take place in the MS/MS experiments.

Indirect rearrangement. As a protonated species, the rearrangement of AP1(T) has a much lower energy barrier of 29.26 kcal mol⁻¹ compared to that of the rearrangement of NP3, as displayed in Fig. 4b. The imaginary frequency of TS2(T) at 753.95i cm⁻¹ corresponds to the cleavage of the C–S bond and the formation of a C–O bond, where the oxygen atom with its lone pair electrons act as a nucleophile. The reaction is highly exothermic, by 25.03 kcal mol⁻¹ to form P2(T) and by 65.30 kcal mol⁻¹ to form the fragment ion B and the cation SOH⁺(T). All these results showed that protonation of A at the oxygen atom was beneficial to the indirect rearrangement reaction, both thermodynamically and kinetically. This might be due to the distribution of the electron density throughout the structures of AP1(T), TS2(T), P2(T) and SOH⁺(T), which all only have stable wavefunctions in the triplet spin state. However, this reaction can not be supported by the experimental result that the fragment ion SOH⁺(T) at m/z 49 has never been reported in the fragmentation of SMX. It reminds us that protonation of the fragment ion A assumed in Fig. 3c should be unlikely to occur in the MS/MS experiments. Therefore, the fragment ion A was considered to be the sole precursor of the indirect rearrangement reaction.

The rearrangement of A could be modeled in the singlet spin state and is depicted in Fig. 4c. The oxygen atom with its lone pair electrons acted as a nucleophile to attack the para position of the aniline ring, to form transition state TS1. The cleavage of the C–S bond and the formation of the C–O bond accomplished the rearrangement reaction to produce the product P1. The optimized structures of TS1 and P1 obtained in this work are consistent with the previous results.¹¹ The energy barrier and exothermicity are 34.55 kcal mol⁻¹ and 11.76 kcal mol⁻¹ respectively, which are also comparable to the values (36.2 kcal mol⁻¹ and 10.9 kcal mol⁻¹) reported before. The energy of the sum of B and SO(T) is −4.99 kcal mol⁻¹, which is slightly higher than that of P1. Hence, the indirect rearrangement reaction from A is more favorable than the direct rearrangement reaction from NP3. However, the wavefunctions of TS1 and P1 were found to be unstable, suggesting that there might be other stationary points with minimized energies.

As expected, we also obtained another transition state structure in the triplet spin state (TS11(T)) with a stable wavefunction as can be seen in Fig. 4c. Its imaginary frequency at 133.22i cm⁻¹ was a stretching vibration of the sulfur atom going to and away from the carbon atom, leading to the formation of the product in the triplet spin state P11(T). This reaction could further proceed via TS12(T) to finish the rearrangement to give P12(T). The imaginary frequency at 392.94i cm⁻¹ was a nucleophilic attack of the oxygen atom at the para position of the aniline ring. The energy barrier was only 6.13 kcal mol⁻¹, starting from P11(T). Considering the low energy level (31.50 kcal mol⁻¹) of TS12(T), TS11(T) should be the transition state of the rate-limiting step. The overall reaction has the energy barrier of 31.93 kcal mol⁻¹ and is exothermic by 17.20 kcal mol⁻¹. In combination with the results in the analysis of both direct and indirect rearrangements, the stepwise mechanism was believed to be most reasonable in the formation of the fragment ion B.

The Fukui function (f⁺) governing nucleophilic attack was then calculated for the different precursors (i.e. NP3, AP1(T), A, and P11(T)) of the rearrangement reactions.²⁶ As shown in Fig. 4d, the maxima of f⁺ were mainly localized around the isoxazole moiety in NP3 and the sulfonyl moiety in A. Both NP3 and A exhibited no reactivity at the para carbon atom of the aniline ring, which was the nucleophilic attack site in the rearrangement reaction. This might be the reason for the high energy barriers of the corresponding reactions and for the unstable wavefunctions of the transition state structures (i.e. TSD and TS1). On the contrary, inspection of f⁺ on AP1(T) obviously showed the nucleophilic reactivity at the para carbon atom of the aniline ring. This is in agreement with the low energy barrier and high exothermicity (Fig. 4b). The result implied us that the protonation of A on the oxygen atom could facilitate the rearrangement reaction. The missing of this reaction pathway should be attributed to the reaction condition, because only the target ion (e.g. molecular ion) was introduced into MS/MS. For the precursor (P11(T)) of the stepwise rearrangement, the maxima of f⁺ could be found at the para carbon atom of the aniline ring, indicating its reactivity with a nucleophile. The result is consistent with the low energy barrier of 6.13 kcal mol⁻¹ by starting from P11(T), because f⁺ could indicate the most energetically favorable site for the electron density increment. Therefore, one would draw the conclusion that the stepwise reaction was initiated by the collision-induced dissociation of C–S bond. Once the P11(T) formed, the rearrangement could occur due to the strong nucleophilicity on the para carbon atom of the aniline ring.

In order to gain a deep insight into the stepwise rearrangement reaction, spin density (SD) analysis was performed as shown in Fig. 4c. For TS11(T) and P11(T), the SD is mainly localized on the nitrogen atom and the ortho and para carbon atoms. Through the C–S bond cleavage, the paired electron of the closed-shell A was separated to two parts. One unpaired electron (SD = 1.12 or 1.29) was localized on the para carbon atom, another (SD = 0.88 or 0.84) was localized on the nitrogen atom and its ortho carbon atoms. This led to the formation of a radical-like structure, the aniline cation of P11(T), in which the carbon atom with its single electron was apt to be attacked by the electron-rich reagent.²⁷ This was the initial driving force of the entire reaction since the prerequisite for the rearrangement process of sulfonamides is the occurrence of a radical structure.²⁸ In contrast, the closed-shell A was considered to be stable and could be isolated in MS/MS/MS experiments.⁹ The intramolecular nucleophilic substitution occurred then to give the rearranged structure P12(T). In this process, the SD shifted from the aniline cation to the terminal SO structure (The red circle with SD = 0.98). Finally, the entire transfer of SD resulted in the formation of the closed-shell B and the open-shell SO(T) in the triplet spin state.

3.4. Formation of the fragment ion C(T)

Formation of the fragment ion C(T) could be also explained as the result of simple bond cleavage. NP3, A, AP1(T), and B were proposed here to be the potential precursors. Heterolytic bond cleavage has been commonly observed in the collision-induced dissociation in the ESI-MS, and is also the direct pathway to give the fragment ion C(T). The homolytic cleavage of the C–S bond was proved by a recent work to be the favorable pathway in the fragmentation of benzenesulfonic and benzenesulfinic acid.²⁹ Therefore, both heterolytic and homolytic cleavage energies of the C–S or C–O bond were estimated and listed in Table 2.

Table 2 Bond length (L in Å); and heterolytic bond cleavage energy (E_Hetero in kcal mol⁻¹), homolytic bond cleavage energy (E_Homo in kcal mol⁻¹) of the C–S or C–O bond; and the activation barrier (E_TS in kcal mol⁻¹) of the rearrangement reaction

	Bond
Parameters	C–S in NP3	C–S in A	C–S in AP1(T)	C–O in B
L	1.7404	1.6837	1.8459	1.2186
EHetero	70.156	29.976	−34.612	139.775
EHomo	88.390	140.089	258.028	292.914
ETS	59.868	31.928	29.261	—

---

It is clear to see that the homolytic bond cleavage of all precursors requires more energy than the corresponding heterolytic bond cleavage. The lowest energy requirement could be found in the heterolytic cleavage of the C–S bond of AP1(T) because it was the sole exothermic process. This result should be attributed to the effect of protonation and the resulting elongation of the C–S bond length from 1.684 Å of A to 1.846 Å in AP1(T).¹² However, the fragment ion SO₂H⁺ at m/z 65 was also not detected previously, further confirming the absence of AP1(T) in the MS/MS experiments. Therefore, A should be most probable precursor in the formation of the fragment ion C(T). In other words, the fragment ion C(T) could not be produced by the collision-induced dissociation of either the molecular ion NP3 or the fragment ion B, due to the high energy requirements of the heterolytic cleavage of their C–S or C–O bonds. It is noteworthy that C–S bond cleavage also played a critical role in the formation of the fragment ion B, because it was considered to be the prerequisite of the rearrangement reaction. This was supported by the results in Table 2, showing that the activation barriers decreased with decreasing heterolytic cleavage energies. Particularly for the fragment ion A, the heterolytic cleavage energy of the C–S bond was comparable to the activation barrier of the corresponding rearrangement reaction, indicating that formation of the fragment ions B and C(T) might be competitive reactions. Note that C(T) only has a stable wavefunction in the triplet spin state, thus should be also easily attacked by SO₂. Therefore, the major difference in the formation of B and C(T) was assumed to be the degree of heterolytic C–S bond cleavage of A.

4. Conclusions

In summary, we performed DFT calculations to investigate the characteristic fragmentation pathways of typical sulfonamide drugs theoretically. By employing SMX as a representative substrate for sulfonamides, the structure of the molecular ion was initially examined to confirm the protonation site at the nitrogen atom of the isoxazole ring. The fragment ion A was then recognized as the result of heterolytic S–N bond cleavage and also as the precursor of the fragment ions B and C(T). Formation of the fragment ion B was attributed to a stepwise rearrangement reaction including heterolytic C–S bond cleavage and intramolecular nucleophilic substitution. The fragment ion C(T) was obtained from the heterolytic C–S bond cleavage of A, which was also the rate-limiting step in the formation of the fragment ion B. These results suggested that formation of the fragment ions B and C(T) were competitive reactions, with the major difference being the degree of the heterolytic C–S bond cleavage.

Acknowledgements

This project was supported by the National Science Fund for Distinguished Young Scholars of China (Grant no. 51225805) and the Fund for the Creative Research Groups of China (Grant no. 51221892).

References

1. S. Thiele-Bruhn, J. Plant Nutr. Soil Sci., 2003, 166, 145–167.
2. R. Lindberg, P. A. Jarnheimer, B. Olsen, M. Johansson and M. Tysklind, Chemosphere, 2004, 57, 1479–1488.
3. W. L. Shelver, H. Hakk, G. L. Larsen, T. M. DeSutter and F. X. Casey, J. Chromatogr. A, 2010, 1217, 1273–1282.
4. R. C. Wei, F. Ge, S. Y. Huang, M. Chen and R. Wang, Chemosphere, 2011, 82, 1408–1414.
5. S. K. Haack, D. W. Metge, L. R. Fogarty, M. T. Meyer, L. B. Barber, R. W. Harvey, D. R. LeBlanc and D. W. Kolpin, Environ. Sci. Technol., 2012, 46, 7478–7486.
6. A. G. Trovo, R. F. P. Nogueira, A. Aguera, C. Sirtori and A. R. Fernandez-Alba, Chemosphere, 2009, 77, 1292–1298.
7. M. C. Dodd and C. H. Huang, Environ. Sci. Technol., 2004, 38, 5607–5615.
8. J. L. Mohatt, L. H. Hu, K. T. Finneran and T. J. Strathmann, Environ. Sci. Technol., 2011, 45, 4793–4801.
9. K. Klagkou, F. Pullen, M. Harrison, A. Organ, A. Firth and G. J. Langley, Rapid Commun. Mass Spectrom., 2003, 17, 2373–2379.
10. N. Hu, Y. P. Tu, K. Z. Jiang and Y. J. Pan, J. Org. Chem., 2010, 75, 4244–4250.
11. H. Y. Wang, X. Zhang, Y. L. Guo, X. C. Dong, Q. H. Tang and L. Lu, Rapid Commun. Mass Spectrom., 2005, 19, 1696–1702.
12. A. Alex, S. Harvey, T. Parsons, F. S. Pullen, P. Wright and J. A. Riley, Rapid Commun. Mass Spectrom., 2009, 23, 2619–2627.
13. J. M. Conley, S. J. Symes, M. S. Schorr and S. M. Richards, Chemosphere, 2008, 73, 1178–1187.
14. M. J. Garcia-Galan, M. S. Diaz-Cruz and D. Barcelo, Environ. Int., 2011, 37, 462–473.
15. M. J. Frisch, et al., Gaussian 09, Revision B.01, Gaussian Inc, Wallingford, CT, 2010.
16. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
17. G. Huschek, D. Hollmann, N. Kurowski, M. Kaupenjohann and H. Vereecken, Chemosphere, 2008, 72, 1448–1454.
18. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
19. U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747–9754.
20. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
21. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
22. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
23. G. F. Xu, T. Huang, J. Zhang, J. K. Huang, T. Carlson and S. C. Miao, Rapid Commun. Mass Spectrom., 2010, 24, 321–327.
24. L. J. Haupert, J. C. Poutsma and P. G. Wenthold, Acc. Chem. Res., 2009, 42, 1480–1488.
25. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
26. R. G. Parr and W. T. Yang, J. Am. Chem. Soc., 1984, 106, 4049–4050.
27. M. Kirchgessner, K. Sreenath and K. R. Gopidas, J. Org. Chem., 2006, 71, 9849–9852.
28. P. R. Tentscher, S. N. Eustis, K. McNeill and J. S. Arey, Chem.–Eur. J., 2013, 19, 11216–11223.
29. X. Zhang, J. Mol. Struct., 2012, 1028, 1–6.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra07737g

---