DOI:
10.1039/C4RA07104B
(Communication)
RSC Adv., 2014,
4, 39552-39557
Dissipative particle dynamics study of nano-encapsulated thermal energy storage phase change material
Received
14th July 2014
, Accepted 12th August 2014
First published on 12th August 2014
Abstract
The nano-encapsulated phase change materials (PCM), which have several good thermophysical properties, were proposed as potential for thermal energy storage. Various PCM have been widely researched on micro and macro perspective by experimental and simulated methods to form a bridge between the microstructure and macroscale properties of the nano-encapsulated PCM. In this study, the dissipative particle dynamics (DPD) simulation method was used to investigate the mesoscopic morphologies and evolution mechanisms of the nano-encapsulated PCM. The coarse-grained and Flory–Huggins-type models were used to obtain the molecular structures and interaction parameters. The results showed that the nano-encapsulated PCM can be fabricated by using n-docosane as a core material and styrene (St), ethyl acrylate (EA) and allyloxy nonyl-phenoxy propanol polyoxyethylene ether ammonium sulfate (DNS-86) as shell materials. The core–shell structures failed to fabricate with excess surfactant and shell materials. The preliminary optimized encapsulation rate of the core material could be useful for the design and experiment of the nano-encapsulated PCM.
1. Introduction
Energy shortage and environmental pollution have attracted worldwide attention in the past decades; simultaneously many researchers throughout the world have devoted their lives to search renewable and energy-saving technologies for the sustainable development of economy and society. To avoid large reduction in energy system, thermal energy storage, which plays a vital role in renewable energy and waste heat recovery, is of growing importance.1 Because of many good thermophysical properties such as suitable phase-transition temperature, high latent heat of transition and good heat transfer, phase change materials (PCM) have been proposed as viable solutions for thermal energy storage.2,3 Moreover, the PCM have been widely used in various fields for thermal management or transportation, including greenhouses,4 buildings,5,6 solar energy,7 electronic devices,8 electric vehicle batteries.9
To overcome the inherent disadvantages, such as corrosive to metal, decomposition, sub-cooling and leakage of different PCM, encapsulation of PCM is an effective solution.10 The PCM capsules in micro and nano-scale (i.e. micro/nano-encapsulated PCM) have been utilized in many fields, especially in latent functionally thermal fluids or slurries.11,12 Compared with micro-encapsulated PCM, the nano-encapsulated PCM showed better performance such as well repeated cycling and lower viscosity that can be used in fluid and textile field.10,13 The PCM capsules have been developed widely, most of the work focus on micro-encapsulated PCM. There is limited literature available to study nano-encapsulated PCM. Zhang et al.14 fabricated nano-capsules containing n-octadecane with melamine-formaldehyde shell and analyzed the effects of stirring rate on the diameters and morphology of the capsules. Later, Fang et al.10 indicated that a stirring rate of 1500 rpm was suitable for the nano-encapsulation. Park et al.15 synthesized polystyrene particles by encapsulating paraffin wax as PCM. Su et al.16 described the heat transfer property of a single-phase liquid by adding nano-encapsulated PCM. All the above mentioned works were carried out at the micro perspective (structure and morphology) and macro perspective (preparation and properties). In our previous work, we have investigated the thermal behavior of the PCM by molecular dynamics (MD) simulations method from the microscopic scale.17–19 However, there is hardly any research addressing nano-encapsulated PCM from the mesoscopic perspective. Dissipative particle dynamics (DPD), introduced by Hoogerbrugge and Koelman,20 has been applied to study the mesostructures and morphology evolution of many materials. The DPD method, with coarse-graining procedure, forms a bridge between fast molecular kinetics and the slow thermodynamic relaxation of macroscale properties.21
In the present work, the DPD method was employed to interpret the mesostructures and morphology evolution of the nano-encapsulated PCM. Compared with our previous study,22,23 the contents of the core and shell materials in the PCM system are more complex. This study also attempts to discuss the effect of shell and core materials content on the morphology of the PCM.
2. Method and model
2.1 DPD theory
In the DPD model, a group of molecules or a volume of fluid was represented as a DPD bead, and many of these interacting beads form a mesoscopic system.24,25 The time evolution of the motion for the DPD beads can be obtained by Newton's equations of motion:26,27| |
 | (1) |
where fi, mi, ri, and vi are the force, mass, position vectors, and velocity vectors of the bead i, respectively. The mass of each bead is usually set to 1 DPD mass unit.26 The force between each pair of the beads is composed of four types:28,29| |
 | (2) |
where FCij, FDij, and FRij are the conservative force, dissipative force, and random force of the bead i and j, respectively. FSi is the spring force. The different parts of the forces are given by,| |
 | (3) |
| |
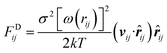 | (4) |
| |
 | (5) |
| |
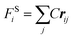 | (6) |
where aij is the maximum repulsion between the beads i and j.30 rij = ri − rj, rij = |rij|, ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij = rij/rij, vij = vi − vj. rc is the cutoff radius, which is always set to 1 unit of length in simulations. ω(r) stands for r-dependent weight function ω(r) = (1 − r) for r < 1 and ω(r) = 0 for r > 1. ξij is a random number with zero mean and unit variance. σ is the noise strength and was set as 3, and δt is the time step of simulation. C is the spring constant and its default value is 4 in this study.
ij = rij/rij, vij = vi − vj. rc is the cutoff radius, which is always set to 1 unit of length in simulations. ω(r) stands for r-dependent weight function ω(r) = (1 − r) for r < 1 and ω(r) = 0 for r > 1. ξij is a random number with zero mean and unit variance. σ is the noise strength and was set as 3, and δt is the time step of simulation. C is the spring constant and its default value is 4 in this study.
In the beginning, Euler-type algorithm was used to integrate the set of positions and velocities.20,28 Then, Groot and Warren developed a modified version of the velocity-Verlet algorithm:26,31
| |
 | (7) |
| | |
ṽi(t + Δt) = vi(t) + λΔtfi(t)
| (8) |
| | |
fi(t + Δt) = fi(r(t + Δt), ṽi(t + Δt))
| (9) |
| |
 | (10) |
As the mass of each bead is set to 1, the force acting on a bead equals its acceleration ṽi(t + Δt), and the force is still updated once per iteration without increase in computational cost. Hence, the modified velocity-Verlet algorithm was used in the current work.
2.2 Models and interaction parameters
To prepare nano-encapsulated PCM, the components used in this study contain water, n-docosane, azodiisobutyronitrile (AIBN), polyvinyl pyrrolidone (PVP), octylphenol polyoxyethylene ether (OP-10), styrene (St), ethyl acrylate (EA) and allyloxy nonylphenoxy propanol polyoxyethylene ether ammonium sulfate (DNS-86). The coarse-grained models in this simulation are shown in Fig. 1. Each molecule of water, AIBN, St and EA are represented as beads a, c, g and h, respectively. An n-docosane molecule was divided into two beads, b. Each monomer of PVP was considered as one bead, d. A molecule of OP-10 was divided into two beads e and f, and DNS-86 was also divided into two beads, i and j.
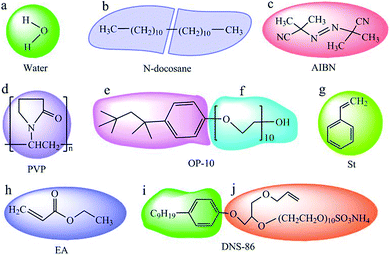 |
| | Fig. 1 Coarse-grained models of water (a), n-docosane (b), AIBN (c), PVP (d), OP-10 (e and f), St (g), EA (h) and DNS-86 (i and j). | |
Before calculating the conservation force, the repulsion parameters aij should be calculated. The link between the repulsive parameter aij and χ-parameters in Flory–Huggins-type models was made by Groot and Warren.26,32 For the beads of the same type, the repulsion parameters aii is shown as:31
where
ρ = 3 and
kBT = 1 were usually used in many previous works.
33–36 ρ is the density,
T is the system temperature and
kB is the Boltzmann constant. The repulsion parameters
aii between the different types of beads, are obtained by following as:
27where the value of
aij can be obtained from solubility parameters:
| |
 | (13) |
where
Vbead is the average molar volume of the two beads.
δi and
δj are the solubility parameters of the bead
i and
j.
The solubility parameters used in the current research were calculated by MD simulations. The details of the MD process can be seen in our previous study.18,23,37 Each MD system consists of more than 1000 atoms in a cubic cell of amorphous structure with periodic boundary conditions. The smart minimization method was used to optimize the geometry. Then, 100 ps in constant-temperature, constant-pressure ensemble (NPT), and 100 ps in constant temperature, constant volume ensemble (NVT) was used to equilibrate the system. After equilibration, 1000 ps were used in NPT ensemble to analyze the molar volume and solubility parameter. All the simulations were performed using Amorphous Cell, Discover and Forcite modules in Materials Studio 5.5 software (Accelrys) with the condensed-phase optimized molecular potentials for atomistic simulation studies (COMPASS) force field.38,39 The simulated molar volumes and solubility parameters of the beads are shown in Table 1. According to eqn (11)–(13), the calculated interaction parameters of the different beads at 298 K used in the following DPD simulation are listed in Table 2. A cubic box with a size of 32 × 32 × 32 with periodic boundary conditions (PBC) was adopted in this work after checking the influence of the box sizes on the simulation results. The total number of the beads was 9.8 × 104. The time step was taken as 0.05 and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps were adopted to obtain equilibration phase. All the simulations were carried out using DPD program incorporated in the Materials Studio 5.5 software (Accelrys) with a constant temperature.
000 steps were adopted to obtain equilibration phase. All the simulations were carried out using DPD program incorporated in the Materials Studio 5.5 software (Accelrys) with a constant temperature.
Table 1 The molar volumes and solubility parameters of the beads
| Bead |
Vbead (cm3 mol−1) |
δ (J cm−3) |
| a |
18.70 |
46.51 |
| b |
205.93 |
16.09 |
| c |
182.23 |
15.69 |
| d |
108.88 |
22.625 |
| e |
214.68 |
16.45 |
| f |
433.11 |
22.629 |
| g |
112.27 |
19.76 |
| h |
106.05 |
20.72 |
| i |
235.86 |
16.89 |
| j |
583.69 |
23.37 |
Table 2 The interaction parameters of the beads in PCM system
| aij |
a |
b |
c |
D |
e |
f |
g |
h |
i |
j |
| a |
25 |
|
|
|
|
|
|
|
|
|
| b |
162.18 |
25 |
|
|
|
|
|
|
|
|
| c |
150.93 |
25.03 |
25 |
|
|
|
|
|
|
|
| d |
73.04 |
33.86 |
34.22 |
25 |
|
|
|
|
|
|
| e |
164.17 |
25.03 |
25.16 |
33.14 |
25 |
|
|
|
|
|
| f |
195.01 |
43.05 |
44.55 |
25.00 |
41.32 |
25 |
|
|
|
|
| g |
86.84 |
27.81 |
28.20 |
26.21 |
27.35 |
27.98 |
25 |
|
|
|
| h |
79.74 |
29.41 |
29.81 |
25.52 |
28.86 |
26.31 |
25.13 |
25 |
|
|
| i |
172.38 |
25.20 |
25.39 |
32.46 |
25.07 |
39.55 |
26.90 |
28.30 |
25 |
|
| j |
237.84 |
52.60 |
54.82 |
25.26 |
50.21 |
25.36 |
30.98 |
28.20 |
47.69 |
25 |
3. Results and discussion
A possible proportion, according to published work such as Fang et al.,10 of the components (n-docosane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) St
St![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EA
EA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNS-86
DNS-86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PVP
PVP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OP-10
OP-10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AIBN) used in the DPD simulation is 10
AIBN) used in the DPD simulation is 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25
0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6
0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.08
0.08![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8
0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04 and the water used was sufficient for the dynamic process. Fig. 2 shows the evolution of the diffusivity of different beads with the simulation time. In a typical simulation, the diffusivity decreases rapidly at the first 400 DPD units (8000 time steps). After about 1600 DPD units, it can be seen that the diffusivity gradually moves to a steady state. This indicates that a time of 2000 DPD units is long enough for the system to achieve equilibrium.
0.04 and the water used was sufficient for the dynamic process. Fig. 2 shows the evolution of the diffusivity of different beads with the simulation time. In a typical simulation, the diffusivity decreases rapidly at the first 400 DPD units (8000 time steps). After about 1600 DPD units, it can be seen that the diffusivity gradually moves to a steady state. This indicates that a time of 2000 DPD units is long enough for the system to achieve equilibrium.
 |
| | Fig. 2 Evolution of the diffusivity of different beads with the simulation time. | |
In the nano-encapsulated PCM system, n-docosane was used as core material and St, EA and DNS-86 were used as shell materials and other components were used as surfactant. Fig. 3 clearly shows the change of aggregates with increasing simulation steps in the simulated nano-encapsulated PCM system with a possible proportion as 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25
0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6
0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.08
0.08![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8
0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04. The beads, which represent water and other components, are not shown in the figures such that the morphologies of the capsule structure could be clearly seen. At first (t = 0 step), different beads, which represent the shell and core materials are distributed randomly in the cubic box. At t = 1000 steps, different structure transitions can be observed. Some n-docosane molecules start to aggregate together at time t = 5000 steps. Finally, ordered spherical capsule structure is formed at t = 30
0.04. The beads, which represent water and other components, are not shown in the figures such that the morphologies of the capsule structure could be clearly seen. At first (t = 0 step), different beads, which represent the shell and core materials are distributed randomly in the cubic box. At t = 1000 steps, different structure transitions can be observed. Some n-docosane molecules start to aggregate together at time t = 5000 steps. Finally, ordered spherical capsule structure is formed at t = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps and the spherical capsule structure did not change significantly until t = 40
000 steps and the spherical capsule structure did not change significantly until t = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. From the capsule structure, we found that the n-docosane molecules are encapsulated with St, EA and DNS-86. The core–shell structure indicated that the nano-encapsulated PCM were formed and the phenomenon also confirmed the feasibility of the DPD method in understanding the aggregates dynamic process of the nano-encapsulated PCM system.
000 steps. From the capsule structure, we found that the n-docosane molecules are encapsulated with St, EA and DNS-86. The core–shell structure indicated that the nano-encapsulated PCM were formed and the phenomenon also confirmed the feasibility of the DPD method in understanding the aggregates dynamic process of the nano-encapsulated PCM system.
 |
| | Fig. 3 Change of aggregates with increasing simulation steps in the simulated PCM system with PBC and a possible proportion of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6 0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.08 0.08![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04. 0.04. | |
In the preparation of the nano-encapsulated PCM, the content of surfactant was far less than the content of the shell and core materials. However, the surfactants in the experiment play a very important roles such as initiator, emulsifier and dispersant. Therefore, in the DPD simulations, the interactions of different surfactants were also considered, although the chemical reaction was ignored in the dynamic process. For preliminarily understanding the effect of the concentration of the surfactant on the capsule structure in the nano-encapsulated PCM system, Fig. 4 shows the isodensity surface of AIBN with different AIBN content: (a) 0.04, (b) 6; and PVP with different PVP content: (c) 0.08, (d) 2; and OP-10 with different OP-10 content: (e) 0.8, (f) 9, at t = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 DPD steps. As can be seen in Fig. 4(a) and (b), the AIBN distributed intricately and showed embedded trends when the proportion of AIBN was equal to possible real proportion. When the proportion of AIBN was ten times higher than the possible proportion, the isodensity surfaces of AIBN were observed as cylindrical structures such that the n-docosane cannot be encapsulated. As can be seen in Fig. 4(c) and (d), the isodensity surface of PVP displayed a cluster structure when the proportion of PVP was excess and it is unnecessary and adverse for fabricating the nano-encapsulated PCM. Similarly, as can be seen in Fig. 4(e) and (f), when the proportion of OP-10 was proper, the OP-10 was distributed uniformly on the surface of the PCM capsule. Moreover, the nano-encapsulated PCM cannot be fabricated when the proportion of OP-10 was excess.
000 DPD steps. As can be seen in Fig. 4(a) and (b), the AIBN distributed intricately and showed embedded trends when the proportion of AIBN was equal to possible real proportion. When the proportion of AIBN was ten times higher than the possible proportion, the isodensity surfaces of AIBN were observed as cylindrical structures such that the n-docosane cannot be encapsulated. As can be seen in Fig. 4(c) and (d), the isodensity surface of PVP displayed a cluster structure when the proportion of PVP was excess and it is unnecessary and adverse for fabricating the nano-encapsulated PCM. Similarly, as can be seen in Fig. 4(e) and (f), when the proportion of OP-10 was proper, the OP-10 was distributed uniformly on the surface of the PCM capsule. Moreover, the nano-encapsulated PCM cannot be fabricated when the proportion of OP-10 was excess.
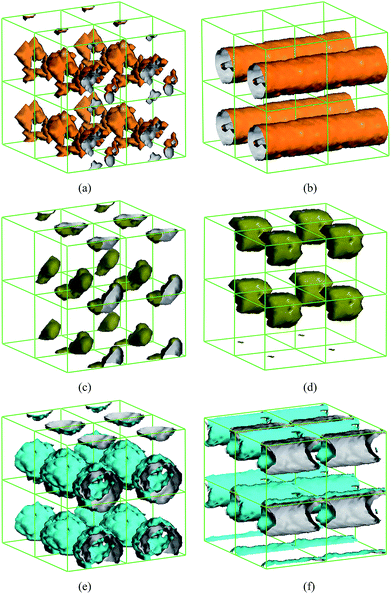 |
| | Fig. 4 Isodensity surfaces of AIBN with different AIBN content under PBC: (a) 0.04, (b) 6; and PVP with different PVP content: (c) 0.08, (d) 2; and OP-10 with different OP-10 content: (e) 0.8, (f) 9, at 4 × 104 DPD steps. | |
The shell material of the nano-encapsulated PCM contains a small amount of EA and DNS-86; moreover, we also varied the isodensity surfaces of the shells by varying the proportion of EA and DNS-86. Fig. 5 shows the isodensity surface of EA at 4 × 104 DPD steps with different EA content: (a) 0.25, (b) 4; and DNS-86 at 4 × 104 DPD steps with different DNS-86 content: (c) 0.6, (d) 3. As can be seen in Fig. 5(a) and (c), both EA and DNS-86 are present with typical spherical shell structure when the proportions of EA and DNS-86 were proper. Likewise, the cylindrical structure can be observed when the contents of EA and DNS-86 were too large. This also indicated that the nano-encapsulated PCM cannot be fabricated.
 |
| | Fig. 5 Isodensity surfaces of EA at 4 × 104 DPD steps with different EA content under PBC: (a) 0.25, (b) 4; and DNS-86 at 4 × 104 DPD steps with different DNS-86 content: (c) 0.6, (d) 3. | |
The shell of the nano-encapsulated PCM contains St, EA and DNS-86 such that it is complex to predict a more possible encapsulation rate of the n-docosane by adjusting the proportion of the shell materials. Therefore, the content of the bead ‘b’, which represents the core material was adjusted in the DPD simulation. Fig. 6 shows the evolution of the diffusivity of the bead ‘b’ with different n-docosane content. It can be seen that the diffusivity of the bead ‘b’ with a content lower than 13 was close to zero at the last 400 DPD units. When the content was higher than 13, such as 14 and 15, the system achieved equilibrium, but the diffusivity was still fluctuating at about 0.7 DPD units. It can also be concluded that the capsule structure of the PCM was not formed. The encapsulation rate, which can be seen as the rate of core material and the whole PCM capsule, of n-docosane was obtained as 54.51% and it can be used as reference for the preparation experiment. As the DPD method was based on the coarse-grained model, more accurate encapsulation rate of the core material is worth further investigating, based on the development of force field.
 |
| | Fig. 6 Evolution of the diffusivity of the bead ‘b’ with different n-docosane content. | |
4. Conclusions
In this work we investigated the mesoscopic morphologies and evolution mechanism of the nano-encapsulated PCM by DPD simulation method. By using n-docosane as the core material and St, EA and DNS-86 as the shell materials, the molecular structures employed in the encapsulation process were coarse-grained with a systematic coarse-graining strategy. When the proportion of the components is proper, a typical core–shell structure of the nano-encapsulated PCM can be obtained. The PCM capsules failed to fabricate with excess surfactant and shell materials. A preliminary optimized encapsulation rate of n-docosane is 54.51% according to the DPD simulations. The DPD model described in this work could be useful in the design and experiment of nano-encapsulated PCM.
Acknowledgements
This work was supported by the natural science foundation of Jiangsu Province (BK20140190) and the Fundamental Research Funds for the Central Universities (China University of Mining and Technology, no. 2014QNA24).
References
- F. Pitie, C. Y. Zhao and G. Caceres, Energy Environ. Sci., 2011, 4, 2117–2124 CAS.
- A. Sharma, V. V. Tyagi, C. R. Chen and D. Buddhi, Renewable Sustainable Energy Rev., 2009, 13, 318–345 CrossRef CAS PubMed.
- E. Oró, A. de Gracia, A. Castell, M. M. Farid and L. F. Cabeza, Appl. Energy, 2012, 99, 513–533 CrossRef PubMed.
- H. Benli and A. Durmuş, Sol. Energy, 2009, 83, 2109–2119 CrossRef CAS PubMed.
- A. M. Khudhair and M. M. Farid, Energy Convers. Manage., 2004, 45, 263–275 CrossRef CAS.
- D. Zhou, C. Y. Zhao and Y. Tian, Appl. Energy, 2012, 92, 593–605 CrossRef CAS PubMed.
- P. C. Eames and P. W. Griffiths, Energy Convers. Manage., 2006, 47, 3611–3618 CrossRef CAS PubMed.
- R. Kandasamy, X. Q. Wang and A. S. Mujumdar, Appl. Therm. Eng., 2008, 28, 1047–1057 CrossRef CAS PubMed.
- Z. H. Rao, S. F. Wang and G. Q. Zhang, Energy Convers. Manage., 2011, 52, 3408–3414 CrossRef CAS PubMed.
- Y. T. Fang, S. Y. Kuang, X. N. Gao and Z. G. Mang, Energy Convers. Manage., 2008, 49, 3704–3707 CrossRef CAS PubMed.
- J. L. Alvarado, C. Marsh, C. Sohn, G. Phetteplace and T. Newell, Int. J. Heat Mass Transfer, 2007, 50, 1938–1952 CrossRef PubMed.
- X. Wang, R. L. Zeng, B. J. Chen, Y. P. Zhang, J. L. Niu, X. C. Wang and H. F. Di, Appl. Energy, 2009, 86, 2661–2670 CrossRef PubMed.
- G. Cho and K. Choi, J. Appl. Polym. Sci., 2011, 121, 3238–3245 CrossRef PubMed.
- X. X. Zhang, Y. F. Fan, X. M. Tao and K. L. Yick, Mater. Chem. Phys., 2004, 88, 300–307 CrossRef CAS PubMed.
- S. J. Park, K. S. Kim and S. K. Hong, Polymer, 2005, 29, 8–13 CAS.
- M. Su, Y. Hong, S. J. Ding, W. Wu, J. J. Hu, A. A. Voevodin, L. Gschwender, E. Snyder and L. Chow, ACS Appl. Mater. Interfaces, 2010, 2, 1685–1691 Search PubMed.
- Z. H. Rao, S. F. Wang, M. C. Wu, Y. L. Zhang and F. H. Li, Energy Convers. Manage., 2012, 64, 152–156 CrossRef CAS PubMed.
- Z. H. Rao, S. F. Wang and F. F. Peng, Int. J. Heat Mass Transfer, 2013, 64, 581–589 CrossRef CAS PubMed.
- Z. Rao, S. Wang and F. Peng, Appl. Energy, 2012, 100, 303–308 CrossRef CAS PubMed.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- S. L. Yuan, X. Q. Zhang and K. Y. Chan, Langmuir, 2009, 25, 2034–2045 CrossRef CAS PubMed.
- Z. H. Rao, S. F. Wang, F. F. Peng, W. Zhang and Y. L. Zhang, Energy, 2012, 44, 805–812 CrossRef CAS PubMed.
- Z. Rao, Y. Huo and X. Liu, RSC Adv., 2014, 4, 20797 RSC.
- Y. Qian, X. D. Guo, L. J. Zhang and J. Zhou, Chem. Eng. J., 2007, 131, 195–201 CrossRef PubMed.
- Z. Y. Lu, H. Wang, Y. T. Liu and H. J. Qian, Polymer, 2011, 52, 2094–2101 CrossRef PubMed.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS PubMed.
- Y. Qian, X. D. Guo, J. P. K. Tan, S. H. Kim, L. J. Zhang, Y. Zhang, J. L. Hedrick and Y. Y. Yang, Biomaterials, 2009, 30, 6556–6563 CrossRef PubMed.
- P. Espanol and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef CAS.
- G. H. Hu, J. G. Gai, H. L. Li, S. P. Zhu and S. Hoppe, Ind. Eng. Chem. Res., 2010, 49, 11369–11379 CrossRef.
- D. Duong-Hong, N. Phan-Thien, K. S. Yeo and G. Ausias, Comput. Meth. Appl. Mech. Eng., 2010, 199, 1593–1602 CrossRef PubMed.
- R. D. Groot and T. J. Madden, J. Chem. Phys., 1998, 108, 8713–8724 CrossRef CAS PubMed.
- H. Wen, H. Wu, J. B. Xu, X. F. He and Y. H. Zhao, Colloids Surf., A, 2006, 290, 239–246 CrossRef PubMed.
- Z. T. Cai, S. L. Yuan, G. Y. Xu and Y. S. Jiang, Chem. Phys. Lett., 2002, 365, 347–353 CrossRef.
- X. R. Cao, G. Y. Xu, Y. M. Li and Z. Q. Zhang, J. Phys. Chem. A, 2005, 109, 10418–10423 CrossRef CAS PubMed.
- H. L. Li, J. G. Gai, C. Schrauwen and G. H. Hu, Polymer, 2009, 50, 336–346 CrossRef PubMed.
- J. W. Jiang and Z. L. Luo, Polymer, 2010, 51, 291–299 CrossRef PubMed.
- Z. Rao, S. Wang and F. Peng, Int. J. Heat Mass Transfer, 2013, 66, 575–584 CrossRef CAS PubMed.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- H. Sun, P. Ren and J. R. Fried, Comput. Theor. Polym. Sci., 1998, 8, 229–246 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here. 


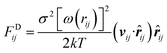

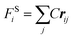
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij = rij/rij, vij = vi − vj. rc is the cutoff radius, which is always set to 1 unit of length in simulations. ω(r) stands for r-dependent weight function ω(r) = (1 − r) for r < 1 and ω(r) = 0 for r > 1. ξij is a random number with zero mean and unit variance. σ is the noise strength and was set as 3, and δt is the time step of simulation. C is the spring constant and its default value is 4 in this study.
ij = rij/rij, vij = vi − vj. rc is the cutoff radius, which is always set to 1 unit of length in simulations. ω(r) stands for r-dependent weight function ω(r) = (1 − r) for r < 1 and ω(r) = 0 for r > 1. ξij is a random number with zero mean and unit variance. σ is the noise strength and was set as 3, and δt is the time step of simulation. C is the spring constant and its default value is 4 in this study.




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps were adopted to obtain equilibration phase. All the simulations were carried out using DPD program incorporated in the Materials Studio 5.5 software (Accelrys) with a constant temperature.
000 steps were adopted to obtain equilibration phase. All the simulations were carried out using DPD program incorporated in the Materials Studio 5.5 software (Accelrys) with a constant temperature.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) St
St![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EA
EA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNS-86
DNS-86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PVP
PVP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OP-10
OP-10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AIBN) used in the DPD simulation is 10
AIBN) used in the DPD simulation is 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25
0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6
0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.08
0.08![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8
0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04 and the water used was sufficient for the dynamic process. Fig. 2 shows the evolution of the diffusivity of different beads with the simulation time. In a typical simulation, the diffusivity decreases rapidly at the first 400 DPD units (8000 time steps). After about 1600 DPD units, it can be seen that the diffusivity gradually moves to a steady state. This indicates that a time of 2000 DPD units is long enough for the system to achieve equilibrium.
0.04 and the water used was sufficient for the dynamic process. Fig. 2 shows the evolution of the diffusivity of different beads with the simulation time. In a typical simulation, the diffusivity decreases rapidly at the first 400 DPD units (8000 time steps). After about 1600 DPD units, it can be seen that the diffusivity gradually moves to a steady state. This indicates that a time of 2000 DPD units is long enough for the system to achieve equilibrium.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25
0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6
0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.08
0.08![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8
0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04. The beads, which represent water and other components, are not shown in the figures such that the morphologies of the capsule structure could be clearly seen. At first (t = 0 step), different beads, which represent the shell and core materials are distributed randomly in the cubic box. At t = 1000 steps, different structure transitions can be observed. Some n-docosane molecules start to aggregate together at time t = 5000 steps. Finally, ordered spherical capsule structure is formed at t = 30
0.04. The beads, which represent water and other components, are not shown in the figures such that the morphologies of the capsule structure could be clearly seen. At first (t = 0 step), different beads, which represent the shell and core materials are distributed randomly in the cubic box. At t = 1000 steps, different structure transitions can be observed. Some n-docosane molecules start to aggregate together at time t = 5000 steps. Finally, ordered spherical capsule structure is formed at t = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps and the spherical capsule structure did not change significantly until t = 40
000 steps and the spherical capsule structure did not change significantly until t = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. From the capsule structure, we found that the n-docosane molecules are encapsulated with St, EA and DNS-86. The core–shell structure indicated that the nano-encapsulated PCM were formed and the phenomenon also confirmed the feasibility of the DPD method in understanding the aggregates dynamic process of the nano-encapsulated PCM system.
000 steps. From the capsule structure, we found that the n-docosane molecules are encapsulated with St, EA and DNS-86. The core–shell structure indicated that the nano-encapsulated PCM were formed and the phenomenon also confirmed the feasibility of the DPD method in understanding the aggregates dynamic process of the nano-encapsulated PCM system.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25
0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6
0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.08
0.08![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8
0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04.
0.04.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 DPD steps. As can be seen in Fig. 4(a) and (b), the AIBN distributed intricately and showed embedded trends when the proportion of AIBN was equal to possible real proportion. When the proportion of AIBN was ten times higher than the possible proportion, the isodensity surfaces of AIBN were observed as cylindrical structures such that the n-docosane cannot be encapsulated. As can be seen in Fig. 4(c) and (d), the isodensity surface of PVP displayed a cluster structure when the proportion of PVP was excess and it is unnecessary and adverse for fabricating the nano-encapsulated PCM. Similarly, as can be seen in Fig. 4(e) and (f), when the proportion of OP-10 was proper, the OP-10 was distributed uniformly on the surface of the PCM capsule. Moreover, the nano-encapsulated PCM cannot be fabricated when the proportion of OP-10 was excess.
000 DPD steps. As can be seen in Fig. 4(a) and (b), the AIBN distributed intricately and showed embedded trends when the proportion of AIBN was equal to possible real proportion. When the proportion of AIBN was ten times higher than the possible proportion, the isodensity surfaces of AIBN were observed as cylindrical structures such that the n-docosane cannot be encapsulated. As can be seen in Fig. 4(c) and (d), the isodensity surface of PVP displayed a cluster structure when the proportion of PVP was excess and it is unnecessary and adverse for fabricating the nano-encapsulated PCM. Similarly, as can be seen in Fig. 4(e) and (f), when the proportion of OP-10 was proper, the OP-10 was distributed uniformly on the surface of the PCM capsule. Moreover, the nano-encapsulated PCM cannot be fabricated when the proportion of OP-10 was excess.



