A DFT study on structure, stabilities and electronic properties of double magnesium doped gold clusters†
Abstract
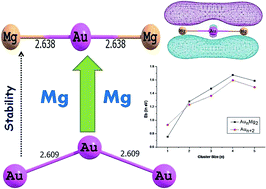
Density functional theory (DFT) with PW91PW91 functional has been applied to investigate the structures, relative stabilities and electronic properties of small bimetallic neutral, cationic and anionic AunMg2 (n = 1–5) clusters. The results show that doping with two Mg atoms dramatically affects the geometries of the ground-states of Aun (n = 1–7) clusters. The relative stabilities of the clusters are compared on the basis of average binding energies, fragmentation energies and second order difference of energies. These parameters show even-odd alternation phenomenon. The electronic properties are calculated using hardness values and this suggests that even numbered clusters are more stable than odd counterparts in both bare, as well as doped ones. The nature of the bonding interaction is also investigated using Bader's quantum theory of atoms in molecules (QTAIM), which indicates the presence of covalent bonding in the studied clusters. The population analysis reveals the transfer of electrons from Mg to Au atoms, which is in turn responsible for the enhanced stability of doped clusters.

 Please wait while we load your content...
Please wait while we load your content...