How much do coulombic interactions stabilize a mesophase? Ion pair and non-ionic binary isosteric derivatives of monocarbaborates and carboranes

Abstract

Replacement of the B⁻ atom in the monocarbaborate anion, 1[10] or 1[12], and the N⁺ atom in the pyridinium cation [Pyr] of a liquid crystalline ion pair with C atoms leads to an isoelectronic and isosteric non-ionic binary liquid crystalline mixture of carborane (2[10] or 2[12]) and benzene ([Ph]) derivatives lacking coulombic interactions. A comparison of mesogenic properties of ion pairs, 1[10]c–[Pyr]c and 1[12]c–[Pyr]c, with their analogous non-ionic mixtures, 2[10]c–[Ph]c and 2[12]c–[Ph]c, shows a 181 K higher clearing temperature, T_c, for the ion pair. This corresponds to a DFT-calculated difference in association energy ΔΔH_a = 24.5 kcal mol⁻¹ in a typical dielectric medium (ε = 2.5). Pure compounds and binary mixtures were characterized using thermal, optical, and XRD methods.

---

Introduction

Ionic liquid crystals (ILC) are capable of anisotropic ion transport,^1–4 and for this reason they are becoming increasingly attractive electrolytes for ion batteries,⁵ photovoltaic^6–8 and other applications.^9,10 In contrast to non-ionic mesogens, typical ILC are binary systems, comprising of a cation and an anion. Consequently, mesogenic properties of ILC are controlled not only by the anisometry of the two components, but also by electrostatic interactions.¹¹ While the first factor is well understood,¹² the effect of coulombic interactions on phase stability is poorly characterized and has only recently become the subject of theoretical considerations.^13,14 Despite the large number of examples of ILC,¹⁰ there exists no single report of a molecular system that permits experimental evaluation of the coulombic component of the phase stability in the absence of other factors. We now report such a molecular system and for the first time assess the effect of coulombic interactions, as the only variable, on mesophase stability in ILC.

During the past several years, we have developed new ILC materials in which anisometric anions derived from monocarbaborates, [closo-1-CB₉H₁₀]⁻ ([10]) and [closo-1-CB₁₁H₁₂]⁻ ([12]), are the driving force to induce mesogenic behaviour.^15–18 Due to the high delocalization of the charge and the resulting weak nucleophilicity of the boron cluster anions,¹⁹ the ion interactions in such ILC, e.g.1a–[Pyr]a (Fig. 1),¹⁶ are non-specific and mainly electrostatic. Such ion pairs typically form SmA and soft crystalline phases, although some exhibit a nematic phase, e.g. azo derivative 1[12]b–[Pyr]a (Fig. 1).¹⁶

Fig. 1 The structure of ions (1 and [Pyr]) and non-ions (2 and [Ph]). In the cage structures, each vertex represents a BH fragment, and the sphere is a carbon atom.

Replacement of the B⁻ (12) atom in anion 1[12]b and the N⁺ atom in cation [Pyr]a with C atoms leads to a non-ionic pair consisting of carborane 2[12]b and benzene derivative [Ph]a. An equimolar mixture of 2[12]b and [Ph]a represents an isosteric, non-coulombic analogue of the mesogenic ion pair 1[12]b–[Pyr]a.

Here, we report the synthesis and detailed thermal, optical and structural (XRD) analysis of ion pairs 1[10]–[Pyr] and 1[12]–[Pyr] as well as their electrically neutral analogues, 2 and [Ph]. We emphasize the comparison of the mesogenic behaviour of ion pairs 1–[Pyr] with the isosteric, non-ionic equimolar mixtures 2–[Ph]. The experimental results are supported with DFT modelling of the association of ions and non-ionic analogues in a dielectric medium.

Results and discussion

Synthesis

Esters 1c and 2c were obtained by reaction of phenol 3c (ref. 15) with appropriate acid chlorides which were prepared from carboxylic acids 4[10],¹⁵4[12],¹⁶5[10] (ref. 20) and 5[12] (Method A, Scheme 1). Without isolation, ion pairs 1c–[NEt₄], obtained from acid 4[10]–[NEt₄] (ref. 15) and 4[12]–[NEt₄],¹⁶ were converted to 1c–[Pyr] by cation exchange with [Pyr]Br as described before for esters 1a–[Pyr]a and 1b–[Pyr]a.^15,16 Esters 2a and 2b were prepared directly from phenols 3a (ref. 16) and 3b,¹⁶ respectively, and carboxylic acid 5 in the presence of DCC (Method B).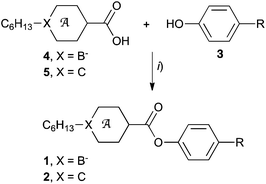

Scheme 1 Synthesis of esters 1 and 2. Reagents and conditions: (i) Method A: (1) (COCl)₂, cat. DMF, CH₂Cl₂; (2) Et₃N, CH₂Cl₂ or Method B: DCC, DMAP, CH₂Cl₂, rt, 12 h.

12-Hexyl-p-carborane-1-carboxylic acid (5[12]) was obtained by alkylation followed by carboxylation of p-carborane (Scheme 2) as described before for the pentyl analogue.²¹

Scheme 2 Synthesis of carboxylic acid 5[12]. Reagents and conditions: (i) (1) BuLi 1 eq, THF −80 °C → rt → −80 °C; (2) C₆H₁₃I 1 eq, 0 °C; (3) BuLi 1 eq, −80 °C → 0 °C; (4) CO₂, (5) HCl.

Pyridinium bromides [Pyr]b–Br and [Pyr]c–Br were prepared by N-alkylation of 4-(trans-4-pentylcyclohexylmethyloxy)-pyridine (6) with appropriate alkyl bromide in MeCN following the procedure described for [Pyr]a–Br (Scheme 3).¹⁵ The substituted pyridine 6 was obtained from 4-chloropyridine and trans-4-pentylcyclohexylmethanol²² (7) in the presence of NaH in DMSO following a general method.²³

Scheme 3 Synthesis of pyridinium salts [Pyr]–Br. Reagents and conditions: (i) NaH, DMSO, rt; (ii) C_nH_2n+1Br, MeCN, reflux.

The cyclohexylmethyl phenyl ethers [Ph] were obtained by alkylation of appropriate 4-alkylphenol (8[n]) with heptyl tosylate (for [Ph]a) or trans-4-pentylcyclohexylmethyl tosylate²²9 for [Ph]b and [Ph]c (Scheme 4). Phenol 8[11] was obtained by alkylation of 4-bromophenol with C₁₁H₂₃MgBr following a general procedure.²⁴

Scheme 4 Synthesis of phenyl ethers [Ph]. Reagents and conditions: (i) K₂CO₃, MeCN, cat Aliquat, reflux.

Thermal analysis

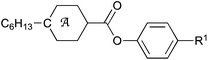
Transition temperatures and enthalpies of the newly prepared compounds were determined by differential scanning calorimetry (DSC) and results are shown in Tables 1 and 2.

Table 1 Transition temperatures for 2^a

R^1	A	Cr		N		I
a Cr-crystal, N-nematic, I-isotropic. Temperatures obtained on heating at 5 K min^−1. Enthalpies are listed in the ESI. b Cr1 104 Cr2. c Ref. 26. d Ref. 17. e Cr1 41 Cr2.
	[10]	˙	114^b	˙	175	˙
	[12]	˙	145	˙	187	˙
	[Ph] ^c	˙	89.5	˙	200	˙
	[10]	˙	67	˙	197	˙
	[12]	˙	85	˙	205	˙
	[Ph] ^d	˙	91	˙	206	˙
	[10]	˙	44^e	(˙	36)	˙
	[12]	˙	46	(˙	45)	˙

---

Table 2 Transition temperatures for binary systems 1–[Pyr] and 2–[Ph]^a

	X	Y	Cr		E		SmA		N		I
a Cr-crystal, SmA-smectic A, E-soft crystalline phase, N-nematic, I-isotropic. Temperatures obtained on heating at 5 K min^−1. Enthalpies are listed in the ESI. For definition of substituents R see Fig. 1. b Cr1 85 Cr2. c Ref. 16. d Cr1 64 Cr2 101 × 107.
1[10]c–[Pyr]c	B^−	N^+	˙	126	˙	163	˙	207			˙
2[10]c–[Ph]c	C	C	˙	27					(˙	26)	˙
1[12]c–[Pyr]c	B^−	N^+	˙	148^b	˙	200	˙	210			˙
2[12]c–[Ph]c	C	C	˙	30					(˙	29)	˙
1[10]c–[Pyr]a ^c	B^−	N^+	˙	107^d							˙
1[12]c–[Pyr]a ^c	B^−	N^+	˙	117							˙
1[12]c–[Pyr]b	B^−	N^+	˙	132	˙	172					˙

---

Single component materials. All six non-ionic carborane derivatives 2 form a nematic phase (Table 1), which is consistent with nematogenic behavior of their benzene analogues. The three-ring compounds 2a and 2b exhibit a wide temperature range enantiotropic phase with clearing temperatures around 200 °C. A comparison of the carborane derivatives with their benzene analogues demonstrates that the phase stability follows the order [10] < [12] < [Ph], which is in agreement with our previous findings.^16,25 The two-ring mesogens, 2c, exhibit monotropic phases with significantly lower N–I transition temperatures.

The phenyl ether [Ph]c is a new member of a known homologous series²⁷ and it exhibits a mesophase identified by XRD analysis as a soft crystalline B phase (Cr 32 SmB_cryst 42 I, Fig. 2a).

Fig. 2 The optical texture of (a) B phase in [Ph]c at 29 °C and (b) nematic phase at 25 °C in 2[12]c–[Ph]c obtained on cooling from the isotropic phase.

DSC, POM, and XRD²⁸ analyses revealed that pyridinium bromide [Pyr]c–Br exhibits a SmA phase and another more ordered unidentified phase. Unfortunately, the salt decomposes at about 165 °C. The shorter analogue, [Pyr]b–Br, is not mesogenic.

Two-component materials. Ion pairs 1a–[Pyr]a and 1b–[Pyr]a were reported before, and they display SmA and nematic phases.¹⁶ Previous results demonstrated that ions pairs 1c–[Pyr]a, in which the total number of rings is 3, melt about 110 °C and do not form liquid crystalline phases.¹⁶ Inclusion of the cyclohexyl ring in the structure of the pyridinium cation increased the melting temperature of ion pair 1[12]c–[Pyr]b and induced an enantiotropic soft crystalline phase E (Table 2). Extension of the butyl chain in the [Pyr]b cation to undecyl in [Pyr]c resulted in the appearance of an enantiotropic SmA phase above the E phase in both ion pairs, 1[10]c–[Pyr]c and 1[12]c–[Pyr]c, with a clearing temperature of about 210 °C (e.g.Fig. 3 and 4). DSC analysis of 1[12]c–[Pyr]c also revealed another soft-crystalline phase X below the E phase.

Fig. 3 DSC trace of 1[12]c–[Pyr]c. The heating and cooling rates are 5 K min⁻¹.

Fig. 4 The optical textures of (a) SmA phase (205 °C) and (b) E phase (175 °C) obtained for 1[12]c–[Pyr]c on cooling from the isotropic phase in the same region of the sample.

These findings are in agreement with our general observations that a total of 4 rings in the ion structures are necessary for induction of mesogenic behavior in ILC of the general structure 1.^16,18 For instance, while 1c–[Pyr]a, a 3-ring ionic compound, does not exhibit mesogenic behaviour, 4-ring ion pairs 1a–[Pyr]a and 1b–[Pyr]a do exhibit enantiotropic SmA and N phases.¹⁶

For comparison purposes, equimolar mixtures of non-ionic analogues of 1–[Pyr] were investigated. Initial studies of 2a–[Ph]a and 2b–[Ph]a demonstrated phase separation upon cooling from the isotropic phase. It was considered that the significant difference in the molecular length and mesogenic behaviour of the two components leads to their incompatibility. Therefore, carboranes 2c and phenyl ether [Ph]c were considered, since the total length of the alkyl chains in each compound is 16 atoms.

POM analysis of equimolar mixtures 2[10]c–[Ph]c and 2[12]c–[Ph]c demonstrated ideal miscibility, and the formation of a monotropic nematic phase with clearing temperatures, T_NI, of 26 °C and 29 °C, respectively (Table 2). A comparison of these transition temperatures with those obtained for the analogous ion pair 1c–[Pyr]c shows a difference in the clearing temperature of 181 K. Since the ion-pair and the non-ionic binary mixture differ only by a molecular charge, the increase in the clearing temperature can be attributed solely to the strong coulombic interactions present in the ion pair and absent in the non-ionic binary mixture.

XRD data

The formation of the SmA phase by ion pairs 1[10]c–[Pyr]c and 1[12]c–[Pyr]c was confirmed by XRD measurements. Diffractograms obtained for the high temperature mesophase in each material showed a series of sharp commensurate reflections consistent with a lamellar structure (Fig. 5). Considering the calculated molecular length²⁸ of about 33.8 Å for both anions 1[10]c and 1[12]c (including van der Waals radius for the terminal H atoms) the measured layer spacing of about 27 Å indicates approximately 20% of interdigitation and/or imperfect orientational order of molecular long axes and molecular folding in both ion-pairs.

Fig. 5 Integrated XRD patterns taken in SmA phase of 1[10]c–[Pyr]c (T = 175 °C, upper red curve) and 1[12]c–[Pyr]c (T = 205 °C, lower black curve). Upper curve is vertically shifted for clarity of presentation.

The wide-angle region of the diffractograms shows an unsymmetric broad halo, which can be deconvoluted into two signals with the maxima about 4.7 Å and 5.1 Å for 1[10]c–[Pyr]c, and 4.8 and 5.3 for 1[12]c–[Pyr]c. The diffused signals correlate with the mean distance between the alkyl chains (former) and the separation between boron clusters (latter).

XRD patterns obtained for oriented samples of 1[10]c–[Pyr]c and 1[12]c–[Pyr]c in the phase formed below the SmA phase could be indexed as an E phase (Table 3 and Fig. 6). However, signals from the full size of the in-plane unit cell were also visible,²⁸ which are typically forbidden for E phase. Signals (100) and (010) are observed due to the binary nature of the ionic materials. This causes the molecule in the center of the unit cell to be different than those in the corners resulting in a unit cell that is not centered. There is also a slight difference between patterns for 1[10]c–[Pyr]c and 1[12]c–[Pyr]c. The pattern for the 12-vertex analogue indicates a regular ABA type stacking of the smectic layers, which leads to a doubling of the unit cell dimension along layer normal (thus doubling of the Miller index l, see Fig 6b). The structure of the E phase formed by ion pair 1[12]c–[Pyr]b is similar to that of 1[10]c–[Pyr]c.

Table 3 Unit cell parameters for E phase in 1c–[Pyr]

	Temperature/°C	a/Å	b/Å	c/Å
1[10]c–[Pyr]c	150	8.99	6.12	29.84
1[12]c–[Pyr]b	150	9.11	6.44	25.26
1[12]c–[Pyr]c	180	9.16	6.50	57.42

---

Fig. 6 2D XRD patterns for E phase of (a) 1[10]c–[Pyr]c at 150 °C and (b) 1[12]c–[Pyr]c at 180 °C. Note the presence of equatorial signals (100) and (010) in (a) and their absence in (b) indicating regular ABA layer stacking for 1[12]c–[Pyr]c.

XRD analysis of the mesophase formed by phenyl ether [Ph]c revealed a soft crystalline B phase (SmB_cry), which is consistent with a relatively large enthalpy of the isotropic transition (12.7 kJ mol⁻¹) and the optical texture (Fig. 2). The measured layer spacing is 31.2 Å which correlates well with the calculated molecular length of 32.8 Å (including van der Waals radius for H atoms).

Molecular modelling

The energy of coulombic interactions in ion pairs 1c–[Pyr]c was assessed computationally by comparison of the association energy for 1[12]c–[Pyr]c and 2[12]c–[Ph]c for an arbitrary chosen relative orientation of the molecules in the pair. The calculations were conducted using the M06-2x functional, which reasonably well reproduces non-covalent interactions.²⁹

Analysis of fully optimized individual structures revealed a nearly linear anion 1[12]c and a bent cation [Pyr]c (Fig. 7). The hexyl chain and the carbonyl group in the former are staggered relative to the {closo-1-CB₁₁} cage. The two carboxyl groups are nearly co-planar with the benzene ring rendering the “organic” half of the molecule planar (Fig. 7a). The angle between the planes of the terminal alkyl chains is 15°, and the molecular length (L, as the H⋯H distance) is 31.6 Å. The carborane analogue 2[12]c has a nearly identical molecular length (L = 31.3 Å). The main difference between 1[12]c and 2[12]c is that the carbonyl group nearly eclipses the B–H bond in the latter, which result in the wider interplanar angle of 27°.

Fig. 7 Equilibrium ground state geometry of ions 1[12]c (a) and [Pyr]c (b) and ion pair 1[12]c–[Pyr]c (c) at the M06-2x/3-21G* level of theory.

The undecyl chain in the pyridnium cation [Pyr]c is orthogonal to the ring plane, which results in a bent molecular structure as shown in Fig. 7b. The interplanar angle is 78° and the H⋯H separation L of 30.3 Å, which is close to the length of anion 1[12]c. Molecular dimensions of the benzene analogue [Ph]c are nearly the same with the interplanar angle of 81° and L = 30.2 Å.

Full geometry optimization of 2[12]c and [Ph]c in vacuum gave a tight molecular pair 2[12]c–[Ph]c, which served as the starting point for geometry optimization of ion pair 1[12]c–[Pyr]c. The resulting close-contact structure is shown in Fig. 7c. A comparison of energies of the individual components and that of the binary system gave the enthalpy of association, ΔH_a after BSSE correction. For the non-ionic pair the association is calculated to be mildly exothermic (ΔH_a = −4.3 kcal mol⁻¹), while for the ion pair, 1[12]c–[Pyr]c, the association enthalpy is dramatically larger ΔH_a = −64.3.0 kcal mol⁻¹ in vacuum. Placing molecules at low strength dielectric medium (ε = 2.5), typical for weakly polar liquid crystals, had little effect on the association enthalpy of 2[12]c–[Ph]c (ΔH_a = −3.4 kcal mol⁻¹). In contrast, the dielectric medium significantly reduced the exotherm of formation of ion pair 1[12]c–[Pyr]c (ΔH_a = −27.9 kcal mol⁻¹). As a result, the difference in association energy, ΔΔH_a, of the non-polar pair and ion pair is 24.5 kcal mol⁻¹ in a weakly dielectric medium. Increasing ε to 10.0, which is reasonable for an ionic liquid,^30,31 the ΔΔH_a value for the two pairs falls to 7.0 kcal mol⁻¹. Thus, the calculated significant difference in association enthalpy in the two model binary systems is consistent with the observed 181 K higher thermal stability of the mesophase in ILC than in the non-ionic binary mixture. Also, the observed tendency for the formation of high-temperature lamellar phases (SmA and E) by the ion pair instead of a nematic phase is a consequence of the tight molecular arrangement dictated by significant coulombic interactions.

Conclusions

For the first time, we have assessed experimentally the impact of coulombic interactions on mesophase stability by comparison of ionic (1c–[Pyr]c) and isosteric non-ionic (2c–[Ph]c) systems in the absence of other factors. Thus, replacement of appropriate carbon atoms in an equimolar binary mixture with B⁻ and N⁺ fragments leads to an isosteric and isoelectronic ion pair. Results show that the difference in the clearing temperature between the two binary systems is 181 K, which corresponds to a difference in association enthalpy of 7 kcal in appropriate dielectric media. The boron cluster size in the ionic material appears to have little effect on the magnitude of this phenomenon. It is possible, however, that the size of the ions is the determining factor. A comparison was demonstrated for components of approximately equal length due to their best compatibility of the electrically neutral compounds (i.e. formation of a homogeneous nematic phase).

The presented concept of isosteric and isoelectronic replacement of C,C with B⁻,N⁺ is applicable to other molecular systems and provides unique experimental models to support theoretical considerations of the liquid crystalline state.

Computational details

Quantum-mechanical calculations were carried out using a Gaussian 09 suite of programs.³² Geometry optimizations for unconstrained conformers of appropriate molecules and ions with the most extended molecular shapes were performed at the M06-2x/3-21G* level of theory²⁹ using default convergence limits. The alkoxy group was set in all-trans conformation maintaining co-planarity with the aromatic ring in the input structure. The aromatic ring and the carboxyl group were staggered with respect to the carborane cage as found experimentally and computationally in related structures. The orientation of the substituents on the cyclohexane ring was set according to results of conformational analysis for model cyclohexane derivatives. Optimized structures of non-polar molecules served as starting points for optimization of the ionic analogues after replacing the carbon atoms with B or N.

For calculations of binary system 2[12]c–[Ph]c, molecules of 2[12]c and [Ph]c at equilibrium geometry (M06-2x/3-21G*) were set parallel to each other at a 4 Å distance, and the geometry of the pair was minimized. The resulting energy was corrected for basis set superposition error (BSSE) by running single point calculations (M06-2x/3-21G*//M06-2x/3-21G*) at the equilibrium geometry with the keyword COUNTERPOISE = 2,³³ and compared to that of isolated molecular components. The optimized geometry of non-polar pair 2[12]c–[Ph]c served as the starting point for calculations involving ion pair 1[12]c–[Pyr]c, after replacement of the two carbon atoms with B and N. Conformational search was not attempted. For each pair, the association energy was calculated as a difference between the energy of the molecular pair and isolated molecules (ΔH_a = H_pair − (H_cat + H_an)).

Thermodynamic parameters were requested with the FREQ keyword. The PCM model³⁴ was implemented using the SCRF (Solvent = Generic, Read) keyword and specified “epsinf = 2.25” and “eps = 2.5” or “eps = 10” and the total energies were obtained in single point calculations with the same method.

Experimental part

General

NMR spectra were obtained at 128 MHz (¹¹B) and 400 MHz (¹H) in CDCl₃ or CD₃CN. Chemical shifts were referenced to the solvent (¹H) or to an external sample of B(OH)₃ in MeOH (¹¹B, δ = 18.1 ppm). Optical microscopy and phase identification were performed using polarized optical microscopy (POM) and a hot stage. Thermal analysis was obtained using a DSC with samples of about 0.5–1.0 mg and a heating rate of 5 K min⁻¹ under a flow of nitrogen gas.

General procedure for the preparation of 1–[Pyr]

To a solution of carboxylic acid 4[12]–[NEt₄] or 4[10]–[NMe₄] (0.1 mmol) in dry CH₂Cl₂ (2 mL) was added oxalyl chloride (5 eq) and a catalytic amount of DMF. The mixture was stirred at rt for 30 min, and the mixture was evaporated to complete dryness. Dry CH₂Cl₂ was added (3 mL) followed by phenol 3 (0.1 mmol) and Et₃N (0.2 mmol), and the reaction was stirred overnight. Organic products were extracted (CH₂Cl₂), the organic layer was dried (Na₂SO₄) and the solvent was evaporated. The residue was passed through a silica gel plug (MeCN/CH₂Cl₂, 1 : 5) giving crude product as either the [NMe₄] or [NEt₄] salt. N-Alkyl-4-alkoxypyridinium bromide ([Pyr]–Br, 1.2 equivalent) was added to a solution of the crude ester 1[10]–[NMe₄] or 1[12]–[NEt₄] (1 eq) in CH₂Cl₂ upon which a white precipitate formed. Water was added, and the biphasic system was stirred overnight. The CH₂Cl₂ layer was separated, and the aqueous layer was extracted with additional CH₂Cl₂. The CH₂Cl₂ layers were combined, washed with H₂O, dried (Na₂SO₄), and the solvent was evaporated. The crude product was purified on a silica gel plug (CH₂Cl₂) and recrystallized from EtOH, EtOH/EtOAc and hexane/EtOAc mixtures providing pure ion pair.

1[12]c–[Pyr]b . Obtained in 68% yield as a white solid: ¹H NMR (400 MHz, CDCl₃) δ 0.50–2.50 (m, 10H), 0.56–0.63 (m, 2H), 0.84 (t, J = 6.9 Hz, 3H), 0.885 (t, J = 6.9 Hz, 3H), 0.888 (t, J = 6.9 Hz, 3H), 0.96 (t, J = 7.4 Hz, 3H), 1.00–1.13 (m, 2H), 1.14–1.44 (m, 32H), 1.73 (quint, J = 7.4 Hz, 2H), 1.76–1.93 (m, 6H), 2.53 (t, J = 7.5 Hz, 2H), 4.07 (d, J = 6.0 Hz, 2H), 4.29 (t, J = 7.5 Hz, 2H), 7.00 (s, 4H), 7.31 (d, J = 7.5 Hz, 2H), 8.32 (d, J = 7.4 Hz, 2H). Anal. calcd for C₄₄H₈₀B₁₁NO₅: C, 64.29; H, 9.81; N, 1.70. Found: C, 64.40; H, 9.71; N, 1.80%.

1[10]c–[Pyr]c . Obtained in 86% yield as a white solid: ¹H NMR (400 MHz, CDCl₃) δ 0.50–2.50 (m, 8H), 0.84–0.94 (m, 12H), 0.98–1.13 (m, 4H), 1.15–1.45 (m, 42H), 1.53–1.63 (m, 2H), 1.78–2.05 (m, 10H), 2.57 (t, J = 7.5 Hz, 2H), 4.01 (d, J = 6.0 Hz, 2H), 4.25 (t, J = 7.5 Hz, 2H), 7.11 (d, J = 7.4 Hz, 2H), 7.25 (d, J = 6.9 Hz, 2H), 7.27 (d, J = 6.9 Hz, 2H), 8.26 (d, J = 7.2 Hz, 2H). Anal. calcd for C₅₁H₉₂B₉NO₅: C, 68.32; H, 10.34; N, 1.56. Found: C, 68.60; H, 10.19; N, 1.47%.

1[12]c–[Pyr]c . Obtained in 61% yield as a white solid: ¹H NMR (400 MHz, CDCl₃) δ 0.50–2.50 (m, 10H), 0.56–0.64 (m, 2H), 0.84 (t, J = 6.7 Hz, 3H), 0.86–0.91 (m, 9H), 0.93–1.13 (m, 4H), 1.16–1.44 (m, 44H), 1.73 (quint, J = 7.4 Hz, 2H), 1.78–1.95 (m, 6H), 2.53 (t, J = 7.5 Hz, 2H), 4.07 (d, J = 6.0 Hz, 2H), 4.28 (t, J = 7.5 Hz, 2H), 7.00 (s, 4H), 7.30 (d, J = 7.4 Hz, 2H), 8.30 (d, J = 7.4 Hz, 2H). Anal. calcd for C₅₁H₉₄B₁₁NO₅: C, 66.57; H, 10.30; N, 1.52. Found: C, 66.82; H, 10.32; N, 1.44%.

General procedure for preparation of esters 2

Method A. To a solution of carboxylic acid 5 (0.1 mmol) in dry CH₂Cl₂ (2 mL) was added oxalyl chloride (5 eq) and a catalytic amount of DMF. The mixture was stirred at rt for 30 min, and the mixture was evaporated to complete dryness. Dry CH₂Cl₂ was added (3 mL) followed by appropriate phenol 3 (ref. 16) (0.1 mmol) and Et₃N (0.2 mmol), and the mixture was stirred overnight. Organic products were extracted (CH₂Cl₂), organic layer was dried (Na₂SO₄) and the solvent was evaporated. The residue was passed through a silica gel plug (hexane/CH₂Cl₂, 4 : 1) giving crude ester 2, which was purified further by recrystallization.

Method B. A solution of carboxylic acid 5 (0.1 mmol) and appropriate phenol 3 (ref. 16) (0.11 mmol) was treated with N,N′-dicyclohexylcarbodiimide (DCC, 31 mg, 0.15 mmol) and a catalytic amount of 4-dimethylaminopyridine. The reaction mixture was stirred overnight. The reaction mixture was then washed with 10% HCl, the CH₂Cl₂ layer separated, dried (Na₂SO₄), and evaporated. The crude material was passed through a silica gel plug (CH₂Cl₂) giving crude ester 2, which was purified further by recrystallization.

2[10]a . Obtained as a white solid from acid 5[10] according to Method B and recrystallized from EtOH: ¹H NMR (400 MHz, CDCl₃) δ 0.88 (t, J = 6.9 Hz, 3H), 0.94 (t, J = 7.0 Hz, 3H), 1.03–1.10 (m, 2H), 1.12–1.31 (m, 6H), 1.32–1.46 (m, 20H), 1.49–1.58 (m, 2H), 1.5–3.5 (m, 8H), 1.95 (quint, J = 7.9 Hz, 2H), 2.49–2.57 (m, 2H), 3.23 (t, J = 8.3 Hz, 2H), 7.18 (d, J = 8.6 Hz, 2H), 7.23 (d, J = 8.6 Hz, 2H); ¹¹B NMR δ −10.3 (d, J = 160 Hz, 8B). Anal. calcd for C₃₁H₅₄B₈O₂: C, 68.29; H, 9.98. Found: C, 68.56; H, 9.95%.

2[12]a . Obtained as a white solid from acid 5[12] according to Method B and recrystallized from EtOH: ¹H NMR (400 MHz, CDCl₃) δ 0.85 (t, J = 7.1 Hz, 3H), 0.87 (t, J = 6.9 Hz, 3H), 1.00–1.07 (m, 2H), 1.08–1.42 (m, 30H), 1.5–3.5 (m, 10H), 1.60–1.64 (m, 2H), 2.42–2.49 (m, 2H), 6.83 (d, J = 8.5 Hz, 2H), 7.09 (d, J = 8.5 Hz, 2H); {¹H}¹¹B NMR δ −13.9 (5B), –12.7 (5B). Anal. calcd for C₃₁H₅₆B₁₀O₂: C, 65.45; H, 9.92. Found: C, 65.74; H, 9.84%.

2[10]b . Obtained as an orange solid from acid 5[10] according to Method B, and recrystallized from iso-octane (3×) and then from EtOH (2×) at −4 °C: ¹H NMR (400 MHz, CDCl₃) δ 0.92 (t, J = 6.8 Hz, 3H), 0.94 (t, J = 7.1 Hz, 3H), 1.5–3.5 (m, 8H), 1.32–1.45 (m, 8H), 1.45–1.55 (m, 4H), 1.83 (quint, J = 7.0 Hz, 2H), 1.97 (quint, J = 7.9 Hz, 2H), 3.24 (t, J = 8.4 Hz, 2H), 4.05 (t, J = 6.5 Hz, 2H), 7.01 (d, J = 8.9 Hz, 2H), 7.45 (d, J = 8.8 Hz, 2H), 7.93 (d, J = 8.9 Hz, 2H), 7.99 (d, J = 8.7 Hz, 2H); {¹H}¹¹B NMR (128 MHz, CDCl₃) δ −10.2. Anal. calcd for C₂₇H₄₂B₈N₂O₃: C, 61.29; H, 8.00; N, 5.29. Found: C, 61.39; H, 7.92; N, 5.30%.

2[12]b . Obtained as an orange solid from acid 5[12] according to Method B and recrystallized from iso-octane (3×) and then from EtOH (2×): ¹H NMR (400 MHz, CDCl₃) δ 0.85 (t, J = 7.1 Hz, 3H), 0.92 (t, J = 7.0 Hz, 3H), 1.13–1.26 (m, 8H), 1.33–1.38 (m, 4H), 1.45–1.52 (m, 2H), 1.5–3.5 (m, 10H), 1.61–1.65 (m, 2H), 1.82 (quint, J = 7.1 Hz, 2H), 4.04 (t, J = 6.6 Hz, 2H), 6.99 (d, J = 9.0 Hz, 2H), 7.10 (d, J = 8.8 Hz, 2H), 7.85 (d, J = 8.9 Hz, 2H), 7.88 (d, J = 9.1 Hz, 2H). Anal. calcd for C₂₇H₄₄B₁₀N₂O₃: C, 58.67; H, 8.02; N, 5.07. Found: C, 58.94; H, 7.97; N, 5.03%.

2[10]c . Obtained in 90% yield as a white solid from acid 5[10] according to Method A and recrystallized from MeCN and EtOH–AcOEt mixture: ¹H NMR (400 MHz, CDCl₃) δ 0.89 (t, J = 6.9 Hz, 3H), 0.94 (t, J = 7.1 Hz, 3H), 1.24–1.45 (m, 14H), 1.49–1.58 (m, 2H), 1.5–3.5 (m, 8H), 1.76 (quint, J = 7.5 Hz, 2H), 1.90–2.02 (m, 2H), 2.57 (t, J = 7.5 Hz, 2H), 3.23 (t, J = 8.3 Hz, 2H), 7.17 (d, J = 9.0 Hz, 2H), 7.32 (d, J = 9.0 Hz, 2H). Anal. calcd for C₂₄H₄₂B₈O₄: C, 59.92; H, 8.80. Found: C, 60.15; H, 8.74%.

2[12]c . Obtained in 93% yield as a white solid from acid 5[12] according to Method A, and recrystallized from MeCN and EtOH–AcOEt mixture: ¹H NMR (400 MHz, CDCl₃) δ 0.85 (t, J = 7.0 Hz, 3H), 0.88 (t, J = 6.3 Hz, 3H), 1.07–1.44 (m, 18H), 1.5–3.5 (m, 10H), 1.58–1.66 (m, 2H), 1.72 (quint, J = 7.4 Hz, 2H), 2.52 (t, J = 7.5 Hz, 2H), 6.97 (d, J = 9.0 Hz, 2H), 7.04 (d, J = 9.0 Hz, 2H). Anal. calcd for C₂₄H₄₄B₁₀O₄: C, 57.11; H, 8.79. Found: C, 57.36; H, 8.70%.

1-Butyl-4-heptyloxybenzene ([Ph]a). A suspension of 4-butylphenol (8[4], 1.00 g, 6.7 mmol), 1-bromoheptane (1.00 mL, 7.0 mmol), K₂CO₃ (2.8 g, 20.1 mmol), and a catalytic amount of Aliquat in dry MeCN (15 mL) was stirred at reflux for 24 h. The solvent was evaporated, and the residue was passed through a silica gel plug (hexane). The crude product was further purified by Kugel-Rohr distillation (160–170 °C/0.5 mm Hg) giving 1.50 g (90% yield) of [Ph]a as a colorless oil: ¹H NMR (400 MHz, CDCl₃) δ 0.89 (t, J = 6.9 Hz, 3H), 0.92 (t, J = 7.3 Hz, 3H), 1.26–1.40 (m, 8H), 1.41–1.48 (m, 2H), 1.53–1.61 (m, 2H), 1.77 (quint, J = 7.0 Hz, 2H), 2.54 (t, J = 7.7 Hz, 2H), 3.93 (t, J = 6.6 Hz, 2H), 6.81 (d, J = 8.6 Hz, 2H), 7.08 (d, J = 8.6 Hz, 2H). Anal. calcd for C₁₇H₂₈O: C, 82.20; H, 11.36. Found: C, 82.38; H, 11.55%.

trans-4-Pentylcyclohexylmethyl 4-undecylphenyl ether ([Ph]c). A suspension of 4-undecylphenol (8[11], 1.0 mmol), tosylate 9 (ref. 22) (1.0 mmol), K₂CO₃ (3.0 mmol), and a catalytic amount of Aliquat in dry MeCN (5 mL) was stirred at reflux for 24 h. The solvent was evaporated, and the residue was passed through a silica gel plug (hexane/CH₂Cl₂, 4 : 1) giving crude product. The product was further purified by multiple recrystallizations from MeCN/AcOEt and EtOH/AcOEt mixtures giving [Ph]c in 78% yield as a white solid: ¹H NMR (400 MHz, CDCl₃) δ 0.85 (t, J = 7.0 Hz, 3H), 0.88 (t, J = 6.3 Hz, 3H), 0.90–1.10 (m, 3H), 1.15–1.44 (m, 26H), 1.58–1.66 (m, 2H), 1.68–1.77 (m, 1H), 1.79 (br d, J = 11.8 Hz, 2H), 1.88 (br d, J = 13.3 Hz, 2H), 2.52 (t, J = 7.7 Hz, 2H), 3.72 (d, J = 6.4 Hz, 2H), 6.80 (d, J = 8.6 Hz, 2H), 7.06 (d, J = 8.5 Hz, 2H). Anal. calcd for C₂₉H₅₀O: C, 83.99; H, 12.15. Found: C, 84.19; H, 12.04%.

4-(trans-4-Pentylcyclohexylmethyloxy)pyridine (6). Following a general literature procedure,^23,35 a suspension of NaH (755 mg, 19.7 mmol, 60% in oil) in dry DMSO (50 mL) was treated with trans-4-pentylcyclohexylmethanol²² (7, 3.00 g, 16.4 mmol) under an Ar atmosphere. The mixture was stirred for 2 h at rt, and then freshly prepared 4-chloropyridine^23,35 was added. The reaction mixture was stirred at rt overnight. Water was added, and the mixture was extracted (hexane). The hexane layer was separated, dried (Na₂SO₄), and evaporated. The crude product was passed through a silica gel plug (CH₂Cl₂/EtOAc, 4 : 1) giving 2.25 g (53% yield) of pyridine 6 as a white solid: mp 72–72 °C; ¹H NMR (400 MHz, CDCl₃) δ 0.89 (t, J = 7.0, 3H), 0.90–1.11 (m, 3H), 1.12–1.36 (m, 10H), 1.70–1.78 (m, 1H), 1.81 (br d, J = 13.8 Hz, 2H), 1.88 (br d, J = 13.8 Hz, 2H), 3.79 (d, J = 6.4 Hz, 2H), 6.78 (d, J = 6.4 Hz, 2H), 8.40 (d, J = 6.4 Hz, 2H). Anal. calcd for C₁₇H₂₇NO: C, 78.11; H, 10.41; N, 5.36. Found: C, 78.15; H, 10.24; N, 5.41%.

1-Butyl-4-(trans-4-pentylcyclohexylmethyloxy)pyridinium bromide ([Pyr]b–Br). A solution of pyridine 6 (300 mg, 1.15 mmol) and 1-bromobutane (1.02 mL, 9.4 mmol) in dry MeCN (10 mL) was refluxed for 15 h. The solvent was evaporated, and the residue was passed through a silica gel plug (MeCN/CH₂Cl₂) yielding 620 mg (62% yield) of pyridinium salt [Pyr]b–Br which was recrystallized from EtOH to give a white solid: DSC Cr₁ 53 Cr₂ 80 107 I; ¹H NMR (400 MHz, CDCl₃) δ 0.88 (t, J = 7.0 Hz, 3H), 0.96 (t, J = 7.3 Hz, 3H), 0.95–1.14 (m, 3H), 1.15–1.34 (m, 10H), 1.40 (sext. J = 6.0 Hz, 2H), 1.75–1.89 (m, 5H), 1.95 (quint, J = 7.6 Hz, 2H), 4.06 (d, J = 6.0 Hz, 2H), 4.73 (t, J = 7.4 Hz, 2H), 7.39 (d, J = 7.2 Hz, 2H), 9.16 (d, J = 7.2 Hz, 2H). Anal. calcd for C₂₁H₃₆BrNO: C, 63.31; H, 9.11; N, 3.52. Anal. calcd for C₂₁H₃₆BrNO·0.5H₂O: C, 61.91; H, 9.15; N, 3.44. Found: C, 62.14; H, 9.02; N, 3.50%.

4-(trans-4-Pentylcyclohexylmethyloxy)-1-undecyl-pyridinium bromide ([Pyr]c–Br). It was prepared in an analogous way to the synthesis of [Pyr]b–Br using 6 and undecyl bromide and isolated as a white solid. The salt was further purified by crystallization (3×) from EtOH containing a few drops of hexane giving a white solid: DSC Cr 75 Sm₁ 146 SmA 163 dec. I; ¹H NMR (400 MHz, CDCl₃) δ 0.87 (t, J = 6.8 Hz, 3H), 0.89 (t, J = 6.9 Hz, 3H), 0.95–1.15 (m, 3H), 1.16–1.39 (m, 26H), 1.76–1.89 (m, 5H), 1.96 (quint, J = 7.1 Hz, 2H), 4.07 (d, J = 6.0 Hz, 2H), 4.70 (t, J = 7.4, 2H), 7.40 (d, J = 7.4 Hz, 2H), 9.09 (d, J = 7.4 Hz, 2H). Anal. calcd for C₂₈H₅₀BrNO: C, 67.72; H, 10.15; N, 2.82. Anal. calcd for C₂₈H₅₀BrNO·H₂O: C, 65.35; H, 10.18; N, 2.72. Found: C, 65.62; H, 10.18; N, 2.75%.

Note added after first publication

This article replaces the version published on 15th October 2014, which contained errors in the formulae of the monocarbaborates in the Introduction section.

Acknowledgements

This work was supported by the NSF grant DMR-1207585.

Notes and references

1. T. Kato, Science, 2002, 295, 2414–2418.
2. H. Shimura, M. Yoshio, K. Hoshino, T. Mukai, H. Ohno and T. Kato, J. Am. Chem. Soc., 2008, 130, 1759–1765.
3. T. Ichikawa, M. Yoshio, A. Hamasaki, T. Mukai, H. Ohno and T. Kato, J. Am. Chem. Soc., 2007, 129, 10662–10663.
4. M. Yoshio, T. Kagata, K. Hoshino, T. Mukai, H. Ohno and T. Kato, J. Am. Chem. Soc., 2006, 128, 5570–5577.
5. Y. Abu-Lebdeh, A. Abouimrane, P.-J. Alarco and M. Armand, J. Power Sources, 2006, 154, 255–261.
6. N. Yamanaka, R. Kawano, W. Kubo, T. Kitamura, Y. Wada, M. Watanabe and S. Yanagida, Chem. Commun., 2005, 740–742.
7. R. Kawano, M. K. Nazeeruddin, A. Sato, M. Grätzel and M. Watanabe, Electrochem. Commun., 2007, 9, 1134–1138.
8. Y. Zhao, J. Zhai, J. He, X. Chen, L. Chen, L. Zhang, Y. Tian, L. Jiang and D. Zhu, Chem. Mater., 2008, 20, 6022–6028.
9. K. Binnemans, Chem. Rev., 2005, 105, 4148–4204.
10. K. V. Axenov and S. Laschat, Materials, 2011, 4, 206–259.
11. Evidence include induction of liquid crystalline phases by quartenization of the nitrogen center in pyridine and imidazole derivatives. For example: X. Cheng, X. Bai, S. Jing, H. Ebert, M. Prehm and C. Tschierske, Chem.–Eur. J., 2010, 16, 4588–4601; L. M. Antill, M. M. Neidhardt, J. Kirres, S. Beardsworth, M. Mansueto, A. Baro and S. Laschat, Liq. Cryst., 2014, 41, 976–985.
12. D. Demus, in Handbook of Liquid Crystals, ed. D. Demus, J. W. Goodby, G. W. Gray, H.-W. Spiess and V. Vill, Wiley-VCH, New York, 1998, vol. 1, pp. 133–187.
13. S. Kondrat, M. Bier and L. Harnau, J. Chem. Phys., 2010, 132, 184901.
14. G. Saielli, Soft Matter, 2012, 8, 10279–10287.
15. B. Ringstrand, H. Monobe and P. Kaszynski, J. Mater. Chem., 2009, 19, 4805–4812.
16. B. Ringstrand, A. Jankowiak, L. E. Johnson, P. Kaszynski, D. Pociecha and E. Górecka, J. Mater. Chem., 2012, 22, 4874–4880.
17. J. Pecyna, A. Sivaramamoorthy, A. Jankowiak and P. Kaszynski, Liq. Cryst., 2012, 39, 965–971.
18. A. Jankowiak, J. Kanazawa, P. Kaszynski, R. Takita and M. Uchiyama, J. Organomet. Chem., 2013, 747, 195–200.
19. C. A. Reed, Acc. Chem. Res., 1998, 31, 133–139.
20. Z. Janoušek and P. Kaszynski, Polyhedron, 1999, 18, 3517–3526.
21. A. G. Douglass, K. Czuprynski, M. Mierzwa and P. Kaszynski, J. Mater. Chem., 1998, 8, 2391–2398.
22. A. Jankowiak, A. Januszko, B. Ringstrand and P. Kaszynski, Liq. Cryst., 2008, 35, 65–77.
23. A. Jankowiak, A. Baliński, J. E. Harvey, K. Mason, A. Januszko, P. Kaszyński, V. G. Young Jr and A. Persoons, J. Mater. Chem. C, 2013, 1, 1144–1159.
24. N. A. Bumagin and E. V. Luzikova, J. Organomet. Chem., 1997, 532, 271–273.
25. P. Kaszynski, in Boron Science. New Technologies and Applications, ed. N. S. Hosmane, CRC Press, New York, 2012, pp. 319–354.
26. R. Dabrowski, J. Dziaduszek, J. Szulc, K. Czupryński and B. Sosnowska, Mol. Cryst. Liq. Cryst., 1991, 209, 201–211.
27. N. Carr and G. W. Gray, Mol. Cryst. Liq. Cryst., 1985, 124, 27–43.
28. For details see the ESI.†.
29. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
30. T. Singh and A. Kumar, J. Phys. Chem. B, 2008, 112, 12968–12972.
31. M.-M. Huang, Y. Jiang, P. Sasisanker, G. W. Driver and H. Weingärtner, J. Chem. Eng. Data, 2011, 56, 1494–1499.
32. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
33. S. Simon, M. Duran and J. J. Dannenberg, J. Chem. Phys., 1996, 105, 11024–11031.
34. M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 and references therein.
35. G. H. Schmid and A. W. Wolkoff, Can. J. Chem., 1972, 50, 1181–1187.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic details for intermediates 5[12] and 8[11], additional computational data, archive of optimized equilibrium geometries for 1[12]c, 2[12]c, [Pyr]c, [Ph]c, and pairs 1[12]c–[Pyr]c and 2[12]c–[Ph]c. See DOI: 10.1039/c4ra06502f

---