Energetic and topological approach for characterization of supramolecular clusters in organic crystals†
Abstract
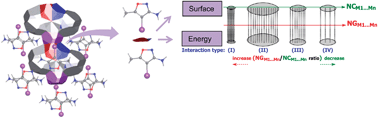
In this work, an approach is proposed for understanding the crystal arrangements of organic compounds. The crystals are studied taking into account the stabilization energy and the topological properties like contact surfaces of a molecule (M1) due to the presence of neighboring Mn (cluster). The molecular system models chosen were five heterocycles and one β-enaminone. The cluster of compounds had a Molecular Coordination Number (MCN) of 14, except for one compound that had an MCN of 16. Our study showed that intermolecular interactions can be divided into four main types: type I, with large energy values and a small contact surface; type II, involving a large value for both the energy and the contact surface; type III, with small and medium energy values, and a medium-sized contact surface; and type IV, with small energy values and a relatively large contact surface. Additionally, from this approach we show that only from the supramolecular cluster is it possible to observe the participation of the topological component during the formation of the crystal. This is demonstrated by the fact that the fragility of the electrostatic interaction between M1 and one Mn in the same plane is compensated by a strong interaction of M1 with a molecule in another plane.

 Please wait while we load your content...
Please wait while we load your content...