Density functional study on the effect of a new ladder-type structure with different substituent groups (R = H, CH₃, OCH₃ and CN) for donor–acceptor copolymers

Abstract

A series of ladder-type fused-ring D–A (donor–acceptor) copolymers have been designed and synthesized as electron donors for BHJ photovoltaic cells, in previous work, and almost all of them focus on electron-rich units. The aim of this paper is to explore the effect of a new ladder-type multifused electron-deficient unit (DCDTBT) with different substituent groups (R = H, CH₃, OCH₃ and CN) on the ground state structure, electronic, optical and charge transfer properties of D–A copolymers for the improvements of photovoltaic performance. Based on the reported D–A copolymer (P1) which was composed of an electron-rich benzo[1,2-b:4,5-b′]dithiophene unit (BDT) and an electron-deficient 4,7-di(4-hexyl-2-thienyl)-2,1,3-benzothiadiazole unit (4DTBT), the 4DTBT unit was replaced with the ladder-type di[4,4-dicyclopenta]dithienylbenzothiadiazole (DCDTBT) unit to form a new copolymer (P2). The calculated results reveal that P2 has better planarity, wider and stronger optical absorption, and smaller reorganization energy than P1. Then the substituent groups (CH₃, OCH₃ and CN) were introduced at the bridging carbons of the DCDTBT unit to design seven new donor copolymers (P2a–P2c, P2a′–P2c′ and P3). From the calculated results, the introduction of the substituent groups into the DCDTBT unit can markedly improve the electronic, optical and charge transfer properties of those copolymers, but have a little influence on molecular backbone planarity. In particular, the introduction of the cyano-group into the DCDTBT unit can obviously reduce the HOMO/LUMO levels of the copolymers. Interestingly, the copolymers (P2c/P2c′) combining the cyano-group and methyl or methoxyl into the same bridging carbon of DCDTBT unit have excellent electronic, optical properties and charge transfer ability, as promising donor polymers for high-efficiency (∼7% for P2c, ∼9% for P2c′) organic solar cells. In this work, a design strategy is used to select a suitable ladder-type electron-deficient unit for further improving the photovoltaic performance of donors in solar cells.

---

1. Introduction

Bulk heterojunction (BHJ) polymer solar cells (PSCs) have been becoming greatly attractive due to their numerous potential advantages over conventional silicon-based solar cells, such as low cost, lightweight, flexibility and solubility to fabricate flexible large-area devices.^1–3 In general, a donor and an acceptor segment constitute the active layers in organic polymer solar cells, assembled either in the form of a blend or in a bilayer structure.⁴ Fullerene and its derivates are generally as acceptor materials for organic solar cells.^5,6 In most cases, people mainly study electron donors in the organic solar cells. Now, the D–A copolymers have been widely used as donor polymers with narrow band gaps in PSCs.^7–10

It is worth mentioning that the main strategies to improve the efficiency of PSCs as follows: (1) reduce the HOMO energy level of a donor molecule to obtain a large open circuit voltage (V_oc), owing to the energy difference between the HOMO of the donor and the LUMO of the acceptor in direct proportion to the V_oc,³ (2) decrease the band gap of a donor molecule to increase the short-circuit current (J_sc),¹¹ (3) keep the LUMO level of a donor to be at least 0.3 eV higher than the LUMO level of the acceptor (fullerene derivatives) to guarantee the efficient charge separation at the donor–acceptor interface and overcome the binding energy of the intrachain exciton.^12–14 Besides, the solubility and morphology of photovoltaic materials significantly influence the efficiency in the fabrication of the bulk heterojunction PSCs.

Di-2-thienyl-2′,1′,3′-benzothiadiazole (DTBT) is extensively used as an efficient electron-deficient (acceptor) unit in high-efficiency BHJ polymer solar cells, because it is convenient to tune the energy levels so as to adjust the absorption spectra.^15,16 In this paper, the D–A copolymer¹⁵ P1 (Fig. 1) that is composed of 4DTBT acceptor unit and donor unit of BDT has been designed and synthesized for PSCs. However, P1 possesses a relatively large energy gap (1.98 eV) and high-lying HOMO level, which results in low short-circuit current (J_sc) and small V_oc, respectively.

Fig. 1 Structural diagrams of P1 and DCDTBT-derivatives (P2, P2a–P2c, P2a′–P2c′ and P3).

Considerable researches have demonstrated that the forced planarization by covalently fastening adjacent aromatic units by a carbon bridge in the electron-rich (donor) units of the polymer backbone includes the following advantages:^17–22 (1) providing an effective way to strengthen the π conjugation and decrease the band gap (broad light absorption spectrum), (2) suppressing the rotational disorder around interannular single bonds to lower the reorganization energy, enhancing charge-carrier mobility and intermolecular hopping, (3) facilitating to introduce different substituent groups at the bridging carbons to adjust the orbital energy levels (such as reducing HOMO/LUMO levels). For instance, Wu and his co-workers²⁰ developed two ladder-type multifused copolymers poly(fluorence-dicyclopentathiophene-alt-benzothiadiazole) (PFDCTBT) and poly(carbazole-dicyclopentathiophene-alt-benzothiadiazole) (PCDCTBT) where the 3-positions of two outer thiophenes are covalently tied with 3,6-positions of central fluorene or carbazole cores by a carbon bridge forming a rigid structure. The rigid structures of PFDCTBT and PCDCTBT possess strong π conjugation, narrow band gaps and high hole mobilities. As expected, the copolymers of PFDCTBT and PCDCTBT both show relatively good performance (2.8% and 3.7%). However, up to now, most of the studies have been focusing on electron-rich units rather than electron-deficient units in D–A donor polymers.

Questions may be raised when a ladder-type electron-deficient unit with different substituent groups (R = H, CH₃, OCH₃ and CN) are introduced in polymer backbone as follows: (1) How do the substituent groups affect the ground state geometries of these copolymers? (2) What is the effect of the substituent groups on the electronic, optical and charge transfer properties of these copolymers as well as the photovoltaic performances? (3) How to make the copolymers possess both low-lying HOMO energy levels and narrow band gaps by introducing the substituents at the bridging carbon of the polymer backbones? In order to elaborate these problems, we devise a ladder-type multifused acceptor unit (DCDTBT) to replace 4DTBT unit on the basis of the concept of Wu and his co-workers. In the unique DCDTBT unit (R = H), all the 3-positions of two outer thiophenes were covalently tied with the 3,3′-position of BT core by a carbon bridge, forming two cyclopentadienyl rings embedded in a rigid pentacyclic structure. Moreover, the substituents (CH₃, OCH₃ and CN) were introduced on the bridging carbon of the DCDTBT unit to adjust the ground state structure, electronic, optical and charge transfer properties of D–A copolymers for the improvements of photovoltaic performance. In this paper, this study presents us with a structural guideline to select a ladder-type multifused acceptor unit for further improving the photovoltaic performance of BHJSCs.

2. Computational details

All the DFT and TD-DFT calculations were performed with the aid of the Gaussian 09 program.²³ Density functional theory (DFT) was used to optimize the neutral, cationic and anionic geometries of the oligomers. For the sake of simplifying the calculation, all the alkyl and alkoxy branched chains (Fig. 1) were replaced by methyl and methoxyl groups, respectively, while hydrogen atoms saturate the terminal groups of the repetitive units.²⁴ To find a appropriate calculated method, P1 was calculated at three famous functionals (B3LYP,^25,26 PBE0 and BHandHLYP²⁷) with 6-31G**and 6-311G** basis sets (on the monomer and dimer models) to predict the HOMO energy level. The PBE0 method is well suited for sulfur-bearing molecules by Jacquemin's reports.^28,29 The related theoretical investigation of P1 has been reported by Zhang's team.³⁰

The calculated results of the HOMO energy levels of M1 (monomer) and D1 (dimer) at B3LYP, PBE0 and BHandHLYP methods with 6-311G** level are listed in Table 1, respectively. By contrast, the calculated HOMO energy levels at the same methods with 6-31G** level for monomer and dimer models are listed in Table S1 (see ESI†). The calculated HOMO energy level was taken from the energy eigenvalue corresponding to the highest occupied (Kohn–Sham) KS orbital on the basis of many papers supporting the physical significance of the highest occupied KS HOMO energy eigenvalue.^31,32

Table 1 HOMO energy (in eV), ΔE_LU–HO (in eV), absorption peaks: λ (in nm) and vertical transition energies of S₀ → S₁: E_g,_TD (in eV) of P1 obtained in the gas phase with PBE0, B3LYP and BHandHLYP methods at 6-311G** basis set

Method	Oligomer	HOMO	ΔELU–HO	λ	Eg,TD	HOMO^a	λ^a
a Experimental values (from ref. 15) “M” and “D” denote monomer and dimer, respectively.
PBE0	M1	−5.40	2.67	563	2.20	−5.40	625
				379			425
	D1	−5.24	2.40	636	1.95
				420
B3LYP	M1	−5.24	2.37	602	2.06
				397
	D1	−5.09	2.13	682	1.82
				445
BHand-HLYP	M1	−6.13	4.30	443	2.80
				311
	D1	−5.96	4.02	476	2.61
				326

---

Two ways have been used to calculate the energy gaps (band gaps) of the copolymer (P1). The first way is to take the difference between HOMO and LUMO energies which is calculated by DFT (ΔE_LU–HO in Table 1 and S1†). Another way is to directly calculate the S₀ → S₁ electronic transition energy with TDDFT (E_g,_TD; in Table 1 and S1†). Likewise, the calculated results with a smaller basis set (B3LYP/6-31G**, PBE0/6-31G** and BHandHLYP/6-31G**) are listed in the Table S1† for comparison with 6-311G**. The calculated band gap with PBE0 functional (dimer model) at the 6-311G** basis set in the TDDFT approach is in excellent agreement with the experimental value of the copolymer (P1). Furthermore, in order to expound the variation of the HOMO levels and energy gaps with increasing conjugation lengths, P1 was calculated at PBE0/6-311G** level on oligomer models (monomer, dimer and trimer) for reducing the calculated cost. As shown in Table S3 (see ESI†), from monomer to trimer, the HOMO levels are gradually increased while the energy gaps are gradually decreased. Moreover, the related investigation has been reported by Zhang's team.³⁰

Compared with the above-mentioned calculated results, they show that PBE0 method with 6-311G** basis set on dimer model is more appropriate for this article. The LUMO level was equal to the HOMO level plus to the TDDFT transition energy (E_LUMO = E_HOMO + E_g,TD) instead of taking from the unreliable KS LUMO eigenvalue.^24,33,34 In order to reduce the error, the reorganization energies for hole (λ_h) and electron (λ_e) of the copolymers were predicted on the dimer model at the PBE0/6-311G** level. In this work, the ground state geometries were calculated by the spin-restricted DFT. Nevertheless, the spin-unrestricted DFT was used to optimize the doublet ion state geometries of the anionic and cationic units. All the calculations of the studied copolymers were carried out only in the gas phase.

3. Results and discussion

3.1. The ground state structural properties

The main optimized ground state structural parameters of P1–P3, P2a–P2c and P2a′–P2c′ are shown in Table 2. The optimized ground state structures of all copolymers are listed in Fig. S1.† As shown in Table 2, the calculated dihedral angles (C1–C2–C3–S1/S1–C4–C5–C6/C7–C8–C9–S2/S2–C16–C17–C18/S3–C19–C20–C21/C22–C23–C24–C25/C26–C27–C28–C29) of P2 are less than the corresponding dihedral angles of P1, meaning that the molecular backbone of P2 has better planarity than that of P1. Herein, P2 possesses a good planar molecular structure due to the following reasons: (1) the two thiophene-rings have alkyl branched-chains in the 4DTBT unit, whereas there is no alkyl branched-chains in the DCDTBT unit; (2) the two outer thiophenes of the DCDTBT unit are covalently tied with the 3,3′-position of BT core by a carbon bridge, forming a rigid pentacyclic structure. Due to the introduction of the DCDTBT electron-deficient unit in P2, it leads to the stronger conjugation effect and the shorter bond lengths (C2–C3/C4–C5/C8–C9/C16–C17/C19–C20/C23–C24/C27–C28) compared with P1.

Table 2 Selected geometrical parameters of the copolymers

	P1	P2	P2a	P2b	P2c	P2a′	P2b′	P2c′	P3
Bond length (Å)
C2–C3	1.446	1.440	1.440	1.440	1.440	1.440	1.440	1.440	1.440
C4–C5	1.449	1.434	1.430	1.431	1.430	1.442	1.436	1.437	1.431
C8–C9	1.449	1.434	1.430	1.429	1.430	1.442	1.442	1.437	1.431
C16–C17	1.445	1.439	1.439	1.439	1.440	1.439	1.439	1.440	1.440
C19–C20	1.445	1.439	1.439	1.440	1.440	1.439	1.440	1.440	1.440
C23–C24	1.449	1.435	1.431	1.432	1.431	1.443	1.437	1.438	1.432
C27–C28	1.452	1.438	1.434	1.434	1.435	1.446	1.446	1.442	1.436
Dihedral angle (°)
C1–C2–C3–S1	−32.17	−15.39	−16.92	11.29	−13.19	−11.95	−12.24	15.67	−13.44
S1–C4–C5–C6	6.57	0.38	3.24	2.87	−0.83	2.93	2.46	−0.28	−1.61
C7–C8–C9–S2	7.33	0.36	2.37	0.17	−1.71	2.48	0.32	−0.46	−2.62
S2–C16–C17–C18	−31.67	−13.89	12.73	10.63	16.18	−12.53	−13.63	15.43	17.40
S3–C19–C20–C21	27.89	14.49	10.75	−16.21	−12.64	10.18	12.80	−16.39	−14.98
C22–C23–C24–C25	−7.93	0.03	1.86	1.37	−1.03	1.78	0.89	0.26	1.26
C26–C27–C28–C29	−5.71	0	1.80	1.09	−1.08	1.86	0.71	0.27	1.25

---

For DCDTBT-based derivatives (P2, P2a–P2c, P2a′–P2c′ and P3), introducing different substituents (R = H, CH₃, OCH₃ and CN) to bridge-carbon only leads a slight geometrical parameter change. For example, compared with P2, the bond lengths (C2–C3/C16–C17/C19–C20) and the dihedral angles (C1–C2–C3–S1/S2–C16–C17–C18/S3–C19–C20–C21) of those copolymers (P2a–P2c, P2a′–P2c′ and P3) have a little variation. It indicates that the interaction between donor units (D) and acceptor units (A) is weakly influenced no matter what or how many R parts are introduced at bridging carbons of the DCDTBT electron-deficient unit. Specifically, for the all oligomers (except P1), the dihedral angles of S1–C4–C5–C6/C7–C8–C9–S2/C22–C23–C24–C25/C26–C27–C28–C29 are close to 0.0° due to the forced planarization by covalently fastening adjacent aromatic units by a carbon bridge. Therefore, the introducing of the different substituent groups into the DCDTBT unit has a little effect on the molecular conjugation effect and planarity.

3.2. Frontier molecular orbitals

We calculated the HOMO/LUMO energy levels of all the copolymers on a dimer model by DFT at the PBE0/6-311G** level. The orbital diagrams of HOMO and LUMO of all dimers are plotted in Fig. 2.

Fig. 2 HOMO and LUMO orbital diagrams of all dimers.

For all of the copolymers, the HOMOs are π-type orbitals which are delocalized over the entire C=C backbone (with a little contribution of the C=N and N–S bonds of the BT unit). But the LUMOs are almost completely focused on the electron-deficient moiety with π* character, and the contribution of thiazole ring (C=N and N–S bonds) is markedly increased in LUMOs. The HOMO → LUMO electron transitions (see Fig. 2 and Table 4) in these copolymers imply the electron transfer from the electron-rich segment to electron-deficient segment. Furthermore, the prerequisite of an effective intramolecular charge transfer is that the HOMO and LUMO plots exhibit certain overlap.

In the Table 3, the values of molecular orbital energies (HOMO and LUMO, E_LUMO = E_HOMO + E_g,TD) and compositions were calculated by DFT for all the copolymers. As shown in Table 3, compared with P1, the HOMO and LUMO energies of P2 are increased. Accordingly, the compositions of the donor fragments in HOMOs and the acceptor fragments in LUMOs decrease from P1 to P2. For instance, in HOMOs, the electron-rich fragments account for 46.7% and 39.2% in P1 and P2, respectively. In LUMOs, the electron-deficient fragments take up 90.4% and 86.8% in P1 and P2, respectively. These orders imply that the energies of HOMO (LUMO) may have a negative correlation with the compositions of the electron-rich fragments (the electron-deficient fragments) in HOMOs (LUMOs). This may be helpful to understand that P2 possesses high-lying HOMO and LUMO energy levels in comparison with P1.

Table 3 Molecular orbital energies (eV) and compositions (%) of all molecules

Oligomers	Orbital	Energy	Donor	Acceptor
P1	HOMO	−5.24	46.7	53.3
	LUMO	−3.29	9.6	90.4
P2	HOMO	−5.08	39.2	60.8
	LUMO	−3.15	13.2	86.8
P2a	HOMO	−5.02	37.4	62.6
	LUMO	−3.18	13.1	86.9
P2b	HOMO	−5.24	41.4	58.6
	LUMO	−3.42	11.8	88.2
P2c	HOMO	−5.46	47.2	52.8
	LUMO	−3.66	10.3	89.7
P2a′	HOMO	−5.23	41.9	58.1
	LUMO	−3.52	9.8	90.2
P2b′	HOMO	−5.39	45.4	54.6
	LUMO	−3.68	9.2	90.8
P2c′	HOMO	−5.54	50.3	49.7
	LUMO	−3.84	8.5	91.5
P3	HOMO	−5.80	62.4	37.6
	LUMO	−4.10	7.9	92.1

---

Based on the above discussion, we come to analyze those copolymers (P2, P2a, P2a′ and P3) which introduce two same substituent groups in the bridging carbons of DCDTBT unit. As shown in Table 3, for P2, P2a, P2a′ and P3, which the substituent groups are H, methyl, methoxyl and cyano-group, the HOMO energies are −5.08, −5.02, −5.23 and −5.80 eV, with the order of P2a > P2 > P2a′ > P3. The compositions of donor fragments in HOMOs are in the order P2a < P2 < P2a′ < P3. It implies that the energies of HOMO have a negative correlation with the compositions of the donor fragments in HOMOs. The sequence of LUMO energies for P2, P2a, P2a′ and P3 is P2 ≈ P2a > P2a′ > P3, the order of their compositions of the electron-deficient fragments in LUMOs is P2 ≈ P2a < P2a′ < P3. Likewise, the orders imply that there is a negative correlation between LUMO energies and the compositions of the electron-deficient fragments in LUMOs. These results manifest that the variations of the molecular orbital energies and compositions for P2, P2a, P2a′ and P3 are primarily influenced by electron-withdrawing strength of the substituent groups. In this paper, the comparison of the electron-withdrawing strength of the substituent groups is via the calculated NBO charge analysis of the corresponding electron-deficient units in Table S2.†

Furthermore, the study for the number of cyano-groups can also certify the above result. As shown in Table 3, from P2a to P2c, as the number of cyano-groups at the bridging carbon increases, the energies of HOMO and LUMO are gradually decreased. There is an increased trend for the compositions of the donor fragments in HOMOs and the acceptor fragments in LUMOs. Similarly, it implies that the energies of HOMO and LUMO have a negative correlation with the compositions of the donor fragments in HOMOs and the acceptor fragments in LUMOs. The results demonstrate again that the variations of molecular orbital energies and compositions for the copolymers (P2a–P2c and P2a′–P2c′) are mainly influenced by electron-withdrawing strength of the substituent groups.

3.3. Absorption spectra

The simulated optical adsorption spectra and vertical singlet–singlet electronic transition energies of all the copolymers were computed with TD-PBE0/6-311/G**//PBE0/6-311G** level on a dimer model. The calculated dipole-allowed absorptions associated with electronic transitions, oscillator strength (f), and dominating configurations are summarized in Table 4 (considering the first 20 excited states). The simulated absorption spectra of the nine copolymers are presented in Fig. 3. In Fig. 3, there are two obvious absorption peaks of these copolymers in the visible and near-infrared regions. The strong transitions (f > 0.8) of all copolymers in the visible range correspond to the transitions from HOMO to LUMO, HOMO to LUMO+2 and HOMO−4 to LUMO. Fig. 2 and S2† show that the electronic transitions in these copolymers are assigned to π–π* type transition.

Table 4 Calculated electronic transitions, oscillator strength (ƒ > 0.8), and main configurations of all these dimers by TD-PBE0/6-311G**//PBE0/6-311G** approach

	Excitation energy (eV and nm)		Transition	Oscillator	Main configuration	λmax,exp (nm)
a From ref. 15.
P1	1.95	636	S0 → S1	1.6978	H → L (92%)	625^a
	2.95	420	S0 → S9	1.0376	H → L+2 (85%)	425^a
P2	1.92	644	S0 → S1	2.0861	H → L (92%)
	2.76	450	S0 → S6	1.7026	H → L+2 (80%)
P2a	1.84	673	S0 → S1	2.0183	H → L (91%)
	2.71	458	S0 → S6	1.6069	H → L+2 (78%)
P2b	1.82	682	S0 → S1	1.9161	H → L (93%)
	2.74	452	S0 → S8	1.6552	H → L+2 (86%)
P2c	1.80	690	S0 → S1	1.8796	H → L (92%)
	2.77	448	S0 → S9	1.5821	H → L+2 (84%)
P2a′	1.71	726	S0 → S1	1.6889	H → L (92%)
	2.72	456	S0 → S8	1.7431	H → L+2 (88%)
P2b′	1.71	726	S0 → S1	1.6796	H → L (92%)
	2.74	452	S0 → S9	1.6330	H → L+2 (85%)
P2c′	1.70	728	S0 → S1	1.6623	H → L (91%)
	2.76	449	S0 → S9	0.8322	H → L+2 (48%) H−4 →L (39%)
	2.78	446	S0 → S10	0.8985	H → L+2 (39%) H−4 →L (42%)
P3	1.70	729	S0 → S1	1.6557	H → L (82%)
	2.79	445	S0 → S10	1.5089	H → L+2 (73%)

---

Fig. 3 Absorption spectra of all the copolymers.

As shown in Table 1, the calculated absorption peaks (P1: 636, 420 nm) reproduce well (within 11 nm of the error in the absorption peak position) the experiment absorption peaks¹⁵ (P1: 625, 425 nm). In Fig. 3a, compared with that of P1, P2 which is introduced ladder-type DCDTBT unit in the polymer backbone possesses stronger and wider light absorption. The lowest transition absorption peak of P2 only shows red-shifted of 8 nm in comparison with P1. However, the lowest transition absorption peaks of P2a–P2c, P2a′–P2c′ and P3 show red-shifted of 29, 38, 46, 82, 82, 84 and 85 nm in comparison with P2 (see Table 4), respectively. Obviously, introducing the substituent groups (CH₃, OCH₃ and CN) at the bridging carbons of the DCDTBT unit can exhibit significantly red-shifted absorptions. In particular, compared to P1 and P2, the copolymers of P2a–P2c, P2a′–P2c′ and P3 have much broader absorption in the visible and infrared region, and their maximum absorption peaks are close to the wavelength of the maximum photon flux density of the solar spectrum (∼700 nm, ∼1.77 eV).¹⁸

Interestingly, for P2a–P2c and P2a′–P2c′, the lowest absorption transition energies are almost no change while raising the number of cyano-groups (n = 0, 1, 2 for P2a–P2c and P2a′–P2c′, respectively.). From Fig. 3 and Table 4, it can be observed that the energy gaps don't change no matter how many cyano-groups are introduced on the ladder-type structure. This may result from the fact that the HOMO and LUMO levels are reduced at the same extent for P2a–P2c and P2a′–P2c′. In addition, the electron density distributions of HOMO and LUMO for P2a–P2c and P2a′–P2c′ have similar character. This may be helpful for us to understand that they have the similar absorption transition energies and the shape of absorption peaks. Likewise, for P2, P2a–P2c, P2a′–P2c′ and P3, the second absorption peaks are also almost invariable, which are mainly caused by the electron excitation from HOMO to LUMO+2. As expected, the electron density distribution plots of HOMO and LUMO+2 also have similar character for the copolymers (P2, P2a–P2c, P2a′–P2c′ and P3) in Fig. 2 and S2.†

3.4. How do the designed copolymers possess both low-lying HOMO energy levels and narrow band gaps?

It is well known that, the HOMO/LUMO energy levels and the band gap of a donor material should be optimized to enhance the PCE of an organic solar cell. An “ideal” conjugated donor polymer should have an appropriate HOMO energy level (−5.4 eV) and a narrow band gap (1.5 eV).¹¹ In fact, introducing the substituents into polymer backbone is often an effective way to adjust electronic and optical properties as well as improve the photovoltaic performance. In the present work, the introduction of methyl or methoxyl into the bridging carbons of DCDTBT-based copolymers (P2a and P2a′) display small band gaps and high-lying HOMO/LUMO levels while P3 possesses deep-lying HOMO/LUMO levels with strong electron-withdrawing group (CN) being introduced at the bridging carbon. In order to get a donor polymer with suitable HOMO/LUMO levels and narrow band gap, we tried to combine the cyano-group and methyl or methoxyl into the bridging carbons of the DCDTBT unit. It is interesting to note that the copolymers (P2c, P2b′ and P2c′) possess low band gaps and appropriate HOMO energy levels while the methyl or methoxyl and cyano-group both are introduced at the DCDTBT unit.

3.5. Charge transfer properties

In order to design a good candidate for the solar cell application, it is significantly important to comprehend the relationship between the charge transport property and the molecular structure. We investigated the charge transport property through the reorganization energy. The inner reorganization energy (λ_int) results from the fast change of the molecular geometry (such as a charge is removed or added from a molecule), and the outer reorganization energy (λ_ext) denotes variations in the surrounding medium owing to the polarization effects.³⁵ When the medium contribution to the relaxation energy is neglected (such as in a thin film), the inner reorganization energies are much larger than their external counterparts (λ_ext).^36,37 Under this circumstance, the external reorganization energy could be ignored. Thus, we would mainly discuss about the λ_int in this paper. In this case, the hole reorganization energy (λ_h) and electron reorganization energy (λ_e) values can be calculated by eqn (1) and (2):^36,38

λ_h = [E⁺₀ − E₊] + [E⁰₊ − E₀] (1)

λ_e = [E⁻₀ − E₋] + [E⁰₋ − E₀] (2)

In the two equations, E₀ represents the energy of neutral segment in neutral geometry. E₊(E₋) is the energy of cation (anion) in cationic (anionic) geometry. E⁰₊(E⁰₋) denotes the energy of neutral segment in cationic (anionic) geometry, while E⁺₀(E⁻₀) represents the energy of cation (anion) in neutral geometry. The calculated λ_h and λ_e are shown in Table 5. Compared with the representative hole transport material N,N′-diphenyl-N,N′-bis(3-methlphenyl)-(1,10-biphenyl)-4,4′-diamine (TPD) (λ_h = 0.290 eV), the λ_h values of the investigated polymers on a dimer model (0.200–0.279 eV) are smaller, which implies that the investigated polymers may have higher hole transfer rates.³⁹ Similarly, the λ_e values (0.119–0.180 eV) are smaller than that of the typical electron transport material tris(8-hydroxyquinolinato)aluminum(III) (Alq3) (λ_e = 0.276 eV), which indicates that the investigated polymers may have higher electron transfer rates.⁴⁰

Table 5 Hole reorganization energy (λ_h) and electron reorganization energy (λ_e) of investigated molecules. All energies are in eV

	P1	P2	P2a	P2b	P2c	P2a′	P2b′	P2c′	P3
λh	0.279	0.208	0.201	0.205	0.205	0.206	0.209	0.206	0.198
λe	0.180	0.141	0.138	0.131	0.126	0.148	0.142	0.135	0.119

---

For P2, the values of λ_h and λ_e both are smaller than that of P1. This result demonstrates that the ladder-type multifused acceptor unit (DCDTBT) can suppress the rotational disorder around interannular single bonds to lower the reorganization energy in comparison with the 4DTBT acceptor unit. Moreover, the difference between λ_h and λ_e values for DCDTBT-based derivative (P2) is smaller than that of 4DTBT-based derivative (P1). It indicates that P2 has better equilibrium property for hole and electron transport than P1.

For DCDTBT-based derivatives, their λ_h values are 0.208, 0.201, 0.205, 0.205, 0.206, 0.209, 0.206 and 0.198 eV for P2, P2a–P2c, P2a′–P2c′ and P3, respectively, and their λ_e values are 0.141, 0.138, 0.131, 0.126, 0.148, 0.142, 0.135 and 0.119 eV, respectively. Surprisingly, the λ_h values of those copolymers are very nearly close. These results suggest that the introduction of the different substituent groups (H, CH₃, OCH₃ and CN) at the bridging carbons of the ladder-type multifused DCDTBT unit has a large effect on λ_e but hardly influence λ_h. This may be due to the fact that these copolymers possess very similar ground state geometric structures. For the copolymers of P2a–P2c, their λ_h values are almost the same, and their λ_e values decrease in the following order: P2a > P2b > P2c. Likewise, the copolymers of P2a′–P2c′ also have the same tendency with P2a–P2c. The results reveal that the raising number (such as n = 0, 1, 2 for P2a–P2c, respectively.) of cyano-groups can decrease the λ_e values gradually but make little effect on λ_h.

3.6. Solar cell performances

In the polymer BHJ solar cells, two equally important parameters in determining the power conversion efficiency (PCE) of a given solar cell are short circuit current density (J_sc) and open circuit voltage (V_oc). Moreover, a desirable polymer donor should exhibit not only a lowest transition energy between 1.2 and 1.9 eV with broad absorption to maximize sunlight absorption but also a highest occupied molecular orbital energy level between −5.2 and −5.8 eV.⁴¹ The V_oc and J_sc are largely influenced by the HOMO energy levels and the band gaps of the conjugated polymers, respectively. As shown in Table 4, the band gaps of P2, P2a–P2c, P2a′–P2c′ and P3 all are lower than that of P1. It may suggest that these newly designed copolymers (P2, P2a–P2c, P2a′–P2c′ and P3) may have larger J_sc than P1. In general, the V_oc is proportion to the built-in potential which is defined as the difference between the HOMO level of a donor polymer and the LUMO level of an acceptor ([6,6]-phenyl-C₆₁-butyric acid methyl ester (PCBM)). Since 1995, PC₆₁BM/PC₇₁BM (PC₇₁BM, [6,6]-phenyl-C₇₁-butyric acid methyl ester) are widely used as the standard acceptor because of good solubility, high electron mobility and commercial availability in organic solar cells.^42–45 In this study,¹⁵ PC₆₁BM is selected as the electron acceptor with the HOMO and LUMO energy levels of −6.1 eV and −4.2 eV, respectively. We can estimate the open circuit voltage (V_oc) value of a conjugated polymer–PCBM solar cell as eqn (1)⁴⁶

V_oc = 1/e(|E^donorHOMO| − |E^PCBMLUMO|) − 0.3 V(3)

where e is the elementary charge, the value of 0.3 V is an empirical factor, E^PCBMLUMO is the lowest occupied molecular orbital (LUMO) energy level (−4.2 eV) of the PC₆₁BM. In this work, the V_oc values of P1–P2, P2a–P2c, P2a′–P2c′ and P3 are 0.74, 0.58, 0.52, 0.74, 0.96, 0.73, 0.89, 1.04 and 1.30 V, respectively. Compared with the V_oc values of P2a–P2c and P2a′–P2c′, the introduction of cyano-group at the ladder-type structure acceptor unit can obviously enhance the open circuit voltage (V_oc). By the qualitative comparison, the copolymers of P2c, P2c′ and P3 may possess larger J_sc and higher V_oc when they are applied to PSCs. As shown in Fig. 4, the differences of LUMO energy levels between those new designed donors (P2, P2a–P2c, P2a′–P2c′ and P3) and the acceptor of PC₆₁BM are corresponding to 1.05, 1.02, 0.78, 0.54, 0.68, 0.52, 0.36 and 0.1 eV, respectively. All of them are properly located above 0.3 eV except P3, which can warrant the formation of a downhill driving force for efficient electron transfer from the donor to the acceptor.^18,46 For P3, the introduction of four cyano-groups into the DCDTBT unit can significantly reduce the HOMO/LUMO levels, but it is not conducive to the electron transfer from the donor to the acceptor. Therefore, when the number of cyano-groups at the bridging carbon increases to a certain extent, it is not beneficial to improve the performance of polymers.

Fig. 4 Frontier molecular orbital energies of P1–P2, P2a–P2c, P2a′–P2c′ and P3. (E_LUMO = E_HOMO + E_g,TD).

In order to estimate the performance of the designed molecules from the qualitative perspective, we used the Scharber diagram⁴⁶ to predict PCEs (%) of the solar cells of those eight donors. From Scharber diagram, the PCE of PSC can be predicted by the band gap and the LUMO level of the constituent donor polymer. Scharber et al. proposed the design rule, which suppose a fill factor (FF) of 0.65 and a carrier mobility of ∼10⁻³ cm² V⁻¹ S⁻¹. For the sake of power conversion efficiencies exceeding 10%, a donor polymer should have a LUMO energy level < −3.92 eV and a band gap < 1.74 eV. Fig. 5 shows that the PCE is more sensitive to the LUMO level of donor polymer than the band gap. Now, many researches have revealed that the LUMO energy levels of D–A donor copolymers mainly rely on the electron-accepting moieties.⁴⁷ We estimate the PCEs of P1 (using the calculated results of E_g,_TD and E_LUMO = E_HOMO + E_g,TD) is ∼4.4% by the Scharber diagram, and it agrees well with the experimental data (5.0% ref. 15).

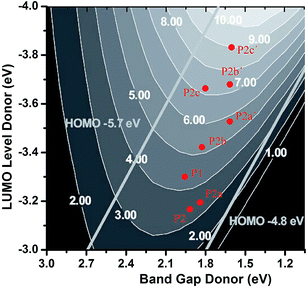Fig. 5 Scharber diagrams to estimate PCEs (%) of the bulk heterojunction solar cells of the copolymers (P1, P2, P2a–P2c and P2a′–P2c′). Adapted with permission from the work of Scharber and coworkers (in ref. 46). Copyright 2006 Wiley-VCH.

According to the Scharber diagram, the corresponding PCEs of these copolymers are ∼3.5% (P2), ∼3.6% (P2a), ∼5% (P2b), ∼7% (P2c), ∼6% (P2a′), ∼7.5% (P2b′), and ∼9% (P2c′), respectively. Compared with that of P1, the results show that P2c, P2b′ and P2c′ have smaller band gaps and deeper LUMO energy levels, and exhibit the higher predicted PCEs (∼7%, ∼7.5% and ∼9% for P2c, P2b′ and P2c, respectively) when combined with PC₆₁BM acceptor in organic solar cells. The results demonstrate that our idea is an efficient way to improve the performance of the D–A conjugated polymers.

4. Conclusion

We presented several polymer donors for elaborating how a ladder-type multifused acceptor unit with different substituent groups (R = H, CH₃, OCH₃ and CN) that are introduced in polymer backbone, affect the ground state structure, electronic, optical and charge transfer properties. First, the introduction of the ladder-type DCDTBT unit to replace 4DTBT unit in the donor not only enhances the π conjugation and the intrachain coplanarity in molecular backbone, but also decreases the band gap and reorganization energy. In addition, compared with the calculated results of P2, the introducing of the substituent groups into DCDTBT unit can further adjust electronic, optical and charge transport properties of the copolymers but with a little effect on molecular backbone planarity. In particular, the introduction of the strong electron-withdrawing cyano-group onto the bridging carbon of DCDTBT unit can evidently reduce HOMO and LUMO levels. Moreover, the calculation shows that P2c and P2c′ have not only a favorable electronic structure (deeper HOMO and LUMO levels) but also lower band gaps and reorganization energies in comparison with P1. Especially the predicted PCEs of these newly designed copolymers (P2c and P2c′) are ∼7% and ∼9%, respectively. Therefore, P2c and P2c′ may be promising donors for organic bulk heterojunction solar cells in the future. These results may provide a design idea for selecting a suitable ladder-type electron-deficient unit for further improving the performance of donors in the PSCs.

Acknowledgements

This work was supported by National Natural Science Foundation of China (Grant no. 21073144), and by Fundamental Research Funds for the Central Universities (grant no. XDJK2010B009).

References

1. G. Yu, J. Gao, J. Hummelen, F. Wudl and A. Heeger, Science, 1995, 270, 1789–1790.
2. R. Friend, R. Gymer, A. Holmes, J. Burroughes, R. Marks, C. Taliani, D. Bradley, D. Dos Santos, J. Bredas and M. Lögdlund, Nature, 1999, 397, 121–128.
3. H.-Y. Chen, J. Hou, S. Zhang, Y. Liang, G. Yang, Y. Yang, L. Yu, Y. Wu and G. Li, Nat. Photonics, 2009, 3, 649–653.
4. Y. Yi, V. Coropceanu and J.-L. Brédas, J. Am. Chem. Soc., 2009, 131, 15777–15783.
5. N. Sariciftci, L. Smilowitz, A. Heeger and F. Wudl, Science, 1992, 258, 1474–1476.
6. H. Imahori, H. Yamada, D. M. Guldi, Y. Endo, A. Shimomura, S. Kundu, K. Yamada, T. Okada, Y. Sakata and S. Fukuzumi, Angew. Chem., 2002, 114, 2450–2453.
7. J. Peet, J. Kim, N. E. Coates, W. L. Ma, D. Moses, A. J. Heeger and G. C. Bazan, Nat. Mater., 2007, 6, 497–500.
8. J. Hou, H.-Y. Chen, S. Zhang, G. Li and Y. Yang, J. Am. Chem. Soc., 2008, 130, 16144–16145.
9. Y. Chen, R. N. Gunasinghe, X.-Q. Wang and Y. Pang, RSC Adv., 2013, 3, 25097–25102.
10. Y. Chen, Y. Xu, Q. Wang, R. N. Gunasinghe, X. Q. Wang and Y. Pang, Small, 2013, 9, 870–875.
11. B. C. Thompson and J. M. Fréchet, Angew. Chem., Int. Ed., 2008, 47, 58–77.
12. Z. He, C. Zhong, X. Huang, W. Y. Wong, H. Wu, L. Chen, S. Su and Y. Cao, Adv. Mater., 2011, 23, 4636–4643.
13. N. Blouin, A. Michaud, D. Gendron, S. Wakim, E. Blair, R. Neagu-Plesu, M. Belletête, G. Durocher, Y. Tao and M. Leclerc, J. Am. Chem. Soc., 2008, 130, 732–742.
14. G. Dennler, M. C. Scharber and C. J. Brabec, Adv. Mater., 2009, 21, 1323–1338.
15. H. Zhou, L. Yang, A. C. Stuart, S. C. Price, S. Liu and W. You, Angew. Chem., 2011, 123, 3051–3054.
16. H. Zhou, L. Yang, S. Liu and W. You, Macromolecules, 2010, 43, 10390–10396.
17. L. Koster, V. Mihailetchi and P. Blom, Appl. Phys. Lett., 2006, 88, 093511–093513.
18. Y.-J. Cheng, S.-H. Yang and C.-S. Hsu, Chem. Rev., 2009, 109, 5868–5923.
19. P. Coppo and M. L. Turner, J. Mater. Chem., 2005, 15, 1123–1133.
20. J.-S. Wu, Y.-J. Cheng, M. Dubosc, C.-H. Hsieh, C.-Y. Chang and C.-S. Hsu, Chem. Commun., 2010, 46, 3259–3261.
21. C.-H. Chen, Y.-J. Cheng, C.-Y. Chang and C.-S. Hsu, Macromolecules, 2011, 44, 8415–8424.
22. R. N. Gunasinghe, D. G. Reuven, K. Suggs and X.-Q. Wang, J. Phys. Chem. Lett., 2012, 3, 3048–3052.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, et al., Gaussian 09, Revision A.01, Gaussian, Inc., Wallingford, CT, 2009.
24. J. Ku, Y. Lansac and Y. H. Jang, J. Phys. Chem. C, 2011, 115, 21508–21516.
25. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
26. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
27. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
28. D. Jacquemin and E. A. Perpète, Chem. Phys. Lett., 2006, 429, 147–152.
29. D. Jacquemin, J. Preat, V. Wathelet, M. Fontaine and E. A. Perpète, J. Am. Chem. Soc., 2006, 128, 2072–2083.
30. L. Zhang, K. Pei, M. Yu, Y. Huang, H. Zhao, M. Zeng, Y. Wang and J. Gao, J. Phys. Chem. C, 2012, 116, 26154–26161.
31. J. P. Perdew and M. Levy, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 16021.
32. D. Chong, O. Gritsenko and E. Baerends, J. Chem. Phys., 2002, 116, 1760.
33. L. Yang, J.-K. Feng and A.-M. Ren, J. Mol. Struct.: THEOCHEM, 2007, 816, 161–170.
34. G. Zhang and C. B. Musgrave, J. Phys. Chem. A, 2007, 111, 1554–1561.
35. V. Lemaur, M. Steel, D. Beljonne, J.-L. Brédas and J. Cornil, J. Am. Chem. Soc., 2005, 127, 6077–6086.
36. S. Tang and J. Zhang, J. Phys. Chem. A, 2011, 115, 5184–5191.
37. N. G. Martinelli, J. Idé, R. S. Sánchez-Carrera, V. Coropceanu, J.-L. Brédas, L. Ducasse, F. Castet, J. Cornil and D. Beljonne, J. Phys. Chem. C, 2010, 114, 20678–20685.
38. W.-Q. Deng and W. A. Goddard, J. Phys. Chem. B, 2004, 108, 8614–8621.
39. N. E. Gruhn, D. A. da Silva Filho, T. G. Bill, M. Malagoli, V. Coropceanu, A. Kahn and J.-L. Brédas, J. Am. Chem. Soc., 2002, 124, 7918–7919.
40. B. C. Lin, C. P. Cheng, Z.-Q. You and C.-P. Hsu, J. Am. Chem. Soc., 2005, 127, 66–67.
41. Y. Zou, A. Najari, P. Berrouard, S. Beaupré, B. Réda Aïch, Y. Tao and M. Leclerc, J. Am. Chem. Soc., 2010, 132, 5330–5331.
42. K.-H. Kim, H. Kang, S. Y. Nam, J. Jung, P. S. Kim, C.-H. Cho, C. Lee, S. C. Yoon and B. J. Kim, Chem. Mater., 2011, 23, 5090–5095.
43. C. Zhang, S. Chen, Z. Xiao, Q. Zuo and L. Ding, Org. Lett., 2012, 14, 1508–1511.
44. Y. Sun, G. C. Welch, W. L. Leong, C. J. Takacs, G. C. Bazan and A. J. Heeger, Nat. Mater., 2011, 11, 44–48.
45. C. J. Brabec, C. Winder, N. S. Sariciftci, J. C. Hummelen, A. Dhanabalan, P. A. van Hal and R. A. Janssen, Adv. Funct. Mater., 2002, 12, 709–712.
46. M. C. Scharber, D. Mühlbacher, M. Koppe, P. Denk, C. Waldauf, A. J. Heeger and C. J. Brabec, Adv. Mater., 2006, 18, 789–794.
47. H. Zhou, L. Yang, S. Stoneking and W. You, ACS Appl. Mater. Interfaces, 2010, 2, 1377–1383.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra05954a

---