Gel, glass and nematic states of plate-like particle suspensions: charge anisotropy and size effects

Abstract

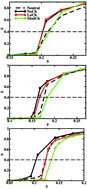
The influence of the charge anisotropy and platelet size on the formation of gel and glass states and nematic phases in suspensions of plate-like particles is investigated using Monte Carlo simulations in the canonical ensemble. The platelets are modeled as discs with charged sites distributed on a hexagonal lattice. The edge sites can carry a positive charge, while the remaining sites are negatively charged giving rise to a charge anisotropy. A screened Coulomb potential plus a short range repulsive potential are used to describe the interactions between the sites of the platelets. The liquid–gel transition is found to be favored by a high charge anisotropy and by large particles. Oppositely, the liquid–glass transition is favored for small particles without charge anisotropy, i.e., fully negatively charged. Finally, we find that the isotropic/nematic transition is disfavored by the charge anisotropy. For a strong charge anisotropy, the nematic phase does not form and, instead, a gel/columnar transition is found.

---

1 Introduction

Minerals often consist of charged disc-shaped particles (clays, gibbsite, …) with a net charge dependent on their surrounding environment (solvent, pH, salt concentration, …).^1–4 Due to their peculiar shape and charge distribution, mineral particles dispersed in an aqueous solution present many interesting properties. The first of them is their ability to undergo a transition from a liquid state to an arrested state (gel, glass, …).^5–11 This has been widely studied in the past due to the important number of industrial applications it is involved in: cosmetics, paint products, drilling fluids, … The comprehension of arrested states is made difficult by the lack of proper definitions of these states. Tanaka et al.¹² give a good description of all the nonergodic states of charged colloidal suspensions. In brief, a disordered state which is percolated and whose characteristic length of the network between two adjacent junctions is much larger than the particle size is defined as a gel. Therefore, gel phases can only be formed when attractive interactions are at play in a system. Similarly, a disordered state whose elasticity originates from caging effect and whose characteristic length scale between two adjacent junctions is about the distance between two particles is defined as a glassy state. One part of the confusion between gel and glassy states arises from the fact that glass can either be attractive or repulsive while gels are only attractive. Then depending on the charge carried by the edges of the platelet, two different transitions are considered, that is, a transition to a gel phase in presence of charge anisotropy and a transition to a glassy state without charge anisotropy. Unfortunately, the experimental characterization of the charge distribution of minerals is not trivial, and to the best of our knowledge no experimental studies of mineral platelets as a function of their charge anisotropy has been reported. In a recent work on a model clay system¹³ we reported three different transitions according to the charge anisotropy of the platelets: a liquid–gel transition is found for high charge anisotropy, a sol–gel transition for a moderate charge anisotropy and a liquid–glass one without charge anisotropy in agreement with experimental observations on laponite.¹³ Studying homogeneously charged platelet by kinetic Monte-Carlo Jabbari-Farouji et al.¹⁴ has recently found the existence a solid-like state at low ionic strengths, in agreement with the observation of a Wigner glass on laponite. Similarly, studies of the influence of particle size on the transition to an arrested state are scarce. In general, when the sol–glass transition involve perfectly exfoliated platelets, the transition is shifted to lower volume fractions for smaller platelets, as observed on montmorillonite,⁹ nontronite^15,16 and beidellite¹⁷ clays.

Another remarkable property of anisotropic plate-like particles, is their ability to form liquid crystalline phases. Langmuir first reported the self assembly of colloidal particles in suspensions of California hectorites.^18,19 The transition from an isotropic to a nematic phase was rationalized by Onsager as a competition between orientational and translational entropy.^20,21 This explanation, first developed for hard rods and then extended to the disc-like particles, has been confirmed by Monte Carlo simulations.²² Since then, efforts have been put into experimental studies in order to understand the isotropic/nematic (I/N) transition of mineral platelets. Gibbsite,^23–25 layered double hydroxides like Ni/Al,²⁶ Mg/Al,²⁷ hydrotalcite,²⁸ copper sulfide²⁹ and many different clays^15,17,30,31 were found to display a transition to a liquid crystalline phase. However, few of these studies present results about the size dependence of the I/N transition. Michot et al.¹⁵ reported an increased formation of a nematic phase when the nontronite particle size was increased, but the opposite trend was found for beidellite clays.¹⁷ According to the authors, this difference in behavior is the result of an incomplete exfoliation of particles in the suspension. Computer simulations of infinitely thin platelets^32,33 and for different aspect ratio³⁴ are in fairly good agreement with experimental results showing that polydispersity disfavors the formation of the nematic phase, while decreasing the aspect ratio (thickness to diameter ratio) enhances its formation. However, more informations about the influence of the charge anisotropy on the I/N transition is needed. Recently, Martínez-Haya et al.³⁵ presented a new potential where the directionality of the interactions between the platelets could be tuned. They show that the nematic stability is favored for homogeneous or weakly directional interactions, i.e. with a low charge anisotropy. Meneses-Juarez et al.³⁶ studied with Monte Carlo simulations the phase behaviour of hard oblate ellipsoids with short ranged oblate-shaped square-well attractions. They found that increasing the shape anisotropy does not shift the I/N transition to low densities. Jabbari-Farouji et al.¹⁴ found that the nematic order is suppressed at low ionic strength for homogeneously charged platelet interacting with a generalized Yukawa potential. Within Onsager–van der Waals density functional theory, Wensink et al.³⁷ further shown that this effect is less noticeable when the platelet is not homogeneously charged but decorated with a few charged patches distributed on a hexagonal lattice. Finally Delhorme et al.³⁸ found that the I/N transition is replaced by a gel/columnar transition when increasing the charge anisotropy.

The aim of this paper is to investigate the influence of both particle size and charge anisotropy on the I/N transition and the transition from an isotropic to a kinetically arrested state. For this purpose, Monte Carlo simulations with a screened Coulomb potential combined with a soft repulsion are used to simulate dispersions of mineral platelets.

2 Model and simulations

2.1 Model

In this study we use the same model and simulation techniques as employed in a previous paper¹³ and they are only briefly described below. A dispersion of N platelets in a 1–1 salt solution is considered. In the model dispersions, the platelets have the same diameter D and are decorated with a collection of n^T sites of diameter L = 1 nm spread on an compact hexagonal lattice with a density of 0.87 site per nm². Beside n^T and D the platelets are characterized by n_e edge sites and n_b basal sites. The edge sites can be positive, neutral or negative and is the total charge of the edges. The n_b basal sites located in the center of the disc are always negatively charged, e. The net charge of a platelet is thus given by Z^net = Z^e − n_be. The platelets are dispersed in a cubic box of volume V_box, where periodic boundary conditions are applied in all directions using the minimum image convention.

The solvent, which is water, is treated as a structure less dielectric continuum and is implicitly represented by its relative permittivity, ε_r, which is assumed to be constant throughout space. Salt and counterion are also implicitly represented through the Debye screening length κ⁻¹, defined as:

where k is the Boltzmann's constant, T the absolute temperature, ε₀ is the permittivity of vacuum, and c_s and c_c the salt and counterion concentration, respectively.

2.2 Interaction potentials

A shifted and truncated Lennard-Jones (LJ) potential is used to account for the finite size of particles. In addition to the shifted LJ potential a screened Coulomb potential is employed to describe the electrostatic contribution. The total interaction between two sites, u^tot(r_ij) = u^el(r_ij) + u^LJ(r_ij), of charge z separated a distance r_ij then reads,where ε_LJ and σ_LJ are the Lennard-Jones parameters, which were set to 0.5k_BT and 10 Å, respectively. The full configurational energy of the N platelets system them becomeswhere indices i, j refer to platelets and indices α, β to sites on these platelets, respectively. It is important to mention that the screened Coulomb potential should be used with care,^39,40 specially for large and highly charged particles. A detailed discussion on the model limitations is given in ref. 13.

2.3 Systems

Three different platelet sizes are considered with n^T = 61, 91 and 199 and n_e = 24, 30 and 48 which correspond to D = 90, 110 and 150 Å, respectively. In addition, four different charge anisotropies are considered:

• high charge anisotropy (HiCh) where all edge sites are positively charged;

• moderate charge anisotropy (ModCh) where half of the edge sites are positive and the other neutral (organized as an alternation of charged and neutral sites);

• low charge anisotropy (LoCh), where only neutral sites on the edges are present;

• without charge anisotropy (NoCh), where all sites on the platelet are negatively charged.

The net charge of the platelets for each charge anisotropy is summed up in Table 1.

Table 1 Net charges for the different platelet sizes and charge anisotropies

D	NoCh	LoCh	ModCh	HiCh
90 Å	−61	−37	−25	−13
110 Å	−91	−61	−46	−31
150 Å	−199	−151	−127	−103

---

Neutral systems, i.e. without electrostatic interactions, for the three sizes of platelets are also considered for comparison. In all calculations, the salt concentration is kept constant at c_s = 10 mM. The particle volume fraction, defined as,

is varied from 0.0007 to 0.3, where V_part = n^Tπσ_LJ³/6 is the volume of a single platelet.

2.4 Simulations

The calculations are carried out using the same procedure as in a previous paper.¹³ In brief, the model is solved using Monte Carlo simulations in the canonical ensemble (N,V,T) and the standard Metropolis algorithm. Collective platelets displacement and multi-level coarse graining are employed. The simulations are performed with 1000/500/200 platelets for the small, medium and big platelets, respectively. An equilibrium run is done with 2 × 10⁶ cycles (in one cycle all platelets have been moved once), and a typical production run involves 4 × 10⁶ cycles.

2.5 Measured quantities

The nematic order parameter, S, is used to characterize the nematic phase. It is evaluated from the tensor:³⁴where N is the number of platelets, u_i is the normal vector to the i^th platelet and I the identity matrix. The highest eigenvalue, λ⁺, is used to evaluate S, S = λ⁺. S is calculated over an average of 2 × 10⁴ cycles for the isotropic and 4 × 10⁶ cycles in the nematic phase. ϕ value at which S = 0.4 is taken as the position of the I/N transition.⁴¹

The percolation of the system and the elasticity of the suspension are evaluated using the same procedure as in the previous study.¹³ In brief, two clay platelets are considered to be “connected” neighbors if the separation between one site of a platelet is located at less than 15 Å from a site of another platelet. A cluster is defined as a collection of connected platelets. From these considerations we calculate:

• 〈N_nei〉 = average number of neighbors around one platelet.

• 〈N_cl〉 = average number of platelets in a cluster.

• 〈P_par〉 = percentage of platelets aggregated in the system.

The elasticity is approximated by calculating the average force fluctuation per platelet in the three Cartesian directions:

The effective osmotic pressure is evaluated from the virial equation,

where F(r_αβ) is the force between two sites in different platelets. It is important to note that when density dependent potentials are used, like here where the interaction between the platelets is described with a Yukawa potential modulated by a density dependent screening length, eqn (7) does not lead to the correct but to an effective osmotic pressure of the system. Although effective, its qualitative behavior is maintained. For a more detailed discussion on the subject see ref. 13, 40 and 42.

The convergence of the measured quantities were tested by either doubling or halving the system size at various particle volume fraction (not shown). Some small but negligible variations were observed.

3 Results

3.1 Nematic phase

The I/N transition is investigated in Fig. 1, which shows the variation of S as a function of volume fraction for various platelet sizes and charge anisotropies in comparison to the neutral platelet case. The estimated I/N transition at S = 0.4 for the various cases treated are summarized in Table 2. All curves present the same behavior – at low ϕ, S is close to zero. This is characteristic of an isotropic phase (I) where the platelets are randomly oriented. When increasing ϕ, a transition from an isotropic to a nematic phase occurs characterized by the rapid rise of the nematic order parameter. In agreement with Onsager's prediction, the transition is found to be shifted toward lower volume fractions as the platelet size is increased – see Table 2. This is an example of the role of the excluded volume in such phase formation. Interestingly, the I/N transition is also found to be dependent of the charge carried by the edges. When the platelet edges bear the same charge as the basal plane (NoCh) or when they are neutral (LoCh), the formation of the nematic phase is favored, i.e. compared to the neutral case. This seems to be true for all platelet sizes, and illustrates the role of the electrostatic repulsions. When the edges are oppositely charged (ModCh) attractive interactions start to play a role and formation of the nematic phase is then disfavored. For high charge anisotropy (HiCh), the I/N transition is replaced by a gel/columnar transition, see below and ref. 38. Note as well that, the smaller the platelets, the less important the effect of the charge anisotropy. The obtained results are consistent with the recent findings of Martínez-Haya et al.³⁵ with the use of anisotropic dispersive potentials.

Fig. 1 Nematic order parameter as a function of the volume fraction ϕ. The diameter of the platelets is, from top to bottom: (a) 90 Å, (b) 110 Å and (c) 150 Å. The NoCh case is represented in full black lines with circles, LoCh in full red lines with squares and ModCh in full green lines with diamonds. The neutral case is given for comparison (black dashed lines).

Fig. 2 Effective equation of state for platelets with various charge anisotropies and sizes, D. From top to bottom: (a) HiCh; (b) ModCh.

Table 2 Volume fractions at which the I/N transition occurs for various platelet sizes, D, and charge anisotropies. The I/N transition is extracted from Fig. 1 at S = 0.4. The statistical error in the calculation of S is ± 0.05

D	Neutral	NoCh	LoCh	ModCh	HiCh
90 Å	0.21	0.20	0.20	0.21	—
110 Å	0.18	0.16	0.16	0.18	—
150 Å	0.12	0.10	0.12	0.13	—

---

3.2 Gel phase

Fig. 2 and 3 display the effective osmotic pressure and structural parameters for dispersions of platelets with various sizes and moderate to high charge anisotropy. As already shown elsewhere,¹³ in the case of strong charge anisotropy, dispersions of platelets (D = 150 Å) experience a first order phase transition as revealed by the van der Waals loop in the effective equation of state. This corresponds macroscopically to a phase separation between a repulsive liquid and a percolated network, see Fig. 3-a and -b, of randomly oriented platelets characteristic of a gel phase. The gel forms due to basal-edge attraction between the platelets. The gel structure is characterized in Fig. 3 through the quantities 〈N_cl〉, 〈N_nei〉 and 〈P_par〉 which all increase with volume fraction. In particular, a percolated network is found above ϕ = 10%, c.f. Fig. 3-b. The steep increase in 〈N_cl〉 and 〈N_nei〉 at low ϕ, in Fig. 3 has been shown to be associated with the formation of the metastable Smectic B phase.¹³ On the other hand, the decrease in the number of neighbors for the largest platelet size, Fig. 3-c, at ϕ > 0.15, is related to the formation of a columnar phase, see ref. 38. When the platelet size is decreased, 〈N_cl〉, 〈N_nei〉 and 〈P_par〉 become monotonically increasing functions. The percolation point, i.e. ϕ at which the system is fully percolated, is seen to increase as the platelet size is reduced, see Fig. 3-b, although, due to a weaker Z^net, smaller platelets start to aggregate earlier, as best seen in Fig. 3-a. The effective equation of state, Fig. 2, shows that the liquid–gel separation is greatly soften when decreasing the platelets size to D = 110 Å and, upon a further decrease in D, is replaced by a continuous sol–gel transition. Using an approximate Maxwell construction (Fig. 2-a), the phase transition from a liquid to a gel is thus found to increase from ϕ ∼ 3% to ∼15% as the platelet size is decreased.

Fig. 3 Structural parameters for dispersions of platelets at two charge anisotropies and with various sizes: (ModCh) = red; (HiCh) = black; D = 90 Å (dashed lines); D = 110 Å (full lines); D = 150 Å (full line with circles). From top to bottom: (a) Percentage of platelets in the simulation box that are included in a cluster, 〈P_par〉. (b) Average number of platelets in a cluster normalized with N_tot, 〈N_cl〉. (c) Number of neighbors around a platelet inside a cluster, 〈N_nei〉. Two clay platelets are considered to be “connected” neighbors if the separation between one site of a platelet is located at less than 15 Å from a site of another platelet. A cluster is defined as a collection of connected platelets.

In the case of platelets with moderate charge anisotropy, a continuous sol–gel transition is found for all D, c.f. Fig. 2-b and 3, respectively. Note that the effective osmotic pressure is approximatively two times bigger for ModCh compared to HiCh as a result of the reduced charge anisotropy (and the related rise of Z^net). The evolution of 〈P_par〉 and 〈N_cl〉 with the platelet size, Fig. 3-a and -b, shows that, although less pronounced, the same conclusion as in the case of strong charge anisotropy can be drawn. That is, the bigger the platelet size is, the easier the sol–gel transition. It should also be noted here, that the screening length is also playing an important role and that the platelet size relative to κ⁻¹ is a determining factor.⁴³ Interestingly the same trend has been observed on dispersions of Ni/Al layered double hydroxide⁴⁴ and nontronite clay¹⁵ at low salt concentration. Although such a rationalization is appealing, a full characterization of the charge anisotropy of these minerals would be needed in order to conclusively ascertain the dependence of the liquid–gel transition with the size of the platelets. A closer look at Fig. 3-c, reveals a step in the increase in the number of neighbors with ϕ for all moderate charge anisotropy curves (ModCh), induced by the spatial reorganization of platelets, characteristic of the I/N transition, c.f. Fig. 1. Note that, however, above this transition a true nematic phase is not observed but, instead, what can be called a nematic gel.

The same conclusions can be drawn from the force fluctuation per platelet shown in Fig. 4, i.e. a measure of the gel elasticity. Indeed, the gel becomes stiffer with increase in platelet size and charge anisotropy. The stiffness goes up with the volume fraction, but slows down at the transition to the nematic gel.

Fig. 4 Force fluctuation per platelet as a function of the volume fraction ϕ for platelets with various sizes and charge anisotropies. Dashed lines: moderate charge anisotropy; full lines: strong charge anisotropy; black curves: D = 90 Å; red curves: D = 110 Å; green curves: D = 150 Å.

The gel formation can also be understood and predicted on the basis of an effective platelet-platelet interaction as in ref. 43. The simulation of a pair of platelets averaging over all angles presents the advantage to be a much faster procedure than that of a bulk system. Fig. 5 presents the free energy of interaction, the thermally averaged energy as well as the minimum energy as a function of the platelet separation for various volume fractions. Fig. 5-a displays several minima, depending on volume fraction, for the free energy of interaction but only for the most anisotropic charge distribution. For the moderate or low anisotropies there are no free energy minima in the interaction curves for any volume fraction. As a matter of fact, the thermally averaged energy of interaction is always positive for moderate and low anisotropies in contrast to the case with large anisotropy – see Fig. 5-b. However, there are still configurations with a net attractive energy, but it is overwhelmed by the orientational entropy. An interesting observation is that the initial minimum at around 120 Å in Fig. 5-a has only a weak effect on the pressure and it is the appearance of the second minimum at 85 Å, corresponding to a T shape configuration, that seems to trigger the van der Waals loop in the effective equation of state i.e. Fig. 2-a. What is more, at the volume fraction corresponding to the minimum in the effective equation of state (ϕ = 10%), a minimum is found in the thermal energy but not in the free energy. This clearly illustrates that multi-body interactions play an important role in such concentrated dispersions.

Fig. 5 From top to bottom: (a) The free energy of interaction between two platelets with D = 150 Å each and high charge anisotropy. The volume fraction is varied and the background electrolyte concentration is 10 mM. The free energy curve for two neutral platelets is also included (with symbols). (b) Free energy and energy of interaction as well as the minimum energy as a function of separation for two platelets with D = 150 Å and either high (full line) or moderate charge (dashed line) anisotropy. the volume fraction is 0.1.

3.3 Glass phase

Fig. 6 presents the structural parameters versus ϕ of dispersions for fully negatively charged platelets, with neutral or negatively charged edge sites. Globally, the same trend is obtained for 〈P_par〉, 〈N_cl〉 and 〈N_nei〉 as compared to the moderate and strong charge anisotropy case. Indeed, due to the repulsive electrostatic interactions that prevail in these systems, the “filled space” by the spatial organization of the platelets is found to be reduced as depicted by the global shift of the curves toward higher volume fractions. This is emphasized when the platelets are large and do not present a charge anisotropy. As an example, the number of close neighbors stays lower than two up to ϕ ∼ 15% for all D when the platelets are fully negatively charged, while at high charge anisotropy and D = 150 Å it drops to ϕ ∼ 2% – see Fig. 3-c and 5-c.

Fig. 6 Structural parameters for dispersions of platelets at two charge anisotropies and with various sizes: (LoCh) = black; (NoCh) = red; D = 90 Å (dashed lines); D = 110 Å (full lines); D = 150 Å (full line with circles). From top to bottom: (a) Percentage of platelets in the simulation box that are included in a cluster, 〈P_par〉. (b) Average number of platelets in a cluster normalized with N_tot, 〈N_cl〉. (c) Number of neighbors around a platelet inside a cluster, 〈N_nei〉.

A striking feature is the change in stiffness of the repulsive glass (Wigner glass) as the volume fraction and the platelet size are increased. The stiffness is found to increase, as expected, with the volume fraction, but contrary to the gel case, it decreases with platelet size. This surprising behavior is illustrated in Fig. 7. Similarly to a previous finding on gels,¹³ 〈f²〉 is found to be proportional to the number of close neighbors, see Fig. 6-c. Indeed, the same qualitative trend is observed, i.e. both the number of close neighbors and glass stiffness decrease when edge sites become negatively charged and platelet size is increased. The liquid–glass transition is thus expected to be favored with small platelets, in agreement with observations in dispersions of nontronite,¹⁶ beidellite¹⁷ and montmorillonite.⁹

Fig. 7 Force fluctuation per platelet as a function of the volume fraction ϕ for platelets with various sizes and charge anisotropies. Full lines: low charge anisotropy; full lines with symbols: no charge anisotropy; black curves: D = 90 Å; red curves: D = 110 Å; green curves: D = 150 Å.

Size fractionated nontronite and beidellite clays are also found to display a true isotropic–nematic transition. That is, the formation of the liquid crystal phase is preempting the transition from a fluid to a kinetically arrested state. The results of our study suggest that a true isotropic–nematic transition would be favored for: (i) large exfoliated platelets, as low aspect ratio platelets favor the formation of the nematic phase and postpone the formation of a glass phase (for low charge anisotropy), and (ii) uniformly charged platelets or carrying a low charge anisotropy. While experimental investigations confirm (i),^15,17 it was also suggested that only clays with a structural charge located in the tetrahedral layers, i.e. closer to the surface, can display a true I/N transition. This suggestion was formulated to explain why a true I/N transition is not observed with montmorillonite (charge located in the octahedral layer) but with nontronite and beidellite. However, Na-fluorohectorite, which charge arises from the octahedral layer, also displays such a transition with stacks of platelets^45,46 indicating that the influence of the location of the structural charge is limited. Instead, our results suggest that part of the answer might be found in the charge heterogeneity. In any case, this issue needs to be further investigated through experiments and simulations.

4 Conclusion

We have provided new insight into the transition from an isotropic liquid to a nematic liquid phase and to various solid phases. Our results shed more light on how the different phases depend on the charge heterogeneity of the platelets. In particular, we find that at high charge anisotropy the liquid–gel transition is favored for dispersions of large platelets and reversely when the platelets are fully negatively charged. These two different regimes (i.e. at low and high charge anisotropy) may explain the differences in the liquid–solid transition observed between, on one hand, montmorillonite, beidellite, and, on the other hand, nontronite, Mg/Al layered double hydroxides, with changes in the platelet size distribution. However, a better characterization of the charge anisotropy of these minerals would be needed in order to conclusively connect of the liquid–solid transition to the platelet size. In addition, we found that the I/N transition is disfavored by the charge anisotropy, and, thus, often found to be pre-empted by a gel phase. Surprisingly, this transition is found to disappear in favor of a gel-columnar transition for strong enough charge anisotropy.

Acknowledgements

The authors acknowledge the support of the CRI of the Université de Bourgogne and Lunarc at Lund University for providing access to the common computer facilities.

References

1. B. Baeyens and M. Bradbury, J. Contam. Hydrol., 1997, 27, 199–222.
2. E. Tombácz and M. Szekeres, Appl. Clay Sci., 2004, 27, 75–94.
3. M. Duc, F. Gaboriaud and F. Thomas, J. Colloid Interface Sci., 2005, 289, 148–156.
4. M. Delhorme, C. Labbez, C. Caillet and F. Thomas, Langmuir, 2010, 26, 9240–9249.
5. G. Lagaly, Appl. Clay Sci., 1989, 4, 105–123.
6. A. Mourchid, A. Delville, J. Lambard, E. Lecolier and P. Levitz, Langmuir, 1995, 11, 1942.
7. F. Pignon, J.-M. Piau and A. Magnin, Phys. Rev. Lett., 1996, 76, 4857.
8. C. Martin, F. Pignon, J.-M. Piau, A. Magnin, P. Lindner and B. Cabane, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 021401.
9. L. J. Michot, I. Bihannic, K. Porsch, S. Maddi, C. Baravian, J. Mougel and P. Levitz, Langmuir, 2004, 20, 10829–10837.
10. B. Ruzicka, L. Zulian and G. Ruocco, Phys. Rev. Lett., 2004, 93, 258301.
11. M. C. D. Mourad, D. V. Byelov, A. V. Petukhov, D. A. M. de Winter, A. J. Verkleij and H. N. W. Lekkerkerker, J. Phys. Chem. B, 2009, 113, 11604–11613.
12. H. Tanaka, J. Meunier and D. Bonn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031404.
13. M. Delhorme, B. Jönsson and C. Labbez, Soft Matter, 2012, 8, 9691–9704.
14. S. Jabbari-Farouji, J. J. Weis, P. Davidson, P. Levitz and E. Trizac, Sci. Rep., 2014, 3, 3559.
15. L. J. Michot, I. Bihannic, S. Maddi, C. Baravian, P. Levitz and P. Davidson, Langmuir, 2008, 24, 3127–3139.
16. L. J. Michot, C. Baravian, I. Bihannic, S. Maddi, C. Moyne, J. F. L. Duval, P. Levitz and P. Davidson, Langmuir, 2009, 25, 125–139.
17. E. Paineau, K. Antonova, C. Baravian, I. Bihannic, P. Davidson, I. Dozov, M. Impéror-Clerc, A. Madsen, P. Levitz, F. Meneau and L. J. Michot, J. Phys. Chem. B, 2009, 113, 15858–15869.
18. I. Langmuir, J. Chem. Phys., 1938, 6, 873–896.
19. Note, however, that California hectorites are lath shaped and that nobody to date has been able to reproduce the experiments.
20. L. Onsager, Phys. Rev., 1942, 62, 558.
21. L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659.
22. J. Vieillard-Baron, Mol. Phys., 1974, 28, 809.
23. F. M. van der Kooij and H. N. W. Lekkerkerker, J. Phys. Chem. B, 1998, 102, 7829–7832.
24. F. M. van der Kooij, K. Kassapidou and H. N. W. Lekkerkerker, Nature, 2000, 406, 868–871.
25. D. van der Beek and H. N. W. Lekkerkerker, Europhys. Lett., 2003, 61, 703.
26. L. Luan, S. Liu and D. Sun, J. Solid State Chem., 2009, 182, 1462–1467.
27. S. Liu, J. Zhang, N. Wang, W. Liu, C. Zhang and D. Sun, Chem. Mater., 2003, 15, 3240.
28. M. C. D. Mourad, E. J. Devid, M. M. van Schooneveld, C. Vonk and H. N. W. Lekkerkerker, J. Phys. Chem. B, 2008, 112, 10142–10152.
29. A. E. Saunders, A. Ghezelbash, D. M. Smilgies, M. B. Sigman and B. A. Kargel, Nano Lett., 2006, 6, 2959–2963.
30. A. Mourchid, E. LeColier, E. van Damme and P. Levitz, Langmuir, 1998, 14, 4718.
31. J. C. P. Gabriel, C. Sanchez and P. Davidson, J. Phys. Chem., 1996, 100, 11139–11143.
32. D. Frenkel and R. Eppenga, Phys. Rev. Lett., 1982, 49, 1089.
33. M. A. Bates and D. Frenkel, J. Chem. Phys., 1999, 110, 6553–6559.
34. J. A. C. Veerman and D. Frenkel, Phys. Rev. A, 1992, 45, 5632.
35. B. Martínez-Haya and A. Cuetos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 020701.
36. E. Meneses-Juarez, S. Varga, P. Orea and G. Odriozola, Soft Matter, 2013, 9, 5277–5284.
37. H. H. Wensink and E. Trizac, J. Chem. Phys., 2014, 140, 024901.
38. M. Delhorme, C. Labbez and B. Jönsson, J. Phys. Chem. Lett., 2012, 3, 1315–1320.
39. A. Agra, E. Trizac and L. Bocquet, Eur. Phys. J. E, 2004, 15, 345–357.
40. J. Dobnikar, R. Castañeda-Priego, H. von Grünberg and E. Trizac, New J. Phys., 2006, 8, 277–307.
41. R. Eppenga and D. Frenkel, Mol. Phys., 1984, 52, 1303.
42. A. A. Louis, J. Phys.: Condens. Matter, 2002, 14, 9187.
43. B. Jönsson, C. Labbez and B. Cabane, Langmuir, 2008, 24, 11406.
44. L. J. Michot, J. Ghanbaja, V. Tirtaatmadja and P. J. Scales, Langmuir, 2001, 17, 2100–2105.
45. H. Hemmen, N. L. Ringdal, E. N. D. Azevedo, M. Engelsberg, E. L. Hansen, Y. Méheust, J. O. Fossum and K. D. Knudsen, Langmuir, 2009, 25, 12507–12515.
46. N. Miyamoto, H. Iijima, H. Ohkubo and Y. Yamauchi, Chem. Commun., 2010, 46, 4166–4168.

---

Footnote

† Present address: Materials Technology, Eindhoven University of Technology, WH 4.139, PO Box 513, 5600 MB Eindhoven, The Netherlands.

---