Going beyond the self-assembled monolayer: metal intercalated dithiol multilayers and their conductance

Abstract

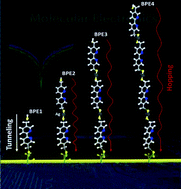
A study of the self-assembly of silver atom intercalated 5,5′-bis(mercaptomethyl)-2,2′-bipyridine (BPD; HS-CH₂-(C₅H₃N)₂-CH₂-SH) and 1,4-benzenedimethanethiol (BDMT; HS-CH₂-(C₆H₄)-CH₂-SH)) dithiol (DT) multilayers on gold is presented. The bilayer of these SAMs can be obtained starting from the exposure of a DT monolayer to a concentrated silver ion solution. After grafting the silver atoms on the sulfur end group, the incubation of the resulting DT–Ag SAM in a DT solution leads to the formation of a DT–Ag–DT bilayer. This process was extended to make a multilayer structure. The corresponding changes in these self-assembled layers on Au are characterized by X-ray photoelectron spectroscopy (XPS), spectroscopic ellipsometry (SE) measurements, and I–V characteristics. Our interpretation of evolution in the absorbed layer are based on changes in intensities of peaks in XPS related to S bound to substrate or Ag and in –SH groups, as well as changes in thickness and absorption features in SE measurements. The latter show the evolution in absorbance wavelength as a function of thickness and indicate a decrease in the HOMO–LUMO gap from about 4.5 eV to 4 eV. The I–V characteristics show a significant bias dependence on the number of the BPD layers and there appears to be a transition from tunneling to a hopping regime when going from the single to the multiple layers.