Theoretical prediction of low-density nanoporous frameworks of zinc sulfide based on ZnnSn (n = 12, 16) nanocaged clusters
Yongliang Yong*ab,
Xiaohong Lia,
Xiping Haoa,
Jingxiao Caoa and
Tongwei Lia
aCollege of Physics and Engineering, Henan University of Science and Technology, Luoyang 471003, People's Republic of China. E-mail: ylyong@haust.edu.cn
bDepartment of Physics, Zhejiang University, Hangzhou 310027, People's Republic of China
First published on 12th August 2014
Abstract
Using density functional theory calculations, the possibility of the formation of different low-density framework materials based on highly stable ZnnSn (n = 12, 16) clusters is systematically investigated. Our cluster building blocks, which have high symmetries and large HOMO–LUMO gaps, are predicted to be strongly energetically preferred. Via the coalescence of ZnnSn (n = 12, 16) building blocks, many kinds of low-density ZnS framework materials of varying porosity are thus proposed. All the frameworks differ from known synthesized materials and are predicted to be energetically stable at room temperature. These new materials are found to be semiconductors with wide bandgaps, indicating that they may have promise for optoelectronic applications. Because of their nanoporous structure, they could be used for gas storage, heterogeneous catalysis, and filtration and so on. The insights we obtained here will be helpful for extending the range of properties and applications of ZnS materials.
1. Introduction
Since the discovery of the excellent properties and applications of aluminosilicate zeolites in the areas of ion-exchange, separations, and catalysis,1–3 the area of inorganic open-framework materials has become one of intense research activity. One of the objectives of the research into open-framework materials is to find materials possessing channels and other features that make them porous or nanoporous. These porous materials play an important role in many technologies related to energy and sustainability, such as catalysis, gas separation, water purification, and batteries.4–11 In addition, in the current search for new and interesting nanoporous open-frameworks, the predictability of the framework architecture and the control of its dimensionality are essential, even if one is confronted with the underlying issue of polymorphism.12On the other hand, the prediction of the structures and properties of new materials from first principles is an important issue in fields as diverse as materials science and pharmacology, since it can be guide synthetic work efficiently towards the formulation of new materials with useful and novel properties, and is a great complementary tool to experimental polymorph screening. There are a number of diverse promising approaches to be used for the prediction of crystal structures, as outlined in a recent comprehensive review by Woodley and Catlow.13 One of the fascinating routes to the production of new materials with nanoporous architectures of different dimensionalities is using stable size-specific clusters as building blocks.13–20
Zinc sulfide (ZnS) has traditionally shown remarkable fundamental properties versatility and is currently of high relevance in technological applications including light-emitting diodes (LEDs), electroluminescence, flat panel displays, infrared windows, sensors, lasers, and biodevices.21–26 Since the transition from bulk systems to small clusters leads to substantial changes in physical and chemical properties, giving rise to unusual properties (such as the size quantization effect) that can result in promising applications, there is growing interest in the study of small clusters.27 Up to now, ZnS clusters have been studied both theoretically and experimentally.28–48 There is a general consensus on the lowest-energy structures for ZnnSn clusters based on the predictions of previous global optimizations studies: the smallest clusters are typically planar with ring-like structures, whereas in the next range of cluster size, the dominant structural motif takes the form of spherical bubbles, where all atoms are three-coordinated. Then the onion-like structures in which one bubble is inside another become more favorable with cluster size increasing, before the dominant structural motif can be built up by cutting from bulk phases. Particularly, the structures of the smallest magic clusters of ZnS (Zn12S12 and Zn16S16) have been identified as fullerene-like,36–41,48 perfect closed cages, or spherical bubbles, where all atoms arrange in tetragonal and hexagonal rings. Importantly, because of the octahedral character of the fullerene-like structures for these clusters, they are suitable for assembling new frameworks.
In this work, we report the results of density functional theory calculations on cluster-assembled materials based on Zn12S12 and Zn16S16, demonstrating the stability and energetic feasibility of new low-density nanoporous structures from ZnS clusters. We would firstly concentrate on the structural and electronic properties of individual Zn12S12 and Zn16S16 clusters. The pairwise interaction of the clusters will then be discussed, where we considered the plausibility of formation of particular frameworks by direct assembly of stable ZnS clusters rather than following more conventional synthetic routes. The structures, energetics, and electronic properties of the assembled-framework architectures will be subsequently discussed.
2. Computational methods
In this work, all calculations are performed using the spin-polarized density functional theory (DFT) implemented in the DMOL3 program (Accelyrs Inc.).49,50 The generalized gradient approximation formulated by Perdew, Burke, and Ernzerhof (PBE)51 is employed to describe the exchange-correlation energy functional. Density-functional semi-core pseudopotentials (DSPPs)52 fitted to all-electron relativistic DFT results, and double numerical basis set including d-polarization functions (i.e., the DND set) are selected. Self-consistent field (SCF) procedures are performed with a convergence criterion of 10−6 a.u. on the energy and electron density. The geometries are fully optimized without any symmetry constraints. We use a convergence criterion of 10−3 a.u. on the gradient and displacement and 10−5 a.u. on the total energy in geometrical optimization. Periodic boundary conditions are employed in the solid-state calculations, and the Brillouin zone is sampled using a 3 × 3 × 3 Monkhorst–Pack53 grid. To further explore the thermal stability of these solids, Born–Oppenheimer molecular dynamics (BOMD) is carried out in a NVT ensemble. A Nosé–Hoover chain of thermostats was used to control the temperature at 300 K. The PBE/DSPPs/DND combination is used here for BOMD. The SCF convergence criterion of 10−6 a.u is performed to ensure the accuracy of calculations.3. Results and discussion
3.1 Individual Zn12S12 and Zn16S16 clusters
The lowest-energy structures of individual Zn12S12 and Zn16S16 clusters are shown in Fig. 1. Zn12S12, the smallest possible high-symmetry magic number cluster, is the first appearance of a fullerene-like cage with high symmetry (D2h), which has six isolated four-membered rings (4Rs) and eight six-membered rings (6Rs) on the cluster surface. The other magic number octahedral cluster, Zn16S16, possesses six 4Rs and twelve 6Rs. It also has a high symmetry (Td). The energy gaps between the highest-occupied molecular orbital (HOMO) and lowest-unoccupied molecular orbital (LUMO) of Zn12S12 and Zn16S16 clusters are 3.436 eV and 3.324 eV, respectively. The equilibrium geometries and electronic properties of Zn12S12 and Zn16S16 clusters we obtained are in agreement with previous theoretical studies,36–41,48 which may confirm that the methods used in our calculations are responsibly. The octahedral configurations, high symmetries, and large HOMO–LUMO gaps demonstrate that the magic Zn12S12 and Zn16S16 clusters are particularly stable, indicating that they could be ideal building blocks to form higher order structures for synthesizing cluster-assembled materials. | ||
| Fig. 1 The optimized structures of Zn12S12 and Zn16S16 clusters. Here and in the following figures, Zn atoms are gray, and S atoms are yellow. | ||
3.2 Cluster–cluster interactions
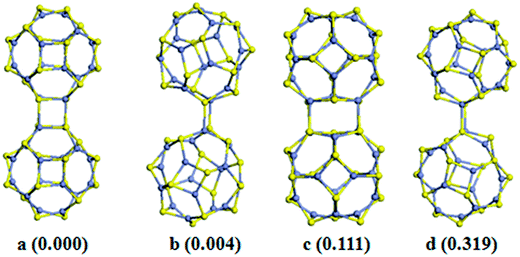
In this subsection, we consider the formation of Zn12S12 and Zn16S16 dimers and their implications for forming framework materials. As shown in Fig. 1, the individual Zn12S12 and Zn16S16 clusters have two types of edges (linear Zn–S), two types of faces (4Rs and 6Rs), and two types of apexes (Zn and S atoms), respectively. Similar to the process of searching the lowest-energy structures of Zn12O12 (ref. 54) and M12N12 (M = Al, Ga)55 dimers, in this work, we checked all possible dimer interactions. The five lowest-energy structures of Zn12S12 dimers are shown in Fig. 2, while four lowest-energy structures of Zn16S16 dimers are shown in Fig. 3. As seen in Fig. 2 and 3, in principle there are five ways for clusters to interact with each other: (i) joining two hexagonal-rings to form a double six-membered ring (D6R) junction, which has two types marked as D6R_1 and D6R_2. For the D6R_1 type, a 6R of one monomer is connected with a 4R of the other monomer, while for the D6R_2 type, a 6R of one monomer is connected with a 6R of the other monomer. (ii) Joining two tetragonal-rings to form a double four-membered ring (D4R) junction. (iii) Joining two edges to form four-membered ring (4R) junction, which has two types marked as 4R_1 and 4R_2. For the 4R_1 type, the 4Rs surrounding the joined edge face to 4Rs of the other monomer, and the 6Rs surrounding the joined edge face to 6Rs of the other monomer. However, for the 4R_2 type, the 4Rs surrounding the joined edge face to 6Rs of the other monomer.For the Zn12S12 dimers, we find that the coalescence via D6R junction is the most energetically favorable [see Fig. 2a and b], and followed by the coalescence via D4R junction. This is very similar to the cases of other fullerene-like X12Y12 (XY = ZnO, AlN, GaN, SiC) clusters.54–56 It is noted that the energy difference between structure a and b, which is formed by D6R_1 and D6R_2 junctions respectively, is very small (only 0.014 eV) as shown in Fig. 2. Meanwhile, the binding energies per ZnS of structure a and b as shown in Fig. 2 are on the whole the same. These facts mean that both of them can be considered to be the ground state. However, for the Zn16S16 dimers, the coalescence via D4R junction is the most stable one. This is different from the case of Zn16O16 dimers. Liu and co-workers have predicted that the most stable isomer of Zn16O16 dimers is the coalescence via D6R junction.57 The coalescence via D6R junction is 0.111 eV higher in energy than the most stable one, indicating that the coalescence on the 6R face becomes energetically unfavourable for larger clusters. This could be attributable to the elastic strain induced on the clusters when interacted with each other at 6R faces. When the 6R face coalescence is taking, the two 6Rs that form the D6R junction are arranged in parallel, which would distort the surface of the cluster [see Fig. 3c]. In this case, the elastic energy lost penalizing the energy that is gained from the formation of Zn–S bonds. It should be noted that the D6R junction has only four Zn–S bonds to be formed, however, as we shall show bellow, the six Zn–S bonds of D6R junction would make contributions in cluster-assembled materials.
The strength of coalescence is quantified by the dimerization energy (Ed), which is defined by:
| Ed = Etot(dimer) − 2 × Etot(monomer) | (1) |
| Eb = (nEZn + nES − EZnS)/n | (2) |
| Species | Isomers | Eb (eV) | Ed (eV) | Eg (eV) |
|---|---|---|---|---|
| Zn12S12 dimers | a | 5.3113 | −0.845 | 3.150 |
| b | 5.3107 | −0.831 | 3.214 | |
| c | 5.308 | −0.771 | 2.296 | |
| d | 5.302 | −0.613 | 3.343 | |
| e | 5.300 | −0.579 | 3.395 | |
| Zn16S16 dimers | a | 5.345 | −0.979 | 3.202 |
| b | 5.345 | −0.975 | 3.213 | |
| c | 5.341 | −0.869 | 3.119 | |
| d | 5.335 | −0.660 | 3.224 |
To further discuss the assembly processes, the transition states are searched by the method of complete linear/quadratic synchronous transit (LST/QST). The reaction paths of Zn12S12 dimers are studied, and take this an example to investigate the assembly processes. The Zn12S12 dimers as shown in Fig. 2 are viewed as products. The reactants are set as two monomers with distances of larger 7 Å and keeping the direction of interactions between monomers unchanged (see Fig. 2). To form the dimer (shown in Fig. 2a), an energy barrier of about 0.44 eV must be overcome, conversely, the reaction to the configuration of b as shown in Fig. 2 only has to overcome a small energy barrier of about 0.08 eV. For the reactions to configurations of c, d, and e, the energy barrier is 0.37 eV, 0.12 eV, and 0.18 eV, respectively. From the kinetic prediction point of view, the reaction path clearly indicates that the interactions of two Zn12S12 monomers, the configuration of a as shown in Fig. 2 are the most favorable.
From Fig. 2 and 3, it is obvious that the structural geometries of monomers can be retained during the coalescences are occurring. Then, we consider the electronic properties of these dimers, since it is expected that some novel properties of isolated monomers would be also retained in cluster-assembled materials. The calculated HOMO–LUMO gaps of these dimers are shown in Table 1. It is found that the HOMO–LUNO gaps of dimers are very similar to that of the corresponding monomers, indicating that the basic electronic properties of monomers can be maintained in dimers.
3.3 Structural and electronic properties of cluster-assembled materials based ZnnSn (n = 12, 16)
We now discuss the periodic systems constructed with ZnnSn (n = 12, 16) clusters. We have considered a large number of possible initial structures of cluster-assembled materials based on ZnnSn (n = 12, 16) clusters, in addition, we also have considered the nanoporous analogues of sodalite structures (SOD) based on ZnnSn (n = 12, 16) clusters, which was recently proposed for nanoporous SiC, MgO, and ZnO.56–60 The optimized stable configurations of Zn12S12- and Zn16S16-assembled frameworks are shown in Fig. 4 and 5, respectively. The junctions of each monomer, space group, lattice parameters, the volume, binding energy, and band gap of the calculated frameworks, together with wurtzite (WZ) and zinc-blende (ZB) ZnS phases, are obtained and summarized in Table 2.| System | Junctiona | S | Lattice constants | V (Å3) | Eb (eV) | Eg (eV) | ||
|---|---|---|---|---|---|---|---|---|
| a (Å) | b (Å) | c (Å) | ||||||
| a Notations: e.g. D4R2 + 4R_12 + 4R_22 represent there are two D4Rs, two 4R_1s, and two 4R_2 junctions for one monomer in the corresponding framework. | ||||||||
| WZ | P63MC | 3.823 | 3.823 | 6.261 | 39.624 | 5.831 | 2.367 | |
| ZB | F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3M 3M |
5.420 | 5.420 | 5.420 | 39.805 | 5.842 | 2.270 | |
| 12-1 | 4R6 | PM![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) M M |
6.552 | 6.552 | 6.552 | 46.880 | 5.559 | 2.820 |
| 12-2 | D6R_18 | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
8.135 | 8.135 | 8.135 | 39.895 | 5.129 | 1.959 |
| 12-3 | D4R6 | FM![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) C C |
13.250 | 13.250 | 13.250 | 68.533 | 5.477 | 2.993 |
| 12-4 | D4R2 + 4R_14 | P2/C | 9.070 | 9.070 | 17.110 | 58.648 | 5.301 | 2.390 |
| 12-5 | 4R_14 + 4R_22 | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
9.050 | 9.050 | 9.170 | 59.752 | 5.352 | 2.240 |
| 12-6 | D6R_12 + 4R_12 + 4R_22 | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
7.754 | 9.178 | 9.178 | 52.920 | 5.396 | 2.558 |
| 12-7 | D6R_14 | FD![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) |
18.89 | 18.89 | 18.89 | 70.214 | 5.416 | 2.530 |
| 12-8 | D6R_12 + | P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1C 1C |
14.000 | 14.000 | 21.000 | 74.259 | 5.373 | 2.150 |
| 16-1 | 4R6 | CMM2 | 22.039 | 22.039 | 15.584 | 47.309 | 5.408 | 2.395 |
| 16-2 | 6R4 + 4R2 | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
6.864 | 6.864 | 15.584 | 45.890 | 5.451 | 2.440 |
| 16-3 | D6R4 + D4R2 | P4/NBM | 13.152 | 13.152 | 9.865 | 53.326 | 5.298 | 2.440 |
| 16-4 | D4R6 | P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3M 3M |
9.865 | 9.865 | 9.865 | 60.003 | 5.357 | 2.721 |
| 16-5 | D4R4 + 4R_22 | P2/C | 9.900 | 9.900 | 23.823 | 62.347 | 5.418 | 2.531 |
| 16-6 | D4R2 + 4R_12 + 4 | P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) |
20.787 | 20.787 | 9.865 | 66.604 | 5.430 | 2.776 |
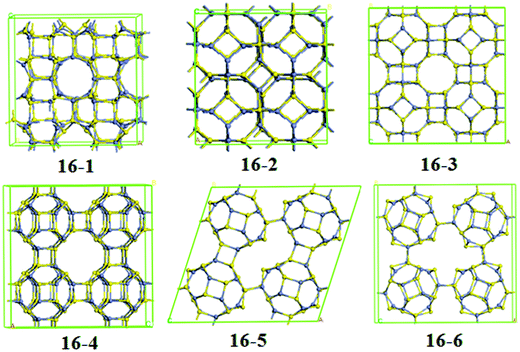
For Zn12S12-assembled frameworks, we have obtained eight kinds of structures, which are shown in Fig. 4. Following the framework notation for the corresponding silicate topologies,61 it is found that structure 12-1, 12-3, 12-7, and 12-8 can be viewed as SOD, LTA, FAU, and EMT phases, respectively. From the analysis of relative energies, the framework 12-1 turns out to be the most stable one among all the frameworks considered, resembling previous studies on ZnO frameworks based on Zn12O12 clusters.54,57,58,60 It should be noted that the SOD–ZnS structure cannot be synthesized via the direct coalescence of Zn12S12 clusters, since the SOD–ZnS is formed via Zn–S edge-to-edge intercage interactions forming four-membered ring linkages. From the perspective of cluster-assembled materials, the most stable one is framework 12-3 among all the frameworks, which is formed via 6 × D4R junctions [see Fig. 4 (12-3)]. This structural framework was also investigated by Matxain et al. in a study on thermally stable solids based on endohedrally doped ZnS clusters.62 Since the centers of Zn12S12 cages favor the bulk fcc structure, they predicted that the structure of the characterized solid has a cubic unit cell with lattice parameters of 13.79 Å, which corresponds to a distance of about 2.5 Å between monomers. In this work, our calculated optimum lattice parameter is found to be 13.25 Å with a distance of 2.546 Å between monomers. It is obvious that the lattice parameter we obtained is a little smaller than that of Matxain et al.62 The differences in lattice parameters may be attributed to bond lengths of the intermonomer Zn–S bonds. We found that each monomer in the structure 12-3 has two types of Zn–S bonds, a longer one (2.458 Å) in four-membered rings and the other shorter one (2.378 Å) connecting the neighboring four-membered rings, which are larger than those of isolated monomers. This feature was also found in other stable solids based on X12Y12 (XY = ZnO, AlN, GaN, and BN) clusters.54,55,63 However, the bond lengths of the corresponding Zn–S bonds reported by Matxain et al. are 2.57 Å and 2.49 Å, respectively, which is larger than our results. Previous computational studies of cluster-assembled materials based on fullerene-like X12Y12 (XY = ZnO, AlN, and GaN) clusters have revealed that the 12-2 phases are more stable than the LTA–XY phases.54,55 On the contrary, in this work, the 12-2 phase [see Fig. 4 (12-2)] is much less stable than the LTA–ZnS phase. It might be due to the fact that the Zn–S bond lengths between monomers are different. The average Zn–S bond length between monomers of the 12-2 ZnS phase is 2.55 Å, larger than that of their corresponding Zn12S12 dimer (2.51 Å). However, the Zn–S bond lengths between monomers of the other Zn12S12-assembled frameworks are smaller than those of corresponding Zn12S12 dimers. The increasing of bond lengths in 12-2 ZnS phase may reduce its stability.
To check for the dynamic behavior and thermal stability of these frameworks, the first-principles Born–Oppenheimer molecular dynamics (MD) simulation was carried out for the selected case, namely, the 12-2 ZnS phase, which is less stable than others. We set a simulation time of 3 ps with a time step of 1 fs, and the structural change was calculated at a constant average temperature of 300 K. Fig. 6 shows how the energies of the framework varies during the simulation. It was observed that the energy of the framework oscillates around the value (about −213215.167 eV) for the duration of the simulation, and the energy-floating ranges are no more than 0.005 eV with the simulation time increasing, a fact that is very supportive of the thermal stability of the calculated structure. This feature was found by Matxain et al. for other ZnS solids based on ZnS clusters.62 Therefore, the 12-2 ZnS phase is predicted to be stable at room temperature for long enough to allow for their characterization. As mentioned above, the other Zn12S12-assembled frameworks are much more structural stability at T = 0 K than the 12-2 ZnS phase. It may be predicted that the other Zn12S12-assembled frameworks are also stable at room temperature.
 | ||
| Fig. 6 Variation in the energy (eV) of the 12-2 ZnS phase (as shown in Fig. 4 (12-2)) as a function of time. | ||
For Zn16S16-assembled frameworks, six kinds of frameworks are found to be stable with characterized positive frequencies. Frameworks 16-1 and 16-2 can be viewed as SOD phases, while frameworks 16-3 and 16-4 are structural analogs of zeolite LTA. For framework 16-1, the coalescences of monomers are formed via the Zn–S edge-to-edge intercage interactions forming four-membered ring (4R) linkages (see Table 2), which is the same as the case of framework 12-1. However, 4R and 6R linkages are found in the framework 16-2. As seen in Fig. 5, the framework 16-3, formed by the (4 × D6R + 2 × D4R) junctions, is the most energetically unfavorable one because of the participation of D6R junctions, which is similar to the case of dimers for Zn16S16 clusters. Frameworks 16-5 and 16-6, which have the 4R junctions, are more stable than frameworks 16-3 and 16-4. Furthermore, framework 16-5 lies energetically very close to the frameworks 16-6, suggesting that the contributions of both 4R_1 and 4R_2 junctions for the formations of different frameworks are almost degenerated in energy.
The volumes per atom of the frameworks we characterized are 15.3–86.6% larger than that of ZB–ZnS phase, especially for the cluster-assembled phases, suggesting that these frameworks are all low-density polymorphs. For SOD–, LTA–, and FAU–MgO phases, Bromley et al.58 have confirmed that their stabilities become weaker with increasing volume per atom. See Table 2, it is found the same feature for the SOD–, LTA–, and FAU–ZnS phases. However, based on an overall analysis of all the frameworks we studied, there is no direct relation between the stability and density. It can be seen from Fig. 4 and 5 that all the characterized frameworks are nanoporous materials. Due to their nanoporous structures, these frameworks based on ZnS clusters could be used in many applications such as gas storage, heterogeneous catalysis, adsorbents, and sensors.7–9
We now investigate the electronic properties of all the predicted frameworks as shown in Fig. 4 and 5. The band structures of all the frameworks have been calculated firstly, and the direct bandgaps are potted in Table 2. Our calculations predict all the frameworks to be semiconductors with wide bandgaps. Particularly, the bandgap values of all the calculated frameworks (expect for frameworks 12-2, 12-5, and 12-8) are larger than that of the ZB–ZnS phase (which is more stable than WZ–ZnS phase at room temperature). Because of the wide bandgap characteristics for these calculated frameworks, it is expected that they should be perspective materials for optoelectronic applications. As we all know, the use of GGA level of density functional theory leads to an underestimation of the one-electron band gap. For example, the calculated bandgap for WZ–ZnS phase is 2.367 eV and for ZB–ZnS phase is 2.27 eV, compared with the experimental values of about 3.77 eV and 3.72 eV, respectively. Therefore, it is predicted that the real bandgap values of all the frameworks should be similarly by about 1.4 eV higher.
To further understand the features in the band edges near the Fermi level, we also calculate the total and partial density of states (PDOS) for the frameworks based on ZnnSn (n = 12, 16) clusters. The results of PDOS for Zn12S12- and Zn16S16-based frameworks are shown in Fig. 6 and 7, respectively. Since the cost of calculation increases rapidly with the size of unit cells, we were able to include only a limited number of the conduction states for larger unit cell materials. Hence, there are only the lower conduction bands that are shown for some frameworks with large unit cell (e.g. frameworks 12-3 and 12-7, i.e. LTA– and FAU–ZnS). It is found that, in general, the PDOS of all frameworks considered exhibits similar features, which could be tracked back to the atomic valence states: Zn 4s and 3d and S 3s and 3p. The valence bands near Fermi level are mainly dominated by the 3p atomic orbitals of S atoms, and the contribution of the other atomic orbitals to the valance bands is very small. The largest contribution to the conduction bands comes from the 4s orbitals of Zn atoms. Moreover, the 3d orbitals of Zn atoms and 3p orbitals of S atoms also provide partial contribution to the conduction bands (Fig. 8).
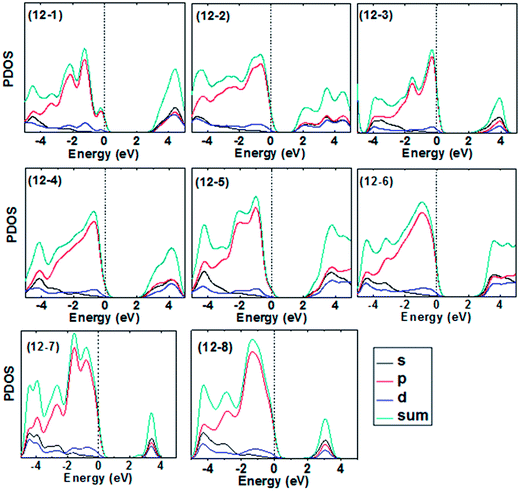 | ||
| Fig. 7 Total and partial density of states for the Zn12S12-based frameworks. The vertical line indicates the Fermi level. | ||
 | ||
| Fig. 8 Total and partial density of states for the Zn16S16-based frameworks. The vertical line indicates the Fermi level. | ||
4. Conclusions
In summary, the possibility of the formation of different low-density framework materials based on highly stable ZnnSn (n = 12, 16) clusters is theoretically investigated using density functional theory calculations. Our cluster building blocks, which have high symmetries and large HOMO–LUMO gaps, are predicted to be strongly energetically preferred.Dimers formed by attaching clusters on tetragonal, hexagonal, or edge (Zn–S) sites, are found to be more stable than others. The energy differences between any two dimers with different junctions are quite small, suggesting that the different junctions may coexist when the cluster assembly is formed. The characterized dimers with different junctions are further used as starting geometries. Via the coalescence of ZnnSn (n = 12, 16) building blocks, many kinds of low-density ZnS framework materials of varying porosity are thus proposed. All frameworks differ from known synthesized materials and are energetically stable at room temperature. These new materials are found to be semiconductors with wide bandgaps, and the values of bandgaps for most of these materials are larger than that of zinc-blende ZnS phase, indicating that they may have a promise for optoelectronic applications. Because of the nanoporous character of these new materials, they could be used for gas storage, heterogeneous catalysis, and filtration and so on.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (no. 11304080 and no. 11104138).References
- D. W. Breck, Zeolite Molecular Sieves: Structure, Chemistry and Use, Wiley-Interscience, New York, 1974 Search PubMed.
- P. B. Venuto, Microporous Mater., 1994, 2, 297–411 CrossRef CAS.
- A. Corma, Chem. Rev., 1995, 95, 559–614 CrossRef CAS.
- D. Bradshaw, J. B. Claridge, E. J. Cussen, T. J. Prior and M. J. Rosseinsky, Acc. Chem. Res., 2005, 38, 273–282 CrossRef CAS PubMed.
- C. J. Kepert, Chem. Commun., 2006, 695–700 RSC.
- S. L. James, Chem. Soc. Rev., 2003, 32, 276–288 RSC.
- D. Maspoch, D. Ruiz-Molina and J. Veciana, Chem. Soc. Rev., 2007, 36, 770–818 RSC.
- R. E. Morris and P. S. Wheatley, Angew. Chem., Int. Ed., 2008, 47, 4966–4981 CrossRef CAS PubMed.
- J. Jiang, R. Babarao and Z. Hu, Chem. Soc. Rev., 2011, 40, 3599–3612 RSC.
- S. T. Meek, J. A. Greathouse and M. D. Allendorf, Adv. Mater., 2011, 23, 249–267 CrossRef CAS PubMed.
- R. Q. Snurr, J. Phys. Chem. Lett., 2011, 2, 1842–1843 CrossRef CAS.
- B. Moulton and M. J. Zaworotko, Chem. Rev., 2001, 101, 1629–1658 CrossRef CAS PubMed.
- S. M. Woodley and C. R. A. Catlow, Nat. Mater., 2008, 7, 937–946 CrossRef CAS PubMed.
- S. N. Khanna and P. Jena, Phys. Rev. Lett., 1992, 69, 1664–1667 CrossRef CAS.
- M. Qian, A. C. Reber, A. Ugrinov, N. K. Chaki, S. Mandal, H. M. Saavedra, S. N. Khanna, A. Sen and P. S. Weiss, ACS Nano, 2010, 4, 235–240 CrossRef CAS PubMed.
- S. A. Claridge, A. W. Castleman Jr, S. N. Khanna, C. B. Murray, A. Sen and P. S. Weiss, ACS Nano, 2009, 3, 244–255 CrossRef CAS PubMed.
- A. W. Castleman Jr and S. N. Khanna, J. Phys. Chem. C, 2009, 113, 2664–2675 Search PubMed.
- S. Mandal, A. C. Reber, M. Qian, P. S. Weiss, S. N. Khanna and A. Sen, Acc. Chem. Res., 2013, 46, 2385–2395 CrossRef CAS PubMed.
- P. Jena, J. Phys. Chem. Lett., 2013, 4, 1432–1442 CrossRef CAS.
- J. Kemsley, Chem. Eng. News, 2013, 95, 24–25 Search PubMed.
- X. Jiang, Y. Xie, J. Lu, L. Y. Zhu and Y. T. Qian, Chem. Mater., 2001, 13, 1213–1218 CrossRef CAS.
- X. S. Fang, C. H. Ye, X. S. Peng, Y. H. Wang, Y. C. Wu and L. D. Zhang, Adv. Funct. Mater., 2005, 15, 63–68 CrossRef CAS PubMed.
- J. Ziegler, S. Xu, E. Kucur, F. Meister, M. Batentschuk, F. Gindele and T. Nann, Adv. Mater., 2008, 20, 4068–4073 CrossRef CAS PubMed.
- J. W. Moreau, P. K. Weber, M. C. Martin, B. Gilbert, I. D. Hutcheon and J. F. Banfield, Science, 2007, 316, 1600–1603 CrossRef CAS PubMed.
- X. S. Fang, Y. Bando, M. Y. Liao, U. K. Gautam, C. Y. Zhi, B. Dierre, B. D. Liu, T. Y. Zhai, T. Sekiguchi, Y. Koide and D. Golberg, Adv. Mater., 2009, 21, 2034–2039 CrossRef CAS PubMed.
- X. S. Fang, Y. Bando, U. K. Gautam, C. H. Ye and D. Golberg, J. Mater. Chem., 2008, 18, 509–522 RSC.
- F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371–423 CrossRef CAS.
- A. Mohajeri and M. Alipour, Int. J. Quantum Chem., 2011, 111, 3841–3850 CAS.
- J. M. Matxain, J. E. Fowler and J. M. Ugalde, Phys. Rev. A, 2000, 61, 053201 CrossRef.
- J. M. Azpiroz, E. Mosconi and F. D. Angelis, J. Phys. Chem. C, 2011, 115, 25219–25226 CAS.
- S. Hamad, C. R. A. Catlow, E. Spano, J. M. Matxain and J. M. Ugalde, J. Phys. Chem. B, 2005, 109, 2703–2709 CrossRef CAS PubMed.
- S. Pal, B. Goswami and P. Sarkar, J. Phys. Chem. C, 2008, 112, 6307–6312 CAS.
- S. Hamad and C. R. A. Catlow, J. Cryst. Growth, 2006, 294, 2–8 CrossRef CAS PubMed.
- S. Pal, R. Sharma, B. Goswami, P. Sarkar and S. P. Bhattacharyya, J. Chem. Phys., 2009, 130, 214703 CrossRef PubMed.
- E. Spanó, S. Hamad and C. R. A. Catlow, Chem. Commun., 2004, 864–865 RSC.
- K. Chuchev and J. J. BelBruno, J. Phys. Chem. A, 2005, 109, 1564–1569 CrossRef CAS PubMed.
- S. Pal, B. Goswami and P. Sarkar, J. Chem. Phys., 2005, 123, 044311 CrossRef PubMed.
- C. R. A. Catlow, S. T. Bromley, S. Hamad, M. Mora-Fonz, A. A. Sokola and S. M. Woodley, Phys. Chem. Chem. Phys., 2010, 12, 786–811 RSC.
- E. Spanó, S. Hamad and C. R. A. Catlow, J. Phys. Chem. B, 2003, 107, 10337–10340 CrossRef.
- X. Zhang, M. Zhao, T. He, W. Li, X. Lin, Z. Wang, Z. Xi, X. Liu and Y. Xia, Solid State Commun., 2008, 147, 165–168 CrossRef CAS PubMed.
- S. Hamad, S. M. Woodley and C. R. A. Catlow, Mol. Simul., 2009, 35, 1015–1032 CrossRef CAS.
- A. Burnin, E. Sanville and J. J. BelBruno, J. Phys. Chem. A, 2005, 109, 5026–5034 CrossRef CAS PubMed.
- A. Burnin and J. J. BelBruno, Chem. Phys. Lett., 2002, 362, 341–348 CrossRef CAS.
- A. Mohajeri, M. Alipour and M. B. Ahmadi, Chem. Phys. Lett., 2011, 503, 162–166 CrossRef CAS PubMed.
- H. Chen, D. Shi, B. Wang and J. Qi, J. Comput. Theor. Nanosci., 2011, 8, 2454–2461 CrossRef CAS PubMed.
- G. Malloci, L. Chiodo, A. Rubio and A. Mattoni, J. Phys. Chem. C, 2012, 116, 8741–8746 CAS.
- D. L. Lalsare and A. Kshirsagar, Bull. Mater. Sci., 2012, 35, 1055–1062 CrossRef CAS.
- K. A. Nguyen, R. Pachter and P. N. Day, J. Chem. Theory Comput., 2013, 9, 3581–3596 CrossRef CAS.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS PubMed.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- D. R. Hamann, M. Schluter and C. Chiang, Phys. Rev. Lett., 1979, 43, 1494–1497 CrossRef CAS.
- K. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- Y. L. Yong, B. Song and P. He, J. Phys. Chem. C, 2011, 115, 6455–6461 CAS.
- Y. L. Yong, B. Song and P. He, Phys. Chem. Chem. Phys., 2011, 13, 16182–16189 RSC.
- M. B. Watkins, S. A. Shevlin, A. A. Sokol, B. Slater, C. R. A. Catlow and S. M. Woodley, Phys. Chem. Chem. Phys., 2009, 11, 3186–3200 RSC.
- Z. Liu, X. Wang, J. Cai, G. Liu, P. Zhou, K. Wang and H. Zhu, J. Phys. Chem. C, 2013, 117, 17633–17643 CAS.
- J. Carrasco, F. Illas and S. T. Bromley, Phys. Rev. Lett., 2007, 99, 235502 CrossRef.
- M. A. Zwijnenburg, F. Illas and S. T. Bromley, Phys. Rev. Lett., 2010, 104, 175503 CrossRef.
- S. M. Woodley, M. B. Watkins, A. A. Sokol, S. A. Shevlin and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2009, 11, 3176–3185 RSC.
- S. M. Auerbach, K. A. Carrado and P. K. Dutta, Handbook of zeolite science and technology, Marcel Dekker, Inc., New York, 2003 Search PubMed.
- J. M. Matxain, M. Piris, X. Lopez and J. M. Ugalde, Chem.–Eur. J., 2009, 15, 5138–5144 CrossRef CAS PubMed.
- J. M. Matxain, L. A. Eriksson, J. M. Mercero, X. Lopez, M. Piris, J. M. Ugalde, J. Poater, E. Matito and M. Sola, J. Phys. Chem. C, 2007, 111, 13354–13360 CAS.
| This journal is © The Royal Society of Chemistry 2014 |