Optimal characteristic nanosizes of mineral bridges in mollusk nacre

Abstract

To date, it is still unclear why all mineral bridges linking neighboring platelets in various types of mollusk nacre have sizes of 10–50 nanometers. We answer this question by investigating the strength of platelet–platelet interfaces and found that only when the mineral bridges have diameters of a few tens of nanometers can the interfaces achieve an optimal strength. It is the uniformity of stress distributions in the mineral bridges that dictates their characteristic sizes. The mechanism underlying interfacial optimization via mineral nanobridges simultaneously optimizes the load-bearing efficiency of the materials. This study provides inspirations for the biomimetic design of advanced composite materials.

---

After millions of years of evolution, natural biological materials have acquired superior mechanical properties via their elegant hierarchical structures from the nanoscale up.^1–4 Mounting evidence has suggested that nanosized structural features play a critical role in enhancing the strength of biological materials.^5–9 Investigations on the size effect of micro/nanostructures in biological materials could help to reveal novel strengthening strategies adopted by nature and could provide inspirations for the biomimetic design of high-performance engineering materials.^10–13

Nacre (or mother-of-pearl) has attracted the interest of many scientists because of its outstanding mechanical strength and fracture toughness in comparison to those of its constituent parts, which mainly include aragonite (∼95 vol%) and a protein-rich organic phase (∼5 vol%) assembled in a hierarchical fashion.^14–22 At the micro scale, nacre has an elegant “brick-and-mortar” structure, which is composed of microsized mineral platelets (“bricks”) interspersed in an organic matrix (“mortar”).^14,15,17 At the nanoscale, the mineral platelets are composed of aragonite nanograins, which are the structural elements when nacre forms.^16,17,21,22 The structural transition from mineral nanograins into microsized platelets and the “brick-and-mortar” structure of nacre is mediated by the formation of nanosized mineral bridges at the platelet–platelet interfaces.^16,17 Interestingly, the diameters of the mineral bridges in various types of mollusk nacre are all of a narrow range of 10–50 nm.^23–27 Regarding the superior mechanical properties of nacre, previous studies have revealed a number of strengthening mechanisms across multiple length scales,^{4,19,23,24,27–37} among which an optimal strength of the platelet–platelet interfaces is of critical importance.^37,38 However, it is still unclear whether and how the characteristic nanosizes (10–50 nm) of the mineral bridges in nacre help to optimize the platelet–platelet interface strength, which further contributes to the outstanding macroscopic mechanical properties of nacre.

To answer this question, we here establish a theoretical model to investigate the size effect of mineral bridges on the interface strength in nacre. According to our dimensional analysis and finite element simulations, it is the optimization of the platelet–platelet interface strength under shear stress that dictates the characteristic sizes of the mineral bridges in the range of about 10–40 nm, which is consistent with relevant experimental observations. By analyzing the stress distribution and the material's load-bearing efficiency, the mechanisms underlying the size effect of the mineral bridges are also revealed, providing insights for the innovative design of high-strength engineering materials mimicking the interface nanostructures of nacre.

On the basis of experimental observations, a theoretical model is established for the microstructure of nacre (Fig. 1). It is composed of a periodic array of mineral bridges linking two neighboring platelets in nacre (Fig. 1a and c). According to the tension-shear chain model of nacre, the platelet–platelet interfaces predominantly transfer shear stresses.²⁹ Therefore, we focus on the interface strength under remote shear stress, τ, applied to the mineral platelets sandwiching the interfacial layer. It is known on the basis of previous experimental observations that an individual mineral bridge has a curvilinear morphology,^23,25–27 which is approximated in our model by a columnar structure with meniscus-like exterior surfaces of curvature radius h/2, where h is the thickness of the two-phase interface layer (Fig. 1b and d). To investigate the size effect of the mineral bridges, their characteristic size is defined by the diameter of their minimal cross-section, 2a. In this model, the interstitial space outside the mineral phase is occupied by a soft organic phase, separating neighboring mineral bridges by periodicity 2c. The dimensionless parameter a/c characterizes the volume percentage of the mineral phase in the interfacial layer. Therefore, we define a/c as a constant in the following analysis in order to provide a control, demonstrating that the size effect we study is not due to simply changing the amount of the load-bearing mineral phase in the interface. We choose the ratio a/c to be 1/3, reflecting the bridge–bridge distance of about 50–80 nm and the average bridge diameter of 25 nm which is observed in nacre.^24,27 Furthermore, since the organic phase is softer than the mineral phase by a factor of 10² to 10³,^19,39 its effect on the interfacial stress is negligible (as we will demonstrate below) and the externally applied shear load is mainly undertaken by the mineral bridges. In the following analysis, we only incorporate the mechanical property of the mineral phase unless mentioned otherwise. For the sake of simplicity, we will first focus on the two-dimensional (2D) model (Fig. 1) and the main conclusions drawn from the 2D analysis will be demonstrated also in a three-dimensional (3D) model.

Fig. 1 2D model of a platelet–platelet interface with mineral bridges in nacre. (a) Interface with a periodic array of mineral bridges (blue) interspersed in a soft organic phase (yellow). (b) Zoomed-in schematic of a representative volume element (dashed blue box in (a)) of the interface. (c) Scanning transmission electron microscopy (STEM) image of the platelet–platelet interface in nacre. An array of mineral bridges was observed in the interfacial layer. The image was adapted with permission.²⁵ (d) TEM image of a single mineral bridge between mineral platelets (the boundary of the mineral phase is marked by yellow dashed lines). The image was adapted with permission.²⁶

Recent experiments have shown that the aragonite phase in nacre is not just a simple brittle monocrystal but composed of nanocrystal grains.^21,22 In addition, the pure aragonite may undergo a certain amount of nanoscale ductile deformation.⁴⁰ Therefore, we reckon it is necessary to include the possibility of ductile failure of nanosized mineral bridges into our model. In particular, we study the interface strength under external shear loading before the occurrence of yielding mineral bridges and choose maximum von Mises equivalent stress, σ^Mises_max, as the failure criterion. It is a function of the following parameters:

σ^Mises_max = f(a, c, h, H, τ, E), (1)

where a is the radius of the mineral bridge at the minimal cross section, c is the spacing between two neighboring mineral bridges, h is the interface thickness or the mineral bridge height, τ is the remote shear stress, 2H is the thickness of a mineral platelet due to the top–bottom symmetry of our model (Fig. 1a), and E is the Young's modulus of the mineral material. The mineral phase, including the mineral bridges and platelets, is treated as a homogeneous and linear elastic material with Poisson's ratio ν = 0.3. Using the Pi theorem for dimensional analysis, eqn (1) reduces to a dimensionless function:

Since a/c is taken as a constant and a/H ≪ 1, eqn (2) can be simplified as

Thus, the failure of the mineral phase depends only on two normalized parameters, a/h and τ/E. The former describes the geometric feature of the mineral bridges and the latter stands for their mechanical property. Given the linear elasticity of the mineral phase and the complete force boundary conditions in the interface model, the theory of elasticity concludes that the stress solution for the problem is independent of the elastic modulus, E.⁴¹ Thus, we suggest a size effect wherein the internal stress and failure of the mineral bridges depend mainly on a single normalized geometric parameter, a/h. That is

To verify the above conclusion derived from the dimensional analysis, 2D plane-strain numerical simulations are performed to calculate the stress distribution using the software Abaqus 6.9.1. For the microstructure-based model of the platelet–platelet interface, illustrated in Fig. 1, the stress state within the mineral bridge is determined from the finite element simulations. Considering the periodic boundary conditions, we only calculate a representative volume element of the interface, as shown in Fig. 1b. Although geometric nonlinearity has been implemented in the finite element simulations, the numerical results (Fig. 2a) agree well with our result from the dimensional analysis, based on the theory of linear elasticity. This shows that the maximum von Mises stress, σ^Mises_max, is indeed independent of the elastic modulus, E, of the mineral phase but highly sensitive to the change in the characteristic size of the mineral bridges, a/h. The value of σ^Mises_max decreases with decreasing a/h and reaches an asymptotic value when a/h is smaller than 0.6 (Fig. 2a).

Fig. 2 Theoretical and numerical results of the size effect. (a) Finite element results on the relationship between the reduced maximum von Mises stress, σ^Mises_max/τ, and the normalized shear stress, τ/E. The effect of the reduced mineral bridge size, a/h, is illustrated as separate curves and the yield condition (orange curve) is also plotted. (b) Finite element results for the relationship between the interface strength, τ_b, and the nanosizes of the mineral bridges. The results both with and without the soft organic phase are shown. The yellow line is drawn for guidance. The insets show 2D finite element models.

In this study, we assume that a mineral bridge will start to fail when its maximum von Mises stress, σ^Mises_max, reaches the critical value σ_b. Thus, the interface strength, τ_b, is defined as the remote shear stress satisfying this critical condition. Since the yield stress of a material is usually smaller than the elastic modulus by orders of magnitude,⁴² we take the yield stress as σ_b/E = 1/200, which is estimated from previous experimental reports⁴³ and represented by a hyperbola in Fig. 2a. Therefore, the interface strength, τ_b, can be determined as the critical shear stress in Fig. 2a, where each horizontal line meets the yielding curve. It has been emphasized that, so far, we have kept the theoretical model dimensionless, in order to demonstrate the dominant role of the mineral bridge aspect ratio, a/h, in the interface strength, as well as the generality of our model for potentially guiding interface designs at different length scales. In the following, however, we will introduce nacre-specific parameters and length scales, to understand how the mineral bridges of diameters 10–50 nm specifically affect the interface strength in nacre.

To more clearly reveal the size effect of the nanosized mineral bridges, we calculate the failure strength of the interface via finite element simulations. On the basis of relevant experiments of nacre, we take the following representative values: E = 80 GPa,⁴³ σ^Mises_b = 400 MPa (tensile strength estimated as a fraction of the measured compressive strength of 1 GPa),⁴³ h = 25 nm, H = 300 nm,^18,19 and c = 3a.²⁷ The characteristic size 2a varies from 14 to 200 nm, wherein the lower limit of 2a is determined by the geometric feature of the mineral bridge and the periodicity in our interface model. Fig. 2b gives the simulation results regarding the dependence of the interface strength, τ_b, on the mineral bridge diameter, 2a. It is clear that τ_b increases almost linearly as the size of the mineral bridge shrinks and it reaches a plateau when the diameter of the mineral bridge is around or smaller than 40 nm. This result unequivocally shows that the characteristic nanometer sizes of the mineral bridges usually observed in nacre, i.e., 10–50 nm in diameter, belong to an optimal range of sizes that maximizes the interface strength under shear stress. As it is well known, enhancing the interface at the nanoscale is of crucial significance for improving the macroscopic tensile strength of materials. In addition, our simulations show that the incorporation of a soft organic phase,³⁹ with E_organic/E = 0.001 and ν_organic = 0.49, has a negligible influence on the interface strength (Fig. 2b), justifying our approach that only considers the mechanical property of the mineral phase. It is also notable that, unlike many size effects of nanomaterials resulting from surface effects, the size effects and the optimal interface strength revealed in this study arise mainly from the nanosized geometry of the mineral bridges and the strength optimization of the nanostructured interface in nacre.

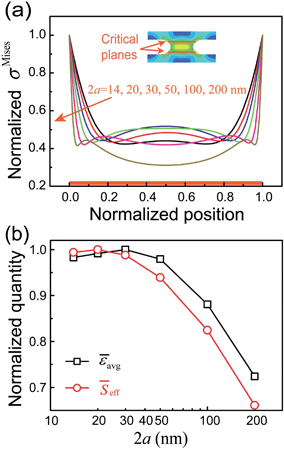
Furthermore, to gain insights into the mechanisms underlying the size effect described above, we look into the stress state within the individual mineral bridges, which are the most important load-bearing elements in the platelet–platelet interfaces. In particular, we examine the von Mises stress distribution across the critical plane within a mineral bridge, where the maximal stress and failure start to occur (Fig. 3a, inset). The simulation results, shown in Fig. 3a, clearly demonstrate that the uniformity of the stress distribution within the mineral bridge is dependent on its size. The global stress distribution becomes more and more uniform as the mineral bridge diameter, 2a, decreases to a value of 50 nm, echoing the linear increase in the interface strength, shown in Fig. 2b. However, when 2a is smaller than 50 nm, the stress distribution in the vicinity of the ends continues to become more uniform, while that in the central region becomes less uniform as the size decreases further. Therefore, the two counteracting trends might cancel each other out and result in a size effect plateau when the diameter of the mineral bridges reaches the optimal range between 10 and 40 nm (Fig. 2b).

Fig. 3 Size-dependent stress distribution and load-bearing efficiency of the material. (a) Normalized distribution of the von Mises stress, σ^Mises, across the critical planes (inset, orange lines) within the mineral bridge at different sizes. (b) Variation of the normalized material efficiency, [small epsilon, Greek, macron]_avg, and normalized effective load-bearing area, S̄_eff, with respect to the mineral bridge size.

In principle, a more uniform distribution of stress suggests a more efficient usage of the material. Here, we introduce the following parameter to describe the load-bearing efficiency of the material:

where σ^Mises (S) is the distribution of the von Mises stress in the critical plane, S_eff is the effective load-bearing area, and S_total is the total area of the critical plane. The parameter ε_avg reflects the average usage of the load-bearing potential of the mineral phase in the critical plane of the individual mineral bridges. It is calculated from the stress distribution curve in the critical plane. Fig. 3b illustrates the relationship between the normalized material efficiency, [small epsilon, Greek, macron]_avg, and the mineral bridge diameter, 2a. An optimal efficiency is found when the diameter is smaller than 40 nm, reflecting a similar size effect as observed in Fig. 2b. In fact, the relationship between the normalized effective load-bearing area, S̄_eff, and the mineral bridge diameter, 2a, is also plotted in Fig. 3b. It also illustrates a similar size effect as [small epsilon, Greek, macron]_avg, although there is a slight difference. This difference is due to the fact that the critical plane is offset from the mid-plane of the mineral bridge (Fig. 3a, inset) because of its curvilinear morphology and, thus, the total area of the critical plane, S_total, undergoes a slight variation for different mineral bridge sizes. Both size effects in [small epsilon, Greek, macron]_avg and S̄_eff reflect an intrinsic optimization mechanism of the interface strength and, thus, implicates that the optimal characteristic size of the mineral bridges is determined by the size-dependent uniformity of the stress distribution and the load-bearing efficiency of the material in the nanostructured interface. In other words, if the mineral bridge diameter is larger than 50 nm, a higher stress concentration would appear, lowering both the load-bearing ability of the platelet–platelet interfaces and the overall utilization efficiency of the material. In contrast, mineral bridges in the size range of 10–50 nm lead to a uniform stress distribution and optimal interface properties.

Additionally, to verify that the size effect and the optimal interface strength mechanism derived from the 2D model have a general meaning, we built three-dimensional (3D) finite element models (Fig. 4a). Using the same values of parameters given above, the results from the 3D simulations are shown in Fig. 4b. It is clear that our conclusions obtained in the 2D context are confirmed by 3D simulations. In spite of the fact that the numerical values of the 2D and 3D results are slightly different, they do share the same optimal characteristic size range of the mineral bridges, 10–40 nm, which correlates with the optimal strength of the interfaces (Fig. 4b). This result verifies that the differences between the 2D and 3D models have no significant effect on the conclusions, which shows the potential of the size effect and our biomimetic theory to help design and optimize real 3D-structured interfaces.

Fig. 4 3D finite element simulation results. (a) Left: 3D interface model with a periodic array of mineral bridges (blue) between two neighboring platelets; right: zoomed-in schematic of a representative element of the interface model. The organic phase filling the interstitial space is not shown for the sake of clarity. (b) Simulation results showing the dependence of the interface strength on the mineral bridge size. The yellow line is drawn for guidance.

In summary, we have unravelled the size effect of nanoscale mineral bridges in nacre. It was found that the mineral bridge diameter in the range of about 10–40 nm optimizes the interface strength. This size effect is attributed to the nanostructure of the platelet–platelet interfaces. The size-dependent uniformity of the stress distribution and the load-bearing efficiency of the material are identified as the dominant mechanisms underlying the size effect of the mineral bridges. The results could deepen our understanding of the role of nanostructures in regulating interface mechanics in natural biological materials and also provide clues for the design and fabrication of materials mimicking nanostructured interfaces.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant no. 31270989), Tsinghua University (20121087991) and the 973 Program of MOST (2012CB934101 and 2013CB933033).

References

1. P. Fratzl and R. Weinkamer, Nature's Hierarchical Materials, Prog. Mater. Sci., 2007, 52, 1263–1334.
2. M. A. Meyers, P. Y. Chen, A. Y. M. Lin and Y. Seki, Biological Materials: Structure and Mechanical Properties, Prog. Mater. Sci., 2008, 53, 1–206.
3. H. D. Espinosa, J. E. Rim, F. Barthelat and M. J. Buehler, Merger of Structure and Material in Nacre and Bone - Perspectives on De Novo Biomimetic Materials, Prog. Mater. Sci., 2009, 54, 1059–1100.
4. G. Mayer, New Toughening Concepts for Ceramic Composites from Rigid Natural Materials, J. Mech. Behav. Biomed. Mater., 2011, 4, 670–681.
5. E. Arzt, Biological and Artificial Attachment Devices: Lessons for Materials Scientists from Flies and Geckos, Mater. Sci. Eng., C, 2006, 26, 1245–1250.
6. H. J. Gao and H. M. Yao, Shape Insensitive Optimal Adhesion of Nanoscale Fibrillar Structures, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 7851–7856.
7. S. Keten, Z. P. Xu, B. Ihle and M. J. Buehler, Nanoconfinement Controls Stiffness, Strength and Mechanical Toughness of Beta-Sheet Crystals in Silk, Nat. Mater., 2010, 9, 359–367.
8. M. J. Buehler, Tu(R)ning Weakness to Strength, Nano Today, 2010, 5, 379–383.
9. M. E. Launey, M. J. Buehler and R. O. Ritchie, On the Mechanistic Origins of Toughness in Bone, Annu. Rev. Mater. Res., 2010, 40, 25–53.
10. F. Barthelat, Biomimetics for Next Generation Materials, Philos. Trans. R. Soc., A, 2007, 365, 2907–2919.
11. B. Bhushan, Biomimetics: Lessons from Nature - an Overview, Philos. Trans. R. Soc., A, 2009, 367, 1445–1486.
12. P. Podsiadlo, A. K. Kaushik, E. M. Arruda, A. M. Waas, B. S. Shim, J. D. Xu, H. Nandivada, B. G. Pumplin, J. Lahann, A. Ramamoorthy and N. A. Kotov, Ultrastrong and Stiff Layered Polymer Nanocomposites, Science, 2007, 318, 80–83.
13. L. J. Bonderer, A. R. Studart and L. J. Gauckler, Bioinspired Design and Assembly of Platelet Reinforced Polymer Films, Science, 2008, 319, 1069–1073.
14. J. D. Currey, Mechanical-Properties of Mother of Pearl in Tension, Proc. R. Soc. B, 1977, 196, 443–463.
15. A. P. Jackson, J. F. V. Vincent and R. M. Turner, The Mechanical Design of Nacre, Proc. R. Soc. B, 1988, 234, 415–440.
16. L. Addadi, D. Joester, F. Nudelman and S. Weiner, Mollusk Shell Formation: A Source of New Concepts for Understanding Biomineralization Processes, Chem.–Eur. J., 2006, 12, 981–987.
17. A. Lin and M. A. Meyers, Growth and Structure in Abalone Shell, Mater. Sci. Eng., A, 2005, 390, 27–41.
18. F. Barthelat and H. D. Espinosa, An Experimental Investigation of Deformation and Fracture of Nacre-Mother of Pearl, Exp. Mech., 2007, 47, 311–324.
19. F. Barthelat, H. Tang, P. D. Zavattieri, C. M. Li and H. D. Espinosa, On the Mechanics of Mother-of-Pearl: A Key Feature in the Material Hierarchical Structure, J. Mech. Phys. Solids, 2007, 55, 306–337.
20. F. Barthelat, Nacre from Mollusk Shells: A Model for High-Performance Structural Materials, Bioinspiration Biomimetics, 2010, 5, 035001.
21. X. D. Li, W. C. Chang, Y. J. Chao, R. Z. Wang and M. Chang, Nanoscale Structural and Mechanical Characterization of a Natural Nanocomposite Material: The Shell of Red Abalone, Nano Lett., 2004, 4, 613–617.
22. Z. W. Huang and X. D. Li, Origin of Flaw-Tolerance in Nacre, Sci. Rep., 2013, 3, 1693.
23. F. Song and Y. L. Bai, Effects of Nanostructures on the Fracture Strength of the Interfaces in Nacre, J. Mater. Res., 2003, 18, 1741–1744.
24. F. Song, J. B. Zhou, X. H. Xu, Y. Xu and Y. L. Bai, Effect of a Negative Poisson Ratio in the Tension of Ceramics, Phys. Rev. Lett., 2008, 100, 245502.
25. K. Gries, R. Kröger, C. Kübel, M. Schowalter, M. Fritz and A. Rosenauer, Correlation of the Orientation of Stacked Aragonite Platelets in Nacre and Their Connection Via Mineral Bridges, Ultramicroscopy, 2009, 109, 230–236.
26. A. G. Checa, J. H. E. Cartwright and M. G. Willinger, Mineral Bridges in Nacre, J. Struct. Biol., 2011, 176, 330–339.
27. F. Song, A. K. Soh and Y. L. Bai, Structural and Mechanical Properties of the Organic Matrix Layers of Nacre, Biomaterials, 2003, 24, 3623–3631.
28. K. Okumura and P. G. de Gennes, Why Is Nacre Strong? Elastic Theory and Fracture Mechanics for Biocomposites with Stratified Structures, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 4, 121–127.
29. H. J. Gao, Application of Fracture Mechanics Concepts to Hierarchical Biomechanics of Bone and Bone-Like Materials, Int. J. Fract., 2006, 138, 101–137.
30. R. Rabiei, S. Bekah and F. Barthelat, Failure Mode Transition in Nacre and Bone-Like Materials, Acta Biomater., 2010, 6, 4081–4089.
31. F. Barthelat and R. Rabiei, Toughness Amplification in Natural Composites, J. Mech. Phys. Solids, 2011, 59, 829–840.
32. R. Z. Wang and H. S. Gupta, Deformation and Fracture Mechanisms of Bone and Nacre, Annu. Rev. Mater. Res., 2011, 41, 41–73.
33. F. Barthelat, A. K. Dastjerdi and R. Rabiei, An Improved Failure Criterion for Biological and Engineered Staggered Composites, J. R. Soc., Interface, 2013, 10, 20120849.
34. J. E. Rim, P. Zavattieri, A. Juster and H. D. Espinosa, Dimensional Analysis and Parametric Studies for Designing Artificial Nacre, J. Mech. Behav. Biomed. Mater., 2011, 4, 190–211.
35. H. D. Espinosa, A. L. Juster, F. J. Latourte, O. Y. Loh, D. Gregoire and P. D. Zavattieri, Tablet-Level Origin of Toughening in Abalone Shells and Translation to Synthetic Composite Materials, Nat. Commun., 2011, 2, 173.
36. K. S. Katti, D. R. Katti, S. M. Pradhan and A. Bhosle, Platelet Interlocks Are the Key to Toughness and Strength in Nacre, J. Mater. Res., 2005, 20, 1097–1100.
37. Y. Shao, H. P. Zhao, X. Q. Feng and H. J. Gao, Discontinuous Crack-Bridging Model for Fracture Toughness Analysis of Nacre, J. Mech. Phys. Solids, 2012, 60, 1400–1419.
38. Y. Shao, H. P. Zhao and X. Q. Feng, On Flaw Tolerance of Nacre: A Theoretical Study, J. R. Soc., Interface, 2014, 11, 20131016.
39. B. H. Ji and H. J. Gao, Mechanical Properties of Nanostructure of Biological Materials, J. Mech. Phys. Solids, 2004, 52, 1963–1990.
40. C. Kearney, Z. Zhao, B. J. F. Bruet, R. Radovitzky, M. C. Boyce and C. Ortiz, Nanoscale Anisotropic Plastic Deformation in Single Crystal Aragonite, Phys. Rev. Lett., 2006, 96, 255505.
41. L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Pergamon Press, Oxford, 1970.
42. J. D. Currey and B. K. Hardness, Young's Modulus and Yield Stress in Mammalian Mineralized Tissues, J. Mater. Sci.: Mater. Med., 1990, 1, 14–20.
43. F. Barthelat, C. M. Li, C. Comi and H. D. Espinosa, Mechanical Properties of Nacre Constituents and Their Impact on Mechanical Performance, J. Mater. Res., 2006, 21, 1977–1986.

---