Recalcitrance of cyanuric acid to oxidative degradation by OH radical: theoretical investigation

Abstract

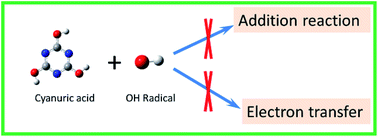
Cyanuric acid (CA) is among the several organic compounds that are resistant to oxidative degradation in advanced oxidation processes (AOPs). In the present study, the reaction between CA and ˙OH radical (the primary reactive oxygen species in AOPs) was investigated by density functional theory and compared with the reaction between 1,3,5-benzenetriol (BT) and ˙OH radical. The results indicate that compared to BT, the two tautomers (enolic form and keto form) of CA have difficulty in thermodynamically and kinetically reacting with ˙OH radical via both the addition to the triazine ring and electron abstraction. Although the reaction for the enolic form of CA was found to be much more favorable than its keto form, the small population of the enolic CA, because of its thermodynamic unstability, makes it less competitive. The reason for the recalcitration of CA to ˙OH radical is attributed to the electron deficiency of the triazine ring because of the higher electro negativity of N atom compared to that of C atom.

---

1. Introduction

Advanced oxidation processes (AOPs), such as semiconductor photocatalysis and (photo)-Fenton process, are considered to be promising technologies for the treatment of wastewater because nearly all kinds of organic compounds can be degraded, even mineralized, by these processes. However, some organic compounds are exceptionally resistant to oxidative degradation in AOP treatments. Among them, cyanuric acid (CA) is the most well-known, although it was reported to be degraded under some harsh conditions.^1–3 The recalcitration of CA by TiO₂ photocatalytic oxidation and Fenton process has been confirmed by comprehensive experimental studies.^4–6 Moreover, although s-triazine and other triazine-based herbicides and dyes undergo rapid degradation under AOP conditions, the degradation always stops at CA as the final product.^7–9

Hydroxyl radical (˙OH) is considered to be the primary reactive oxygen species in AOPs. The reactions between ˙OH and organic compounds have been extensively studied by experimental and theoretical methods, and three possible pathways have been proposed: (1) addition to the aromatic ring, (2) electron transfer, and (3) H-atom abstraction.¹⁰ In general, ˙OH reacts with aromatic substrates via pathways 1 and 2, while the last pathway is dominant for aliphatics. Therefore, when explaining the oxidative resistance of CA to ˙OH, only the first two pathways were considered, and the proposed hypotheses include:¹¹ (1) the reaction between ˙OH and CA is very slow to compete with other processes such as the recombination of photogenerated carriers and the coupling of ˙OH; (2) ˙OH reacts with CA via electron transfer followed by H⁺ loss but the formed radical is stable enough to avoid further oxidation before it re-couples with another electron or hydrogen atom; (3) the addition of ˙OH to the CA ring does occur but the adduct rapidly loses ˙OH in a reversible manner. Jenks et al.¹¹ reported that no oxygen exchange between CA and H₂O was observed under photocatalytic condition (using ¹⁸O-enriched CA as the substrate), which excludes the third hypothesis. However, the question as to why CA is resistant to ˙OH is still unclear and is difficult to answer by experimental methods. Alternatively, theoretical calculation offers a complementary approach to gain deep insight into the mechanism behind the recalcitrance of CA. Although there are several theoretical studies on the reaction between ˙OH and susceptive aromatic compounds, such as quinoline,¹² phenols,¹³ benzene,¹⁴ xylenes,¹⁵ to the best of our knowledge, the relevant reaction of CA has not been calculated yet.

In this work, in an attempt to elucidate the mechanism of the recalcitrance of CA to AOPs, the ˙OH addition and electron transfer pathways were examined by density functional theory. For comparison, the corresponding reactions of 1,3,5-benzenetriol (BT), which is iso-electronic and iso-symmetric with CA, was parallelly examined at the same theory level. Our results reveal that the reaction of CA with ˙OH radical is thermodynamically and kinetically difficult for both the addition to triazine ring and electron abstraction, which provides a deeper insight into the resistance of CA to the oxidative degradation in AOPs.

2. Computational methods

All geometry optimizations, harmonic vibrational frequencies and zero-point energy (ZPE) calculations were performed by the density functional theory^16,17 (DFT, with the B3LYP functional^18–20 and the 6-311++G(d,p) basis set). The minimum or transition state (TS) nature of the stationary points was verified by frequency analysis. The effect of solvation was investigated with the most recent version of the polarizable continuum model, that is, integral equation formalism PCM (IEF-PCM)²¹ to calculate the solvation free energies. (Geometry optimizations and frequency calculations were recalculated in water, the radii scale factor is 1.2 (ref. 22 and 23).) All the stationary point energies reported here have underwent a ZPE correction (unscaled), and all the energies are plotted relative to the total energy of the initial reactants (˙OH and CA or BT). Symmetry was not included in all the calculations.

To obtain the transition state, a search on potential surface was usually carried out by scanning the bond length of the formation of C⋯OH or N⋯OH bond in the range of 1.3–2.4 Å before the optimization of TS. Then, geometry optimizations were performed at the peak positions from this rough energy diagram to obtain the exact structures and energies of transition states. Such strategy was always successful for the addition of ˙OH to 1,3,5-benzenetriol and to the C position of CA. However, for the ˙OH addition to the N position of cyanuric acid, the length scan of the formation of N–O bond showed that the energy increases monotonically with the reduction in N⋯OH distance, and no peak could be obtained.

The rate constants for the addition of ˙OH to the aromatic ring were calculated by the classical transition state theory according to the following equation:

where k_B is the Boltzmann constant, h is the Plank's constant, T is the temperature (298 K), E₀ is the reaction activation energy (E_TS − E_R − E_˙OH, including ZPE corrections), and Q_TS, Q_R and Q_˙OH are the total partition functions for TS, substrate (CA or BT) and ˙OH, respectively. The Gaussian 03 package²⁴ was used for all the calculations.

3. Results and discussion

3.1. Substrate structure

CA is a weak acid in aqueous media (pK_a1 = 7.0, pK_a2 = 11.3, and pK_a3 = 14.5). In aqueous solutions, it exists as a mixture of tautomers, namely the enolic form (cyanuric acid, CAe) and the keto form (isocyanuric acid, CAk). In alkaline condition, the enolic form is dominant, whereas in acidic media (pH < 6), the keto form is more stable.¹ Accordingly, both the enolic form and keto form were examined in the present study. The optimized structures of CAk and CAe, as well as BT in both the gas phase and water solution with selected bond lengths are shown in Fig. 1. It is found that the length of the C–O bonds in CAe and CAk are 1.332 (1.327) and 1.206 (1.217) Å (gas phase and (water solution)), respectively, whereas the C–N bonds are 1.332 (1.334) and 1.391 (1.382) Å, respectively. It suggests that the C–O single bond in CAe transforms partly into the C=O double bond in CAk, and the aromaticity of C–N bonds in CA becomes lower as the proton shifts from O atom to N atom. The C–O bond of CAe (1.332 (1.334) Å) is remarkably shorter than that of BT (1.367 (1.366) Å), which implies that the O atom of CAe participates in the conjugation system of the aromatic ring to a larger extent than that of BT. The larger extent of O atom conjugation has an excess stabilization effect on the CAe molecule relative to BT. For these three molecules, the optimized structures in the gas phase and water solution are very close, indicating that the change in geometry caused by the solvation effect is not significant. The free energy comparison shows that in both the gas phase and water solution, CAk is more stable than CAe (by 30.1 and 29.3 kcal mol⁻¹, respectively), indicating that CA exists mainly in the keto form at room temperature. This result is consistent with earlier reports.¹ To give a more comprehensive understanding of the reaction of CA, both the reactions starting from CAk and CAe were investigated in this work.

Fig. 1 Optimized structures for CAe, CAk and BT in the gas phase and water solution (in parentheses) obtained at the B3LYP/6-311++G(d,p) level of theory. Atom representation: blue for N, gray for C, red for O, and white for H.

3.2. ˙OH addition

Because ˙OH reacts with aromatic substrates commonly via addition to the ring, we first examined the energy change accompanied by the formation of OH-adduct radical. CAe, CAk and BT all have two types of positions on the ring for the attack by ˙OH (C and N positions for CAe and CAk, ipso-C and ortho-C positions relative to hydroxyl for BT). Table 1 summarizes the changes in thermodynamic functions (ΔH, ΔS and ΔG) and estimated equilibrium constants and the activation energy of the formation of OH-adduct radicals with different structures. For CAe and CAk, only the structures of C–OH adduct radicals could be optimized to a stationary point. The comparison of the energy of the formed HO-adduct radical with the sum of the energy of ˙OH and the substrate shows that the C–OH addition is endothermic with an enthalpy increase of 0.41 (3.83) and 6.27 (9.54) kcal mol⁻¹ for CAe and CAk, respectively. The addition reactions have negative values of entropy change (ΔS) because the formed C–O/N–O bonds restrict the relative motion of ˙OH and the substrate and accordingly decrease the degree of freedom of system. Accordingly, the Gibbs energy changes (ΔGs) of the calculated ˙OH addition processes are generally larger than the enthalpy changes (ΔHs). The corresponding equilibrium constants are 5.58 × 10⁻⁸ (1.83 × 10⁻¹⁰) and 2.91 × 10⁻¹³ (1.91 × 10⁻¹⁵), respectively. The remarkable increase in Gibbs free energy and the small equilibrium constants for the C–OH adducts indicate that this process is thermodynamically unfavorable and equilibrates near the dissociative substrate and ˙OH, especially for CAk, the dominant species under room temperature. For the ˙OH addition to the N position, the energy increases with the reduction of N–O distance monotonically in the range of 1.3–2.4 Å but no minima could be obtained (Fig. S1, ESI†). The energies in Table 1 for the addition of N position were obtained with the fixation of the N–O bond at typical length (1.43 Å)²⁵ and indicate that this process is highly endothermic. The difficulty of N position addition could be explained by the fact that the standard bond energy of N–O (55 kcal mol⁻¹) is significantly lower than that of C–O (85.5 kcal mol⁻¹)²⁶ and by the high electronegativity of N atom. In contrast, the addition of ˙OH to BT at both ipso-C and ortho-C positions are quite exothermic. The enthalpy changes (ΔH) for these two additions are −13.92 (−11.20) and −16.83 (−12.92) kcal mol⁻¹, respectively, which makes these processes to proceed towards completion (with equilibrium constants of 1.81 × 10³ (16.3) and 1.27 × 10⁵ (2.81 × 10²)).

Table 1 Changes in thermodynamic functions (ΔH, ΔS and ΔG), equilibrium constants, activation energy and estimated rate constants for ˙OH addition

Reactant	Product	g/s	ΔH^b	ΔS^c	ΔG^b	K	ΔG^#^b	K^d
a The structure optimization and thermodynamic calculation were carried out with the length of the formed N–O bond fixed to 1.43 Å.b Unit: kcal mol^−1.c Unit: cal mol^−1 K^−1.d Unit: M^−1 s^−1.
		g	0.41	−31.8	9.89	5.58 × 10^−8	11.9	2.15 × 10^−3
		s	3.83	−31.7	13.27	1.83 × 10^−10	15.4	6.40 × 10^−6
		g^a	28.22	−35.1	38.69	4.07 × 10^−29	—	—
		s^a	36.54	−31.3	45.86	2.26 × 10^−34	—	—
		g	6.27	−36.3	17.09	2.91 × 10^−13	13.2	1.99 × 10^−4
		s	9.54	−35.3	20.06	1.91 × 10^−15	16.8	5.20 × 10^−7
		g^a	55.06	−33.7	65.12	1.64 × 10^−48	—	—
		s^a	63.38	−29.9	72.29	9.08 × 10^−54	—	—
		g	−13.92	−31.8	−4.44	1.81 × 10^3	0.1	2.31 × 10^6
		s	−11.20	−32.0	−1.65	16.3	1.9	1.26 × 10^5
		g	−16.83	−33.1	−6.95	1.27 × 10^5	−6.7	1.65 × 10^11
		s	−12.92	−32.1	−3.34	2.81 × 10^2	−4.8	1.29 × 10^−10

---

It should be noted that in the C–OH adducts of CAe and CAk, the formed C–O bonds are 1.40 (1.40) and 1.39 (1.38) Å, respectively, shorter than those for ˙OH-addition in BT (1.45 (1.45) Å for ipso-C and 1.46 (1.47) Å for ortho-C), which implies that the thermodynamic difference shown in Table 1 cannot be attributed to the bond energy of the formed C–O bond. To explain the thermodynamic difference in the ˙OH-addition among CAe, CAk and BT, an examination of the electrostatic potential of these substrates was carried out (Fig. 2). The triazine ring in CA, especially for CAk, the more stable form, is more positive than the aromatic ring of BT. Quantitatively, the electron deficiency of the ring can be expressed with the sum of the Mulliken charges of the atoms on the ring (six C atoms for BT, three C and three N atoms for CAe and CAk). The charge sums of the aromatic rings of BT, CAe and CAk are −0.617 (−0.819), −0.343 (−0.341) and −0.172 (−0.052), respectively, which shows that the triazine ring is significantly less negative than the benzene ring. Because of the electrophilic nature of ˙OH, these results indicate that ˙OH is more likely to react with BT relative to the two forms of CA. Another line of explanation of the thermodynamic difference comes from the spin density analysis of the formed HO-adduct radicals (Fig. 3). For the C–OH adduct radical of CAe, ipso-C and ortho-C OH-adduct radicals of BT, the uncoupled electron distributes mainly around the aromatic ring. In contrast, the uncoupled electron distributes primarily around the O atom bonded to the attacked C atom in the C–OH adduct radical of CAk, which may be caused by the single bond nature of C–N bond restricting the delocalization of the uncoupled electron around triazine ring. The localization of the uncoupled electron could explain that the HO-addition to the C atom of CAk is the most energetically unfavorable among the four investigated processes.

Fig. 2 Electrostatic potential of CAe, CAk and BT, mapped on the surface of molecular electron density at an isodensity of 0.004 e Bohr⁻³.

Fig. 3 Spin density distribution of HO-adduct radicals. (a) C–OH adduct radical of CAe. (b) C–OH adduct radical of CAk. (c) ipso-C OH-adduct radical of BT. (d) ortho-C OH-adduct radical of BT.

Although a stable reactant complex is observed for the ˙OH addition to the BT rings, no reactant complex was obtained for CA. This is clearly because of the electron deficiency of the CA ring, which makes the stationary point for such a complex on the potential surface disappear because of the presence of other stronger interactions near the potential stationary point. In fact, all the efforts to localize the reactant complexes between OH, CAe and CAk converged to the H-bonding-based complex, in which the OH radical interacts with the proton of CA in the plane.

To investigate the kinetic characteristics of ˙OH addition, the energy diagrams of these reactions were scanned. In both the gas phase and water solution, typical reaction diagrams of reactant (R)—transition state (TS)—product (P) are shown for the ˙OH additions to CAe and CAk (Fig. 4 and S2, ESI†). The TSs for the ˙OH addition to CAe and CAk are located at 11.95 (15.39) and 13.17 (16.77) kcal mol⁻¹ above the reactants (CA + ˙OH), respectively. The high energy barriers would make these ˙OH addition processes kinetically reluctant. Estimated with TST, their rate constants are 21.5 (1.99) × 10⁻⁴ and 64.0 (5.20) × 10⁻⁷ M⁻¹ s⁻¹, respectively, which are significantly lower than those of the reactions between ˙OH and other organics (normally 10⁷−10¹⁰ M⁻¹ s⁻¹).²⁷ The ˙OH formed in the oxidation system would be primarily consumed by other coexisting substrates or coupling with H₂O₂ rather than inducing the degradation of CA. In contrast, in the reaction between ˙OH and BT, besides a shared reactant complex (RC), two low-lying TSs are located corresponding to the ipso- and ortho-additions, respectively. The TS energy of the ipso-addition is slightly higher than that of the reactant (by 0.08 (1.94) kcal mol⁻¹), and even the ortho-addition gives a negative activation energy (−6.75 (−4.78) kcal mol⁻¹), which makes these two processes kinetically feasible with the estimated rate constants of 23.1 (1.26) × 10⁵ and 16.5 (1.29) × 10¹⁰ M⁻¹ s⁻¹, respectively. The rate constant of ortho-addition is considerably larger than that of the ipso-addition, showing that the ˙OH addition would primarily occur at the ortho-site. This priority for the ortho-addition is in accordance with the reported results,^28,29 and may be explained with the ortho–para directing ability of the original hydroxyl groups and the electrophilic nature of ˙OH.

Fig. 4 Energy diagram of ˙OH addition to (a) CAe, (b) CAk, and (c) BT in gas phase.

A comparison of the structures of reactants, TSs and products clearly reveal the intermediate features of these TSs. For example, in addition to the formation of C–O bonds, the addition of ˙OH to CAe mainly leads to an elongation of the two C–N bonds adjacent to the site of addition, which is a reflection of the electron transfer from the aromatic π orbitals to the newly formed C–O bonds. These C–N bonds are lengthened by 0.044 (0.044) Å from the original CAe to TS and by 0.067 (0.066) Å from the TS to the HO-adduct radical (Δr^R→TS_C–N/Δr^TS→P_C–N = 0.66 (0.67)). The ˙OH addition to CAk causes the elongation of the C–O bond at the addition site. This bond is lengthened by 0.074 (0.065) Å from the reactant to TS, and by 0.067 (0.075) Å from TS to the product (Δr^R→TS_C–O/Δr^TS→P_C–O = 1.10 (0.87)). In contrast, the TSs for the ˙OH addition to BT are more reactant-like, and the closeness for the ortho addition is more serious than the ipso one. For example, the C–C bonds adjacent to the added site (corresponding to the above-mentioned C–N bonds in the case of CAe) is lengthened by 0.026 (0.028) Å from the original BT to TS and the lengthening is 0.072 (0.071) Å from the TS to the product in the ortho-attacking process (Δr^R→TS_C–C/Δr^TS→P_C–C = 0.36 (0.39)). For the ipso-addition, the lengthening of adjacent C–C bonds is 0.037 (0.036) Å from the original BT to TS and 0.067 (0.067) Å from the TS to the products (Δr^R→TS_C–C/Δr^TS→P_C–C = 0.55 (0.54)). It is obvious that the ˙OH addition to BT proceeds via “early” TSs. These results are in accordance with the Hammond's postulate, and the thermodynamic results of the ˙OH addition to BT are more exothermic than the additions to CAe and CAk.

3.3. Electron transfer

The possibility of the direct one-electron oxidation of CA (or BT) by ˙OH is judged by the comparison of the ionization potentials (IPs) of CA (or BT) with the electron affinity of ˙OH (Table 2). It is observed that the calculated EA of ˙OH was 1.8 and 5.2 eV in the gas phase and water solution, respectively, which is comparable to the experimental values (1.9 and 6.3, respectively)³⁰ For all the three substrates (CAe, CAk and BT), the structures of their cationic radicals (Fig. S3, ESI†) were found to be very close to their neutral molecules, which is indicative of low reorganization energy for the electron transfer. As shown in Fig. 2, the triazine rings of CAe and CAk are more positive than the benzene ring of BT, which suggests that CAs are more resistant to oxidation than BT. The calculation of the IPs of CAs and BT confirmed this assumption. In both the gas phase and aqueous solution, the two forms of CA have similar IPs (10.0 (7.5) eV for CAe and 10.3 (7.8) eV for CAk), which are significantly higher than that of BT (8.1 (5.8) eV). The IPs of CAe, CAk and BT in the aqueous solution are about 2.3–2.5 eV lower than those in the gas phase, which is caused by the more remarkable stabilization effect of solvent on the cation, rather than on the neutral molecule, and falls well in the range of 2–4 eV, estimated by Pearson.³¹ In both the gas phase and aqueous solution, the EA of ˙OH is significantly lower than the IPs of CAe and CAk, which implies that the direct oxidation of the two forms of CA by ˙OH is thermodynamically unfavorable. The EA of ˙OH is still lower than the IP of BT but the difference is quite small, particularly in the solution phase (5.2 vs. 5.8 eV), which is consistent with the estimation proposed by Tripathi:³² whether electron transfer or addition is the first step in the reaction is determined by the IP of the aromatic substrate. As with most of the aromatic substrates (IP > 5.4 eV), BT reacts with ˙OH through the addition of ˙OH, rather than direct electron transfer.

Table 2 Calculated IPs of CAe, CAk and BT and EA of ˙OH

Substrate	IP (eV)
a Ionization potentials.b Electron affinity.
CAe^a	10.0 (7.5)
CAk^a	10.3 (7.8)
BT^a	8.1 (5.8)
OH^b	1.8 (5.2)

---

4. Conclusion

The theoretical calculations indicate that both the addition and electron transfer reactions between ˙OH and CA are energetically unfavorable, which is attributed to the electron deficiency of the triazine ring endowed by the high electronegativity of N atom. In agreement with the previous experimental observations, our results exclude the assumption that the addition of ˙OH to the CA ring does occur but the formed adduct rapidly loses ˙OH in a reversible manner. Moreover, earlier mechanistic proposals for the resistance of CA to ˙OH attack, such as the slow reaction rate and the stability of the CA radical formed through direct oxidation followed by deprotonation, are also ruled out by the calculation.

References

1. E. Garcia-Lopez, G. Marci, N. Serpone and H. Hidaka, J. Phys. Chem. C, 2007, 111, 18025–18032.
2. R. Varghese, U. K. Aravind and C. T. Aravindakumar, J. Hazard. Mater., 2007, 142, 555–558.
3. S. Horikoshi, Y. Wada, N. Watanabe, H. Hidaka and N. Serpone, New J. Chem., 2003, 27, 1216–1223.
4. A. Jańczyk, E. Krakowska, G. Stochel and W. Macyk, J. Am. Chem. Soc., 2006, 128, 15574–15575.
5. T. A. Tetzlaff and W. S. Jenks, Org. Lett., 1999, 1, 463–466.
6. N. Watanabe, S. Horikoshi, H. Hidaka and N. Serpone, J. Photochem. Photobiol., A, 2005, 174, 229–238.
7. C. L. Bianchi, C. Pirola, V. Ragaini and E. Selli, Appl. Catal., B, 2006, 64, 131–138.
8. E. Pelizzetti, V. Maurino, C. Minero, V. Carlin, M. L. Tosato, E. Pramauro and O. Zerbinati, Environ. Sci. Technol., 1990, 24, 1559–1565.
9. C. Hu, J. C. Yu, Z. Hao and P. K. Wong, Appl. Catal., B, 2003, 42, 47–55.
10. G. N. R. Tripathi, J. Am. Chem. Soc., 1998, 120, 4161–4166.
11. T. A. Tetzlaff and W. S. Jenks, Org. Lett., 1999, 1, 463–466.
12. A. R. Nicolaescu, O. Wiest and P. V. Kamat, J. Phys. Chem. A, 2005, 109, 2829–2835.
13. M. Altarawneh, B. Z. Dlugogorski, E. M. Kennedy and J. C. Mackie, J. Phys. Chem. A, 2008, 112, 3680–3692.
14. M. P. DeMatteo, J. S. Poole, X. Shi, R. Sachdeva, P. G. Hatcher, C. M. Hadad and M. S. Platz, J. Am. Chem. Soc., 2005, 127, 7094–7109.
15. J. Fan and R. Zhang, J. Phys. Chem. A, 2008, 112, 4314–4323.
16. J. W. Labannowski and J. Andzelm, Density Functional Methods in Chemistry, Springer, New York, 1991.
17. R. G. Parr and W. Yang, Density Functional Theory in Atom and Molecules, Oxford University Press, New York, 1989.
18. A. D. BecKe, J. Chem. Phys., 1993, 98, 5648.
19. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639.
20. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
21. M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54.
22. V. Barone, M. Cossi and J. Tomasi, J. Chem. Phys., 1997, 107, 3210–3221.
23. R. Cammi, B. Mennucci and J. Tomasi, J. Phys. Chem. A, 2000, 104, 4690–4698.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian, Inc., Wallingford CT, 2004.
25. W. J. Orville-Thomas, Chem. Rev., 1957, 57, 1179–1211.
26. R. T. Sanderson, Chemical bonds and bond energy, ed. R. T. Sanderson, Academic Press, New York, 1971.
27. G. V. Buxton, C. L. Greenstock, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1988, 17, 513–886.
28. C. Xu and L. Wang, J. Phys. Chem. A, 2013, 117, 2358–2364.
29. G. Albarran and R. H. Schuler, J. Phys. Chem. A, 2007, 111, 2507–2510.
30. P. Wardman, J. Phys. Chem. Ref. Data, 1989, 18, 1637–1755.
31. R. G. Pearson, J. Am. Chem. Soc., 1986, 108, 6109–6114.
32. G. N. R. Tripathi, J. Am. Chem. Soc., 1998, 120, 4161–4166.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra04687k

---