Monte Carlo simulation of temperature-induced reversible morphological changes between sphere and vesicle formed by AB diblock copolymers

Abstract

Temperature-induced reversible morphological changes of micelles formed by AB diblock copolymers in a selective solvent for A blocks was studied through Monte Carlo simulation. When only hydrophobic B blocks are temperature-sensitive, the micelle morphology changes from sphere at high temperature to vesicle with a decrease in temperature. When the system was heated back to high temperature, the vesicles transform into spheres, indicating reversible morphological changes with temperature. However, the simulation results show that the pathways of morphological changes between sphere and vesicle depend on temperature change rate. The pathway of the sphere changing into vesicle under a quenching process is different from the pathway of the vesicle changing into sphere when the system was directly heated to the higher temperature. Moreover, the time consumed in the simulation for vesicle transformation into sphere upon heating is significantly shorter than that for the reverse process upon quenching. By contrast, when changing the temperature gradually, the pathways of morphological transitions from sphere to vesicle and from vesicle to sphere are almost identical. Moreover, the time consumed in the simulation for the annealing and gradual heating processes are nearly the same. This pathway differences observed when directly and gradually changing the temperature of the system are further elucidated by investigating the contact number variation between B blocks and solvents with simulation time. On the other hand, when the hydrophilic blocks and hydrophobic blocks are both temperature-sensitive, the introduction of the temperature-sensitivity of hydrophilic blocks hinders the morphological transition from sphere to vesicle under annealing conditions, and only larger spheres can be obtained after the annealing process when the degree of temperature-sensitivity of blocks A is rather high. Meanwhile, the simulation results show that the morphological transitions are still reversible under a slow temperature change rate when the hydrophilic blocks and hydrophobic blocks are both temperature-sensitive.

---

1. Introduction

In the past decades, amphiphilic block copolymers have been given significant attention because of their ability to self-assemble into micelles with various morphologies in selective solvents.^1–3 Controlling micelle morphology is an important factor for extensive applications of polymer micelles in various areas, such as controlled release,⁴ drug delivery⁵ and nanocontainers.⁶ Intensive experimental^7–14 and theoretical^15–21 studies show that micelle morphology can be tuned by adjusting molecular parameters (such as block species and polymerization degree of different blocks) and solution parameters (such as solvent species and content of selective solvent). Among the parameters, temperature adjustment has been employed as an effective method to control the self-assembly behavior of block copolymers because temperature can be adjusted easily without changing any other experimental parameters. Qin et al.²² synthesized a well-defined diblock copolymer poly(ethylene oxide)-b-poly(N-isopropylacrylamide) with one temperature-sensitive block poly(N-isopropylacrylamide). The diblock copolymers become amphiphilic in water above body temperature and can self-assemble into vesicles, encapsulating both hydrophilic and hydrophobic molecules. In addition, a decrease in temperature can trigger the disassembly of vesicles, thereby releasing the encapsulants. This temperature-sensitive diblock copolymer shows significant potential for drug delivery applications.

Given that temperature-dependent micellization and demicellization are specifically important for temperature-driven drug delivery, numerous studies have been conducted to investigate the kinetics of temperature-induced micelle morphological changes.^23–30 LaRue et al.²⁵ reported temperature-induced reversible morphological changes of poly(styrene-b-isoprene) micelles. They observed a reversible change from vesicles to cylindrical micelles. The morphological change upon heating is found to be much faster than the reverse process upon cooling. Abbas et al.²⁷ investigated the self-assembly behavior of poly(styrene-b-dimethylsiloxane) in dilute solution. Thermo-reversible changes from vesicles to cylinders and then to spheres are observed. The change from cylinder to vesicle shows a little hysteresis, whereas the transition from sphere to cylinder is completely reversible during the experiments. Bhargava et al.²⁸ investigated thermo-reversible morphological changes of poly(styrene-b-ethylene oxide) micelles and obtained similar results. Their experimental results showed no hysteresis in the entire reversible morphological change processes during heating and cooling.

Although numerous studies on the kinetics of temperature-induced morphological changes have been conducted, some problems remain unsolved. For example, some experimental results show that the morphological change upon heating is significantly faster than the reverse process upon cooling,²⁵ whereas other experimental results show that no hysteresis is observed in the morphological changes during heating and cooling.²⁸ What factors affect the pathway of morphological change induced by temperature? The reversible morphological changes of micelles formed by amphiphilic AB diblock copolymers were studied through Monte Carlo simulation to address the foregoing question.

2. Model and simulation

The dynamic Lattice Monte Carlo simulation method is used in this study. The self-assembly of coarse-grained chains, that is, A₂-b-B₅ (numbers 2 and 5 refer to the repeat units for corresponding molecules), in a selective solvent for blocks A is considered. The diblock copolymer concentration is 8.75%. The system is embedded in a simple cubic lattice box of volume V = L × L × L with L = 40(larger box with L = 50 has also been employed, and the simulation result is shown in Fig. S1 in the ESI.† The simulation result shown in Fig. S1† indicates that the simulation results obtain in the box with L = 40 are not influenced by the finite size effect). Periodic boundary conditions are imposed in all of the three directions. Each monomer occupies one lattice site, and the monomers are self- and mutually avoiding, which ensures that no more than one monomer exists per lattice site. The single-site bond fluctuation model proposed by Carmesin and Kremer³¹ and by Larson^32,33 is used in this study. The permitted bond length is 1 and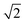 ; thus, each lattice site has 18 nearest neighbor sites in a three-dimensional space. The chain configuration evolution is achieved through monomer motions. Each step of the motion is generated through a microrelaxation model, which is highly efficient in relaxing local chain conformation on the lattice³⁴ and is suitable for dynamic process studies.^35,36 The microrelaxation mode is defined as follows: a monomer is randomly chosen to exchange with one of its 18 nearest neighbors. If the neighbor is a solvent molecule, then the exchange move is attempted. If the exchange does not violate the bond length restriction and retains no bond crossing, then the exchange is allowed. This process constitutes a single movement. If the exchange would break two chain connections, then it is not allowed. If the exchange creates a single break in the chain, then the solvent molecule continues to exchange with subsequent monomers along the chain until the reconnection of a bond. The acceptance or rejection of the attempted move is further governed by the Metropolis importance sampling rule,³⁷ that is, if the energy change ΔE is negative, then the exchange is accepted; otherwise, the exchange is accepted with a probability of p = exp[−ΔE/(k_BT)], where is the energy change caused by the attempted move; ΔN_ij is the number difference of the nearest neighbor pairs between components i and j before and after the movement, where i, j = A, B, and solvent, respectively; ε_ij is the interaction energy between components i and j; k_B is the Boltzmann constant; and T is the temperature. The reduced interaction energy ε^*_ij can be written as ε^*_ij = ε_ij/k_BT. The parameter ε^*_AS is set as negative, whereas ε^*_BS is set as positive, corresponding to the amphiphilic nature of the block copolymer. The parameter ε^*_AB is set as positive because of the incompatibility between A and B blocks. The simulation time is measured in units of Monte Carlo step (MCS). One MCS indicates that on the average, every monomer has attempted one exchange.

In the literature, many experiments show that a change in temperature leads to a change in the solubility of block copolymers.^23,25–28 Typically, the hydrophobicity of hydrophobic blocks changes greatly when the solution temperature is changed, whereas the hydrophilicity of hydrophilic blocks remains almost unchanged²⁸ or changes slightly compared to the change in the hydrophobicity of hydrophobic blocks.²⁵ In order to realize the temperature-dependence of the solubility of different blocks, two parameters T* and Δ_i are introduced. T* is defined as the reduced temperature, which reflects the changes in solubility induced by temperature, and it increases with decreasing temperature. Δ_i (i = A or B) is a constant which reflects the degree of temperature-sensitivity of the solubility of each block. Thereafter, the hydrophilicity of blocks A becomes 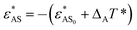, and the hydrophobicity of block B turns into . and are the hydrophilicity of blocks A and hydrophobicity of blocks B at the initial temperature (T* = 0), and , . In addition, the incompatibility between A and B blocks is set as , and Δ_AB = 1, indicating that ε^*_AB is less sensitive to temperature compared to ε^*_BS. On the other hand, although ε^*_AS is considered to be insensitive to temperature,^25,28 the effect of the temperature-dependence of block A (Δ_A > 0) on the morphological changes is also investigated for the purpose of comparison.

3. Results and discussion

3.1 Effect of the temperature change rate on the morphological changes of diblock copolymers

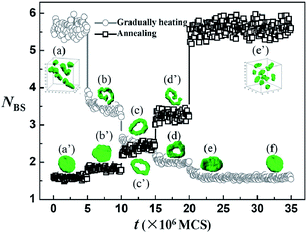
In this section, we mainly focus on the effect of temperature change rate on the reversible morphological changes between sphere and vesicle formed by the diblock copolymers with only blocks B being temperature-sensitive (i.e., Δ_A = 0, Δ_B = 8). First, the micelles formed by AB diblock copolymers at different temperatures are obtained by quenching the system from athermal state (i.e., homogenous initial state) to different given temperatures (i.e., T^* = 0 − 0.02). Fig. 1 shows the micelle morphologies obtained at different temperature values. The full sequence of sphere (Fig. 1a), cylinder (Fig. 1b), ring (Fig. 1c), lamella (Fig. 1d), and vesicle (Fig. 1e) can be obtained by decreasing the given quenching temperature. This phase sequence is similar to the phase sequence in experimental²⁷ and simulation¹⁵ reports. According to the phase sequence (Fig. 1), two temperatures (i.e., T^* = 0 and T^* = 0.02) at which the copolymers can respectively self-assemble into sphere and vesicle are chosen as the initial (final) temperatures. Two temperature change rates are employed in the current paper. When quenching (or directly heating) is performed by changing T^* from 0 directly to 0.02 (or from 0.02 to 0), the temperature change rate is considered to be rapid. By contrast, when annealing (or gradually heating) is performed by changing T^* from 0 to 0.02 (from 0.02 to 0) via a step of 0.005 per 5 × 10⁶ MCS, the temperature change rate is considered to be slow.

Fig. 1 Micelle morphologies of AB diblock copolymers in dilute solution at different quenching temperatures. (a) T^* = 0, (b) T^* = 0.004, (c) T^* = 0.008, (d) T^* = 0.015, (d) T^* = 0.02. Only B domains are shown in this and the following Figures.

Fig. 2a–e shows the pathway of morphological change from sphere to vesicle under quenching condition. Spheres first merge into small membranes (Fig. 2b), and then continue to fuse into a big oblate membrane (Fig. 2c). Finally, the oblate membrane closes up to form a vesicle [Fig. 2d–e]. This morphological change process [Fig. 2a–e] lasts for approximately 4.0 × 10⁶ MCS. Subsequently, the vesicle obtained under quenching condition (Fig. 2e) is heated back to T^* = 0 by increasing the temperature from 0.02 directly to 0 to investigate the disassembly of vesicles. Fig. 2f–j shows the morphological change pathway from vesicle to sphere upon directly heating condition. The vesicle first changes into a perforated vesicle (Fig. 2g), which then evolves into cage-like micelle (Fig. 2h). Later, the cage-like micelle breaks up and transforms into rod-like micelle (Fig. 2i). Finally, the rod-like micelle turns into sphere (Fig. 2j). Fig. 2 indicates that when the solution system is quenched to a lower temperature and then heated back to the original higher temperature, the micelle morphology changes from sphere to vesicle, and then from vesicle back to sphere. This simulation result indicates that the micelle morphology variation with temperature is reversible. However, the disassembly process from vesicle to sphere upon heating is significantly rapid. The disassembly process lasts for approximately 1.5 × 10⁵ MCS, which is much shorter than the quenching process. These simulation results are similar to the experimental results reported by LaRue et al.²⁵ In their experiment, a reversible transition from vesicles to cylindrical micelles is observed upon heating from 25 °C directly to 40 °C, and the change in morphology upon heating is significantly faster than the morphology change in reverse process upon quenching.

Fig. 2 Snapshots at different stages showing the pathway of transformation between sphere and vesicle under rapid temperature change rate (a)–(e) quenching process; (f)–(j) directly heating process. (a) 2000 MCS, (b) 1.0 × 10⁶ MCS, (c) 3.0 × 10⁶ MCS, (d) 3.4 × 10⁶ MCS, (e) 4.0 × 10⁶ MCS, (f) 0 MCS, (g) 250 MCS, (h) 2000 MCS, (i) 1.0 × 10⁴ MCS, (j) 1.5 × 10⁵ MCS. For the purpose of clarity, the cross sections of the micelles are given in (e)–(g).

Fig. 2 shows that the morphological change pathway from sphere to vesicle [Fig. 2a–e] is different from the pathway from vesicle back to sphere [Fig. 2f–j], indicating that the kinetic pathway of the micelle morphological change is irreversible during quenching and heating. To understand the irreversibility of the kinetic pathways further (Fig. 2), the contact number for each B monomer is calculated. Three species are in contact with B monomer, namely, A monomer, B monomer, and solvent. The total contact number for each B monomer should be 18 (the number of the nearest neighbors). The average contact number for each B monomer with solvents is represented by N_BS. N_BS can reflect the interfacial area between B monomers and solvents. A change in N_BS indicates that morphological change occurs in the solution. Fig. 3 shows the variations of N_BS with simulation time (MCS) under directly heating and quenching conditions. Under directly heating conditions, N_BS rapidly increases from a low value to a high value within approximately 5.0 × 10⁴ MCS and then remains almost constant. However, under quenching conditions, N_BS initially decreases rapidly. Thereafter, N_BS undergoes several flat regions to reach the minimum value until the simulation time is up to 3.7 × 10⁶ MCS. Meanwhile, Fig. 3 also indicates that the lowest N_BS value corresponds to the state in which the vesicle is formed, whereas the highest N_BS value corresponds to the state in which sphere is formed. Therefore, a sharp increase in N_BS indicates that the vesicle disassembles into small spheres very rapidly when the system is heated directly from low to high temperature. By contrast, a gradual decrease in N_BS indicates that the change process from sphere to vesicle is much more time consuming when the system is quenched directly from high to low temperature. Moreover, the flat regions of the N_BS curve upon quenching indicate that the morphological change pathway from sphere to vesicle undergoes many metastable states (typical morphologies of the metastable states are shown in Fig. 3). The change in N_BS is accomplished by the movement of polymer chains. The sharp increase in N_BS reflects that the polymer chains have high mobility upon directly heating. By contrast, upon quenching, the polymer chains have low mobility. At the same time, the coalescence of small spheres to form big oblate membrane and the close up of the big membrane to form vesicle are time consuming, particularly at low temperature. These phenomena can result in almost direct disassembly of vesicles into small spheres under directly heating condition, whereas spheres have to undergo several metastable states to form vesicles upon quenching.

Fig. 3 Variations of contact numbers (N_BS) between blocks B and solvents with simulation time under quenching and directly heating conditions respectively. The snapshots in this Figure are the typical morphologies in each time period under quenching condition.

The effect of slow temperature change rate on micelle morphological changes is also investigated. Fig. 4 and 5 show the pathway of morphological changes between sphere and vesicle under slow rate of temperature change. The simulation results show totally different phenomenon from the one observed under rapid temperature change rate. Under annealing condition, spheres first merge into short rods (Fig. 4b), which further merge into a very long rod (Fig. 4d). Then, the two ends of the long rod connect to form a ring-shaped micelle (Fig. 4e). The ring-shaped micelle fuses into a big oblate membrane (Fig. 4h), which eventually closes up to form vesicle. Fig. 4 shows that the morphological change under annealing condition is significantly more complicated than the one observed under quenching condition. Fig. 5 shows the morphological change process under gradually heating condition. The system follows a vesicle (Fig. 5a) to membrane (Fig. 5c) to ring (Fig. 5f) to rod (Fig. 5h) to sphere (Fig. 5j) pathway, which is almost the reverse process upon annealing (Fig. 4). Moreover, the simulation time cost for the morphological changes upon gradually heating is almost the same as that upon annealing. Bhargava et al.²⁸ reported similar experimental results. Their studies showed completely reversible morphological changes, that is, vesicle (room temperature) to long rod (50 °C) to short rod (60 °C) to sphere (70 °C), with step-by-step increase in temperature. Their results showed no hysteresis in the morphological changes during heating and annealing. Our simulation results are consistent with their experimental results, except that two other micelles, namely, membrane (Fig. 5c) and ring-shaped micelles (Fig. 5f), are observed when the system evolves from vesicle into rod in the simulation. In addition, aside from the classical morphologies (i.e., sphere, rod, and vesicle), perforated membranes [Fig. 4(f–g) and 5(d–e)] and tailed ring (Fig. 5g) are observed in our simulation upon slow temperature change rate.

Fig. 4 Snapshots at different stages showing the pathway of transformation from sphere to vesicle under annealing condition. (a) 2.0 × 10⁶ MCS, (b) 5.6 × 10⁶ MCS, (c) 1.06 × 10⁷ MCS, (d) 1.1 × 10⁷ MCS, (e) 1.3 × 10⁷ MCS, (f) 1.51 × 10⁷ MCS, (g) 1.52 × 10⁷ MCS, (h) 1.6 × 10⁷ MCS, (i) 2.8 × 10⁷ MCS, (j) 2.91 × 10⁷ MCS. (j′) is the cross section of (j).

Fig. 5 Snapshots at different stages showing the pathway of transformation from vesicle to sphere under gradually heating condition. (a) 2.0 × 10⁶ MCS, (b) 1.02 × 10⁷ MCS, (c) 1.04 × 10⁷ MCS, (d) 1.16 × 10⁷ MCS, (e) 1.17 × 10⁷ MCS, (f) 1.3 × 10⁷ MCS, (g) 1.9 × 10⁷ MCS, (h) 2.0 × 10⁷ MCS, (i) 2.001 × 10⁷ MCS, (j) 2.6 × 10⁷ MCS. (a′) is the cross section of (a).

To elucidate the simulation results observed upon slow temperature change rate, N_BS variations with simulation time (MCS) under gradually heating and annealing conditions are given in Fig. 6. N_BS increases step by step with an increase in simulation time upon gradually heating condition. N_BS requires five steps to reach its highest value. Moreover, the N_BS value remains almost constant at each step, indicating that the morphologies at each step are stable. Similar N_BS variations are observed under annealing condition (Fig. 6), that is, N_BS decreases step by step with an increase in simulation time. Compared with Fig. 3, N_BS variations with simulation time upon slow temperature change rate (Fig. 6) are totally different from those observed upon rapid temperature change rate. In the slow temperature change process, the temperature is changed step by step; thus, the system experiences five temperature stages during the heating or annealing process. The simulation is performed long enough for chain relaxation, which is beneficial for the system to reach its equilibrium state at each temperature stage. In Fig. 6, the equilibrium values of N_BS and the typical micelle morphologies at the same temperature stage are almost the same no matter whether the system is in gradually heating or annealing process. Therefore, under slow temperature change rate, the micelle morphology obtained at a certain temperature in simulation is stable and independent of whether the system is annealed or heated. Bhargava et al.²⁸ reported that the micelle morphologies observed in their experiments are in equilibrium states, which are confirmed by our simulation results. Furthermore, a slight difference in N_BS curves is found between heating and annealing process, that is, the heating process takes five steps, whereas the annealing process involves six steps. This difference is due to the mobility of polymer chains, which worsen at low temperature during the later stage of the annealing process. Therefore, more time is needed for the membrane to change into vesicle. Besides the slight difference, the morphological changes between different micelle morphologies under gradually heating and annealing conditions are almost the same, indicating that no hysteresis is observed in the morphological changes during heating and annealing.

Fig. 6 Variations of contact number (N_BS) between block B and solvents with simulation time under gradually heating and annealing conditions respectively. The snapshots in this Figure are the typical morphologies in each time period under gradually heating and annealing conditions.

Therefore, when the temperature change rate is rapid, many metastable states are observed in the morphological changes, indicating that the system experiences a significantly non-equilibrium process. The metastable states are uncertain in a non-equilibrium process, which results in the irreversibility of the morphological change pathway under rapid temperature change rate. However, when the temperature change rate is slow, on the basis of the simulation results, the system experiences a relatively equilibrium process. The equilibrium states at different temperatures are unique, which explains why the morphological change process is completely reversible upon slow temperature change rate.

In order to test whether the aforementioned simulation results are reproducible, the simulations are repeated with two different initial states (the initial state used for the aforementioned simulations is named as initial state 1, and the two new initial states are named as initial state 2 and 3 respectively). The simulation results are given in Fig. S2–5 in the ESI.† The simulation results show that almost all the morphologies and phase sequences shown in Fig. 2, 4 and 5 can be reproduced when changing the initial states, which proves that the morphological pathways under different temperature change rate are reproducible. Only the tailed ring shown in Fig. 5g in the gradually heating process can not be reproduced, which indicates that the tailed ring is a metastable state and is sensitive to the initial state.

Furthermore, five stable micelle morphologies in slow temperature change process (i.e., sphere, cylinder, ring, lamella, and vesicle in Fig. 4 and 5 and S4–S5†) have been quantitatively investigated. Radius of the spheres, radius and aspect ratio of the cylinders and rings, thickness of the lamella, thickness and the inner radius of the vesicles are calculated, respectively. The statistical results are shown in Table 1. It can be seen that the micelles sizes, especially the sizes of spheres and vesicles, obtained with different initial states are quite similar. This indicates that the simulation results shown in Fig. 2,4 and 5 are quantitatively reproducible. In addition, it is found that the radius of the spheres, cylinders and rings are very similar. This indicates that the spheres tend to fuse into a very long cylinder with a large aspect ratio rather than a thick cylinder with a small aspect ratio, and the cylinder is further connected end to end to form a ring under annealing condition. Moreover, the thicknesses of the lamellas and the vesicles are also quite similar, which indicates that the vesicles are formed via the bending of the lamellas. These statistical results further confirm the pathways of morphological changes observed under slow temperature change rate shown in Fig. 4 and 5.

Table 1 Size statistics of the micelles obtained from different initial state under slow temperature change rate

	Annealing process				Gradually heating process
	Radius	Radius/aspect ratio	Radius/aspect ratio	Thickness	Thickness/inner layer radius	Thickness	Radius/aspect ratio	Radius/aspect ratio	Radius
Initial state 1	4.27 ± 0.38	4.18 ± 0.52/9.92	4.10 ± 0.43/10.48	5.76 ± 0.58	5.52 ± 0.56/5.52 ± 0.50	6.01 ± 1.61	3.94 ± 0.47/10.56	3.75 ± 0.87/13.02	4.62 ± 0.69
Initial state 2	4.45 ± 0.24	3.86 ± 0.48/12.95	3.69 ± 0.53/12.11	7.11 ± 0.91	5.68 ± 0.57/5.58 ± 0.42	5.41 ± 0.61	3.79 ± 0.32/12.21	3.68 ± 0.64/14.00	4.62 ± 0.44
Initial state 3	4.29 ± 0.16	3.76 ± 0.63/14.50	3.05 ± 0.41/10.43	6.75 ± 0.72	5.68 ± 0.43/5.18 ± 0.44	5.91 ± 1.25	3.80 ± 0.37/12.01	3.67 ± 0.49/13.33	4.32 ± 0.54

---

In the case of rapid temperature change rate, most of the micelle morphologies observed during the transition are metastable. Therefore, only the average radius and radius distribution of the spheres in the final stable states (Fig. 2j, S2j and S3j†) were calculated and shown in Fig. 7a–c. It is found that the average radius of the sphere and the peak position of the radius distribution in Fig. 7a–c are quite similar, which indicates that the size of sphere is independent of initial states. For the purpose of comparison, the average radius and radius distribution of the spheres in the slow temperature change process (Fig. 5j, S4h and S5h†) are also given in Fig. 7d–f. It is seen that the sphere size and size distribution width of the spheres finally obtained upon different temperature change rate are similar, which means that the sphere size is independent of temperature change rate.

Fig. 7 Averaged radius and radius distribution of the spheres obtained under rapid (a)–(c) and slow (d)–(f) temperature change rate.

The effect of temperature change rate on the morphological changes between sphere and vesicle has been investigated. By altering the temperature change rates, simulation results that are consistent with the experimental results reported by LaRue et al.²⁵ and Bhargava et al.²⁸ have been obtained. Although the temperature change rates are not mentioned in both experiments, the temperature change rate is concluded to be the key factor in determining whether the system experiences a non-equilibrium process or equilibrium process, which further determines the kinetic pathway of the morphological changes.

3.2 Effect of the temperature-dependence of the hydrophilicity of blocks A on the morphological changes of diblock copolymers

In this section, the temperature-dependence of the hydrophilicity of blocks A is also considered, i.e., with Δ_A > 0. Three values of Δ_A are employed, i.e., Δ_A = 1, 3, 8. As stated in the Model and simulation section, Δ_A is the parameter reflecting the degree of temperature-sensitivity of the hydrophilicity of blocks A. Therefore, the larger the value of Δ_A is, the higher temperature-sensitivity |ε^*_AS| has. Other interaction parameters including Δ_B remain the same as those in Section 3.1. The temperature change rate in this section is slow, which is the same as the slow temperature change rate adopted in Section 3.1.

Fig. 8 shows the variations of the contact number N_BS with simulation time under annealing and gradually heating conditions when Δ_A = 1. The pathways of morphological changes under annealing [Fig. 8a–f] and gradually heating [Fig. 8a′–e′] conditions are also given in Fig. 8. It is seen that the variation curves of N_BS shown in Fig. 8 is quite similar to the curves shown in Fig. 6 when Δ_A = 0. However, the final micelles (Fig. 8f) obtained in the annealing process in the case of Δ_A = 1 is lamella instead of the vesicle obtained in the case of Δ_A = 0. This phenomenon results from the introducing of temperature-dependence of the hydrophilicity of blocks A. Once the temperature-dependence of the hydrophilicity of blocks A is introduced (Δ_A = 1), |ε^*_AS| will be increased with an increase in T*. However, it was found that the effect of increasing the hydrophilicity of blocks A is equivalent with the effect of decreasing the hydrophobicity of blocks B on the phase behaviors of block copolymers in a selective solvent.³⁸ Therefore, when T* is increased, an increase in |ε^*_AS| will hinder the morphological transition induced by increasing ε^*_BS. However, because the value of Δ_A is much smaller than Δ_B, the effect of increasing |ε^*_AS| is relatively weaker than the effect of increasing ε^*_BS. Therefore, only the last morphology in the phase sequence shown in Fig. 4, i.e., vesicle, can not be obtained in the case of Δ_A = 1.

Fig. 8 . Variations of N_BS with simulation time in the case of Δ_A = 1. (a)–(f) and (a′)–(e′) are the corresponding morphologies observed under annealing and gradually heating conditions, respectively. (a) initial state, (b) 1.0 × 10⁷ MCS, (c) 1.5 × 10⁷ MCS, (d) 2.0 × 10⁷ MCS, (e) 2.2 × 10⁷ MCS, (f) 3.5 × 10⁷ MCS, (a′) initial state, (b′) 1.0 × 10⁷ MCS, (c′) 1.5 × 10⁷ MCS, (d′) 1.8 × 10⁷ MCS, (e′) 2.5 × 10⁷ MCS.

For the purpose of comparison, Δ_A is increased to 3. The pathways of morphological changes in the case of Δ_A = 3 are shown in Fig. 9. It can be seen that the spheres (Fig. 9a) can only evolved into a long cylinder (Fig. 9d) under annealing condition in the case of Δ_A = 3. This indicates that the effect of increasing |ε^*_AS| turns to be much stronger in the case of Δ_A = 3 than that in the case of Δ_A = 1. When Δ_A is further increased to 8, the morphological change under annealing condition becomes almost invisible, i.e., the spheres (Fig. 10a) only change into larger spheres (Fig. 10b) after annealing. This indicates that the morphological transition from sphere to vesicle is almost completely hindered by increasing |ε^*_AS|.

Fig. 9 . Snapshots at different stages showing the pathway of morphological changes in the case of Δ_A = 3. (a)–(d) annealing process; (e)–(h) gradually heating process. (a) 5.0 × 10⁶ MCS, (b) 1.0 × 10⁷ MCS, (c) 1.5 × 10⁷ MCS, (d) 5.0 × 10⁷ MCS, (e) 5.0 × 10⁶ MCS, (f) 1.5 × 10⁷ MCS, (g) 2.0 × 10⁷ MCS, (h) 2.5 × 10⁷ MCS.

Fig. 10 . Snapshots showing the morphological changes in the case of Δ_A = 8. (a) initial state; (b) the snapshot at 1.0 × 10⁸ MCS after annealing from the initial state; (c) the snapshot at 1.0 × 10⁸ MCS after gradually heating from the spheres shown in (b).

From the simulation results shown in Fig. 8–10, it can be seen that introducing temperature-dependence into the hydrophilic blocks will hinder the morphological transition under annealing condition. The morphologies turn to be less variable with an increase in the degree of temperature-sensitivity of blocks A (Δ_A). At the same time, from the heating processes shown in Fig. 8a′–e′, 9e–h, and 10b and c, it can be seen that the morphological changes are still reversible under a slow temperature change rate when Δ_A changes from 1 to 8.

4. Conclusion

In this study, the effect of temperature change rate on temperature-induced reversible morphological changes of micelles formed by AB diblock copolymers was studied through Monte Carlo simulation. When only hydrophobic B blocks are temperature-sensitive, the simulation results show that the temperature-induced morphological changes are reversible under different temperature change rates. However, the kinetic pathways of morphological changes between sphere and vesicle depend on temperature change rate. Under rapid temperature change condition, the pathway during heating is different from the pathway during quenching. By contrast, the pathways during gradually heating and annealing are identical under slow temperature change condition. These simulation results indicate that the temperature change rate is the key factor in determining whether the system experiences a non-equilibrium process or an equilibrium process, which further determines the kinetic pathway of the morphological changes. On the other hand, when the hydrophilic blocks and hydrophobic blocks are both temperature-sensitive, the introduction of the temperature-sensitivity of hydrophilic blocks hinders the morphological transition from sphere to vesicle under annealing condition, and only larger sphere can be obtained after the annealing process when the degree of temperature-sensitivity of blocks A is rather high. Meanwhile, the simulation results show that the morphological transitions are still reversible under a slow temperature change rate when the hydrophilic blocks and hydrophobic blocks are both temperature-sensitive. Although the solution environment and the polymer properties in experiments are more complicated than those in simulations, the simulation results can still offer an insight into temperature-induced morphological change behavior and provide useful information for morphology control in experiments.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China for Youth Science Funds (21104078), the Science and Technology Development Projects of Jilin Province (201201096), and the Scientific Research Starting Foundation for the Jilin Agricultural University, China (201212).

References

1. L. F. Zhang and A. Eisenberg, Science, 1995, 268, 1728–1731.
2. L. F. Zhang and A. Eisenberg, J. Am. Chem. Soc., 1996, 118, 3168–3181.
3. J. F. Ding and G. J. Liu, Macromolecules, 1997, 30, 655–657.
4. A. Mecke, C. Dittrich and W. Meier, Soft Matter, 2006, 2, 751–759.
5. O. Onaca, R. Enea, D. W. Hughes and W. Meier, Macromol. Biosci., 2009, 9, 129–139.
6. P. Broz, S. Driamov, J. Ziegler, N. Ben-Haim, S. Marsch, W. Meier and P. Hunziker, Nano Lett., 2006, 6, 2349–2353.
7. K. Mortensen, Curr. Opin. Colloid Interface Sci., 1998, 3, 12–19.
8. G. J. Liu, Chin. J. Polym. Sci., 2000, 18, 255–262.
9. S. Jain and F. S. Bates, Science, 2003, 300, 460–464.
10. J. J. Yuan, R. Ma, X. Q. Li, K. Zhuang, S. Y. Cheng, L. Jiang, L. X. Feng and Z. Q. Fan, Chin. J. Polym. Sci., 2003, 22, 17–23.
11. A. Choucair, C. Lavigueur and A. Eisenberg, Langmuir, 2004, 20, 3894–3900.
12. J. Bang, S. Jain, Z. Li, T. P. Lodge, J. S. Pedersen, E. Kesselman and Y. Talmon, Macromolecules, 2006, 39, 5583.
13. Y. Y. He, Z. B. Li, P. Simone and T. P. Lodge, J. Am. Chem. Soc., 2006, 128, 2745–2750.
14. Y. Jiang, J. T. Zhu, W. Jiang and H. J. Liang, J. Phys. Chem. B, 2005, 109, 21549–21555.
15. P. C. Sun, Y. H. Yin, B. H. Li, T. H. Chen, Q. H. Jin, D. T. Ding and A. C. Shi, J. Chem. Phys., 2005, 122, 204905.
16. J. T. Zhu, Y. Jiang, H. J. Liang and W. Jiang, J. Phys. Chem. B, 2005, 109, 8619–8625.
17. X. A. Li, P. Tang, F. Qiu, H. D. Zhang and Y. L. Yang, J. Phys. Chem. B, 2006, 110, 2024–2030.
18. Y. T. Zhu, X. P. Yang, W. X. Kong, Y. P. Sheng and N. Yan, Soft Matter, 2012, 8, 11156–11162.
19. L. Wang, T. Jiang and J. Lin, RSC Adv., 2013, 3, 19481–19491.
20. Ws. Kong, B. Li, Q. Jin, D. Ding and A.-C. Shi, J. Am. Chem. Soc., 2009, 131, 8503–8512.
21. Y. P. Sheng, X. P. Yang, N. Yan and Y. T. Zhu, Soft Matter, 2013, 9, 6254–6262.
22. S. H. Qin, Y. Geng, D. E. Discher and S. Yang, Adv. Mater., 2006, 18, 2905–2909.
23. P. W. Zhu and D. H. Napper, Langmuir, 2000, 16, 8543–8545.
24. J. Bang, K. Viswanathan, T. P. Lodge, M. J. Park and K. Char, J. Chem. Phys., 2004, 121, 11489–11500.
25. I. LaRue, M. Adam, M. Pitsikalis, N. Hadjichristidis, M. Rubinstein and S. S. Sheiko, Macromolecules, 2006, 39, 309–314.
26. H. Wei, X. Z. Zhang, Y. Zhou, S. X. Cheng and R. X. Zhuo, Biomaterials, 2006, 27, 2028–2034.
27. S. Abbas, Z. B. Li, H. Hassan and T. P. Lodge, Macromolecules, 2007, 40, 4048–4052.
28. P. Bhargava, Y. F. Tu, J. X. Zheng, H. M. Xiong, R. P. Quirk and S. Z. D. Cheng, J. Am. Chem. Soc., 2007, 129, 1113–1121.
29. Z. D. Wang and W. Jiang, Soft Matter, 2010, 6, 3743–3746.
30. E. V. Korchagina, X.-P. Qiu and F. o. M. Winnik, Macromolecules, 2013, 46, 2341–2351.
31. I. Carmesin and K. Kremer, Macromolecules, 1988, 21, 2819–2823.
32. R. Larson, J. Chem. Phys., 1989, 91, 2479.
33. R. Larson, J. Chem. Phys., 1992, 96, 7904.
34. W. Hu, J. Chem. Phys., 1998, 109, 3686.
35. K. Haire, T. Carver and A. Windle, Comput. Theor. Polym. Sci., 2001, 11, 17–28.
36. S. Ji and J. Ding, Langmuir, 2006, 22, 553–559.
37. N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087.
38. J. J. Fan, Y. Y. Han and W. Jiang, Chem. J. Chin. Univ., 2011, 32, 1651.

---

Footnote

† Electronic supplementary information (ESI) available: The simulation results obtained in larger simulation box L = 50, and the repeated simulation results with different initial states. See DOI: 10.1039/c4ra04112g

---