Effect of DC trend removal and window functioning methods on correlation between electrochemical noise parameters and EIS data of stainless steel in an inhibited acidic solution
Seyed Yousef Armana,
Reza Naderi*b and
Bijan Pouryosefi Markhalia
aMining and Metallurgical Engineering Department, Amirkabir University of Technology, Tehran, Iran
bSchool of Metallurgy and Materials Engineering, College of Engineering, University of Tehran, Tehran, Iran. E-mail: rezanaderi@ut.ac.ir; Fax: +98 21 8800 6076; Tel: +98 21 8208 4075
First published on 6th August 2014
Abstract
For the case of stainless steel in HCl containing thiourea as a well-known organic inhibitor, the effect of a data pretreatment approach on the interpretation of electrochemical noise results, as well as the correlation between electrochemical noise data and electrochemical impedance spectroscopy parameters, were investigated in this paper. Accordingly, the impact of different window functions as drift removal methods in the frequency domain on the correlation was studied. Evaluation of the effect of five window functions implemented in NOVA software on the power spectral density plots and characteristic charge calculated from shot noise theory indicated that Hann and Bartlett window functions could be appropriate choices. Through taking advantage of the window functions, a good correlation was observed between electrochemical noise data and the results of electrochemical impedance spectroscopy. Because selecting too high and too low values for p in a moving-average removal method to remove DC trend from electrochemical noise time records was found to result in data misinterpretation, a proper p value was tried and proposed.
1. Introduction
Basically, the term electrochemical noise refers to spontaneous current and potential fluctuations occurring on the electrode surface in a particular solution.1,2 In order to measure the fluctuations there is no need to apply external perturbations, leading to minimal interface with the system.3 The electrochemical current noise and electrochemical potential noise contain valuable information about the ongoing process in the electrochemical system under study, which could be analyzed in the time domain as well as the frequency domain.4 In the case of electrochemical noise time series, to interpret data properly a possible continual drift between adjacent data points called DC trend should be removed.5 To transfer data from time records to the frequency domain, fast Fourier transform (FFT) or maximum entropy method (MEM) are usually applied.6 Since the FFT algorithm makes the time record repetitive, if there exists a drift between the first and last data points, large discontinuities would emerge, corrupting the obtained results. So, an appropriate window function should be used to avoid large discontinuities; otherwise the obtained power spectral density (PSD) plots would be misleading.7 In addition to interpretation of the electrochemical noise (EN) data, many efforts have been made to find a correlation between them and the corresponding electrochemical impedance spectroscopy (EIS) parameters.8–10One of the most efficient approaches to protect metallic structures against acidic corrosion attack is to use organic inhibitors. Various organic molecules which often contain π bonds and aromatic rings as well as heteroatoms such as oxygen, nitrogen and sulfur, are believed to hinder corrosion attack. This may be attributed to formation of a thin protective layer on the metal surface, resulting in blocking of the active sites.11,12 Among a variety of organic molecules, thiourea (TU) has already proved to be an effective inhibitor in acidic solutions, particularly on iron and steel substrates.13–15
This work intends to study the correlation between electrochemical noise data and the results of EIS in the case of stainless steel in an inhibited acidic solution. In this sense, the behaviour of TU as a well-known corrosion inhibitor in 1 M HCl was assessed, through taking advantage of electrochemical noise measurements (ENM). TU was chosen to examine the accuracy and reliability of the ENM method for evaluation of the inhibition performance of organic inhibitors in acidic solutions on metallic substrates. Also, the impact of EN data pretreatments, including DC trend removal in the time domain and window functioning in the frequency domain, on the correlation was evaluated. Since electrochemical noise measurement has the advantage that no external current is forced through the system, the paper aims to compare the values of inhibition efficiency obtained from EN and EIS data.
2. Experimental
2.1 Materials
Fig. 1 shows the chemical structure of TU used as a corrosion inhibitor in this work. The organic inhibitor of analytical grade was purchased from Merck and used without further purification. In order to prepare the inhibited electrolytes, different concentrations of TU was added to 1 M HCl solutions. The electrochemical measurements were performed on 1 cm2 of austenitic stainless steel panels (composition (wt%): C: 0.04, P: 0.08, Si: 0.75, Ni: 8, Cr: 18, Mn: 2, N: 0.1, S: 0.8 and Fe: balance) exposed to hydrochloric acid solutions containing 0, 25, 50, 100, 200 and 400 ppm (weight/volume) of the corrosion inhibitor at 25 °C without de-aeration. The stainless steel plates, supplied by Tianjin TISCO & TPCO Stainless Steel Co. Ltd, were cut as rectangular specimens. During the immersion period, the temperature was kept constant using a water bath. Prior to immersion, the specimen surface was abraded with abrasive papers starting from 80 to 2000 grit size. The samples were rinsed with distilled water and dried in air, followed by acetone degreasing. One surface of the samples was connected to a copper wire for electrical connection. To seal the edges and back sides of the steel panels, they were covered with a beeswax–colophony mixture, leaving an area of 1 cm2 unmasked.2.2 Methods
After 4 h of immersion, electrochemical measurements were carried out employing Autolab instrument model PGstat 302N. To perform EIS measurements, a conventional three-electrode cell including the stainless steel specimen as working electrode, a platinum counter electrode and a saturated Ag/AgCl reference electrode was used. Impedance spectra were plotted at open circuit potential (OCP) within the frequency domain 10 kHz to 0.01 Hz using a perturbation sine wave of 10 mV amplitude peak to peak.Electrochemical potential and current noise were simultaneously measured in a freely corroding system employing two nominally identical stainless steel working electrodes of the same area (preparation method is mentioned in Section 2.1) and a saturated Ag/AgCl reference electrode. The area of each electrode exposed to the solution was about 1.0 cm2. The three electrodes were immersed in 1 M HCl solution containing different concentrations of the inhibitor at 25 °C without de-aeration. The reference electrode was placed in the middle of a 1 cm distance between the two working electrodes. During the electrochemical measurements, the cell was placed in a Faraday cage to minimize possible external electromagnetic interference. The noise data were recorded for 1024 s at a sampling rate of 1 s. EN measurements were carried out with an apparatus containing a noise module with the input range of ±2.5 V, maximum potential resolution of 760 nV and potential accuracy of 300 μV. The potential and current noise data collected in the time domain were transformed in the frequency domain through the fast Fourier transform (FFT) and maximum entropy method (MEM). All data analysis was carried out using NOVA 1.8 software.
3. Results and discussion
3.1 Electrochemical impedance spectroscopy
The Bode and Nyquist plots of stainless steel samples immersed in 1 M HCl solutions in the absence and presence of different concentrations of TU are depicted in Fig. 2, where Z′ is the real part of the impedance, Z′′ is the imaginary part of the impedance and Z is the magnitude of the impedance.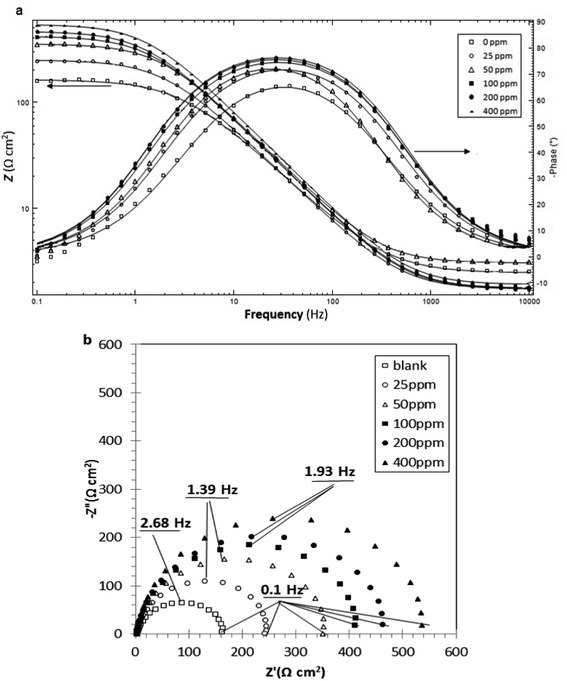 | ||
| Fig. 2 Bode (a) and Nyquist (b) plots of stainless steel samples exposed to 1 M HCl solutions containing 0–400 ppm of TU. | ||
Both Nyquist and Bode plots revealed one time constant for EIS response of all samples, indicating that the corrosion process is under charge transfer control in the absence and presence of different concentrations of TU.16 Moreover, the similarity between EIS spectra obtained from the samples exposed to solutions with and without TU could show that the corrosion reaction mechanisms are not affected by the inhibitor.17
From Fig. 2, all Nyquist plots revealed damped semicircles. The deviation from a perfect semicircle, occurring due to roughness and/or inhomogeneity of the surface, is called frequency depression.18,19 The high frequency capacitive loops might be related to the charge transfer process.20 The diameters which are proportional to the charge transfer resistance (Rct) could be calculated from the difference in impedance at lower and higher frequencies.21 As the concentration of TU increased, a continuous expansion of the loops revealed an increasing trend of the charge transfer resistance. Considering the spectra characterized by one time constant, it could be deduced that TU molecules hindered the corrosion reaction through interfering in the charge transfer process which is accomplished by blocking the active sites.
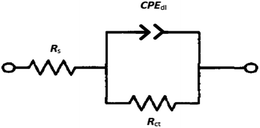
Fig. 3 displays the simple Rs(CPEdl//Rct) equivalent circuit to fit the impedance data. The circuit is commonly used to model the spectra involving a simple faradaic reaction.22,23
In Fig. 3, Rs represents solution resistance, Rct the charge transfer resistance, and CPEdl the constant phase element of double layer. CPE consists of two other parameters, namely admittance magnitude (Y0) and exponent (n). The parameter n ranging from 0 to 1 is a good indication of surface condition, i.e. it approaches one for more homogenous electrode surfaces.24 It should be noted that the solid lines in the Bode plots are simulated results using the equivalent circuit depicted in Fig. 3. It is clear from Fig. 2 that the model could generate spectra which are different from the experimental results for a small quantity.
The parameters extracted from the EIS data in the presence and absence of TU are listed Table 1. To calculate inhibition efficiency (η) and double layer capacitance (Cdl), eqn (1) and (2) were used, respectively:20,25
 | (1) |
| Cdl = Y0(2πfmax)n−1 | (2) |
| Conc. (ppm) | Rct (Ω cm2) | CPE | Cdl (μF cm−2) | η (%) | |
|---|---|---|---|---|---|
| Y0 (Ω−1 cm−2 (s)n) | n | ||||
| 0 | 163 | 0.000483 | 0.873 | 337 | |
| 25 | 253 | 0.000410 | 0.901 | 321 | 35 |
| 50 | 359 | 0.000351 | 0.904 | 276 | 54 |
| 100 | 424 | 0.000330 | 0.909 | 271 | 61 |
| 200 | 469 | 0.000316 | 0.919 | 265 | 65 |
| 400 | 541 | 0.000264 | 0.924 | 224 | 70 |
It is clear that the charge transfer resistance as well as inhibition efficiency showed an increasing trend as the inhibitor concentration increased. Furthermore, the increase in TU concentration caused the value of n to approach one. This means that the samples exposed to the uninhibited solution may encounter nonuniform corrosion attack, which leads to more inhomogeneity of the surface in comparison with samples exposed to the inhibited solutions. The decreasing trend of double layer capacitance as a result of the increase in TU concentration could also be connected to the decrease in local dielectric constant arising from replacement of water molecules on the sample surface by TU molecules.26,27 In other words, the trend of Cdl may confirm the adsorption of TU molecules on the stainless steel surface. In summary, EIS data revealed efficient corrosion inhibition offered by TU, acting as an adsorptive inhibitor on stainless steel in HCl solutions.
3.2 Electrochemical noise measurement
 | ||
| Fig. 4 The time records of electrochemical current noise associated with the samples immersed into HCl solutions with (a) 0 and (b) 400 ppm of TU. | ||
It is believed that each point in an array of the observed potential (and current) records is composed of a real potential component and a DC trend. Considering a recorded potential time series consisting of K data points, eqn (3) could be written for any data point i:33,34
| Vi,obs = Vi,real + Vi,DC | (3) |
 | (4) |
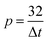 | (5) |
Eqn (5), emerging from a wavelet analysis, is based on the fact that various electrochemical events have different lifetimes. Therefore, the measured signal could be over-filtered and misinterpreted in the case of too low p values. In a previous publication,34 the findings confirmed the validity of eqn (5).
To study the effect of p on the time record analysis of electrochemical noise data, p values of 3, 10, 16, 32, 64 and 192 were examined for DC trend removal. Fig. 5 demonstrates the effect of p values on the electrochemical current noise data recorded for the samples in HCl solutions containing 0 and 400 ppm of TU. A significant dependency of the shape, amplitude and particularly the width of individual transients upon the value of p is clearly visible from the figure. In addition, regardless of p values the specimens in the inhibited solutions revealed lower amplitudes in comparison with those exposed to the uninhibited solutions, confirming the effective performance of TU. Fig. 5 also shows that too high values of p in the DC trend removal process could lead to a kind of drift.
 | ||
| Fig. 5 Removing DC trend from the electrochemical current noise with the use of p values: (a) 3, (b) 10, (c) 16, (d) 32, (e) 64 and (f) 192. | ||
The noise resistance (Rn) obtained through dividing the standard deviation of potential by the standard deviation of current (σv/σI) is a measure of inhibitive performance.34,35,37 In this paper, this parameter was used to study the effect of p value on analysis of the electrochemical noise time records (Table 2).
| Conc. (ppm) | Rn (Ω cm2) | ||||||
|---|---|---|---|---|---|---|---|
| p = 0 | p = 3 | p = 10 | p = 16 | p = 32 | p = 64 | p = 192 | |
| 0 | 219 | 241 | 251 | 262 | 271 | 313 | 265 |
| 25 | 3668 | 166 | 228 | 318 | 466 | 662 | 1290 |
| 50 | 1499 | 330 | 399 | 464 | 613 | 790 | 937 |
| 100 | 1611 | 380 | 484 | 631 | 971 | 850 | 570 |
| 200 | 1011 | 1030 | 1760 | 2020 | 2620 | 1750 | 889 |
| 400 | 3066 | 1310 | 2720 | 2730 | 3990 | 3370 | 1780 |
Although TU revealed an effective corrosion inhibition behavior, in the case of p = 0 no clear trend was observed for the noise resistance, which is in contrast to results obtained from the EIS method. Pre-treating time series with p values of 3 and 10, one can also detect no continuous increasing trend for Rn. The noise resistance encountered a decrease when 25 ppm of TU was added to the HCl solution. So, choosing low p values could lead to misinterpretation of the noise data. A good trend correlation was observed between Rn and the parameters extracted from EIS when p values increased to 16, 32 and 64. Considering the sampling rate of 1 s, the p value calculated by eqn (5) could place it within the proper range. Despite the trend correlation, it is noteworthy that the magnitude of Rn differed from the corresponding polarization resistance as reported in the literature.10,35,36 From Table 2, it is clearly seen that taking too high p values (i.e. p = 192) could also result in electrochemical noise data misinterpretation.
Another possible problem, corrupting the obtained FFT data, is frequency leakage which will be explained later. Before that, it is necessary to take a deeper look at the mathematics of a power spectrum estimation method named periodogram. To compute the discrete Fourier transform of a function c(t) sampled at N points, eqn (6) is used:39
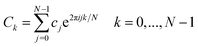 | (6) |
 represents complex number, j and k are the counter of summation and index of Fourier transform, respectively. The periodogram estimate of the power spectrum is defined at N/2 + 1 frequencies:39
represents complex number, j and k are the counter of summation and index of Fourier transform, respectively. The periodogram estimate of the power spectrum is defined at N/2 + 1 frequencies:39
 | (7) |
where P(0) is the energy of the signal and fk is defined for the zero and positive frequencies. It can be shown that eqn (7) is normalized in a way such that the sum of N/2 + 1 values of P is equal to the mean squared amplitude of the function cj. Since fk is the representative of a frequency bin extending from halfway from the preceding discrete frequency to halfway to the next one, P(fk) is an average of P(f) over a narrow window function as the functions,
 | (8) |
This window function (known as square window function) has oscillatory lobes with slow fall-off that results in significant leakage from one frequency to the adjacent ones. To compensate for this phenomenon, the input data are multiplied by a window function wi, which tends gradually from zero at both ends to a maximum 1 in the middle. Consequently, eqn (7) is modified in the following manner:39
 | (9) |
where
 .
.
Fig. 6 depicts the plots of Bartlett  , Hann
, Hann  and square window functions having the length of 256, as well as their corresponding frequency leakages. It is clear from the figure that the shape of window functions strongly affects the side lobes and consequently the frequency leakage. Square window function, which has a broader top and a steep manner, could reveal larger side lobes and more frequency leakage. In contrast, the window functions such as Bartlett and Hann, which approach from both ends toward the middle with more gentle slopes and have a point-wise middle, may reduce the chance of frequency leakage from a certain frequency to its adjacent points. The larger the frequency leakage, the more the magnitude and slopes of PSD plots would be affected.
and square window functions having the length of 256, as well as their corresponding frequency leakages. It is clear from the figure that the shape of window functions strongly affects the side lobes and consequently the frequency leakage. Square window function, which has a broader top and a steep manner, could reveal larger side lobes and more frequency leakage. In contrast, the window functions such as Bartlett and Hann, which approach from both ends toward the middle with more gentle slopes and have a point-wise middle, may reduce the chance of frequency leakage from a certain frequency to its adjacent points. The larger the frequency leakage, the more the magnitude and slopes of PSD plots would be affected.
 | ||
| Fig. 6 (a) The plots of Bartlett, Hann and square window functions for the length of 256 and (b) their corresponding frequency leakages.40 | ||
To study the effect of different window functions on the data interpretation in the frequency domain, five window functions implemented in NOVA software, namely Bartlett, Blackman, Hamming, Hann and square window functions, were used. It is important to point out that before applying the window functions to data series, the baseline was removed by the software. Fig. 7 and 8 represent the impact of window function on PSD(I) plots of the samples in 1 M HCl solutions containing 200 ppm TU obtained from FFT and MEM methods, respectively.
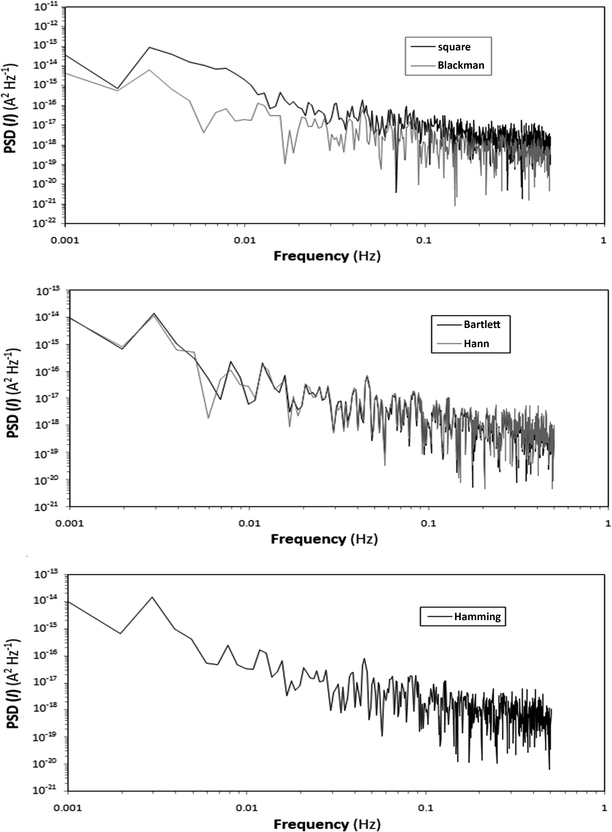 | ||
| Fig. 7 PSD(I) plots of the samples in 1 M HCl solutions containing 200 ppm TU, obtained by the FFT method. | ||
 | ||
| Fig. 8 PSD(I) plots of the samples in 1 M HCl solutions containing 200 ppm TU, obtained by the MEM method. | ||
Based on shot noise theory by considering some restrictive assumptions, the charge of each electrochemical event, q, could be obtained by the following equation:41,42
 | (10) |
| Conc. (ppm) | q (C) | ||||
|---|---|---|---|---|---|
| Hann | Bartlett | Hamming | Blackman | Square | |
| 0 | 1.21 × 10−6 | 1.08 × 10−6 | 1.27 × 10−6 | 9.96 × 10−7 | 4.14 × 10−6 |
| 25 | 4.75 × 10−7 | 3.76 × 10−7 | 3.97 × 10−7 | 4.00 × 10−7 | 5.98 × 10−6 |
| 50 | 3.19 × 10−7 | 2.76 × 10−7 | 3.54 × 10−7 | 1.72 × 10−7 | 9.29 × 10−6 |
| 100 | 2.19 × 10−7 | 2.46 × 10−7 | 4.92 × 10−7 | 1.40 × 10−7 | 9.24 × 10−6 |
| 200 | 1.18 × 10−7 | 1.08 × 10−7 | 1.92 × 10−8 | 8.28 × 10−8 | 3.99 × 10−6 |
| 400 | 1.11 × 10−7 | 7.03 × 10−8 | 7.50 × 10−8 | 8.76 × 10−8 | 7.30 × 10−8 |
According to the PSD plots, a sharper slope is observed in the presence of inhibitor. This means that the PSD energy distributes over a broader area in the more aggressive condition, whereas for the inhibited system the PSD energy distribution is sharper and is concentrated in just a few frequencies. The distributions of ψI (PSD of current) throughout the frequency domain in the presence and absence of TU are plotted in Fig. 9. The dimensionless value presented on the y axis (PSD distribution) is calculated for each frequency point (k) using eqn (11):
 | (11) |
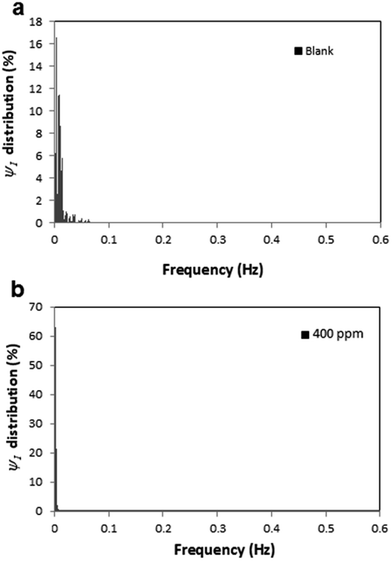 | ||
| Fig. 9 PSD (I) distributions of samples immersed in 1 M HCl (a) without inhibitor and (b) with 400 ppm of TU. | ||
The current study confirms the previous findings43 about the correlation between PSD energy distribution and inhibition efficiency. In other words, the behaviour could indicate that ψI distribution over a broader frequency range might be a measure of corrosion intensity.
3.3 Inhibition efficiency obtained from electrochemical noise measurement
On the basis of published data, the corrosion inhibition efficiency of an inhibitor can be obtained using different methods.44–46 According to eqn (12), the electrochemical noise data can be used to calculate the inhibition efficiency allowing evolution of Gibbs energy:
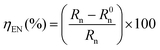 | (12) |
| Conc. (ppm) | Rct (Ω cm2) | ηEIS (%) | Rn (p = 32) (Ω cm2) | ηEN (%) |
|---|---|---|---|---|
| 0 | 163 | 271 | ||
| 25 | 253 | 35 | 466 | 41.84 |
| 50 | 359 | 54 | 613 | 55.79 |
| 100 | 424 | 61 | 971 | 72.09 |
| 200 | 469 | 65 | 2620 | 89.65 |
| 400 | 541 | 70 | 3990 | 93.20 |
From Table 4, the η and resistance parameters followed an increasing trend with increasing inhibitor concentration. Regardless of the trend, the values of ηEN were higher than those of ηEIS. In the case of EIS, the effect of external perturbation on the adsorption–desorption process might lead to lower adsorption of inhibitor on the surface. Moreover, longer experimental duration of EN (about 17 min) in comparison with EIS (about 13 min) may be another reason contributing to higher values of ηEN.
3.4 Inhibition mechanism and adsorption isotherm
The inhibition action of TU could be linked to coverage of the surface sites, most active in the process of discharge. Water molecules on the substrate surface are removed and an electron exchange between the inhibitor molecules and iron could take place through changing the composition of the electrical double layer. This behaviour is more likely to be a consequence of electrostatic forces between ionic charge or dipoles of adsorbed species and the electric charge on the metal surface which is known as surface charge.44 On the basis of published data, the anodic dissolution of steel in acidic solution leads to positively charged metal surface.45 Therefore, an electrostatic attraction would occur between Cl− ions in the solution and positively charged surface. In this condition, the TU molecule may exist in the protonated form in acidic media:46| H2N–CS–NH2 + H+ → [H2N–CSH–NH2]+ | (13) |
In the presence of Cl− ions on the surface, the chloride salt [H2N–CSH–NH2]+Cl− might be formed. TU, as an organosulfur molecule, consists of two C–N groups as well as a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S group. The electronegativity values of nitrogen and sulfur are greater than that of carbon, which leads to withdrawal of electrons by these atoms and causes localization of electrons towards these atoms. In addition to the physical adsorption, the chemical adsorption of TU on steel surface arises from the donor–acceptor interaction through both nitrogen and sulfur atoms and the vacant d orbital of iron.47 This could lead us to believe that physical adsorption is the first and crucial step before adsorption/interaction between TU and the steel/solution interface. In order to assess the adsorption behaviour of the inhibitor, several adsorption isotherms were examined. Of them, the Langmuir adsorption isotherm was found to be the best suited. This isotherm, describing the adsorption of TU molecules on the surface of stainless steel in 1 M HCl, can be expressed using eqn (14):48
S group. The electronegativity values of nitrogen and sulfur are greater than that of carbon, which leads to withdrawal of electrons by these atoms and causes localization of electrons towards these atoms. In addition to the physical adsorption, the chemical adsorption of TU on steel surface arises from the donor–acceptor interaction through both nitrogen and sulfur atoms and the vacant d orbital of iron.47 This could lead us to believe that physical adsorption is the first and crucial step before adsorption/interaction between TU and the steel/solution interface. In order to assess the adsorption behaviour of the inhibitor, several adsorption isotherms were examined. Of them, the Langmuir adsorption isotherm was found to be the best suited. This isotherm, describing the adsorption of TU molecules on the surface of stainless steel in 1 M HCl, can be expressed using eqn (14):48
 | (14) |
 | (15) |
 | (16) |
The interaction between the inhibitor molecules and metal surface could be characterized using the Gibbs free energy value arising from the following equation:49
ΔG0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(55.5Kads) ln(55.5Kads)
| (17) |
3.5 SEM studies
The surfaces of stainless steels exposed to 1 M HCl solutions without and with 400 ppm of thiourea after 4 h were analyzed using SEM (Fig. 11). In the absence of thiourea, a pitting corrosion effect is clearly visible in Fig. 11a. On the other hand, Fig. 11b reveals less damage on the surface of the metallic plate immersed in the acid solution with 400 ppm of the inhibitor. In agreement with the electrochemical data, this behaviour may reflect the effectiveness of thiourea as a corrosion inhibitor in 1 M HCl for stainless steel. | ||
| Fig. 11 SEM micrographs of stainless steel after 4 h of immersion in 1 M HCl with 0 (a) and 400 ppm (b) of thiourea. | ||
4. Conclusion
Thiourea as a well-known organic inhibitor was chosen to examine the accuracy and reliability of the EN method for evaluation of the inhibition performance of organic inhibitors in acidic solutions on metallic substrates. Other methods including EIS and SEM were employed to verify the validity of electrochemical noise data. It has been shown that the EN method is highly sensitive to the data pretreatment, especially for the applied DC trend removal approach. In this case, the MAR DC trend removal method was chosen for the time domain DC trend removal. On the other hand, since the necessity of choosing window functions for the appropriate interpretation of frequency domain data has been established before, the staggering collection of different window functions calls for finding the most appropriate one for the system. Consequently, the correlation between electrochemical noise data and the results obtained from other methods was studied in this work, leading to the following experimental evidences:1. The electrochemical noise data interpretation was strongly dependent upon the approach used for DC trend removal. Moving average removal (MAR) as a common method to eliminate DC trend from EN data was shown to be significantly affected by the choice of initial p values. Taking too low p values may lead to over-filtering of wider transients. Too high p values, on the other hand, could introduce some kinds of drifts into the system. The obtained data in this study could verify the formula introduced by Liu for choosing appropriate p values.
2. Investigation of the effects of window functions on electrochemical noise analysis in the frequency domain showed that application of window functions before performing any analysis of the frequency domain is necessary.
3. Among the window functions, a good trend correlation was observed between the noise data obtained from Hann and Bartlett window functions, which makes them good choices for similar systems.
4. Although the inhibition effectiveness of TU in HCl solution on stainless steel was confirmed using Blackman and Hamming window functions, they failed to show a decreasing trend for corrosion events with increasing TU concentration.
5. PSD energy distribution over the frequency domain was introduced to be a measure of corrosion intensity.
6. The inhibition efficiency values calculated using EN data were higher than those obtained from EIS, indicating the impact of external perturbation on the adsorption–desorption process of TU. The ΔG0 values revealed no effect of electrochemical technique on governing the adsorption behavior of TU on the surface of stainless steel in the acidic medium.
Notes and references
- C. J. Park and H. S. Kwon, Mater. Chem. Phys., 2005, 91, 355 CrossRef CAS PubMed.
- Y. Shao, C. Jia, G. Meng, T. Zhang and F. Wang, Corros. Sci., 2009, 51, 371 CrossRef CAS PubMed.
- X. F. Liu, J. Zhan and Q. J. Liu, Corros. Sci., 2009, 51, 1460 CrossRef CAS PubMed.
- A. Aballe, M. Bethencourt, F. J. Botana and M. Marcos, Electrochim. Acta, 1999, 44, 4805 CrossRef CAS.
- F. Mansfeld, Z. Sun, C. H. Hsu and A. Nagiub, Corros. Sci., 2001, 43, 341 CrossRef CAS.
- P. R. Roberge, J. Appl. Electrochem., 1993, 23, 1223 CrossRef CAS.
- U. Bertocci, J. Frydman, C. Gabrielli and F. Huet, J. Electrochem. Soc., 1998, 8, 2780 CrossRef PubMed.
- F. Mansfeld and L. Han, J. Electrochem. Soc., 1996, 143, 286 CrossRef PubMed.
- M. Hernandez and J. Genesca, Corros. Sci., 2009, 51, 499 CrossRef CAS PubMed.
- J. M. Sanchez-Amaya, R. M. Osuna and M. Bethencourt, Prog. Org. Coat., 2007, 60, 248 CrossRef CAS PubMed.
- C. M. Goulart, A. Esteves-Souza, C. A. Martinez-Huitle, C. J. Ferreira Rodrigues, M. A. Medeiros Maciel and A. Echevarria, Corros. Sci., 2013, 67, 281 CrossRef CAS PubMed.
- P. A. Schweitzer, Corrosion engineering handbook: Corrosion of linings and coatings cathodic and inhibitor protection and corrosion monitoring, CRC. Press, 2007 Search PubMed.
- A. M. Fekry and R. R. Mohamed, Electrochim. Acta, 2010, 55, 1933 CrossRef CAS PubMed.
- A. E. Stoyanova and S. D. Peyerimhoff, Electrochim. Acta, 2002, 47, 1365 CrossRef CAS.
- Z. D. Stankovic and M. Vukovic, Electrochim. Acta, 1996, 41, 2529 CrossRef CAS.
- M. Mahdavian and S. Ashhari, Prog. Org. Coat., 2010, 68, 259 CrossRef CAS PubMed.
- Q. B. Zhang and Y. X. Hua, Electrochim. Acta, 2009, 54, 1881 CrossRef CAS PubMed.
- U. Rammelt and G. Reinhard, Corros. Sci., 1987, 4, 373 CrossRef.
- M. A. Migahed and I. F. Nassar, Electrochim. Acta, 2008, 53, 2877 CrossRef CAS PubMed.
- I. Ahamed, R. Prasad and M. A. Quraishi, Corros. Sci., 2010, 52, 933 CrossRef PubMed.
- M. Bouklah, A. Ouassini, B. Hammouti and A. E. Idrissi, Appl. Surf. Sci., 2005, 250, 50 CrossRef CAS PubMed.
- X. Li, S. Deng and H. Fu, Corros. Sci., 2010, 52, 2786 CrossRef CAS PubMed.
- F. G. Liu, M. Du, J. Zhang and M. Qiu, Corros. Sci., 2009, 51, 102 CrossRef CAS PubMed.
- H. J. Guadalupe, E. Garcia-Ochoa, P. J. Maldonado-Rivas, J. Cruz and T. Pandiyan, J. Electroanal. Chem., 2011, 655, 164 CrossRef CAS PubMed.
- P. Bommersbach, C. Alemany-Dumont and J. P. Millet, Electrochim. Acta, 2006, 51, 4011 CrossRef CAS PubMed.
- N. Muthukumar, A. Ilangovan, S. Maruthamuthu and N. Palaniswamy, Electrochim. Acta, 2007, 52, 7183 CrossRef CAS PubMed.
- M. Outirite, M. Lagrenee, M. Lebrini, M. Traisnel, C. Jama, H. Vezin and F. Bentiss, Electrochim. Acta, 2010, 55, 1670 CrossRef CAS PubMed.
- D. Seifzadeh, H. Basharnavaz and A. Bezaatpour, Mater. Chem. Phys., 2013, 138, 794 CrossRef CAS PubMed.
- L. Hu, S. Zhang, W. Li and B. Hou, Corros. Sci., 2010, 52, 2891 CrossRef CAS PubMed.
- R. Naderi and M. M. Attar, Corros. Sci., 2009, 51, 1671 CrossRef CAS PubMed.
- Y. Yang, T. Zhang, Y. Shao, G. Meng and F. Wang, Corros. Sci., 2010, 52, 2697 CrossRef CAS PubMed.
- X. Liu, T. Zhang, Y. Shao, G. Meng and F. Wang, Corros. Sci., 2010, 52, 892 CrossRef CAS PubMed.
- Y. J. Tan, S. Bailey and B. Kinselia, Corros. Sci., 1996, 38, 1681 CrossRef CAS.
- B. P. Markhali, R. Naderi, M. Mahdavian, M. Sayebani and S. Y. Arman, Corros. Sci., 2013, 75, 269 CrossRef CAS PubMed.
- H. Ashassi-Sorkhabi and D. Seifzadeh, J. Appl. Electrochem., 2008, 38, 1545 CrossRef CAS.
- Y. Tan, S. Bailey and B. Kinsella, Corros. Sci., 1998, 40, 513 CrossRef CAS.
- G. Meszaros, I. Szenes and B. Lengyel, Electrochem. Commun., 2004, 6, 1185 CrossRef CAS PubMed.
- J. Smulko, K. Darwicki and A. Zielinski, Electrochem. Commun., 2002, 4, 388 CrossRef CAS.
- W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery, Numerical Recipes in C, The Art of Scientific Computing, Cambridge University Press, 1997 Search PubMed.
- B. Kahsay, Numerical Recipes in FORTRAN 77: The Art of Scientific Computing, Cambridge University Press, 1992 Search PubMed.
- J. M. Sanchez-Amaya, R. A. Cottis and F. J. Botana, Corros. Sci., 2005, 47, 3280 CrossRef CAS PubMed.
- R. A. Cottis, Corrosion, 2001, 57, 265 CrossRef CAS.
- B. P. Markhali, R. Naderi and M. Mahdavian, J. Electroanal. Chem., 2014, 56 CrossRef CAS PubMed.
- S. M. A. Hosseini and A. Azimi, Corros. Sci., 2009, 51, 728 CrossRef CAS PubMed.
- A. Yuce, B. Mert, G. Kardas and B. Yazıcı, Corros. Sci., 2014, 83, 310 CrossRef PubMed.
- S. M. Haleem, S. Wanees, E. E. Aal and A. Farouk, Corros. Sci., 2013, 68, 1 CrossRef PubMed.
- X. Wang, H. Yang and F. Wang, Corros. Sci., 2011, 53, 113 CrossRef CAS PubMed.
- M. Mehdipour, B. Ramezanzadeh and S. Y. Arman, J. Ind. Eng. Chem., 2014 DOI:10.1016/j.jiec.2014.02.041.
- B. Ramezanzadeh, S. Y. Arman, M. Mehdipour and B. P. Markhali, Appl. Surf. Sci., 2014, 289, 129 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |